线面平行、垂直练习题(精.选)

线面、面面平行和垂直的判定和性质

班别：姓名：

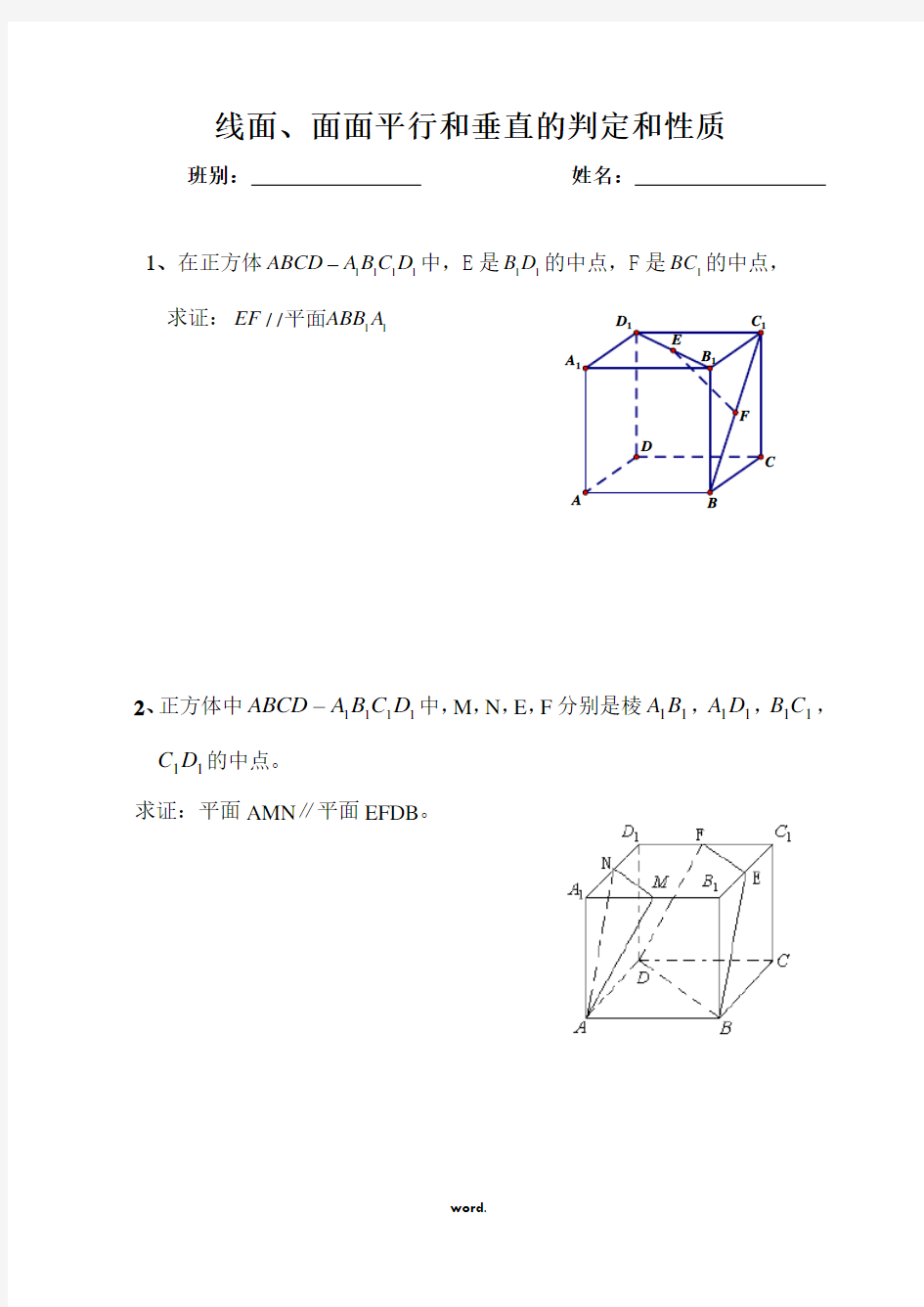
1、在正方体1111ABCD A B C D -中，E 是11B D 的中点，F 是1BC 的中点，求证：11//EF ABB A 平面

2、正方体中1111D C B A ABCD -中，M ，N ，E ，F 分别是棱11B A ，11D A ，11C B ，11D C 的中点。

求证：平面AMN ∥平面EFDB 。

D 1

C 1

B 1

3．如图，四棱锥P ABCD -中，底面ABCD 为平行四边

60,2,DAB AB AD PD ∠==⊥o 底面ABCD ，证明：PA BD ⊥

4．如图，已知四棱锥P ABCD -的底面ABCD 是菱形, PA ⊥平面ABCD , 点

F 为PC 的中点. （Ⅰ）求证://PA 平面BDF ; （Ⅱ）求证:平面PAC ⊥平面BDF .

5、如图，P 为ABC ?所在平面外一点，PA ┴面BAC ，90,ABC ∠=o AE ┴PB 于E ，AF ┴PC 于F ，求证：（1）BC ┴面PAB ，（2）AE ┴面PBC ，（3）PC ┴面AEF 。

6. 如图，棱长为1的正方体ABCD-A 1B 1C 1D 1中，

(1)求证：AC ⊥平面B 1D 1DB; (2)求三棱锥B-ACB 1体积．

D 1

C 1

B 1

A 1

7.如图，ABCD 是正方形，O 是正方形的中心，PO ⊥底面ABCD ，E 是PC 的中点。求证：（1）PA ∥平面BDE ；（2）BD ⊥平面PAC

8、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。求证：（1）⊥AB 平面CDE;

（2）平面CDE ⊥平面ABC 。

最新文件仅供参考已改成word 文本。方便更改

线线垂直、线面垂直、面面垂直的判定与性质

空间中得垂直关系 1.线面垂直直线与平面垂直得判定定理:如果,那么这条直线垂直于这个平面。推理模式: 直线与平面垂直得性质定理:如果两条直线同垂直于一个平面,那么这两条直线。 2.面面垂直两个平面垂直得定义:相交成得两个平面叫做互相垂直得平面。两平面垂直得判定定理:(线面垂直面面垂直) 如果,那么这两个平面互相垂直。推理模式: 两平面垂直得性质定理:(面面垂直线面垂直) 若两个平面互相垂直,那么在一个平面内垂直于它们得得直线垂直于另一个平面。一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直线面垂直面面垂直.这三者之间得关系非常密切,可以互相转化,从前面推出后面就是判定定理,而从后面推出前面就是性质定理.同学们应当学会灵活应用这些定理证明问题.在空间图形中,高一级得垂直关系中蕴含着低一级得垂直关系,下面举例说明. 例题:1.如图,AB就是圆O得直径,C就是圆周上一点,PA⊥平面ABC. (1)求证:平面PAC⊥平面PBC; (2)若D也就是圆周上一点,且与C分居直径AB得两侧,试写出图中所有互相垂直得各对平面. 2、如图,棱柱得侧面就是菱形, 证明:平面平面 3、如图所示,在长方体中,AB=AD=1,AA 1=2,M就是棱CC 1 得中点 (Ⅰ)求异面直线A 1M与C 1 D 1 所成得角得正切值; (Ⅱ)证明:平面ABM⊥平面A 1B 1 M 1

4、如图,就是圆Ｏ得直径,Ｃ就是圆周上一点,平面ABC .若AE ⊥PC ,Ｅ为垂足,Ｆ就是PB 上任意一点,求证:平面AEF ⊥平面PBC . 5、如图,直三棱柱ABC —A 1B 1C 1 中,AC ＝BC ＝1,∠ACB ＝90°,AA 1 ＝,D 就是A 1B 1 中点.(1)求证C 1D ⊥平面A 1B ;(2)当点F 在BB 1 上什么位置时,会使得AB 1 ⊥平面C 1DF ？并证明您得结论 6、S 就是△ABC 所在平面外一点,SA ⊥平面ABC,平面SAB ⊥平面SBC,求证AB ⊥BC 、 7、在四棱锥中,底面ABCD 就是正方形,侧面VAD 就是正三角形,平面VAD ⊥底面ABCD 证明:AB ⊥平面VAD V D C B A S A B

立体几何线面平行垂直,线面角二面角的证明方法

A P B C E D 一：线面平行的证明方法： 1、用“近似平行法”先找到面上与已知直线平行的直线（一般为表示面的三角形的边界直线，或三角形某边上的中线）看找到的这条线与已知线的长度关系，1）若相等应该构造平行四边形；2）若不相等一般利用三角形中位线的性质（将这两个不相等的线段的端点连结并延长即会出现关键三角形）。 2、若既不能构造平行四边形也不能性用中位线性质，则应再构造一个此直线所在的平面，证明此平面与已知平面平行（先证面面平行，推出线面平行）例一：如图，已知菱形ABCD ，其边长为2， 60BAD ∠= ，ABD ?绕着BD 顺时针旋转120 得到PBD ?，M 是PC 的中点．（1）求证：//PA 平面MBD ；（2）求直线AD 与平面PBD 所成角的正弦值．例二：已知四棱锥P-ABCD ，底面ABCD 是 60=∠A 、边长为a 的菱形，又ABCD PD 底⊥，且PD=CD ，点M 、N 分别是棱AD 、PC 的中点．（1）证明：DN//平面PMB ；（2）证明：平面PMB ⊥平面PAD ；（3）求点A 到平面PMB 的距离．例三：如图，已知点P 是平行四边形ABCD 所在平面外的一点，上的点且PE EA BF FD =∶∶，求证：EF //平面PBC ．二：线面垂直的证明方法：通过线线垂直，证明线面垂直 1）利用勾股定理逆定理及三角形中两个角和为90°； 2）利用等边、等腰三角形（中线即高线），正方形、矩形邻边垂直，正方形菱形对角线垂直等； 3）通过线面垂直，反推线线垂直； 4）利用面面垂直的性质，证明垂直于交线即垂直于另一个平面。例四：如图,四边形ABCD 为矩形，CF ⊥平面ABCD ，DE ⊥平面ABCD ， AB=4a ，BC= CF=2a,P 为AB 的中点. (1)求证：平面PCF ⊥平面PDE ； (2)求四面体PCEF 的体积. C

线面平行与垂直的证明题

线面平行与垂直的证明1：如图，在棱长为1的正方体ABCD-A1B1C1D1中. （1）求证：AC⊥平面B1BDD1；（2）求三棱锥B-ACB1体积． 2：如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中点．求证：（1）PA∥平面BDE；（2）平面PAC⊥平面BDE． D1 C1 B1 A1 C D B A

3：如图：在底面是直角梯形的四棱锥S —ABCD 中， ∠ABC = 90°，SA ⊥面ABCD ，SA = AB = BC = 1，2 1 AD ．（Ⅰ）求四棱锥S —ABCD 的体积；（Ⅱ）证明：平面SBC ⊥平面SCD . 4：已知多面体ABCDFE 中，四边形ABCD 为矩形，AB ∥EF ，AF ⊥BF ，平面ABEF ⊥平面ABCD ， O 、M 分别为AB 、FC 的中点，且AB = 2，AD = EF = 1. （Ⅰ）求证：AF ⊥平面FBC ；（Ⅱ）求证：OM ∥平面DAF .

5：．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是P C的中点，作EF⊥PB交PB于点F．（1）证明PA//平面EDB；（2）证明PB⊥平面EFD； 6：已知正方形ABCD和正方形ABEF所在的平面相交于AB，点M，N分别在AC和BF上，且 AM=FN. C

求证：MN ‖平面BCE. 7：如图，正方体1111D C B A ABCD -中，棱长为a （1）求证：直线//1B A 平面1ACD （2）求证：平面1ACD ⊥平面D BD 1；

8：如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2a,DC=a,F是BE的中点，求证：(1) FD∥平面ABC (2) AF⊥平面EDB. 9：如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是CB、CD、CC1的中点，（1）求证：平面A B1D1∥平面EFG; （2）求证：平面AA1C⊥面EFG.

线面垂直判定经典证明题

线面垂直判定 1、已知：如图，PA⊥AB，PA⊥AC。求证：PA⊥平面ABC。 ] 2、已知：如图，PA⊥AB，BC⊥平面PAC。求证：PA⊥BC。 ' 3、如图，在三棱锥V-ABC中，VA=VC，AB=BC。求证：VB⊥AC | 4、在正方体ABCD-EFGH中，O为底面ABCD中心。求证：BD⊥平面AEGC 5、如图，AB是圆O的直径，PA⊥AC, PA⊥AB, 求证：BC⊥平面PAC ;

6、如图，AD ⊥BD, AD ⊥DC,AD=BD=CD,∠BAC=60° 求证： BD ⊥平面ADC : 7、.如图所示，PA ⊥矩形ABCD 所在平面，M 、N 分别是AB 、PC 的中点. (1)求证：MN ∥平面PAD . (2)求证：MN ⊥CD . (3)若∠PDA ＝45°，求证：MN ⊥平面PCD . 《 . 8、已知：如图，P 是棱形ABCD 所在平面外一点，且PA=PC 求证：AC PBD 平面： A D ~ C B P

9、已知四面体ABCD 中，CD BD AC AB ==,,平面⊥ABC 平面BCD ,E 为棱BC 的中点。（1）求证：⊥AE 平面BCD ; （2）求证：BC AD ⊥; \ 10、三棱锥A-BCD 中，AB=1，BC=2，BD=AC=3 AD=2，求证：AB ⊥平面BCD > ! 11、在四棱锥S-ABCD 中，SD ⊥平面ABCD ，底面ABCD 是正方形求证：AC ⊥平面SBD > ? 12、如图，正方形ABCD 所在平面与三角形CDE 所在平面相交于CD ，AE ⊥平面CDE ，求证：AB ⊥平面ADE ； · C B A E D A B

必修2直线与平面垂直的判定与性质试题及答案

直线与平面垂直的判定与性质一、选择题 1．两异面直线在平面α内的射影（） A．相交直线B．平行直线 C．一条直线—个点D．以上三种情况均有可能 2．若两直线a与b异面，则过a且与b垂直的平面（） A．有且只有—个B．可能存在也可能不存在 C．有无数多个D．—定不存在 3．在空间，下列哪些命题是正确的（） ①平行于同一条直线的两条直线互相平行； ②垂直于同一条直线的两条直线互相平行； ③平行于同一个平面的两条直线互相平行； ④垂直于同—个平面的两条直线互相平行． A．仅②不正确B．仅①、④正确C．仅①正确D．四个命题都正确 4．若平面α的斜线l在α上的射影为l′，直线b∥α，且b⊥l′，则b与l（）A．必相交B．必为异面直线C．垂直D．无法确定 5．下列命题 ①平面的每条斜线都垂直于这个平面内的无数条直线； ②若一条直线垂直于平面的斜线，则此直线必垂直于斜线在此平面内的射影； ③若平面的两条斜线段相等，则它们在同一平面内的射影也相等； ④若一条线段在平面外并且不垂直于这个平面，则它的射影长一定小于线段的长．其中，正确的命题有（） A．1个B．2个C．3个n 4个 6．在下列四个命题中，假命题为（） A．如果一条直线垂直于平面内的无数条直线，那么这条直线和这个平面垂直 B．垂直于三角形两边的直线必垂直于第三边 C．过点A垂直于直线a的所有直线都在过点A垂直于a的平面内 D．如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面 7．已知P是四边形ABCD所在平面外一点且P在平面ABCD内的射影在四边形ABCD 内，若P到这四边形各边的距离相等，那么这个四边形是（） A．圆内接四边形B．矩形C．圆外切四边形D．平行四边形 8．在△ABC中，AB＝AC＝5，BC＝6，P A⊥平面ABC，P A＝8，则P到BC的距离等于（） 2C．35D．45 A．5B．5 二、填空题 9．AB是平面α的斜线段，其长为a，它在平面α内的射影A′B的长为b，则垂线A′A_________． 10．如果直线l、m与平面α、β、γ满足：l＝β∩γ，l⊥α，m α和m⊥γ，现给出以下四个结论： ①α∥γ且l⊥m；②αγ且m∥β③αβ且l⊥m；④αγ且l⊥m；其中正确的为“________”．（写出序号即可） 11．在空间四面体的四个面中，为直角三角形的最多有____________个． 12．如图，正方形ABCD，P是正方形平面外的一点，且P A⊥平面A BCD则在△P AB、△PBC、△PCD、△P AD、△P AC及△PBD中，为直角三角形有_________个．

线面、面面平行和垂直的八大定理

线面、面面平行和垂直的八大定理一、线面平行。 1、判定定理：平面外一条直线与平面内一条直线平行，那么这条直线与这个平面平行。符合表示： β ββ////a b a b a ??? ????? 2、性质定理：如果一条直线与平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。符号表示： b a b a a a ////??? ?????=??βαβαα 二、面面平行。 1、判定定理：如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线，那么这两个平面平行。符号表示： β α//////????? ?????==N n m M b a a m b n 2、性质定理：如果两个平面平行同时与第三个平面相交，那它们的交线平行。符号表示： d l d l ////??? ???==γβγαβα （更加实用的性质：一个平面内的任一直线平行另一平面）三、线面垂直。 1、判定定理：如果一条直线与一个平面内的两条相交直线都垂直，那么这条直线垂直这个平面。符号表示： α⊥?????? ??????=⊥⊥a M c b b a c a ＄：三垂线定理：（经常考到这种逻辑）在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

符号表示： PA a A oA a po oA a ⊥??? ? ????=⊥⊥??ααα 2、性质定理：垂直同一平面的两条直线互相平行。（更加实用的性质是：一个平面的垂线垂直于该平面内任一直线。）四、面面垂直。 1、判定定理：经过一个平面的垂线的平面与该平面垂直。 βααβ⊥??⊥a a , 2、性质定理：已知两个平面垂直，在一个平面内垂直于交线的直线垂直于另一个平面。βαβαβα⊥?⊥?=?⊥a b a a b ,,，

立体几何大题线面平行与垂直的证明题

线面平行与垂直的证明 1：如图，在棱长为1的正方体ABCD-A 1B 1C 1D 1中. （1）求证：AC ⊥平面B 1BDD 1；（2）求三棱锥B-ACB 1体积． 2：如图，ABCD 是正方形，O 是正方形的中心， PO ⊥底面ABCD ，E 是PC 的中点．求证：（1）PA∥平面BDE ；（2）平面PAC ⊥平面BDE ． 3：如图：在底面是直角梯形的四棱锥S —ABCD 中， ∠ABC = 90°，SA ⊥面ABCD ，SA = AB = BC = 1，2 1=AD ．（Ⅰ）求四棱锥S —ABCD 的体积；（Ⅱ）证明：平面SBC ⊥平面SCD . 4：已知多面体ABCDFE 中，四边形ABCD 为矩形，AB ∥EF ，AF ⊥BF ，平面ABEF ⊥平面ABCD ， O 、M 分别为AB 、FC 的中点，且AB = 2，AD = EF = 1. （Ⅰ）求证：AF ⊥平面FBC ；（Ⅱ）求证：OM ∥平面DAF . 5：．如图，在四棱锥P-ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD =DC ，E 是P C 的中点，作EF ⊥PB 交PB 于点F ．（1）证明 P A //平面EDB ；（2）证明PB ⊥平面EFD ； D 1 C 1 B 1 A 1 C D B A D A B C O E P A B C D P E F

6：已知正方形ABCD 和正方形ABEF 所在的平面相交于AB ，点M ，N 分别在AC 和BF 上，且AM=FN. 求证：MN ‖平面BCE. 7：如图，正方体1111D C B A ABCD -中，棱长为a （1）求证：直线//1B A 平面1ACD （2）求证：平面1ACD ⊥平面D BD 1； 8：如图，已知△ABC 是正三角形，EA 、CD 都垂直于平面ABC ，且EA=AB=2a,DC=a,F 是BE 的中点，求证：(1) FD ∥平面ABC (2) AF ⊥平面EDB. 9：如图，在正方体ABCD-A 1B 1C 1D 1中，E 、F 、G 分别是CB 、CD 、CC 1的中点，（1）求证：平面A B 1D 1∥平面EFG; （2）求证：平面AA 1C ⊥面EFG. B C D E F N M F G E C1D1 A1 B1 D C B F E D C A M

高中数学立体几何线面垂直的证明

立体几何证明【知识梳理】 1. 直线与平面平行判定定理：如果平面外一条直线和这个平面内一条直线平行，那么这条直线和这个平面平行.（“线线平行?线面平行”）性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.（“线面平行?线线平行”） 2.．直线与平面垂直判定定理一如果一条直线和一个平面内的两条相交直线都垂直，那么这两条直线垂直于这个平面.（“线线垂直?线面垂直”）判定定理二：如果平行线中一条直线垂直于一个平面，那么另一条也垂直于这个平面. 性质1.如果一条直线垂直于一个平面，那么这条直线垂直于这个平面内的所有直线。（线面垂直?线线垂直）性质2：如果两条直线同垂直于一个平面，那么这两条直线平行. 三。平面与平面空间两个平面的位置关系：相交、平行. 1. 平面与平面平行判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行.（“线面平行?面面平行”） 2. 两个平面垂直判定定理：如果一条直线与一个平面垂直，那么经过这条直线的平面垂直于这个平面.（“线面垂直?面面垂直”）性质定理：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.（面面垂直?线面垂直）

知识点一【例题精讲】 1.在棱长为2的正方体1111D C B A ABCD -中，E 、F 分别为1DD 、DB 的中点。（1）求证：EF//平面11D ABC ；（2）求证：平面B 11D C C B 1⊥ EF C B 1⊥；（3）求三棱锥EFC B -1的体积V. 2.如图所示, 四棱锥P -ABCD 底面是直角梯形, ,,2,BA AD CD AD CD AB PA ⊥⊥=⊥底面ABCD , E 为PC 的中点, PA ＝AD ＝AB ＝1. （1）证明: //EB PAD 平面; （2）证明: BE PDC ⊥平面; （3）求三棱锥B -PDC 的体积V . 3、如图所示，在四棱锥P ﹣ABCD 中，PA ⊥底面 ABCD ，AB ⊥AD ，AC ⊥CD ，∠ABC=60°，PA=AB=BC ，E 是PC 的中点，证明：（1）AE ⊥CD （2）PD ⊥平面ABE ．

线线平行线面平行面面平行的练习题

线线平行、线面平行、面面平行部分的练习题 1．如图2-3-3所示,已知α∩β=CD,α∩γ=EF,β∩γ=AB,AB ∥α.求证：ＣＤ∥EF. 2.已知直线a ∥平面α，直线a ∥平面β，平面αI 平面β=b ，求证//a b ． 3. 正方形ABCD 交正方形ABEF 于AB （如图所示）M 、N 在对角线AC 、FB 上且AM= FN 。求证：MN //平面BCE 4．如图2-3-7所示，正三棱柱ABC —A1B1C1中，D 是BC 的中点，试判断A1B 与平面ADC1的位置关系，并证明你的结论. 5．、已知⊥PA 矩形ABCD 所在的平面，M 、N 分别是AB 、PC 的中点，求证：MN//平面PAD. 6.在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，设M 、N 、E 、F 分别是棱A 1B 1、A 1D 1、C 1D 1、B 1C 1的中点.求证：(1)E 、F 、B 、D 四点共面；（2）面AMN ∥面EFBD. 7．已知在正方体ABCD －1111D C B A 中，M 、N 分别是11D A 、11B A 的中点，在该正方体中作出与平面AMN 平行的平面，并证明你的结论。

8．已知点是△ 所在平面外一点，点，，分别是△ ，△ ，△ 的重心，求证：平面平面． 9. 已知三棱锥Ｐ—ＡＢＣ，Ａ′，B ′C ′是△PBC,△PCA,△PAB 的重心. (1)求证：面Ａ′Ｂ′Ｃ′∥面ＡＢＣ； (2)求S △A ′B ′C ′： S △ABC . . 10. 如图所示11 1 ABC A B C -中，平面ABC//平面A 1B 1C 1 ，若D 是棱1 CC 的中点，在棱AB 上是否存在一点E ，使 11//C AB DE 证明你的结论答案与提示： 1.证明：∵AB β,AB α,又∵AB ∥α,α∩β =CD,∴AB ∥CD,同理ＡＢ∥ＥＦ，∴ＣＤ∥ＥＦ. 2. 证明：经过a 作两个平面γ和δ，与平面α和β分别相交于直线c 和d ， ∵a ∥平面α，a ∥平面β， ∴a ∥c ，a ∥d ，∴c ∥d ，又∵d ?平面β，c ?平面β， ∴c ∥平面β， d c b a δ γ β α

高一数学必修2线、面垂直的判定与性质

α β a A 线、面垂直的判定与性质一、线、面垂直的判定与性质 1.线面垂直的定义：如果直线 l 与平面α内的任意一条直线都垂直，我们说直线 l 与平面α 互相垂直. 2.线面垂直的判定：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．直线与平面垂直 3. （1）的射影所成的角（2）（3一条直线与平面所成的角的取值范围是 4.二面角相关概念：以二面角的棱上任意一点为顶点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角. ∠AOB 即为二面角α -AB-β的平面角注意：二面角的平面角必须满足：（1）角的顶点在棱上.（2）角的两边分别在两个面内. （3）角的边都要垂直于二面角的棱. 二面角的取值范围 5.面面垂直的定义：一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.记为β⊥α 6.判定定理：如果一个平面经过另一个平面的垂线，则这两个平面垂直． 7.直线与平面垂直的性质定理：垂直于同一个平面的两条直线平行 8.面面垂直的性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直. 面面垂直?线面垂直 α ⊥l 记为???????? l a l ⊥b l ⊥α?a α?b A b a = ] 90,0[0[]] 0[180,000π，或a β?a α⊥面?βα⊥ //a a b b αα⊥???⊥?a b α a b l a a l αβαββ⊥??=?????⊥?a α?⊥

二、例题解析题型一、判断问题例1、直线l与平面α内的无数条直线垂直，则直线l与平面α的关系是() A．l和平面α相互平行B．l和平面α相互垂直C．l在平面α内D．不能确定变式：如果一条直线垂直于一个平面内的：①三角形的两边；②梯形的两边；③圆的两条直径； ④正六边形的两条边．则能保证该直线与平面垂直() A．①③B．①②C．②④D．①④ 例2、已知直线a∥平面α，a⊥平面β，则( ) A．α⊥βB．α∥βC．α与β不垂直D．以上都有可能变式：下列命题中错误的是( ) A．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β B．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β C．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l，那么l⊥平面γ D．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β 例3、已知b⊥平面α，a?α，则直线a 与直线b 的位置关系是( ) A．a∥b B．a⊥b C．直线a 与直线b 垂直相交D．直线a 与直线b 垂直且异面变式1：下面四个命题，其中真命题的个数为( ) ①如果直线l 与平面α内的无数条直线垂直，则l⊥α； ②如果直线l 与平面α内的一条直线垂直，则l⊥α； ③如果直线l 与平面α不垂直，则直线l 和平面α内的所有直线都不垂直； ④如果直线l 与平面α不垂直，则平面α内也可以有无数条直线与直线l 垂直． A．1 个B．2 个C．3 个D．4 个变式2：已知平面α⊥平面β，则下列命题正确的个数是() ①α内的直线必垂直于β内的无数条直线；②在β内垂直于α与β的交线的直线必垂直于α内的任意一条直线；③α内的任何一条直线必垂直于β；④过β内的任意一点作α与β交线的垂线，则这条直线必垂直于α. A．4 B．3C．2D．1 题型二：求角问题（线面角、面面角）例1、在正方体ABCD－A1B1C1D1中， (1)求直线A1C与平面ABCD所成的角的正切值． (2)求直线A1B与平面BDD1B1所成的角．变式：如图所示，Rt△BMC中，斜边BM＝5且它在平面ABC上的射影AB长为4，∠MBC＝60°，求MC与平面ABC所成角的正弦值．

线面平行与垂直的证明题

线面平行与垂直的证明 1：如图,在棱长为1的正方体ABCD-A 1B 1C 1D 1中. (1）求证:AC ⊥平面B １ＢＤD １; （２）求三棱锥B-ACB 1体积. 2：如图,ＡBC Ｄ是正方形,O 是正方形的中心, PO ⊥底面ABCD ，E 是ＰＣ的中点. 求证:（１）ＰＡ∥平面BD Ｅ；（2)平面P ＡC ⊥平面BDE ．３：如图:在底面是直角梯形的四棱锥S —ABCD 中， ∠AB Ｃ = 90°,SA ⊥面ABCD,SA = AB ＝ BC = 1,2 1 = AD ． (Ⅰ）求四棱锥S —A ＢＣD 的体积; （Ⅱ）证明:平面SBC ⊥平面SCD . D 1 C 1 B 1 A 1 C D B A D A B C O E P

4:已知多面体ABCDFE中, 四边形ABCD为矩形,AB ∥EF,AＦ⊥BF,平面AＢＥＦ⊥平面AＢCＤ, Ｏ、M 分别为AＢ、FC的中点,且ＡB= 2，AD = ＥF= １. （Ⅰ)求证:AＦ⊥平面FBC; (Ⅱ）求证:ＯM∥平面ＤＡF. 5:．如图,在四棱锥P-ABCD中，底面ＡＢCD是正方形，侧棱PD⊥底面AＢCD，PＤ=DＣ,E是P C的中点，作EF ⊥PB交PB于点Ｆ. (１)证明ＰA//平面EDB；（2)证明PB⊥平面EFＤ; 6:已知正方形AＢCＤ和正方形ABＥF所在的平面相交于AＢ,点M,N分别在AC和BF上,且AM=FN．求证：ＭＮ‖平面ＢCE. A B C D P E F B C D E F N M

７：如图,正方体1111D C B A ABCD -中，棱长为a （1）求证:直线//1B A 平面1ACD （2)求证：平面1ACD ⊥平面D BD 1; 8: 如图,已知△ABC 是正三角形,EA 、ＣD 都垂直于平面AB Ｃ，且EA=AB ＝2a,DC=a,F 是BE 的中点, 求证：(１) FD ∥平面ＡＢC (2) A Ｆ⊥平面ＥDB ． 9:如图,在正方体ＡBCD-A １Ｂ1C 1D 1中,E 、F 、G 分别是CB 、ＣD 、ＣC 1的中点，（1）求证：平面Ａ B １D 1∥平面ＥFG; (２) 求证:平面AA 1C ⊥面EFG ． F E C1D1 A1 B1 D B F E D C A M

(完整版)线面平行证明的常用方法

线面平行证明的常用方法张磊立体几何在高考解答题中每年是必考内容，必有一个证明题；重点考察：平行与垂直（线线平行、线面平行、面面平行、线线垂直、线面垂直、面面垂直等），我们现在对线面平行这一方面作如下探讨：方法一：中位线型：找平行线。例1、如图⑴，在底面为平行四边形的四棱锥P ABCD -中，点E 是PD 的中点.求证：//PB 平面AEC 分析：如图⑴ 如图⑵ 如图⑶ 方法二：构造平行四边形，找平行线例2、如图⑵, 平行四边形ABCD 和梯形BEFC 所在平面相交，BE//CF ，求证：AE//平面DCF. 分析：过点E 作EG//AD 交FC 于G ， DG 就是平面AEGD 与平面DCF 的交线，那么只要证明AE//DG 即可。方法三：作辅助面使两个平面是平行, 即：作平行平面，使得过所证直线作与已知平面平行的平面例3、如图⑷，在四棱锥O ABCD -中，底面ABCD 为菱形， M 为OA 的中点，N 为BC 的中点，证明：直线MN OCD 平面‖ 分析：：取OB 中点E ，连接ME ，NE ，只需证平面MEN 平面OCD 。方法四：利用平行线分线段成比例定理的逆定理证线线平行。例4、已知正方形ABCD 和正方形ABEF AC 和BF 上，且AM=FN. 求证：MN ‖平面BCE. 如图⑷ 如图⑸ 如图⑹ E B A D C G F F y C B E D A S z _ M _ D _ A B _ O E P E D C B O A B C D E F N M

例5．如图⑸，已知三棱锥Ｐ—ＡＢＣ，Ａ′，B ′，C ′是△PBC,△PCA,△PAB 的重心. (1)求证：Ａ′Ｂ′∥面ＡＢＣ； (2)求S △A ′B ′C ′：S △ABC . 方法五：（向量法）所证直线与已知平面的法向量垂直，关键：建立空间坐标系（或找空间一组基底）及平面的法向量。例6、如图⑹，在四棱锥S ABCD -中，底面ABCD 为正方形，侧棱SD ⊥底面ABCD E F ，，分别为AB SC ，的中点．证明EF ∥平面SAD ；分析：因为侧棱SD ⊥底面ABCD ，底面ABCD 是正方形，所以很容易建立空间直角坐标系及相应的点的坐标。证明：如图，建立空间直角坐标系D xyz -．设(00)(00)A a S b ，，，，，，则(0)(00)B a a C a ，，，，，， 00222a a b E a F ???? ? ????? ，，，，，， 02b EF a ??=- ?? ?u u u r ，，．因为y 轴垂直与平面SAD ，故可设平面的法向量为n r =（0，1，0）则：02b EF n a ??=- ?? ?u u u r r g g ，，（0，1，0）=0 因此 EF n ⊥u u u r r 所以EF ∥平面SAD ．

直线、平面垂直的判定及其性质

直线、平面垂直的判定及其性质最新考纲 1.以立体几何的定义、公理和定理为出发点，认识和理解空间中线面垂直的有关性质与判定定理；2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题 . 知识梳理 1.直线与平面垂直 (1)直线和平面垂直的定义如果一条直线l 与平面α内的任意直线都垂直，就说直线l 与平面α互相垂直. (2)判定定理与性质定理 (1)定义：一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角，一条直线垂直于平面，则它们所成的角是直角；一条直线和平面平行或在平面内，则它们所成的角是0°的角. (2)范围：??? ???0，π2. 3.二面角 (1)定义：从一条直线出发的两个半平面所组成的图形叫做二面角；

(2)二面角的平面角：在二面角的棱上任取一点，以该点为垂足，在两个半平面内分别作垂直于棱的两条射线，这两条射线所构成的角叫做二面角的平面角. (3)二面角的范围：[0，π]. 4.平面与平面垂直 (1)平面与平面垂直的定义两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直. (2)判定定理与性质定理 1.两个重要结论 (1)若两平行线中的一条垂直于一个平面，则另一条也垂直于这个平面. (2)若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法). 2.使用线面垂直的定义和线面垂直的判定定理，不要误解为“如果一条直线垂直于平面内的无数条直线，就垂直于这个平面”. 基础自测 1.判断下列结论正误(在括号内打“√”或“×”) (1)直线l 与平面α内的无数条直线都垂直，则l ⊥α.( ) (2)垂直于同一个平面的两平面平行.( ) (3)若两平面垂直，则其中一个平面内的任意一条直线垂直于另一个平面.( )

线面平行垂直知识点

线面平行垂直知识点Revised on November 25, 2020

立体几何知识点总结一、平面通常用一个平行四边形来表示. 平面常用希腊字母α、β、γ…或拉丁字母M、N、P来表示，也可用表示平行四边形的两个相对顶点字母表示，如平面AC. 在立体几何中，大写字母A，B，C，…表示点，小写字母，a,b,c,…l,m,n,…表示直线，且把直线和平面看成点的集合，因而能借用集合论中的符号表示它们之间的关系，例如： a)A∈l—点A在直线l上；A?α—点A不在平面α内； b)l?α—直线l在平面α内； c)a?α—直线a不在平面α内； d)l∩m=A—直线l与直线m相交于A点； e)α∩l=A—平面α与直线l交于A点； f)α∩β=l—平面α与平面β相交于直线l. 二、平面的基本性质公理1 如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内. 公理2 如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线. 公理3 经过不在同一直线上的三个点，有且只有一个平面. 根据上面的公理，可得以下推论. 推论1 经过一条直线和这条直线外一点，有且只有一个平面. 推论2 经过两条相交直线，有且只有一个平面. 推论3 经过两条平行直线，有且只有一个平面. 公理4 平行于同一条直线的两条直线互相平行三、证题方法 (1) ) 直线在平面内—有无数个公共点 (2)直线和平面直线不在平面内平行—没有公共点 (直线在平面外) 相交—有且只有一公共点 (3)平面与平面相交—有一条公共直线(无数个公共点) 平行—没有公共点五、异面直线的判定证明两条直线是异面直线通常采用反证法. 有时也可用定理“平面内一点与平面外一点的连线，与平面内不经过该点的直线是异面直线”. 六、线面平行与垂直的判定 (1)两直线平行的判定 ①定义：在同一个平面内，且没有公共点的两条直线平行. ②如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行，即若a∥α,a∥β ④垂直于同一平面的两直线平行，即若a⊥α，b⊥α，则a∥b（线面垂直的性质定理） ⑤两平行平面与同一个平面相交，那么两条交线平行，即若α∥β,α∩γ,β∩γ=b,则a∥b（面面平行的性质公理） ⑥中位线定理、平行四边形、比例线段……，α∩β=b,则a∥b.（线面平行的判定定理） ③平行于同一直线的两直线平行，即若a∥b,b∥c,则a∥c.（公理4）

线线,线面平行与垂直专项练习

线面、面面平行 1、已知m、n、l1、l2表示不同直线，α、β表示不同平面．若m?α，n?α， l1?βl2?β，l1∩l2＝M，则能得到结论α∥β的选项是( ) A．m∥β且l1∥αB．m∥β且n∥β C．m∥β且n∥l1 D．m∥l1且n∥l2 2、a，b是两条直线，α，β是两个平面，则能使a⊥b成立的条件是( ) A．a⊥α，b∥β，α⊥βB．a⊥α，b⊥β，α∥β C．a?α，b⊥β，α∥βD．a?α，b∥β，α⊥β 3、若有直线m、n和平面α、β，下列四个命题中，正确的是( ) A．若m∥α，n∥α，则m∥n B．若m?α，n?α，m∥β，n∥β，则α∥β C．若α⊥β，m?α，则m⊥β D．若α⊥β，m⊥β，m?α，则m∥α 4、能使平面α∥平面β成立的条件是( ) A．存在一条直线a，a∥α，a∥β B．存在一条直线a，a?α，a∥β C．存在两条平行直线a、b，a?α、b?β、a∥β、b∥α D．存在两条异面直线a、b，a?α、b?β、a∥β、b∥α 5、已知平面α∩β＝l，m是α内不同于l的直线，那么下列命题中错误的( ) A．若m∥β，则m∥l B．若m∥l，则m∥β C．若m⊥β，则m⊥l D．若m⊥l，则m⊥β 6、设m、n表示不同直线，α、β表示不同平面，则下列命题中正确的是( ) A．若m∥α，m∥n，则n∥α B．若m?α，n?β，m∥β，n∥α，则α∥β C．若α∥β，m∥α，m∥n，则n∥β D．若α∥β，m∥α，n∥m，n?β，则n∥β 7、设m，n为两条直线，α，β为两个平面，则下列四个命题中，正确的命题是( ) A．若m?α，n?α，且m∥β，n∥β，则α∥β B．若m∥α，m∥n，则n∥α

立体几何线面、面面平行的证明

Q D C B A P C 1 B 1 A 1D 1 D C B A D A 1 C 1 C B 1 B 理科数学复习专题立体几何线面平行与面面平行专题复习【题型总结】题型一小题：判断正误 1. a 、b 、c 是直线，,,αβγ是平面，下列命题正确的是_____________ α αβ βααβαβαγαγββααα////a ,//a //a //,//a ////a ,//a ////,////a //,//a //a //,//a b b b b c c b b 则⑥则⑤则④则③则②则① 归纳：_______________________________________ 题型二线面平行的判定 1、如图，在四棱锥P —ABCD 中，底面ABCD 是矩形，E 、F 分别是ＰＢ，ＰＣ的中点，求证：EF 归纳： 3、在正方体中，Ｅ，Ｆ分别为C1D1和BC 的中点，求证： FE 1111111//. ABCD A B C D AB D C BC -在正方体中，求证：平面平面11111111111,,:(1)//;(2)//. ABC A B C D AC BC AB D D AC B DA BC D -2、如图已知正三棱柱中，点为的中点求证平面为的中点，求证：平面平面111ABC A B C -AB AC =,,M N P 11,,BC CC BB 1//A N AMP

【综合练习】一、选择题 1、直线和平面平行是指该直线与平面内的（） (A)一条直线不相交 (B)两条直线不相交 (C)无数条直线不相交(D)任意一条直线都不相交 2、已知a b ||,αα?，则必有（） ()||(),A a b B a b 异面 (),C a b 相交 (),D a b 平行或异面 3、若直线a,b 都与平面?平行，则a 和b 的位置关系是（） (A)平行 (B)相交 (C)异面 (D)平行或相交或是异面直线 4.已知平面α、β和直线m ，给出条件：①m ∥α；②m ⊥α；③m ?α；④α⊥β；⑤α∥β.为使m ∥β，应选择下面四个选项中的 ( ) A ．①④ B ．①⑤ C ．②⑤ D ．③⑤ 5．下列命题正确的是（） A 一直线与平面平行，则它与平面内任一直线平行 B 一直线与平面平行，则平面内有且只有一个直线与已知直线平行 C 一直线与平面平行，则平面内有无数直线与已知直线平行，它们在平面内彼此平行 D 一直线与平面平行，则平面内任意直线都与已知直线异面 6. 以下命题（其中a ，b 表示直线，?表示平面） ①若a ∥b ，b ??，则a ∥? ②若a ∥?，b ∥?，则a ∥b ③若a ∥b ，b ∥?，则a ∥? ④若a ∥?，b ??，则a ∥b 其中正确命题的个数是（）个个个个二、解答题 1．如图，E D ,分别是正三棱柱111ABC A B C -的棱1AA 、11B C 的中点，求证：1//A E 平面1BDC ； 2、如图，在四棱锥P-ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD=DC=1，点E 是PC 的中点，作EF PB 交PB 于点

线面垂直与面面垂直的判定与性质

立体几何之垂直关系【知识要点】空间中的垂直关系如果一条直线与平面内的两条相交直线垂直，则这条直线与这个平面垂直．如果一个平面过另一个平面的一条垂线，则两个平面互相垂直．如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．解决空间问题的重要思想方法：等价转化——化空间问题为平面问题．空间平行、垂直关系证明的基本思想方法——转化与联系，如图所示．题型1 平移证明线线垂直例1 如图，在四棱锥ABCD P -中，N M AD BC AB AD BC BC AB ,.2,1,,===⊥分别为DC PD ,的中点，求证：AC MN ⊥ 例2 底面ABCD 是正方形，Q G BE PD PD BE ,,2,=‖分别为AP AB ,的中点，求证：CG QE ⊥

例3 如图，在正方形1111D C B A ABCD -中，M 为1CC 的中点，F E ,分别为11,D A CD 的中点，AC 交BD 于点O ，求证：OM EF ⊥ 题型2 线面垂直判定例1 如图，在三棱锥ABC P -中，PAB ?是等边三角形。 ①若ABC ?是等边三角形，证明：PC AB ⊥ ②若 90=∠=∠PBC PAC ，证明：PC AB ⊥ 例 2 已知四棱台1111D C B A ABCD -的上下底面边长分别是2和4的正方形， 41=AA 且

ABCD AA 底面⊥1，点P 为1DD 的中点，求证：PBC AB 面⊥1 例3 如图，在三棱柱111C B A ABC -中，AC AB BAC ==∠,90 ，1A 在底面ABC 的射影为BC 的中点，D 为11C B 的中点。证明：⊥D A 1平面BC A 1 题型3 线面垂直性质证明线线垂直例1 如图，在三棱柱111C B A ABC -中，侧棱垂直于底面，D AA AC ACB ,2 1,901= =∠ 是棱1AA 的中点，求证：BD DC ⊥1 例2 已知正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直，M 为AC 上一点，N 为BF 上一点，且FN AM =。求证：AB MN ⊥

线面平行与垂直关系的转化

三垂线定理一、温故 1.线面平行的判定及性质定理 2.线面垂直的判定及性质定理 3.求线面所成角步骤二、探究思考1：面的垂线垂直于平面内的每一条直线；平面的斜线不能垂直于平面的每一条直线，但也不是与每一条直线都不垂直。那么平面的斜线与平面内的直线在什么情况下是垂直的呢？例1：已知：,PA PO 分别是平面α的垂线和斜线，AO 是PO 在平面α的射影,, a α?a AO ⊥。求证：a PO ⊥；例2.已知P 是平面ABC 外一点，,PA ABC AC BC ⊥⊥。求证：PC BC ⊥。 P B

例3.已知：点O 是ABC ?的垂心，PO ABC ⊥平面，垂足为O ，求证：PA BC ⊥ 例4.已知PA ⊥正方形ABCD 所在平面，O 为对角线BD 的中点。求证：,PO BD PC BD ⊥⊥。例5.在正方体1AC 中，求证：1111 1,AC B D AC BC ⊥⊥；例6．已知：,PA PO 分别是平面α的垂线和斜线，AO 是PO 在平面α的射影,, a α?a PO ⊥。求证：a AO ⊥； P B 1 A C O D A C B P

例7．在空间四边形ABCD 中，设,AB CD AC BD ⊥⊥。求证：（1）AD BC ⊥；（2）点A 在底面BCD 上的射影是BCD ?的垂心；线面平行与垂直关系的转化 1.对于命题：①b a a b b a ⊥?⊥,//； ②αα//,b a b a ?⊥⊥； ③ c a b a c b a ////,,,?=???βαβα；④ c b a c a b ////,,,?=?=?=?ααγγββα，其中正确的命题个数是 2.若直线a ，b 没有公共点，则下列命题：①存在与a ，b 平行的直线；②存在与a ，b 垂直的平面；③存在经过a 而与b 垂直的平面；④存在经过a 而与b 平行的平面. 其中正确的命题序号是 3.已知a ，b 和平面α，下列推理：①α⊥a 且b a a b ⊥??；②αα⊥?⊥b a b a 且//；③b a a //b //??αα且；④ααα??⊥⊥a a b a 或且//b ，其中正确的命题序号是 4.下列说法：①如果一条直线和平面内的一条直线垂直，该直线与这个平面必相交；②如果一条直线和平面的一组平行线垂直，该直线必在这个平面内；④如果一条直线和一个平面垂直，该直线垂直于平面内的任何直线，其中正确的个数是 5.空间四边形ABCD 的四条边相等，则它的对角线AD 、BC 的关系是 6.对于命题：① αα⊥????⊥a b b a //；②αα////a b b a ?????；③αα⊥?? ?? ⊥a b b a //；④ αα//b b a a ?? ?? ⊥⊥其中正确的命题是 7.在正方体ABCD-A ?B ?C ?D ?中，边对角线BD ?的一个平面交AA ?于E ，交CC ?于F ， D A B C