第2章 关系模型与关系代数

第2章关系模型与关系代数
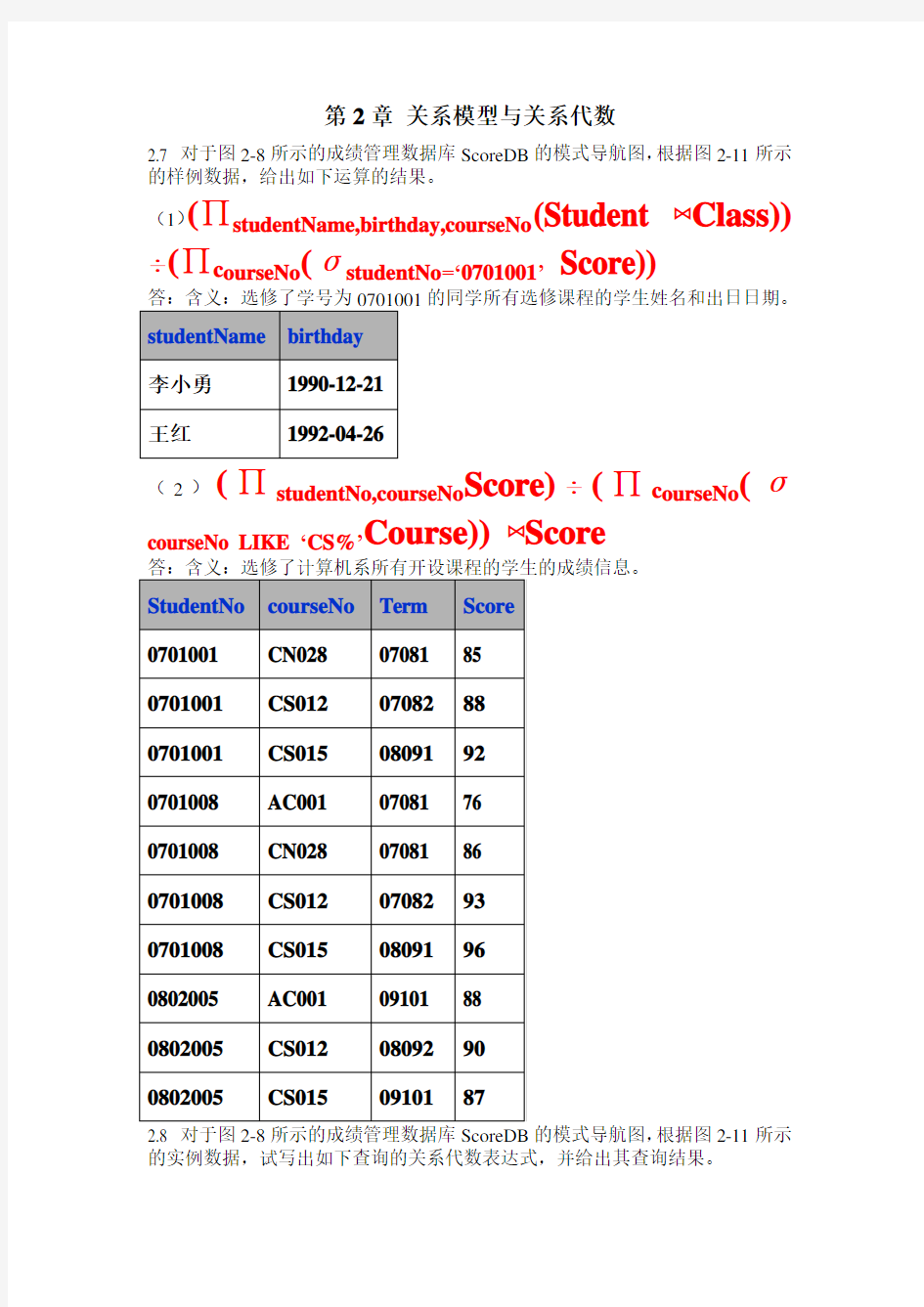
2.7 对于图2-8所示的成绩管理数据库ScoreDB的模式导航图,根据图2-11所示的样例数据,给出如下运算的结果。
(1)(∏studentName,birthday,courseNo(Student ?Class))÷(∏c ourseNo(σstudentNo=‘0701001’ Score))
的同学所有选修课程的学生姓名和出日日期。
(2)(∏studentNo,courseNo Score)÷(∏c ourseNo(σ
Course))?Score
courseNo LIKE ‘CS%’
的模式导航图,根据图2-11所示的实例数据,试写出如下查询的关系代数表达式,并给出其查询结果。
(1)查找籍贯为“上海”的全体学生。
答:σnative LIKE ‘上海%’(Student)
(2)查找1992年元旦以后出生的全体男同学。
答:σyear(birthday)>=1992∧sex='男’(Student)
(3)查找信息学院非汉族同学的学号、姓名、性别及民族。
答:∏studentNo,studenName,sex,nation(σnation!=’汉族’(Student) ?(σinstitute=’信息学院’(Class)))
(4)查找08-09学年第二学期(08092)开出课程的编号、名称和学分。
答:∏courseNo,courseName,courseHour(Course ?(σterm=’08092’Score))
(5)查找选修了“操作系统”的学生学号、成绩及姓名。
答:∏studentNo,studenName,score(Student ?(Score ?(∏courseNo(σcourseName=’操作系Course)))
统’
(6)查找班级名称为“会记学08(3)班”的学生在07-08学年第一学期(07081)选课情况,要求显示学生姓名、课程号、课程名称和成绩。
答:∏studenName, courseNo,courseName,score( (σ
Class) ?Student?className=’会计学08(3)班’
(σterm=’07081’ Score) ?Course)
(7)查找至少选修了一门其直接先修课编号为CS012的课程的学生学号和姓名。
答:∏studenNo, studentName( (σ
Course) ?Score ?priorCourse=’CS012’
Student)
(8)查找选修了08-09学年第一学期(08091)开出的全部课程的学生学号和姓名。
答:∏studenNo, studentName(Score÷(∏
(σterm=’08091’ Score)) ?Student) courseNo
(9)查找至少选修了学号为0703010的学生所选课程的学生学号和姓名。答:∏studenNo, studentName(Score÷(∏
(σstudentNo=’0703010’Score)) ?courseNo
Student)
2.9 对于图2-10所示的学生选课数据库SCDB的模式导航图,试写出如下查询的关系代数表达式。
(1)查找2008级蒙古族学生信息,包括学号、姓名、性别和所属班级。答:∏studenNo,studentName,sex,classNo((σnation=’蒙
Student) ?(σgrade=2008Class))
古族’
(2)查找“C语言程序设计”课程的课程班号、上课时间以及上课地点。答:∏cClassNo,time,location((σcourseName=’C语言程
Course) ?CourseClass ?序设计’
Classroom)
(3)查找选修了先修课程为“计算机概论”的学生学号、课程号和成绩。
答:∏studenNo,courseNo,score((∏C1.courseNo((ρCourse) ?C1.priorCourse=C2.courseNo(σC1
(ρC2Course)))) ?SC) courseName=’计算机概论’
(4)查找李勇老师08-09学年第二学期(08092)开出的课程号、课程名和学分。答:∏courseNo,courseName,creditHour((∏
(σteacherName=’李勇’Teacher))?(σteacherNo
CourseClass)?Course)
term=’08092’
(5)查找信息学院学生选课情况,要求显示学生姓名、课程号、课程名、课程班号、成绩和任课教师。
答:∏studentName,courseNo,courseName,cClassNo,score,teacher
((∏instituteNo(σinstituteName=’信息学院’Name
Institute)) ?Class ?Student ?SC ?Course ?CourseClass ?Teacher)
四种线性代数模型
线性代数是高等学校理工科和经济类学科相关专业的一门重要基础课,它不仅是其他数学课程的基础,也是物理、力学、电路等专业课程的基础。作为处理离散问题工具的线性代数,也是从事科学研究和工程设计的科研人员必备的数学工具之一。 实验一 生物遗传模型 1.工程背景 设一农业研究所植物园中某植物的基因型为AA 、Aa 和aa 。常染色体遗传的规律是:后代是从每个亲体的基因对中个继承一个基因,形成自己的基因对。如果考虑的遗传特征是由两个基因A 、a 控制的,那末就有三种基因对,记为AA 、Aa 和aa 。研究所计划采用Aa(AA)型的植物与每一种基因型植物相结合的方案培育植物后代。问经过若干年后,这种植物的任意一代的三种基因型分布如何 2.问题分析 分析双亲体结合形成后代的基因型概率,如表6-4所示。 表6-4基因型概率矩阵 后代 基因对 父体—母体的基因对 AA —AA AA —Aa AA —aa Aa —Aa Aa —aa aa —aa AA 1 1/2 0 1/4 0 0 Aa 0 1/2 1 1/2 1/2 0 aa 1/4 1/2 1 3.模型建立与求解 设,,n n n a b c 分别表示第n 代植物中基因型AA 、Aa 、aa 型的植物占植物总数的百分率。则 第n 代植物的基因型分布为() n n n n a x b c ?? ?= ? ???,0(0)00a x b c ?? ? = ? ??? 表示植物型的初始分布。依据上述基因型概率矩阵,有1112n n n a a b --=+,111 2 n n n b b c --=+,0n c =,1n n n a b c ++=,表示为矩阵形式 11111/2001/21000n n n n n n a a b b c c ---?????? ? ??? = ? ??? ? ?????????
线性代数第3章习题解答(rr)
1.已知向量:112[5,1,3,2,4],34[3,7,17,2,8],T T ααα=--=-- 求1223αα+ 解: ∵ 21{[3,7,17,2,8][15,3,9,6,12]}4T T α=----- 1[12,4,8,8,4][3,1,2,2,1]4 T T =-----=- ∴ 1223[10,2,6,4,8][9,3,6,6,3][19,1,0,10,11]T T T αα+=-+-= 2.设 12[2,5,1,3],[10,1,5,10],T T αα== 3123[4,1,1,1],3()2()5()0T ααααααα=--++-+=并且 求 α 解: ∵ 1236325αααα=+- [6,15,3,9][20,2,10,20][20,5,5,5][6,12,18,24], T T T T =+--= ∴ [1,2,3,4].T α= 3.判断下列命题是否正确,为什么? (1)如果当 120m k k k ====L 时, 11220m m k k k ααα+++=L 成立, 则向量组12,,m αααK 线性相关 解:不正确.如:[][]121,2,3,4T T αα==,虽然 12000,αα+=但12,αα线性无关。 (2) 如果存在m 个不全为零的数12,,,,m k k k L 使 11220,m m k k k ααα+++≠L 则向量组12,,,m αααL 线性无关。 解: 不正确. 如[][]11121,2,2,4,1,2,T T k αα====存在k 使 121220,,.αααα+≠但显然线性相关 (3) 如果向量组12,,,m αααL 线性无关,则其中任何一个向量都 不能由其余向量线性表出. 解: 正确。(反证)如果组中有一个向量可由其余向量线性表示,则向量组 12,,,m αααL 线性相关,与题没矛盾。 (4) 如果向量组123,,ααα线性相关,则3α一定可由12,αα线性表示。 解:不正确。例如:[][][]1230,0,0,0,1,0,0,0,1,T T T ααα===向量组123,,ααα线性相关,但3α不能由12,αα线性表示。 (5) 如果向量β可由向量123,,ααα线性表示,即: 112233,k k k βααα=++则表示系数 123,,k k k 不全为零。 解:不正确。例如:[][][]120,0,0,1,0,0,0,1,0,T T T βαα=== []31230,0,1,000T αβααα==++,表示系数全为0。 (6) 若向量12,αα线性相关,12,ββ线性无关,则1212,,,ααββ线性相关.
线性代数公式大全最全最完美
线性代数公式大全——最新修订 1、行列式 1. n 行列式共有2n 个元素,展开后有!n 项,可分解为2n 行列式; 2. 代数余子式的性质: ①、ij A 和ij a 的大小无关; ②、某行(列)的元素乘以其它行(列)元素的代数余子式为0; ③、某行(列)的元素乘以该行(列)元素的代数余子式为A ; 3. 代数余子式和余子式的关系:(1)(1)i j i j ij ij ij ij M A A M ++=-=- 4. 设n 行列式D : 将D 上、下翻转或左右翻转,所得行列式为1D ,则(1)2 1(1) n n D D -=-; 将D 顺时针或逆时针旋转90o ,所得行列式为2D ,则(1)2 2(1)n n D D -=-; 将D 主对角线翻转后(转置),所得行列式为3D ,则3D D =; 将D 主副角线翻转后,所得行列式为4D ,则4D D =; 5. 行列式的重要公式: ①、主对角行列式:主对角元素的乘积; ②、副对角行列式:副对角元素的乘积(1)2 (1) n n -? -; ③、上、下三角行列式( = ◥◣):主对角元素的乘积; ④、 ◤和 ◢:副对角元素的乘积(1)2 (1)n n -? -; ⑤、拉普拉斯展开式: A O A C A B C B O B ==、 (1)m n C A O A A B B O B C ==-g ⑥、范德蒙行列式:大指标减小指标的连乘积; ⑦、特征值; 6. 对于n 阶行列式A ,恒有:1(1)n n k n k k k E A S λλλ-=-=+-∑,其中k S 为k 阶主子式; 7. 证明0A =的方法: ①、A A =-; ②、反证法; ③、构造齐次方程组0Ax =,证明其有非零解; ④、利用秩,证明()r A n <; ⑤、证明0是其特征值; 2、矩阵 1. A 是n 阶可逆矩阵: ?0A ≠(是非奇异矩阵); ?()r A n =(是满秩矩阵) ?A 的行(列)向量组线性无关; ?齐次方程组0Ax =有非零解; ?n b R ?∈,Ax b =总有唯一解; ?A 与E 等价; ?A 可表示成若干个初等矩阵的乘积;
线性代数公式模板
线性代数公式 1、行列式 1. n 行列式共有2n 个元素,展开后有!n 项,可分解为2n 行列式; 2. 代数余子式的性质: ①、ij A 和ij a 的大小无关; ②、某行(列)的元素乘以其它行(列)元素的代数余子式为0; ③、某行(列)的元素乘以该行(列)元素的代数余子式为A ; 3. 代数余子式和余子式的关系:(1)(1)i j i j ij ij ij ij M A A M ++=-=- 4. 设n 行列式D : 将D 上、下翻转或左右翻转,所得行列式为1D ,则(1)2 1(1) n n D D -=-; 将D 顺时针或逆时针旋转90 ,所得行列式为2D ,则(1)2 2(1)n n D D -=-; 将D 主对角线翻转后(转置),所得行列式为3D ,则3D D =; 将D 主副角线翻转后,所得行列式为4D ,则4D D =; 5. 行列式的重要公式: ①、主对角行列式:主对角元素的乘积; ②、副对角行列式:副对角元素的乘积(1)2 (1) n n -? -; ③、上、下三角行列式( = ◥◣):主对角元素的乘积; ④、 ◤和 ◢:副对角元素的乘积(1)2 (1)n n -? -; ⑤、拉普拉斯展开式: A O A C A B C B O B ==、(1)m n C A O A A B B O B C ==- ⑥、范德蒙行列式:大指标减小指标的连乘积; ⑦、特征值; 6. 对于n 阶行列式A ,恒有:1(1)n n k n k k k E A S λλλ-=-=+-∑,其中k S 为k 阶主子式; 7. 证明0A =的方法: ①、A A =-; ②、反证法; ③、构造齐次方程组0Ax =,证明其有非零解; ④、利用秩,证明()r A n <; ⑤、证明0是其特征值; 2、矩阵 8. A 是n 阶可逆矩阵: ?0A ≠(是非奇异矩阵); ?()r A n =(是满秩矩阵) ?A 的行(列)向量组线性无关; ?齐次方程组0Ax =有非零解; ?n b R ?∈,Ax b =总有唯一解;
数据库系统原理与设计(第2版)-万常选版-第2章-关系模型与关系代数--课后答案
3.简述如下概念,并说明它们之间的联系与区别:。 (1)域,笛卡尔积,关系,元组,属性 答:域:域是一组具有相同数据类型的值的集合。 笛卡尔积:给定一组域D1,D2,…,Dn,这些域中可以有相同的。这组域的笛卡尔积为:D1×D2×…×Dn={(d1,d2,…,dn)|di?Di,i=1,2,…,n }其中每一个元素(d1,d2,…,dn)叫作一个n元组(n-tuple)或简称元组(Tuple)。元素中的每一个值di叫作一个分量(Component)。 关系:在域D1,D2,…,Dn上笛卡尔积D1×D2×…×Dn的子集称为关系,表示为 R(D1,D2,…,Dn) 元组:关系中的每个元素是关系中的元组。 属性:关系也是一个二维表,表的每行对应一个元组,表的每列对应一个域。由于域可以相同,为了加以区分,必须对每列起一个名字,称为属性(Attribute)。 (2)超码,主码,候选码,外码 答:超码:对于关系r的一个或多个属性的集合A,如果属性集A可以唯一地标识关系r中的一个元组,则称属性集A为关系r的一个超码 (superkey) 。 候选码:若关系中的某一属性组的值能唯一地标识一个元组,则称该属性组为候选码(Candidate key)。 主码:若一个关系有多个候选码,则选定其中一个为主码(Primary key)。 外码:设F是基本关系R的一个或一组属性,但不是关系R的码,如果F与基本关系S 的主码Ks相对应,则称F是基本关系R的外码(Foreign key),简称外码。 基本关系R称为参照关系(Referencing relation),基本关系S称为被参照关系(Referenced relation)或目标关系(Target relation)。关系R和S可以是相同的关系。 (3)关系模式,关系,关系数据库 答:关系模式:关系的描述称为关系模式(Relation Schema)。它可以形式化地表示为:R(U,D,dom,F) 其中R为关系名,U为组成该关系的属性名集合,D为属性组U中属性所来自的域,dom 为属性向域的映象集合,F为属性间数据的依赖关系集合。 关系:在域D1,D2,…,Dn上笛卡尔积D1×D2×…×Dn的子集称为关系,表示为 R(D1,D2,…,Dn) 关系是关系模式在某一时刻的状态或内容。关系模式是静态的、稳定的,而关系是动态的、随时间不断变化的,因为关系操作在不断地更新着数据库中的数据。 关系数据库:关系数据库也有型和值之分。关系数据库的型也称为关系数据库模式,是对关系数据库的描述,它包括若干域的定义以及在这些域上定义的若干关系模式。关系数据库的值是这些关系模式在某一时刻对应的关系的集合,通常就称为关系数据库。 2.3.为什么需要空值null? 答:引入空值,可以方便于数据库的维护和建立,数字或者字符有时并不能解决想要解决的问题,毕竟它们是真实的存在,有了空值,那么有些操作,比如查询,插入,删除都可以更加方便,比如公司的部门,新增的部门,信息是不存在的,是之后数据库人员进行添加之后才有的,所以让它为空,比给它0更加贴近实际。空值是所有可能的域的一个取值,表明值未知或不存在。 2.3.关系模型的完整性规则有哪些? 答:关系模型的完整性规则是对关系的某种约束条件。关系模型中可以有三类完整性约束:实体完整性、参照完整性和用户定义的完整性。 其中实体完整性和参照完整性是关系模型必须满足的完整性约束条件,被称作是关系的
最全线性代数公式笔记
线性代数公式必记 1、行列式 1. n 行列式共有2n 个元素,展开后有!n 项,可分解为2n 行列式; 2. 代数余子式的性质: ①、ij A 和ij a 的大小无关; ②、某行(列)的元素乘以其它行(列)元素的代数余子式为0; ③、某行(列)的元素乘以该行(列)元素的代数余子式为A ; 3. 代数余子式和余子式的关系:(1)(1)i j i j ij ij ij ij M A A M ++=-=- 4. 设n 行列式D : 将D 上、下翻转或左右翻转,所得行列式为1D ,则(1)2 1(1) n n D D -=-; 将D 顺时针或逆时针旋转90 ,所得行列式为2D ,则(1)2 2(1)n n D D -=-; 将D 主对角线翻转后(转置),所得行列式为3D ,则3D D =; 将D 主副角线翻转后,所得行列式为4D ,则4D D =; 5. 行列式的重要公式: ①、主对角行列式:主对角元素的乘积; ②、副对角行列式:副对角元素的乘积(1)2 (1) n n -? -; ③、上、下三角行列式( = ◥◣):主对角元素的乘积; ④、 ◤和 ◢:副对角元素的乘积(1)2 (1)n n -? -; ⑤、拉普拉斯展开式: A O A C A B C B O B ==、 (1)m n C A O A A B B O B C ==- ⑥、范德蒙行列式:大指标减小指标的连乘积; ⑦、特征值; 6. 对于n 阶行列式A ,恒有:1(1)n n k n k k k E A S λλλ-=-=+-∑,其中k S 为k 阶主子式; 7. 证明0A =的方法: ①、A A =-; ②、反证法; ③、构造齐次方程组0Ax =,证明其有非零解; ④、利用秩,证明()r A n <; ⑤、证明0是其特征值; 2、矩阵 1. A 是n 阶可逆矩阵: ?0A ≠(是非奇异矩阵); ?()r A n =(是满秩矩阵) ?A 的行(列)向量组线性无关; ?齐次方程组0Ax =有非零解; ?n b R ?∈,Ax b =总有唯一解;
线性代数公式大全——最新修订(突击必备)
线性代数公式大全 1、行列式 1. n 行列式共有2 n 个元素,展开后有!n 项,可分解为2n 行列式; 2. 代数余子式的性质: ①、ij A 和ij a 的大小无关; ②、某行(列)的元素乘以其它行(列)元素的代数余子式为0; ③、某行(列)的元素乘以该行(列)元素的代数余子式为A ; 3. 代数余子式和余子式的关系:(1)(1)i j i j ij ij ij ij M A A M ++=-=- 4. 行列式的重要公式: ①、主对角行列式:主对角元素的乘积; ②、副对角行列式:副对角元素的乘积(1)2 (1) n n -? -; ③、上、下三角行列式( = ◥◣):主对角元素的乘积; ④、 ◤和 ◢:副对角元素的乘积(1)2 (1) n n -? -; ⑤、拉普拉斯展开式:A O A C A B C B O B ==、(1)m n C A O A A B B O B C ==- ⑥、范德蒙行列式:大指标减小指标的连乘积; ⑦、特征值; 5. 对于n 阶行列式A ,恒有:1(1) n n k n k k k E A S λλλ-=-=+-∑,其中k S 为k 阶主子式; 6. 证明0A =的方法: ①、A A =-; ②、反证法; ③、构造齐次方程组0Ax =,证明其有非零解; ④、利用秩,证明()r A n <; ⑤、证明0是其特征值; 2、矩阵 1. A 是n 阶可逆矩阵: ?0A ≠(是非奇异矩阵); ?()r A n =(是满秩矩阵) ?A 的行(列)向量组线性无关; ?齐次方程组0Ax =有非零解; ?n b R ?∈,Ax b =总有唯一解;
?A 与E 等价; ?A 可表示成若干个初等矩阵的乘积; ?A 的特征值全不为0; ?T A A 是正定矩阵; ?A 的行(列)向量组是n R 的一组基; ?A 是n R 中某两组基的过渡矩阵; 2. 对于n 阶矩阵A :* * AA A A A E == 无条件恒成立; 3. 1* *1 11**()()()()()()T T T T A A A A A A ----=== * * * 1 1 1 ()()()T T T AB B A AB B A AB B A ---=== 4. 矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和; 5. 关于分块矩阵的重要结论,其中均A 、B 可逆: 若12 s A A A A ?? ? ?= ? ?? ? ,则: Ⅰ、12s A A A A = ; Ⅱ、1 1112 1s A A A A ----?? ? ?= ? ? ?? ? ; ②、1 11A O A O O B O B ---?? ?? = ? ????? ;(主对角分块) ③、1 11O A O B B O A O ---?? ??= ? ? ???? ;(副对角分块) ④、1 1111A C A A CB O B O B -----?? -?? = ? ????? ;(拉普拉斯) ⑤、1 111 1A O A O C B B CA B -----?? ?? = ? ?-???? ;(拉普拉斯) 3、矩阵的初等变换与线性方程组 1. 一个m n ?矩阵A ,总可经过初等变换化为标准形,其标准形是唯一确定的:r m n E O F O O ???= ???; 等价类:所有与A 等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵; 对于同型矩阵A 、B ,若()()r A r B A B = ? ; 2. 行最简形矩阵:
关系代数习题
习题四 1. 试述关系模型的三个组成部分。 .关系是由(R,U,D,dom,F )组成,R 为关系名,关系结构、关系操作、关系完整性约束 U 位组成关系的元组属性集合,D 为属性集合U 来自的域,dom 为对象关系的映像集合,F 为属性依赖关系集合。关系操作为关系代数、关系演算、关系映象操作,此语言表达能和功能强大,约束:参照完整性约束,用户自定义约束,实体完整性约束。 2. 试述关系数据语言的特点和分类。 关系操作语言灵活方便、语言表达能力和功能强,其特点:操作一体化,操作方式一次一集合,高度的非过程化的操作,关系操作语言包括:关系代数语言、关系演算语言、基于映像 的语言,关系代数语言是对关系的运算来表达查询的语言,关系演算语言查询元组的应该满足的谓词条件的运算查询语言, 基于映像的语言具有关系代数与关系演算的语言的双重特点 语言查询!
3. 定义并解释下列术语,说明它们之间的联系与区别。 主码、候选码、外码。)1 在一个关系中某个属性(或属性组)能够唯一标识一个元组,则称该属性为候选码,选择其 R 中属性F 不是R 的码,h 为K 关系的主码,如果F 与h 相对应,中一个为主码,在关系 则称 F 为管系R 的外码 笛卡尔积、关系、元组、属性、域。2)给定一组域D1,D2,D3 3)关系、关系模式、关系数据库。 4. 试述关系模型的完整性规则。在参照完整性中,为什么外码属性的值也可以为空?什么 情况下才可以为空? 5. 试述等值连接与自然连接的区别和联系。 6. 对于学生选课关系,其关系模式为: 学生(学号,姓名,年龄,所在系); 课程(课程名,课程号,先行课); 选课(学号,课程号成绩)。 用关系代数完成如下查询。 求学过数据库课程的学生的姓名和学号。1) 求学过数据库和数据结构的学生姓名和学号。2)求没学过数
第2章 关系模型与关系代数参考答案
第2章关系模型与关系代数 2.7 对于图2-8所示的成绩管理数据库ScoreDB的模式导航图,根据图2-11所示的样例数据,给出如下运算的结果。 (1)(∏studentName,birthday,courseNo(Student ?Class))÷(∏c ourseNo(σstudentNo=‘0701001’ Score)) 的同学所有选修课程的学生姓名和出日日期。 (2)(∏studentNo,courseNo Score)÷(∏c ourseNo(σ Course))?Score courseNo LIKE ‘CS%’ 的模式导航图,根据图2-11所示的实例数据,试写出如下查询的关系代数表达式,并给出其查询结果。
(1)查找籍贯为“上海”的全体学生。 答:σnative=‘上海’Student (2)查找1992年元旦以后出生的全体男同学。 答:σyear(birthday)>=1992∧sex='男’Student (3)查找信息学院非汉族同学的学号、姓名、性别及民族。 答:∏studentNo,studenName,sex,nation(Student ?(σinstitute=’信息学院’Class)) (4)查找08-09学年第二学期(08092)开出课程的编号、名称和学分。 答:∏courseNo,courseName,courseHour(Course ?(σterm=’08092’Score)) (5)查找选修了“操作系统”的学生学号、成绩及姓名。 答:∏studentNo,studenName,score(Student ?(Grade ?(σcourseName=’操作系统’Course)) (6)查找班级名称为“会记学08(3)班”的学生在07-08学年第一学期(07081)选课情况,要求显示学生姓名、课程号、课程名称和成绩。 答:∏studenName, courseNo,courseName,score( (σ Class) ?Student?className=’会计学08(3)班’ (σterm=’07081’ Score) ?Course) (7)查找至少选修了一门其直接先修课编号为CS012的课程的学生学号和姓名。答:∏studenNo, studentName( (σ
线性代数应用题
线性代数应用题集锦 郑波 重庆文理学院数学与统计学院 2011年10月
目录 案例一. 交通网络流量分析问题 (1) 案例二. 配方问题 (4) 案例三. 投入产出问题 (6) 案例四. 平板的稳态温度分布问题 (8) 案例五. CT图像的代数重建问题 (10) 案例六. 平衡结构的梁受力计算 (12) 案例七. 化学方程式配平问题 (15) 案例八. 互付工资问题 (17) 案例九. 平衡价格问题 (19) 案例十. 电路设计问题 (21) 案例十一. 平面图形的几何变换 (23) 案例十二. 太空探测器轨道数据问题 (25) 案例十三. 应用矩阵编制Hill密码 (26) 案例十四. 显示器色彩制式转换问题 (28) 案例十五. 人员流动问题 (30) 案例十六. 金融公司支付基金的流动 (32) 案例十七. 选举问题 (34) 案例十八. 简单的种群增长问题 (35) 案例十九. 一阶常系数线性齐次微分方程组的求解 (37) 案例二十. 最值问题 (39) 附录数学实验报告模板 (40)
这里收集了二十个容易理解的案例. 和各类数学建模竞赛的题目相比, 这些案例确实显得过于简单. 但如果学生能通过这些案例加深对线性代数基本概念、理论和方法的理解, 培养数学建模的意识, 那么我们初步的目的也就达到了. 案例一. 交通网络流量分析问题 城市道路网中每条道路、每个交叉路口的车流量调查,是分析、评价及改善城市交通状况的基础。根据实际车流量信息可以设计流量控制方案,必要时设置单行线,以免大量车辆长时间拥堵。 图1 某地交通实况 图2 某城市单行线示意图 【模型准备】某城市单行线如下图所示, 其中的数字表示该路段每小时按箭头方向行驶的车流量(单位: 辆).
线性代数在实际生活中的应用
线性代数在生活中的实际应用 大学数学就是自然科学的基本语言,就是应用模式探索现实世界物质运动机理的主要手段。学习数学的意义不仅仅就是学习一种专业的工具而已。 ;;;初等的数学知识 学习线性代数数学建模 函数模型的建立及应用,作为变化率的额倒数在几何学、物理学、经济学中的应用,抛体运动的数学建模及其应用,最优化方法及其在工程、经济、农业等领域中的应用,逻辑斯谛模型及其在人口预测、新产品的推广与经济增长预测方面的应用,网络流模型及其应用,人口迁移模型及其应用,常用概率模型及其应用,等等。 线性代数中行列式 实质上就是又一些竖直排列形成的数表按一定的法则计算得到的一个数。早在1683年与1693年,日本数学家关孝与与德国数学家莱布尼茨就分别独立的提出了行列式的概念。之后很长一段时间,行列式主要应用与对现行方程组的而研究。大约一个半世纪后,行列式逐步发展成为线性代数的一个独立的理论分支。1750年瑞士数学家克莱姆也在她的论文中提出了利用行列式求解线性方程组的著名法则——克莱姆法则。随后1812年,法国数学家柯西发现了行列式在解析几何中的应用,这一发现机器了人们对行列式的应用进行探索的浓厚兴趣。如今,由于计算机与计算软件的发展,在常见的高阶行列式计算中,行列式的数值意义虽然不大,但就是行列式公式依然可以给出构成行列式的数表的重要信息。在线性代数的某些应用中,行列式的只就是依然非常重要。 例如:有甲、乙、丙三种化肥,甲种化肥每千克含氮70克,磷8克,钾2克;乙种、 化肥每千克含氮64克,磷10克,钾0、6克;丙种化肥每千克含氮70克,磷5克,钾1、4克.若把此三种化肥混合,要求总重量23千克且含磷149克,钾30克,问三种化肥各需多少千克? 解: 题意得方程组 依千克、、各需设甲、乙、丙三种化肥32,1x x x ??? ??=++=++=++. 304.16.02,1495108,23321 321321x x x x x x x x x ,527- =D 此方程组的系数行列式81275 81 321-=-=-=D D D ,,又 由克莱姆法则,此方程组有唯一解:3=x 1;52=x ;.153=x 即甲乙丙三种化肥各需 3千克 5千克 15千克、 矩阵实质上就就是一张长方形的数表,无论就是在日常生活中还就是科学研究中,矩阵就是一种非常常见的数学现象。学校课表、成绩单、工厂里的生产进度 表、车站时刻表、价目表、故事中的证劵价目表、科研领域中的数据分析表,它就是表述或处理大量的生活、生产与科研问题的有力的工具。矩阵的重要作用主要就是它能把头绪纷繁的十五按一定的规则清晰地展现出来,使我们不至于背一些表面瞧起来杂乱无章的关系弄得晕头转向。塌还可以恰当的给出事物之间内在的联系,并通过矩阵的运算或变换来揭示事物之间的内在联系。它也就是我们求解数学问题时候“数形结合”的途径。矩阵的运算就是非常重要的内容。
线性代数第三章习题与答案(东大绝版)
第三章 习题与答案 习题 A 1.求向量123(4,1,3,2),(1,2,3,2),(16,9,1 ,3)T T T =--=-=-ααα的线性组合12335.+-ααα 解 12341161293535331223?????? ? ? ? ? ? ?+-=+- ? ? ?-- ? ? ?-??????ααα1251613109491512561037???????? ? ? ? ? ? ? ? ?=+-= ? ? ? ?--- ? ? ? ?--???????? . 2.从以下方程中求向量α 1233()2()5()-++=+αααααα, 其中123(2,5,1,3),(10,1,5,10),(4,1 ,1,1).T T T ===-ααα 解 由方程得1233322550-++--=αααααα, 1232104651112 632532515118310124???????? ? ? ? ? ? ? ? ?=+-=+-= ? ? ? ?- ? ? ? ?????????αααα 故12 34?? ? ?= ? ??? α,即(1,2,3,4)T =α. 3.求证:向量组12i s α,α,,α,α 中的任一向量i α可以由这个向量组线性表出. 证 120010(1,2,,)i i s i s =+++++= ααααα 4.证明: 包含零向量的向量组线性相关. 证 设向量组为1211α,α,,α,0,α,,αi i s -+ ,则有 12110α0αα00α0α0,0i i s k k -++++++++=≠ 而0,0,,0,,0,,0k 不全为0,故向量组线性相关. 5.设有m 个向量12α,α,,αm ,证明: 若αα()i j i j =≠,则向量组12α,α,,αm 线性相关. 证 显然有1210α0αα0α()α0α0,0i i j m k k k +++++++-++=≠ , 而0,,0,,0,,0,,0,,0k k - 不全为0.故向量组线性相关. 6.判断下列向量组的线性相关性
线性代数在数模中的应用
线性代数在数学建模中的应用举例 1 基因间“距离”的表示 在ABO 血型的人们中,对各种群体的基因的频率进行了研究。如果我们把四种等位基因A 1,A 2,B ,O 区别开,有人报道了如下的相对频率,见表1.1。 表1.1基因的相对频率 问题 一个群体与另一群体的接近程度如何?换句话说,就是要一个表示基因的“距离”的合宜的量度。 解 有人提出一种利用向量代数的方法。首先,我们用单位向量来表示每一个群体。为此目的,我们取每一种频率的平方根,记ki ki f x = .由于对这四种群 体的每一种有14 1 =∑=i ki f ,所以我们得到∑==4 1 2 1i ki x .这意味着下列四个向量的每个都 是单位向量.记 .444342414,343332313,242322212,141312111???? ? ? ??????=????????????=????????????=????????????=x x x x a x x x x a x x x x a x x x x a
在四维空间中,这些向量的顶端都位于一个半径为1的球面上. 现在用两个向量间的夹角来表示两个对应的群体间的“距离”似乎是合理的.如果我们把a 1和a 2之间的夹角记为θ,那么由于| a 1|=| a 2|=1,再由内只公式,得 21cos a a ?=θ 而 .8307.03464.02943.03216.0,8228.01778.00000.05398.021???? ? ? ??????????????? ???=a a 故 9187.0c o s 21=?=a a θ 得 2.23=θ°. 按同样的方式,我们可以得到表1.2. 表1.2基因间的“距离” 由表1.2可见,最小的基因“距离”是班图人和英国人之间的“距离”,而爱斯基摩人和班图人之间的基因“距离”最大. 2 Euler 的四面体问题 问题 如何用四面体的六条棱长去表示它的体积?这个问题是由Euler (欧拉)提出的. 解 建立如图2.1所示坐标系,设A ,B ,C 三点的坐标分别为(a 1,b 1,c 1),( a 2,b 2,c 2)和(a 3,b 3,c 3),并设四面体O-ABC 的六条棱长分别为.,,,,,r q p n m l 由立体几何知道,该四面体的体积V 等于以向量→ → → OC OB OA ,,组成右手系时,以它们为棱的平行
线性代数第三章(答案)
第三章 矩阵的初等变换与线性方程组 一、填空题 1、 设???? ?? ? ??=n n n n n n b a b a b a b a b a b a b a b a b a A 2 1 2221 212111,其中),,2,1(,0,0n i b a i i =≠≠,则=)(A R ____ 2、 设n 阶矩阵A 的各行元素之和均为零,且=)(A R n -1,则线性方程组AX =0 的通解为________ 3、 设四阶方阵的秩为2,其伴随矩阵的秩为_______ 4、 设?????? ? ??=---112 11 22 221 21n n n n n n a a a a a a a a a A ,??????? ??=n x x x X 21,???? ??? ??=111 B ,其中 ),,2,1,,(n j i j i a a j i =≠≠,则线性方程组B AX =的解是________ 5、 已知????? ? ?=10 0210 002 P ,??? ? ? ? ?=20 0020 001A ,则=-1001)(AP P ________ 6、 设A ,B 均为n 阶矩阵AB =0,且A +B=E,则=+)()(B R A R _________ 7、 设矩阵n m A ?的秩为r ,P 为m 阶可逆矩阵,则)(PA R =________ 8、 矩阵??? ?? ??--34031302 1201 的行最简形矩阵为___________ 9、 矩阵??? ? ? ? ?----17 4 03430 1320的行最简形矩阵为__________ 10、 从矩阵A 中划去一行得到矩阵B ,则)(______)(B R A R 从矩阵A 中增加一行得到矩阵B ,则)(______)(B R A R
线性代数在实际生活中的应用
线性代数在生活中的实际应用 大学数学是自然科学的基本语言,是应用模式探索现实世界物质运动机理的主要手段。学习数学的意义不仅仅是学习一种专业的工具而已。 ;;;初等的数学知识 学习线性代数数学建模 函数模型的建立及应用,作为变化率的额倒数在几何学、物理学、经济学中的应用,抛体运动的数学建模及其应用,最优化方法及其在工程、经济、农业等领域中的应用,逻辑斯谛模型及其在人口预测、新产品的推广与经济增长预测方面的应用,网络流模型及其应用,人口迁移模型及其应用,常用概率模型及其应用,等等。 线性代数中行列式 实质上是又一些竖直排列形成的数表按一定的法则计算得到的一个数。早在1683年与1693年,日本数学家关孝和与德国数学家莱布尼茨就分别独立的提出了行列式的概念。之后很长一段时间,行列式主要应用与对现行方程组的而研究。大约一个半世纪后,行列式逐步发展成为线性代数的一个独立的理论分支。1750年瑞士数学家克莱姆也在他的论文中提出了利用行列式求解线性方程组的著名法则——克莱姆法则。随后1812年,法国数学家柯西发现了行列式在解析几何中的应用,这一发现机器了人们对行列式的应用进行探索的浓厚兴趣。如今,由于计算机和计算软件的发展,在常见的高阶行列式计算中,行列式的数值意义虽然不大,但是行列式公式依然可以给出构成行列式的数表的重要信息。在线性代数的某些应用中,行列式的只是依然非常重要。 例如:有甲、乙、丙三种化肥,甲种化肥每千克含氮70克,磷8克,钾2克;乙种、 化肥每千克含氮64克,磷10克,钾0.6克;丙种化肥每千克含氮70克,磷5克,钾1.4克.若把此三种化肥混合,要求总重量23千克且含磷149克,钾30克,问三种化肥各需多少千克? 解: 题意得方程组 依千克、、各需设甲、乙、丙三种化肥32,1x x x ??? ??=++=++=++. 304.16.02,1495108,23321 321321x x x x x x x x x ,527- =D 此方程组的系数行列式81275 81 321-=-=-=D D D ,,又 由克莱姆法则,此方程组有唯一解:3=x 1;52=x ;.153=x 即甲乙丙三种化肥各需 3千克 5千克 15千克、 矩阵实质上就是一张长方形的数表,无论是在日常生活中还是科学研究中,矩阵是一种非常常见的数学现象。学校课表、成绩单、工厂里的生产进度表、车站 时刻表、价目表、故事中的证劵价目表、科研领域中的数据分析表,它是表述或处理大量的生活、生产与科研问题的有力的工具。矩阵的重要作用主要是它能把头绪纷繁的十五按一定的规则清晰地展现出来,使我们不至于背一些表面看起来杂乱无章的关系弄得晕头转向。塌还可以恰当的给出事物之间内在的联系,并通过矩阵的运算或变换来揭示事物之间的内在联系。它也是我们求解数学问题时候
线性代数公式大全
概率论公式大全(2010版) 1.随机事件及其概率 吸收律:A AB A A A A =?=??Ω=Ω?)( A B A A A A A =???=??=Ω?)( )(AB A B A B A -==- 反演律:B A B A =? B A AB ?= n i i n i i A A 11=== n i i n i i A A 11=== 2.概率的定义及其计算 )(1)(A P A P -= 若B A ? )()()(A P B P A B P -=-? 对任意两个事件A , B , 有 )()()(AB P B P A B P -=- 加法公式:对任意两个事件A , B , 有 )()()()(AB P B P A P B A P -+=? )()()(B P A P B A P +≤? )()1()()()()(2111111n n n n k j i k j i n j i j i n i i n i i A A A P A A A P A A P A P A P -≤<<≤≤<≤==-+++- =∑∑∑ 3.条件概率 ()=A B P ) ()(A P AB P 乘法公式 ())0)(()()(>=A P A B P A P AB P
()() ) 0)(()()(12112112121>=--n n n n A A A P A A A A P A A P A P A A A P 全概率公式 ∑==n i i AB P A P 1)()( )()(1i n i i B A P B P ?=∑= Bayes 公式 )(A B P k )()(A P AB P k = ∑==n i i i k k B A P B P B A P B P 1 ) ()()()( 4.随机变量及其分布 分布函数计算 ) ()()()()(a F b F a X P b X P b X a P -=≤-≤=≤< 5.离散型随机变量 (1) 0 – 1 分布 1,0,)1()(1=-==-k p p k X P k k (2) 二项分布 ),(p n B 若P ( A ) = p n k p p C k X P k n k k n ,,1,0,)1()( =-==- *Possion 定理 0lim >=∞ →λn n np 有 ,2,1,0!)1(l i m ==---∞→k k e p p C k k n n k n k n n λλ (3) Poisson 分布 )(λP ,2,1,0,!)(===-k k e k X P k λλ
四种线性代数模型
线性代数就是高等学校理工科与经济类学科相关专业的一门重要基础课,它不仅就是其她数学课程的基础,也就是物理、力学、电路等专业课程的基础。作为处理离散问题工具的线性代数,也就是从事科学研究与工程设计的科研人员必备的数学工具之一。 实验一 生物遗传模型 1、工程背景 设一农业研究所植物园中某植物的基因型为AA 、Aa 与aa 。常染色体遗传的规律就是:后代就是从每个亲体的基因对中个继承一个基因,形成自己的基因对。如果考虑的遗传特征就是由两个基因A 、a 控制的,那末就有三种基因对,记为AA 、Aa 与aa 。研究所计划采用Aa(AA)型的植物与每一种基因型植物相结合的方案培育植物后代。问经过若干年后,这种植物的任意一代的三种基因型分布如何? 2、问题分析 分析双亲体结合形成后代的基因型概率,如表6-4所示。 表6-4基因型概率矩阵 后代 基因对 父体—母体的基因对 AA —AA AA —Aa AA —aa Aa —Aa Aa —aa aa —aa AA 1 1/2 0 1/4 0 0 Aa 0 1/2 1 1/2 1/2 0 aa 1/4 1/2 1 3、模型建立与求解 设,,n n n a b c 分别表示第n 代植物中基因型AA 、Aa 、aa 型的植物占植物总数的百分率。 则第n 代植物的基因型分布为() n n n n a x b c ?? ?= ? ???,0(0)00a x b c ?? ?= ? ???表示植物型的初始分布。依据上述基 因型概率矩阵,有1112n n n a a b --=+,111 2 n n n b b c --=+,0n c =,1n n n a b c ++=,表示为矩阵形 式 11111/2001/21000n n n n n n a a b b c c ---?????? ? ??? = ? ??? ? ????????? 记11/2001/21000M ?? ?= ? ??? ,则()(1) 2(2)3(3)(0)n n n n n x Mx M x M x M x ---=====L 。 于就是问题归结为如何计算n M ,可将M 对角化。易于计算M 的特征值为1、1/2、0, 其相应的特征向量为(1,0,0)T ,(0,1,0)T -,(1,2,1)T -。 令101012001P ?? ?=-- ? ???,则1 11/2001/21000M P P -?? ?= ? ??? 。
线性代数第三章习题解
线性代数第三章习题解 1. 计算下列行列式: 1) 4 321; 2) 2 2b b a a ; 3) 7 04 0- 解: 1) 26432414 321-=-=?-?=; 2) )(222 2a b ab b a ab b b a a -=-=; 3) 0)4(0707 40=-?-?=-. 2. 计算下列三阶行列式: 1) 241130 4 21--; 2) 320001753-; 3) b a c a c b c b a 解: 1) 将行列式按第一列展开 2) 将行列式按第二行展开 3) 3. 计算下列行列式: 1) 0 00 0000005 5 4433 2222211111b a b a b a e d c b a e d c b a ; 2) x y y x y x y x D n 0 0000 000 00 =; 3) f e d c b a 00000000 解: 1) 将行列式按第一列展开后, 得到的各子式再按第二列展开, 这样展开后的后三列构成的任何三阶子式都至少包括一行0, 因此后三列任何三阶子式均为0, 整个行列式的值D =0. 2) 将行列式按第一列展开得 3) 先对第一列展开, 然后对第二列展开, 得 4. 利用行列式的性质计算下列行列式
1) 2 60 5 232112131412 -; 2) ef cf bf de cd bd ae ac ab ---; 3) 2 2 2 2 2222 2 2222222)3()2()1()3()2()1()3()2()1()3()2()1(++++++++++++d d d d c c c c b b b b a a a a 解: 下面都将所求行列式的值设为D . 1) 因为第1行加到第2行以后, 第2行将和第4行相等, 因此行列式的值D =0; 2) 首先从第1,2,3行分别提取公因子a ,d ,f , 再从第1,2,3列提取公因子b ,c ,e , 得 3) 将第2,3,4列都展开, 并统统减去第1列, 得 再将第3列减去2倍的第2列, 第4列减去3倍的第2列, 得 5. 把下列行列式化为上三角形行列式, 并计算其值 1) 1 5 2 3 21353140422 -----; 2) 2 1 6 4 72954 1732152----- 解: 1) 2) 6. 计算下列n 阶行列式 1) 12125 4 3 1432321-n n n 2) a b b b a b a 解: 1) 设此行列式的值为D , 将第2,3,…,n 列均加于第一列, 则第一列的所有元素均为 )1(2 1 321+= ++++n n n , 将此公因式提出, 因此有 再令第n 行减去第n -1行, 第n -1行减去第n -2行, …, 第2行减去第1行, 可得 2) 此题和第3题的2)一样, 因此有n n n b a D 1 )1(+-+= 7. 证明下列行列式 1) ))()((1 11 a c c b b a ab ca bc c b a ---=
