五年级奥数专题：图形的计数

九图形的计数(A)

年级班姓名得分

一、填空题

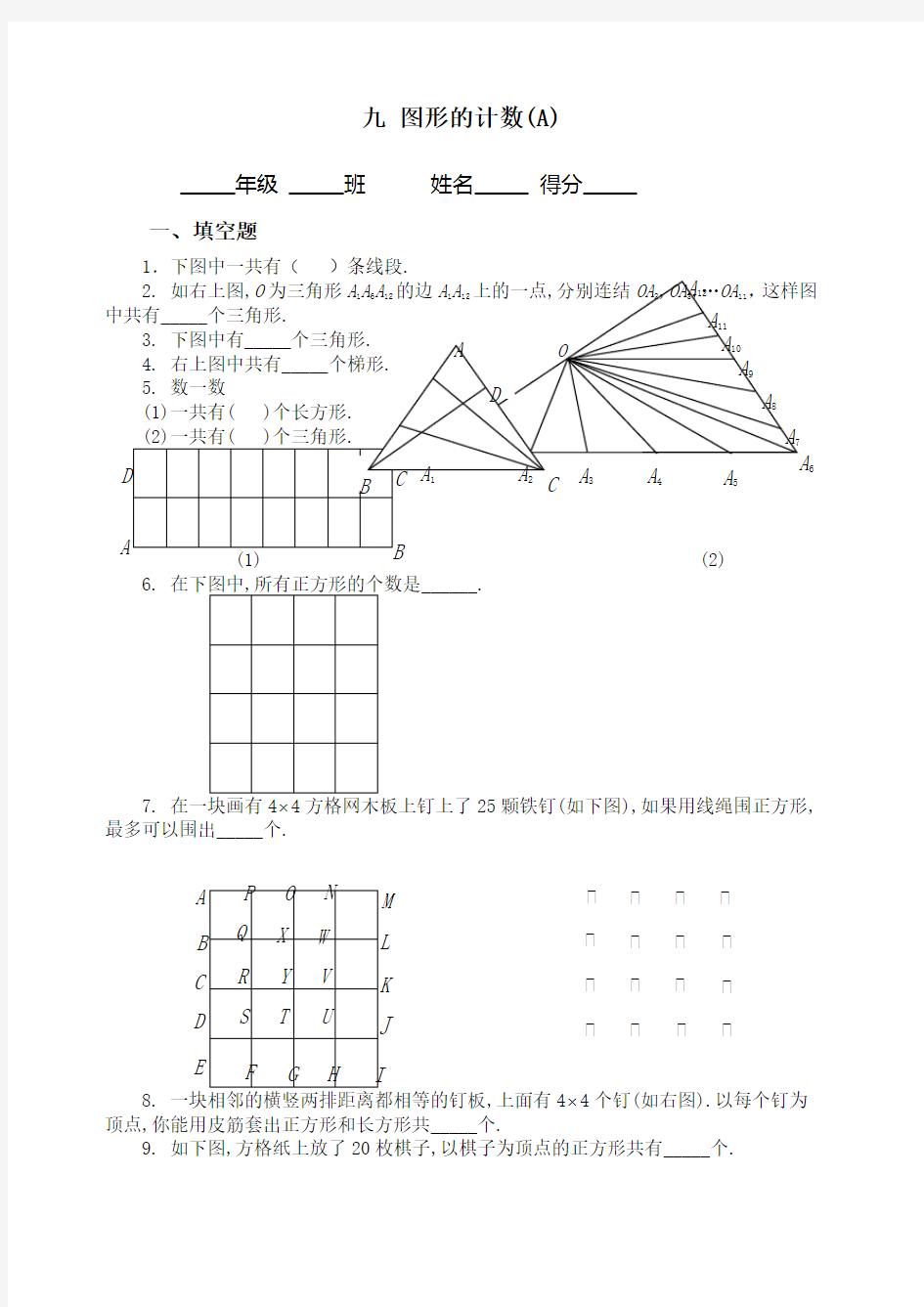
1．下图中一共有（）条线段.

6. ______.

7. 25颗铁钉(如下图),如果用线绳围正方形,最多可以围出_____个.

8. ,上面有4?4个钉(如右图).以每个钉为顶点,你能用皮筋套出正方形和长方形共_____个.

9. 如下图,方格纸上放了20枚棋子,以棋子为顶点的正方形共有_____个.

10. 数一数.要注意那些看不见的.

二、解答题

11. 右图中共有7层小三角形，求白色小三角形的个数与黑色小三角形的个数之比.

12. 下图中,AB 、CD 、EF 、MN 互相平行，则图中梯形个数与三角形个数的差是多少？ 13．现在都是由边长为1厘米的红色、白色两种正方形分别组成边长为2厘米、4厘米、8厘米、9厘米的大小不同的正方形、它们的特点都是正方形的四边的小正方形都是涂有红颜色的小正方形，除此以外，都是涂有白色的小正方形，要组成这样4个大小不同的正方形，总共需要红色正方形多少个？白色正方形多少个？ 14．将 ABC 的每一边4等分，过各分点作边的平行线，在所得下图中有多少个平行四边形？ 7 6

2 1 N

M F E D

C B A O

九图形的计数（B）

年级班姓名得分

一、填空题

1. 下图中长方形（包括正方形）总个数是_____.

2. 右上图中有正方形_____个,三角形_____个,平行四边形_____个,梯形_____个.

3. 下图中共出现了_____个长方形.

4. 先把正方形平均分成8个三角形.再数一数,它一共有_____个大小不同的三角形.

5. 图形中有_____个三角形.

6．如右上图,一个三角形分成36个小三角形.把每个小三角形涂上红色或蓝色,两个有公共边的小三角形要涂上不同的颜色,已知涂成红色的三角形比涂成蓝色的三角形多,那么多_____个.

7. 下图是由小立方体码放起来的,其中有一些小方体看不见.图中共有_____个小立方体.

8. 右上图中共有_____个正方形.

9. 有九张同样大小的圆形纸片,其中标有数码“1”的有1张；标有数码“2”的有2张；标有数码“3”的有3张，标有数码“4”的也有3张。把这九张圆形纸片如下图所示放置在一起，但标有相同数码的纸片不许靠在一起，问：

如果M位上放置标有数码“3”的纸片，一共有_____种不同的放置方法.

10. 如下图,在2×2方格中,画一条直线最多可穿过3个方格,在3×3方格中,画一条直线最多可穿过5个方格.那么10×10方格中,画一条直线最多可穿过_____个方格.

二、解答题

11. 把一条长15cm的线段截为三段，使每条线段的长度是整数，用这三条线段可以组成多少个不同的三角形？（当且仅当两三角形的三条边可以对应相等时，我们称这两个三角形是相同的.）

12. 有一批长度分别为1,2,3,4,5,6,7,8,9,10和11厘米的细木条,它们的数量都足够多,从中适当选取3根木条作为三条边.可围成一个三角形,如果规定底边是11厘米长,你能围成多少个不同的三角形?

13. 下图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?

14. 有同样大小的立方体27个,把它们竖3个,横3个,高3个,紧密地没有缝隙地搭成一个大的立方体(见图).如果用1根很直的细铁丝扎进这个大立方体的话,最多可以穿透几个小立方体?

———————————————答案

——————————————————————

1． 30

由例1注可知图形中每边有3+2+1=6（条）线段，因此整个图形中共有6?5=30条线段.

2. 37

1A 6A 12分解成以OA 6为公共边的两个三角形1A 6中共有5+4+3+2+1=15(个)三角形, OA 6A 12中共有+1=21(个)三角形,这样,图中共有15+21+1=37(个)三角形. 3. 15

这样的问题应该通过分类计数求解.此题中的三角形可先分成含顶点C 的和不含顶点C 的两大类.含顶点C

的又可分成另外两顶点在线段AB 上的和在线段BD

上的两小类.分类图解如下:

6?3=18(个)梯形. 5. 108,36

(1)因为长方形是由长和宽组成的,因此可分别考虑所有长方形的长和宽的可能种数.按照前面所介绍的线段的计数方法可分别求出长和宽的线段条数,将它们相乘就是所有长方形的个数.

因为AB 边上有8+7+6+…+2+1=2

9?=36条线段，AD 边上有2+1=3条线段，所以图中

一共有36?3=108个长方形.

(2)三角形一共有6行,每行都有3+2+1=6(个),所以一共有6?6=36(个)三角形. 6. 30

由例5注可知整个图形中共有12+22+32+42=30个正方形. 7. 50

此类问题一般用分类方法计数.对正方形的边长分八类计数如下: 边长为AB 的正方形有16个；边长为AC 的正方形有9个；边长为AD 的正方形有4个；边长为AE 的正方形有1个；边长为DF 的正方形有9个；边长为CF 的正方形有8个；边长为BF 的正方形有2个；边长为CG 的正方形有1个. 所以,最多可围出50个正方形. 8. 44

因为正方形是特殊的长方形,所以可以把正方形看成长方形,这样就不必分别求正方

形和长方形的个数,仍用分类计数的方法求解.

先考虑有一组对边平行于BC 的长方形有多少个.这一类按其水平边的位置可分为6小类,即位置在BF 、FE 、EC 、FC 、BE 、BC .同样,其竖直边也分为6类.所以这一类有6?6=36个长方形.

,分解图如下页图所示,其中分别有6

所以，共有9+4+2+4+2=2110． 30

将原立体图形从左至右分类计算，共有11+7+5+7=30个.

11. 白色小三角形个数=1+2+3+…+6=2

)61(?+=21，

黑色小三角形个数=1+2+3+…+7=2

)71(?+=28，

所以它们的比=2821=4

12. 解法一

本图中三角形的个数为(1+2+3+4)?4=40(个).下面求梯形的个数.梯形由两底唯一确定.首先在AB ,CD ,EF ,MN 中,考虑两底所在的线段,共有(4?3)÷2=6(种)选法；对上述四条线段中确定的两条线段，共有10（10=4+3+2+1）个梯形.共60个梯形.故所求差为20.

解法二

4个三角形,6个梯形,梯形比三角图形图形多2个.而在题图中,这种恰有10个.故题图中,梯形个数与三角形的个数之差为2?10=20(个).

13. 边长2厘米的正方形:

2?2=4(个) ……红色边长4厘米的正方形

(4-1)?4=12(个) ……红色 (4-2)?(4-2)=4(个) ……白色

边长8厘米的正方形

(8-1)?4=28(个) ……红色

(8-2)?(8-2)=36(个) ……白色

边长9厘米的正方形

(9-1)?4=32(个) ……红色

(9-2)?(9-2)=49(个) ……白色

所以,红色小正方形共有

4+12+28+32=76(个)

白色小正方形共有

4+36+49=89(个)

[注]本题的要求是由边长为1厘米的红色和白色两种正方形,分别组成边长是2厘米,4厘米,8厘米,9厘米的大小不同的正方形,可以看作方阵问题来解.四周的小正方形是涂红色的,可看成是空心方阵,因此,涂红色正方形的个数等于4?(n-1).其他小正方形是涂白色的，可当作实心方阵，所以，涂白色的正方形的个数等于(n-2)?(n-2).比如,由边长为1厘米的正方形组成边长为9厘米的正方形,涂红色的小正方形的个数是:4?(9-1)=32(个),涂白色的小正方形的个数是:(9-2)?(9-2)=49(个).

14. 将平行四边形分为三类:①尖角在上、下方；②尖角在左下、右上方；③尖角在左上、右下方.

就第①类而言: 型6个；型3个，与其对称的3个；

型1个，与其对称的1个；型1个；共15个.同理,第②、③类也分别含15个，故上述三类平行四边形共45个.

[注]这样数平行四边行,很麻烦,又易出错.我们试图找到一种对应关系:先考虑任一边不与BC平行的平行四边形,延长各边必与BC有4个交点,特殊情况下,第二个交点与第三个交点重合；反过来，BC上的任意四点或三点决定一个平行四边形，也就是说，边不与BC平行的平行四边形的个数与BC上的四交点组和三交点组的数目一样多。

由于BC上有5个交点，其中可构成5个4点组；10个3点组，即边不平行于BC的平行四边形有15个。

同理分别考虑边不平行AB、CD的平行四边行。

由此可知，共有45个平行四边形。

———————————————答案——————————————————————

1. 90

利用例1和例4公式可直接计算:

(5+4+3+2+1)×(3+2+1)

=15×6

=90(个)

[注]注意,由长方形、正方形的意义可知，正方形一定是长方形，但反之不然.故求长方形个数时,不必把正方形分开考虑.

2. 3个正方形; 18个三角形; 6个平行四边形; 8个梯形.

3. 18

根据这个图形的特点,我们先数出下图(1)中长方形的个数为(2+1)×(2+1)=9个；然后在图(1)的内部添上一个长方形得到图(2).这时新产生的长方形有(2+1)×(2+1)=9个.至此已将图(1)还原为题图,同时题图中的长方形已全部数完.因此,原图中共有长方形.

(2+1)×(2+1)+ (2+1)×(2+1)=18(个).

(1) (2)

4. 16

具体分法如下图所示.基中小三角形有8个,由两个小三角形组成的三角形有4个,由四个小三角形组成的三角形有4个,所以共有三角形8+4+4=16(个).

5. 72

把图中最小三角形作为基数,然后按含有几个基数的三角形分类进行解答.

含一个基数的三角形,共有16个；含两个基数的三角形，共有24个；含四个基数的三角形，共有20个；含八个基数的三角形，共有8个；含十六个基数的三角形，共有4个.因此,整个图形中共有

16+24+20+8+4=72(个)三角形.

6. 6

图中的三角形可分成两种,一种是尖头向上的,一种是尖头向下的.从图上可以看出,每种三角形必须涂成同一颜色.为了使涂红色的三角形比涂蓝色的三角形多,尖头向上的三角形要涂红色.

每一横排,尖头向上的三角形要比尖头向下的三角形多一个,共有6排,因此,涂红色的比涂蓝色的三角形多6个.

7. 38

将原立体图形从左至右分类计算,共有16+9+5+7+1=38个.

8. 115

单独的一个4×4的方格中有12+22+32+42=30个正方形,两个4×4的方格如原图重叠后,重叠部分有5个正方形.所以原图中一共有30×4-5×3=115个正方形.

9. 6

根据标有相同数码的纸片不许靠在一起的条件，当M位置上放标有数码“3”的纸片时，其余两个标有数码“3”的纸片，只能放置在下面左右两边两个圆圈内.如下图所示.

这样圆圈绕M

,回到初始状态,可知共有六种不同的放

置方法.

10. 19

,则与所有的横边产生11个交点,与竖边至多9个交点,共20

如果直线与大正方形的一横边和一竖边有交点,则与横边至多产生10个交点,与竖边至多产生10个交点,共20个交点.

20个交点,将直线分成21部分,其中在大正方形有内有19部分,故至多穿过19个方格.

[注]穿过一个方格,在直线上截出一条线段,线段由直线上的交点决定,关键是求交点个数.

对小学生来说,通常总是从简单情况入手,即由1×1方格,2×2方格,3×3方格等的情况,归纳出一般的规律,从而得出10×10方格的结果.请同学们用归纳法试一试!

11. 最大边为7时,另两边之和为8,可构成4个(1+7,2+6,3+5,4+4)不同的三角形；最大边为6时，另两边之和为9，可构成2个（3+6，4+5）不同的三角形;最大边为5时,可构成1个(5+5)不同的三角形.所以一共可组成7个不同的三角形.

12. 由三角形的一边为11厘米,及其他边长必为1,2,.…，11厘米，根据三角形两边之和大于第三边的性质，可知两边之和应介于12厘米和22厘米之间（包含12厘米和22厘米）.这样,共可围成36个不同的三角形.

12:(1,11),(2,10),(3,9),(4,8),(5,7),(6,6)； 13:(2,11),(3,10),(4,9),(5,8),(6,7)； 14:(3,11),(4,10),(5,9),(6,8),(7,7)； 15:(4,11),(5,10),(6,9),(7,8)； 16:(5,11),(6,10),(7,9),(8,8)； 17:(6,11),(7,10),(8,9)； 18:(7,11),(8,10),(9,9)； 19:(8,11),(9,10)； 20:(9,11),(10,10)； 21:(10,11)； 22:(11,11)

所以，一共可以围成36个不同的三角形.

13. 为方便起见,不妨设原正方形的边长为3,则小正方形的边长是1,阴影三角形的面积是2

×2×3=3.所求的三角形可分两种情形:

(1)三角形的一边长为2,这边上的高是3.这时,长为2的边只能在原正方形的边上,这样的三角形有2×4×4=32(个)；

(2)三角形的一边长为3,这边上的高是2.这时长为3的边是原正方形的一边或平行于一边的分割线.其中与(1)重复的三角形不再算入,这样的三角形有8×2=16(个).

因此,所求的三角形共32+16=48(个)(包括图中开始给的三角形.) 14. 最多可以穿透7个小立方体.提示:仿题10.