数学建模过河

一、模型假设

由题中条件可解，不需假设其他外界条件

二、模型构成

记人、猫、鸡、米的数量分别为1x 、2x 、3x 、4x ，第k 次渡河前此岸的人、猫、鸡、米的数量分别为k S =（1x ，2x ，3x ，4x ），则彼岸的人、猫、鸡、米的数量分别为k S ’=（1-1x 、1-2x 、1-3x 、1-4x ）

由题中条件得在安全渡河条件下的允许状态合集

S ={(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0)}

及其相对应的S ’。不难验证，S 对此岸和彼岸都是安全的。

第k 次渡河时穿上的人、猫、鸡、米的数量分别为1u 、2u 、3u 、4u ，决策方案即为乘船方案k d =（1u ，2u ，3u ，4u ），允许决策合集为

D ={(1,1,0,0),(1,0,1,0),(1,0,0,1),(1,0,0,0)}

因为k 为奇数时船从此岸驶向彼岸，k 为偶数时船由彼岸驶回此岸，所以状态k S 随决策k d 变化的规律是

()k

d k k s k s 11-+=+ 求决策k d ∈D （k=1,2,...,n ），使状态k s ∈S 按照上式，由初始状态1s =（1,1,1,1）经有限步n 到达状态1+n s =（0,0,0,0）。

三、模型求解

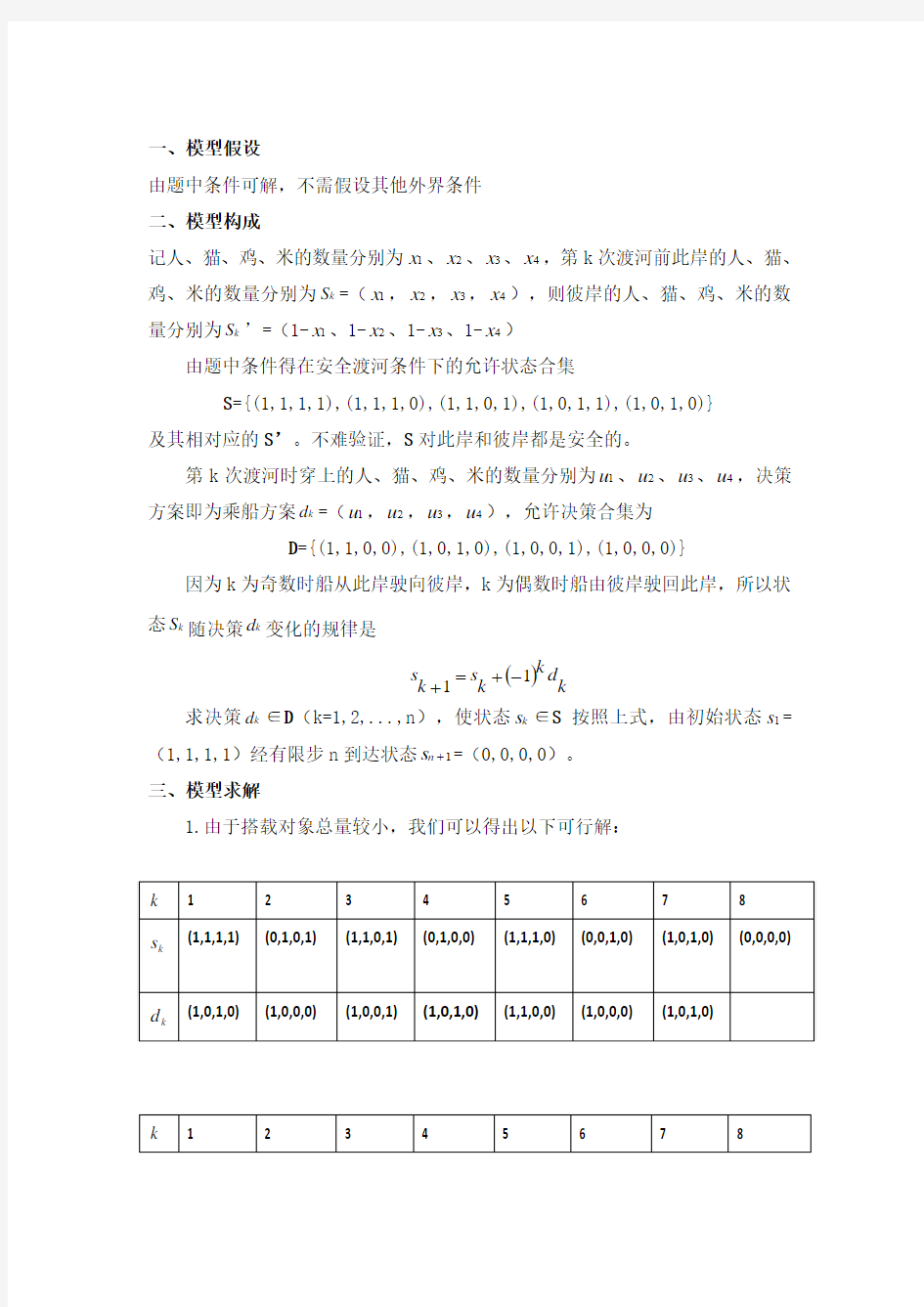
1.由于搭载对象总量较小，我们可以得出以下可行解：

2.若使用MATLAB编程

A向量定义为状态变量

B向量定义为运载变量

（1）xduhe.m文件：

clear;clc;

A=[1,1,1,1];

B=[1,0,1,0;1,1,0,0;1,0,0,1;1,0,0,0];

M=[1,1,1,0;0,0,0,1;1,1,0,1;0,0,1,0;1,0,1,1;0,1,0,0;1,0,1,0;0,1,0,1]; duhe(A,B,M,1);

（2）、duhe.m文件：

function duhe(L,B,M,s); [h,l]=size(L);

for k=s:h

for i=1:4

C=mod(L(k,:)+B(i,:),2);

if C==[0,0,0,0]

print(B(i,:),C,s);

fprintf('渡河成功\n\n');

break;

else if fuhe(C,M)==1

print(B(i,:),C,s);

S=[L;C];

if Panduan(S)==1

duhe(S,B,M,s+1);

else

fprintf('此渡河方案不可行\n\n'); end

end

end

end

End

（3）、fuhe.m文件：

function y=fuhe(C,M)

y=0;

for i=1:8

if(C==M(i,:))

y=1;

break;

end

end

（4）、Panduan.m文件：

function z=Panduan(S)

z=1;

[m,n]=size(S);

for p=1:m

for q=(p+1):m

if S(p,:)-S(q,:)==[0,0,0,0]

z=0;

break;

end

end

end

（5）、print.m文件：

function print(K,C,s)

fprintf('第%d次渡河:',s);

if K(1)==1

fprintf('人, ');

end

if K(2)==1

fprintf('猫, ');

end

if K(3)==1

fprintf('鸡, ');

end

if K(4)==1

fprintf('米, ');

end

if C(1)==0

fprintf('从左岸到达右岸\n');

else

fprintf('从右岸回到左岸\n');

End

四、模型分析

该问题的最优方案是：

①人先带鸡过河，然后人再回来，把米带过河，然后把鸡运回河岸，人再把猫带过河，最后人回来把鸡带过去。

②人先带鸡过河，然后人再回来，把猫带过河，然后把鸡运回河岸，人再把米带过河，最后人回来把鸡带过去。