常见均质刚体转动惯量的研究

常见均质刚体转动惯量的研究

胡辰

（陕西理工学院物理与电信工程学院物理学104班，陕西 汉中 72300）

指导老师：王亚辉

[摘要]本文通过对常见均质刚体转动惯量的研究，利用刚体在形状方面的联系，找出了能够代表一些常见均质

刚体的固定模型。通过对该模型转动惯量参量的变换，可以容易的得到相关均质刚体的转动惯量。这将方便了我们对转动惯量的计算和使用。

[关键词]均质刚体；转动惯量；模型

引言

转动惯量是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度。其量值取决于刚体的形状、质量分布及转轴的位置。对于转动惯量国内外主要集中于对其计算方法上的研究。文献中，对于转动惯量的计算主要有一下几种方法：积分法、质量投影法[1]

、垂直轴定理、平行轴定理、组合法[2]

、标度变换法[3]

、量纲分析法[4]

等。本文在刚体质量、转轴相同情况下，从形状入手。首先对常见均质刚体转动惯量进行计算与分析，利用不同刚体间在形状方面的联系，找出了能够代表一些常见均质刚体的固定模型。通过对该模型转动惯量参量的变换，便可以容易的得到相关均质刚体的转动惯量。这将使在使用过程中，我们只需要记住几个刚体模型转动惯量的表达式，就可以在应用中很方便地推出其它相关刚体的转动惯量，减小了工作量，使转动惯量使用更加容易和方便。

1 转动惯量概念的导出及其物理意义

若各质点绕共同的Z 轴作圆周运动，质点系对Z 轴角动量写作 i i i z v m r L ∑= （1.1）

将该式用于刚体，则刚体对轴角动量为

t v m L i i z ∑=，因i z i r t v ω=，故有 ()z

i

i

z r m L ω∑=

2

等式右方括号内为各质元质量与其到转轴垂直距离平方成积之和，

∑2

i

i r

m 叫作刚体对它转

动轴z 的转动惯量，用z I 表示[5]

?∑==dm r r m I i i z 22

（1.2）

转动惯量的单位是：2

m kg ? ，量纲为2

ML

转动惯量的物理意义可从刚体对转动轴角动量与平动动量的对比中得出，转动惯量相当于惯性质量m ，转动角速度对应于平动速度v ，诸如此类的对应关系还有，如：转动动能

22ωI E k =对应于平动动能22νm E k =，动量守恒定律∑=c mv （常量）对应于

∑=c I ω（常量）[6]，定轴转动定理αI M =对应于牛顿第二定律ma F =[7]。从这种相比

拟的关系中可以得到，转动惯量是表征转动中对一定轴转动惯性大小的量度。

2 对常见均质刚体转动惯量的计算

2.1 圆环的转动惯量

2.1.1 绕中心轴的转动惯量

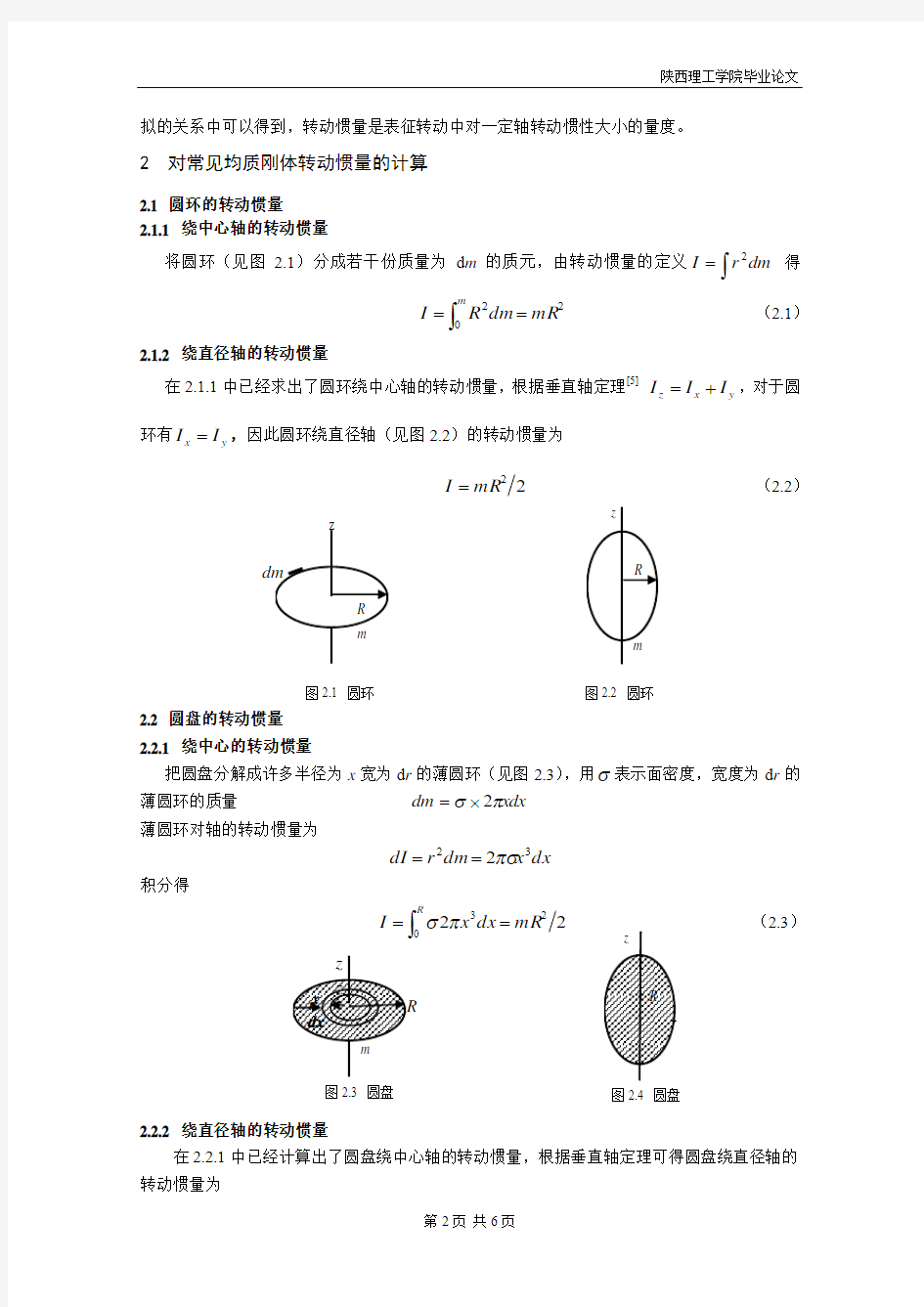
将圆环（见图 2.1）分成若干份质量为d m 的质元，由转动惯量的定义?

=dm r I 2

得

?==m

mR dm R I 0

22 （2.1）

2.1.2 绕直径轴的转动惯量

在2.1.1中已经求出了圆环绕中心轴的转动惯量，根据垂直轴定理[5] y x z I I I +=，对于圆环有y x I I =，因此圆环绕直径轴（见图2.2）的转动惯量为

22mR I = （2.2）

2.2 圆盘的转动惯量 2.2.1 绕中心的转动惯量

把圆盘分解成许多半径为x 宽为d r 的薄圆环（见图2.3），用σ表示面密度，宽度为d r 的薄圆环的质量 xdx dm πσ2?= 薄圆环对轴的转动惯量为

dx x dm r dI 322πσ==

积分得 22230

mR dx x I R

==?

πσ （2.3）

2.2.2 绕直径轴的转动惯量

在2.2.1中已经计算出了圆盘绕中心轴的转动惯量，根据垂直轴定理可得圆盘绕直径轴的转动惯量为

R

m

z 图2.2 圆环

图2.1 圆环

m

R

z

dm

R

z

图2.4 圆盘

图2.3 圆盘

m

R

r

z

z dx

x

42mR I = （2.4）

2.3 实心圆柱体的转动惯 2.

3.1 绕中心轴的转动惯量

在2.1.1中，已经计算了圆盘绕中心轴的转动惯量2

mR I =，因为对中心轴的转动惯量与厚度L 无关，因为厚度归并到质量中去了[6]。故以圆柱体的中心轴线为转轴（见图2.5）的转动惯量为

2mR I = （2.5）

2.3.2 绕中心直径的转动惯量

如图2.6，把圆柱分成若干份厚度为d x 的薄圆盘，设圆柱体密度为ρ，则薄圆盘质量为

dx R dm 2πρ=。已知薄圆盘绕直径轴的转动惯量42mR I =，根据平行轴定理2md I I c +=

得 dm x dm R dI 224+=

即

积分得

12

4)4(222

2

224

mL mR dx

x R R

I L L +=+=

?-πρρπ

2.4 环形圆盘的转动惯量 2.4.1 绕中心轴的转动惯量

如图2.7，把环形圆盘分成若干份半径为r 宽度为d x 的圆环，用σ表示环形圆盘密度。 则 dr r dm σπ2= 根据定义 dr r dm r dI 3

22πσ==

积分得 ?+==2

1

2)(22

2213

R R R R m dr r I σπ （2.7）

2.4.2 绕直径轴的转动惯量

在2.4.1中已经求出了环形圆盘绕中心轴的转动惯量2)(2

2211R R m I +=，根据垂直轴定理，得环形圆盘绕直径轴（见图2.8）的转动惯量为

4)(22

22

11R R m I I +== （2.8）

2.5 杆的转动惯量

如图2.7在棒上取长度元d x ，d x 距离转轴z 的距离为x ，则质量元dx dm λ=（L

m =λ图2.5 圆柱体

L

z

R

m

z

R

x L

m

图2.6 圆柱体

dx

dx x R dx R dI 2244πρρπ+=

（2.6）

为线密度），根据定义 ?

=dm r I 2

得 ?

=

=2

22

12

1

2L

mL dx r I λ （2.9）

3 模型类比推理

以上分别计算了圆环、圆盘、圆柱、环形圆盘、杆，等几种常见均质刚体绕不同轴的转动惯量。从刚体的形状上看，某些刚体之间可以通过形状的变换得到；从计算结果上看，在转轴类似的情况下，刚体的转动惯量之间存在着相等、相似、叠加等关系。如何寻找这种潜在的规律？已知，决定刚体转动惯量的三个重要因素是刚体的质量、刚体的形状、转动轴。所以，可以在刚体质量、转轴相同情况下，从形状入手。以上所计算的常见的均质刚体质量都为m ，转轴分为两类：或是中心轴线，或是中心直径。仔细分析，不难发现以上刚体可以通过空心圆柱体绕以下两类转轴（如图3.1）（如图3.2）变换得到。

空心圆柱体绕中心轴线转动时（见图3.1），它的转动惯量为

2)(2

221R R m I += [8]

（

3.1） 经参量变换，由（3.1）式可导出以下常见均质刚体绕中心轴线的转动惯量： ⑴ 当21R R =时，得到圆环（如图2.1）的转动惯量，2

mR I = ⑵ 当L =0，01=R 时，得到圆盘（如图2.3）的转动惯量，22

mR I =

⑶ 当01=R 时，得到实心圆柱体（如图2.5）的转动惯量，22mR I = ⑷ 当L =0时，得到环形圆盘（如图2.7）的转动惯量，2)(222

1R R m I +=

图2.7 环形圆盘

1R 2

R

z

m

dx

r

1R

2R

z

m

图2.8 环形圆盘

L

z

x dx 图2.9 杆

m

L

1R 2R

z 图3.1 空心圆柱体

z

1R 2R

m

L

图3.2 空心圆柱体

若空心圆柱体的转轴为中心直径时（见图3.2），它的转动惯量为

(

)

12

4

2

2

2

21mL

R R m I ++= （3.2）

由参量变换，从（3.2）式可导出以下常见均质刚体绕中心直径的转动惯量： ⑴当L =0，21R R =时，得到圆环（如图2.2）的转动惯量，22mR I = ⑵当L =0，01=R 时，得到圆盘（如图2.4）的转动惯量，42mR I =

⑶当01=R 时，得到实心圆柱体（如图2.6）的转动惯量，1242

2mL mR I +=

⑷当L=0时，得到环形圆盘（如图2.8）的转动惯量，4)(2

221R R m I +=

⑸当021==R R 时，得到棒（见图2.9）的转动惯量，122

mL I =

同理，我们还可以从均质六面体（见图3.3）的转动惯量[9]，导出其它常见的均质刚体的转动惯量。通过质量投影法和垂直轴定理可算得，均质六面体的转动惯量为

(

)

12

2

2

21L L m I += （3.3）

由均质六面体转动惯量的变换，可以得到一下几种刚体绕z 轴的转动惯量：

⑴当L L L L ===321时，得到正方体绕z 轴（见图3.4）的转动惯量，62

mL I =

⑵当01=L 时，得到长为2L ，宽为3L 的长方形（见图3.5）绕z 轴的转动惯量，122

2mL I = ⑶当3L =0时，得到长为1L ，宽为2L 的长方形（见图3.6）绕z 的转动惯量，12)(2

22

1L L m I +=

4 总结

转动惯量的计算方法居多，但有时为了方便我们没必要对常见均质刚体的转动惯量进行着个计算。因形状上的联系，这些常见均质刚体的转动惯量之间也存在联系。所以我们只需要掌握几个固定刚体模型的转动惯量表达式，就可以在应用中很方便地推出与其相关刚体的转动惯量。由以上讨论可知这些模型有空心圆柱体、六面体。除此外我们亦可由空心球体绕中心直径轴的转动惯量导出实心球、薄壁球壳、球面扇形体、贝球绕中心直径轴的转动惯量[10]。

m

1L

3L

2L

z

图3.3 六面体

m

L

z

图3.4 正方体

m

2L

3L

z

图3.5 长方形

m

2L

1L

z

图3.6 长方形

用这种思想方法来计算常见均质刚体的转动转动惯量，将会对转动惯量的学习、应用和从事相关的研究都具有一定的指导意义。

参考文献

[1]王永超.刚体转动惯量的质量投影法[J].大学物理,2010,1(9):37-39.

[2]王正清.普通物理: 力学[M] .北京: 高等教育出版社,1990. 220-230.

[3] Robert Rabinoff,俞志毅. 用标度变换求转动惯量[J]. 大学物理,1987,6 (7) : 31-32.

[4]杨忠.用量纲分析法求平面物体的转动惯量[J].大学物理,1997,16 (4) : 45-46.

[5]漆安慎,杜婵硬.普通物理学教程: 力学[M] .北京: 高等教育出版社，2005.222-224.

[6]郑祖诒.转动惯量及其计算[J]. 邯郸师专学报(自然科学报),1991,1 (2):13-14.

[7]张三慧.大学物理学: 力学、电磁学[M].北京: 清华大学出版社,2009.157-159.

[8][苏]A.A杰特拉夫, 亚沃尔斯基.物理学手册[M] .北京: 科学出版社,1986.62-67.

[9]周雪润.对几种刚体转动惯量的研究[J].贵阳学院学报(自然科学报),2011,6 (3) : 11-13.

[10]秦瑶.常见均质刚体转动惯量的求法讨论[J].大学物理,2002, 21(2) : 39-41.

Study on the rotational inertia of common uniform

rigid bodies

HU Chen

(Grade10,Class04,Major physics, School of physics and telecom engineering ,

Shaanxi University of Technology, Hanzhong723000, Shaanxi）

Tutor:WANG Yahui

[Abstract] In this paper, the rotational inertia of the common rigid uniform quality were to be https://www.360docs.net/doc/d918710244.html,ing the contact between the rigid body in shape, identified a fixed models which can represent some uniform common rigid body.By discussed the rotational inertia of the model .We can easily get the moment of inertia of some rigid which associated with the model.This will allow us in the course, you only need to remember a few formulas.

[Key words] Uniform rigid body; rotational inertia; shaft; model