Rosenbrock函数极小值

导数运用极大值与极小值(含答案)
极大值与极小值 一、基础过关 1.函数y =f (x )的定义域为(a ,b ),y =f ′(x )的图象如图,则函数y =f (x )在开区间(a ,b )内取得极小值的点有________个. 2.下列关于函数的极值的说法正确的是________.(填序号) ①导数值为0的点一定是函数的极值点; ②函数的极小值一定小于它的极大值; ③函数在定义域内有一个极大值和一个极小值; ④若f (x )在(a ,b )内有极值,那么f (x )在(a ,b )内不是单调函数. 3.函数y =x 3-3x 2-9x (-2
函数极小值
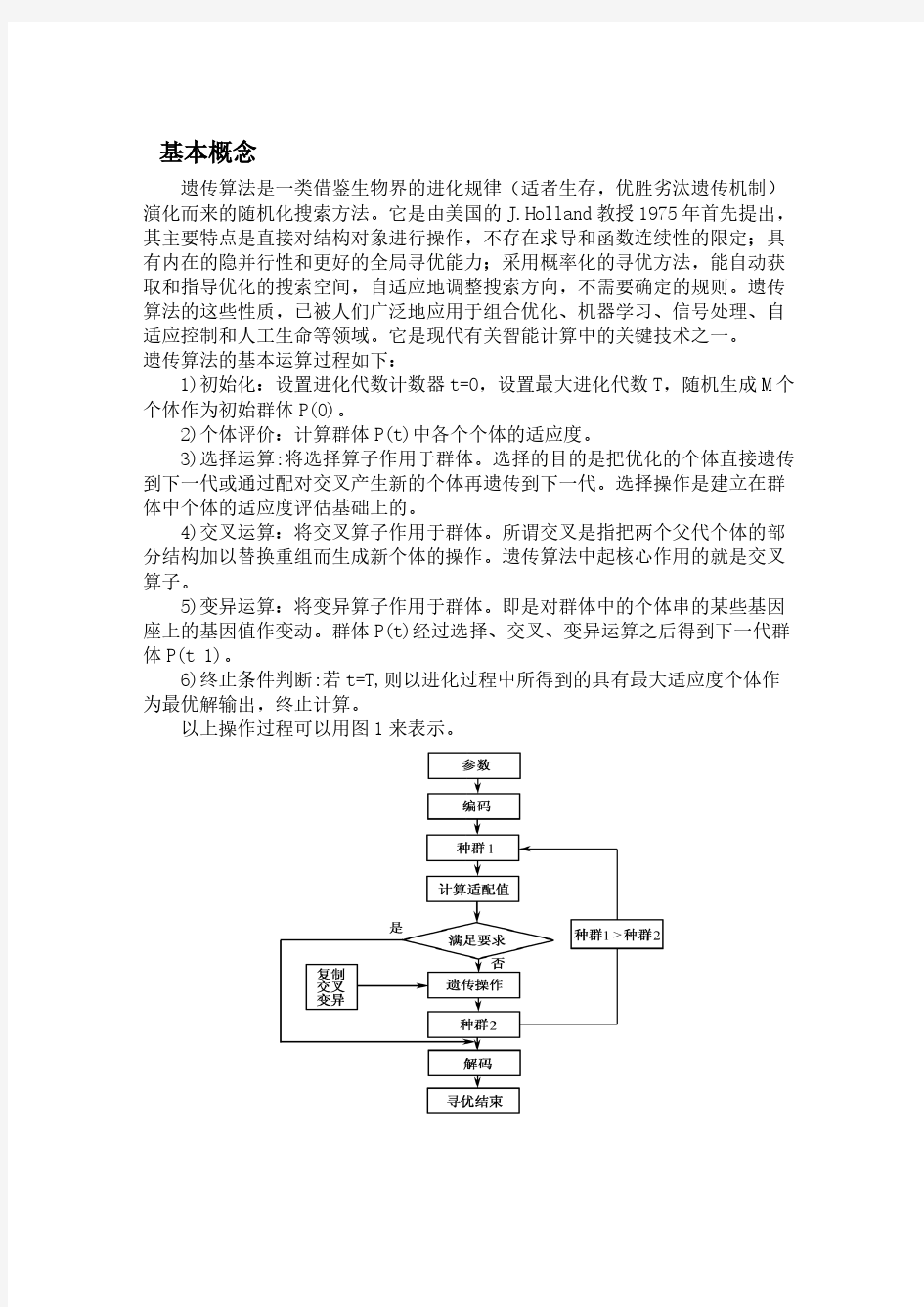
基本概念 遗传算法是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法。它是由美国的J.Holland教授1975年首先提出,其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。遗传算法的这些性质,已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。它是现代有关智能计算中的关键技术之一。 遗传算法的基本运算过程如下: 1)初始化:设置进化代数计数器t=0,设置最大进化代数T,随机生成M个个体作为初始群体P(0)。 2)个体评价:计算群体P(t)中各个个体的适应度。 3)选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。 4)交叉运算:将交叉算子作用于群体。所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。遗传算法中起核心作用的就是交叉算子。 5)变异运算:将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t 1)。 6)终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。 以上操作过程可以用图1来表示。
图1 遗传算法流程图 利用遗传算法求Rosenbrock 函数的极小值 求解该问题遗传算法的构造过程: (1)确定决策变量和约束条件; (2)建立优化模型; (3)确定编码方法 用长度为15位的二进制编码串来分别表示两个决策变量x1,x2。10位二进制编码串可以表示从0到2^15-1之间的个2^15不同的数,故将x1,x2的定义域离散化为1023个均等的区域,包括两个端点在内共有1024个不同的离散点。 从离散点-100到离散点100 ,分别对应于从000000000000000(0)到111111*********(1023)之间的二进制编码。 将x1,x2分别表示的两个15位长的二进制编码串连接在一起,组成一个30位长的二进制编码串,它就构成了这个函数优化问题的染色体编码方法。使用这种编码方法,解空间和遗传算法的搜索空间就具有一一对应的关系。 例如 x :000000000110111 000001101110001 表示一个个体的基因型,其中前10位表示x1,后10位表示x2 4)确定解码方法:解码时需要将30位长的二进制编码串切断为两个15位长的二进制编码串,然后分别将它们转换为对应的十进制整数代码,分别记为y1和y2。 依据个体编码方法和对定义域的离散化方法可知,将代码y 转换为变量x 的解码公式为 )2,1(1001 15^2200=--?=i yi xi 例如,对个体x :00000000110111 000001101110001 它由两个代码所组成 上述两个代码经过解码后,可得到两个实际的值239.722,247.891=-=x x (5) 确定个体评价方法:由于Rosenbrock 函数的值域总是非负的,并且优 化目标是求函数的最小值,故可将个体的适应度直接取为对应的目标函数值,即 选个体适应度的倒数作为目标函数 (6)设计遗传算子:选择运算使用比例选择算子,交叉运算使用单点交叉算子,变异运算使用基本位变异算子。 (7)确定遗传算法的运行参数:群体大小M=40,终止进化代数G=500,交叉???=≤≤--+-=)2,1(100100)1()(100),(212221212i x x x x x x f i 881 ,5521==y y ) ,()(21x x f x F =)(1)(x F x J =
梯度下降法求函数极小值
%%%%%%%%%%%%%%% 梯度下降法求函数极小值%%%%%%%%%%%%%%%%%% % 函数:f(x,y)=(x-2)^2+(y-4)^2 % 目的:求极小值和对应的极小值点坐标 % 方法:梯度下降法 % 理论: % 方向导数:偏导数反应的是函数沿坐标轴方向的变化率,但许多物理现象告诉我们,只考虑函数沿坐标轴方向的变化率是不够的,有必要研究函数沿任一指定方向的变化率。 % 函数f(x,y)在点P0(x0,y0)可微分,那么函数在改点沿任一方向l的方向导数存在,其值为: f'x(x0,y0)*cos(α)+f'y(x0,y0)*cos(β),其中,cos(α),cos(β)是方向l % 的方向余弦。 % 梯度:是与方向导数有关联的另一个概念,梯度是一个向量,表示为:f'x(x0,y0)*i+f'y(x0,y0)*j。 % 关系: % f'x(x0,y0)*cos(α)+f'y(x0,y0)*cos(β) % =grad f(x0,y0)*el % =|grad f(x0,y0)|*cos(θ),其中el=(cos(α),cos(β))是与方向l同方向的单位向量。 % 变化率:函数沿某个方向的变化率指的是函数值沿这个方向变化的快慢。 % θ=0,el与梯度同向,函数增加最快,函数在这个方向的方向导数达到最大值,这个最大值就是梯度的模;% θ=π,el与梯度反向,函数减少最快,函数在这个方向的方向导数达到最小值; % θ=π/2,el与梯度方向正交,函数变化率为零; %% clear
syms x y b f=2*(x-2)^2+(y-4)^2; %求解函数的极小值点 Grad=[diff(f,x),diff(f,y)]; %求梯度 eps=1e-3; v=[x,y]; v0=[0,0]; Grad0=subs(Grad,v,v0);%求V0的梯度值 M=norm(Grad0);%梯度的模,方向导数 n=0; %% while n<=100 d=-Grad0;%寻优搜索方向 fval=subs(f,v,v0);%函数值 %% %%%%%%%%%%%%%%%%%%%%%%%求出最优步长,然后确定下一刻的坐标点%%%%%%%%%%%%%%%%%%%%%%% %设步长变量为b,将v0=v0+b*d带入函数,求导,令导数等于零,解出最佳步长b1,此为一维寻优。得到下一刻坐标点v0=v0+b1*d ft=subs(f,v,v0+b*d);%将步长变量带入函数 dft=diff(ft);%求导 b1=solve(dft);%得到该方向的最优步长
例说求函数的最大值和最小值的方法
例说求函数的最大值和最小值的方法 例1.设x 是正实数,求函数x x x y 32+ +=的最小值。 解:先估计y 的下界。 55)1(3)1(5)21(3)12(222≥+- +-=+-+ ++-=x x x x x x x y 又当x =1时,y =5,所以y 的最小值为5。 说明 本题是利用“配方法”先求出y 的下界,然后再“举例”说明这个下界是可以限到的。“举例”是必不可少的,否则就不一定对了。例如,本题我们也可以这样估计: 77)1(3)1(7)21(3)12(222-≥-+ +-=-++ ++-=x x x x x x x y 但y 是取不到-7的。即-7不能作为y 的最小值。 例2. 求函数1 223222++--=x x x x y 的最大值和最小值。 解 去分母、整理得:(2y -1)x 2+2(y +1)x +(y +3)=0. 当2 1≠y 时,这是一个关于x 的二次方程,因为x 、y 均为实数,所以 ?=[2(y +1)]2-4(2y -1)(y +3)≥0, y 2+3y --4≤0, 所以 -4≤y ≤1 又当3 1-=x 时,y =-4;x =-2时,y =1.所以y min =-4,y max =1.
说明 本题求是最值的方法叫做判别式法。 例3.求函数152++-=x x y ,x ∈[0,1]的最大值 解:设]2,1[1∈=+t t x ,则x =t 2-1 y = -2(t 2-1)+5t = -2t 2+5t +1 原函数当t =169,45=x 即时取最大值8 33 例4求函数22 3,5212≤≤+--=x x x x y 的最小值和最大值 解:令x -1=t ( 121≤≤t ) 则t t t t y 4142+=+= y min =5 1,172max =y 例5.已知实数x ,y 满足1≤x 2+y 2≤4,求f (x )=x 2+xy +y 2的最小值和最大值 解:∵)(2 122y x xy +≤ ∴6)(23 ),(2222≤+≤++=y x xy y x y x f 又当2==y x 时f (x ,y )=6,故f (x ,y )max =6 又因为)(2122y x xy +- ≥
函数的极值和最值(讲解)
函数的极值和最值 【考纲要求】 1.掌握函数极值的定义。 2.了解函数的极值点的必要条件和充分条件. 3.会用导数求不超过三次的多项式函数的极大值和极小值 4.会求给定闭区间上函数的最值。 【知识网络】 【考点梳理】 要点一、函数的极值 函数的极值的定义 一般地,设函数)(x f 在点0x x =及其附近有定义, (1)若对于0x 附近的所有点,都有)()(0x f x f <,则)(0x f 是函数)(x f 的一个极大值,记作 )(0x f y =极大值; (2)若对0x 附近的所有点,都有)()(0x f x f >,则)(0x f 是函数)(x f 的一个极小值,记作 )(0x f y =极小值. 极大值与极小值统称极值. 在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值. 要点诠释: 求函数极值的的基本步骤: ①确定函数的定义域; ②求导数)(x f '; ③求方程0)(='x f 的根; ④检查'()f x 在方程根左右的值的符号,如果左正右负,则f(x)在这个根处取得极大值;如果左负右正,则f(x)在这个根处取得极小值.(最好通过列表法) 要点二、函数的最值 1.函数的最大值与最小值定理 若函数()y f x =在闭区间],[b a 上连续,则)(x f 在],[b a 上必有最大值和最小值;在开区间),(b a 内连 函数的极值和最值 函数在闭区间上的最大值和最小值 函数的极值 函数极值的定义 函数极值点条件 求函数极值
续的函数)(x f 不一定有最大值与最小值.如1 ()(0)f x x x = >. 要点诠释: ①函数的最值点必在函数的极值点或者区间的端点处取得。 ②函数的极值可以有多个,但最值只有一个。 2.通过导数求函数最值的的基本步骤: 若函数()y f x =在闭区间],[b a 有定义,在开区间(,)a b 内有导数,则求函数()y f x =在],[b a 上的最大值和最小值的步骤如下: (1)求函数)(x f 在),(b a 内的导数)(x f '; (2)求方程0)(='x f 在),(b a 内的根; (3)求在),(b a 内使0)(='x f 的所有点的函数值和)(x f 在闭区间端点处的函数值)(a f ,)(b f ; (4)比较上面所求的值,其中最大者为函数()y f x =在闭区间],[b a 上的最大值,最小者为函数 ()y f x =在闭区间],[b a 上的最小值. 【典型例题】 类型一:利用导数解决函数的极值等问题 例1.已知函数.,33)(23R m x x mx x f ∈-+=若函数1)(-=x x f 在处取得极值,试求m 的值,并求 )(x f 在点))1(,1(f M 处的切线方程; 【解析】2'()363,.f x mx x m R =+-∈ 因为1)(-=x x f 在处取得极值 所以'(1)3630f m -=--= 所以3m =。 又(1)3,'(1)12f f == 所以)(x f 在点))1(,1(f M 处的切线方程312(1)y x -=- 即1290x y --=. 举一反三: 【变式1】设a 为实数,函数()22,x f x e x a x =-+∈R . (1)求()f x 的单调区间与极值;
1.3.2函数的极大值与极小值同步检测
《函数的极大值与极小值》同步检测 一、基础过关 1.函数y =f (x )的定义域为(a ,b ),y =f ′(x )的图象如图,则函数y =f (x )在开区间(a ,b )内取得极小值的点有________个. 2.下列关于函数的极值的说法正确的是________.(填序号) ①导数值为0的点一定是函数的极值点; ②函数的极小值一定小于它的极大值; ③函数在定义域内有一个极大值和一个极小值; ④若f (x )在(a ,b )内有极值,那么f (x )在(a ,b )内不是单调函数. 3.函数y =x 3-3x 2-9x (-2 ①函数y =f (x )在区间????-3,-1 2内单调递增; ②函数y =f (x )在区间????-1 2,3内单调递减; ③函数y =f (x )在区间(4,5)内单调递增; ④当x =2时,函数y =f (x )有极小值; ⑤当x =-1 2时,函数y =f (x )有极大值. 则上述判断正确的是________.(填序号) 二、能力提升 8.若a >0,b >0,且函数f (x )=4x 3-ax 2-2bx +2在x =1处有极值,则ab 的最大值等于________. 9.若函数y =x 3-3ax +a 在(1,2)内有极小值,则实数a 的取值范围是________. 10.求下列函数的极值: (1)f (x )=x 3-12x ; (2)f (x )=x 3-2 2(x -1)2 . 11.已知f (x )=x 3+12mx 2-2m 2x -4(m 为常数,且m >0)有极大值-5 2,求m 的值. 12.设a 为实数,函数f (x )=x 3-x 2-x +a . (1)求f (x )的极值; (2)当a 在什么范围内取值时,曲线y =f (x )与x 轴仅有一个交点? 三、探究与拓展 13.已知函数f (x )=(x 2+ax -2a 2+3a )e x (x ∈R ),其中a ∈R . (1)当a =0时,求曲线y =f (x )在点(1,f (1))处的切线的斜率; (2)当a ≠2 3 时,求函数f (x )的单调区间与极值. 函数的最大值和最小值教案 1.本节教材的地位与作用本节主要研究闭区间上的连续函数最大值和最小值的求法和实际应用,分两课时,这里是第一课时,它是在学生已经会求某些函数的最值,并且已 经掌握了性质:“如果f(x)是闭区间[a,b]上的连续函数,那么 f(x)在闭区间[a,b]上有最大值和最小值” ,以及会求可导函数的极值之后进行学习的,学好这一节,学生将会求更多的函数的 最值,运用本节知识可以解决科技、经济、社会中的一些如何使成本最低、产量最高、效益最大等实际问题.这节课集中体现了数形结合、理论联系实际等重要的数学思想方法,学好本节,对于进一步完善学生的知识结构,培养学生用数学的意识都具有极为重要的意义. 2.教学重点会求闭区间上连续开区间上可导的函数的最值. 3.教学难点高三年级学生虽然已经具有一定的知识基础,但由于对求函数极值还不熟练,特别是对优 化解题过程依据的理解会有较大的困难,所以这节课的难点是理解确定函数最值的方法. 4.教学关键本节课突破难点的关键是:理解方程f′(x)=0的解,包含有指定区间内全部可能的极值点. 【教学目标】根据本节教材在高中数学知识体系中的地位和作用,结合学生已有的认知水平,制定本节如下的 教学目标: 1.知识和技能目标 (1)理解函数的最值与极 值的区别和联系. (2)进一步明确闭区间[a,b]上的连续函数 f(x),在[a,b]上必有最大、最小值. (3)掌握用导数法求上述 函数的最大值与最小值的方法和步骤. 2.过程和方法目标(1)了解开区间内的连续函数或闭区间上的不连续函数不一定有 最大、最小值. (2)理解闭区间上的连续函数最值存在的可能 位置:极值点处或区间端点处. (3)会求闭区间上连续,开区 间内可导的函数的最大、最小值. 3.情感和价值目标 (1) 认识事物之间的的区别和联系. (2)培养学生观察事物的能力,能够自己发现问题,分析问题并最终解决问题. (3)提高 学生的数学能力,培养学生的创新精神、实践能力和理性精神. 【教法选择】根据皮亚杰的建构主义认识论,知识是个体在 与环境相互作用的过程中逐渐建构的结果,而认识则是起源于主 客体之间的相互作用. 本节课在帮助学生回顾肯定了闭区间 上的连续函数一定存在最大值和最小值之后,引导学生通过观察 闭区间内的连续函数的几个图象,自己归纳、总结出函数最大值、最小值存在的可能位置,进而探索出函数最大值、最小值求解的 方法与步骤,并优化解题过程,让学生主动地获得知识,老师只是 进行适当的引导,而不进行全部的灌输.为突出重点,突破难点, 这节课主要选择以合作探究式教学法组织教学. 【学法指导】对于求函数的最值,高三学生已经具备了良好的知识基础,剩下 的问题就是有没有一种更一般的方法,能运用于更多更复杂函数 的求最值问题?教学设计中注意激发起学生强烈的求知欲望,使 得他们能积极主动地观察、分析、归纳,以形成认识,参与到课堂 3.8函数的最大值和最小值(第1课时) 嵊州市马寅初中学袁利江 【教学目标】 根据本节教材在高中数学知识体系中的地位和作用,结合学生已有的认知水平,制定本节如下的教学目标: 1.知识和技能目标 (1)理解函数的最值与极值的区别和联系. (2)进一步明确闭区间[a,b]上的连续函数f(x),在[a,b]上必有最大、最小值. (3)掌握用导数法求上述函数的最大值与最小值的方法和步骤. 2.过程和方法目标 (1)了解开区间内的连续函数或闭区间上的不连续函数不一定有最大、最小值. (2)理解闭区间上的连续函数最值存在的可能位置:极值点处或区间端点处. (3)会求闭区间上连续,开区间内可导的函数的最大、最小值. 3.情感和价值目标 (1)认识事物之间的的区别和联系. (2)培养学生观察事物的能力,能够自己发现问题,分析问题并最终解决问题. (3)提高学生的数学能力,培养学生的创新精神、实践能力和理性精神. 【教学重点】 会求闭区间上连续开区间上可导的函数的最值. 【教学难点】 高三年级学生虽然已经具有一定的知识基础,但由于对求函数极值还不熟练,特别是对优化解题过程依据的理解会有较大的困难,所以这节课的难点是理解确定函数最值的方法.【难点突破】 本节课突破难点的关键是:理解方程f′(x)=0的解,包含有指定区间内全部可能的极值点.【教法选择】 根据皮亚杰的建构主义认识论,知识是个体在与环境相互作用的过程中逐渐建构的结果,而认识则是起源于主客体之间的相互作用. 本节课在帮助学生回顾肯定了闭区间上的连续函数一定存在最大值和最小值之后,引导学生通过观察闭区间内的连续函数的几个图象,自己归纳、总结出函数最大值、最小值存在的可能位置,进而探索出函数最大值、最小值求解的方法与步骤,并优化解题过程,让学生主动地获得知识,老师只是进行适当的引导,而不进行全部的灌输.为突出重点,突破难点,这节课主要选择以合作探究式教学法组织教学. 【学法指导】 对于求函数的最值,高三学生已经具备了良好的知识基础,剩下的问题就是有没有一种更一般的方法,能运用于更多更复杂函数的求最值问题?教学设计中注意激发起学生强烈的求知欲望,使得他们能积极主动地观察、分析、归纳,以形成认识,参与到课堂活动中,充分发挥他们作为认知主体的作用. 专项训练:导数的极大值与极小值 一、单选题 1.已知函数f(x)=x ln x-a e x(e为自然对数的底数)有两个极值点,则实数a的取值范围是( ) A.B.(0,e) C.D.(-∞,e) 2.函数y=xe x的最小值是( ) A.-1B.-e C.-D.不存在 3.当函数y=x·2x取极小值时,x=( ) A.B.- C.-ln 2D.ln 2 4.已知函数,则() A.有个零点B.在上为减函数 C.的图象关于点对称D.有个极值点 5.设a∈R,若函数y=e ax+3x,x∈R有大于零的极值点,则( ) A.a>-3B.a<-3 C.a>-D.a<- 6.当函数y=x·2x取极小值时,x=( ) A.B.- C.-ln 2D.ln 2 7.已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( ) A.?x0∈R,f(x0)=0 B.函数y=f(x)的图像是中心对称图形 C.若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)单调递减 D.若x0是f(x)的极值点,则f′(x0)=0 8.若函数,当时,函数的单调减区间和极小值分别为() A.,B.,C.,D., 9.若函数在上有最小值,则实数的取值范围是()A.B.C.D. 10.已知在上递减的函数,且对任意的,总有,则实数的取值范围为() A.B.C.D. 11.若函数,当时,函数的单调减区间和极小值分别为() A.B.C.D. 12.若函数在上恰有两个极值点,则的取值范围为() A.B.C.D. 13.已知是常数,函数的导函数的图像如图所示,则函数的图像可能是() A.B.C. D. 14.已知,函数,若在上是单调减函数,则的取值范围是( ) A.B.C.D. 15.设,则函数 A.仅有一个极小值B.仅有一个极大值 C.有无数个极值D.没有极值 16.若函数在内有且仅有一个极值点,则实数的取值范围是() 导数在函数求最大值和最小值中的应用 例1.求函数f (x )=5x + . 解析:由3040x x +??-? ≥≥得f (x )的定义域为-3≤x ≤4,原问题转化为求f (x )在区间[-3, 4]上的最值问题。 ∵ y ’=f ’(x ) =5 在[-3,4]上f ’(x )>0恒成立, ∴ f (x )在[-3,4]上单调递增. ∴ 当x =-3时y min =-15-7, 当x =4时y max =20+27, ∴ 函数的值域为[-15-7,20+27]. 例2.设32f (a ),f (-1) 4.3.2 函数的极大值和极小值 教学目标: 1.理解极大值、极小值的概念; 2.能够运用判别极大值、极小值的方法来求函数的极值; 3.掌握求可导函数的极值的步骤; 教学重点:极大、极小值的概念和判别方法,以及求可导函数的极值的步骤. 教学难点:对极大、极小值概念的理解及求可导函数的极值的步骤. 教学过程: 一.创设情景 观察图3.3-8,我们发现,t a =时,高台跳水运动员距水面高度最大.那么,函数()h t 在此点的导数是多少呢?此点附近的图像有什么特点?相应地,导数的符号有什么变化规律? 放大t a =附近函数()h t 的图像,如图3.3-9.可以看出()h a ';在t a =,当t a <时,函数()h t 单调递增,()0h t '>;当t a >时,函数()h t 单调递减,()0h t '<;这就说明,在t a =附近,函数值先增(t a <,()0h t '>)后减(t a >,()0h t '<).这样,当t 在a 的附近从小到大经过a 时,()h t '先正后负,且()h t '连续变化,于是有()0h a '=. 对于一般的函数()y f x =,是否也有这样的性质呢? 附:对极大、极小值概念的理解,可以结合图象进行说明.并且要说明函数的极值是就函数在某一点附近的小区间而言的. 从图象观察得出,判别极大、极小值的方法.判断极值点的关键是这点两侧的导数异号 二.新课讲授 1.问题:图 3.3-1(1),它表示跳水运动中高度h 随时间t 变化的函数 2() 4.9 6.510 h t t t =-++的图像,图3.3-1(2)表示高台跳水运动员的速度v 随时间t 变化的函数'()()9.8 6.5v t h t t ==-+的图像. 运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别? 通过观察图像,我们可以发现: (1) 运动员从起点到最高点,离水面的高度h 随时间t 的增加而增加,即()h t 是 增函数.相应地,' ()()0v t h t =>. (2) 从最高点到入水,运动员离水面的高度h 随时间t 的增加而减少,即()h t 是 减函数.相应地,'()()0v t h t =<. 2.函数的单调性与导数的关系 观察下面函数的图像,探讨函数的单调性与其导数正负的关系. 如图 3.3-3,导数'0()f x 表示函数()f x 在点00(,)x y 处的切线的斜率.在0x x =处, 二次函数的最大值和最小值问题 ————————————————————————————————作者: ————————————————————————————————日期: 二次函数的最大值和最小值问题 高一数学组主讲人---------蒋建平 本节课的教学目标: 重点:掌握闭区间上的二次函数的最值问题 难点:理解并会处理含参数的二次函数的最值问题 核心: 区间与对称轴的相对位置 思想: 数形结合、分类讨论 一、复习引入 1、二次函数相关的知识点回顾。 (1)二次函数的顶点式: (2)二次函数的对称轴: (3)二次函数的顶点坐标: 2、函数的最大值和最小值的概念 设函数)(x f 在0x 处的函数值是)(0x f ,如果不等式)()(0x f x f ≥对于定义域内任意x 都成立,那么)(0x f 叫做函数)(x f y =的最小值。记作)(0min x f y = 如果不等式)()(0x f x f ≤对于定义域内任意x 都成立,那么)(0x f 叫做函数)(x f y =的最小值。记作)(0max x f y = 二、新课讲解:二次函数最大值最小值问题探究 类型一:无限制条件的最大值与最小值问题 例1、(1)求二次函数322 ++-=x x y 的最大值 . (2)求二次函数x x y 422-=的最小值 . 本题小结:求无条件限制时二次函数最值的步骤 1、配方,求二次函数的顶点坐标。 2、根据二次函数的开口方向确定是函数的最大值还是最小值。 3、求出最值。 类型二:轴定区间定的最大值与最小值问题 例2、(1)求函数])1,3[(,232-∈-+=x x x y 的最大值 ,最小值 . (2)求函数])3,1[(232∈-+=x x x y 的最大值 ,最小值 . (3)求函数])2,5[(232 --∈-+=x x x y 的最大值 与最小值 . 本题小结:求轴定区间定时二次函数最值的步骤 1、配方,求二次函数的顶点坐标或求对称轴,画简图。 2、判断顶点的横坐标(对称轴)是否在闭区间内。 3、计算闭区间端点的值,并比较大小。 类型三:轴动区间定的最大值与最小值问题 例3、求函数)(32R a ax x y ∈++=在]1,1[-上的最大值。 《3.3.2 函数的极大值和极小值》教案 教学目标: 1.理解极大值、极小值的概念; 2.能够运用判别极大值、极小值的方法来求函数的极值; 3.掌握求可导函数的极值的步骤; 教学重点: 极大、极小值的概念和判别方法,以及求可导函数的极值的步骤. 教学难点: 对极大、极小值概念的理解及求可导函数的极值的步骤. 教学过程: 一.创设情景 观察图3.3-8,我们发现,t a =时,高台跳水运动员距水面高度最大.那么,函数()h t 在此点的导数是多少呢?此点附近的图像有什么特点?相应地,导数的符号有什么变化规律? 放大t a =附近函数()h t 的图像,如图3.3-9.可以看出()h a ';在t a =,当t a <时,函数()h t 单调递增,()0h t '>;当t a >时,函数()h t 单调递减,()0h t '<;这就说明,在t a =附近,函数值先增(t a <,()0h t '>)后减(t a >,()0h t '<).这样,当t 在a 的附近从小到大经过a 时,()h t '先正后负,且()h t '连续变化,于是有()0h a '=. 对于一般的函数()y f x =,是否也有这样的性质呢? 附:对极大、极小值概念的理解,可以结合图象进行说明.并且要说明函数的极值是就函数在某一点附近的小区间而言的. 从图象观察得出,判别极大、极小值的方法.判断极值点的关键是这点两侧的导数异号 二.新课讲授 1.问题:图 3.3-1(1),它表示跳水运动中高度h 随时间t 变化的函数2() 4.9 6.510h t t t =-++的图像,图3.3-1(2)表示高台跳水运动员的速度v 随时间t 变化的函数' ()()9.8 6.5v t h t t ==-+的图像. 【学习目标】 1.理解极大值、极小值的概念. 2.能够运用判别极大值、极小值的方法来求函数的极值. 3.掌握求可导函数的极值的步骤 【重点与难点】 极大、极小值的概念和判别方法,以及求可导函数的极值的步骤 【学法提示】 讲练结合 【课前预习】 用导数法求下列函数的单调区间. (1) 2()2f x x x =-- (2)311433 y x x = -+ 1.极大值: 2.极小值: 3.极大值与极小值统称为极值 取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值。请注意以下几点: (ⅰ)极值是一个局部概念由定义,并不意味着它在函数的整个的定义域内最大或最小 (ⅱ)函数的极值不是唯一的即函数在某区间上或定义域内极大值或极小值可以不止一个 (ⅲ)极大值与极小值之间无确定的大小关系即一个函数的极大值未必大于极小值,如下图所示,1x 是极大值点,4x 是极小值点,而)(4x f >)(1x f (ⅳ)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点 4. 判别f (x 0)是极大、极小值的方法: 若0x 满足 0)(0='x f ,且在0x 的两侧)(x f 的导数异号,则0x 是)(x f 的极值点,)(0x f 是极值,并且如果)(x f '在0x 两侧满足“左正右负”,则0x 是)(x f 的极大值点,)(0x f 是极大值;如果)(x f '在0x 两侧满足“左负右正”,则0x 是)(x f 的极小值点,)(0x f 是极小值 5. 求可导函数f (x )的极值的步骤: (1)确定函数的定义区间,求导数/()f x (2)求方程/()f x =0的根 (3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列表.检查/()f x 在方程根左右的值的符号,若左正右负,那么f (x )在这个根处取得极大值;若左负右 § 4函数的最大值最小值问题 最值与极值的重要区别: 极值是一点X 。局部的形态; 最值是某区间整体的形态。 先讨论必要 性: X 。是f (x)在(a b 内的最大(小)值, =X 。必是f (x)在(a,b)的极大(小)值点, =X 。是f (x)的稳定点或不可导点. 稳定点 f(x)在[a,b ]的可能的最值点:S 不可导点 ,区间端点 F 面就两种常见的情形给出判别法,以最大值为例说明. 1 ?闭区间情形 设f (x)在a,b 1连续,这时f (x)在l.a, b 1必有最大值. 则将所有稳定点、不可导点和区间端点的函数值进行比较 (如果可能的 话),最大者即是最大值. 2.开区间情形 设f(x)在(a,b)可导,且在(a,b)有最大值.若在(a,b)内有唯一的 稳定点X 。,则X 。是最大值点. 注意强调最值的存在性 例1 一块边长为a 的正方形,在四个角上截去同样大小的正方形, 做成无盖的盒,问截去多大的小方块能使盒的容积最大? 图5-13 解设x为截去的小方块的边长,则盒的容积为 V(x)二x(a 2,) ,x 100,) 显然,V(x)在(0,a)可导,且 2 ' 2 V (x) =(a _2x) _4x(a _2x) =(a_2x)(a _6x) 令V (x) = 0得x =—或x =—。因此在(0,—)中有唯一一的稳定点—o 2 6 2 6 由实际问题本身知V(x)在(0,-)中必有最大值,故知最大值为 2 V(—) -a3。即截去的小的方块边长为-时,盒的容积最大。 6 2 7 6 例2求函数f (x) = 2x3 -9x2 +12x在1-1,3】的最大值和最小值 解2x3-9x212x =x 2(x-9)2 15, IL 4 8 因此f(x) =(2x3-9x2 12x)sgnx,x 〔-1,3 1, f (x) =(6x2-18x 12)sgn x = 6(x-1)(x -2)sgn x, x (T,0) _? (0,3) 故f (x)的稳定 点为x=1,x=2,不可导为x=0。 比较所有可能的最值点的函数值: f(-1)= 2 3f, (0) f 0, =(1f) 5〒(f2) =4, 即得最大值为f(-1) = 23,最小值为f(0)=0。 例3 在正午时,甲船恰在乙船正南82处,以速度V1=20km h向正东开出;乙船也正以速度v =16km h向正南开去(图5—15).已知两船航向不变,试证:下午二时,两船相距最近. 3.3.2 极大值与极小值 1.函数f(x)=x 3-3x 的极小值为________. 解析:令f′(x)=3x 2-3=0,得x =±1,可求得f(x)的极小值为f(1)=-2. 答案:-2 2.函数f(x)=x 3-12x 的极大值与极小值之和为________. 解析:函数的定义域为R ,f′(x)=3x 2-12,令f′(x)=0,解得x 1=-2或x 2=2.列表: x (-∞,-2) -2 (-2,2) 2 (2,+∞) f′(x) + 0 - 0 + f(x) ↗ 极大值 16 ↘ 极小值 -16 ↗ ∴当x =-2时,函数有极大值f(-2)=16.当x =2时,函数有极小值f(2)=-16. ∴极大值与极小值之和为f(2)+f(-2)=0. 答案:0 3.已知命题甲:f′(x 0)=0,命题乙:点x 0是可导函数f(x)的极值点,则甲是乙的________条件.(填充分不必要,必要不充分或充要) 解析:f ′(x 0)=0不能得出点x 0是可导函数f(x)的极值点,即甲不是乙的充分条件;但点x 0是可导函数f(x)的极值点可得出f′(x 0)=0,故甲是乙的必要条件. 答案:必要不充分 4.若函数f(x)=x 3+mx 2-m 2x +1(m 为常数,且m>0)有极大值9,则m 的值是________. 解析:由f′(x)=3x 2+2mx -m 2=(x +m)(3x -m)=0,得x =-m 或x =1 3m , 当x 变化时,f′(x)与f(x)的变化情况如下表: x (-∞,-m) -m ? ???-m ,13m 1 3m ??? ?13m ,+∞ f′(x) + - + 导数--函数的最大值与最小值练习题 【典型例题】 例1:求下列各函数的最值: (1)()[]32362,1,1f x x x x x =-+-∈-;(2)( )[]0,4f x x x =+∈。 例2:设 213a <<,函数()3232f x x ax b =-+在区间[]1,1-上的最大值为1 ,最小值为数的解析式。 【当堂练习】 1、函数()3223125f x x x x =--+在区间[]0,3上的最大值和最小值分别是( ) A 、5,15- B 、5,4- C 、4,15-- D 、5,15-- 2、函数()[],0,4x f x x e x -=?∈的最大值为( ) A 、0 B 、 1 e C 、 4 4e D 、 2 2e 3、已知函数()2 23f x x x =--+在[],2a 上的最大值为154 ,则a =( ) A 、32- B 、12 C 、12- D 、12-或32 - 4、若函数()1sin sin 33f x a x x =+在3 x π =处有最值,则a =( ) A 、2 B 、1 C D 、0 5、当0,2x π?? ∈ ???时,函数()()sin f x tx x t R =-∈的值恒小于零,则t 的取值范围是( ) A 、2t π≤ B 、2t π≤ C 、2t π≥ D 、2 t π< 6、点P 是曲线2ln 2y x =-上任意一点,则点P 到直线y x =-的最小距离为( ) A 、 4 B 、 4 C D 7.下列说法正确的是 A.函数的极大值就是函数的最大值 B.函数的极小值就是函数的最小值 C.函数的最值一定是极值 D.在闭区间上的连续函数一定存在最值 8.函数y =f (x )在区间[a ,b ]上的最大值是M ,最小值是m ,若M =m ,则f ′(x ) A.等于0 B.大于0 C.小于0 D.以上都有可能 9.函数y = 2 342 13141x x x ++,在[-1,1]上的最小值为( ) A.0 B.-2 C.-1 D.12 13 10.函数y =1 22+-x x x 的最大值为( )A.33 B.1 C.21 D. 2 3 11.设y =|x |3,那么y 在区间[-3,-1]上的最小值是( )A.27 B.-3 C.-1 D.1 12.设f (x )=ax 3-6ax 2+b 在区间[-1,2]上的最大值为3,最小值为-29,且a >b ,则( ) A.a =2,b =29 B.a =2,b =3 C.a =3,b =2 D.a =-2,b =-3 二、填空题 13.函数y =2x 3-3x 2-12x +5在[0,3]上的最小值是___________. 14.函数f (x )=sin2x -x 在[- 2π,2 π ]上的最大值为_____;最小值为____ 15.将正数a 分成两部分,使其立方和为最小,这两部分应分成____和____. 16.使内接椭圆22 22b y a x +=1的矩形面积最大,矩形的长为_____,宽为______ 17.在半径为R 的圆内,作内接等腰三角形,当底边上高为______时,它的面积最大. 18、函数()3 2 43365f x x x x =+-+在[)2,-+∞上的最大值为 ,最小值为 。 19、若函数()3 32f x x x m =+ +在[]2,1-上的最大值为9 2,则m = 。 20、设函数()3 31f x ax x =-+对于任意[]1,1x ∈-,都有()0f x ≥成立,则a = 。 21、已知()()()2 4 f x x x a =--,若()10f '-=,求()f x 在[]2,2-上的最大值和最小值。 三、解答题 22、已知0a >,函数()ln f x x ax =-。 (1)设曲线()y f x =在点()( ) 1,1f 处的切线为l ,若l 与圆()2 2 11x y ++=相切,求a 的值;(2) 求()f x 的单调区间;(3)求函数()f x 在(]0,1上的最大值。 23.一条水渠,断面为等腰梯形,如图所示,在确定断面尺寸时,希望在断面ABCD 的面积为定值S 时,使得湿周l =AB +BC +CD 最小,这样可使水流阻力小,渗透少,求此时的高h 和下底边长b . b函数的最大值和最小值教案.doc
函数的最大值和最小值(教案与课后反思)
函数的极大值与极小值
导数在函数求最大值和最小值中的应用解读
函数的极大值和极小值
二次函数的最大值和最小值问题
《3.3.2 函数的极大值和极小值》教案
函数的极大值、极小值
函数的最大值最小值问题
苏教版数学高二- 选修1-1试题 极大值与极小值
导数--函数的最大值与最小值练习题
