二次函数中的存在性问题讲义及答案

二次函数中的存在性问题（讲义）

一、知识点睛

解决“二次函数中存在性问题”的基本步骤：

①____________．研究确定图形，先画图解决其中一种情形．

②____________.先验证①的结果是否合理，再找其他分类，

类比第一种情形求解．

③____________.结合点的运动范围，画图或推理，对结果

取舍．

二、精讲精练

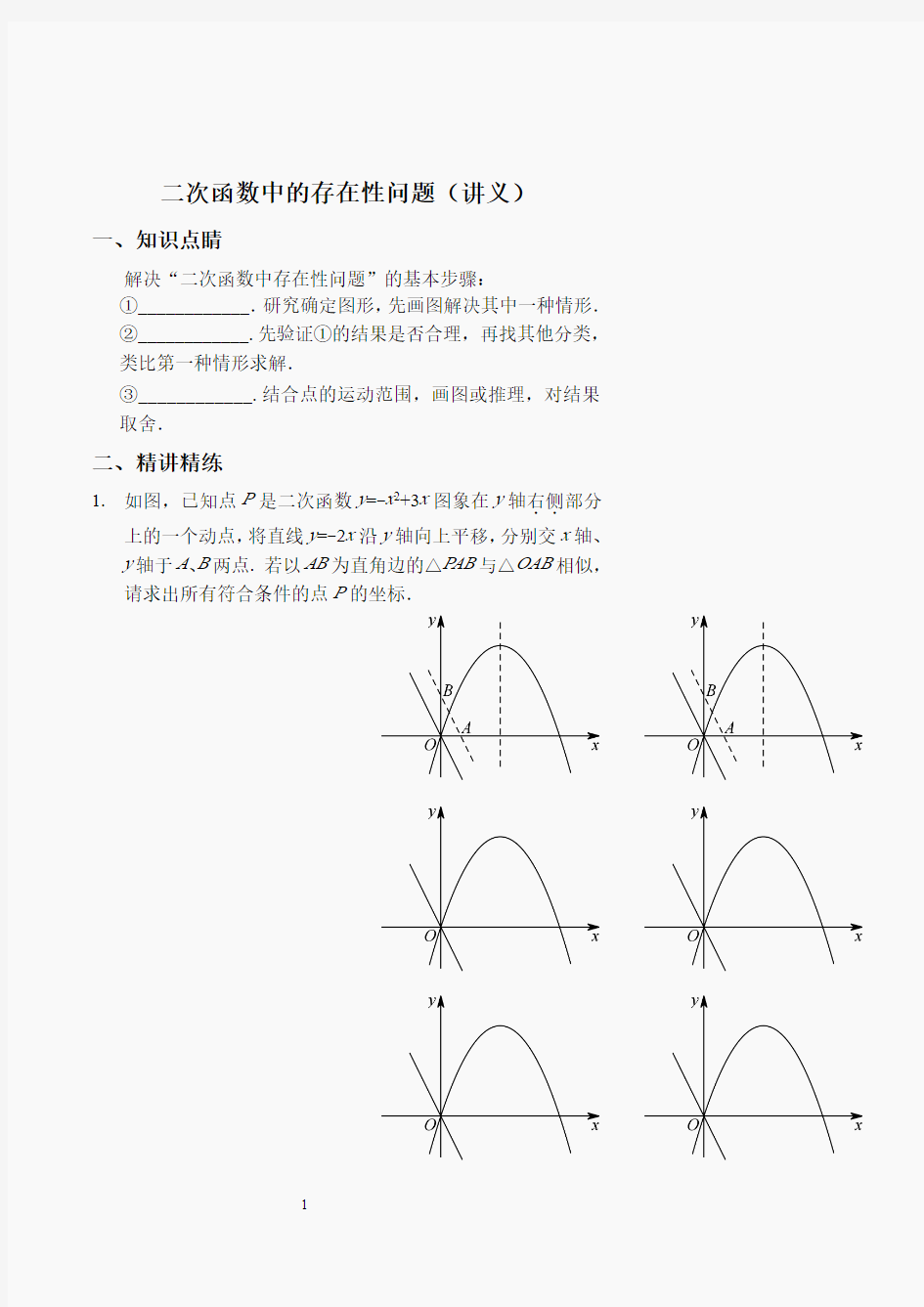
1.如图，已知点P是二次函数y=-x2+3x图象在y轴右侧

．．部分上的一个动点，将直线y=-2x沿y轴向上平移，分别交x轴、y轴于A、B两点.若以AB为直角边的△P AB与△OAB相似，请求出所有符合条件的点P的坐标．

2.抛物线()21134

y x =--+与y 轴交于点A ，顶点为B ，对称轴BC 与x 轴交于点C ．点P 在抛物线上，直线PQ //BC 交x 轴于点Q ，连接BQ ．

（1）若含45°角的直角三角板如图所示放置，其中一个顶点与点C 重合，直角顶点D 在BQ 上，另一个顶点E 在PQ 上，求直线BQ 的函数解析式；

（2）若含30°角的直角三角板的一个顶点与点C 重合，直角顶点D 在直线BQ 上（点D 不与点Q 重合），另一个顶点E 在PQ 上，求点P 的坐标．

3.如图，矩形OBCD 的边OD 、OB 分别在x 轴正半轴和y 轴

负半轴上，且OD ＝10，OB ＝8．将矩形的边BC 绕点B 逆时针旋转，使点C 恰好与x 轴上的点A 重合．

（1）若抛物线c bx x y ++-=23

1经过A 、B 两点，则该抛物线的解析式为______________________；

（2）若点M 是直线AB 上方抛物线上的一个动点，作MN ⊥x 轴于点N ．是否存在点M ，使△AMN 与△ACD 相似？若存在，求出点M 的坐标；若不存在，说明理由．

4.已知抛物线2=23y x x --经过A 、B 、C 三点，点P （1，k ）

在直线BC ：y=x -3上，若点M 在x 轴上，点N 在抛物线上，

是否存在以A 、M 、N 、P 为顶点的四边形为平行四边形？若存在，请求出点M 的坐标；若不存在，请说明理由．

5.抛物线22

12-+=x x y 与y 轴交于点C ，与直线y =x 交于A (-2，-2)、B (2，2)两点．如图，线段MN 在直线AB 上移动，且2MN =，若点M 的横坐标为m ，过点M 作x 轴的垂线与x 轴交于点P ，过点N 作x 轴的垂线与抛物线交于点Q ．以P 、M 、Q 、N 为顶点的四边形能否为平行四边形？若能，请求出m 的值；若不能，请说明理由．

三、回顾与思考

__________________________________________________________________________________________________________________________________________________________________

【参考答案】

一、知识点睛1画图分析②分类讨论③验证取舍

二、精讲精练

1.解：由题意，设OA =m ，则OB =2m ；

当∠BAP =90°时，△BAP ∽△AOB 或△BAP ∽△BOA ；1若△BAP ∽△AOB ，如图1，

可知△PMA ∽△AOB ，相似比为2：1；则P 1（5m ，2m ），

代入x x y 32+-=，可知2513=m ，)25

26,513(1P 2若△BAP ∽△BOA ，如图2，

可知△PMA ∽△AOB ，相似比为1：2；则P 2（2m ，2

m ），代入x x y 32+-=，可知811=m ，)1611,411(2P

当∠ABP =90°时，△ABP ∽△AOB 或△ABP ∽△BOA ；3若△ABP ∽△AOB ，如图3，

可知△PMB ∽△BOA ，相似比为2：1；则P 3（4m ，4m ），

代入x x y 32+-=，可知2

1=m ，)2,2(3P 4若△ABP ∽△BOA ，如图4，

可知△PMB ∽△BOA ，相似比为1：2；则P 4（m ，m 25），代入x x y 32+-=，可知21=m ，415(,)24P 2.解：（1）由抛物线解析式()21134

y x =--+可得B 点坐标（1，3）.

要求直线BQ 的函数解析式，只需求得点Q 坐标即可，即求CQ 长度.

过点D 作DG ⊥x 轴于点G ，过点D 作DF ⊥QP 于点F .

则可证△DCG ≌△DEF .则DG =DF ，

∴矩形DGQF 为正方形.

则∠DQG =45°，则△BCQ 为等腰直角三角形.

∴CQ =BC =3，此时，Q 点坐标为（4，0）

可得BQ 解析式为y =－x +4.

（2）要求P 点坐标，只需求得点Q 坐标，然后根据横坐标相同来求点P 坐标即可.

而题目当中没有说明∠DCE =30°还是∠DCE =60°，所以分两种情况来讨论.1当∠DCE =30°时，

a ）过点D 作DH ⊥x 轴于点H ，过点D 作DK ⊥QP 于点K .

则可证△DCH ∽△DEK .则

3DH DC DK DE

==，在矩形DHQK 中，DK =HQ ，

则3DH HQ

=.在Rt △DHQ 中，∠DQC =60°.

则在Rt △BCQ 中，

3BC CQ

=∴CQ =3，此时，Q 点坐标为（1+3,0）

则P 点横坐标为1+3.代入()21134y x =-

-+可得纵坐标.∴P （1+3,94

）.b ）又P 、Q 为动点，∴可能PQ 在对称轴左侧，与上一种情形关于对称轴对称.

由对称性可得此时点P 坐标为（1－3,

94）2当∠DCE =60°时，

a)过点D 作DM ⊥x 轴于点M ，过点D 作DN ⊥QP 于点N .

则可证△DCM ∽△DEN .则13

DM DC DN DE ==，在矩形DMQN 中，DN =MQ ，则13

DM MQ =.在Rt △DMQ 中，∠DQM =30°.

则在Rt △BCQ 中，

13

BC CQ =∴CQ =3BC =33，此时，Q 点坐标为（1+33，0）则P 点横坐标为1+33.代入()21134y x =--+可得纵坐标.∴P （1+33,154

－）.b ）又P 、Q 为动点，∴可能PQ 在对称轴左侧，与上一种情形关于对称轴对称.

由对称性可得此时点P 坐标为（1－33,154－）综上所述，P 点坐标为（1+3,94），（1－3,94），（1+33,154－）或（1－33,154

－）.3．解：（1）∵AB =BC =10，OB =8

∴在Rt △OAB 中，OA =6

∴A （6，0）

将A （6，0），B （0，-8）代入抛物线表达式，得，8310312

-+-=x x y （2）存在：

如果△AMN 与△ACD 相似，则21=AN MN 或2=AN

MN 设M ),(8310312

-+-m m m （0

当21=AN MN 时，2

168310312=-+-m m m ，即2

164631=---m m m ))((∴25=m ∴),(4

725-M 如图2验证一下：

当2=AN MN 时，268310312=-+-m

m m ，即

264631=---m

m m ))((∴2-=m （舍）2）如果点M 在x 轴上方的抛物线上：当21=AN MN 时，2168310312=--+-m m m ，即2

164631=----m m m ))((∴211=m ∴M ),(41211此时41=MN ,21=AN ∴2

1=AN MN ∴△AMN ∽△ACD

∴M ),(4

1211满足要求当2=AN MN 时，268310312=--+-m

m m ，即264631=----m

m m ))((∴m =10（舍）

综上M 1),(4725-,M 2),(4

12114.解：满足条件坐标为：

1(36,0)-M 2(36,0)+M 3(12,0)-+M 4(12,0)

--M 思路分析：A 、M 、N 、P 四点中点A 、点P 为顶点，则AP 可为平行四边形边、对角线；

(1)如图，当AP 为平行四边形边时，平移AP ；

∵点A 、P 纵坐标差为2

∴点M 、N 纵坐标差为2；

∵点M 的纵坐标为0

∴点N 的纵坐标为2或-2

①当点N 的纵坐标为2时

解：2232

--=x x 得16

=±x 又∵点A 、P 横坐标差为2

∴点M 的坐标为：

1(36,0)-M 、2(36,0)

+M ②当点N 的纵坐标为-2时

解：2232

--=-x x 得12

=±x 又∵点A 、P 横坐标差为2

∴点M 的坐标为：

3(12,0)-+M 、4(12,0)

--M (2)当AP 为平行四边形边对角线时；

设M 5（m ,0）

MN 一定过AP 的中点（0，-1）

则N 5（-m ，-2）

N 5在抛物线上

∴2232

+-=-m m 12=-±m （负值不符合题意，舍去）∴12

=-+m ∴5(12,0)

-+M 综上所述:

符合条件点P 的坐标为：

1(36,0)-M 2(36,0)+M 3(12,0)-+M 4(12,0)

--M 5．解：分析题意，可得：MP ∥NQ ，若以P 、M 、N 、Q 为顶点的四边形为平行四边形，只需MP =NQ 即可

由题知：(,)M m m ，(,0)P m ，(1,1)N m m ++，

21(1,(1)+(1)2)2

Q m m m +++-故只需表达MP 、NQ 即可.表达分下列四种情况：

①如图1，PM m =-，21(1)22

QN m =+-，令PM =QN ，解得：1=2+7m -（舍去），2=27m --；

②如图2，PM m =-，21(1)+22

QN m =-+，令PM =QN ，解得：1=3m （舍去），1=3m -；

③如图3，PM m =，21(1)+22

QN m =-+，令PM =QN ，解得：1=2+7m -，2=27m --（舍去）；④如图4，PM m =，21(1)22

QN m =+-，令PM =QN ，解得：1=3m ，1=3m -（舍去）；

综上，m 的值为1=27m --、2=3m -、3=2+7m -、4=3m ．