数学建模_电力生产问题
电力生产最优化问题
摘要
本文解决的是发电机使用的非线性最优化问题。为满足每日电力需求,且总成本最小,可把每天分为七个时间段,要计算一天的最小成本即是分别求出每个时间段的最小成本,从而累加得出一天的最小总成本。我们采用了LINGO 软件实现整个流程,最终求出七个时段总成本的最优解,即每天使用发电机的总成本的最小值,并进行了误差分析,模型的评价与推广。
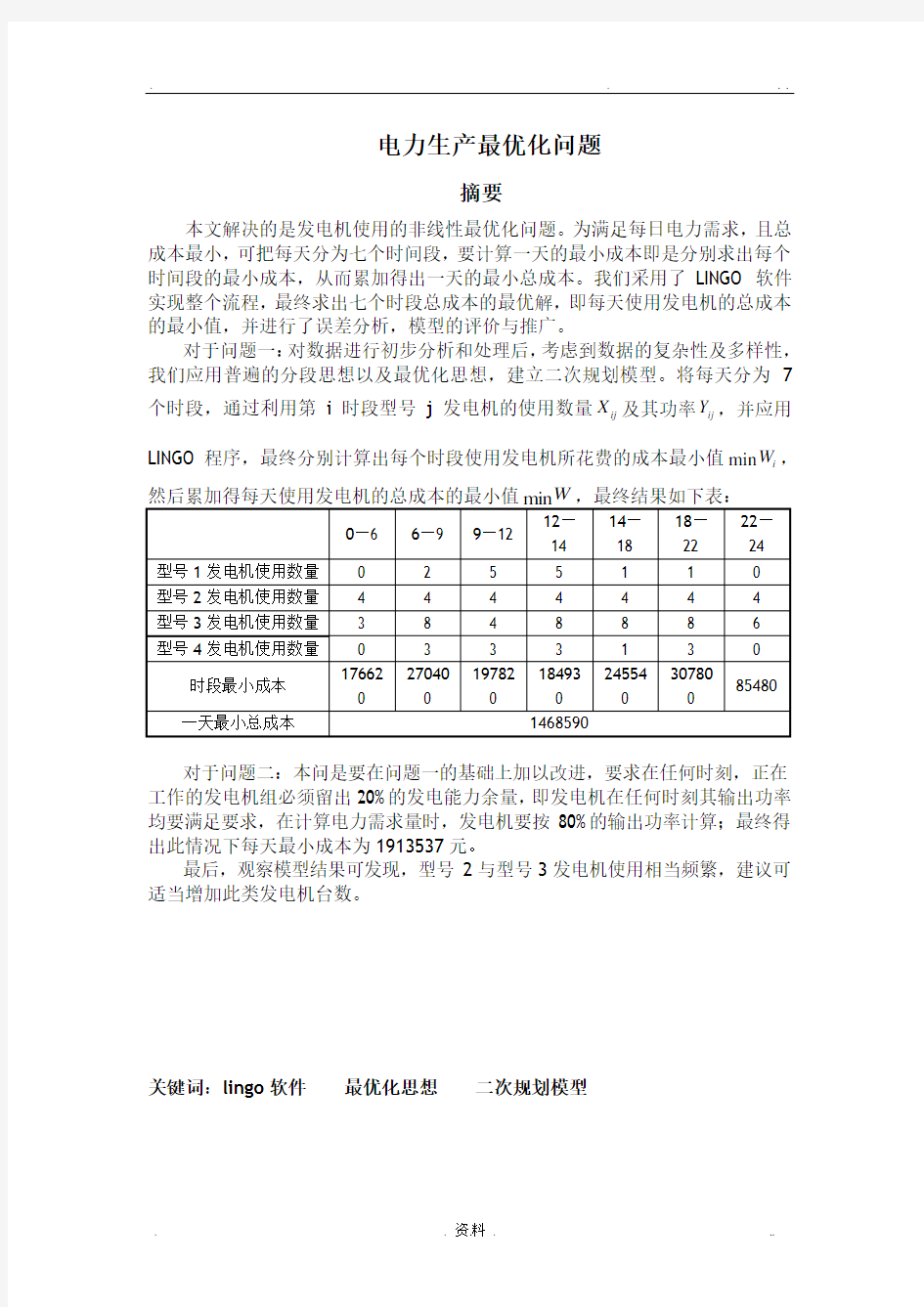
对于问题一:对数据进行初步分析和处理后,考虑到数据的复杂性及多样性,我们应用普遍的分段思想以及最优化思想,建立二次规划模型。将每天分为7个时段,通过利用第i 时段型号j 发电机的使用数量ij X 及其功率ij Y ,并应用LINGO 程序,最终分别计算出每个时段使用发电机所花费的成本最小值min i W ,
对于问题二:本问是要在问题一的基础上加以改进,要求在任何时刻,正在工作的发电机组必须留出20%的发电能力余量,即发电机在任何时刻其输出功率均要满足要求,在计算电力需求量时,发电机要按80%的输出功率计算;最终得出此情况下每天最小成本为1913537元。
最后,观察模型结果可发现,型号2与型号3发电机使用相当频繁,建议可适当增加此类发电机台数。
关键词:lingo 软件 最优化思想 二次规划模型
一.问题重述
问题背景:
电是我们这个社会不可缺少的资源之一。我们身边处处都需要电,小到电灯、电扇,大到飞机、卫星。对电力资源的合理利用是目前重要任务之一。在可持续发展的社会中,如何节约资源、提高效率是当前社会面临的重要问题之一,本题即是要求合理分配发电机使用数量,以减小发电成本的问题。
题目要求:
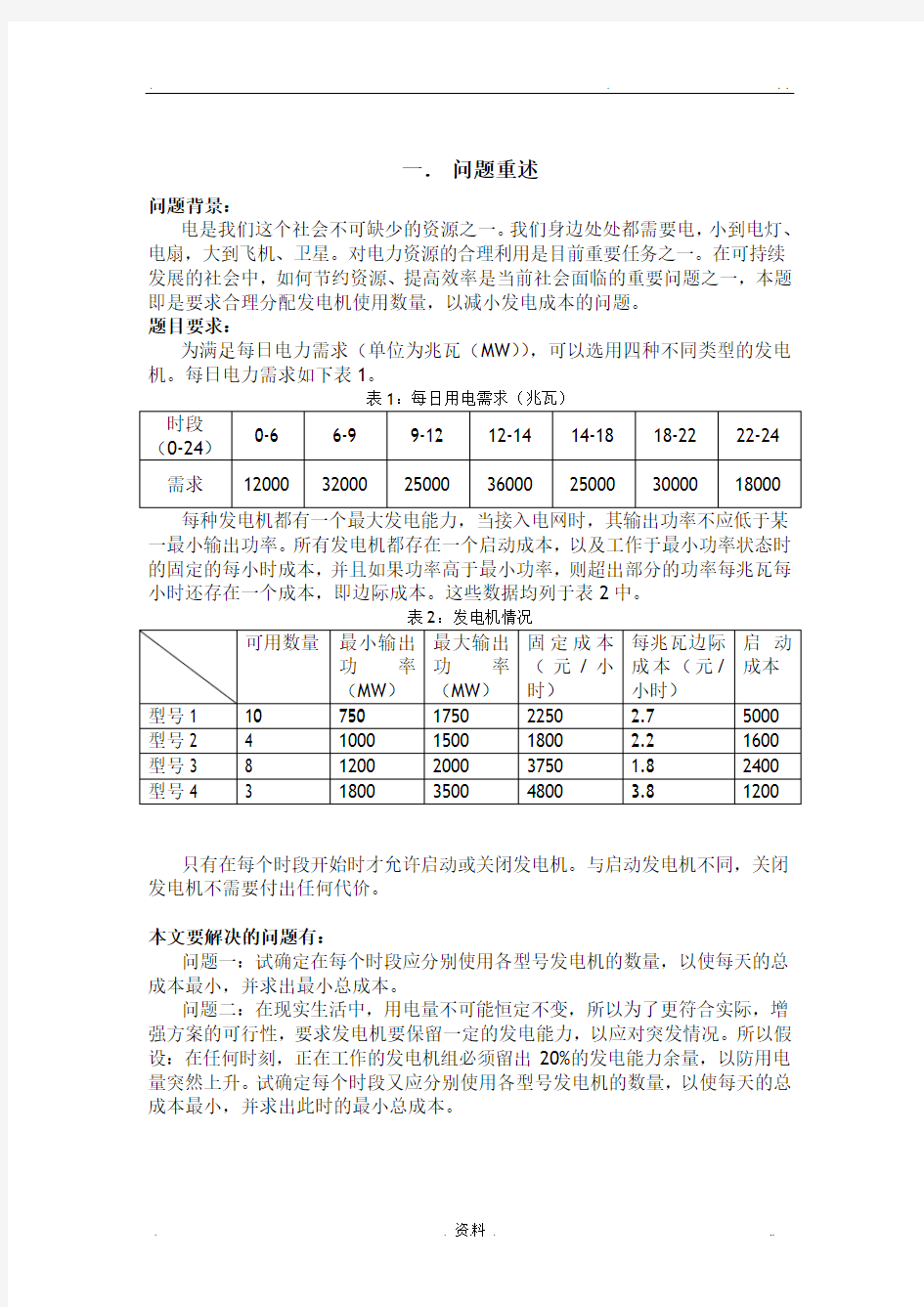
为满足每日电力需求(单位为兆瓦(MW)),可以选用四种不同类型的发电机。每日电力需求如下表1。
一最小输出功率。所有发电机都存在一个启动成本,以及工作于最小功率状态时的固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。这些数据均列于表2中。
只有在每个时段开始时才允许启动或关闭发电机。与启动发电机不同,关闭发电机不需要付出任何代价。
本文要解决的问题有:
问题一:试确定在每个时段应分别使用各型号发电机的数量,以使每天的总成本最小,并求出最小总成本。
问题二:在现实生活中,用电量不可能恒定不变,所以为了更符合实际,增强方案的可行性,要求发电机要保留一定的发电能力,以应对突发情况。所以假设:在任何时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升。试确定每个时段又应分别使用各型号发电机的数量,以使每天的总成本最小,并求出此时的最小总成本。
二.模型的假设
假设1:在每个时段开始时才允许启动或关闭发电机。
假设2:发电机工作期间不发生任何故障。
假设3:发电机之间的摩擦不消耗功率。
假设4:发电机输出过程其功率始终保持不变。
假设5:关闭发电机过程不做任何考虑。
假设6:关闭和启动发电机时均是瞬时完成,不记相应使用的时间。假设7:发电机自身不消耗功率。
G相等。
假设8:在一时段内,每小时所需要的功率
i
三.符号说明
四. 模型的建立与求解
问题(一)
1.1 模型分析
该问题是一个分段求解问题,比较复杂不易求出精确的最优解,故只能近似求出其最优解来。
我们把每天分为7个时段,通过求每个时段发电机使用的总成本来求每天的总成本,即为各各时段总成本之和。然后要确定发电机在每个时段所使用的发电机的型号以及所使用的数量和输出的实际功率,而每个时段的总成本是由三个部分组成的,分别为:固定成本、启动成本、边际成本。据此对每个时段建立模型及其相应的约束条件,又各各时段中若已经启动的发电机就不用再启动,所以无需相应的额外启动成本,故第1时段与后6个时段计算情况不同,所以我们要分时段来求各时段的启动成本。 1.2 模型的建立 1.2.1 确定目标函数
我们确定的目标函数是为了解决电力生产优化问题。在满足需求量的情况下,为了使每天发电成本最低,则需要每个时段有最小成本,所以我们建立如下目标函数
7
1min min i i W W ==∑
为了解决问题,我们进一步研究每个时段的最小成本,由于成本由启动成本、固定成本、边际成本组成,所以我们经分析可得出第i 时段的总成本为:
4
1[**()***]i ij j ij i ij j j i ij j W F A X T Y M B T X ==++-∑
因为ij F 代表第i 时段j 型号发电机的总启动成本,在第1是时段时,开多少发电机,就需要多少次启动成本。而从第二次开始,如果比上一时间段开机少,本时段就不需要此启动成本;如果开机比上一时段多,则只需要计算多出发电机的启动成本。所以,我们最终得出第i 时段j 型号的启动成本公式为:
(1)(1)(1)*,1*(),2,3,4,5,6,7,0,j ij ij j ij i j ij i j ij i j
C X i F C X X i X X X X ---?=?
=-=>??
≤?
1.2.2确定约束条件
ⅰ. 因为ij X 代表第i 时段型号j 发电机使用数量,所以ij X 应小于等于本型号发电机总的数量,且为整数,即:
1234010040803
i i i i X X X X <=<=??<=<=?
?
<=<=??<=
<=? (ij X 为整数)
ⅱ. 同时由于ij Y 代表第i 时段单个型号j 的功率,所以ij Y 的大小应该介于最小输出功率与最大输出功率之间,即:
12
347501500100017501200200018003500
i i i i Y Y Y Y <=<=??<=<=??<=<=??<=<=?
ⅲ. 发电机的发电量要满足电量需求,而i G 代表第i 时段每小时所需要的功率,所以每小时发电量要大于等于i G ,即: 4
1*i ij ij j G X Y =<=∑
1.2.3 综上所述,得到问题一的最优化模型
7
1
4
1min min [**()***]i i i ij j ij i ij j j i ij j W W W F A X T Y M B T X ==?
=????=++-??
∑∑
41
112233
44*010,7501500;..04,10001750;
08,12002000;
03,18003500;i ij ij
j i i i i i i i i G X Y X Y s t X Y X Y X Y =?
<=??
?<=<=<=<=?<=<=<=<=??<=<=<=<=?
?<=<=<=<=??
∑(ij X 必须取整数)
1.3 模型的求解.
首先,我们分析题目得到,总成本由启动成本、固定成本、边际成本组成。 启动成本:分析易知,启动成本只与本型号发电机的数量有关,与其输出功率无关。其值为:各型号发电机数量与其各自的启动成本之积的求和。
固定成本:因为当发电机接入电网时,其输出功率不应低于其最小输出功率,
数学建模竞赛简介
数学建模竞赛简介 数学建模就是建立、求解数学模型的过程和方法,首先要通过分析主要矛盾,对各种实际问题进行抽象简化,并按照有关规律建立起变量,参数间的明确关系,即明确的数学模型,然后求出该数学问题的解,并通过一定的手段来验证解的正确性。 数学建模竞赛于1985年起源于美国,起初竞赛题目通常由工业部门、军事部门提出,然后由数学工作者简化或修正。1989年我国大学生开始参加美国大学生数学建模竞赛,1990年我国开始创办我国自己的大学生数学建模竞赛。1993年国家教委(现教育部)高教司正式发文,要求在全国普通高等学校中开展数学建模竞赛。从1994年开始,大学生数学建模竞赛成为教育部高教司和中国工业的应用数学学会共同主办,每年一届的,面向全国高等院校全体大学生的一项课外科技竞赛活动。2010年全国共有30省(市、自治区)九百多所院校一万多个队三万多名大学生参赛,成为目前全国高等学校中规模最大的课外科技活动。数学建模竞赛是教育主管部门主办的大学生三大竞赛之一。 现在的竞赛题目来源于更广泛的领域,都是各行各业的实际问题经过适当简化,提炼出来的极富挑战性的问题,每次两道题,学生任选一题,可以使用计算机、软件包,可以参阅任何资料(含上网参阅任何资料)。竞赛以三人组成的队为单位,三人之间通力合作,在三天三夜内完成一篇论文。不给论文评分,而是按论文的水平为四档:全国一等奖、全国二等奖、赛区一等奖,赛区二等奖,成功参赛奖。我校于2001年开始参加这项竞赛活动。多次获全国一等奖、二等奖、湖北赛区一等奖、二等奖。 数学建模竞赛活动培养了学生的创造力、应变能力、团队精神和拼搏精神,适应了21世纪经济发展和人才培养的挑战。不少参加过全国大学生数学建模竞赛的同学都深有感触,他们说:“参加这次活动是我们大学四年中最值得庆幸的一件事,我们真正体会这几年内学到了什么,自己能干什么。”“那不寻常的三天在我们记忆中留下了永恒的一瞬,真是一次参赛,终身受益。”团队精神贯穿在数学建模竞赛的全过程,它往往是成败的关键。有些参赛队员说:“竞赛使我们三个人认识到协作的重要性,也学会了如何协作,在建模的三天中,我们真正做到了心往一处想,劲往一处使,每个人心中想的就是如何充分发挥自己的才华,在短暂的时间内做出一份尽量完善的答卷。三天中计算机没停过,我们轮流睡觉、轮流工作、轮流吃饭,可以说是抓住了每一滴可以抓住的时间。”“在这不眠的三天中,我们真正明白了团结就是力量这个人生真谛,而这些收获,将会伴随我们一生,对我们今后的学习,工作产生巨大的影响。”
三峡大学数学建模第一题电力生产问题
电力生产问题 为满足每日电力需求(单位为兆瓦(MW)),可以选用四种不同类型的发电机。每日电力需求如下表1。 所有发电机都存在一个启动成本,以及工作于最小功率状态时的固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。这些数据均列于表2中。 ( 只有在每个时段开始时才允许启动或关闭发电机。与启动发电机不同,关闭发电机不需要付出任何代价。 问题(1)在每个时段应分别使用哪些发电机才能使每天的总成本最小,最小总成本为多少? 问题(2)如果在任何时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升。那么每个时段又应分别使用哪些发电机才能使每天的总成本最小,此时最小总成本又为多少? 电力生产问题的数学模型 摘要 本文解决的是电力生产问题,在发电机的发电量能满足每日的电力需求的条件下,为了使每日的总成本达到最低,我们建立了一个最优化模型。 对于问题一:由已知条件可知有固定成本、边际成本、启用成本,据此,我们确定了三个指标:即固定总成本、边际总成本、启动总成本。总成本即为这三项总成本之和。每天分为七个时段,发电机共有四种型号,方案结果应该包括每个时段每种型号平均功率及该时段该型号发电机的数量,一共有56个未知数,为减少未知数,并将非线性约束条件转化为线性约束条件,将整数规划转化为非整数规划,我们以每个时段每种型号的几个发电机发出的总功率为变量,并列出相应的约束条件,然后通过LINGO求出个时段各种型号发电机的总功率,再采用分支定界法求出最小总成本为
146.9210万元。再根据总功率利用Matlab软件计算出总功率所对应的该型号发电机的数量(见表一)。 对于问题二:题目要求在任何时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升。其他条件与问题一相同,因此,只需增加一个约束条件,即发电机机组所能发出的最大总功率乘以80%后大于用电需求。为锻炼编程技术,故在第二问改用Matlab软件编程来求解,将所要求的7个时段4种型号的发电机的平均功率一共28个未知数用X1,X2,,,,X28表示,将其对应的发电机数量用X29,X30,,,X56表示,并利用矩阵列出约束条件和目标函数,然后编程并运行求解,得到的发电机数量有的不为整数,然后采用分支定界法,得到调整后的结果,最小总成本为157.5426万元。 ! 关键词:线性规划、总功率、使用数量、总成本 1.问题重述 1.1问题背景 为满足每日电力需求(单位为兆瓦(MW)),可以选用四种不同类型的发电机。每日电力需求如下表1。 所有发电机都存在一个启动成本,以及工作于最小功率状态时的固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。这些数据均列于表2中。 任何代价。 1.2需要解决的问题 问题(1)在每个时段应分别使用哪些发电机才能使每天的总成本最小,最小总成本为多少? 问题(2)如果在任何时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升。那么每个时段又应分别使用哪些发电机才能使每天的总成本最小,此时最小总成本又为多少? 2.模型假设 假设1:调整发电机功率没有成本 :
数学建模实验报告第十一章最短路问答
实验名称:第十一章最短路问题 一、实验内容与要求 掌握Dijkstra算法和Floyd算法,并运用这两种算法求一些最短路径的问题。 二、实验软件 MATLAB7.0 三、实验内容 1、在一个城市交通系统中取出一段如图所示,其入口为顶点v1,出口为顶点v8,每条弧段旁的数字表示通过该路段所需时间,每次转弯需要附加时间为3,求v1到v8的最短时间路径。 V1 1 V2 3 V3 1 V5 6 V6 V4 2 V7 4 V8
程序: function y=bijiaodaxiao(f1,f2,f3,f4) v12=1;v23=3;v24=2;v35=1;v47=2;v57=2;v56=6;v68=3;v78=4; turn=3; f1=v12+v23+v35+v56+turn+v68; f2=v12+v23+v35+turn+v57+turn+v78; f3=v12+turn+v24+turn+v47+v78; f4=v12+turn+v24+v47+turn+v57+turn+v56+turn+v68; min=f1; if f2 f4 实验结果: v1到v8的最短时间路径为15,路径为1-2-4-7-8. 2、求如图所示中每一结点到其他结点的最短路。V110 V3V59 V6 floy.m中的程序: function[D,R]=floyd(a) n=size(a,1); D=a for i=1:n for j=1:n R(i,j)=j; end end R for k=1:n for i=1:n for j=1:n if D(i,k)+D(k,j) 201数学建模生产计划 摘要 本文主要研究足球生产计划的规划问题。 对于问题一足球总成本包括生产成本与储存成本,又由于足球各月的生产成本、储存成本率及需求量已知,故各月足球的生产量对总成本起决定因素。在此建立总成本与足球生产量之间的关系,运用Matlab求出了总成本的最优解。 对于问题二储存成本率的大小影响了储存成本的高低,要使总成本最低,在储存成本率变化的情况下必须不断调整足球各月生产量,我们在Matlab中运用散点法,取了501个点,进而对图形进行线性拟合,得出储存成本率减小时各月足球生产量的变化情况。 对于问题三考虑到储存容量不能用储存成本率直接由函数表达,因此在Matlab 采用散点法结合表格分析法对501个点进行分析可得到储存成本率为0.39%时,储存容量达到最大。 关键词:最优解散点法线性拟合表格分析法 问题的重述 皮革公司在6个月的规划中根据市场调查预计足球需求量分别是10,000、15,000、30,000、35,000、25,000和10,000,在满足需求量的情况下使总成本最低,其包括生产成本及库存成本。根据预测,今后六个月的足球的生产单位成本分别是$12.50、$12.55、$12.70、$12.80、$12.85和$12.95,而每一个足球在每个月中的持有成本是该月生产成本的5%。目前公司的存货是5,000,每个月足球最大产量为30,000,而公司在扣掉需求后,月底的库存量最多只能储存10,000个足球。 问题一、建立数学模型,并求出按时满足需求量的条件下,使生产总成本和储存成本最小化的生产计划。 问题二、如若储存成本率降低,生产计划会怎样变化? 问题三、储存成本率是多少时?储存容量达到极限。 问题的分析 问题一要求在足球的需求量一定的情况下,使生产总成本和储存成本最小。又足球的生产成本和储存成本率已知,故只需要建立生产总成本和储存成本与各月足球的生产量之间的优化模型,运用Matlab即可求出足球生产总成本和储存成本的最优化组合。 基于最短路问题的研究及应用 : Fanmeng 学号: 指导老师: 摘要 最短路问题是图论中的一大问题,对最短路的研究在数学建模和实际生活中具有很重要的实际意义,介绍最短路问题的定义及这类问题的解决办法Dijkstra算法,并且能够在水渠修建实例运用到此数学建模的方法,为我们解决这类图论问题提供了基本思路与方法。 关键字数学建模最短路问题 Dijkstra算法水渠修建。 目录 第一章.研究背景 (1) 第二章.理论基础 (2) 2.1 定义 (2) 2.2 单源最短路问题Dijkstra求解: (2) 2.2.1 局限性 (2) 2.2.2 Dijkstra算法求解步骤 (2) 2.2.3 时间复杂度 (2) 2.3 简单样例 (3) 第三章.应用实例 (4) 3.1 题目描述 (4) 3.2 问题分析 (4) 3.3符号说明 (5) 3.4 模型假设 (5) 3.5模型建立与求解 (5) 3.5.1模型选用 (5) 3.5.2模型应用及求解 (5) 3.6模型评价 (5) 第四章. 参考文献 (6) 第五章.附录 (7) 第一章.研究背景 在现实生活中中,我们经常会遇到图类问题,图是一种有顶点和边组成,顶点代表对象,在示意图中我们经常使用点或者原来表示,边表示的是两个对象之间的连接关系,在示意图中,我们使用连接两点G点直接按的下端来表示。顶点的集合是V,边的集合是E的图记为G[V,E] ,连接两点u和v的边用e(u,v)表示[1]。最短问题是图论中的基础问题,也是解决图类问题的有效办法之一,在数学建模中会经常遇到,通常会把一个实际问题抽象成一个图,然后来进行求的接任意两点之间的最短距离。因此掌握最短路问题具有很重要的意义。 常见评价模型简介 评价类数学模型是全国数学建模竞赛中经常出现的一类模型,如2005年全国赛A题长江水质的评价问题,2008年B题高校学费标准评价体系问题等。主要介绍三种比较常用的评价模型:层次分析模型,模糊综合评价模型,灰色关联分析模型,以期帮助大家了解不同背景下不同评价方法的应用。 层次分析模型 层次分析法(AHP)是根据问题的性质和要求,将所包含的因素进行分类,一般按目标层、准则层和子准则层排列,构成一个层次结构,对同层次内诸因素采用两两比较的方法确定出相对于上一层目标的权重,这样层层分析下去,直到最后一层,给出所有因素相对于总目标而言,按重要性程度的一个排序。其主要特征是,它合理地将定性与定量决策结合起来,按照思维、心理的规律把决策过程层次化、数量化。 运用层次分析法进行决策,可以分为以下四个步骤: 步骤1 建立层次分析结构模型 深入分析实际问题,将有关因素自上而下分层(目标—准则或指标—方案或对象),上层受下层影响,而层内各因素基本上相对独立。 步骤2构造成对比较阵 对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,借助1~9尺度,构造比较矩阵; 步骤3计算权向量并作一致性检验 由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验,若通过,则最大特征根对应的特征向量做为权向量。 步骤4计算组合权向量(作组合一致性检验) 组合权向量可作为决策的定量依据 通过一个具体的例子介绍层次分析模型的应用。 例(选择旅游地决策问题)如何在桂林、黄山、北戴河3个目的地中按照景色、费用、居住条件、饮食、旅途条件等因素进行选择。 步骤1 建立系统的递阶层次结构 将决策问题分为3个层次:目标层O,准则层C,方案层P;每层有若干元素,各层元素间的关系用相连的直线表示。 电力生产问题数学模型 ————————————————————————————————作者:————————————————————————————————日期: 电力生产问题数学模型 摘要 本文研究电力生产问题中的最优化电力资源配置,属于求解优化电力配置下的最小成本问题。由于电力生产有非线性、多变量等特点,所以我们基于在每一时间段非线性局部最优的前提下,建立整体的单目标多变量的非线性最优化模型 。 因此对于研究的课题,我们建立了一个有约束条件的目标函数的最优化模型来求解。在该模型的基础上我们建立起解决问题所需模型。 解决问题(1)时,我们运用LINGO 工具求解所建立的数学模型,得到每个时段的台数和成本如下表:(详细数据见) 时段1 时段2 时段3 时段4 时段5 时段6 时段7 总成本/元 型号1 0 2 0 2 0 1 0 0 1750 750 1750 1000 1300 750 … … … … … … … … 型号4 0 3 3 3 3 3 3 0 2166.6 1800 3500 1800 1800 解决问题(2)时,我们从节约能源和成本的前提出发,让在工作的每一台发电机保留出20%的发电能力,而不是让其发出多于需求电量的20%白白浪费,因此我们将“每个时段的电力需求”这个约束条件由问题(1)中的j ij j D P m ≤≤改为 8.0?≤≤j ij j D P m 。得到每个时段的台数和成本如下表:(详细数据见) 时段1 时段2 时段3 时段4 时段5 时段6 时段7 总成本/元 型号1 0 5 0 8 1 5 0 0 1400 1400 1400 1400 1400 0 … … … … … … … … 型号4 3 3 3 3 3 3 3 1866.6 2466.6 2466.6 2400 2000 1800 1800 关键词:非线性 整体最优化 LIGNO 软件 时 段 型 号 时 段 型 号 数学建模简介 当需要从定量的角度分析和研究一个实际问题时,人们就要在深入调查研究、了解对象信息、作出简化假设、分析内在规律等工作的基础上,用数学的符号和语言作表述,也就是建立数学模型,然后用通过计算得到的结果来解释实际问题,并接受实际的检验。这个建立数学模型的全过程就称为数学建模。 数学建模的广泛应用 数学建模的应用逐渐变的广泛,数学建模大量用于一般工程技术领域,用于代替传统工程设计中的现场实验、物理模拟等手段;在高新科技领域,成为必不可少的工具,无论是在通信、航天、微电子、自动化都是创新工艺、开发新 产品的必要手段;在新的科研领域在用数学方法研究 其中的定量关系时,数学建模就成为首要的、关键的 步骤和这些学科发展和应用的基础。 将计算机技术和数学建模进行紧密结合,使得原 本抽象的数学模型生动具体的呈现在研究者面前,使 得问题得到更好的解决。 数学建模的分支——数据挖掘 数据挖掘(Data Mining,DM)是目前人工智能和数 据库领域研究的热点问题,所谓数据挖掘是指从数据库 的大量数据中揭示出隐含的、先前未知的并有潜在价值 的信息的非平凡过程。数据挖掘是一种决策支持过程, 它主要基于人工智能、机器学习、模式识别、统计学、 数据库、可视化技术等,高度自动化地分析企业的数据, 做出归纳性的推理,从中挖掘出潜在的模式,帮助决策 者调整市场策略,减少风险,做出正确的决策。 数据挖掘是通过分析每个数据,从大量数据中寻找其规律的技术,主要有数据准备、规律寻找和规律表示3个步骤。数据准备是从相关的数据源中选取所需的数据并整合成用于数据挖掘的数据集;规律寻找是用某种方法将数据集所含的规律找出来;规律表示是尽可能以用户可理解的方式(如可视化)将找出的规律表示出来。 数据挖掘的任务有关联分析、聚类分析、分类分析、异常分析、特异群组分析和演变分析,等等。 数学建模之电力的生产问 题 Prepared on 22 November 2020 电力生产最小成本 摘要 本文是需解决发电机厂每天在不同时间段用电需求量不同的情况下,根据给定不同型号不同数量的发电机,合理分配各台发电机在不同时间段的开启和关闭以及运行时的输出功率,既使得一天内总发电成本最小,又使发电机组在一天中各个时段的总输出功率达到用电需求的问题,为解决这个问题,采用了单目标非线性规划方法,建立了所求问题的最优化模型,借助Lingo软件对模型进行求解,得到每日最小发电总成本,以此制定发电机组的启停计划。 问题一:为了使发电厂一天总的发电成本最低,同时还要考虑到不同时间段开机数量不同对启动成本的相互影响,将七个时间段的成本统一考虑,其中,启动成本与发电机开启数量有关,要让成本少,应在满足相应约束条件下尽量减少开机数量,尽量让上一阶段的发电机下一阶段依然工作,边际成本与开启发电机台数、输出功率、最小功率、时长有关,固定成本与开启发电机台数、时长有关,选取相应的约束条件对目标函数进行约束,从而给出优化模型,运用非线性规划的方法,利用Lingo编程求解,得到发电厂每天最小发电总成本为:1427179 元。具体的发电机使用方案见附录一中表一、表二。 问题二:根据题目的要求,在任何时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升,在建模时将每台发电机的实际输出功率降至80%,所以可以按照问题一建立的模型,将其约束条件中每个时间段的实际输出功率改为功率的80%但同时要满足用电量,同样利用Lingo编程求解,得到发电厂每天最小发电总成本为:1444670元。具体的发电机使用方案见附录一中表三、表四。 在得到上述两个问题的结果后,对结果的正确性性进行检验,并且对所得结果进行分析,给出自己的评价,并且对所建模型的合理性进行判断,以及对模型做了适当的推广。 关键词:单目标非线性规划发电机的合理搭配电力生产最优解 电力生产问题 摘要 本文解决的是电力生产中发电机的安排问题,在满足每日各时间段电力需求的条件下,安排各型号发电机来供电,以期获得最小的成本。为解决此问题,我们建立了两个最优化模型。 针对问题一:建立了非线性单目标最优化模型。从已知条件、目标函数、约束条件三方面进行综合分析可知,每天的总成本由总固定成本、总边际成本、总启动成本组成,确定总成本为目标函数,各时段各型号发电机工作数量及其总超出功率为主要变量,并列出相应约束条件。最后通过Lingo软件[2]求出最小成本为1540770元,并得出各时段各型号发电机的数量及其功率如下表(具体见表三): 针对问题二:建立了线性单目标最优化模型。引入非负变量,即为各时段新增开的各型号的发电机台数,通过此变量线性表示出启动成本。以总成本为目标函数,在模型一的基础上,只需改变一个约束条件,即发电机组在任意时间段内所能发出的最大总功率的80%要大于等于该时段的用电需求。最后通过lingo软件求出最小成本为1885420元,并得出各时段各型号发电机的数量及其功率。 关键词:非线性最优化模型线性最优化模型最小生产成本 1 问题重述 1.1 问题背景 在电力生产过程中,为满足每日的电力需求并且使生产成本达到最小,因不同发电性能的发电机成本不同,故可以选用不同型号的发电机组合使用。 1.2 题目信息 题中给出了一天中七个时段的用电需求(见表一)及四种发电机的发电性能和相应成本(见表二)。其中,所有发电机都有一个最大发电能力,当接入电网时,其输出功率不应低于其最小输出功率,且所有发电机均存在一个启动成本,以及工作于其最小功率状态时固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。 问题(1):在每个时段应分别使用哪些发电机才能使每天的总成本最小,最小总成本为多少? 问题(2):如果在任何时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升。那么每个时段又应分别使用哪些发电机才能使每天的总成本最小,此时最小总成本又为多少? 2 模型假设 假设1:不计发电机启动时所需时间; 假设2:各发电机均在24时关闭,即不考虑循环过程; 假设3:各发电机的输出功率在时段初调整好后,保持不变; 假设4:题目所列出的成本以外的成本消耗不计。 运输问题 摘要 本文主要研究的是货物运输的最短路径问题,利用图论中的Floyd算法、Kruskal算法,以及整数规划的方法建立相关问题的模型,通过matlab,lingo编程求解出最终结果。 关于问题一,是一个两客户间最短路程的问题,因此本文利用Floyd算法对其进行分析。考虑到计算的方便性,首先,我们将两客户之间的距离输入到网络权矩阵中;然后,逐步分析出两客户间的最短距离;最后,利用Matlab软件对其进行编程求解,运行得到结果:2-3-8-9-10总路程为85公里。 关于问题二,运输公司分别要对10个客户供货,必须访问每个客户,实际上是一个旅行商问题。首先,不考虑送货员返回提货点的情形,本文利用最小生成树问题中的Kruskal算法,结合题中所给的邻接矩阵,很快可以得到回路的最短路线: 1-5-7-6-3-4-8-9-10-2;然后利用问题一的Floyd算法编程,能求得从客户2到客户1(提货点)的最短路线是:2-1,路程为50公里。即最短路线为:1-5-7-6-3-4-8-9-10-2-1。但考虑到最小生成树法局限于顶点数较少的情形,不宜进一步推广,因此本文建立以路程最短为目标函数的整数规划模型;最后,利用LINGO软件对其进行编程求解,求解出的回路与Kruskal算法求出的回路一致。 关于问题三,是在每个客户所需固定货物量的情况下,使得行程之和最短。这样只要找出两条尽可能短的回路,并保证每条线路客户总需求量在50个单位以内即可。因此我们在问题二模型的基础上进行改进,以货车容量为限定条件,建立相应的规划模型并设计一个简单的寻路算法,对于模型求解出来的结果,本文利用Kruskal算法结合题中所给的邻接矩阵进行优化。得到优化结果为:第一辆车:1-5-2-3-4-8-9-1,第二辆车:1-7-6-9-10-1,总路程为280公里。 关于问题四,在问题一的基础上我们首先用Matlab软件编程确定提货点到每个客户点间的最短路线,然后结合一些限定条件建立一个目标模型,设计一个较好的解决方案进行求解可得到一种很理想的运输方案。根据matlab运行结果分析得出4条最优路线分别为:1-5-2,1-4-3-8,1-7-6,1-9-10。最短总路线为245公里,最小总费用为645。 关键词: Floyd算法 Kruskal算法整数规划旅行商问题 一、问题重述 某运输公司为10个客户配送货物,假定提货点就在客户1所在的位置,从第i个客户到第j个客户的路线距离(单位公里)用下面矩阵中的(,) i j(,1,,10) i j=位置上的数表示(其中∞表示两个客户之间无直接的路线到达)。 1、运送员在给第二个客户卸货完成的时候,临时接到新的调度通知,让他先给客户10送 货,已知送给客户10的货已在运送员的车上,请帮运送员设计一个到客户10的尽可能短的行使路线(假定上述矩阵中给出了所有可能的路线选择)。 2、现运输公司派了一辆大的货车为这10个客户配送货物,假定这辆货车一次能装满10个 客户所需要的全部货物,请问货车从提货点出发给10个客户配送完货物后再回到提货点所行使的尽可能短的行使路线?对所设计的算法进行分析。 3、现因资源紧张,运输公司没有大货车可以使用,改用两辆小的货车配送货物。每辆小 数学建模常用的十大算法==转 (2011-07-24 16:13:14) 转载▼ 1. 蒙特卡罗算法。该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟来检验自己模型的正确性,几乎是比赛时必用的方法。 2. 数据拟合、参数估计、插值等数据处理算法。比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用MA TLAB 作为工具。 3. 线性规划、整数规划、多元规划、二次规划等规划类算法。建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo 软件求解。 4. 图论算法。这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备。 5. 动态规划、回溯搜索、分治算法、分支定界等计算机算法。这些算法是算法设计中比较常用的方法,竞赛中很多场合会用到。 6. 最优化理论的三大非经典算法:模拟退火算法、神经网络算法、遗传算法。这些问题是用来解决一些较困难的最优化问题的,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用。 7. 网格算法和穷举法。两者都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具。 8. 一些连续数据离散化方法。很多问题都是实际来的,数据可以是连续的,而计算机只能处理离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。 9. 数值分析算法。如果在比赛中采用高级语言进行编程的话,那些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。 10. 图象处理算法。赛题中有一类问题与图形有关,即使问题与图形无关,论文中也会需要图片来说明问题,这些图形如何展示以及如何处理就是需要解决的问题,通常使用MA TLAB 进行处理。 以下将结合历年的竞赛题,对这十类算法进行详细地说明。 以下将结合历年的竞赛题,对这十类算法进行详细地说明。 2 十类算法的详细说明 2.1 蒙特卡罗算法 大多数建模赛题中都离不开计算机仿真,随机性模拟是非常常见的算法之一。 举个例子就是97 年的A 题,每个零件都有自己的标定值,也都有自己的容差等级,而求解最优的组合方案将要面对着的是一个极其复杂的公式和108 种容差选取方案,根本不可能去求解析解,那如何去找到最优的方案呢?随机性模拟搜索最优方案就是其中的一种方法,在每个零件可行的区间中按照正态分布随机的选取一个标定值和选取一个容差值作为一种方案,然后通过蒙特卡罗算法仿真出大量的方案,从中选取一个最佳的。另一个例子就是去年的彩票第二问,要求设计一种更好的方案,首先方案的优劣取决于很多复杂的因素,同样不可能刻画出一个模型进行求解,只能靠随机仿真模拟。 2.2 数据拟合、参数估计、插值等算法 数据拟合在很多赛题中有应用,与图形处理有关的问题很多与拟合有关系,一个例子就是98 年美国赛A 题,生物组织切片的三维插值处理,94 年A 题逢山开路,山体海拔高度的插值计算,还有吵的沸沸扬扬可能会考的“非典”问题也要用到数据拟合算法,观察数据的 一、数学建模的意义 数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象、简化建立能近似刻画并"解决"实际问题的一种强有力的数学手段。 数学建模就是用数学语言描述实际现象的过程。这里的实际现象既包涵具体的自然现象比如自由落体现象,也包涵抽象的现象比如顾客对某种商品所取的价值倾向。这里的描述不但包括外在形态,内在机制的描述,也包括预测,试验和解释实际现象等内容。 我们也可以这样直观地理解这个概念:数学建模是一个让纯粹数学家(指只懂数学不懂数学在实际中的应用的数学家)变成物理学家,生物学家,经济学家甚至心理学家等等的过程。 数学模型一般是实际事物的一种数学简化。它常常是以某种意义上接近实际事物的抽象形式存在的,但它和真实的事物有着本质的区别。要描述一个实际现象可以有很多种方式,比如录音,录像,比喻,传言等等。为了使描述更具科学性,逻辑性,客观性和可重复性,人们采用一种普遍认为比较严格的语言来描述各种现象,这种语言就是数学。使用数学语言描述的事物就称为数学模型。有时候我们需要做一些实验,但这些实验往往用抽象出来了的数学模型作为实际物体的代替而进行相应的实验,实验本身也是实际操作的一种理论替代。 应用数学去解决各类实际问题时,建立数学模型是十分关键的一步,同时也是十分困难的一步。建立教学模型的过程,是把错综复杂的实际问题简化、抽象为合理的数学结构的过程。要通过调查、收集数据资料,观察和研究实际对象的固有特征和内在规律,抓住问题的主要矛盾,建立起反映实际问题的数量关系,然后利用数学的理论和方法去分析和解决问题。这就需要深厚扎实的数学基础,敏锐的洞察力和想象力,对实际问题的浓厚兴趣和广博的知识面。数学建模是联系数学与实际问题的桥梁,是数学在各个领械广泛应用的媒介,是数学科学技术转化的主要途径,数学建模在科学技术发展中的重要作用越来越受到数学界和工程界的普遍重视,它已成为现代科技工作者必备的重要能力之。为了适应科学技术发展的需要和培养高质量、高层次科技人才,数学建模已经在大学教育中逐步开展,国内外越来越多的大学正在进行数学建模课程的教学和参加开放性的数学建模竞赛,将数学建模教学和竞赛作为高等院校的教学改革和培养高层次的科技人才的个重要方面,现在许多院校正在将数学建模与教学改革相结 第一题:生产计划安排 2)产品ABC的利润分别在什么范围内变动时,上述最优方案不变 3)如果劳动力数量不增,材料不足时可从市场购买,每单位元,问该厂要不要购进原材料扩大生产,以购多少为宜 4)如果生产一种新产品D,单件劳动力消耗8个单位,材料消耗2个单位,每件可获利3元,问该种产品是否值得生产 答: max3x1+x2+4x3! 利润最大值目标函数x1,x2,x3分别为甲乙丙的生产数量 st!限制条件 6x1+3x2+5x3<45! 劳动力的限制条件 3x1+4x2+5x3<30! 材料的限制条件 End!结束限制条件 得到以下结果 1.生产产品甲5件,丙3件,可以得到最大利润,27元 2.甲利润在—元之间变动,最优生产计划不变 3. max3x1+x2+4x3 st 6x1+3x2+5x3<45 end 可得到生产产品乙9件时利润最大,最大利润为36元,应该购入原材料扩大生产,购入15个单位 4. max3x1+x2+4x3+3x4 st 6x1+3x2+5x3+8x4<45 3x1+4x2+5x3+2x4<30 end ginx1 ginx2 ginx3 ginx4 利润没有增加,不值得生产 第二题:工程进度问题 某城市在未来的五年内将启动四个城市住房改造工程,每项工程有不同的开始时间,工程周期也不一样,下表提供了这些项目的基本数据。 工程1和工程4必须在规定的周期内全部完成,必要时,其余的二项工程可以在预算的限制内完成部分。然而,每个工程在他的规定时间内必须至少完成25%。每年底,工程完成的部分立刻入住,并且实现一定比例的收入。例如,如果工程1在第一年完成40%,在第三年完成剩下的60%,在五年计划范围内的相应收入是*50(第二年)+*50(第三年)+(+)*50(第四年)+(+)*50(第五年)=(4*+2*)*50(单位:万元)。试为工程确定最优的时间进度表,使得五年内的总收入达到最大。 答: 假设某年某工程的完成量为Xij, i表示工程的代号,i=1,2,3,j表示年数,j=1,2,3,如第一年工程1完成X11,工程3完成X31,到第二年工程已完成X12,工程3完成X32。 另有一个投入与完成的关系,即第一年的投入总费用的40%,该工程在年底就完成40%,工程1利润: 50*X11+50*(X11+X12)+50*(X11+X12+X13)+50*(X11+X12+X13) 工程2利润: 70*X22+70*(X22+X23)+70*(X22+X23+X24) 工程3利润: 20*X31+150*(X31+X32)+150*(X31+X32+X33)+150*(X31+X32+X33+X34) 工程4利润: 20*X43+20*(X43+X44) max(50*X11+50*(x11+x12)+50*(X11+X12+X13)+50*(X11+X12+X13))+(70*X22+70*(X22+X23) )+70*(X22+X23+X24)+(150*X31+150*(X31+X32)+150*(X31+X32+X33)+150*(X31+X32+X33+X34)) +(20*X43+20*(X43+X44)) st 5000*X11+15000*X31=3000 5000*X12+8000*X22+15000*X32=6000 5000*X13+8000*X23+15000*X33+1200*X43=7000 8000*X24+15000*X34+12000*X44=7000 8000*X25+15000*X35=7000 X11+X12+X13=1 X22+X23+X24+X25≥ X22+X23+X24+X25≤1 X31+X32+X33+X34+X35≥ X31+X32+X33+X34+X35≤1 X43+X44=1 全为大于零的数 基于最短路问题的研究及应用令狐采学 姓名:Fanmeng 学号: 指导老师: 摘要 最短路问题是图论中的一大问题,对最短路的研究在数学建模和实际生活中具有很重要的实际意义,介绍最短路问题的定义及这类问题的解决办法Dijkstra算法,并且能够在水渠修建实例运用到此数学建模的方法,为我们解决这类图论问题提供了基本思路与方法。 关键字数学建模最短路问题Dijkstra算法水渠修建。 目录 第一章.研究背景1 第二章.理论基础2 2.1 定义2 2.2 单源最短路问题Dijkstra求解:2 2.2.1 局限性2 2.2.2 Dijkstra算法求解步骤2 2.2.3 时间复杂度2 2.3 简单样例3 第三章.应用实例4 3.1 题目描述4 3.2 问题分析4 3.3符号说明4 3.4 模型假设5 3.5模型建立与求解5 3.5.1模型选用5 3.5.2模型应用及求解5 3.6模型评价5 第四章. 参考文献5 第五章.附录6 第一章.研究背景 在现实生活中中,我们经常会遇到图类问题,图是一种有顶点和边组成,顶点代表对象,在示意图中我们经常使用点或者原来表示,边表示的是两个对象之间的连接关系,在示意图中,我们使用连接两点G点直接按的下端来表示。顶点的集合是V,边的集合是E的图记为G[V,E] ,连接两点u和v的边用e(u,v)表示[1]。最短问题是图论中的基础问题,也是解决图类问题的有效办法之一,在数学建模中会经常遇到,通常会把一个实际问题抽象成一个图,然后来进行求的接任意两点之间的最短距离。因此掌握最短路问题具有很重要的意义。 第二章.理论基础 2.1 定义 最短路问题(short-path problem ):若网络中的每条边都有一个数值(长度、成本、时间等),则找出两节点,(通常是源节点和目标节点)之间总权和最小的路径就是最短路问题。最短路问题是网络理论解决的典型问题之一,可用来解决管道铺设,线路安装,厂区布局和设备更新等实际问题[2]。 2.2 单源最短路问题Dijkstra 求解: 2.2.1局限性 Dijkstra 算法不能够处理带有负边的图,即图中任意两点之间的权值必须非负。 2.2.2Dijkstra 算法求解步骤 (1).先给图中的点进行编号,确定起点的编号。 (2).得到图的构成,写出写出图的矩阵 0000(,)(,) (,) (,) n n n n u u u u G u u u u = (3).根据要求求出发点S 到终点E 的最短距离,那么需要从当前没被访问过的结点集合 unvist={u | u {1,2,3...}}n ∈中找到一个距离已经标记的点的集合中vist={u | u {1,2,3...}}n ∈的最短距离,得到这个顶点; (4).利用这个顶点来松弛其它和它相连的顶点距离S 的值 (5).重复步骤(2)和(3),直到再也没有点可以用来松弛其它点,这样我们就得到了由起点S 到其它任意点的最短距离。 2.2.3时间复杂度 时间复杂度达到 2 ()O N A题机组组合问题 当前的科学技术还不能有效地存储电力,所以电力生产和消费在任何时刻都要相等,否则就会威胁电力系统安全运行。又由于发电机组的物理特性限制,发电机组不能够随心所欲地发出需要的电力。为了能够实时平衡变化剧烈的电力负荷,电力部门往往需要根据预测的未来电力负荷安排发电机组起停计划,在满足电力系统安全运行条件下,追求发电成本最小。 在没有电力负荷损耗以及一个小时之内的电力负荷和发电机出力均不变的前提下,假定所有发电机组的发电成本都是由3部分组成,它们是启动成本(Startup Cost),空载成本(No load cost)和增量成本(Incremental Cost)。需要考虑的约束有: 1.负荷平衡约束:任何小时,电力负荷之和必须等于发电机发电出力之和。 2.系统备用约束:处于运行状态的发电机的最大发电能力减去其出力称为该发电机的备用容量,处于停运状态的发电机的备用容量为0。任何小时,发电机的备用容量之和必须大于系统备用要求。 3.输电线路传输容量约束:线路传输的电能必须在它的传输容量范围内。 4.发电机组出力范围约束:处于运行状态的发电机组的发电出力必须小于其最大发电能力(Pmax, MW)。 5.机组增出力约束(Ramp Up, MW/h):发电机组在增加发电出力时,不能太快,有一个增加出力的速度上限,在一定时间内(通常是10分钟,为简单起见,本题取1个小时)不能超过额定范围。 6.机组降出力约束(Ramp Down, MW/h):与机组增出力约束类似,发电机组在减少发电出力时也有一个减少出力的速度上限。 问题1:3母线系统 有一个3母线系统,其中有2台机组、1个负荷和3条输电线路,已知4个小时的负荷和系统备用要求。请求出这4个小时的最优机组组合计划。最终结果应该包括总成本、各小时各机组的状态、各小时各机组的发电出力和各小时各机组提供的备用。所有数据请见下面图及表格,“3BusData”目录中还有包含了本题所有表格数据的5个xml文件。 《数学建模》课程简介 20053025 数学建模 4.5 Mathematical Modeling 4-1 预修要求:微积分、线性代数 面向对象:竺可桢学院工程高级班 内容简介: 本课程以物理、生态、环境、医学、管理、经济、信息技术等领域的一些典型实例为背景,阐述如何通过建立数学模型的方法来研究、解决实际问题的基本方法和技能。开设本课程的目的是,在传授知识的同时,通过典型建模实例的分析和参加建模实践活动,培养和增强学生自学能力、创新素质。参加数学建模课的学习,应自己动手解决一、二个实际问题,以求在实际参与中获取真知。 本课程包括一定学时的讨论班,学生可利用课外时间自己参与建模实践活动并自愿参加由指导教师组织的讨论班活动。选修本课程的本科生经双向选择还有机会参加全国大学生数学建模竞赛(每年约90人)和美国大学生数学建模竞赛(每年为21人)。 推荐教材或参考书: “数学建模”,杨启帆、谈之奕、何勇编著,浙江大学出版社出版,2006年7月 《数学建模》教学大纲 20053025 数学建模 4.5 Mathematical Modeling 4-1 预修要求:微积分、线性代数 面向对象:竺可桢学院工程高级班 一、教学目的与基本要求: 通过典型数学模型分析和课外建模实践,使学生基本掌握运用数学知识建立数学模型来研究科研问题或实际课题的基本技能与基本技巧,本课程教学除传授知识外还要求学生在实际建模中注意培养和提高自身的能力,以便提高自己的综合素质与实际本领。 二、主要内容及学时分配: 1.数学建模概论,3学时 2.初等模型,8学时:舰艇的汇合,双层玻璃的功效,崖高的估算,经验模型,参数 识别,量纲分析法建模,方桌问题、最短路径与最速方案等 3.微分方程建模,14学时:马尔萨斯模型和罗杰斯蒂克模型,为什么要用三级火箭发 射人造卫星,药物在体内的分布,传染病模型,捕食系统的P-P模型,双种群生态 系统研究等 1 预测模块:灰色预测、时间序列预测、神经网络预测、曲线拟合(线性回归); 2 归类判别:欧氏距离判别、fisher判别等; 3 图论:最短路径求法; 4 最优化:列方程组用lindo 或lingo软件解; 5 其他方法:层次分析法马尔可夫链主成分析法等; 6 用到软件:matlab lindo (lingo)excel ; 7 比赛前写几篇数模论文。 这是每年参赛的赛提以及获奖作品的解法,你自己估量着吧…… 赛题解法 93A非线性交调的频率设计拟合、规划 93B足球队排名图论、层次分析、整数规划 94A逢山开路图论、插值、动态规划 94B锁具装箱问题图论、组合数学 95A飞行管理问题非线性规划、线性规划 95B天车与冶炼炉的作业调度动态规划、排队论、图论 96A最优捕鱼策略微分方程、优化 96B节水洗衣机非线性规划 97A零件的参数设计非线性规划 97B截断切割的最优排列随机模拟、图论 98A一类投资组合问题多目标优化、非线性规划 98B灾情巡视的最佳路线图论、组合优化 99A自动化车床管理随机优化、计算机模拟 99B钻井布局0-1规划、图论 00A DNA序列分类模式识别、Fisher判别、人工神经网络 00B钢管订购和运输组合优化、运输问题 01A血管三维重建曲线拟合、曲面重建 01B 工交车调度问题多目标规划 02A车灯线光源的优化非线性规划 02B彩票问题单目标决策 03A SARS的传播微分方程、差分方程 03B 露天矿生产的车辆安排整数规划、运输问题 04A奥运会临时超市网点设计统计分析、数据处理、优化 04B电力市场的输电阻塞管理数据拟合、优化 05A长江水质的评价和预测预测评价、数据处理 05B DVD在线租赁随机规划、整数规划 第十三章线性规划与数学建模简介 【授课对象】理工类专业学生 【授课时数】6学时 【授课方法】课堂讲授与提问相结合 【基本要求】1、了解数学模型的基本概念、方法、步骤; 2、了解线性规划问题及其数学模型; 3、了解线性规划问题解的性质及图解法. 【本章重点】线性规划问题. 【本章难点】线性规划问题、线性规划问题解的性质、图解法. 【授课内容】 本章简要介绍数学建模的基本概念、方法、步骤,并以几个典型线性规划问题为例,介绍构建数学模型的方法及其解的性质。 §1 数学建模概述 一、数学建模 数学建模是构造刻划客观事物原型的数学模型并用以分析、研究和解决实际问题的一种科学方法。运用这种科学方法,必须从实际问题出发,遵循从实践到认识再实践的认识规律,围绕建模的目的,运用观察力、想象力的抽象概括能力,对实际问题进行抽象、简化,反复探索,逐步完善,直到构造出一个能够用于分析、研究和解决实际问题的数学模型。因此,数学建模是一种定量解决实际问题的创新过程。 二、数学模型的概念 模型是人们对所研究的客观事物有关属性的模拟。例如在力学中描述力、 量和加速度之间关系的牛顿第二定律F=ma就是一个典型的(数学)模型。一般地,可以给数学模型下这样的定义:数学模型是磁于以部分现实世界为一定目的而做的抽象、简化的数学结构。 通俗而言,数学模型是为了一定目的对原型所作的一种抽象模拟,它用数学式子,数学符号以及程序、图表等描述客观事物的本质特征与内在联系。 三建立数学模型的方法和步骤 建立数学模型没有固定模式。下面介绍一下建立模型的大体过程: 1.建模准备 建模准备是确立建模课题的过程。这类课题是人们在生产和科研中为了使 认识和实践过一步发展必须解决的问题。因此,我们首先要发现这类需要解决的实际问题。其次要弄清所解决问题的目的要求并着手收集数据。进行建模筹划,组织必要的人力、物力等,确立建模课题。 2.模型假设 作为建模课题的实际问题都是错综复杂的、具体的。如果不对这些实际问题进行抽象简化,人们就无法准确把握它的本质属性,而模型假设就是根据建模的目的对原型进行抽象、简化,抓住反映问题本质属性的主要因素,简化掉那些非本质的次要因素。有了这些假设,就可以在相对简单的条件下,弄清各因素之间的关系,建立相应的模型。 合理的假设是建立理想模型的必要条件和基本保证。如果假设是合理的,则模型切合实际,能解决实际问题;如果假设不合理中或过于简化,则模型与实际情况不符或部分相符,就解决不了问题,就要修改假设,修改模型。 3.构造模型数学建模生产计划有关问题解析
数学建模模最短路
数学建模常见评价模型简介
电力生产问题数学模型
数学建模简介
数学建模之电力的生产问题
数学建模电力安排问题
数学建模运输问题
数学建模中常见的十大模型
数学建模的介绍
数学建模 生产计划问题
数学建模模最短路
数模A题:机组组合问题
数学建模课程简介
数学建模常见问题
线性规划与数学建模简介
