二次互反律

二次互反律
在数论中,特别是在同余理论里,二次互反律是一个用于判别二次剩余,即二次同余方程()q p x mod 2≡之整数解的存在性的定律。二次互反律揭示了方程()q p x mod 2≡可解和 ()q p x mod 2≡可解的简单关系。运用二次互反律可以将模数较大的二次剩余判别问题转为模数较小的判别问题,并最后归结为较少的几个情况,从而在实际上解决了二次剩余的判别问题。然而,二次互反律只能提供二次剩余的存在性,对于二次同余方程的具体求解并没有实际帮助。
二次互反律常用勒让德符号表述:对于两个奇素数p 和q ,
其中
是勒让德符号。但是对于更一般的雅可比符号和希尔伯特符号也有对应的二次互反律。
欧拉和勒让德都曾经提出过二次互反律的猜想。但第一个严格的证明是由高斯在1796年作出的,随后他又发现了另外七个不同的证明[1]。在《算数研究》一书和相关论文中,高斯将其称为“基石”。私下里高斯把二次互反律誉为算术理论中的宝石,是一个黄金定律[2]。
高斯之后雅可比、柯西、刘维尔、克罗内克、弗洛贝尼乌斯等也相继给出了新的证明。至今,二次互反律已有超过200个不同的的证明。二次互反律可以推广到更高次的情况,如三次互反律等等。 相关术语
一个整数a 是模整数n 的二次剩余,是指它与某个整数的平方关于模n 同余。直观来说,是指二次同余方程()n a x mod 2≡有整数解。如果这样的整数解不存在,则称a 是模整数n 的二次非剩余。术语中的“二次”一词是为了表示平方同余,在不至于混淆的行文中,可以略掉。当模数是质数时,通常将0的情况区别讨论,因此有:
在模为质数时,二次剩余与二次非剩余的个数是相等的。
在模为质数时,剩余与剩余、非剩余与非剩余的乘积都是剩余,剩余与非剩余的乘积是非剩余。
几个简单情况
有了上节的关于乘积的性质,可以发现:研究一个合数是否是模某个质数p 的剩余,只需将这个合数进行质因数分解,研究其每个质因数是不是模p 的剩余即可。因此,为了寻找模质数的二次剩余的规律,可以先研究对于前几个质数2、3、5等的情况,看对于什么样的质数p ,2、3、5等是模它们的剩余。此外为了
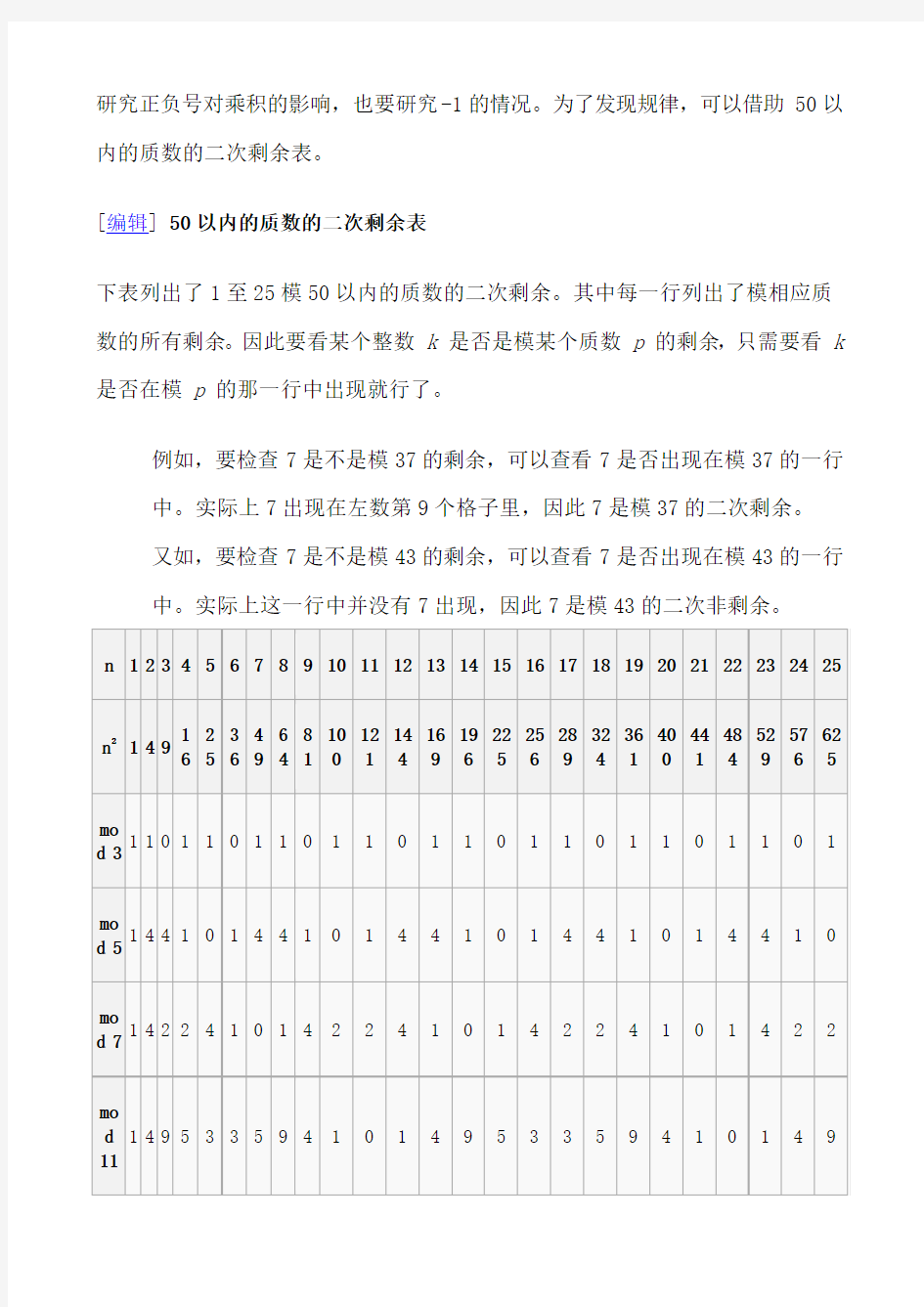
研究正负号对乘积的影响,也要研究-1的情况。为了发现规律,可以借助50以内的质数的二次剩余表。
[编辑] 50以内的质数的二次剩余表
下表列出了1至25模50以内的质数的二次剩余。其中每一行列出了模相应质数的所有剩余。因此要看某个整数k是否是模某个质数p的剩余,只需要看k 是否在模p的那一行中出现就行了。
例如,要检查7是不是模37的剩余,可以查看7是否出现在模37的一行中。实际上7出现在左数第9个格子里,因此7是模37的二次剩余。
又如,要检查7是不是模43的剩余,可以查看7是否出现在模43的一行中。实际上这一行中并没有7出现,因此7是模43的二次非剩余。
n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
n2 1 4 9 1
6
2
5
3
6
4
9
6
4
8
1
10
12
1
14
4
16
9
19
6
22
5
25
6
28
9
32
4
36
1
40
44
1
48
4
52
9
57
6
62
5
mo
d 3
1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1
mo
d 5
1 4 4 1 0 1 4 4 1 0 1 4 4 1 0 1 4 4 1 0 1 4 4 1 0
mo
d 7
1 4
2 2 4 1 0 1 4 2 2 4 1 0 1 4 2 2 4 1 0 1 4 2 2
mo
d
11
1 4 9 5 3 3 5 9 4 1 0 1 4 9 5 3 3 5 9 4 1 0 1 4 9
mo
d 13 1 4 9 3
1
2
1
1
1
2
3 9
4 1 0 1 4 9 3 12 10 10 12 3 9 4 1
mo
d 17 1 4 9
1
6
8 2
1
5
1
3
1
3
15 2 8 16 9 4 1 0 1 4 9 16 8 2 15 13
mo
d 19 1 4 9
1
6
6
1
7
1
1
7 5 5 7 11 17 6 16 9 4 1 0 1 4 9 16 6 17
mo
d 23 1 4 9
1
6
2
1
3
3
1
8
1
2
8 6 6 8 12 18 3 13 2 16 9 4 1 0 1 4
mo
d 29 1 4 9
1
6
2
5
7
2
6
2
3
13 5 28 24 22 22 24 28 5 13 23 6 20 7 25 16
mo
d 31 1 4 9
1
6
2
5
5
1
8
2
1
9
7 28 20 14 10 8 8 10 14 20 28 7 19 2 18 5
mo
d 37 1 4 9
1
6
2
5
3
6
1
2
2
7
7 26 20 33 21 11 3 34 30 28 28 30 34 3 11 21 33
mo
d 41 1 4 9
1
6
2
5
3
6
8
2
3
4
18 39 21 5 32 20 10 2 37 33 31 31 33 37 2 10
mo
d 43 1 4 9
1
6
2
5
3
6
6
2
1
3
8
14 35 15 40 24 10 41 31 23 17 13 11 11 13 17 23
[编辑]–1的情况
首先,看看对于什么样的质数,–1是模它的二次剩余。查对上表后可以发现:–1对于模5,13,17,29,37是二次剩余,而对3,7,11,19,23,31,43则不是。比如:–1 ≡ 2 (mod 3),–1 ≡ 4 (mod 5),–1 ≡ 10 (mod 11),等等。
可以发现前者都是模4余1的质数,后者都是模4余3的质数。于是可以猜想:
同余方程有解当且仅当。
[编辑] 2的情况
接下来看对什么样的质数,2是模它的二次剩余。同样查对上表后可以发现:对于模8余±1的质数,如7,17,23,31,41,47,2是模它的二次剩余。对于模8余±3的质数如3,5,11,13,19,29,37 等则不然。
[编辑] 3的情况
3是模11、13、23、37和47的剩余,但不是模5、7、17、19、29、31、41或43的剩余。
前者模12都余±1,后者都模12余±5。
–3是模7、13、19、31、37和43的剩余,但不是模5、11、17、23、29、41或47的剩余,前者模3都余1,后者模3都余2。
由于模3的剩余只有1,可以发现一个规律:对于所有为模3的剩余的质数,-3是模它的剩余。
[编辑] 5的情况
5是模11、19、29、31和41的剩余,但不是模3、7、13、17、23、37、43或47的剩余,前者模5都余±1,后者模5都余±2。
由于模5的剩余只有±1,可以发现规律:对于所有为模5的剩余的质数,5是模它的剩余。
[编辑]高斯和勒让德的叙述
对于一般的情况,也有类似的规律。在此基础上,高斯和勒让德提出了两个一般性的叙述(没有使用勒让德符号),两者是等价的。
[编辑]高斯的叙述
如果那么可解当且仅当可解。
如果那么可解当且仅当
可解。借助于以下变量:,命题可以简化为:
可解当且仅当可解。
在高斯的叙述中已经可以见到“互反”的体现,即将的可解性与的可解性联系起来。在下表中可以看出,这表现了一种对称性(反对称性)。
下表列明了质数之间相互是否为二次剩余的情况。方格内为R表示对应的q(横列元素)为对应的p(竖列元素)的二次剩余,N则表示相反情况(此表示法由高斯创造)。可以看到白格内的元素是关于对角线对称的,黄格内则关于对角线反对称。可以说黄格代表了一种“特殊情况”[3]。
q
3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
p
3 N R N R N R N N R R N R N N N R R N R R N N R 5 N N R N N R N R R N R N N N R R N R N R N R N 7 N N R N N N R R N R N R N R N N R R N R N N N 11 R R N N N N R N R R N N R R R N R R N N N R R 13 R N N N R N R R N N N R N R N R N N N R N N N 17 N N N N R R N N N N N R R R R N R N N N R R N 19 N R R R N R R N N N N R R N N R N N R N R N N 23 R N N N R N N R R N R N R N R N N R R N N N N 29 N R R N R N N R N N N N N R R N R R N N R N N 31 N R R N N N R N N N R N R N R N R R N N N N R 37 R N R R N N N N N N R N R R N N R R R N R N N
41 N R N N N N N R N R R R N N R R N N R N R N N
43 N N N R R R N R N R N R R R R N R N N R R N R
47 R N R N N R N N N N R N N R R R N R N R R R R
53 N N R R R R N N R N R N R R R N N N N N N R R
59 R R R N N R R N R N N R N N R N N R N R N N N
61 R R N N R N R N N N N R N R N N N N R N R N R
67 N N N N N R R R R N R N N R N R N R R N R R N
71 R R N N N N R N R N R N R N N N N N R R R R N
73 R N N N N N R R N N R R N N N N R R R R N R R
79 N R N R R N R R N R N N N N N N N R N R R R R
83 R N R R N R N R R R R R N N N R R N N N N N N
89 N R N R N R N N N N N N N R R N N R R R R N R
97 R N N R N N N N N R N N R R R N R N N R R N R [编辑]勒让德的叙述
观察上表中黄格的情况,可以看出相对应的两个质数都是模4余3的。因此勒让德的陈述为:
如果或者那么
可解当且仅当可解。
如果那么
可解当且仅当不可解。
[编辑]研究历史
二次互反律曾被不少的数学家研究,因此二次互反律的叙述有很多种。要注意的是当时的数学记号并不统一。欧拉和勒让德并没有高斯的同余记号,高斯也不知道勒让德符号。
下文中的p和q总是不相等的正奇质数。
[编辑]前期探索
费马曾经证明了[4](或声称证明了[5])一系列关于将质数表示成平方和的定理
当且仅当p = 2 或
p = x2 + 2y2当且仅当p = 2 或
p = x2 + 3y2当且仅当p = 3 或
他并没有给出二次互反律的陈述,尽管由此类的定理可以得到–1、±2和±3的情况。
此外欧拉曾经猜想(后被勒让德证明)[6]:
如果那么
如果那么pq = x2 + 5y2.
证明费马的这类命题是导致二次互反律的发现的因素之一。
[编辑]定理的首次叙述:欧拉
欧拉在1783年曾经写过[7](以现今的符号表示):
1) 如果q≡ 1 (mod 4) 那么q是模p的二次剩余当且仅当p≡r (mod q),其中r是一个模q的二次剩余。
2) 如果q≡ 3 (mod 4) 那么q是模p的二次剩余当且仅当p≡±b2(mod 4q), 其中b为奇数但不被q整除。
这是二次互反律首次被完整地陈述[8]。欧拉也证明了[9] 2的情况。
[编辑]勒让德与他的符号
勒让德用a和A表示模4余1的正质数,用b和B表示模4余3的正质数。他
建立了一个有8个定理的表格,这8个定理合起来就是二次互反律[10]。
III
VII
VIII
勒让德认为表达式出现了太多次,可以简写为:
其中N 、c 为互质的数[11]。
这个符号就是现在使用的勒让德符号[12]: 对于所有的整数a 以及任意奇质数p :
. ; .
.
勒让德使用勒让德符号的叙述为:
如果p 整除a ;
如果a 是模p 的二次剩余且p 不整除a
如果a 是模p 的二次非剩余。
,如果或
,如果
他也提到上面的两种情况可以合并为:
勒让德完整地证明了八种情况中的第一、第二和第七种。在证明第八种情况时,勒让德作了一个可以等价于狄利克雷定理的假设。正如高斯在其《算术研究》中指出的。勒让德实际上证明了二次互反律是狄利克雷定理成立的情况下的一个推论[13]。
[编辑]首次的证明:高斯
1801年出版的《算术研究》第131篇的部分,列出了二次互反律的8种情况
第一个完整地给出二次互反律的证明的人是德国数学家高斯。高斯在1796年给出了二次互反律的第一个证明[14]。高斯首先证明了[15]-1和2的情况。作为进行数学归纳法的开始,他证明了[16]±3和±5的情况。他注意到-3和+5的情况较有规律,容易叙述[17],因此把定理叙述为[18]:
如果p是形式为4n + 1,那么p(如果p是形式为4n + 3那么?p)是模每个为模p的二次剩余(非剩余)的质数的二次剩余(非剩余)。
在下一句中,高斯将其列为“基本定理”(但没有用到“互反律”的称谓)。在引进()表示a是模b的二次剩余(非剩余)后,高斯令a和表示模4余1的质数,用b和表示模4余3的,于是写出了勒让德得到的8种情况:
在接下来的文章中他将其推广到关于所谓的雅可比符号,以下的大写字母表示的意思和相应的小写字母一样,但不再是质数。
情况如果那么
9) ±a R A±A R a
10) ±b R A +A R b –A N b
11) +a R B±B R a
12) –a R B±B N a
13) +b R B –B N b +N R b
14) –b R B +B R b –B N b
最后他分各种情况分别运用强数学归纳法将其证明[19]。证明中高斯用到了[20]一个引理:
如果是质数,那么存在奇质数使得
如果使用勒让德符号,那么高斯的陈述就是
令,也就是说 | q* | = | q | 且。
那么
高斯一生中给出了二次互反律的八个证明,其中他最为满意的是第五个证明。[编辑]其它陈述
[编辑]欧拉
如果那么[21]
[编辑]艾森斯坦
艾森斯坦[22]曾声称:
如果并且那么
[编辑]莫德尔
莫德尔[23]证明了以下命题与二次互反律等价:
令a,b和c为整数,那么对每个整除abc的质数p有:
如果有一个非平凡解,那么
也有。
[编辑]关于雅可比符号的互反律
雅可比符号是勒让德符号的一个推广,与后者主要的区别是“分母”只需为正奇数,而不需要一定是质数。当“分母”为质数时,两者意义相同。雅可比符号的运算规律与勒让德符号相同,即:
如果两个数都是正奇数,那么二次互反律对雅可比符号也成立:
然而,当雅可比符号为+1,“分母”为合数时,“分子”不一定是“分母”的二次剩余。高斯的第九至十四种情况可以被表示为:
由于p为质数,上式左边是勒让德符号,于是我们可以知道M是否是模p的剩余。
以上各节的公式对雅可比符号仍然成立。欧拉的公式可以写作:
其中n为整数,
举例来说:2是模7、23、31的剩余,但2是模5的非剩余,因此也不是模15的。这与勒让德提出过的一个问题有关:若已知,我们知道a是模m + 4a、m + 8a、……中所有质数的非剩余,如果这种质数存在的话。但此种质数的存在性直到数十年后才由狄利克雷证明。艾森斯坦的公式则需要两数互质才能成立:如果a,b,a',b' 是正奇数,且gcd(a,b) = gcd(a',b') = 1,那么
如果且,则
[编辑]使用希尔伯特符号的互反律
二次互反律也可以用希尔伯特符号:(a,b)v来叙述。其中a、b是两个非零的有理数,v则可代表任意非平凡的有理数绝对值(p的常用的或p进的绝对值)。希尔伯特符号:(a,b)v的值取1或?1。按照定义,它的值取1当且仅当方程ax2 + by2 = z2在有理数关于v的完备空间中有除了x = y = z = 0之外的解。希尔伯特二次互反律声称:对于固定的a、b,当v变动时,除了对有限个v以外,(a,b)v的值都是1,并且取遍所有v时,所有 (a,b)v的乘积为1(这与复分析中的留数定理相似)。
希尔伯特二次互反律的证明可以归结到几个特殊情况,可以证明其中非平凡的情况与勒让德符号下的二次互反律的两个辅助定理(-1和2的情况)是等价的。在希尔伯特二次互反律中其实并没有“互反”的情形,它的名字只是表明它的历史来源是作为二次互反律的研究成果。不同于二次互反律要考虑正负问题,并要区分2的情况,希尔伯特二次互反律对所有的有理数都是平等的。因此使用希尔伯特符号的二次互反律推广起来更为自然:其推广到整体域时只需做出很少改变,并对所有的整体域都适用[24]。
[编辑]应用
以二次互反律配合以下两个辅助定理
即能迅速地计算勒让德符号,从而解决二次剩余的判别问题。
例如判别37是否是模89的二次剩余:
所以
因此37是不是模89的二次剩余。
[编辑]推广
二次互反律的推广主要是在代数数论中。
例如:高斯考察过四次互反律。在他的[25]首篇论文里他证明了一系列定理,其中最重要的是:如果,那么有解当且仅当p= a2+ 64b2,其中a、b是整数。如果,那么模p的二次剩余必然是四次剩余。
在第二篇论文中[26],高斯引进了著名的高斯整数。高斯证明了模4余1的质数总能分解为两个高斯整数中质数的乘积、唯一分解定理等其它代数数论的基础定理,并引进了一些基本概念,如范数和单位元。在高斯整数中,四次互反律的叙述十分简单。高斯并且注意到在艾森斯坦整环中,三次互反律最为简单。一部分的原因是高斯整数中1有4个四次方根,而艾森斯坦整数中1有3个三次方根。
其它的推广是在以上整环中的二次互反律。高斯率先研究了高斯整数中的二次互反律[27]。
参见
?同余
?同余方程
?二次剩余
?高斯引理
?二次互反律的证明
?三次互反律
?阿廷互反律
[编辑]注释及参考来源
1.^ Gauss, DA § 4, arts 107-150
2.^例如在其1796年4月8日(他初次证明二次互反律的日子)的数学日志里,参
看Felix Klein 的《19世纪数学进程》
3.^蕭文強,數學=證明?
4.^ Lemmermeyer, pp. 2-3
5.^ Gauss, DA, art. 182
6.^ Lemmermeyer, p. 3
7.^ Lemmermeyer, p. 5, Ireland & Rosen, p 54, 61
8.^Proving the law of guadratic reciprocity
9.^ Ireland & Rosen, pp. 69-70. 他的证明基于后来所称的“高斯和”。
10.^ Lemmermeyer, pp. 6-8
11.^ Comm e les quantités analogues se renconteront fréquemment dans le
cours de nos recherches, nous emploierons le caractères abrégés pour
exprimer le reste que donne di visé par c, reste qui suivant ce qu'on vient de voir ne peut être que +1 ou -1. --(法語)Adrien-Marie Legendre (1788年).Recherche d'analyse indéterminée, Histoire de l'Académie Royale des Sciences.
12.^由欧拉判别法,两者等价
13.^ Lemmermeyer, pp. 8
14.^Proving the law of quadratic reciprocity
15.^ Gauss, DA, arts 108-116
16.^ Gauss, DA, arts 117-123
17.^ Gauss, DA, arts 130
18.^ Gauss, DA, Art 131
19.^ Gauss, DA, arts 135-144
20.^ Gauss, DA, arts. 125-129
21.^ Ireland & Rosen, p 60-61.
22.^ Lemmermeyer, Th. 2.28, pp 63-65
23.^ Lemmermeyer, ex. 1.9, p. 28
24.^诺丁汉大学数学线上教程:希尔伯特符号及希尔伯特二次互反律证明
25.^ C. F. Gauss, Theorie der biquadratischen Reste, Comm. Soc. Reg. Sci.
Gottingen (1828); 重印于Untersuchungen uber hohere Arithmetik, pp.
511-533
26.^ C. F. Gauss, Theoria residuorum biquadraticorum. Commentatio secunda.,
Comm. Soc. Reg. Sci. Gottingen 7 (1832) 1-34; 重印于Untersuchungen uber hohere Arithmetik, pp. 534-589
27.^四次互反律的首篇论文Lemmermeyer, p.154中给出了狄利克雷的一个用到二次
互反律的简单证明。Ireland & Rosen, p. 64, ex. 26
Gauss, Carl Friedrich & Arthur A. (translator into English) Clarke (1986), Disquisitiones Arithemeticae (Second, corrected edition), New York: Springer, ISBN 0387962549
幂函数指数函数和对数函数·反函数
幂函数、指数函数和对数函数·反函数 教学目标 1.使学生正确理解反函数的概念,初步掌握求反函数的方法. 2.培养学生分析问题、解决问题的能力及抽象概括的能力. 3.使学生思维的深刻性进一步完善. 教学重点与难点 教学重点是求反函数的技能训练. 教学难点是反函数概念的理解. 教学过程设计 一、揭示课题 师:今天我们将学习函数中一个重要的概念——反函数. (板书:反函数 1.反函数的概念) 二、讲解新课 师:什么是反函数呢?让我们一起来思考这样一个问题:在函数y=2x+1中,如果把x当作因变量,把y当作自变量,能否构成一个函数呢? 生:可以构成一个函数. 师:为什么是个函数呢? 一的x与之相对应. 师:根据这位同学的表述,这是符合函数定义的,也就是说,按照上述原则,函数y=2x+1是存在反函数的.这个反函数的解析式是怎样的呢?
师:这种表示方法是没有问题的,但不符合我们的习惯,按习惯用字母x 表示自变量,用字母y表示因变量,故这个函数的解析式又可以 是不是同一函数呢? 生:是. 师:能具体解释一下吗? 和值域,皆为R,同时对应法则都是自变量减1除以2得因变量,也是相同的,所以它们是相同的函数. 生:有.就是y=2x+1. 那么,是不是所有函数都会有反函数呢? 生:不是所有函数都有反函数. 师:能举个例子说明吗? 生:如函数y=x2,将y当作自变量,x当作因变量,在y允许取值范围内,一个y可能对应两个x,如y=1,则对应x=±1,因此不能构成函数,说明它没有反函数. 师:说得非常好.如果从形的角度来解释,会看得更清楚,见图1,从图中可看出给出一个y能对应两个x.
幂法及反幂法
随机产生一对称矩阵,对不同的原点位移和初值(至少取3个)分别使用幂法求计算矩阵的主特征值及主特征向量,用反幂法求计算矩阵的按模最小特征值及特征向量。 要求 1)比较不同的原点位移和初值说明收敛性 2)给出迭代结果,生成DOC 文件。 3)程序清单,生成M 文件。 解答: >> A=rand(5) %随机产生5*5矩阵 求随机矩阵 A = 0.7094 0.1626 0.5853 0.6991 0.1493 0.7547 0.1190 0.2238 0.8909 0.2575 0.2760 0.4984 0.7513 0.9593 0.8407 0.6797 0.9597 0.2551 0.5472 0.2543 0.6551 0.3404 0.5060 0.1386 0.8143 >> B=A+A' %A 矩阵和A 的转置相加,得到随机对称矩阵B B = 1.4187 0.9173 0.8613 1.3788 0.8044 0.9173 0.2380 0.7222 1.8506 0.5979 0.8613 0.7222 1.5025 1.2144 1.3467 1.3788 1.8506 1.2144 1.0944 0.3929 0.8044 0.5979 1.3467 0.3929 1.6286 B=??? ???? ???? ?? ???6286.13929.03467.15979.08044.03929.00944.12144.18506.13788.13467.12144.15025.17222.08613.05979.08506.17222.02380.09173.08044.03788.18613.09173.04187.1
幂法_反幂法求解矩阵最大最小特征值和对应的特征向量
数值计算解矩阵的按模最大最小特征值及对应的特征向量 一.幂法 1. 幂法简介: 当矩阵A 满足一定条件时,在工程中可用幂法计算其主特征值(按模最大)及其特征向量。矩阵A 需要满足的条件为: (1) 的特征值为A i n λλλλ,0||...||||21 ≥≥≥> (2) 存在n 个线性无关的特征向量,设为n x x x ,...,,21 1.1计算过程: i n i i i u x x αα,1 ) 0()0(∑==,有对任意向量不全为0,则有 1 11111221 12111 1 1 11 1 011)()(...u u a u a u λu λαu αA x A Ax x k n n k n k k n i i k i i n i i i k )(k (k))(k αλλλλλα++++=+=+++≈? ? ????+++======∑∑Λ 可见,当||1 2 λλ越小时,收敛越快;且当k 充分大时,有1)1111)11111λαλαλ=??? ???==+++(k )(k k (k k )(k x x u x u x ,对应的特征向量即是)(k x 1+。 2 算法实现 . ,, 3,,1 , ).5() 5(,,,,||).4();max(,).3() (max(;0,1).2(,).1()() () (停机否则输出失败信息转置若转否则输出若计算最大迭代次数,误差限,初始向量输入矩阵βλβεβλβλε←+←<<-←←= ←←k k N k y x Ay x x abs x y k N x A k k k 3 matlab 程序代码
function[t,y]=lpowerA,x0,eps,N) % t 为所求特征值,y是对应特征向量 k=1; z=0; % z 相当于λ y=x0./max(abs(x0)); % 规范化初始向量 x=A*y; % 迭代格式 b=max(x); % b 相当于β if abs(z-b) 〖2.3〗幂函数 (1)幂函数的定义 一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数. (图象关. ②过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1). ③单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴. ④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当q p α= (其中,p q 互质,p 和q Z ∈),若 p 为奇数q 为奇数时,则q p y x =是奇函数,若p 为奇数q 为偶数时,则q p y x =是偶函数,若p 为偶数q 为奇数时,则q p y x =是非奇非偶函数. ⑤图象特征:幂函数 ,(0,)y x x α=∈+∞,当1α>时,若01x <<,其图象在直线y x =下方,若1x >,其图象在直线y x =上方,当1α<时,若01x <<,其图象在直线y x =上方,若1x >,其图象在直线y x =下方. 反函数 反函数的基本知识点 一.定义:设式子)(x f y = 表示y 是x 的函数,定义域为A ,值域为C ,从式子)(x f y =中解出x ,得到式子)(y x ?=,如果对于y 在C 中的任何一个值,通过式子)(y x ?=,x 在A 中都有唯一确定的值和它对应,那么式子)(y x ?=就表示x 是y 的函数(y 是自变量),这样的函数,叫做)(x f y =的反函数 ,记作)(1y f x -=,即()y f y x 1)(-==?,一般习惯上对调()y f x 1-=中的字母y x ,,把它改写成)(1x f y -=。 (1).反函数存在的条件:从定义域到值域上的一一映射确定的函数才有反函数; (2).原函数的定义域、值域分别是反函数的值域、定义域, ()图象在点图象上)在(点几何语言: )(),(,)()(11x f y a b P x f y b a P a b f b a f --='?==?= (3).()y f x =与1()y f x -=的图象关于y x =对称. 二.求反函数的一般步骤 (1) 确定原函数的值域,也就是反函数的定义域 (2) 由)(x f y =的解析式求出)(y x ?= (3) 将y x ,对换,得反函数的一般表达式)(1x f y -=,标上反函数的定义 域(反函数的定义域不能由反函数的解析式求得) 分段函数的反函数可以分别求出各段函数的反函数后再合成。 三.掌握下列一些结论 《数值分析》计算实习题目 第一题: 1. 算法设计方案 (1)1λ,501λ和s λ的值。 1)首先通过幂法求出按模最大的特征值λt1,然后根据λt1进行原点平移求出另一特征值λt2,比较两值大小,数值小的为所求最小特征值λ1,数值大的为是所求最大特征值λ501。 2)使用反幂法求λs ,其中需要解线性方程组。因为A 为带状线性方程组,此处采用LU 分解法解带状方程组。 (2)与140k λλμλ-5011=+k 最接近的特征值λik 。 通过带有原点平移的反幂法求出与数k μ最接近的特征值 λik 。 (3)2cond(A)和det A 。 1)1=n λλ2cond(A),其中1λ和n λ分别是按模最大和最小特征值。 2)利用步骤(1)中分解矩阵A 得出的LU 矩阵,L 为单位下三角阵,U 为上三角阵,其中U 矩阵的主对角线元素之积即为det A 。 由于A 的元素零元素较多,为节省储存量,将A 的元素存为6×501的数组中,程序中采用get_an_element()函数来从小数组中取出A 中的元素。 2.全部源程序 #include 当前位置:第7章>>第1节>>7.1.3 逆幂法 逆幂法是求实方阵按模最小特征值及相应的特征向量的一种反迭代方法。 1. 求A按模最小的特征值 设非奇异矩阵A的n 个特征值为,其相应的特征向量为e ,则的特征值为 其相应的特征向量仍为。 按模最大的特征值的倒数则为矩阵A按模最小的特征值。 利用乘幂法求按模最大的特征值。 任取初始非零初始向量,作迭代序列 它等价于(7.5) 我们可以通过反迭代过程,即解方程组. 求得. 当k 充分大时,则有 在实际计算中,为了减少运算量,先将矩阵A作三角分解A=LR 然后再求解方程组 2.求在附近的特征值 设与最接近的特征值为即有 作矩阵,它的特征值和相应的特征向量为 若用逆幂法于矩阵,则有 则可求出矩阵的按模最小的特征值和相应的特征向量为 于是得A在附近的特征值和相应的特征向量为 (7.6) 例3 用逆幂法求矩阵在3.4附近的特征值和相应的特征向量 解对进行三角分解得: 用半次迭代法,取,则 得 再解 得 再解 得 于是 练习7.1 1.用乘幂法求矩阵按模最大特征值与特征向量 . 乘幂法的计算公式 设矩阵A的n个特征值按模的大小排列为: 其相应的特征向量为且它们是线性无关的。 先任取非零初始向量,作迭代序列 首先将表示为 所以 为了得出计算和的公式,下面分三种情况讨论 1.为实根,且。 当不为0,k充分大时,则有 所以(7.1)2.为实根,且。 当不为0,k充分大时,则有 (7.2)于是得 从而有 (7.3)3.,且。当k充分大时,则有 在实际应用幂法时,可根据迭代向量个分量的变化情况判断属于那种情况。 若迭代向量各分量单调变化,且有关系式,则属于第1种情况; 若迭代向量各分量不是单调变化,但有关系式,则属于第2种情况; (一)指数与指数函数 1.根式 (1)根式的概念 (2).两个重要公式 ①?? ??????<-≥==)0()0(||a a a a a a a n n ; ②a a n n =)((注意a 必须使n a 有意义)。 2.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂:0,,1)m n m n a a a m n N n *=>∈>、且; ②正数的负分数指数幂: 10,,1)m n m n m n a a m n N n a a - *= = >∈>、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义. 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r as =a r+s (a>0,r 、s∈Q); ②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r bs (a>0,b>0,r ∈Q );. 3.指数函数的图象与性质 y =a x a>1 0 图象 定义域R 值域(0,+∞) 性质(1)过定点(0,1) (2)当x>0时,y>1; x<0时,0 幂法和反幂法的matlab实现 幂法求矩阵主特征值及对应特征向量 摘要 矩阵特征值的数值算法,在科学和工程技术中很多问题在数学上都归结为矩阵的特征值问题,所以说研究利用数学软件解决求特征值的问题是非常必要的。实际问题中,有时需要的并不是所有的特征根,而是最大最小的实特征根。称模最大的特征根为主特征值。 幂法是一种计算矩阵主特征值(矩阵按模最大的特征值)及对应特征向量的迭代方法,它最大的优点是方法简单,特别适用于大型稀疏矩阵,但有时收敛速度很慢。 用java来编写算法。这个程序主要分成了四个大部分:第一部分为将矩阵转化为线性方程组;第二部分为求特征向量的极大值;第三部分为求幂法函数块;第四部分为页面设计及事件处理。其基本流程为幂法函数块通过调用将矩阵转化为线性方程组的方法,再经过一系列的验证和迭代得到结果。 关键字:主特征值;特征向量;线性方程组;幂法函数块 POWER METHOD FOR FINDING THE EIGENVALUES AND CORRESPONDING EIGENVECTORS OF THE MATRIX ABSTRACT Numerical algorithm for the eigenvalue of matrix, in science and engineering technology, a lot of problems in mathematics are attributed matrix characteristic value problem, so that studies using mathematical software to solve the eigenvalue problem is very necessary. In practical problems, sometimes need not all eigenvalues, but the maximum and minimum eigenvalue of real. The characteristic value of the largest eigenvalue of the modulus maximum. Power method is a calculation of main features of the matrix values (matrix according to the characteristics of the largest value) and the corresponding eigenvector of iterative method. It is the biggest advantage is simple method, especially for large sparse matrix, but sometimes the convergence speed is very slow. Using java to write algorithms. This program is divided into three parts: the first part is the matrix is transformed into linear equations; the second part for the sake of feature vector of the maximum; the third part is 幂函数 (1)幂函数的定义: 一般地,函数y x α =叫做幂函数,其中x 为自变量,α是常数. ①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于y 轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限. ②过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1). ③单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限,图象无限接近x 轴与y 轴. ④奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当q p α= (其中,p q 互质,p 和q Z ∈),若p 为奇数q 为奇数时,则q p y x =是奇函数,若p 为奇数q 为偶数时,则q p y x =是偶函数,若p 为偶数q 为奇数时,则q p y x =是非奇非偶函数. ⑤图象特征:幂函数,(0,)y x x α =∈+∞,当1α>时,若01x <<,其图象在直线y x =下 方,若1x >,其图象在直线y x =上方,当1α<时,若01x <<,其图象在直线y x =上 方,若1x >,其图象在直线y x =下方. 幂函数练习题 一、选择题: 1.下列函数中既是偶函数又是(,)-∞0上是增函数的是 ( ) A .y x =43 B .y x =32 C .y x =-2 D .y x =-14 2.函数2 -=x y 在区间]2,2 1[上的最大值是 ( ) A . 4 1 B .1- C .4 D .4- 3.下列所给出的函数中,是幂函数的是 ( ) A .3 x y -= B .3 -=x y C .3 2x y = D .13 -=x y 4.函数3 4x y =的图象是 ( ) A . B . C . D . 5.下列命题中正确的是 ( ) A .当0=α时函数α x y =的图象是一条直线 B .幂函数的图象都经过(0,0)和(1,1)点 C .若幂函数αx y =是奇函数,则α x y =是定义域上的增函数 D .幂函数的图象不可能出现在第四象限 6.函数3 x y =和3 1 x y =图象满足 ( ) A .关于原点对称 B .关于x 轴对称 C .关于y 轴对称 D .关于直线x y =对称 7. 函数R x x x y ∈=|,|,满足 ( ) A .是奇函数又是减函数 B .是偶函数又是增函数 C .是奇函数又是增函数 D .是偶函数又是减函数 8.如图1—9所示,幂函数α x y =在第一象限的图象,比较1,,,,,04321αααα的大小( ) A .102431<<<<<αααα B .104321<<<<<αααα 1α 4α 2α 幂法反幂法求解矩阵大小特征值及其对应的特征向量 ————————————————————————————————作者:————————————————————————————————日期: 数值计算解矩阵的按模最大最小特征值及对应的特征向量 一.幂法 1. 幂法简介: 当矩阵A 满足一定条件时,在工程中可用幂法计算其主特征值(按模最大)及其特征向量。矩阵A 需要满足的条件为: (1) 的特征值为A i n λλλλ,0||...||||21 ≥≥≥> (2) 存在n 个线性无关的特征向量,设为n x x x ,...,,21 1.1计算过程: i n i i i u x x αα,1 ) 0()0(∑==,有对任意向量不全为0,则有 1 11111221 12111 1 1 11 1 011)()(...u u a u a u λu λαu αA x A Ax x k n n k n k k n i i k i i n i i i k )(k (k))(k αλλλλλα++++=+=+++≈? ? ????+++======∑∑ 可见,当||1 2 λλ越小时,收敛越快;且当k 充分大时,有1)11 11)11111λαλαλ=??????==+++(k )(k k (k k )(k x x u x u x ,对应的特征向量即是)(k x 1+。 2 算法实现 . ,, 3,,1 , ).5() 5(,,,,||).4();max(,).3() (max(;0,1).2(,).1()() () (停机否则输出失败信息转置若转否则输出若计算最大迭代次数,误差限,初始向量输入矩阵βλβεβλβλε←+←<<-←←= ←←k k N k y x Ay x x abs x y k N x A k k k 3 matlab 程序代码 数值分析之幂法及反幂法C 语言程序实例 1、算法设计方案: ①求1λ、501λ和s λ的值: s λ:s λ表示矩阵的按模最小特征值,为求得s λ直接对待求矩阵A 应用反幂法即可。 1λ、501λ:已知矩阵A 的特征值满足关系 1n λλ<< ,要求1λ、及501λ时,可 按如下方法求解: a . 对矩阵A 用幂法,求得按模最大的特征值1m λ。 b . 按平移量1m λ对矩阵A 进行原点平移得矩阵1m B A I λ=+,对矩阵B 用反幂法 求得B 的按模最小特征值2m λ。 c . 321m m m λλλ=- 则:113min(,)m m λλλ=,13max(,)n m m λλλ=即为所求。 ②求和A 的与数5011 140 k k λλμλ-=+最接近的特征值 ik λ(k=0,1,…39): 求矩阵A 的特征值中与k μ最接近的特征值的大小,采用原点平移的方法: 先求矩阵 B=A-k μI 对应的按模最小特征值k β,则k β+k μ即为矩阵A 与k μ最接近的特征值。 重复以上过程39次即可求得ik λ(k=0,1,…39)的值。 ③求A 的(谱范数)条件数2cond()A 和行列式det A : 在(1)中用反幂法求矩阵A 的按模最小特征值时,要用到Doolittle 分解方法,在Doolittle 分解完成后得到的两个矩阵分别为L 和U ,则A 的行列式可由U 阵求出,即:det(A)=det(U)。 求得det(A)不为0,因此A 为非奇异的实对称矩阵,则: max 2()s cond A λλ= ,max λ和s λ分别为模最大特征值与模最小特征值。 指数对数幂函数知识点总 结 篇一:指数、对数、幂函数知识点 指数、对数、幂函数知识归纳 知识要点梳理 知识点一:指数及指数幂的运算1.根式的概念 的次方根的定义:一般地,如果 ; 当为奇数时,正数的次方根为正数,负数的次方根是负数,表示为当为偶数时,正数的次方根有两个,这两个数互为相反数可以表示为. 负数没有偶次方根,0的任何次方根都是0.式子 叫做根式,叫做根指数,叫做被开方数. ; ,那么叫做的次方根,其中 2.n次方根的性质:(1)当为奇数时, ; (2)当为偶数时, 3.分数指数幂的意义: ; 注意:0的正分数指数幂等与0,负分数指数幂没有意义. 4.有理数指数幂的运算性质:(1)(2)(3) 知点二:指数函数及其性质1.指数函数概念:一般地,函数变量,函数的定义域为 . 叫做指数函数,其中是自 1.(2013·北京高考理科·T5)函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)= ( ) A.ex+1 B.ex-1 C.e-x+1 D.e-x-1 2.(2013·上海高考文科·T8)方程 3.(2013·湖南高考理科·T16)设函数 f(x)?ax?bx?cx,其中c?a?0,c?b?0. 9x 的实数解为. ?1?3x 3?1 且a=b?,(1)记集合M??(a,b,c)a,b,c不能构成一个三角形的三条边长, 则(a,b,c)?M所对应的f(x)的零点的取值集合为____. (2)若a,b,c是?ABC的三条边长,则下列结论正确的是. (写出所有正确结论的序号) ①?x????,1?,f?x??0; ②?x?R,使得ax,bx,cx不能构成一个三角形的三边长;③若?ABC为钝角三角形,则?x??1,2?,使f?x??0. 知识点三:对数与对数运算1.对数的定义(1)若叫做底数, 叫做真数. ,则叫做以为底 的对数,记作 , (2)负数和零没有对数. (3)对数式与指数式的互化:2.几个重要的对数恒等式: , , . . 3.常用对数与自然对数: 常用对数: ,即 ;自然对数: ,即 (其中 …). 4.对数的运算性质如果 ①加法: 数值分析幂法与反幂法 matlab程序 随机产生一对称矩阵,对不同的原点位移和初值(至少取3个)分别使用幂法求计算矩阵的主特征值及主特征向量,用反幂法求计算矩阵的按模最小特征值及特征向量。 要求 1)比较不同的原点位移和初值说明收敛性 2)给出迭代结果,生成DOC文件。 3)程序清单,生成M文件。 解答: >> A=rand(5) %随机产生5*5矩阵求随机矩阵 A = 0.7094 0.1626 0.5853 0.6991 0.1493 0.7547 0.1190 0.2238 0.8909 0.2575 0.2760 0.4984 0.7513 0.9593 0.8407 0.6797 0.9597 0.2551 0.5472 0.2543 0.6551 0.3404 0.5060 0.1386 0.8143 >> B=A+A' %A矩阵和A的转置相加,得到随机对称矩阵B B = 1.4187 0.9173 0.8613 1.3788 0.8044 0.9173 0.2380 0.7222 1.8506 0.5979 0.8613 0.7222 1.5025 1.2144 1.3467 1.3788 1.8506 1.2144 1.0944 0.3929 0.8044 0.5979 1.3467 0.3929 1.6286 B=?? ????? ???? ?? ???6286.13929.03467.15979.08044 .03929.00944 .12144.18506 .13788.13467.12144.15025.17222.08613.05979.08506.17222.02380.09173.08044.03788.18613 .09173 .04187.1 编写幂法、反幂法程序: function [m,u,index,k]=pow(A,u,ep,it_max) % 求矩阵最大特征值的幂法,其中 % A 为矩阵; % ep 为精度要求,缺省为1e-5; % it_max 为最大迭代次数,缺省为100; % m 为绝对值最大的特征值; % u 为对应最大特征值的特征向量; % index ,当index=1时,迭代成功,当index=0时,迭代失败 if nargin<4 it_max=100; end if nargin<3 ep=1e-5; end n=length(A); index=0; k=0; m1=0; m0=0.01; % 修改移位参数,原点移位法加速收敛,为0时,即为幂法 I=eye(n) T=A-m0*I while k<=it_max v=T*u; [vmax,i]=max(abs(v)); m=v(i); u=v/m; if abs(m-m1) (一)指数函数的定义 一般地,函数y =a x (a >0,且a ≠1)叫做指数函数,其中x 是自变量,函数的定义域是R 。 将a 如数轴所示分为:a <0,a =0,01五部分进行讨论: (1)如果a <0, 比如y =(-4)x ,这时 对于等,在实数范围内函数值不 存在; (2)如果a =0,、 (3)(3)如果a =1,y =1x =1,是个常值函数,没有研究的必要; (4)4)如果01即a >0且a ≠1,x 可以是任意实数。 (四)指数函数性质的简单应用 例 2: 比较下列各题中两个值的大小 : (l)1.72.5,1.73; (2)0.8-01,0.8-02 ; (3)(0.3)-0.3,(0.2)-0.3 (4)1.70.3,0.93.1 解 :(1) 考察指数函数 y =1.7x , 由于底数 1.7>1, 所以指数函数 y =1.7x 在R 上是增函数 因为 2.5< 3, 所以 1.72.5<1.73 (2) 考察指数函数 y =0.8x , 由于底数0<0.8 第四讲 幂函数、与反函数 一、知识梳理 1.幂函数: ①定义:形如a y x =(a 为常数)的函数叫幂函数。 当0>a 时,图象过定点)0,0(和)1,1(;当0a 时,函数图象在第一象限剧烈增长; 当0n 时,都过)0,0(和)1,1(,0 指数与指数幂的运算 【学习目标】 1.理解有理指数幂的含义,掌握幂的运算. 2.理解指数函数的概念和意义,理解指数函数的单调性与特殊点. 3.理解对数的概念及其运算性质. 4.重点理解指数函数、对数函数、幂函数的性质,熟练掌握指数、对数运算法则,明确算理,能对常见的指 数型函数、对数型函数进行变形处理. 5.会求以指数函数、对数函数、幂函数为载体的复合函数的定义域、单调性及值域等性质. 6.知道指数函数与对数函数 互为反函数(a >0,a ≠1). 【要点梳理】 要点一、幂的概念及运算性质 1.整数指数幂的概念及运算性质 2.分数指数幂的概念及运算性质 为避免讨论,我们约定a>0,n ,m ∈N * ,且 m n 为既约分数,分数指数幂可如下定义: 1 n a = m m n a == -1m n m n a a = 3.运算法则 当a >0,b >0时有: (1)n m n m a a a +=?; (2)() mn n m a a =; (3)()0≠>=-a n m a a a n m n m ,; (4)()m m m b a ab =. 要点诠释: (1)根式问题常利用指数幂的意义与运算性质,将根式转化为分数指数幂运算; (2)根式运算中常出现乘方与开方并存,要注意两者的顺序何时可以交换、何时不能交换.如 244 2)4()4(-≠-; (3)幂指数不能随便约分.如2 14 2)4()4(-≠-. 要点二、根式的概念和运算法则 1.n 次方根的定义: 若x n =y(n ∈N * ,n>1,y ∈R),则x 称为y 的n 次方根,即x=n y . n 为奇数时, y 的奇次方根有一个,是负数,记为n y ;零的奇次方根为零,记为00=n ; n 为偶数时,正数y 的偶次方根有两个,记为;负数没有偶次方根;零的偶次方根为零,0=. 2.两个等式 (1)当1n >且* n N ∈时, n a =; 一、问题的描述及算法设计 (一)问题的描述 我所要做的课题是:对称矩阵的条件数的求解设计 1、求矩阵A 的二条件数 问题 A=?? ?? ? ?????----210121012 2、设计内容: 1)采用幂法求出A 的 . 2)采用反幂法求出A 的 . 3)计算A 的条件数 ⅡA Ⅱ2* ⅡA -1Ⅱ2=cond2(A )=/ .(精度要求为10-6) 3、设计要求 1)求出ⅡA Ⅱ2。 2)并进行一定的理论分析。 (二)算法设计 1、幂法算法 (1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1. (2)计算 v )(k =Au )1(-k ,m k =max(v )(k ), u )(k = v )(k / m k (3)若| m k = m 1-k |<ε,则停止计算(m k 作为绝对值最大特征值1λ,u )(k 作为相应的特征向量)否则置k=k+1,转(2) 2、反幂法算法 (1)取初始向量u )0((例如取u )0(=(1,1,…1)T ),置精度要求ε,置k=1. (2)对A 作LU 分解,即A=LU (3)解线性方程组 Ly )(k =u )1(-k ,Uv )(k =y )(k (4)计算 m k =max(v )(k ), u )(k = v )(k / m k (5)若|m k =m 1-k |<ε,则停止计算(1/m k 作为绝对值最小特征值n λ,u )(k 作为相应的特征向量);否则置k=k+1,转(3). 二、算法的流程图(一)幂法算法的流程图 (二)反幂法算法的流程图 三、算法的理论依据及其推导 (一)幂法算法的理论依据及推导 幂法是用来确定矩阵的主特征值的一种迭代方法,也即,绝对值最大的特征值。稍微修改该方法,也可以用来确定其他特征值。幂法的一个很有用的特性是它不仅可以生成特征值,而且可以生成相应的特征向量。实际上,幂法经常用来求通过其他方法确定的特征值的特征向量。 1、幂法的迭代格式与收敛性质 设n 阶矩阵A 的特征值1λ,2λ,…,n λ是按绝对值大小编号的,x i (i=1,2,…,n)为对应i λ的特征向量,且1λ为单根,即 |1λ|>|2λ|≥…≥|n λ| 则计算最大特征值与特征向量的迭代格式为 v )(k =Au )1(-k ,m k =max(v )(k ), u )(k = v )(k / m k (1) 其中max(v )(k )表示向量v )(k 绝对值的最大分量。 2、对于幂法的定理 按式(1)计算出m k 和u )(k 满足 ∞ >-k lim m k =1λ, ∞ >-k lim u )(k = ) max(11 x x (二)反幂法算法的理论依据及推导 反幂法是用来计算绝对值最小的特征值忽然相应的特征向量的方法。是对幂法的修改,可以给出更快的收敛性。 1、反幂法的迭代格式与收敛性质 设A 是非奇异矩阵,则零不是特征值,并设特征值为 |1λ|≥|2λ|≥…≥|1-n λ|>|n λ| 则按A 1-的特征值绝对值的大小排序,有 | n λ1 |>| 1 1 -n λ|≥…≥| 1 1 λ| 对A 1-实行幂法,就可得A 1-的绝对值最大的特征值1/n λ和相应的特征向量,即A 的绝对值最小的特征值和相应的特征向量。 由于用A 1-代替A 作幂法计算,因此该方法称为反幂法,反幂法的迭代格式 (一)指数与指数函数 1.根式 (1)根式的概念 (2).两个重要公式 ① ? ? ? ? ? ? ? ? < - ≥ = = )0 ( )0 ( | | a a a a a a a n n; ②a a n n= ) ((注意a必须使n a有意义)。 2.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂:0,,1) m n m n a a a m n N n * =>∈> 、且; ②正数的负分数指数幂: 1 0,,1) m n m n m n a a m n N n a a - * ==>∈> 、且 ③0的正分数指数幂等于0,0的负分数指数幂没有意义. 注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。 (2)有理数指数幂的性质 ①a r a s=a r+s(a>0,r、s∈Q); ②(a r)s=a rs(a>0,r、s∈Q); ③(ab)r=a r b s(a>0,b>0,r∈Q);. 3.指数函数的图象与性质 y=a x a>1 0 图象 定义域R 值域(0,+∞) 性质(1)过定点(0,1) (2)当x>0时,y>1; x<0时,0幂函数 反函数 反比例
北航数值分析大作业第一题幂法与反幂法
乘幂反幂法
指数函数、对数函数、幂函数的图像和性质知识点总结
幂法和反幂法的matlab实现
幂函数知识点总结与练习题
幂法反幂法求解矩阵大小特征值及其对应的特征向量
数值分析之幂法及反幂法C语言程序实例
指数对数幂函数知识点总结
数值分析幂法与反幂法-matlab程序
幂函数与指数函数及其性质
第四讲 幂函数及反函数(教师)
指数、对数、幂函数总结归纳
数值分析试验幂法与反幂法matlab
指数函数、对数函数、幂函数的图像和性质知识点总结
