第6章 特征编辑-阵列

阵列
阵列用于一次创建一个特征的多个副本。阵列特征按照不同的规则生成新的特征,每个特征称为源特征的一个实例。阵列形式有矩形阵列、环形阵列和填充阵列。
特征阵列操作步骤:
1、选择源特征
在模型树或者图形区选择预阵列的源特征
2、选择命令【编辑】/【阵列】
3、选择阵列方式在图标板的【阵列方式】列表中选择合适的阵列方式,
共七种方式。
●尺寸:选择尺寸作为参照,生成矩形阵列或者环形阵列,参照尺寸为线性尺
寸时,可以创建矩形阵列,参照尺寸选取角度尺寸时,可以创建环形阵列。
●方向:选取方向作为参照,在选定方向上设置阵列特征的数目和距离,只能
创建矩形阵列。
●轴:选取轴线或者立体的直线型边线作为参考,以此线为旋转轴线进行环形
阵列,可以设置阵列特征的数目和阵列各实例之间的夹角,只能用于环形阵列。
●填充:选取或草绘平面图形作为参照,在图形范围内按照一定规则阵列出多
个实例。
●表:通过使用阵列表并为每一阵列实例指定尺寸值来创建阵列。
●参照:通过参照另一阵列来创建阵列。
●曲线:通过指定阵列成员的数目或阵列成员间的距离来沿着草绘曲线创建阵
列。
4、设置阵列参数
在图标板上定义阵列的各参数。
5、完成阵列
一.尺寸阵列
1. 根据左图所示模型,创建2行3列矩形阵列,列间距为70,行间距为60。在列方向上,小圆柱下一实例比上一实例增高20,在行方向上,小圆柱下一实例比上一实例底面直径增加10,如右图所示。名称为“cczl-jx”。
cczl-jx
PS:图中长方体尺寸为180×110×5mm
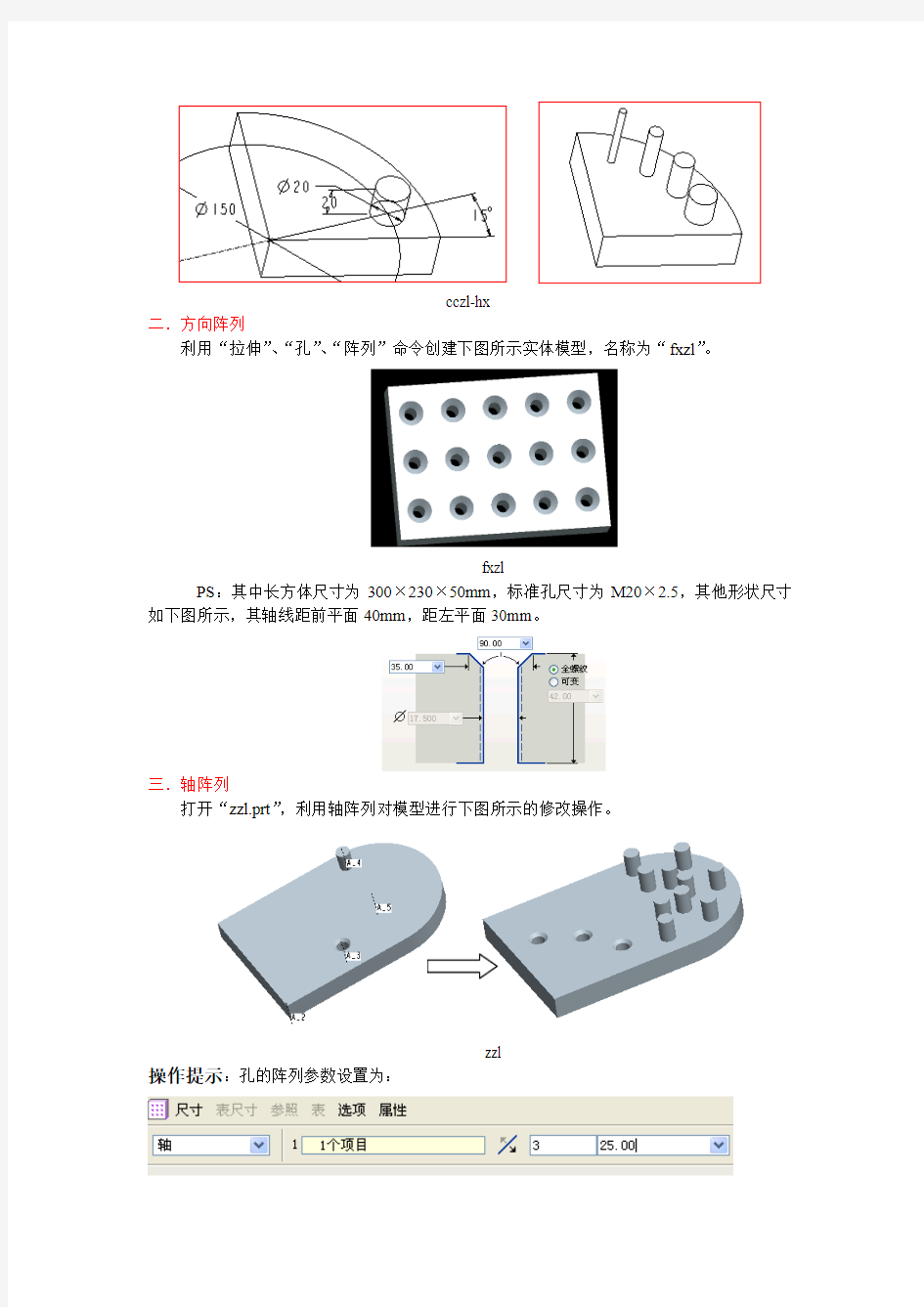
2. 根据左图模型创建环行阵列,各实例夹角为20度,共有4个实例。每个实例比上个实例高度增加10,直径减少3,如右图所示。名称为“cczl-hx”。
cczl-hx
二.方向阵列
利用“拉伸”、“孔”、“阵列”命令创建下图所示实体模型,名称为“fxzl”。
fxzl
PS:其中长方体尺寸为300×230×50mm,标准孔尺寸为M20×2.5,其他形状尺寸如下图所示,其轴线距前平面40mm,距左平面30mm。
三.轴阵列
打开“zzl.prt”,利用轴阵列对模型进行下图所示的修改操作。
zzl
操作提示:孔的阵列参数设置为:
圆柱体的阵列参数设置为:
四.填充阵列
打开“tczl.prt”,利用填充阵列对模型进行下图所示的修改操作。
tczl
操作提示:阵列参数设置为:
五.表阵列
打开“biaozl.prt”,利用表阵列对模型进行下图所示的修改操作。
biaozl
操作提示:阵列参数设置为:
阵列表的参数设置为:
六.参照阵列
打开“czzl.prt”,利用倒角(倒角距离为2)、阵列(参数根据模型自定义)命令对模型进行下图所示的修改操作。
czzl
七.曲线阵列
打开“qxzl.prt”,利用曲线阵列对模型进行下图所示的修改操作,名称分别为“qxzl-1.prt”、“qxzl-2.prt”、“qxzl-3.prt”。
qxzl qxzl-1
qxzl-2 qxzl-3
第九章矩阵特征值问题的数值方法
第9章矩阵特征值问题的数值 方法 9.1 特征值与特征向量 9.2 Hermite矩阵特征值问题 9.3 Jacobi方法 9.4 对分法 9.5 乘幂法 9.6 反幂法 9.7 QR方法
9.1 特征值与特征向量设A是n阶矩阵,x是非零列向量. 如果有数λ存在,满足, (1) 那么,称x是矩阵A关于特征值λ的特征向量.
如果把(1)式右端写为 ,那么(1)式又可写为: x λ ()0 I A x λ-=||0 I A λ-=即1110 ()||...n n n f I A a a a λλλλλ--=-=++++记 它是关于参数λ的n 次多项式,称为矩阵A 的特 征多项式, 其中a 0=(-1)n |A |. (2)
显然,当λ是A的一个特征值时,它必然 是的根. 反之,如果λ是的根,那么齐次方程组(2)有非零解向量x,使(1)式 成立. 从而,λ是A的一个特征值. A的特征值也称为A的特征根 . ()0 fλ= ()0 fλ=
矩阵特征值和特征向量有如下主要性质: 定理9.1.1 n阶矩阵A是降秩矩阵的充分必要 条件是A有零特征值. 定理9.1.2 设矩阵A与矩阵B相似,那么它们 有相同的特征值. 定理9.1.3 n阶矩阵A与A T有相同的特征值. 定理9.1.4 设λ ≠λj是n阶矩阵A的两个互异特 i 征值,x、y分别是其相应的右特征向 量和左特征向量,那么,x T y=0 .
9.2 Hermite矩阵特征值问题?设A为n阶矩阵,其共轭转置矩阵记为A H. 如果A=A H,那么,A称为Hermite矩阵.
矩阵特征问题的求解
矩阵特征问题的求解 在科学技术的应用领域中,许多问题都归为求解一个特征系统。如动力学系统和结构系统中的振动问题,求系统的频率与振型;物理学中的某些临界值的确定等等。 设A 为n 阶方阵,n n ij R a A ?∈=)(,若)0(≠∈x R x n ,有数λ使 Ax= λx (5.1) 则称λ为A 的特征值,x 为相应于λ的特征向量。因此,特征问题的求解包括两方面: 1.求特征值λ,满足 0)det()(=-=I A λλ? (5.2) 2.求特征向量)0(≠∈x R x n ,满足齐方程组 0)(=-x I A λ (5.3) 称?(λ)为A 的特征多项式,它是关于λ的n 次代数方程。 关于矩阵的特征值,有下列代数理论, 定义1 设矩阵A, B ∈R n ?n ,若有可逆阵P ,使 AP P B 1 -= 则称A 与B 相似。 定理1 若矩阵A, B ∈R n ?n 且相似,则 (1)A 与B 的特征值完全相同; (2)若x 是B 的特征向量,则Px 便为A 的特征向量。 定理2 设A ∈R n ?n 具有完全的特征向量系,即存在n 个线性无关的特征向量构成R n 的一组基底,则经相似变换可化A 为对角阵,即有可逆阵P ,使 ????? ????? ? ?= =-n D AP P λλλ 2 11 其中λi 为A 的特征值,P 的各列为相应于λi 的特征向量。 定理3 A ∈R n ?n ,λ1, …, λn 为A 的特征值,则 (1)A 的迹数等于特征值之积,即 ∑∑=== ≡ n i i n i ii a A tr 1 1 )(λ (2)A 的行列式值等于全体特征值之积,即 n A λλλ 21)det(= 定理4 设A ∈R n ?n 为对称矩阵,其特征值λ1≥λ2≥…≥λn ,则 (1)对任A ∈R n ,x ≠0, 1) ,(),(λλ≤≤ x x x Ax n
矩阵特征值求解
矩阵特征值求解的分值算法 12组 1. 1矩阵计算的基本问题 (1) 求解线性方程组的问题.即给定一个n 阶非奇异矩阵A 和n 维向量b ,求 一个n 维向量X,使得 Ax =b (1.1.1 ) (2) 线性最小二乘问题,即给定一个mx n 阶矩阵A 和m 维向量b ,求一个n 维向量 使得 |A X -b | =min{ |Ay -比严 R n } (3) 矩阵的特征问题,即给定一个n 阶实(复)矩阵A ,求它的部分或全部特 征值 以及对应的特征向量,也就是求解方程 Ax = Z x A 的属于特征值A 的特征向量。 在工程上,矩阵的特征值具有广泛的应用,如大型桥梁或建筑物的振动问题: 机械和机件的振动问题;飞机机翼的颤振问题 ;无线电电子学及光学系统的电磁 振动问题;调节系统的自振问题以及声学和超声学系统的振动问题 .又如天文、地 震、信息系统、经济学中的一些问题都与矩阵的特征值问题密切相关。 在科学上,计算流体力学、统计计算、量子力学、化学工程和网络排队的马 尔可夫链模拟等实际问题,最后也都要归结为矩阵的特征值问题.由于特征值问 题在许多科学和工程领域中具有广泛的应用,因此对矩阵的特征值问题的求解理 论研究算法的开发软件的制作等是当今计算数学和科学与工程计算研究领域的 重大课题,国际上这方面的研究工作十分活跃。 1.2矩阵的特征值问题研究现状及算法概述 对一个nxn 阶实(复)矩阵A,它的特征值问题,即求方程(I.1.3)式的非平凡 解,是数值线性代数的一个中心问题.这一问题的内在非线性给计算特征值带来 许多计算问题.为了求(1.1.3)式中的A , —个简单的想法就是显式地求解特征方 程 det(A —几I) = 0 除非对于个别的特殊矩阵,由于特征方程的系数不能够用稳定的数值方法由 行列式的计算来求得,既使能精确计算出特征方程的系数,在有限精度下,其特征 多项式f ") =det(A-ZJ)的根可能对多项式的系数非常敏感 能在理论上是有意义的,实际计算中对一般矩阵是不可行的 数 较大,则行列式det(A -几I)的计算量将非常大;其次,根据 数大于四的多项式求根不存在一种通用的方法 ,基于上述原因,人们只能寻求其 它途径.因此,如何有效地!精确地求解矩阵特征值问题,就成为数值线性代数领 域的一个中心问题. 目前,求解矩阵特征值问题的方法有两大类:一类称为变换方法,另一类称为 向 X, (1.1.2 ) (1.1.3 ) 一对解(4 X),其中R(C),x- R n (C n ),即A 为矩阵A 的特征值,X 为矩阵 (121 ) .因此,这个方法只 .首先,若矩阵A 的阶 Galois 理论,对于次
第五章矩阵特征问题的求解
第五章 矩阵特征问题的求解 5.1 引言 在科学技术的应用领域中,许多问题都归为求解一个特征系统。如动力学系统和结构系统中的振动问题,求系统的频率与振型;物理学中的某些临界值的确定等等。 设A 为n 阶方阵,n n ij R a A ?∈=)(,若)0(≠∈x R x n ,有数λ使 Ax= λx (5.1) 则称λ为A 的特征值,x 为相应于λ的特征向量。因此,特征问题的求解包括两方面: 1.求特征值λ,满足 0)det()(=-=I A λλ? (5.2) 2.求特征向量)0(≠∈x R x n ,满足齐方程组 0)(=-x I A λ (5.3) 称?(λ)为A 的特征多项式,它是关于λ的n 次代数方程。 关于矩阵的特征值,有下列代数理论, 定义1 设矩阵A, B ∈R n ?n ,若有可逆阵P ,使 AP P B 1-= 则称A 与B 相似。 定理1 若矩阵A, B ∈R n ?n 且相似,则 (1)A 与B 的特征值完全相同; (2)若x 是B 的特征向量,则Px 便为A 的特征向量。 定理2 设A ∈R n ?n 具有完全的特征向量系,即存在n 个线性无关的特征向量构成R n 的一组基底,则经相似变换可化A 为对角阵,即有可逆阵P ,使 ????? ???? ?? ?==-n D AP P λλ λO 211 其中λi 为A 的特征值,P 的各列为相应于λi 的特征向量。 定理3 A ∈R n ?n ,λ1, …, λn 为A 的特征值,则 (1)A 的迹数等于特征值之积,即 ∑∑===≡ n i i n i ii a A tr 1 1 )(λ (2)A 的行列式值等于全体特征值之积,即 n A λλλΛ21)det(= 定理4 设A ∈R n ?n 为对称矩阵,其特征值λ1≥λ2≥…≥λn ,则 (1)对任A ∈R n ,x ≠0,
矩阵特征根的有关问题
矩阵特征根的有关问题 吴晗 数学系 数学与应用数学 06180226 [摘 要] 首先给出了矩阵特征根的定义,接着介绍了矩阵特征根的有关求法,其次讨论了矩 阵特征根的性质,最后利用其求法与性质解决一些代数问题。 [关键字] 矩阵 特征根 特征向量 求法 性质 应用 矩阵,线性代数研究的基本对象。按照矩阵的观点,线性代数就是研究矩阵在各种意义下的分类问题及其标准型理论。在矩阵的有关内容之中其特征根就是一个非常重要的内容,与之相对应的就是在指定特征根下的特征向量。在多数《高等代数》教材中,特征值与特征向量的引入是为了研究线性空间中线性变换A 的属性,描述为线性空间中线性变换A 的特征值与特征向量;而在大部分《线性代数》教材中,特征值与特征向量的讨论被作为矩阵理论研究的一个重要组成,定义为n 阶矩阵A 的特征值与特征向量。 所以二者有相辅相成之意。涉及到矩阵特征根的有关问题将在如下文之中列举: 1 矩阵的特征根的定义 设() ij A a =是数域F 上的一个n 阶矩阵,行列式 ()11 12121 22212.......... ............n n A n n nn x a a a a x a a f x xI A a a x a ------=-=--- 叫做矩阵A 的特征多项式,而在复数域内的根就叫做矩阵A 的特征根。即在方程中求解出x (x 在复数域内),其中I 是n 阶单位矩阵。而在矩阵的特征根研究中,我们不只是就仅仅要知道特征根是什么,它不是一个孤立存在的知识点,往往与它紧密联系在一起的就是特征向量。就像前面所说特征值与特征向量的引入是为
矩阵特征问题的求解
矩阵特征问题的求解 5.1 引言 在科学技术的应用领域中,许多问题都归为求解一个特征系统。如动力学系统和结构系统中的振动问题,求系统的频率与振型;物理学中的某些临界值的确定等等。 设A 为n 阶方阵,n n ij R a A ?∈=)(,若)0(≠∈x R x n ,有数λ使 Ax= λx (5.1) 则称λ为A 的特征值,x 为相应于λ的特征向量。因此,特征问题的求解包括两方面: 1.求特征值λ,满足 0)det()(=-=I A λλ? (5.2) 2.求特征向量)0(≠∈x R x n ,满足齐方程组 0)(=-x I A λ (5.3) 称?(λ)为A 的特征多项式,它是关于λ的n 次代数方程。 关于矩阵的特征值,有下列代数理论, 定义1 设矩阵A, B ∈R n ?n ,若有可逆阵P ,使 AP P B 1-= 则称A 与B 相似。 定理1 若矩阵A, B ∈R n ?n 且相似,则 (1)A 与B 的特征值完全相同; (2)若x 是B 的特征向量,则Px 便为A 的特征向量。 定理2 设A ∈R n ?n 具有完全的特征向量系,即存在n 个线性无关的特征向量构成R n 的一组基底,则经相似变换可化A 为对角阵,即有可逆阵P ,使 ????? ???? ?? ?==-n D AP P λλ λ 211 其中λi 为A 的特征值,P 的各列为相应于λi 的特征向量。 定理3 A ∈R n ?n ,λ1, …, λn 为A 的特征值,则 (1)A 的迹数等于特征值之积,即 ∑∑===≡ n i i n i ii a A tr 1 1 )(λ (2)A 的行列式值等于全体特征值之积,即 n A λλλ 21)det(= 定理4 设A ∈R n ?n 为对称矩阵,其特征值λ1≥λ2≥…≥λn ,则 (1)对任A ∈R n ,x ≠0,
3矩阵特征值与特征向量的计算
第3章 矩阵特征值与特征向量的计算 一些工程技术问题需要用数值方法求得矩阵的全部或部分特征值及相关的特征向量。 3.1 特征值的估计 较粗估计ρ(A ) ≤ ||A || 欲将复平面上的特征值一个个用圆盘围起来。 3.1.1 盖氏图 定义3.1-1 设A = [a ij ]n ?n ,称由不等式∑≠=≤-n i j j ij ii a a z 1 所确定的复区域为A 的第i 个盖氏图, 记为G i ,i = 1,2,…,n 。 >≤-=<∑≠=}:{1n i j j ij ii i a a z z G 定理3.1-1 若λ为A 的特征值,则 n i i G 1 =∈ λ 证明:设Ax = λx (x ≠ 0),若k 使得∞ ≤≤==x x x i n i k 1max 因为 k n j j kj x x a λ=∑=1 ?∑≠= -n k j j kj k kk x a x a )(λ ?∑∑∑ ≠=≠=≠≤≤= -n k j j kj n k j j k j kj n k j k j kj kk a x x a x x a a 11λ ? n i i k G G 1 =? ∈λ 例1 估计方阵????? ?? ?? ???----=41 .03.02.05.013.012.01 .035.03.02.01.01A 特征值的范围 解:
G 1 = {z :|z – 1|≤ 0.6};G 2 = {z :|z – 3|≤ 0.8}; G 3 = {z :|z + 1|≤ 1.8};G 4 = {z :|z + 4|≤ 0.6}。 注:定理称A 的n 个特征值全落在n 个盖氏圆上,但未说明每个圆盘内都有一个特征值。 3.1.2 盖氏圆的连通部分 称相交盖氏圆之并构成的连通部分为连通部分。 孤立的盖氏圆本身也为一个连通部分。 定理3.1-2 若由A 的k 个盖氏圆组成的连通部分,含且仅含A 的k 个特征值。 证明: 令D = diag(a 11,a 12,…,a nn ),M = A – D ,记 )10(00 0)(2 1 22111222 11≤≤?? ?? ? ? ? ??+??????? ? ?=+=εεεε n n n n nn a a a a a a a a a M D A 则显然有A (1) = A ,A (0) = D ,易知A (ε)的特征多项式的系数是ε的多项式,从而A (ε)的特征 值λ1(ε),λ2(ε),…,λn (ε)为ε的连续函数。 A (ε)的盖氏圆为:)10(,}||||:{)(11≤≤?=≤ -=∑∑≠=≠=εεεεi n i j j ij n i j j ij ii i G a a a z z G 因为A (0) = D 的n 个特征值a 11,a 12,…,a nn ,恰为A 的盖氏圆圆心,当ε由0增大到1时,λi (ε)画出一条以λi (0) = a ii 为始点,λi (1) = λi 为终点的连续曲线,且始终不会越过G i ; 不失一般性,设A 开头的k 个圆盘是连通的,其并集为S ,它与后n – k 个圆盘严格分离,显然,A (ε)的前k 个盖氏圆盘与后n – k 个圆盘严格分离。 当ε = 0时,A (0) = D 的前k 个特征值刚好落在前k 个圆盘G 1,…,G k 中,而另n – k 个特征值则在区域S 之外,ε从0变到1时, k i i G 1 )(=ε与 n k i i G 1 )(+=ε始终分离(严格) 。连续曲线始终在S 中,所以S 中有且仅有A 的k 个特征值。 注:1) 每个孤立圆中恰有一个特征值。 2) 例1中G 2,G 4为仅由一个盖氏圆构成的连通部分,故它们各有一个特征值,而G 1,G 3构成的连通部分应含有两个特征值。 3) 因为例1中A 为实方阵,所以若λ为A 的特征值,则λ也是A 的特征值,所以G 2,G 4
