线性代数答案人大出版社,第四版赵树嫄主编

线性代数习题
习题一(A )
1,(6)
2222
2
2222
2
2
12(1)4111(1)2111t t
t t
t t t t t
t t --+++==+--++ (7)
1log 0log 1
b a a
b =
2,(3)-7
(4)0
4,234
10001
k k k k k -=-=,0k =或者1k =.
5,23140240,0210x
x x x x x x
=-≠≠≠且.
8,(1)4 (2)7 (3)13
(4) N ( n (n-1)…21 )=(n-1)+(n —2)+…+2+1=(1)
2
n n - 10, 列号为3k42l,故k 、l 可以选1或5;若k=1,l=5,则N(31425)=3,为负号;故k=1,l=5。
12,(1)不等于零的项为132234411a a a a =
(2)(234...1)11223341,1...(1)!(1)N n n n n n a a a a a n n --=-=-! 13,(3)
2112342153521534215100061230
61230002809229092280921000280921000
c c r r --=
(4)将各列加到第一列,
2()
2()2()x y y
x y D x y x y
x x y x
y
++=+++1
2()1
1y x y x y x
y x y
x
+=+---
12()0
0y x y
x y x y x y
x
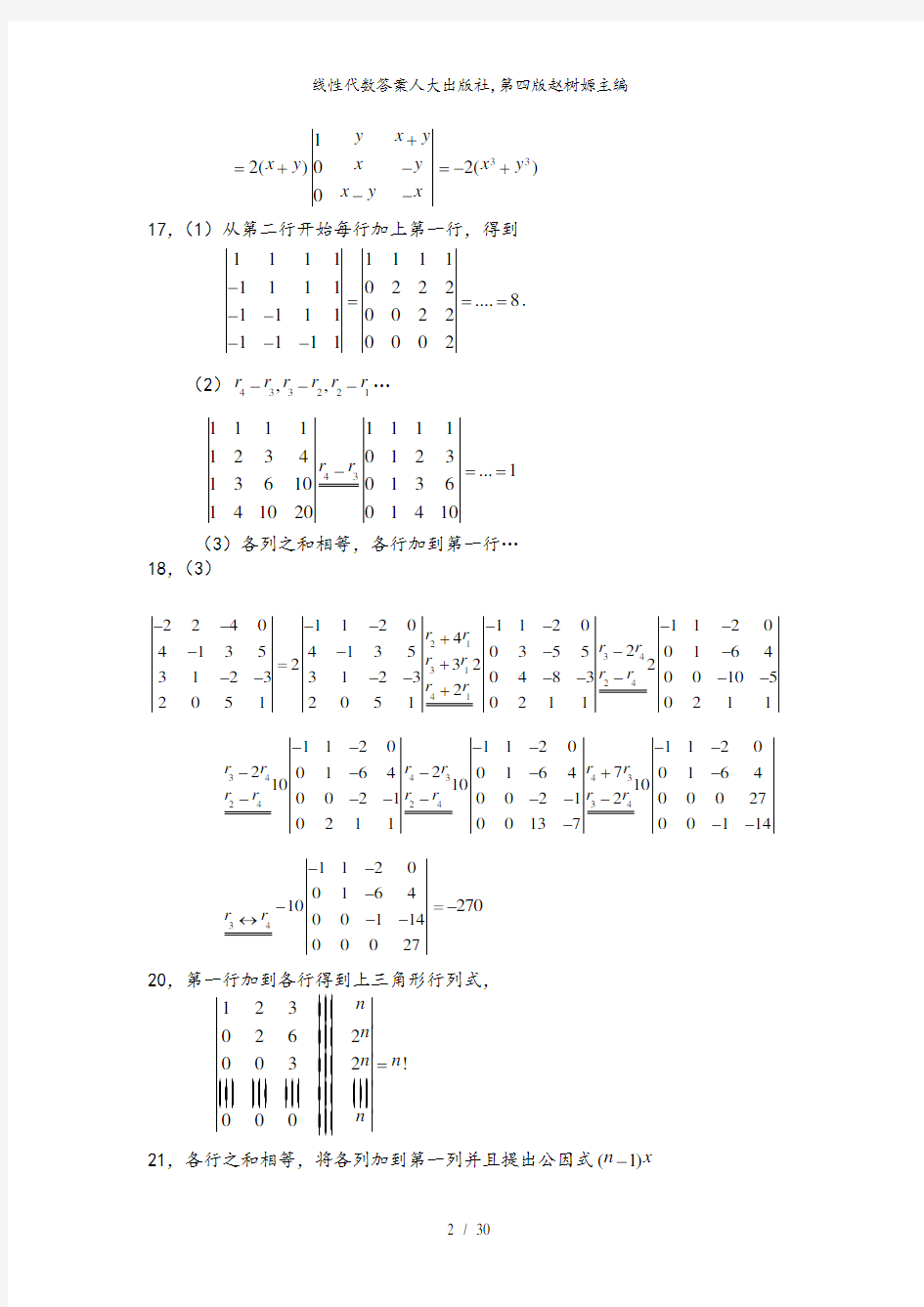
+=+---332()x y =-+ 17,(1)从第二行开始每行加上第一行,得到
1
1
11
1111
11110222 (811)
1
10022
1111
0002
-===-----. (2)433221,,r r r r r r ---…
431111
111
112340123
(113)
6
10013
6
14102001410
r r -== (3)各列之和相等,各行加到第一行…
18,(3)
21
34312441
224011201
1201120
42413541350
3550
164
232
2
312331230
483001052205120510
2110211r r r r r r r r r r --------+-----=+---------+
4334433424
241
120112*********
1640
1640
164
1010
10
002100210002720
21100
1370
0114
r r r r r r r r r r r r ------+---------------
3411200164
10
01140
0027
r r ----?--270=-
20,第一行加到各行得到上三角形行列式,
1
230
262!0
0320
n
n n n n
= 21,各行之和相等,将各列加到第一列并且提出公因式(1)n x -
11
0(1)1010x x x x x x x
n x
x x x x x x -从第二行开始各行减去第一行得到
1111
00
(1)(1)(1)(1)(1)000000
0n n n n x x x x x n x
n x x n x x x
-----=--=----
22,最后一列分别乘以121,,...n a a a ----再分别加到第1,2,…n-1列得到上三角形行列式
11223122313
112101001(
)()...()00010
1
n n n n n n n n x a a a a a a a x a a a a a x a a a x a x a x a x a ------------=----
23,按第一列展开
122110
3110
00111111110
0000000000000000000
00
n n n n n n
a a a a D a a a a a a a +--=-+ 11
222
431
11111111110000
00000000000
0...(1)00000000
n n
n a a a a a a a a +--++- 01223413412311201
1
..................()n
n n n n n i i
a a a a a a a a a a a a a a a a a a a a a -==----=-∑
24,将第二列加第一列,然后第三列加第二列,….第n 列加第n-1列,最后按第一行展开。
D =
12200 (000)
(00)
....................................000 (1)
2
1
...
1
1n
n a a a a a ---1
200...0000...
00..................
..................000 (01)
2
3...
1
n
a a a n
n --=-+ 12(1)(1)...n n n a a a =-+.
25,(1)
2143
22
2222
1123112312220100(1)(4)0231
5
231
5
2
3
190
04r r r r x x x x x x ----=--=--
1
2
x x =±=± (2)各行之和相等… (3)与22题类似…
(4)当0,1,2,3,...2x n =-时,代入行列式都会使行列式有两行相同,所以它们都是方程的根。
28,414243441040140140
2112(6)212(6)030180600
111111
1111
A A A A --+++=
=--=--=- 29,111213141
111
d c b b
A A A A b b b
b
c
d
a d
+++=
其中1,3两行对应成比例,所以为零。 32,从第二行开始每一行乘以(-1)加到上一行然后按第一列展开
123401111
112310111
11122001111
130001112000011
1
1
1
n n x x n x D x x n x x x x x
x
x
x
x
x
----==--
1
11111111110111
1(1)000110
11n x
x x +--=--
1
1121,2 (1)
0000001000000
10000
(1)(1)001000
0000000
11
i i r r n n n i n x x x x x x x x x x
+-++-=---????→-=--←????- 33,按第一列展开
100000000000000000000000000000
n a b a b a b a b a a D a a b
a b
b
a
b
a
-????→=
←????按第一列
展开
阶
1
0000000000000000
n b a
b a b b b a
b
++(-1)1n n n
a b +=+(-1)
34,原方程化为
21211
123122(2)(4)00212002x x x x x x x x =
=--…。
35,
12
34
11110
0111
1
1111
1111001
1
111
1
11r r r r x x x x x y y y y
y
--+--???→←???+--
2211001100111100
0001
1
001
1
1
1
110
0x x xy
xy
x y y y
--===--=0
解得0x =或者0y =
36,
11111213
(21)(11)(12)(31)(32)(31)4814191
8
127
-=++-+--=--(范德蒙行列式) 37,解
12
2322222
22
22
11()()11a b x b x a a x
b a
x a x a c c x a b x a
a b b a x b a b c c
x a b x a a b b x a a b b +++--++---=----------- 2121111
()()00()()()
x a
r r a x b a x a b a x b a x a b x a a b
x a a b b ++--++=---++-------- ()()()()x a b a x b x b a =++---
40,(3)D=63,D 1=63,D 2=126, D 3=189
123
1
23x x x =??
=??=? (6)D=20,D 1=60,D 2=—80, D 3=--20,D 4=20
12
343411
x x x x =??=-??
=-??=? 42,∵221069
12412458201822---=---2323
3330182205
--=-=-=--
∴原方程仅有零解。
43,令1
1
22
113102112
11
k
k k k --=
---(2)(1)6k k =---2340k k =--=, 得 1k =-或4k =;故当1k =-或4k =时原齐次方程组有非零解. 44,原齐次方程组的系数行列式
1120011310(2)(1)0211
2
1
1
k k k k k k -+-=
-=+-≠--
即当1k ≠且2k ≠-时原齐次方程组仅有零解.
习题二(A)
2,(1)
1315 38282
37913 A B
??
??-=??
??
??
-
(2)
141387 232525
2165 A B
??
??
=??
??
??+--
(3)
3111
4040
1335 x B A
-
??
??=-=--
??
??
----
??
(4)由(2A—Y)+2(B—Y)=0得 3Y=2(A+B)
∴
2
()
3
Y A B
=+
5533
2
0202
3
1133
??
??
=??
??
??
1010
22
33
44
00
33
22
22
33
??
??
??
??
=
??
??
??
??
??
3,因为
2324
20
274
x u v
A B C
x y y v
+-+
??
+-==
??
-++-+
??
得方程组230
27
240
40
x u
x y
v
y v
+-=
?
?-++
?
?
+=
?
?-+=
?
解得x=-5,y=-6,u=4,v=-2
5,(2)
1041 431??????
-
--
(3)
123
246
369
??
??
??
??
??
14
(7)
10
5117629
15
161532
02
??
????
??
????
??
????
??
??
-
--
=
11,(1)设
a c
X
b d
??
??
??
=,则
2546
1321
a c
b d
-
??????
=
??????
??????
2525463321a b c d a b c d ++-????
=????++????,得到方程组 254
32
a b a b +=??
+=?解得20a b =??=?, 与25631c d c d +=??+=?-解得23
8c d =??=?-.
2230
8X ??
????-=。 (2)54245974X ??????
????
--=--2-- (3)设x X y z ??????????=,111221131116x y z -??????
??????-=??????????????????
, 2236x y z x y z x y z +-=??-++=??++=?
,解得132x y z =??=??=?于是132X ??????
????=。 13.设所有可交换的矩阵为a b X c d ??=????则11110101a b a b c d c d ????????
=????????????????
, a c b d a a b c d c c d +++????=????+????解得0
a
b
c d a
???
?=??=?从而0a b X a ??=????。 16,(3)因为111111000000??????
=??????
??????,所以11110000n
????=????????。 (4)因为2
1111111201010101????????
==????????????????用数学归纳法可以推得 1110101n
n ????
=????
????
. (5)因为2
111111221121111112211??????????
===????????????????????
故可以推出
111111111...211111111n
n -????????==????????????????
。 20,334()mA m A m m m -=-=-=- 21,122(2)2T T n T n n A A mA m A m +===。
28,因为()()T T T T T T A A A A A A ==,所以T AA 为对称矩阵.
因为()()T T T T T T AA A A AA ==,所以T AA 为对称矩阵.
31, (1),原矩阵为1
211
12241
23
431
3244421120
32A A A B A B A B B B A A A B A B A B B -??
+???????
?==-?
???????+????????-??
,其中 1112021111A B --??????
==????
??-??????
[]1224121010111101112A B A B -????????????
+=+-=+=????????????----????????????; [][]3100331A B ??
==????
;
[][][][][][]3244103210220A B A B ??
+=+-=+-=-????;
(3),记原矩阵为00aI
I cI I bI dI ????
?
???????
,则有 00aI I cI I bI dI ?????????
??? 2
2
22aI acI I
cI bdI ??=??+?? ()aI
acI
I
c b
d I ??=??+??
001000
1
a ac
a ac c bd c bd ??
????=??
+??+??
.
33,312313234242A A A A A A A A --=--- 12
31
2
34288A A A A A A =-=-=-
34,(2)因为0a b
ad bc c d =-≠,所以1
1a b d b c d c a ad bc --????
=????--????
. (4)因为1A =-,故可逆.*143153164A -????=-????--??,1143153164A ---??
??=--??
??-??
. (6)因为12...0n A a a a =≠,故可逆。 1211...(12...)ii i i n A a a a a a i n -+==,
23*
121 (00)
n
n a a a A a a a -?? ?=
?
?
?
?,11
1100
n a A a -??
??
??
=?
????????
?
。 40, (1)1
254635462231321122108X -----??????????
===??????????
-??????????
。 (21
1
10
113111113542224322104321114521251111253197412
2X -????---????
????
??????
????==--=--????????????????????---????
????
--????) (3)1
1
10331112211
112113332
36
1116621
10
22X -?
?
-
??-?????????
?
????????
??=-==??????????????????????????????-???
?
。 42, 由2AX I A X +=+得到2AX X A I -=-,()()()A I X A I A I -=-+,
1()()()()I A I A I X A I A I ----=--()A I +
201140022X A I -??
??=+=??
????
。 44, 两边同乘以121()()()(...)k k I A I A I A I A A A I A I ----=-++++=-=. 45, 由2240A A I --=得到()(3)A I A I I +-=,于是A I +可逆并且
