02第二章 线性规划的基本性质

第二章 线性规划的基本性质

在生产、经济、技术领域，许多工程技术和管理问题实际上是线性的，或者是可以用线性函数近似表达的，所以线性规划的研究是很有意义的。而且对线性规划的理论的研究要比非线性规划领域成熟的多。掌握线性规划的基本理论和求解方法是本课程最重要的目标之一。

§2.1 线性规划解的几何特征

借助于平面图形可以直观地了解线性规划解的几何特征，具体介绍一个实例。 设有两个决策变量x 1和x 2的线性规划： min - 2 x 1 - x 2

s.t. -3 x 1 -4 x 2 ≥-12 （2.1） - x 1 + 2 x 2 ≥ -2 x 1,x 2, ≥ 0

首先在x 1O x 2平面上画出（2.1）的可行域：

12121212{(,)|-3 -4 -12,- + 2 -2, , 0}T

K x x x x x x x x =≥≥≥

为此，只要画出K 的边界：

-3 x 1 -4 x 2 ≥-12

- x 1 + 2 x 2 ≥ -2 x 1 = 0,x 2 = 0

该可行域如图 2.1所示，它是一个由四条直线组成的凸多边形。任何一个含两个变量的线性规划的可行域都是以直线为边的凸多边形。

观察目标函数： f(x ) = - 2 x 1 - x 2

对于任一给定的实数a ，方程 - 2 x 1 - x 2 =a 表示一条直线，称为f 的等值线。变动a 可以得到一族相互平行的直线。把f 的等值线向函数值a 减小的方向移动，它与凸多边形K 的最后一个交点即为的最优解。最优解是凸多边形的一个顶点。

设目标函数f(x ) = c 1 x 1 +c 2 x 2它是x 1和x 2的函数，它的斜率是12

c c -，它在任意一点

的梯度：

()1212,,T

T

f f f c c x x ?????== ?????

它与目标函数的等值线垂直，由高等数学的有关知识可知，当点()12,T

x x 沿着梯度方向移动时，f 的值将随之增大，沿着梯度负方向移动时，f 的值将随之减小。

对于式（2.1），不妨在原点做梯度()()12,2,1T

T

f c c ?==--，从原点至点()2,1T

--作一个向量即为该梯度。过原点作梯度向量的垂直线（用虚线表示），它为过原点且a=0的等值线：

- 2 x 1 - x 2=0

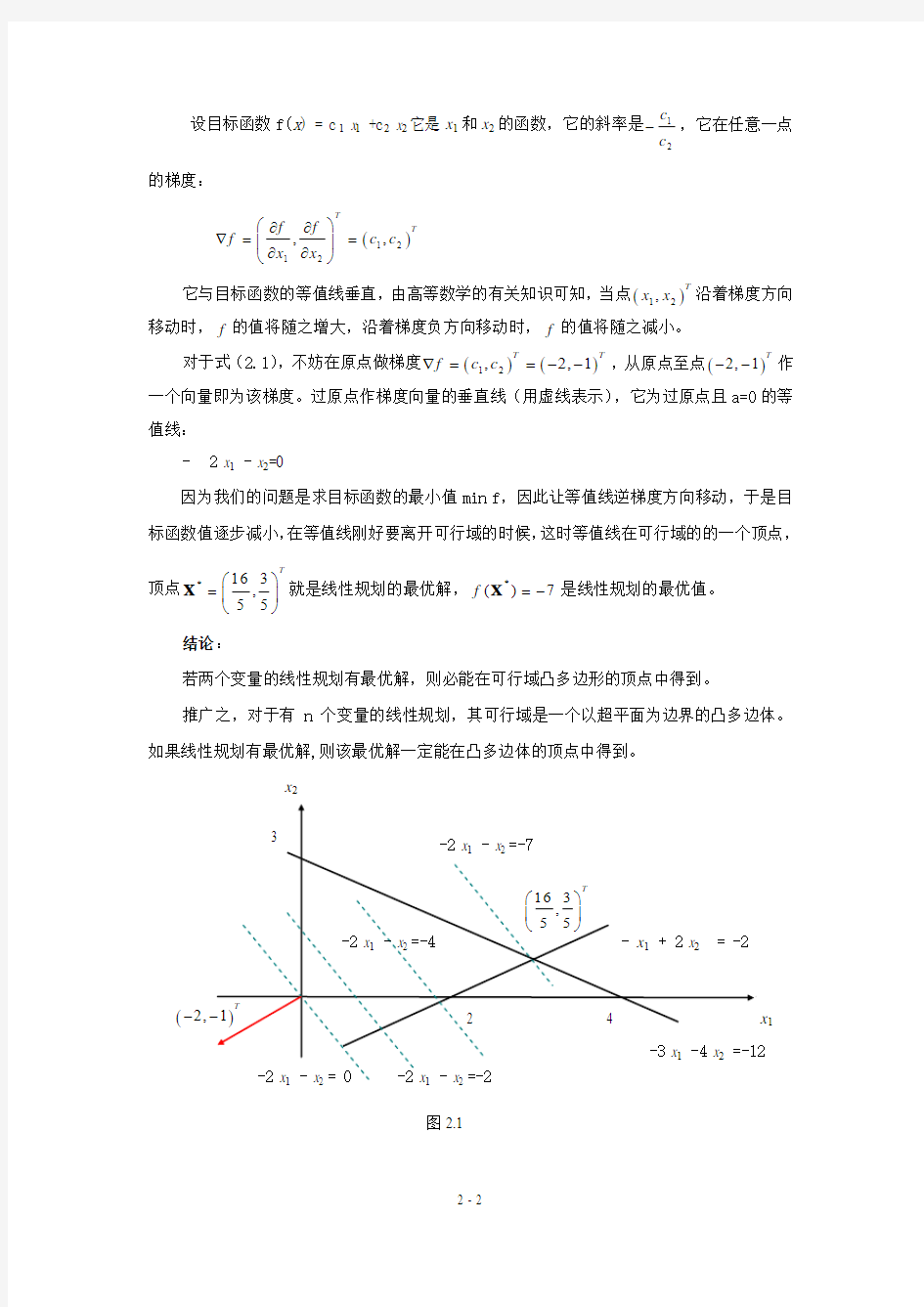
因为我们的问题是求目标函数的最小值min f ，因此让等值线逆梯度方向移动，于是目标函数值逐步减小，在等值线刚好要离开可行域的时候，这时等值线在可行域的的一个顶点，顶点*163,55T

??= ???

X 就是线性规划的最优解，*

()7f =-X 是线性规划的最优值。

结论：

若两个变量的线性规划有最优解，则必能在可行域凸多边形的顶点中得到。

推广之，对于有n 个变量的线性规划，其可行域是一个以超平面为边界的凸多边体。如果线性规划有最优解,则该最优解一定能在凸多边体的顶点中得到。

x 1

x 2

图2.1

(2,-

以上的结论对于求解线性规划有重大的价值，因为原本我们要在可行域的无穷多个点中去寻找最优解，现在根据结论我们只要在可行域的有限个顶点中寻找最优解即可。

§2.2 线性规划解的标准形

为了研究方便，定义下列形式为线性规划的标准形：

11

m in ..

,

1,2, 0

1,2,...,n

j

j

j n

ij

j i j j z c

x s t a

x b i m x j n

===

==≥=∑∑ （2.2）

对于目标函数，一律定义为求最小值，决策变量一律定义为非负变量，约束条件除变量的非负条件之外，一律为等式约束。

各种形式的线性规划模型都可以化为标准形。

1、 若问题的目标函数是求最大值1

m ax n

j

j j z c

x ==

∑，那么可以令：f z =-，把原问题

化为在相同的约束条件下求最小值：min f ，显然，新问题和原问题是同解的。

2、 如果约束条件中有不等式约束：1

n

ij j i j a x b =≤∑，则可以引进一个新变量'

i x ，并用下

面两个约束条件来代替原有的不等式约束：

'

'

1

,

0n

ij

j i i i j a

x x b x =+=≥∑

称变量'

i x 为松弛变量。

3、 如果约束条件中有不等式约束：1

n

ij j i j a x b =≥∑，则可以引进一个新变量"

i x ，并用下

面两个约束条件来代替原有的不等式约束：

"

"

1

,

0n

ij

j i i i j a

x x b x =-=≥∑

称变量"

i x 为剩余变量。

4、 如果约束条件中出现(0)j j j x h h ≥≠，则可以引进一个新变量j j j y x h =-替代原

问题中的变量j x ，于是，问题中原有的约束就化为0j y ≥。

5、 如果变量j x 的符号不受约束，则可以引进两个新变量'

j y 和"

j y ，并以'"

j j j x y y =-代

入原问题的目标函数和约束条件消去j x ，同时在约束条件中增加'

"

0,0j j y y ≥≥。

例2.1 把线性规划

121212121m ax ..

23674230

z x x s t x x x x x x x =++≤+≥-=≥ 化为标准形。

解 该题有四个地方与标准形不符，a.目标函数是求最大值；b.决策变量2x 的符号没有约束；c.第一、第二约束条件为不等式。

1、令：12()f z x x =-=-+，求m ax z 改为求min f

2、令：23434,0,0x x x w here x x =-≥≥

3、对不等式约束条件分别引入为松弛变量5x 和剩余变量6x ，从而将原问题化为标准形：

13413451346134m in ..

2336774230,1,3,4,5,6

j f x x x s t x x x x x x x x x x x x j =--++-+=+--=-+=≥=

§2.3 线性规划解的基本定理

观察(2.1)式，其相应的标准形为：

12

123124m in 2..

3412220,1,2,3,4

j x x s t x x x x x x x j -----=--+-=-≥=

它的可行域有四个顶点，在标准形的形式下所对应的解为：

163(0,0,12,2),(0,3,0,8),(

,,0,0),(2,0,6,0)55

T

T

T T

四个顶点的共同之处是所对应的变量值中均有两个的坐标为0。仔细分析后可知，作为平面上凸多边形的顶点必然是两条边界直线的交点。若边界直线为坐标轴，则相应的一个坐标为0，若边界直线非坐标轴，则化标准形时所引进的松弛变量或剩余变量就应为0，因此

在仅有两个决策变量的线性规划标准形的形式下，顶点所对应的变量的值为0的个数不少于两个是一般规律。这里的变量可以是决策变量、松弛变量或剩余变量。

我们利用代数的这个特征引入基本可行解这个概念来替代几何意义上顶点这个名词，并用以表述线性规划的基本定理。

线性规划的标准形（2.2）用矩阵表示为：

m in ..

T

z s t ==≥C x

A x

B x （2.3） 其中，

121212(,,...,),(,,...,),(),

(,,...,)

T

T

n n T

ij m n m c c c x x x a b b b ?====C x A B

不妨设矩阵A 的秩()r m =A ，即线性方程组=A x B 没有多余的方程。于是线性规划（2.2）的可行解就等价于求线性方程组=A x B 的非负解。

线性方程组=A x B 有n 个变量，且()r m =A ，因此当=A x B 的一个解中非零分量都是线性无关时，则非零分量的个数不会超过()r m =A ，即零分量的个数不少于n-m 。

线性方程组=A x B 中对应非零分量呈线性无关的解就是式（2.3）的基本解；其中非负基本解称为基本可行解。

定理2.1 基本可行解的存在定理，对于线性规划的标准形（2.3） 1、 若有可行解，则一定有基本可行解； 2、 若有最优解，则一定有最优基本可行解；

当矩阵A 的秩()r m =A 时，基本可行解的个数是在n 个变量中取m 个线性无关的变量的组合，其个数不会超过：

!

!()!n n m m n m ??= ?-??

（2.4）