初升高数学之衔接专题：专题六 二次函数的最值问题

专题六 二次函数的最值问题

【要点回顾】

1．二次函数2 (0)y ax bx c a =++≠的最值．

二次函数在自变量x 取任意实数时的最值情况(当0a >时，函数在2b x a

=-

处取得最小值2

44ac b a

-，无最大值；当0a <时，函数在2b x a =-处取得最大值

2

44ac b a

-，无最小值． 2．二次函数最大值或最小值的求法．

第一步确定a 的符号，a ＞0有最小值，a ＜0有最大值； 第二步配方求顶点，顶点的纵坐标即为对应的最大值或最小值． 3．求二次函数在某一范围内的最值．

如：2y ax bx c =++在m x n ≤≤（其中m n <）的最值． 第一步：先通过配方，求出函数图象的对称轴：0x x =； 第二步：讨论：

[1]若0a >时求最小值或0a <时求最大值，需分三种情况讨论： ①对称轴小于m 即0x m <，即对称轴在m x n ≤≤的左侧； ②对称轴0m x n ≤≤，即对称轴在m x n ≤≤的内部； ③对称轴大于n 即0x n >，即对称轴在m x n ≤≤的右侧。

[2] 若0a >时求最大值或0a <时求最小值，需分两种情况讨论：

①对称轴02m n

x +≤，即对称轴在m x n ≤≤的中点的左侧；

②对称轴02

m n

x +>，即对称轴在m x n ≤≤的中点的右侧；

说明：求二次函数在某一范围内的最值，要注意对称轴与自变量的取值

范围相应位置，具体情况，参考例4。

【例题选讲】

例1求下列函数的最大值或最小值．

（1）5322--=x x y ； （2）432+--=x x y ．

分析：由于函数5322--=x x y 和432+--=x x y 的自变量x 的取值范围是全体实数，所以只要确定它们的图象有最高点或最低点，就可以确定函数有最大值或最小值． 解：（1）因为二次函数5322--=x x y 中的二次项系数2＞0，所以抛物线

5322--=x x y 有最低点，即函数有最小值．因为5322--=x x y =8

49

)43(22-

-x ，所以当43

=x 时，函数5322--=x x y 有最小值是8

49-．

（2）因为二次函数432+--=x x y 中的二次项系数-1＜0，所以抛物线

432+--=x x y 有最高点，

即函数有最大值．因为432+--=x x y =4

25

)23(2++-x ，所以当2

3

-=x 时，函数432+--=x x y 有最大值425．

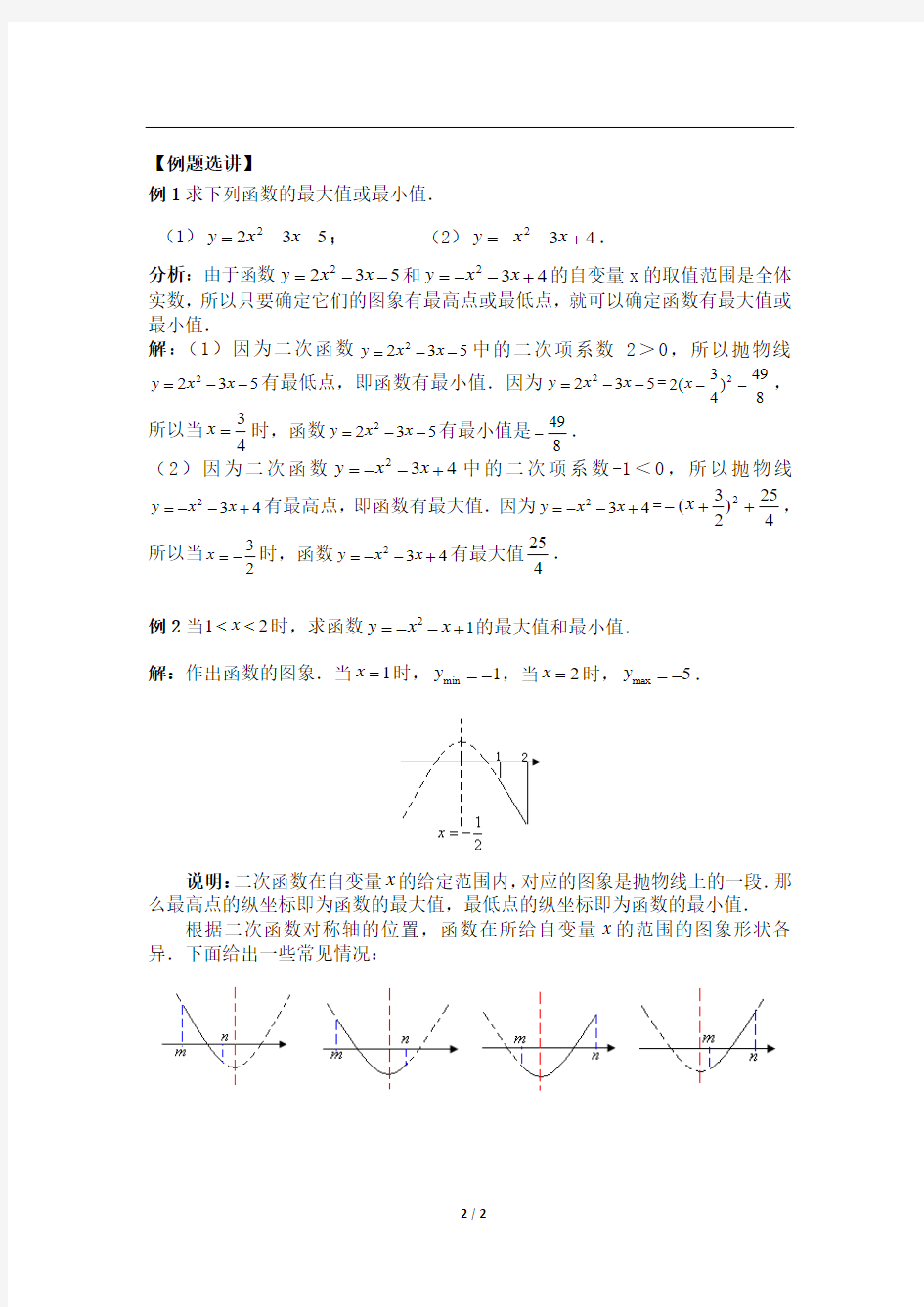
例2当12x ≤≤时，求函数21y x x =--+的最大值和最小值． 解：作出函数的图象．当1x =时，min 1y =-，当2x =时，max 5y =-．

说明：二次函数在自变量x 的给定范围内，对应的图象是抛物线上的一段．那么最高点的纵坐标即为函数的最大值，最低点的纵坐标即为函数的最小值．

根据二次函数对称轴的位置，函数在所给自变量x 的范围的图象形状各异．下面给出一些常见情况：

例3当0x ≥时，求函数(2)y x x =--的取值范围． 解：作出函数2(2)2y x x x x =--=-在0x ≥内的图象．

可以看出：当1x =时，min 1y =-，无最大值．所以，当0x ≥时，函数的取值范围是1y ≥-

例4当1t x t ≤≤+时，求函数215

22

y x x =

--的最小值(其中t 为常数)． 分析：由于x 所给的范围随着t 的变化而变化，所以需要比较对称轴与其范围的相对位置．

解：函数215

22

y x x =--的对称轴为1x =．画出其草图．

(1) 当对称轴在所给范围左侧．即1t >时：当x t =时，2min 15

22

y t t =--；

(2) 当对称轴在所给范围之间．即1101t t t ≤≤+?≤≤时： 当1x =时，

2m i n

1511322

y =?--=-； (3) 当对称轴在所给范围右侧．即110t t +

22min 151

(1)(1)3222

y t t t =+-+-=-．

综上所述：2

213,023,0115

,1

2

2t t y t t t t ?-

=-≤≤???-->?

例5某商场以每件30元的价格购进一种商品，试销中发现这种商品每天的销售

量m (件)与每件的销售价x (元)满足一次函数1623,3054m x x =-≤≤．

(1) 写出商场卖这种商品每天的销售利润y 与每件销售价x 之间的函数关系式；

(2) 若商场要想每天获得最大销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？

解：(1) 由已知得每件商品的销售利润为(30)x -元，那么m 件的销售利润为

(30)y m x =-，又

1

m x =-．2 (30)(1623)32524860,3054y x x x x x ∴=--=-+-≤≤

(2) 由(1)知对称轴为42x =，位于x 的范围内，另抛物线开口向下

∴当42x =时，2max 342252424860432y =-?+?-=

∴当每件商品的售价定为42元时每天有最大销售利润，

最大销售利润为432元．

【巩固练习】

1．抛物线2(4)23y x m x m =--+-，当m = _____ 时，图象的顶点在y 轴上；当

m = _____ 时，图象的顶点在x 轴上；当m = _____ 时，图象过原点．

2．用一长度为l 米的铁丝围成一个长方形或正方形，则其所围成的最大面积为 ________ ．

3．设0a >，当11x -≤≤时，函数21y x ax b =--++的最小值是4-，最大值是0，求,a b 的值．

4．已知函数221y x ax =++在12x -≤≤上的最大值为4，求a 的值．

5．求关于x 的二次函数221y x tx =-+在11x -≤≤上的最大值(t 为常数)．

【巩固练习】答案

1．4 14或2，3

2

2．

2

2

16

l

m 3．2,2

a b

==-． 4．

1

4

a=-或1

a=-．

5．当0

t≤时，

max 22

y t

=-，此时1

x=；当0

t>时，

max 22

y t

=+，此时1

x=-．