高中数学专题讲义-数列的概念

【例1】 请写出下面数列的一个通项公式．

⑴2，0，2，0，2，…

⑵12-，16，112-，120

，…

⑶请写出下面数列的一个通项公式：0.9,0.99,0.999,0.9999,L

【例2】 ⑴ 请写出下面数列的一个通项公式：12，2，92，8，25

2

…，

⑵ 请写出下面数列的一个通项公式：1，2，3，4，5，8，7，16，9…，

【例3】 观察下列等式：

2111,22n i i n n ==+∑ 2

321111,326n i i n n n ==++∑ 3

4321111,424n i i n n n ==++∑ 4

54311111,52330n i i n n n n ==++-∑ 5

654211151,621212n i i n n n n ==++-∑ 6

7653111111,722642n i i n n n n n ==++-+∑ ……………………………………

212

112101

,n

k k k k k k k k k i i a n a n a n a n a n a +--+--==++++???++∑ 可以推测，当2n ≥时，1111

,,12

k k k a a a k +-===+ 2k a -= .

典例分析

数列的概念

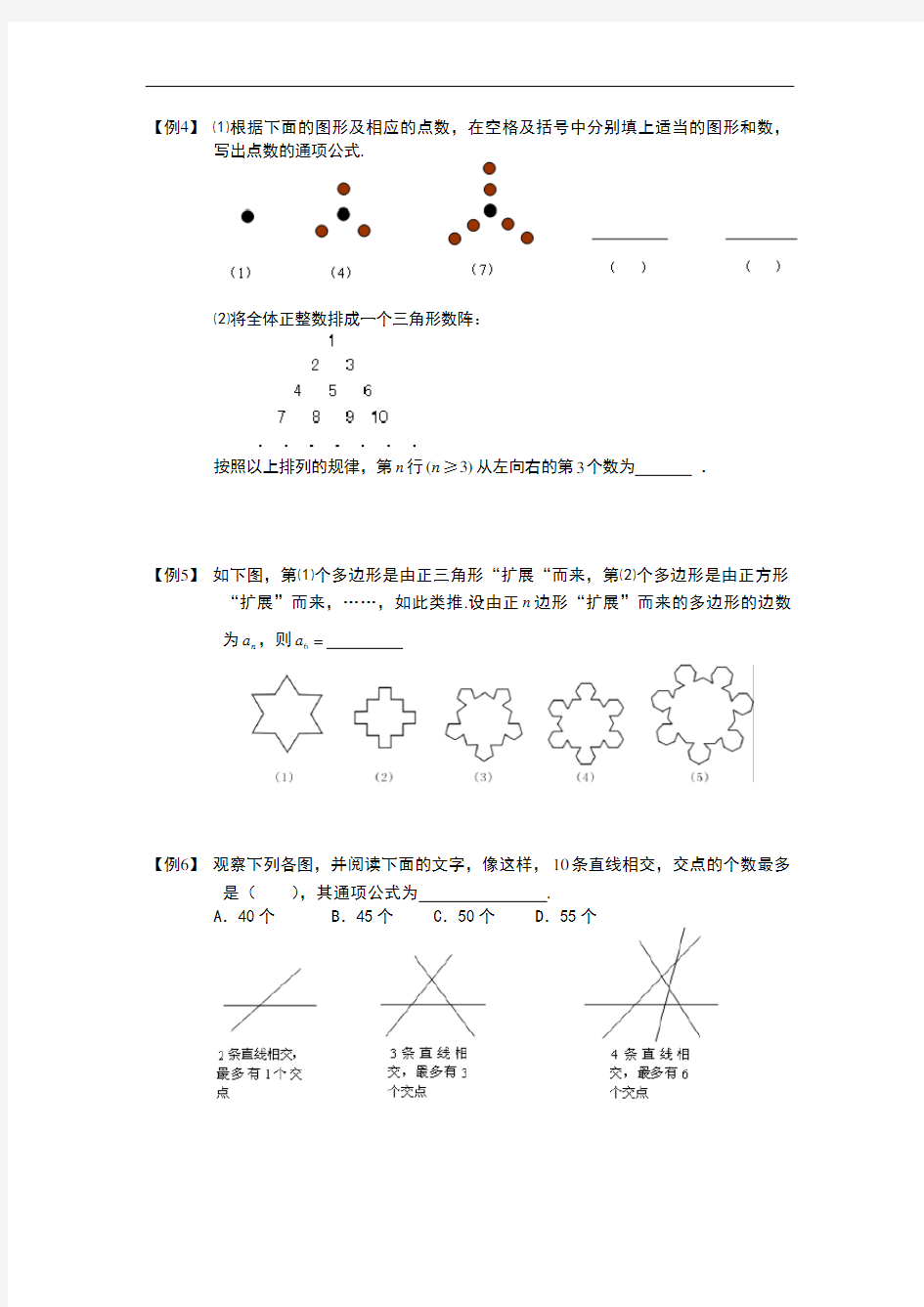
【例4】 ⑴根据下面的图形及相应的点数，在空格及括号中分别填上适当的图形和数，

写出点数的通项公式.

⑵将全体正整数排成一个三角形数阵：

按照以上排列的规律，第n 行(3)n ≥从左向右的第3个数为 ．

【例5】 如下图，第⑴个多边形是由正三角形“扩展“而来，第⑵个多边形是由正方形

“扩展”而来，……，如此类推.设由正n 边形“扩展”而来的多边形的边数为n a ，则6a

【例6】 观察下列各图，并阅读下面的文字，像这样，10条直线相交，交点的个数最多

是（ ），其通项公式为 .

A ．40个

B ．45个

C ．50个

D ．55个

【例7】 将正ABC ?分割成2n （2≥n ，n *∈N ）个全等的小正三角形（图2，图3分别

给出了2n =，3的情形），在每个三角形的顶点各放置一个数，使位于ABC ?的三边及平行于某边的任一直线上的数（当数的个数不少于3时）都分别依次成等差数列．若顶点A ，B ，C 处的三个数互不相同且和为1，记所有顶点上的数之和为()f n ，则有(2)2f =，(3)f =_________，L ，()f n =_____________．

图3

图2

【例8】 已知一个数列的通项公式是230n a n n =+-.

⑴ 问60-是否是这个数列中的项？ ⑵ 当n 分别为何值时，000n n n a a a =><，，？ ⑶ 当n 为何值时，n a 有最大值？并求出最大值.

【例9】 一个数列的通项公式是2813n a n n =-+，写出此数列的前五项，并求此数列的

最小项的值？

【例10】 数列{}n a 中，11a =，对所有的2n ≥，都有2123n a a a a n ????=L ，求数列{}n a 的

通项公式n a ．

【例11】 已知整数以按如下规律排成一列：()1,1、()1,2、()2,1、()1,3、()2,2，()3,1，

()1,4，()2,3，()3,2，()4,1，……，则第60个数对是（ ）

A ．()10,1

B ．()2,10

C ．()5,7

D ．()7,5

【例12】 已知数列()1212:,,,0,3n n A a a a a a a n <<

(),1i j i j n ≤≤≤，j i a a +与j i a a -两数中至少有一个是该数列中的一项．现

给出以下四个命题：

① 数列0,1,3具有性质P ；

② 数列0,2,4,6具有性质P ； ③ 若数列A 具有性质P ，则10a =；

④ 若数列()123123,,0a a a a a a <<≤具有性质P ，则1322a a a +=． 其中真命题有（ ）

A ．4个

B ．3个

C ．2个

D ．1个

【例13】 在数列{}n a 中，若221n n a a p --=，

（2,n n *∈N ≥，p 为常数），则称{}n a 为“等方差数列”．下列是对“等方差数列”的判断：

①若{}n a 是等方差数列，则{}

2

n a 是等差数列；

②{}

(1)n -是等方差数列；

③若{}n a 是等方差数列，则{}kn a （k *∈N ，k 为常数）也是等方差数列； ④若{}n a 既是等方差数列，又是等差数列，则该数列为常数列．

其中正确命题序号为 ．（将所有正确的命题序号填在横线上）

【例14】 数列{}n a 满足11a =，23a =，()12n n a n a λ+=-（1,2,n =L ），则3a 等于（ ）

A ．15

B ．10

C ．9

D ．5

【例15】 在一个数列中，若每一项与它的后一项的乘积都同为一个常数（有限数列最

后一项除外），则称该数列为等积数列，其中常数称公积．若数列{}n a 是等积数列，且62a =，公积为6，则159********a a a a a ????????的值是（ ）

A ．5022

B ．5023

C ．5032

D ．5033