用解析法解平面几何问题

解析法

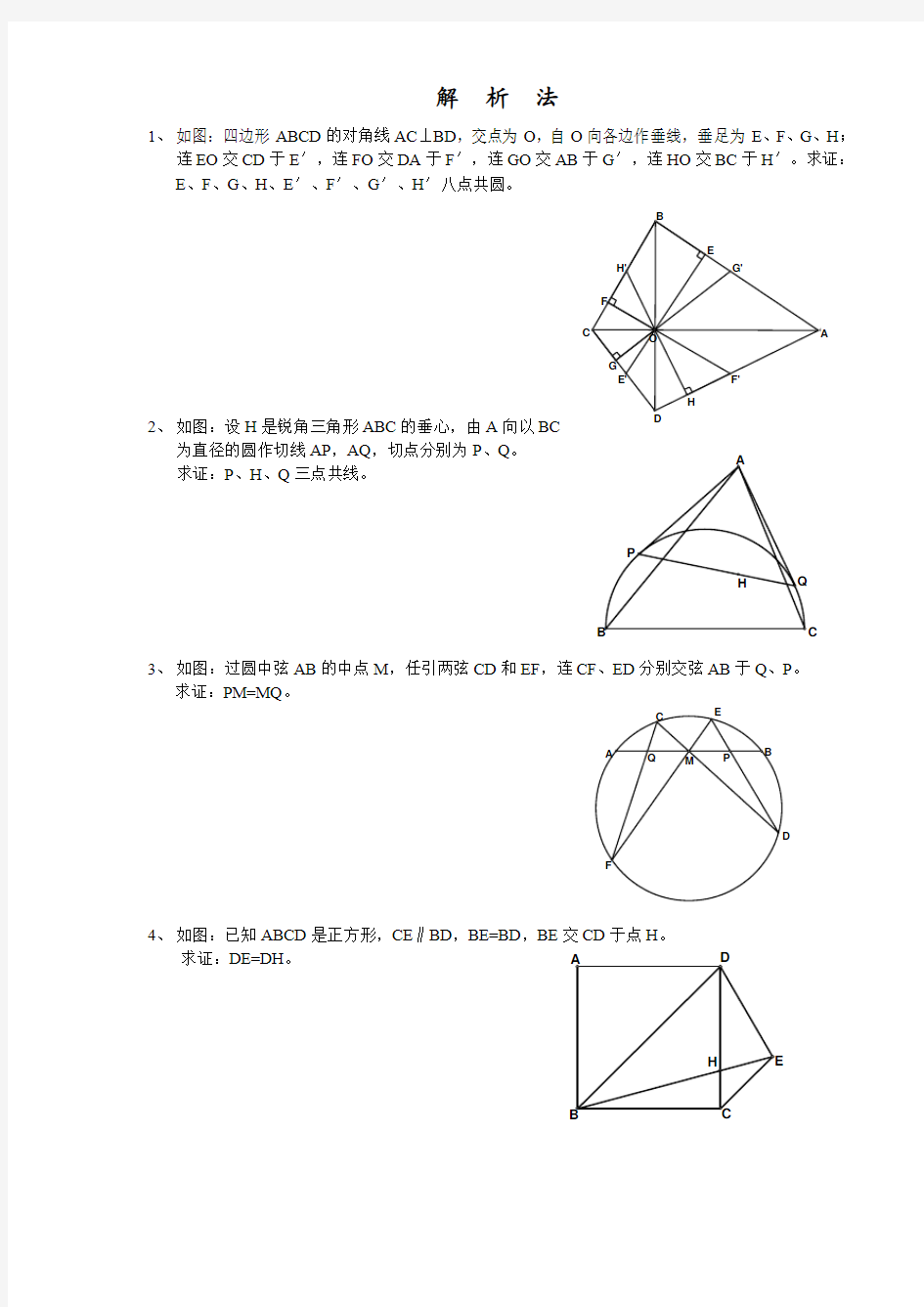
1、如图：四边形ABCD 的对角线AC ⊥BD ，交点为O ，自O 向各边作垂线，垂足为E 、F 、G 、H ；

连EO 交CD 于E ′，连FO 交DA 于F ′，连GO 交AB 于G ′，连HO 交BC 于H ′。求证：E 、F 、G 、H 、E ′、F ′、G ′、H ′八点共圆。

2、如图：设H 是锐角三角形ABC 的垂心，由A 向以BC

为直径的圆作切线AP ，AQ ，切点分别为P 、Q 。求证：P 、H 、Q 三点共线。

3、如图：过圆中弦AB 的中点M ，任引两弦CD 和EF ，连CF 、ED 分别交弦AB 于Q 、P 。

求证：PM=MQ 。

4、如图：已知ABCD 是正方形，CE ∥BD ，BE=BD ，BE 交CD 于点H 。

求证：DE=DH 。

5、用解析法证明圆的切割线定理。

6、用解析法证明半角的正切公式：

θθθ

sin cos 1cos 1sin 2

tan

-=+=

。

7、已知???

?∈≠-≠???=+=+Z k k abc c b a c b a ,2,

0sin cos sin cos πθ???θθ 求证：

cos

sin

cos

θ?

θ-=+=+c

8、设a>0，b>0，c>0，求证：bc c b ab b a -++-+2222≥ac c a ++22说明等号何时成立。练习题：

1、已知方程|x|=ax+1有一个负根但没有正根，则a 的取值范围是。

2、已知()21x x f +=，若b a R b a ≠∈,,，则()()||||b a b f a f --与的大小关系为（）（A ）()()||||b a b f a f -<- （B ）()()||||b a b f a f -=- （C ）()()||||b a b f a f ->- （D ）不能确定

3、函数()1

sin 3

cos --=

ααx f 的值域为。

4、对一切实数a 有的最小值为则M M a a a a ,|11|

22<+--++ 。

5、求证三角形的三条高交于一点。

参考答案

1、[证明] 以CA 为x 轴，DB 为y 轴建立坐标系，并记直线AB 与OG 的方程分别为

y d x b y a x ==+,1 联立可解得??? ??++bd ac abc bd ac abd

G ,'

同理可得??

? ??++bd ac abc bd ac bcd

H ,'，

???

??++bd ac acd bd ac bcd E ,'，??

? ??++bd ac acd bd ac abd

F ,'

由于F ′与G ′，E ′与H ′的横坐标相同，有F ′G ′//E ′H ′//y 轴；由于G ′与H ′，E ′与F ′的纵坐标相同，有G ′H ′//E ′F ′//x 轴；所以四边形E ′F ′G ′H ′是矩形，以它的对角线为直径作圆，这圆过E ′，F ′，G ′，H ′.又由∠G ′EE ′=∠G ′GE ′=∠H ′FF ′=∠H ′HF ′=90°知，这圆也过E ，G ，F ，H ，得证八点共圆．

2、[证明]以BC 为x 轴，线段BC 的垂直平分线为y 轴建立直角坐

标系，记ΔABC 的顶点坐标为A （a ，b ），B （—R ，0），C （R ，

0）（R>0），则以BC 为直径的圆的方程为222R y x =+ ① 而过P ，Q 的切线方程分别为

yy xx R yy xx Q Q P P =+=+因为两切线过点A ，故有

by ax R by ax Q Q P P =+=+

这表明：P （x P ,y P ），Q （x Q ,y Q ）在直线2

R by ax =+ ②

上，但过P ，Q 的直线是唯一的，故②就是直线PQ 的方程。

又由锐角三角形知，AB ，AC 与圆相交，记交点为E ，F ，则BF ⊥AC ，CE ⊥AB ，且BF 与CE 交于ΔABC 的垂心H 。由直线AC 的斜率为

R a b -知，直线BF 的斜率为b

R -，得直线BF 的方程为 ();2aR R by x R a -=+- ③

同理CE 的方程为();2

aR R by x R a +=++ ④

由③+④得②知：BF 与CE 的交点在PQ 上，即PQ 通过ΔABC 的垂心。

3、[证明]以M 为原点，直线AB 为轴建立直角坐标系，

则已知圆可表示为022

2=+-+f by y x ① 直线CD ，EF 可表示为x k y x k y 21,==合并为

()()021=--x k y x k y

②

于是，过①、②交点C 、E 、D 、F 的二次曲线系可表

示为()()022122=--++-+x k y x k y f by y x λ ③

其与x 轴的交点P ，Q 的横坐标满足方程()01221=++f x k k λ，由P ，Q 的存在性知：这方程必有两个不相等的实根，且0=+Q P x x ，这说明：原点M 是P ，Q 的中点，从而PM=MQ 。 4、[证明]如图：以BC 所在直线为x 轴，CD

1，则A （—1，1），B （—1，0），C （0，0），D （0，1）

因为

CE//BD ，所以∠ECX=∠DBC=45°，因此直线

CE 的方程为y=x ，设E （a ，a ），由|BE|=|BD|=2知，

()212

2=++a a 由于a>0，故2

3-=

a ，因此|DE|=13-，又BE 的方程为

321

-=+x y

，设H （0，b ），代入上述方程得32-=b ，于是|DH|=13-

所以|DE|=|DH|。

5、设P 是圆O 外一点，PT 是圆的切线，PAB 是圆的割线，以圆心为原点建立直角坐标系，设圆的方程为222r y x =+ ①

点P 的坐标为()()

000,r y x y x P >+，点A ，B 的坐标为

()()()2,1,,,,2222211==+i r y x y x y x i i ，过点P 的直线方程为()00x x k y y -=- ②

有 PA=||1012x x k -+，PB=||1022

x x k -+，22

020222r y x OT PO PT -+=-=

把②代入①得()

()()()02122

00002

02=-++-++-+r y x x x x ky x x k

由韦达定理得()()2

02002011k

r y x x x x x +-+=-- 从而 ()

()()222

0020121PT r y x x x x x k PB PA =-+=--+=?。

6、[证明]如图：对任意角()ππθθ+≠k 2作单位圆与始边ox 轴正向交于C ，与终边交于A ，有()()0,1,s i n ,c o s

C A θθ又角

的终边在点A 、C 的对称轴上，或为射线OB ，或为射线OB ′，而直线BB ′的方程为2

t a n

x y =。由AC ⊥BB ′知

s i n c o s 12

t a n -=

，又AC 的中点在BB ′上，有

2tan 2cos 12sin θθθ?+=，即θ

θcos 1sin 2tan +=。所以θ

θθθsin cos 1cos 1sin 2tan -=+=。

7、[证明]对a ，b 不为0，已知条件表明，不同的两点()()??θθsin ,cos ,sin ,cos B A 在直线

c by ax =+ ①

上，又AB 所确定的直线方程为()()()()0sin cos cos cos sin sin =-----??θ??θy x 即 2

cos

sin

cos

θ?

θ-=+++y x ②

由两点确定一条直线知①，②重合，得

cos

sin

cos

θ?

θ-=

+=+c b

8、如图在直角坐标系中取点()???

??-???? ??c c C b B a a A 23,2,0,,23,2有ab b a AB -+=22||，cb b c BC -+=22||，ac c a AC ++=22||由|AB|+|BC|≥|AB|即得所求。

当A 、B 、C 三点共线时取等号，此时由面积S ΔAOC=S ΔAOB+S ΔBOC 得

?+?=?60sin 2160sin 21120sin 21bc ab ac 即c

a b 1

11+=时取等号。练习题： 1、 a ≥1 2、 A 3、 ),3

4[+∞ 4、 1 5、略

利用复数妙解三角几何等问题

利用复数妙解三角几何等问题摘要复数在高中涉及的知识点较少，在高考中占据的分数也不多，但却是很有特色的内容。因为复数的代数形式、几何形式、向量形式、三角形式以及指数形式与三角、几何、代数等学科有着密切的联系。本文罗列了复数的代数形式、几何形式、向量形式、三角形式以及指数形式，从解三角函数、几何、不等式、方程等几个问题论述复数在解决非复数数学问题的具体应用，充分认识、深刻理解、熟悉掌握和灵活运用复数的几个表示形式去解答，对学生的创新性思维素质和能力的培养具有重要意义。关键字：复数；形式；解题；妙解复数是高三最后一章的内容，短短几页，只有三节，但在高考中却占着一定的分值。高考中复数主要是以选择题与填空题的形式出现，只要掌握了复数的概念以及运算规律，就很容易得出答案。因此，教材的编排只简单介绍了复数的概念，复数的运算以及数系的扩充，没有作过多的介绍，其三角形式和指数形式只是在背景材料中提到过，并没有作详细的介绍。但在实际应用中，很多的数学问题，比如：三角问题、几何问题等我们也可以用复数的知识去解答。在高中数学中，复数把三角、平面几何、解析几何、代数在一定的程度上相互链接起来了，那我们应该如何巧妙地利用复数的不同表示形式去解答这类问题呢下面分别对这几方面进行探究。 1复数的不同表示形式简介复数的代数形式 =+（其中x、y为实数），其中“i”叫做虚数复数的代数形式表示为z x yi

单位，21i =-，x 和y 分别叫做复数的实部和虚部。复数的几何形式图在复平面上，每一个复数z x yi =+都能够由复平面上坐标为（x ，y ）的点来表示，复数集C 和复平面上的点所称的集合之间建立了一个一一对应的关系：“任何一个复数z x yi =+都可以由复平面的唯一的一个点（x ，y ）来表示，反之，复平面内的任何一个点（x ，y ）都可以表示唯一的复数z x yi =+。” 复数z x yi =+←???→一一对应复平面内的点（x ，y ），这就是复数的几何表示形式。复数的向量形式我们知道，任何一个复数都与平面直角坐标系中的点构成一一对应的关系，即：复数z x yi =+←???→一一对应复平面内的点M （x ，y ），而点M （x ，y ） ←???→一一对应平面向量。所以，复数z x yi =+←???→一一对应平面向量OM ，也就是说复数z x yi =+也可以用起点为原点，点M （x ，y ）为终点的向量OM 表示，OM 这个向量即是复数的向量表示形式。

解析法证明平面几何经典问题--举例

五、用解析法证明平面几何问题----极度精彩！充分展现数学之美感！何妨一试？例1、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引两条直线分别交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）（例1图）（例2图）例2、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、 BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．【部分题目解答】例1、(难度相当于高考压轴题) ；，、点的方程为：直线的方程为：设直线方程为：轴建立坐标系，设圆的为为原点，轴，为如图，以)(),(,AD ,,)-(2211222y x C y x B nx y mx y AB r a y x Y AO A x MN ===+ 、；则，、，C B )()(4433y x E y x D , 1 - ;12-2-)1,{)-(22 2212212222222+=+=+=++=+=m r a x x m am x x r a amx x m y r a y x mx y 由韦达定理知：得：（消去,1- ;1222 243243+=+=+n r a x x n an x x 同理得： ),-(---23 23 22x x x x y y y y CD = 方程为：直线 ,--Q 3 23 223Q y y y x y x x = 点横坐标：由此得 , --P 1 41441P y y y x y x x = 点横坐标：同理得 ,------1 41441323223P Q y y y x y x y y y x y x x x AQ AP ===；即证：，只需证明：故，要证明 N B

“割补法”求解不规则几何体体积

“割补法”求解不规则几何体体积我们通常把不是棱柱、棱锥、棱台和圆柱、圆锥、圆台等的几何体，称为不规则几何体．而解决不规则几何体的方法，常用割补法，即通过分割或补形，将它变成规则的几何体．我们可以从不规则几何体的来源上，即它是由何种常见的几何体所截得的来分类．一、来自三棱柱的截体例1 如图1，正四面体A BC D -中，E F G H ，，，分别是棱 A B A C B D C D ，，，的中点，求证：平面EFH G 把正四面体分割成的两部分几何体的体积相等．分析：显然正四面体被分割成的两部分都是不规则的几何体，因此我们可使用割补法来推导．那么我们应选择割，还是补呢？如果选择补，那么补成什么样子呢？显然只能是正四面体，这就说明我们应该选择割．证明：连结C E C G A G A H ，，，，左右两个不规则几何体都被分割成了一个四棱锥和一个三棱锥，如图1．易证左右的两个四棱锥的体积相等，两个三棱锥的体积也相等，于是两部分体积相等．当然此题还有其他的分割方法，比如分成一个三棱柱和一个三棱锥等，也同样好证．二、来自正方体的截体例2 如图2，已知多面体ABC D EFG -中，A B A C A D ，，两两互相垂直，平面ABC ∥平面D E F G ，平面BEF ∥平面A D G C ， 2AB AD D C ===，1AC EF ==，则该多面体的体积为（）Ａ．2 Ｂ．4 Ｃ．6 Ｄ．8 解法一（割）：如图3，过点C 作C H D G ⊥于H ，连结EH ，这样就把多面体分割成一个直三棱柱D EH ABC -和一个斜三棱柱BEF C H G -．于是所求几何体的体积为： DEH BEF V S AD S DE =?+?△△11212212422????=???+???= ? ?????．解法二（补）：如图4，将多面体补成棱长为2的正方体，那么显然所求的多面体的体积即为该正方体体积的一半．于是所求几何体的体积为31242V = ?=．三、来自圆柱的截体例3 如图5，如图5，一圆柱被一平面所截，已知被截后几何体的最长侧面母线长为4，最短侧面母线长为1，且圆柱底面半径长为2，则该几何体的体积等于_______．解法一（割）：如图6，该几何体的体积等于下面的圆柱的体积与上

复数与平面几何数学竞赛

复数与平面几何本篇着重讨论三角形巧合点的复数表示以及计算彼此之间的距离复数方法，复数方法虽然很少用到，但是但凡用到无不是一击制胜。最经典的自然是那个将垂心变幻的那个IMO 题，不过自这一题之后除了解析性质比较明显，或者是涉及到变换之类的多有用复数证法，原汁原味的复数证法已鲜见，笔者在那道IMO 题之后感触颇深，经过研究，对三角形巧合点的复数形式做了一个小结。引论：已知△ABC ，以外心O 为原点的复平面A,B,C 对应点的复数为,,A B C z z z 则重心G 对应点复数3 A B C G z z z z ++=(可以通过重心的性质易得，或者通过重心坐标容易得到) 2 1××1 221312 B C B C A A B C G z z BC z z z z z z z +++++==+中点为由定比分点公式垂心H 对应点的复数z H A B C z z z =++下面我们来证明这个性质，无妨令A,B,C 在平面上逆时针排列（这个性质验证是极其容易的，直接得到却要费些功夫）证法一：由欧拉定理G 在O,H 连线上，而且HG=2OG 以下就直接得到证法二： 2222222 2 2cos tan tan tan tan cos 2,sin 2, +=++B C A H Ai A H B C A H B C A H B C A H B C A H B C A H B C A AH R A z z i A A A z z e A A A z z z z z z z z z z z z z z z z z z z z z z z z z =-==-=----+------= --∑∏C B C B 利用垂心性质即易得（利用该式易证） z 考虑与A 有关的量：z 利用万能代换表示出（）（）2（）（）z 则z （）-（）（）-（）（）（）（++H B C A H B C H A B C A H B C z z z z z z z z z z z z z z z --+--= ?=+--+） (也可因此易得欧拉公式) 最后推导z I 的表示 z I 的推导一度十分困难，笔者尝试良久仍未见效，最终在向量表示方法中找到了影子，可

解析法在几何中的应用 -

解析法在几何中的应用姓名：周瑞勇学号：201001071465 专业：物理学指导教师：何巍巍

解析法在几何的应用周瑞勇大庆师范学院物理与电气信息工程学院摘要：通过分析几何问题中的各要素之间的关系，用最简练的语言或形式化的符号来表达他们的关系，得出解决问题所需的表达式，然后设计程序求解问题的方法称为解析法。关键词：几何问题，表达关系，表达式，求解问题一前言几何学的历史深远悠久，欧几里得总结前人的成果，所著的《几何原本》。一直是几何学的坚固基石，至今我国中学教学的几何课本仍未脱离他的衣钵。长期的教学实践证明，采用欧式体系学习几何是培养学生逻辑思维能力的行之有效的方法。但是，事物都有两重性。实践同样证明，过多强调它的作为也是不适当的。初等几何的构思之难，使人们为此不知耗费了多少精力，往往为寻求一条神奇、奥秘的辅助线而冥思苦索。开辟新的途径，已是势在必行。近些年来，用解析法、向量法、复数法、三角法证明几何问题，受到越来越多的数学工作者的重视。由于平面几何的内容，只研究直线和园的问题，所以我们完全可以用解析法来研究几何问题。解析法不仅具有几何的直观性，而且也还有证明方法的一般性。综合几何叙述较简，但构思困难，而解析法思路清晰，过程简捷，可以作为证明几何问题中一种辅助方法，两者课去唱补短，想得益彰。二解析法概述几何数学主要是从几何图形这个侧面去研究客观事物的，其基本元素是点，代数学则主要是从数量关系这个侧面来研究客观事物，其基本元素是数。笛卡尔综合了前人的成果，创立了坐标概念，把代数学和几何学结合起来，于是产生了以研究点的位置和一对有序实数的关系、方程和曲线以及有研究连续运动而产生

高考数学用补形法解立体几何题

高考数学用补形法解立体几何题 1. 正四面体补为正方体例1. 求棱长为1的正四面体的体积。图1 分析：常规的思路是直接用三棱锥的体积公式去求，但要首先求出此三棱锥的高，求高比较繁琐。如果将正四面体ABCD补形为正方体（如图1），那么此正方体的棱长为，因此，求正四面体的体积便有了新的求解思路：例2. 如图2，正三棱锥S-ABC的侧棱与底面边长都相等，如果E、F、G分别是SC、AB、AC的中点，那么异面直线EF与BG所成角的余弦值等于__________。图2

分析：常规的思路是“平移法”，取GA的中点H，连结EH、FH，则∠EFH即为所求，但解△EFH的运算量较大。联想到正四面体可补形为正方体（如图3），相当于求与BG所成角的余弦值。在此正方体的左边补上一个大小相同的正方体，构成一个长方体（如图4），则相当于求长方体对角线BD与侧棱所成角的余弦值。设正方体边长为1，则长方体对角线BD的长为。在中， 2. 三条侧棱两两垂直的三棱锥或对棱相等的三棱锥或一条侧棱垂直于底面的三棱锥都可以考虑补形为长方体例3. 如图5，是直二面角，，，那么AB与面β所成的角等于（）图5 A. 90° B. 60° C. 45° D. 30°

分析：由α⊥β，BD⊥CD，得BD⊥α同理得：AC⊥β因此，AC ⊥CD，BD⊥CD，AC⊥BD不妨把三棱锥A-BCD补形为长方体（如图5），易得∠ABC为所求的角。在Rt△ABC中，，选D。例4. 如图6，四面体P-ABC中，侧棱PA、PB、PC两两垂直，O为面ABC 上一点，且O到平面PAB、平面PAC、平面PBC的距离分别为2，3，4，求OP的长度。分析：可补一个“小”长方体（如图6），由此可得“小”长方体的长、宽、高分别为2，3，4，求OP长可转化为求该“小”长方体的对角线长，得： 3. 一般三棱锥（三棱柱）可补形为三棱柱（平行六面体）例5. 已知三棱锥P-ABC中，PA⊥BC，PA＝BC＝a，PA、BC的公垂线段DE＝h，求证三棱锥的体积是。分析：以ABC为底面，PA为侧棱补形为一个三棱柱ABC－，进一步补形为平行六面体ABCD－（如图7），那么

中考复习数学思想方法之二：割补法“补形”在初中几何问题中的应用

中考复习数学思想方法之一：割补法“补形”在初中几何问题中的应用平面几何中的“补形”就是根据题设条件，通过添加辅助线，将原题中的图形补成某种熟悉的，较规则的，或者较为简单的几何基本图形，使原题转化为新的易解的问题．从“补形”的角度思考问题，常能得到巧妙的辅助线，而使解题方向明朗化，所以，补形是添加辅助线的重要方法．下面举例加以说明，供参考．例1 如图1，六边形ABCDEF的六个内角都相等，若AB=1，BC=CD=3，DE=2，则这个六边形的周长等于．解析题中六边形是不规则的图形，现将它补形为较规则的正三角形，分别向两方延长AB、CD、EF相交于G、H、I (如图2)． ∵六边形ABCDEF的六个内角都相等， ∴六边形的各角为120°， ∴△AFI、△BCG、△DEH均是正三角形，从而△GHI为正三角形，则有 GC=BC=3，DH=EH=DE=2， IF=AF, IH=GH=GC+CD+DH =3+3+2=8， ∴IE=IH－EH=8－2=6． ∴六边形的周长等于： AB+BC+CD+DE+EF+F A =AB+BC+CD+DE+IE =1+3+3+2+6=15．注：本题亦可补成平行四边形求解，如图3．例2 如图4，在Rt△ABC中，AC=BC，AD是∠A的平分线，过点B作AD的垂线交AD的延长线于点E，求证：AD=2BE．解析从等腰三角形的性质得到启示：顶角平分线垂直底边且平分底边．结合AE平分∠CAB，B E⊥AE，启发我们补全一个等腰三角形．所以延长BE交AC的延长线于点F(如

图5)，易证△ABF 为等腰三角形，∴ BF =2BE ，再证△ACD ≌△BCF ，全等的条件显然满足，故结论成立．例3 某片绿地的形状如图6所示，其中∠A =60°，A B ⊥BC ，C D ⊥AD ，AB =200m ，CD =100m ，求AD ，BC 的长．解析由题设∠A=60°，A B ⊥BC ，可将四边形补成图7所示的直角三角形．易得∠E =30°，AE =400，CE =200，然后再由勾股定理或三角函数求出BE ， DE 由此得到AD =400－200。例4 如图8，在平面直角坐标系中直线y =x －2与y 轴相交于点A ，与反比例函数在第一象限内的图像相交于点B (m ，2)． (1) 求反比例函数的关系式； (2) 将直线y =x －2向上平移后与反比例函数图像在第一象限内交于点C ，且△ABC 的面积为18，求平移后的直线的函数关系式．解析 (1) 所求解析式为y =8 x ； (2) 本题方法不一，下面着重对此题进行分析解答．

立体几何巧思妙解之割补法

立体几何巧思妙解之割补法在立体几何解题中，对于一些不规则几何体，若能采用割补法，往往能起到化繁为简、一目了然的作用。一、求异面直线所成的角例1、如图1，正三棱锥S-ABC 的侧棱与底面边长相等，如果E 、F 分别为SC 、AB 的中点，那么异面直线EF 与SA 所成的角等于（） 000090604530A B C D 分析：平移直线法是求解异面直线所成角最基本的方法。如图1，只要AC 的中点G ，连EG ，FG ，解△EFG 即可.应该是情理之中的事。若把三棱锥巧妙补形特殊的正方体，定会叫人惊喜不已。巧思妙解：如图2，把正三棱锥S-ABC 补成一个正方体11AGBH ACB S -， 1//,EF AA ∴异面直线EF 与SA 所成的角为0145A AS ∠=。故选C 。二、体积问题例2、如图3，已知三棱锥子P —ABC ，10,PA BC PB AC PC AB ======锥子P —ABC 的体积为（）。 4080160240A B C D 分析：若按常规方法利用体积公式求解，底面积可用海伦公式求出，但顶点到底面的高无法作出，自然无法求出。若能换个角度来思考，注意到三棱锥的有三对边两两相等，若能把它放在一个特定的长方体中，则问题不难解决。巧思妙解：如图4所示，把三棱锥P —ABC 补成一个长方体AEBG —FPDC ，易知三棱锥P —ABC 的各边分别是长方体的面对角线。 PE=x,EB=y,EA=z 不妨令，则由已知有： 2222221001366,8,10164x y x z x y z y z ?+=?+=?===??+=? ，从而知 416810468101606 P ABC AEBG FPDC P AEB C ABG B PDC A FPC AEBG FPDC P AEB V V V V V V V V --------=----=-=??-????= 例3、如图5，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且BCF ADE ??、均为正三角形，EF ∥AB ，EF=2，则该多面体的体积为（）（A ） 32 （B ）33 （C ）34 （D ）23

平面几何证明题的一般思路及方法简述

平面几何证明题的一般思路及方法简述【摘要】惠特霍斯曾说过,“一般地,解题之所以成功,在很大程度上依赖于选择一种最适宜的方法。”灵活、恰当地选择解题方法是求解平面几何问题的良好途径。解决任何一道平面几何证明题,都要应用这样或那样的方法,而选择哪一种方法,就取决于我们用什么样的解题思路。本文试对平面几何证明题中常用的几种解题思路及方法进行分析。【关键词】平面几何证明题思路方法平面几何难学,是很多初中生在学习中的共识,这里面包含了很多主观和客观因素,而学习不得法,没有适当的解题思路则是其中的一个重要原因。波利亚曾说过,“解题的成功要靠正确思路的选择,要靠从可以接近它的方向去攻击堡垒。为了辨别哪一条思路正确,哪一个方向可接近它,就要试探各种方向和思路。”由此可见,掌握证明题的一般思路、探索证题过程中的数学思维、总结证题的基本规律是求解几何证明题的关键。常见的证题思路有直接式思路和间接式思路。一、直接式思路证题时,首先应仔细审查题意,细心观察题目,分清条件和结论,并尽量挖掘题目中隐含的一些解题信息,以在缜密审题的基础上,根据定义、公式、定理进行一系列正面的逻辑推理,最后得出命题的证明,这种证题的思路被称为直接式思路。由于思维方式的逆顺,在证题时运用的方法主要有“分析法”和“综合法”。 1.分析法。分析法是从命题的结论入手,先承认它是正确的,执果索因,寻求结论正确的条件,这样一步一步逆而推之,直到与题设会合,于是就得出了由题设通往结论的思维过程。在由结论向已知条件的寻求追溯过程中,则由于题设条件的不同,或已知条件之间关系的隐含程度不同等,寻求追溯的形式会有一定差异,因而常把分析法分为以下四种类型。 (1)选择型分析法。选择型分析法解题,首先要从题目要求解的结论A出发,逐步把问题转化为分析要得出结论A需要哪些充分条件。假设有条件B,就有结论A,那么B就成为选择找到的使A成立的充分条件,然后再分析在什么条件下能选择得到B……最终追溯到命题中的某一题设条件。 (2)可逆型分析法。如果再从结论向已知条件追溯的过程中,每一步都是推求的充分必要条件,那么这种分析法又叫可逆型分析法,因而,可逆型分析法是选择型分析法的特殊情形。用可逆型分析法证明的命题用选择型分析法一定能证明,反之用选择型分析法证明的命题,用可逆型分析不一定能证明。 (3)构造型分析法。如果在从结论向已知条件追溯的过程中,在寻找新的充分条件的转化“三岔口”处,需采取相应的构造型措施:如构造一些条件,作某些辅助图等,进行探讨、推导,才能追溯到原命题的已知条件的分析法叫做构造型分析法。 (4)设想型分析法。在向已知条件追溯的过程中,借助于有根据的设想、假定,形成“言之成理”的新构思,再进行“持之有据”的验证,逐步地找出正确途径的分析法称为设想型分析法。 2.综合法。综合法则是由命题的题设条件入手,由因导果,通过一系列的正确推理,逐步靠近目标,最终获得结论。再从已知条件着手,根据已知的定义、公式、定理,逐步推导出结论。在这一过程中,由于思考角度不同,立足点不同,综合法常分为四种类型: (1)分析型综合法。我们把分析法解题的叙述倒过来,稍加整理而得到的解法称为分析型综合法。 (2)奠基型综合法。当由已知条件着手较难,或没有熟悉的模式可供归纳推导,就可转而寻找简单的模式,然后再将一般情形化归到这个简单的模式中来,这样的综合法称为奠基型综合法。 (3)媒介型综合法。当问题给出的已知条件较少,且看不出与所求结论的直接联系时,或条

三角法与向量法解平面几何题(正)

第27讲三角法与向量法解平面几何题相关知识在ABC ?中,R 为外接圆半径,r 为内切圆半径,2 a b c p ++=,则 1,正弦定理: 2sin sin sin a b c R A B C ===, 2,余弦定理:2 2 2 2cos a b c bc A =+-,2 2 2 2cos b a c ac B =+-,2 2 2 2cos c a b ab C =+-. 3,射影定理:cos cos a b C c B =+,cos cos b a C c A =+,cos cos c a B b A =+. 4,面积:211sin 2sin sin sin 224a abc S ah ab C rp R A B C R = ==== = (sin sin sin )rR A B C ++ 2 221(cot cot cot )4 a A b B c C = ++. A 类例题例1．在ΔABC 中，已知b =asinC ,c =asin (900 -B )，试判断ΔABC 的形状。分析条件中有边、角关系, 应利用正、余弦定理, 把条件统一转化为边或者是角的关系, 从而判定三角形的形状。解由条件c = asin (900 - B ) = acosB = c b c a ac b c a a 222 22222-+=-+ 2 2222c b c a =-+? 是直角A b c a ?+=?2 22 1sin sin sin =?=A A C c A a 是直角?? ?C a c C c a sin sin =?=?. Q C a b sin =?=? c b ΔABC 是等腰直角三角形。例2．（1）在△ABC 中，已知cosA =13 5，sinB =53 ，则cosC 的值为（） A ．6516 B ．6556 C ．65566516或 D ． 65 16- 解 ∵C = π - (A + B ),∴cosC = - cos (A + B ),又∵A ∈(0, π),∴sinA = 13 12,而sinB =53 显然sinA > sinB ,∴A > B , ∵A 为锐角, ∴B 必为锐角, ∴ cosB = 5 4 ∴cosC = - cos (A + B ) = sinAsinB - cosAcosB =65 1654135531312=?-?.选A . 说明 △ABC 中,sinA > sinB ?A > B . 根据这一充要条件可判定B 必为锐角。（2）在Rt △ABC 中，C ＝90°，A ＝θ，外接圆半径为R ，内切圆半径为r ，

第56讲解析法证几何题教学内容

第56讲解析法证几何题

第56讲解析法证几何题解析法是利用代数方法解决几何问题的一种常用方法．其一般的顺序是：建立坐标系，设出各点坐标及各线的方程，然后根据求解或求证要求进行代数推算．它的优点是具有一般性与程序性，几何所有的平面几何问题都可以用解析法获解，但对于有些题目演算太繁．此外，如果建立坐标系或设点坐标时处理不当，也可能增加计算量．建系设点坐标的一般原则是使各点坐标出现尽量多的0，但也不可死搬教条，对于一些“地位平等”的点、线，建系设点坐标时，要保持其原有的“对称性”． A类例题收集于网络，如有侵权请联系管理员删除

斜边AB及直角边BC为边向三角形两侧作正方形ABDE、CBFG．求证：DC⊥FA．分析只要证k CD·k AF＝－1，故只要求点D的坐标．证明以C为原点，CB为x轴正方向建立直角坐标系．设A(0，a)，B(b，0)，D(x，y)．则直线AB的方程为ax＋by－ab＝0．故直线BD的方程为bx－ay－(b·b－a·0)＝0，即bx－ay－b2＝0． ED方程设为ax＋by＋C＝0．由AB、ED距离等于|AB|，得 |C＋ab| ＝a2＋b2， a2＋b2 解得C＝±(a2＋b2)－ab．如图，应舍去负号．收集于网络，如有侵权请联系管理员删除

所以直线ED方程为ax＋by＋a2＋b2－ab＝0．解得x＝b－a，y＝－b．(只要作DH⊥x轴，由△DBH≌△BAC就可得到这个结果)．即D(b－a，－b)．因为k AF＝b－a b，k CD＝－b b－a，而k AF·k CD＝－1．所以 DC⊥FA．例2．自ΔABC的顶点A引BC的垂线，垂足为D，在AD上任取一点H，直线BH交AC于E，CH交AB于F．试证：AD平分ED与DF所成的角．证明建立直角坐标系，设A(0，a)，B(b，0)，C(c，0)，H(0，h)，于是 BH：x b＋ y h＝1 AC：x c＋ y a＝1 x

例谈构造平行六面体解立体几何题

例谈构造平行六面体解立体几何题立体几何题的题设中若有“垂直”(包括线线垂直、线面垂直及面面垂直)可以试着构造长方体来求解，若没有“垂直”也可尝试构造平行六面体来求解.本文以普通高中课程标准实验教科书《数学·选修2-1·A 版》(人民教育出版社，2007年第2版)(下简称教科书)中的题目及几道高考题来谈谈这种解题方法. 题1 (教科书第106页例2)如图1，甲站在水库底面上的点A 处，乙站在水坝斜面上的点B 处.从,A B 到直线l (库底与水坝的交线)的距离AC 和BD 分别为a 和b ，CD 的长为c ，AB 的长为d .求库底与水坝所成二面角的余弦值. 图1 图2 解可在如图2所示的平行六面体中求解：因为,//CD AC AC A D '⊥，所以CD A D '⊥.又CD BD ⊥，所以CD ⊥面A DB '，得AA A B ''⊥，所以222A B d c '=-. 在A BD '?中，由余弦定理可求得2222 cos 2a b c d A DB ab ++-'∠=，此即所求二面角的余弦值. 题 2 (教科书第107页练习第2题)如图3，60?的二面角棱上有,A B 两点，直线,AC BD 分别在这个二面角的两个半平面内，且都垂直于AB .已知4,6,8AB AC BD ===，求CD 的长. 图3 图4 解可在如图4所示的平行六面体中求解：在ACE ?中，6,6,60AC AE BD CAE ===∠=?，由余弦定理可求得252CE =.

可证BA ⊥面ACE ，所以有DE CE ⊥，在CDE ?中可求得217CD =. 题3 (教科书第113页第12题)一条线段夹在一个直二面角的两个半平面内，它与两个半平面所成的角都是30?，求这条线段与这个二面角的棱所成角的大小. 解可在如图5所示的长方体中求解：30ADB DAE ∠=∠=?，可不妨设2AD =，得1,3,2DE CB AB AE BD BE CD =======，所以在Rt ACD ?中可求得45ADC ∠=?，即夹在直二面角A BE D --的线段AD 与棱BE 所成角的大小是45?. 图5 题 4 已知两平行平面,αβ的距离为23，点,A B α∈，点,C D β∈，且3,2AB CD ==，异面直线,AB CD 成60?角，求四面体ABCD 的体积. 解可在如图6所示的平行六面体中求解：图6 在图6所示的平行六面体中，60A CD '∠=?或120?， 133,23sin 322 A CD A C A B S A CD '?''===??∠=，所以13323332 A BCD A BCD V V '--===. 题 5 (2012·安徽·文·15) 若四面体ABCD 的三组对棱分别相等，即,,A B CD A C B D AD BC ===，则下列命题正确的是 (写出所有正确命题的编号)。 ①四面体ABCD 每组对棱相互垂直 ②四面体ABCD 每个面的面积相等 ③从四面体ABCD 每个顶点出发的三条棱两两夹角之和大于90°而小于180° ④连接四面体ABCD 每组对棱中点的线段相互垂直平分 ⑤从四面体ABCD 每个顶点出发的三条棱可作为一个三角形的三边长

平面几何问题的复数解法.许兴华

平面几何问题的复数解法.许兴华复数是高中数学的重要内容之一,在中学数学中,有许多数学问题,如果我们能够根据题目的具体特征,将其转化为复数问题,那么这类数学问题往往可以得到复巧解妙证. 用复数方法解解平面几何的基本思路是,首先运用复数表示复平面上的点,然后利用复数的模和幅角的有关性质,复数运算的几何意义以及复数相等的条件,化几何问题为复数问题来处理. 1.用于证三角形为正三角形典型1.求证:若三角形重心与其外心重合,则该三角形必为正三角形. 证明思路分析以三角形的相重合的外心(重心),为原点O 建立起复平面上的直角坐标系.设321,,Z Z Z 表示三角形的三个顶点,其对应的复数是.,,321z z z 因O 为外心,故,||||||321r z z z ===又O 为重心，故,033 21=++z z z 即,0321=++z z z 于是由,321z z z -=+得2 2123||||z z z +=)()(2121z z z z ++= ,||||21212221z z z z z z +++=即,22121r z z z z -=+ 22123|||| z z z -=∴)()(2121z z z z --=),(||||21212221z z z z z z +-+=.3|z -z | 21r =∴ 同理可得：.3|z -z | |z -z | 1323r ==∴ 故321,,z z z 在复平面上是正三角形.

2.用于证明几何中的角度相等典型2.已知正方形OBCD 中（如图），E 是CD 的中点，F 是CE 的中点，求证：FOB DOC ∠=∠2 1. 证明思路分析建立如图所示的复平面上的直角坐标系，设 ,1||=OD 则,1=OD ,,4 31,211i OB i OF i OE =+=+= DOE ∠=α是 OD 与OE 的夹角，有 ),43arg(i)21arg(12 ),211arg(2i i +=+=+=αα又 )],43(2516arg[431arg i i i FOB +=+=∠=β ,2βα=∴即FOB DOC ∠=∠21. 3.用于证明几何中的不等式典型3.在凸四边形ABCD 中，求证：BD AC BC AD CD AB ?≥?+?. 证明思路分析建立如图所示的复平面上的直角坐标系，设C,D,A 对应的复数分别是 .,,321z z z 则|, ||||,||||,||||,|||213312z z CD z AB z z CA z DB -==-==|,|||32z z AD -= ||||||||||||||||132213z z z z z z BC AD CD AB ?-+-?=?+? ||||31213231z z z z z z z z -+-=.|||||)(|312BD AC z z z ?=-=

静力学分析中的几何法或解析法

静力学分析中的几何法或解析法作者：王晓鹍{摘要}：静力学研究的内容主要是研究作用于物体上力系的平衡。通过静力学公理具体研究以下三个问题①物体的受力分析②力系的等效替换③力系的平衡条件。根据几何法的三步骤：确定受力体，画出脱离体和已知受力，解除约束体，画出受力方向的步骤。从而根据几何作图解决问题。至于解析法可以根据平衡力系中，合力必为零以及力多边形自行闭合的特点分析问题。 {关键词} 静力学二力平衡公理质点 {英文摘要} { the }: Statics study is the main content of research on object on the equilibrium of force system. The axioms of statics study the following three problems of objects in the stress analysis in power system equivalent substitution of the force equilibrium condition. According to the geometric method in three steps: determining force body, draw out of body and the known force, lift the restriction, draw the step stress direction.According to the geometry problem solving. As for the analytical method based on balanced force, force will be zero and the force polygon self closing characteristic analysis. { the } Statics two force balance axiom particle 静力学是力学的一个分支，它主要研究物体在力的作用下处于平衡的规律，以及如何建立各种力系的平衡条件。平衡是物体机械运动的特殊形式，严格地说，物体相对于惯性参照系处于静止或作匀速直线运动的状态，即加速度为零的状态都称为平衡。对于一般工程问题，平衡状态是以地球为参照系确定的。静力学还

复数与平面几何题

用复数解平面几何题的尝试宿迁市泗洪县育才实验学校周文化文武光华数学工作室潘成华【摘要】用复数法解决某些平面几何题往往显得简洁而特别，尤其是那些规则的，容易得出较简洁表达式的问题。本文通过具体的问题谈谈对复数解平面几何题的若干尝试。关键词复数，共轭复数，平面几何为使符号表示简明，文中约定使用复数时，①用AB 表示“A B -”，代替通常的写法AB ，②AB 表示复数AB 的共轭复数，③引入符号“1≡”及“i ≡”： y x 1≡表示Re(x)=Re(y),即复数x,y 的实部相等；y x i ≡表示Im(x)=Im(y),即复数x,y 的虚部部相等. 由此约定不难得出，“p 是实数”等价于“p i ≡0” ，“p 是纯虚数”等价于“p 1≡ 0”. 命题1. 设i b a x 11+=，i b a y 22+=，其中R ∈i i b a ，，2,1=i ； (1)y x ⊥? 011≡?≡?y x y x ； (2) y x //? 0i i y x y x ≡?-≡?. 证明：只证充分性（1）当y x ⊥时，易知02121=+b b a a ；由i b a x 11+=可得i b a x 11-=，故i b a b a b b a a i b a i b a y x ?-++=+?-=?)()()()(122121212211，于是Re (y x ?)=2121b b a a +=0，即01≡?y x ，再由共轭复数的性质可得01≡?y x . (2)由(1)可知i b a b a b b a a y x ?-++=?)()(12212121，当y x //时，易知01221=-b a b a ， ∴Im (y x ?)=1221b a b a -=0，即0i y x ≡?，再由共轭复数的性质可得0i y x ≡?-. 注：实际上y x ?的实部、虚部分别对应于向量)(11b a ，及)(22b a ，的内积、外积.

高二数学几何解析法

几何解析法教学要求：更进一步熟练运用两点间的距离公式、定比分点的坐标公式、线段的中点坐标公式，掌握用解析法研究几何问题。教学重点：解析法的运用。教学难点：如何抓住几何特征建系、设点、列式。教学过程：一、复习准备： 1. λ＝＝＝； 2.定比分点???==__________y x 、中点??? ==__________y x 、重心G ???==_____ _____ y x 二、讲授新课： 1.教学解析法例题： ①出示例：正方形ABCD 中，过顶点D 作DE ∥CA ，|CE|＝|CA|，且CE 交边DA 于F ，求证：|AE|＝|AF|。 ②分析：本题用解析法证明时，如何建立直角坐标系？如何设各点的坐标？ → 由几何特点设A(0,1)、B(1,1)、C(1,0)，E(x ，-x)后，如何求 B E F D C

F 点的坐标？（由所点E 、C 的坐标及F 的x 坐标，求出F 分EC 的定比，再求F 的y 坐标） ③师生共同写出证明过程。 ④讨论：如何用几何方法证明？ 2.练习：用解析法证明：到三角形三个顶点的距离的平方和最小的点是三角形的重心。解法：建系设点→列出距离平方和的式子→分拆成两个二次函数研究。 3、小结：解析法步骤（建系设点→列式→求解）；注意抓住几何特征建系、设点、列式。三、巩固练习： 1.已知A(-1,1)、B(2,-1)，求满足下列条件的点P ： ① 反向延长AB 到P ，使|BP|＝35|AB|； ② 点P 在直线AB 上，又在x 轴上。（解法关键：计算λ） 2. 设P 、A 、B 、C 是同一直线上任意四点，求证：PA ×BC ＋PB ×CA ＋PC ×AB ＝0 3.课堂作业：书P47、 1、3题。 A B x

用补形法解立体几何题的常用策略

用补形法解立体几何题的常用策略罗建中一、棱锥补成棱柱例1 一个四面体的所有棱长都为 2，四个顶点在同一球面上，则球的表面积为 A. π3 B. π 4 C. π3 3 D. π 6 分析：正四面体可看作是正方体经过切割而得到，因而构造一个棱长为1的正方体ABCD1 1 1 1 D C B A -，则四面体D BC A 1 1 -就是棱长为2的正四面体，而正方体的外接球就是四面体的外接球，又正方体的对角线长就是球的直径，易知对角线长度为3，故球表面积 2 2 3 4 S?? ? ? ? ? π = π =3。评注：对棱长全相等的正四面体通常把它补成正方体。若是相对棱长相等的四面体，则可考虑把它补成长方体。例2 如图1，在底面是直角梯形的四棱锥ABCD S-中，∠ABC=? 90，SA⊥面ABCD，SA=AB=BC=1，AD=2 1 。（1）求四棱锥ABCD S-的体积；（2）求面SCD与面SBA所成的二面角的正切值。解：（1）解答略。（2）以SA为棱，构造正方体AECB-SFGH，如图2，分别取棱SF、HG中点M、N，连结DM、MN、SN、ND，设ND与SC相交于O，连接MO。则有面MDN∥面SAB，且SM⊥面MDN，所以所求的二面角等于二面角S-DN-M。在正方体AECB-SFGH中，△NSD与△NMD都是等腰三角形，所以SO⊥DN， MO⊥DN，所以∠SOM是二面角S-DN-M的平面角。又MO2 1 = SB=2 2 ，SM=2 1 ，所以2 2 MO SM SOM tan= = ∠ ，故所求二面角的正切值是2 2 。

评注：从一顶点出发的三条棱互相垂直的锥体通常可考虑把它补成长方体或正方体。二、三棱柱可补成四棱柱例3 已知斜三棱柱的侧面11ACC A 与平面ABC 垂直，∠ABC=?90，BC=2，AC=32，且C A AA 11⊥，C A AA 11=，求点C 到侧面11ABB A 的距离。解：把斜三棱柱ABC 111C B A -补成如图3所示的平行六面体，设所求的距离为d ，则d 也是平面11A ABB 与平面 11C CMM 间距离，作AC D A 1⊥于点D ，作AB E A 1⊥于点F ，因为C A AA 11=，32AC =，C A AA 11⊥，所以 3 D A 1=，又∠ABC=?90，BC=2，所以22AB =，因侧面11ACC A 与底面ABC 垂直，AC D A 1⊥于点D ，所以 AB D A 1⊥，又AB E A 1⊥，知AB ⊥面ED A 1，因而AB ⊥ED ，又∠ABC=?90，所以DE ∥BC ，D 为AC 中点，且 1BC 21 DE == ，故 2 DE D A E A 2211=+=，而 d S D A S V 11ABB A 1ABMC ?=?=平行六面体。所以 3 2 3 2S D A S d 11ABB A 1ABMC ==?= 。评注：本例通过斜三棱柱补成四棱柱，从而达到把线面距离转化为面面距离，再通过等积变换达到简化解题之目的。三、棱台补成棱锥例4 如图4，三棱柱ABC 111C B A -中，若E 、F 分别为AB 、AC 的中点，平面F C EB 11将三棱柱分成体积为1V 、2 V 的两部分，那么21V :V 等于多少？

复数问题的题型与方法

复数问题的题型与方法复数一节的题型主要是讨论复数的概念，复数相等，复数的几何表示，计算复数模，共轭复数，解复数方程等．一、数学规律： 1．共轭复数规律， 2．复数的代数运算规律i4n 1=i，i4n 2= 1，i4n 3= i； 1）i 4n=1 n n 1 n 2 n 3 n n 1 n 2 n 3 （3）i · i · i ·i = 1，i ＋i ＋i ＋i =0；； 3．辐角的运算规律（1）Arg（z1·z2）＝Argz1＋Argz 2 3）Argzn=nArgz （n∈N） ?，n 1。或z∈R 。要条件是|z|＝|a|。

（6）z 1·z 2 ≠0，则 4．根的规律复系数一元 n 次方程有且只有 n 个根，实系数一元 n 次方程的虚根成对共轭出现。 5．求最值时，除了代数、三角的常规方法外，还需注意几何法及不等式 ||z 1| |z 2 ||≤|z 1± z 2 |≤ |z 1 |+|z 2 |的运用。即|z 1±z 2 |≤ |z 1 |+|z 2 |等号成立的条件是： z 1 ， z 2所对应的向量共线且同向。 |z 1±z 2 |≥|z 1| |z 2 |等号成立的条件是： z 1，z 2 所对立的向量共线且异向。二、主要的思想方法和典型例题分析： 1．化归思想复数的代数、几何、向量及三角表示，把复数与实数、三角、平面几何和解析几何有机地联系在一起，这就保证了可将复数问题化归为实数、三角、几何问题。反之亦然。这种化归的思想方法应贯穿复数的始终。分析】这是解答题，由于出现了复数 z 和 z ，宜统一形式，正面求解。解】解法一设 z ＝x ＋yi （ x ， y ∈R ），原方程即为 x 2 y 2 3y 3xi 1 3i 用复数相等的定义得： ∴ z 1= 1， z 2 = 1+3i.