第5章(5.5.2)均方误差准则(MSE)和LMS算法

5.5.2均方误差准则（MSE ）和LMS 算法

引言：均方误差准则同时考虑ISI 及噪声的影响，使其最小化。

本节讨论问题： 1. 均方误差准则；

2. 无限长LMS 均衡器（C (z )，J min ）；

3. 有限长LMS 均衡器（C opt ，J min ）；

4. LMS 算法；

5. 均衡器的操作；

6. 递推LMS 算法收敛特性的分析。

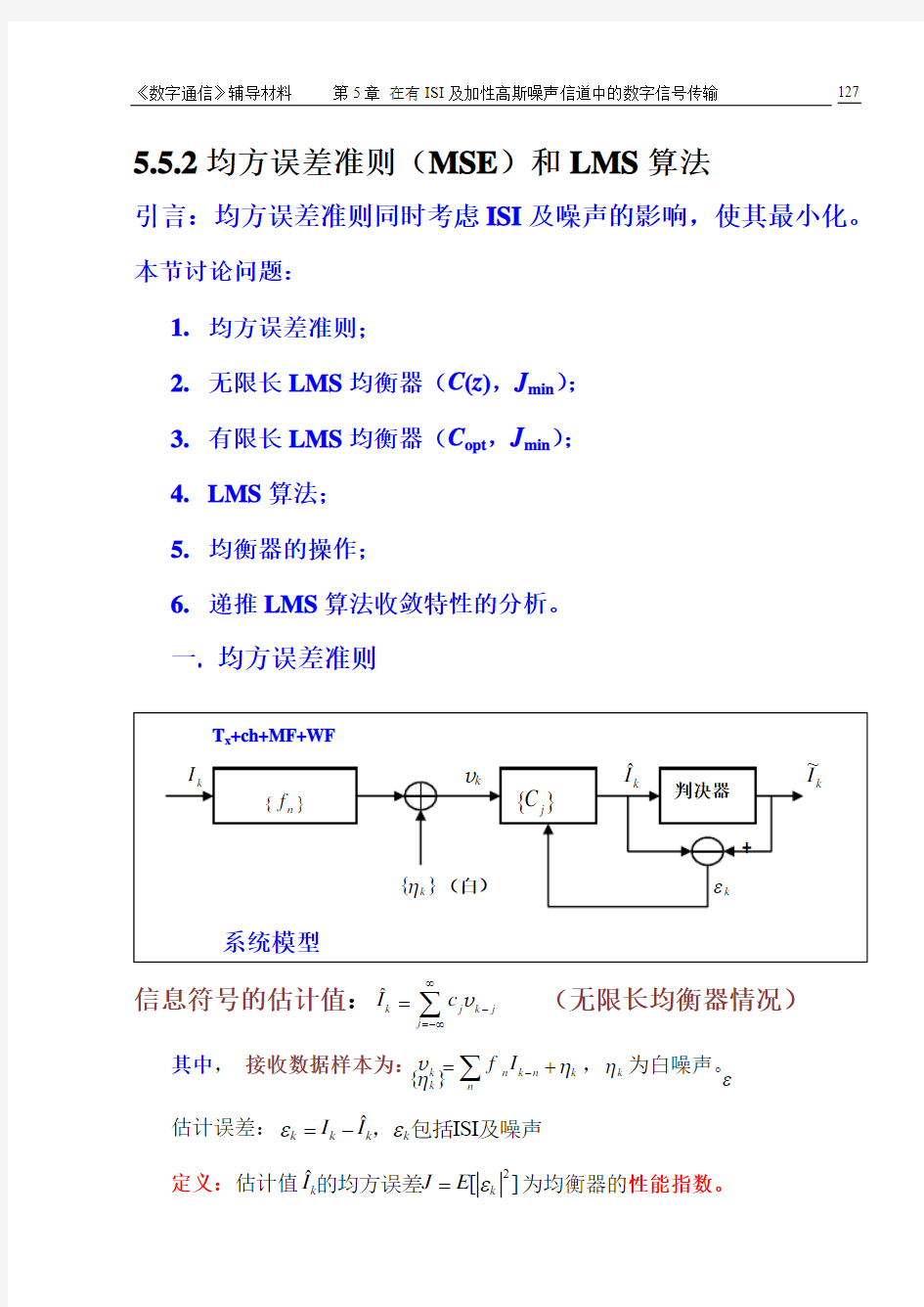
一. 均方误差准则

信息符号的估计值：?k j k j

j I c ∞

-=-∞

=

∑v （无限长均衡器情况）

其中， 接收数据样本为：k n k n k n f I η-=+∑v ，k η为白噪声。 估计误差：?ISI k k k k

I I εε=-，包括及噪声 定义：估计值2?[]k k

I J E ε=的均方误差为均衡器的性能指数。 }{k ηε

均方误差准则：使均方误差性能指数J 最小（min J ），此准则同时考虑使ISI 及噪声影响最小。

获得min J 的途径：调整{}j c ，当min J J =时，opt C C =(最佳抽头系数)

寻找opt C 的方法：1)根据正交性原理（线性均方估计）：*

[]0k k l E l ε-=，所有v 。（注：与ZF 准则不同的是，这里的输入是经过两个输入滤波器的数据样本k v ，这就包含了噪声）。即*?[]0kkl E l ε-=，所有I 。

2)求函数极值方法：令

?0=→=??opt k

J

C C 2013年5月3日星期五上午讲于此处，已经是第十次矣。

这两种方法是等价的，证明如下。

证明：求导置零方法与正交性原理等价。

?l i m K

k

j

k

j j k

j

K j j K

I c c

∞

--→∞

=-∞

=-==∑

∑v v

lim T k K →∞

=V c

假如均衡器为有限长，则

?T k k

I =V c 其中

11T

k k K k K k

k K k K v v v v v ++--+-??=??V ，以及 1

1

T

K

K K K c c c c c --+-??=??c 。

()2

??[][()()]k k k k k

J E E I I I I ε**==--c *

[()]T k k k E I ε=-V c

故

{}k k J E ε*

?=-?V c

另一种方法：

()2

2

*??[][()()] {()()}

[][][][]

k k k k k k i k i k j k j i

j

k i k k i j k k j i j k i k j i

j

i

j

J E E I I I I E I c I c E I c E I c E I c c E ε*****

--****----==--=--=--+∑∑∑∑∑∑c v v v v v v

2

*[][][][]k i k k i j k k j i j k i k j i

j

i

j

E I c E I c E I c c E ****----=--+∑∑∑∑v v v v

可见，()J c 是{}j c 的平方函数（二次型）。求导置零可得：

*0k k l j k l k j j

l J E I c E c **

---?????=-+=?????∑v v v 即， ***0, k j k j k l j l J E I c l c --???????=--=-∞<<∞???????????

∑v v

()()**

00k k i k k i E E εε--∴==，或v v ，i -∞<<∞

{}k k J E ε*

?=-?V c

1

1

T

k k K

k K k

k K k K v v v v v ++--+-??=??V

结论：求导方法与正交性原理是等价的，满足正交条件，就可以获得最小MSE 。

二、无限长LMS 均衡器（()min J z C ，性能）

1. 求()z C ：从正交原理出发，

()*

0k k l E ε-=v

(10-2-27)

即

*

[()]0k j k j

k l j E I c ∞

--=-∞

-

=∑v

v

即

()()

*

j

k -j

k -l k k l j c E E I ∞

-=-∞

=∑*v

v v （*） 正交条件

注: k l -v 是收数据样本，其中的噪声已经白化。

在（*）式左边可以得到：

{}********

0 k j k l n k j n k j m k l m k l n m n m k j n k l m k j k l n m n m k j n k l m lj

n

m

E E f I f I E f f I I f f E I I N ηηηηδ*------------------????????=++????????

????????=+??

??

=+∑∑∑∑∑∑v v

式中利用了[]0k n k n k k n

f I E ηη-=+=∑，v 。

注：j k jk j k kj j k ,)(δδδδδ==-==-都是Kroenecker 冲激或离散冲激的不同写法。 因此我们有：

***

,00[]k j k l n m n m l j lj m m l j lj n

m

m

E f f N f f N δδδ--+-+-=+=+∑∑∑v v

*

00

L

n n l j

lj n f f

N δ+-==+∑0 0,

l j lj x N l j L

else δ-?+-≤?=??? (A)

注：()()(1/)X z F z F z **=，()1F z **-代表了()F z 序列的共轭颠倒序列。或者说

()1F z **-代表了()F z 的MF(零时延)。

()()(1/)X z F z F z **=

()101L L f f z f z --=++

+1

1110()L L L L L z f f z f z f z **-*-+*--??++++?

?

000

L

L

L

L

L i

j

L

i j i

L j

i

L j i j i j z

f

z

f

z

z

f

f z -*

-*----======∑∑∑∑

00

L

L

L

i j i

L j i j z

f

f z *---===∑∑

00

L L

n i i n i n f f z *-===∑∑

L L

l n l n l L n f

f z

*-+=-==

∑∑（注：令l i n =-） 故

*0

L

l n n l n x f f +==∑，其支撑为：L l L -≤≤

或者说，可以得到

*

**

*

*0

L

L k

k n n

l

k l l l k n n k

n n k l

l

n n x f f

f f f f f f

f f ----+++===*====∑∑∑∑

也可以写为

j l j l L n j

l n n L

n j

l n n x f

f

f f

---=-+=-+==

∑∑)

(0

*

*

（*）式右边：

,*******

, 1

(){[]}{}{}k k l n k k l k n k l n k l n k k l n k k l n

n

c c E I E I f I f E I I E I δηη---------==+=+∑∑v

式中，,,10k k l n l n n l n l

δδ---=-?==?≠-?，当，当

由此可得

{}** , 0

l k k l

f L l E I --?-≤≤=??v (B)

将（A ）、（B ）两式代入（*）式：

*0[]j

l j

lj l j c x

N f δ∞

--=-∞

+=∑

上式就是: *

0l l l l c x N c f -?+=

取Z 变换： ()()110[()]()C z F z F z N F z **-**-+= (10-2-31)

则MMSE 均衡器 ()11

0()

()()F z C z F z F z N **-**-=+ (10-2-32) 等效MMSE 均衡器： ()()100

11

()()C z F z F z N X z N **-'=

=++

(10-2-33)

k

I ^

()

z C '

2. 求min J （最小均方误差） （1） 时域

2*****?[][()][][]k k k k k k k j k j

j

J E E I I E I E c εεεε-==-=-∑v 利用正交原理第二项为零，所以

2**min ?[()][][()]k k k k k j k j

j

J E I I I E I E I c -=-=-∑v *

[]j k j k j j j

j

c c E I c c f --=-=-∑∑v （利用(B)式）

令信息符号的平均功率为1，则

2

[]1k c E I ==

min 0

11j

j l l

l j J c

f c f ∞

-==-∞

=-

=-?∑

（2）频域

通过z 变换及令，T j e z ω=将min J 式的{}关系变换成n f J ~min

()

()关系ωωH e X J T j ?~min

全传输系统响应：{}()()()0

N z X z X z B b n +=? (10-2-35)

以z 反变换（留数法）求：

()112n-n c

b B z z dz j

π=

?

()()()1001122c

c

X z b B z z dz dz j

j

z X z N ππ-∴=

=

+????

?

?

(10-2-36)

j T z e T

ωπ

ω=≤

令，且，

()

()()()

()00

1

2 2j T T

j T j T j T T j T

T j T

T

X e b e e jT d j X e N X e

T

d X e

N

ωπ

ωωπωωπ

π

ωω

πω

π

---

=

??+=

+?? (10-2-37)

代入 min 01J b =-，得

()0

m i n 0

2T j T

T

N T

J d X e

N

π

π

ωωπ

-

=

+?

将()j T X e ω以信道折叠谱表示。因为

()()()

k t kT

x x kT h t h t *===?-

()()h t h t *?-的傅里叶变换为2

()H ω，故

2

12()FT

k k n n x t kT H T T πδω∞

∞=-∞

=-∞??-←?→+ ???∑∑

又

22()()()j ft j fkT k k k k k k k FT x t kT x t kT e dt x e DTFT x ππδδ∞

∞∞∞

--=-∞=-∞

=-∞-∞??-=-==????∑∑∑?

所以

()2

12 j T

n n X e H T T T ωππωω∞=-∞??=+≤ ?

??∑， (10-2-18) 所以

min

2

for ISI 0

212T T

n T T

N J d n H N T T π

π

ωπ

πω-

∞

=-∞===?

?++ ???

?∑ (10-2-38)

所以，当ISI=0时， 0

min min 0

011N J J N =

<<+， (10-2-39) 因k k k I I ?-=ε，故?k k k I I ε=+,22?[||]||k k k E I E I ε=-，利用正交原理*?[]0k k l

E ε-=I ，易证：

222?||||||k k k E I E I E ε=+，即2min ?[]1k E I J =-。 输出SNR: 2min

2

min

?[]1[]

k k E I J J E γε∞-=

=

(10-2-40)

三、有限长LMS 均衡器 (opt C ,

min J )

均方误差：()2

2

?[]K k k k j k j

j K J k E I I E I c -=-??

??=-=-????∑v {}k k J E ε*

?=-?V C

101T

K K K K c c c c c --+-??=??C 1

1T

k k K

k K k

k K k K v v v v v ++--+-??=??V

k

I =

1、求opt C ：无限长均衡器

*0[]j

l j

lj l j c x

N f δ∞

--=-∞

+=∑

仿上面无限长均衡器的推导： 根据正交条件：

[]

*0l K

K

j lj j

l j

f N x

c --=-=+∑δ

令0lj l j lj x N δ-??Γ=+??

则0 0,l j lj lj x N l j L δ-?+-≤?Γ=???，

其他

（注: l x 的支撑为l L ≤。）

令 *

00 l l f L l ξ-?-≤≤?=???，

，

其他

得

∑-==Γ

K

K

j l lj

j

c ξ （10-2-43）

矩阵形式：ΓC =ξ （10-2-46）

所以， 1opt -=C Γξ （10-2-47）

说明：opt C , ξ为有)12(+K 个元素的列向量

Γ为(2K+1)×(2K+1)的Hermitian 矩阵。

因为自相关函数*k k x x -=且*lj jl δδ=，所以ij ??=Γ??

Γ中元素满足*

ij ji Γ=Γ。Γ是共轭转置阵（Hermite ）阵。

2、求均衡器的性能即求最小能达到的均方差min J ： 前已经证明min 1j

j j J c

f ∞

-=-∞

=-

∑

将opt C 代入()K J min 式：

1min ()111j j opt j K

J K c f **--=-''=-

=-=-∑

ξC ξΓξ (10-2-48)

注：j f 的支撑为0j L ≤≤。

工程实用方法： 采用简单的迭代过程——最速下降法。

四. LMS 算法：

内容: a)算法：k k k G C C ?-=+1 (理论算法)

b)梯度： ()k k k k

dJ E d ε*

=

=-G V C c) 工程实用算法：1??k k k k ε*++?C =C V d) 均衡器结构：图11-1-2

1、算法：LMS 算法是一种最陡下降法，其实质是一个迭代过程，而迭代过程是通过递推运算来进行的。 设{}j c 有（2K +1）个抽头

递推运算： ()()()K K j k c k c k c j j j ，，，，

0 1-=+=+δ 每次迭代变化量： ()()k G k c j j ?-∝δ 令 ()()k G k c j j ?-=δ 则 ()()()k G k c k c j j j ?-=+1 或矩阵形式： k k k G C C ?-=+1，

式中?为调节阶距（步长）注：可以看到

()()

()K K j k G k c k c j j j ，，，，0 1

1-=?-=-+，

即强制要求抽头系数向着误差下降的方向变化。 则 ()()()k G k c k c j j j ?-=+1 或矩阵形式： k k k G C C ?-=+1，

式中?为调节阶距（步长step ），其中第k 符号时间的抽头系数列矢量（即

均衡器）为：

101()()

()

()()T

k K K K K c k c k c k c k c k --+-?

?=??C

,j opt j j ()()()

曲线的梯度次迭代时，为第j j j c J k k dc k dJ k G ~=

2、梯度：

{}k k k k

dJ E d ε*

=

=-G V C

{}k k k k

dJ E d ε*

=

=-G V C 11T

k k K

k K k

k K k K v v v v v ++--+-??=??V

讨论：1)理想情况下，经过若干次迭代（时0k k =），

0min

{}0()opt k k k

E J k J ε*

=??

=-=??

=??C C G V

2)实际情况中，计算k G 困难

*[]k k k E ε=-G V 统计平均, 不实时

为克服这一困难，用估计值k

G ?取代梯度真值k G *

[]k k k E ε=-G V

对k G 的无偏估计有：?{}k k E =G G 则

k

k k V G *?ε-= k G 为梯度真值，k

G ?为真值k G 的无偏估计量。

3. 工程实用LMS 算法：

k k k G C C ???1?-=+ (11-1-9) 即 *1??k

k k k V C C ε?+=+ (11-1-11) 或 k

k k k V C C *1??ε?+=+

在商用的自适应均衡器中，为简化乘法运算次数，仅取k v 和（或）k ε的正负号进行运算，而不管大小。其优点是简单，易实现，运算次数少；缺点是收敛慢。 如：

()()()()

*

1csgn csgn j j k k j c k c k v ε-+=+? (11-1-14)

定义复符号函数：()()()()

()()()()()()()()()1 Re 0Im 01 Re 0Im 0csgn 1 Re 0Im 01 Re 0Im 0j x x j x x x j x x j x x ?+>>?

->??

--<

，

，

(11-1-15)

4. 均衡器结构

图11-1-2 基于MSE 准则的线性自适应均衡器

五. 均衡器的操作过程 1. 方框图

2. 两种工作模式（状态）

（1）训练模式（training mode ）: k

k k I I ?-=ε （2

）工作模式（run mode ）: k k k I I ?~-=ε, 2

10-

，即使有错判，由于?很小，由此引起的误调整影响很小。

3. 步长?选择与收敛特性

训练时：1? 1?大—加速初始调整，接近m i n J 工作时：2? 2?小—稳态误差小，m i n J J ≈ 步长?选择考虑：●稳定且收敛快

● 稳态MSE 小

k

I

六. 递推LMS 算法收敛特性的分析

1、引言

说明三个问题：要解决什么问题；分析从何入手；分析的方法。 （1） 算法表示 理论上LMS 算法： k k k G C C ?-=+1， （A ）

实用的递推算法：

*1??k

k k k V C C ε?+=+ （B ）

梯度向量有噪无偏估计值：*?k

k k V G ε-= （2） 问题

● 收敛特性与?的关系？ ● 如何选择?，以确保收敛？

因为{}

k k E G G ?=，即k

G ?为真值k G 的无偏估计， 所以，?对收敛特性的影响，对（A ）（B ）两式是相同的。 为数学分析方便，我们只研究（A ）式的收敛特性。

（3） 收敛特性的分析方法

采用反馈系统稳定性的分析方法：

● 建立以1+k C 输出的闭环系统模型，定性分析?的影响； ● 建立系统的差分方程，定量分析?的影响。

2、闭环系统模型——定性分析收敛特性

算法： 1k k k +=-?C C G （A ）

式中， ()k k k =--G =ΓC -ξξΓC （B ）

Γ－接收信号自相关矩阵，由[]k j k l E v v *--确定。

ξ－互相关矩阵，由[]k k l E I v *-确定。

分析：由（A ）式可看出

（1）k C 的迭代过程可以看作：每次迭代增量(k k δ=-?C G )的累积过程

—由保持器实现；

（2）第k 时刻计算的增量(k -?G )应在第(k+1)时刻反映出来

—由延迟(Z -1)来实现。

结论：对闭环输出1k +C 收敛特性影响因素：, ?Γ

3、系统的差分方程——定量分析收敛特性

由(A)式 1=()k k k k k +=-?-?C C G C ΓC -ξ

得

1()k k +=-?+?C I ΓC ξ （A '） (11-1-20)

为一阶差分方程组，即

1(21)k k C I C K ξ+????????

?

?

????????=-?Γ

+?+?????????????????????

??????

因为Γ不是对角矩阵，故，（2K+1）个一阶差分方程是相互耦合的，必须联解。所以，用解联立方程组来定量分析收敛特性是困难的。 解决方法：利用线性变换（酉变换）来解耦。

①Γ为Hermite （厄米特）矩阵，可用U (酉矩阵)表示为

*'=ΓU ΛU (U -1) (11-1-21)

1

2

N λλλ?????

?=?????

?

Λ 式中，U (酉矩阵)由Γ的特征向量确定。

Λ(对角矩阵)的对角元素为Γ的特征值，特征值{}i λ为特征方程

0λ-=ΓI 的根。

②再利用U 矩阵的性质： *'=U U I (U -2)

③将(U -1)式代入(A ')式，两边再乘*'U ，然后利用(U -2)式，可得 1()k k +=-?+?ξΛC I C (11-1-22)

式中， 11

k k k k *++**'?=?

'=??'=?

C U C C U C ξU ξ

1 ()

()

() k k k k +=-?+

?ΛC I C ξ

信道特性反映迭代生不迭代而化的化量与与有产随变变无关关

说明：(1)因为Λ为对角矩阵，所以一阶差分方程组是线性不相关的（即解耦）。

(2) 收敛特性取决于其齐次方程组：

1()k k +=-?C I ΛC (11-1-23)

即表示成（2K+1）个一阶差分方程组：

,(1),()0,(1)0,()0

,(1),()111K k K k K

k k K k K k K C C C C C C λλλ-+--++????

-??????

??????

?????????=-????

??????

????

???

??-??

?????

可见，（2K+1）个{}i λ与（2K+1）个{}i C 对应。 对第j 个抽头系数C j 的差分方程为

,(1)

,()(1)j k j j k C C λ+=-?

,,0,

,0,1,2,

j K K k =-=

其相应的闭环系统模型为： 系统函数为：

1

1

1(1)j z λ---?

令11(1)0j z λ---?=，得极点：1j z λ=-? 要使迭代过程收敛，应使极点在单位圆内，即

11j λ-?< (11-1-24)

即，

111j λ-<-?<

,()

j k C ,(1)

j k C +

又因为{}j λ为Γ的(2K+1)个特征值；而Γ为自相关矩阵、Hermite 型、正定

的，因此，0 ( )j all j λ>，则 2

0j

λ

又因为各抽头用统一的步长?，为保证稳定收敛，以max λ确定?。

因此，若步长?满足：max

2

0λ

，

则递推算法是稳定的，收敛的。 式中，max λ是Γ的最大特征值，其上界为 max ,00trace (21)(21)()K

j

j j j K

K K x N λλ

=-<

==+Γ=++∑Γ

,0,000(21)(), all j j K x N j Γ=Γ=++

4、收敛特性的分析

（1）收敛特性～?

在满足稳定递推运算条件下（即max

2

0λ

），

??↑?↑?

?↑??

收速度差敛稳态误矛盾解决方法：分12 ??，

(一般21 /10 ??＝)。 LMS 算法的优点：简单，各抽头用同一个?。

LMS 算法每次迭代时，一个抽头做两次计算（一次乘法，一次加法），

则N 个抽头（这里N=2K+1），每次迭代计算量为2N+1≈2N 。

LMS 算法的缺点：收敛慢。

因为按max λ确定?，牺牲了大多数抽头乃至整个系统的收敛速度。

（2）收敛特性～λ（max λ，min λ）

收敛速度～max

min λ

λ??

???

比值有关。

若max

min 1λλ??

→ ???

，选择适当的Δ，可快速收敛。

若max

min

1λλ??

>> ???

，收敛慢。 (3) 收敛特性～信道频率响应()C f 的关系 ~~~~()j n x f C f λΓ

对有深度衰减的信道，max

min 1λ

λ??

>> ???

，收敛慢。