乙烷-高斯程序应用
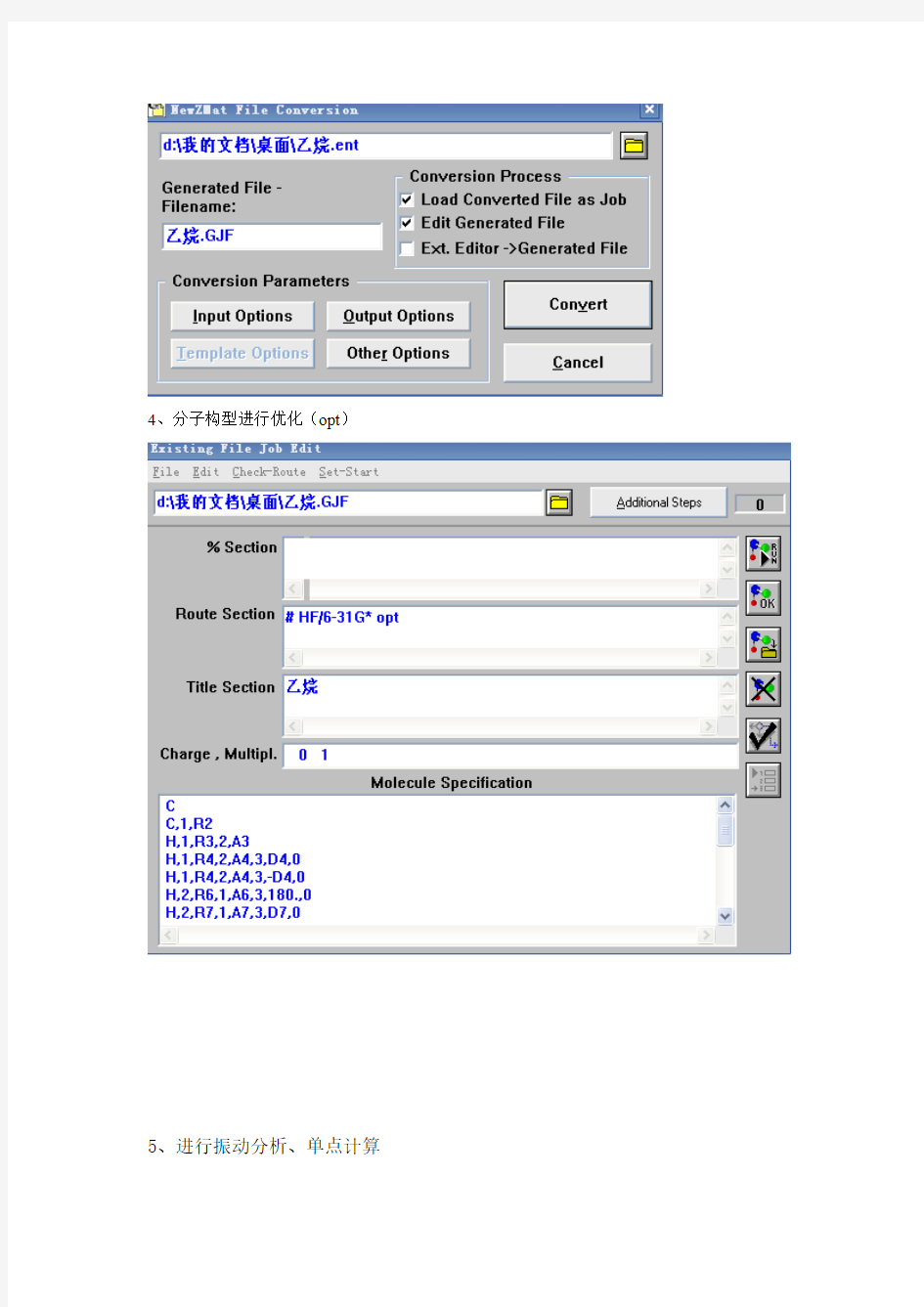
乙烷分子高斯程序应用1、用HyperChem程序画乙烷分子图,保存为*.PDB格式
2、设置工作环境
3、格式转化:
4、分子构型进行优化(opt)
5、进行振动分析、单点计算
6、计算结果输出:
优化结果输出:
Final structure in terms of initial Z-matrix: C
C,1,R2
H,1,R3,2,A3
H,1,R4,2,A4,3,D4,0
H,1,R4,2,A4,3,-D4,0
H,2,R6,1,A6,3,180.,0
H,2,R7,1,A7,3,D7,0
H,2,R7,1,A7,3,-D7,0
V ariables:
R2=1.52714912
R3=1.0851582
R4=1.08516911
R6=1.08517148
R7=1.08518242
A3=111.18808808
A4=111.18735176
A6=111.18983868
A7=111.18910141
D4=119.99975739
D7=-60.00024238
1|1|GINC-UNK|FOpt|RHF|6-31G(d)|C2H6|PCUSER|11-Jan-1911|0||# HF/6-31G*
OPT||乙烷||0,1|C,0.0000021919,0.,-0.7635805116|C,-0.0000021919,0.,0.76
35686082|H,1.0118036956,-0.0000000002,-1.1557871264|H,-0.5059007695,-0
.8762601514,-1.155782425|H,-0.5059007693,0.8762601516,-1.155782425|H,-
1.0118041011,0.0000000002,1.1558109401|H,0.5059009868,-0.8762605204,1.
1558062284|H,0.5059009871,0.8762605202,1.1558062284||V ersion=x86-Win32
-G94RevE.1|State=1-A'|HF=-79.2287541|RMSD=5.028e-010|RMSF=1.707e-004|D
ipole=0.,0.,-0.0000069|PG=CS [SG(C2H2),X(H4)]||@
HE WHO LAUGHS LAST PROBA BLY DIDN'T GET THE JOKE.
Job cpu time: 0 days 0 hours 0 minutes 8.0 seconds.
File lengths (MBytes): R WF= 5 Int= 0 D2E= 0 Chk= 2 Scr= 1
Normal termination of Gaussian 94
振动分析结果:
1 2 3
A" A' A" Frequencies -- 320.9807 887.6569 887.6878
Red. masses -- 1.0078 1.0562 1.0562
Frc consts -- .0612 .4903 .4904
IR Inten -- .0000 2.4997 2.4996
Raman Activ -- .0000 .0000 .0000
Depolar -- .0000 .7500 .7500
Atom AN X Y Z X Y Z X Y Z
1 6 .00 .00 .00 -.05 .00 .00 .00 .00 .05
2 6 .00 .00 .00 -.05 .00 .00 .00 .00 .05
3 1 .00 .00 .41 .16 .51 .00 .00 .00 -.22
4 1 .3
5 .00 -.20 .20 -.2
6 -.03 .03 .44 -.17
5 1 -.35 .00 -.20 .20 -.2
6 .03 -.03 -.44 -.17
6 1 .00 .00 .41 .16 .51 .00 .00 .00 -.22
7 1 -.35 .00 -.20 .20 -.26 .03 -.03 -.44 -.17
8 1 .35 .00 -.20 .20 -.26 -.03 .03 .44 -.17
4 5 6
A' A' A" Frequencies -- 1062.1629 1337.0508 1337.0597
Red. masses -- 3.1308 1.4544 1.4544
Frc consts -- 2.0811 1.5319 1.5320
IR Inten -- .0000 .0000 .0000
Raman Activ -- 13.9063 3.1051 3.1046
Depolar -- .3025 .7500 .7500
Atom AN X Y Z X Y Z X Y Z
1 6 .00 .31 .00 .14 .00 .00 .00 .00 .14
2 6 .00 -.31 .00 -.14 .00 .00 .00 .00 -.14
3 1 .02 .37 .00 -.06 -.51 .00 .00 .00 -.25
4 1 -.01 .37 -.01 -.20 .2
5 .08 .08 .44 -.11
5 1 -.01 .37 .01 -.20 .25 -.08 -.08 -.44 -.11
6 1 -.02 -.3
7 .00 .06 .51 .00 .00 .00 .25
7 1 .01 -.37 -.01 .20 -.25 .08 .08 .44 .11
8 1 .01 -.37 .01 .20 -.25 -.08 -.08 -.44 .11
7 8 9
A' A' A' Frequencies -- 1546.7873 1578.7780 1643.8192
Red. masses -- 1.1984 1.2740 1.0212
Frc consts -- 1.6893 1.8709 1.6259
IR Inten -- .1468 .0000 .0000
Raman Activ -- .0000 4.1660 38.8356
Depolar -- .6187 .7157 .7500
Atom AN X Y Z X Y Z X Y Z
1 6 .00 .09 .00 .00 -.11 .00 -.0
2 .00 .00
2 6 .00 .09 .00 .00 .11 .00 .02 .00 .00
3 1 -.17 -.37 .00 .18 .36 .00 -.12 -.28 .00
4 1 .08 -.37 .14 -.09 .36 -.1
5 .34 .14 -.26
5 1 .08 -.37 -.14 -.09 .3
6 .15 .34 .14 .26
6 1 -.16 -.3
7 .00 -.1
8 -.36 .00 .12 .28 .00
7 1 .08 -.37 -.14 .09 -.36 -.15 -.34 -.14 -.26
8 1 .08 -.37 .14 .09 -.36 .15 -.34 -.14 .26
10 11 12
A" A" A' Frequencies -- 1643.8212 1649.7178 1649.7193
Red. masses -- 1.0212 1.0628 1.0628
Frc consts -- 1.6259 1.7041 1.7041
IR Inten -- .0000 5.7101 5.7108
Raman Activ -- 38.8364 .0001 .0001
Depolar -- .7500 .7500 .7500
Atom AN X Y Z X Y Z X Y Z
1 6 .00 .00 -.0
2 .00 .00 -.05 .05 .00 .00
2 6 .00 .00 .02 .00 .00 -.05 .05 .00 .00
3 1 .00 .00 .49 .00 .00 .52 .12 .22 .00
4 1 -.26 .24 .04 -.28 .19 .04 -.36 -.11 .28
5 1 .2
6 -.24 .04 .28 -.19 .04 -.36 -.11 -.28
6 1 .00 .00 -.49 .00 .00 .52 .12 .22 .00
7 1 -.26 .24 -.04 .28 -.19 .04 -.36 -.11 -.28
8 1 .26 -.24 -.04 -.28 .19 .04 -.36 -.11 .28
13 14 15
A' A' A" Frequencies -- 3203.2175 3209.3460 3253.3299
Red. masses -- 1.0340 1.0379 1.1032
Frc consts -- 6.2510 6.2986 6.8798
IR Inten -- 72.4201 .0057 .0008
Raman Activ -- .0175 221.0308 150.1856
Depolar -- .0191 .0193 .7500
Atom AN X Y Z X Y Z X Y Z
1 6 .00 .03 .00 .00 -.04 .00 .00 .00 -.07
2 6 .00 .0
3 .00 .00 .0
4 .00 .00 .00 .07
3 1 .38 -.1
4 .00 -.39 .14 .00 .00 .00 -.01
4 1 -.19 -.14 -.33 .19 .14 .33 .24 .18 .40
5 1 -.19 -.14 .33 .19 .14 -.33 -.24 -.18 .40
6 1 .39 -.14 .00 .38 -.14 .00 .00 .00 .01
7 1 -.19 -.14 .34 -.19 -.14 .33 .24 .18 -.40
8 1 -.19 -.14 -.34 -.19 -.14 -.33 -.24 -.18 -.40
16 17 18
A' A" A' Frequencies -- 3253.3981 3278.4462 3278.5130
Red. masses -- 1.1032 1.1037 1.1037
Frc consts -- 6.8801 6.9891 6.9894
IR Inten -- .0008 101.4189 101.4133
Raman Activ -- 150.1842 .0011 .0011
Depolar -- .7500 .7500 .7500
Atom AN X Y Z X Y Z X Y Z
1 6 -.07 .00 .00 .00 .00 .07 .07 .00 .00
2 6 .07 .00 .00 .00 .00 .07 .07 .00 .00
3 1 .5
4 -.20 .00 .00 .00 .01 -.54 .21 .00
4 1 .12 .10 .24 -.24 -.18 -.40 -.13 -.10 -.24
5 1 .12 .10 -.24 .24 .18 -.40 -.13 -.10 .24
6 1 -.54 .20 .00 .00 .00 .01 -.54 .21 .00
7 1 -.12 -.10 .24 .24 .18 -.40 -.12 -.10 .24
8 1 -.12 -.10 -.24 -.24 -.18 -.40 -.12 -.10 -.24
Zero-point vibrational energy 209475.1 (Joules/Mol)
50.06574 (Kcal/Mol)
WARNING-- EXPLICIT CONSIDERATION OF 1 DEGREES OF FREEDOM AS VIBRATIONS MAY CAUSE SIGNIFICANT ERROR
VIBRATIONAL TEMPERA TURES: 461.82 1277.13 1277.18 1528.21 1923.71 (KELVIN) 1923.72 2225.47 2271.50 2365.08 2365.08
2373.56 2373.56 4608.69 4617.51 4680.79
4680.89 4716.93 4717.02
Zero-point correction= .079785 (Hartree/Particle)
Thermal correction to Energy= .083192
Thermal correction to Enthalpy= .084136
Thermal correction to Gibbs Free Energy= .056714
Sum of electronic and zero-point Energies= -79.148969
Sum of electronic and thermal Energies= -79.145563
Sum of electronic and thermal Enthalpies= -79.144618 Sum of electronic and thermal Free Energies= -79.172040
牛顿迭代法文献综述
“牛顿迭代法”最新进展文献综述牛顿法是一种重要的迭代法,它是逐步线性化的方法的典型代表。牛顿迭代法又称为牛顿-拉夫逊方法,它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根。另外该方法广泛用于计算机编程中。 介绍一下牛顿迭代法研究的前沿进展,1992年南京邮电学院基础课部的夏又生写的一篇题名一类代数方程组反问题的牛顿迭代法,对一类代数方程组反问题提出了一个可行的迭代解法。从算法上看,它是一种解正问题—迭代—解正问题迭代改善的求解过程。湖南师范大学的吴专保;徐大发表的题名堆浸工艺中浸润面的非线性问题牛顿迭代方法,为了研究堆浸工艺的机理,用牛顿迭代公式寻求浸润面的非线性方程的数值解,经过14次迭代的误差达到了,说明此算法收敛有效。浙江大学电机系的林友仰发表的牛顿迭代法在非线性电磁场解算中的限制对非线性电磁场解算中的限制做了分析,求解非线性方程组时迭代法是不可避免的。牛顿—拉斐森迭代法由于它的收敛速度快常被优先考虑。应用这个方法的主要问题是求雅可比矩阵。因为雅可比矩阵元素的计算非常费时。然而,本文要说明的是当利用以三角形为单元的有限元法求解非线性方程组时,应用牛顿法其雅可比矩阵容易求得,并且它保持了原系数的对称性和稀疏性,因而节省了时间。与此相反,若在差分法中应用牛顿迭代,并且按习惯用矩形网格进行剖分,则雅可比阵的计算很费时,而且不再保持原有对称性,这就使得存贮量和计算时间大为增加。南株洲工学院信息与计算科学系的吕勇;刘兴国发表的题名为牛顿迭代法加速收敛的一种修正格式,主要内容牛顿迭代法是求解非线性方程的一种重要的数值计算方法,在通常情况下,它具有至少平方收敛。本文利用文献[4]所建立的迭代格式xn+1=xn-αf(xfn)(x+n)f′(xn),对迭代格式中的参数α的讨论,实现了牛顿迭代法加速收敛的一种修正格式。
ICA使用牛顿迭代法对FastICA算法经行改进
ICA用牛顿迭代法改进的FastICA算法 ICA算法原理: 独立分量分析(ICA)的过程如下图所示:在信源()st中各分量相互独立的假设下,由观察xt通过结婚系统B把他们分离开来,使输出yt逼近st。 图1-ICA的一般过程 ICA算法的研究可分为基于信息论准则的迭代估计方法和基于统计学的代数方法两大类,从原理上来说,它们都是利用了源信号的独立性和非高斯性。基于信息论的方法研究中,各国学者从最大熵、最小互信息、最大似然和负熵最大化等角度提出了一系列估计算法。如FastICA算法, Infomax算法,最大似然估计算法等。基于统计学的方法主要有二阶累积量、四阶累积量等高阶累积量方法。本实验主要讨论FastICA算法。 1. 数据的预处理 一般情况下,所获得的数据都具有相关性,所以通常都要求对数据进行初步的白化或球化处理,因为白化处理可去除各观测信号之间的相关性,从而简化了后续独立分量的提取过程,而且,通常情况下,数据进行白化处理与不对数据进行白化处理相比,算法的收敛性较好。 若一零均值的随机向量 满足 , 其中:I为单位矩阵,我们称这个向量为白化向量。白化的本质在于去相关,这同主分量分析的目标是一样的。在ICA中,对于为零均值的独立源信号 , 有: , 且协方差矩阵是单位阵cov( S ) = I,因此,源信号 S( t )是白色的。对观测信号X( t ),我们应该寻找一个线性变换,使X( t )投影到新的子空间后变成白化向量,即:
其中,W0为白化矩阵,Z为白化向量。 利用主分量分析,我们通过计算样本向量得到一个变换 其中U和 分别代表协方差矩阵XC的特征向量矩阵和特征值矩阵。可以证明,线性变换W0满足白化变换的要求。通过正交变换,可以保证 因此,协方差矩阵: 再将 代入 且令 有 由于线性变换A~连接的是两个白色随机矢量Z( t )和S( t ),可以得出A~ 一定是一个正交变换。如果把上式中的Z( t )看作新的观测信号,那么可以说,白化使原来的混合矩阵A简化成一个新的正交矩阵A~。证明也是简单的: 其实正交变换相当于对多维矢量所在的坐标系进行一个旋转。 在多维情况下,混合矩阵A是N*N 的,白化后新的混合矩阵A~ 由于是正交矩阵,其自由度降为N*(N-1)/2,所以说白化使得ICA问题的工作量几乎减少了一半。 白化这种常规的方法作为ICA的预处理可以有效地降低问题的复杂度,而且算法简单,用传统的PCA就可完成。用PCA对观测信号进行白化的预处理使得原来所求的解混合矩阵退化成一个正交阵,减少了ICA的工作量。此外,PCA本身具有降维功能,当观测信号的个数大于源信号个数时,经过白化可以自动将观测信号数目降到与源信号维数相同。
牛顿迭代法
牛顿迭代法 李保洋 数学科学学院信息与计算科学学号:060424067 指导老师:苏孟龙 摘要:牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,即牛顿迭代法.迭代法是一种不断用变量的旧值递推新值的过程.跟迭代法相对应的是直接法或者称为一次解法,即一次性解决问题.迭代法又分为精确迭代和近似迭代.“牛顿迭代法”属于近似迭代法,本文主要讨论的是牛顿迭代法,方法本身的发现和演变和修正过程,避免二阶导数计算的Newton迭代法的一个改进,并与中国古代的算法,即盈不足术,与牛顿迭代算法的比较. 关键词:Newton迭代算法;近似求解;收敛阶;数值试验;中国古代数学; 九章算术;Duffing方程;非线性方程;收敛速度;渐进性 0 引言: 迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法或者称为一次解法,即一次性解决问题.迭代法又分为精确迭代和近似迭代.“二分法”和“牛顿迭代法”属于近似迭代法. 迭代算法是用计算机解决问题的一种基本方法.它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值.具体使用迭代法求根时应注意以下两种可能发生的情况: (1)如果方程无解,算法求出的近似根序列就不会收敛,迭代过程会变成死循环,因此在使用迭代算法前应先考察方程是否有解,并在程序中对迭代的次数给予限制. (2)方程虽然有解,但迭代公式选择不当,或迭代的初始近似根选择不合理,也会导致迭代失败. 所以利用迭代算法解决问题,需要做好以下三个方面的工作: 1、确定迭代变量.在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量. 2、建立迭代关系式.所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系).迭代关系式的建立是解决迭代问题的关键,通常可以使用递推或倒推的方法来完成. 3、对迭代过程进行控制,在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题.不能让迭代过程无休止地重复执行下去.迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定.对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析出用来结束迭代过程的条件. 1牛顿迭代法:
Newton迭代法实例
基于牛顿迭代法的圆形断面临界水深直接计算 学院:建筑工程学院学号:2111206052 姓名:王瑞峰 一、问题来源 圆形断面由于具有受力条件好、适应地形能力强、水力条件好等优点,已成为农田灌溉、城市给水排水等工程较常采用的断面形式。而临界水深的计算则是进行圆形断面水力计算的关键,但其计算较繁杂,要求解高次隐函数方程,且未知量包含在三角函数中,求解难度大。自20世纪90年代,对圆形断面临界水深的计算进行了大量研究,获得了较多成果。鉴此,本文应用牛顿迭代算法,得到一种较简洁且可提供高精度算法程序的近似计算公式。 二、数学模型 相应于断面单位能量最小值的水深称为临界水深,其计算公式为: 需满足的临界流方程为: 其中 式中,d为洞径;为临界水深对应的圆心角,rad;n为流速分布不均匀系数(不特殊说明时取1.0);Q为流量,m3Is;g为重力加速度(通常取9.81 m/s2);分别为临界流对应的过水断面面积和水面宽度。 无压流圆形断面的水力要素见图1 将式(1)、(3)、(4)代入式(2)得: 将式(5)整理即得临界水深的非线形方程: 由此可知.式(6)为临界水深h。的高次隐函数方程,且未知量包含在三角函数中。 即圆形断面临界水深的求解即为式(6)的求根问题。在现行工程实际中计算临界水深时均采用近似公式或试算法,所得结果精度不高且效率较低。 三、方法选择 牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根。 解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种近似方法。把f(x)在x0点
附近展开成泰勒级数f(x) = f(x0)+(x-x0)f'(x0)+(x-x0)^2*f''(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f'(x0)(x- x0)=f(x)=0 设f'(x0)≠0则其解为x1=x0-f(x0)/f'(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f'(x(n))。 在对式(6)的求解方法中,应首选牛顿迭代法,因为牛顿迭代法可快速求解出其他方法求不出或难以求出的解。 引入无量纲参数k: 将式(7)代入式(6)得: 的一阶、二阶导函数分别为: 由牛顿迭代法可得: 式中,=0,1,2…为迭代次数;为的初值。 将式(8)、(9)代入式(10),可得相应于式(6)临界水深对应中心角的牛顿迭代公式: 由式(11)迭代计算出临界水深对应的中心角后,代入式(1)即可得临界水深。 根据文献,为避免渡状水面有可能接触洞顶引起水流封顶现象。洞内水面线以上的空间不宜小于隧洞断面面积的15%,且高度不小于0.4m。可得临界水深对应的中心角的最大值一般不超过4.692,相应可得无量纲参数值的上限为0.5044。故取值范围为[O.000 0,0.504 4]。 查阅文献与的近似公式: 若将式(12)视为初值函数,代入式(11)进行一次迭代计算,不仅得到了直接计算的公式,且提高了计算结果的精度。 其中 将式(13)代入式(1)即得圆形断面临界水深。 计算实例: 某引水式电站输水隧洞为圆形断面,已知洞径d=3.0 m,试确定设计流量Q=8.0m3/s时的临界水深。 四、编程实现 本文采用Fortran软件求解,程序的代码如下:
各种迭代法编程
雅可比迭代法: function x=jacobi(a,b,p,delta,n) %a为n维非奇异矩阵;b为n维值向量 %p为初值;delta为误差界;n为给定的迭代最高次数 N=length(b); for k=1:n for j=1:N x(j)=(b(j)-a(j,[1:j-1,j+1:N])*p([1:j-1,j+1:N]))/a(j,j); end err=abs(norm(x’-p)); p=x’; if(err function [x,k,err,p]=ddf(f,x0,tol,n) %ddl.m为用迭代法求非线性方程的解 %f为给定的迭代函数;x0为给定的初始值 %tol为给定的误差界;n为所允许的最大迭代次数 %k为迭代次数;x为不动点的近似值;err为误差 p(1)=x0; for k=2:n p(k)=feval(f,p(k-1)); k, err=abs(p(k)-p(k-1)) x=p(k); if(err 用牛顿迭代法求近似根 ————————————————————————————————作者:————————————————————————————————日期: 第四题 题目:用Newton 法求方程在 74 28140x x -+= (0.1,1.9)中的近似根(初始近似值取为区间端点,迭代6次或误差小于0.00001). 解:此题是用牛顿迭代法求解近似根的问题 1. Newton 迭代法的算法公式及应用条件: 设函数在有限区间[a,b]上二阶导数存在,且满足条件 ⅰ. ()()0f a f b <; ⅱ. ()''f x 在区间[a,b]上不变号; ⅲ. ()'0f x ≠; ⅳ. ()()'f c f c b a ≤-,其中c 是a,b 中使()()''min(,)f a f b 达到的一个. 则对任意初始近似值0[,]x a b ∈,由Newton 迭代过程 ()()() 1'k k k k k f x x x x f x +=Φ=-,k=0,1,2… 所生成的迭代序列{ k x }平方收敛于方程()0f x =在区间[a,b]上的唯一解а. 对本题: )9.1()9.1(0 )8(4233642)(0 )16(71127)(0 )9.1(,0)1.0(,1428)(3225333647>?''<-=-=''<-=-='<>+-=f f x x x x x f x x x x x f f f x x x f Θ 故以1.9为起点 ?? ???='-=+9.1)()(01x x f x f x x k k k k 2. 程序编写 #include CENTRAL SOUTH UNIVERSITY 数值分析实验报告 非线性方程组的牛顿迭代法的应用 一、问题背景 非线性是实际问题中经常出现的,并且在科学与工程计算中的地位越来越重要,很多我们熟悉的线性模型都是在一定条件下由非线性问题简化的,为得到更符合实际的解答,往往需要直接研究非线性科学,它是21世纪科学技术发展的重要支柱,非线性问题的数学模型有无限维的如微分方程,也有有限维的。道遥咏计算机进行科学计算都要转化为非线性的单个方程或方程组的求解。从线性到非线性是一个质的变化,方程的性质有本质不同,求解方法也有很大差别。本文主要介绍的是非线性方程组的牛顿迭代法的数值解法。 二、数学模型 对于方程()0=x f ,如果()x f 湿陷性函数,则它的求根是容易的。牛顿法实质上是一种线性化方法,其基本思想是将线性方程()0=x f 逐步归结为某种线性方程来求解。 设已知方程()0=x f 有近似根k x (假定()0'≠k x f ),将函数()x f 在点k x 展开,有 ()()()()k k k x x x f x f x f -+≈', 于是方程()0=x f 可近似地表示为 ()()()0'=-+k k k x x x f x f 这是个线性方程,记其根为1+k x ,则1+k x 的计算公式 ()() k k k k x f x f x x ' 1- =+, ,1,0=k 这就是牛顿法。 三、算法及流程 对于非线性方程 ()()()???? ????????=n n n n x L x x f M x L x x f x L x x f f ,,,,,,,,,2 1212211 在()k x 处按照多元函数的泰勒展开,并取线性项得到 非线性回归预测法 前面所研究的回归模型,我们假定自变量与因变量之间的关系是线性的,但社会经济现象是极其复杂的,有时各因素之间的关系不一定是线性的,而可能存在某种非线性关系,这时,就必须建立非线性回归模型。 一、非线性回归模型的概念及其分类 非线性回归模型,是指用于经济预测的模型是曲线型的。常见的非线性回归模型有下列几种: (1)双曲线模型: i i i x y εββ++=1 2 1 (3-59) (2)二次曲线模型: i i i i x x y εβββ+++=2321 (3-60) (3)对数模型: i i i x y εββ++=ln 21 (3-61) (4)三角函数模型: i i i x y εββ++=sin 21 (3-62) (5)指数模型: i x i i ab y ε+= (3-63) i i i x x i e y εβββ+++=221110 (3-64) (6)幂函数模型: i b i i ax y ε+= (3-65) (7)罗吉斯曲线: i x x i i i e e y εββββ++=++1101101 (3-66) (8)修正指数增长曲线: i x i i br a y ε++= (3-67) 根据非线性回归模型线性化的不同性质,上述模型一般可细分成三种类型。 第一类:直接换元型。 这类非线性回归模型通过简单的变量换元可直接化为线性回归模型,如:(3-59)、(3-60)、(3-61)、(3-62)式。由于这类模型的因变量没有变形,所以可以直接采用最小平方法估计回归系数并进行检验和预测。 第二类:间接代换型。 这类非线性回归模型经常通过对数变形的代换间接地化为线性回归模型,如:(3-63)、(3-64)、(3-65)式。由于这类模型在对数变形代换过程中改变了因变量的形态,使得变形后模型的最小平方估计失去了原模型的残差平方和为最小的意义,从而估计不到原模型的最佳回归系数,造成回归模型与原数列之间的较大偏差。 第三类:非线性型。 1.填空 1) 计算 f=(2-1)6 , 取2=1.4 , 利用下列算式,那个得到的结果最好?答:C (A) 6121 )(-, (B) (3-22)2, (C) 32231)(+, (D) 99-702 2) 称序列{x n }是p 阶收敛的条件为c x x x x p n n n =--+∞→** lim 1 3) 在等式∑==n k k k n x f a x x x f 010)(],,,[ 中, 系数a k 与函数f (x ) 无 关。 (限填“有”或“无”) 4) 设P k (x k ,y k ) , k =1,2,…,5 为函数y =x 2-3x +1上的5个互异的点,过P 1,…,P 5且次数不超过4次的插值多项式是 x 2-3x +1 。 5) 设f (x )∈C [a ,b ], f (x )的最佳一致逼近多项式是__一定___存在的。 6) 求解微分方程数值解的E ul e r 法的绝对稳定区间是(-2,0) 。 7) n 个节点的插值型求积公式的代数精度不会超过2n -1次。 8) 高次插值容易产生________龙格(R u n g e )现象。 9) R n 上的两个范数||x||p , ||x||q 等价指的是_?C,D ∈R,_C_||x||q _≤||x||p ≤D ||x||q _; R n 上的两个范数_一定__是等价的。(选 填“一定”或“不一定”)。 2.曲线151.03+-=x x y 与89.14.22-=x y 在点(1.6,1)附近相切,试用牛顿迭代法求切点横坐标的近似值1+k x ,使5110-+≤-k k x x 。 解 两曲线的导数分别为51.032-='x y 和x y 8.4=',两曲线相切,导数相等,故有 051.08.432=--x x 令51.08.43)(2--=x x x f ,则f(1)<0,f(2)>0,故区间[1,2]是f(x)=0的有根区间,又当]2,1[∈x 时,08.46)(>-='x x f ,因此f(x)=0在[1,2]上有惟一实根x*,对f(x)应用牛顿迭代法,得计算公式 ,2,1,0,8 .4651.08.4321=----=+k x x x x x k k k k k 由于06)(>=''x f ,故取20=x 迭代计算一定收敛,计算结果如表7-6所示。 表7-6 k k x k k x 0 2.0 3 1.706815287 1 2.293055556 4 1.700025611 2 1.817783592 5 1.7 继续计算仍得7.16=x ,故7.1*=x 。 注 本题也可令89.14.2151.02 3-=+-x x x ,解得切点横坐标满足方程089.2514.2)(23=+--=x x x x f ,用有重根时的牛顿迭代法(7.15)式计算,此时m=2,仍取x0=2,经四步可得x*=1.7。 高斯消元法1.程序: clear format rat A=input('输入增广矩阵A=') [m,n]=size(A); for i=1:(m-1) numb=int2str(i); disp(['第',numb,'次消元后的增广矩阵']) for j=(i+1):m A(j,:)=A(j,:)-A(i,:)*A(j,i)/A(i,i); end A end %回代过程 disp('回代求解') x(m)=A(m,n)/A(m,m); for i=(m-1):-1:1 x(i)=(A(i,n)-A(i,i+1:m)*x(i+1:m)')/A(i,i); end x 2.运行结果: 高斯选列主元消元法1.程序: clear format rat A=input('输入增广矩阵A=') [m,n]=size(A); for i=1:(m-1) numb=int2str(i); disp(['第',numb,'次选列主元后的增广矩阵']) temp=max(abs(A(i:m,i))); [a,b]=find(abs(A(i:m,i))==temp); tempo=A(a(1)+i-1,:); A(a(1)+i-1,:)=A(i,:); A(i,:)=tempo disp(['第',numb,'次消元后的增广矩阵']) for j=(i+1):m A(j,:)=A(j,:)-A(i,:)*A(j,i)/A(i,i); end A end %回代过程 disp('回代求解') x(m)=A(m,n)/A(m,m); for i=(m-1):-1:1 x(i)=(A(i,n)-A(i,i+1:m)*x(i+1:m)')/A(i,i); end x 2.运行结果: 编号 毕业设计(论文)题目 Newton Raphson 算法及其应用 二级学院数学与统计学院 专业信息与计算科学 班级108010101 学生姓名侯杰学号10801010106 指导教师职称 时间 目录 摘要 (3) Abstract (3) 一、绪论 (4) 1.1 选题的背景和意义 (4) 1.2 牛顿迭代法的优点及缺点 (4) 二、Newton Raphson 算法的基本原理 (5) 2.1 Newton Raphsn算法 (5) 2.2 一种修正的Newton Raphsn算法 (7) 2.3 另外一种Newton Raphsn算法的修正 (11) 三、Newton Raphson 算法在计算方程中的应用 (18) 四、利用牛顿迭代法计算附息国债的实时收益率 (21) 4.1附息国债实时收益率的理论计算公式 (22) 4.2附息国债实时收益率的实际计算方法 (22) 4.3利用牛顿迭代法计算 (23) 五、结论 (26) 致谢 (27) 参考文献 (28) 摘要 牛顿在17世纪提出的一种近似求解方程的方法,即牛顿拉夫森迭代法.迭代法是一种不断的用变量的旧值递推新值的过程.跟迭代法相对应的是直接法或被称为一次解法,即一次性解决的问题.迭代法又分为精确迭代以及近似迭代.“牛顿迭代法”就属于近似迭代法,本文主要讨论的就是牛顿迭代法,方法本身的发现到演变到修正的过程,避免二阶导数计算的Newton迭代法的一个改进,以及用牛顿迭代法解方程,利用牛顿迭代法计算国债的实时收益率。 关键词:Newton Raphson迭代算法;近似解;收益率; Abstract In the 17th century,Newton raised by an approximate method of solving equations,that is Newton Iteration,a process of recursion new value constantly with the old value of variable. Correspond with the iterative method is a direct method or as a solution,that is a one-time problem solving. Iteration is divided into exact iterative and approximate iterative. "Newton Iterative Method" are approximate iterative method. This article mainly focuses on the Newton Iteration. The main contents of this article include the discovery,evolution and amendment process of this methods; an improve of avoiding calculating Newton Iteration with second-order derivative; Newton Raphson iterative method of solving equations and Calculating the real-time yield of government bonds. Keywords: Newton Iterative Algorithm; approximate solution; Yield; 例1、已知函数表 求() f x的Lagrange二次插值多项式和Newton二次插值多项式。 解: (1)由题可知 插值基函数分别为 故所求二次拉格朗日插值多项式为 (2)一阶均差、二阶均差分别为 均差表为 故所求Newton 二次插值多项式为 例2、 设2()32f x x x =++,[0,1]x ∈,试求()f x 在[0, 1]上关于()1x ρ=,{}span 1,x Φ=的 最佳平方逼近多项式。 解: 若{}span 1,x Φ=,则0()1x ?=,1()x x ?=,且()1x ρ=,这样,有 所以,法方程为 011231261192 34a a ??????????=?????????? ?????????? ,经过消元得012311 62110123a a ??? ???????=???????????????????? 再回代解该方程,得到14a =,011 6 a = 故,所求最佳平方逼近多项式为* 111 ()46 S x x = + 例3、 设()x f x e =,[0,1]x ∈,试求()f x 在[0, 1]上关于()1x ρ=,{}span 1,x Φ=的最佳平 方逼近多项式。 解: 若{}span 1,x Φ=,则0()1x ?=,1()x x ?=,这样,有 所以,法方程为 解法方程,得到00.8732a =,1 1.6902a =, 故,所求最佳平方逼近多项式为 例4、 用4n =的复合梯形和复合辛普森公式计算积分1?。 解: (1)用4n =的复合梯形公式 由于 2h =,()f x =,()121,2,3k x k k =+=,所以,有 (2)用4n =的复合辛普森公式 由于2h =,()f x =,()121,2,3k x k k =+=,()1 2 220,1,2,3k x k k +=+=,所以,有 例5、 用列主元消去法求解下列线性方程组的解。 解:先消元 再回代,得到33x =,22x =,11x = 非线性方程组的牛顿迭代法的应用 CENTRAL SOUTH UNIVERSITY 数值分析实验报告 非线性方程组的牛顿迭代法的应用 一、问题背景 非线性是实际问题中经常出现的,并且在科学与工程计算中的地位越来越重要,很多我们熟悉的线性模型都是在一定条件下由非线性问题简化的,为得到更符合实际的解答,往往需要直接研究非线性科学,它是21世纪科学技术发展的重要支柱,非线性问题的数学模型有无限维的如微分方程,也有有限维的。道遥咏计算机进行科学计算都要转化为非线性的单个方程或方程组的求解。从线性到非线性是一个质的变化,方程的性质有本质不同,求解方法也有很大差别。本文主要介绍的是非线性方程组的牛顿迭代法的数值解法。 二、数学模型 对于方程()0=x f ,如果()x f 湿陷性函数,则它的求根是容易的。牛顿法实质上是一种线性化方法,其基本思想是将线性方程()0=x f 逐步归结为某种线性方程来求解。 设已知方程()0=x f 有近似根k x (假定()0'≠k x f ),将函数()x f 在点k x 展开,有 ()()()()k k k x x x f x f x f -+≈', 于是方程()0=x f 可近似地表示为 ()()()0'=-+k k k x x x f x f 这是个线性方程,记其根为1+k x ,则1+k x 的计算公式 () () k k k k x f x f x x ' 1- =+, ,1,0=k 这就是牛顿法。 三、算法及流程 对于非线性方程 ()()()???? ????????=n n n n x L x x f M x L x x f x L x x f f ,,,,,,,,,2 12 12211 在()k x 处按照多元函数的泰勒展开,并取线性项得到 非线性回归预测法——高斯牛顿法(詹学朋) 非线性回归预测法 前面所研究的回归模型,我们假定自变量与因变量之间的关系是线性的,但社会经济现象是极其复杂的,有时各因素之间的关系不一定是线性的,而可能存在某种非线性关系,这时,就必须建立非线性回归模型。 一、非线性回归模型的概念及其分类 非线性回归模型,是指用于经济预测的模型是曲线型的。常见的非线性回归模型有下列几种: (1)双曲线模型: i i i x y εββ++=1 2 1 (3-59) (2)二次曲线模型: i i i i x x y εβββ+++=2321 (3-60) (3)对数模型: i i i x y εββ++=ln 21 (3-61) (4)三角函数模型: i i i x y εββ++=sin 21 (3-62) (5)指数模型: i x i i ab y ε+= (3-63) i i i x x i e y εβββ+++=221110 (3-64) (6)幂函数模型: i b i i ax y ε+= (3-65) (7)罗吉斯曲线: i x x i i i e e y εββββ++=++1101101 (3-66) (8)修正指数增长曲线: i x i i br a y ε++= (3-67) 根据非线性回归模型线性化的不同性质,上述模型一般可细分成三种类型。 第一类:直接换元型。 这类非线性回归模型通过简单的变量换元可直接化为线性回归模型,如:(3-59)、(3-60)、(3-61)、(3-62)式。由于这类模型的因变量没有变形,所以可以直接采用最小平方法估计回归系数并进行检验和预测。 第二类:间接代换型。 这类非线性回归模型经常通过对数变形的代换间接地化为线性回归模型,如:(3-63)、(3-64)、(3-65)式。由于这类模型在对数变形代换过程中改变了因变量的形态,使得变形后模型的最小平方估计失去了原模型的残差平方和为最小的意义,从而估计不到原模型的最佳回归系数,造成回归模型与原数列之间的较大偏差。 第三类:非线性型。 高斯牛顿法 高斯—牛顿迭代法的基本思想是使用泰勒级数展开式去近似地代替非线性回归模型,然后通过多次迭代,多次修正回归系数,使回归系数不断逼近非线性回归模型的最佳回归系数,最后使原模型的残差平方和达到最小。高斯—牛顿法的一般步骤为: (1)初始值的选择。其方法有三种,一是根据以往的经验选定初始值;二是用分段法求出初始值;三是对于可线性化的非线性回归模型,通过线性变换,然后施行最小平方法求出初始值。 (2)泰勒级数展开式。设非线性回归模型为: i=1,2,…,n (3-68) 其中r为待估回归系数,误差项~N(0, ),设: ,为待估回归系数的初始值,将(3-68)式在g点附近作泰勒展开,并略去非线性回归模型的二阶及二阶以上的偏导数项,得 (3-69) 将(3-69)式代入(3-68)式,则 移项: 令: 则:i=1,2,…,n 用矩阵形式表示,上式则为:(3-70) 其中: (3)估计修正因子。用最小平方法对(3-70)式估计修正因子B, 则:(3-71) 设g为第一次迭代值,则: (4)精确度的检验。设残差平方和为: ,S为重复迭代次数,对于给定的允许误差率K,当时,则停止迭代;否则,对(3-71)式作下一次迭代。 (5)重复迭代。重复(3-71)式,当重复迭代S次时,则有:修正因子: 第(S+1)次迭代值: 四、应用举例 设12个同类企业的月产量与单位成本的资料如下表: 表3-9 间接代换法计算表 企业编号单位产品成 本(元) 月产量 1 2 3 4 5 6 7 8 9 10 11 12 160 151 114 128 85 91 75 76 66 60 61 60 10 16 20 25 31 36 40 45 51 56 60 65 (注:资料来源《社会经济统计学原理教科书》第435页) 试配合适当的回归模型分析月产量与单位产品成本之间的关系。 解:(1)回归模型与初始值的选择。根据资料散点图的识别,本数据应配合指数模型:对指数模型两边取对数,化指数模型为线性回归模型,然后施行最小平方法求出初始 值。即: 则上述指数模型变为: 对分别求反对数,得,带入原模型, 得回归模型: 高斯—牛顿迭代法 初始回归模型: 目录 一牛顿迭代法的简介 (4) 1.1 牛顿迭代法的产生背景 (4) 1.2 牛顿迭代法的概述 (4) 1.3 牛顿迭代法的优点 (4) 二牛顿迭代法的分析 (4) 2.1 牛顿迭代法的思想 (4) 2.2 牛顿迭代法的要求 (5) 2.3 牛顿.迭代法 (6) 三牛顿迭代求根的方法 (7) 四牛顿迭代法具体例子的实现 (7) 伍牛顿迭代法的收敛性 (10) 六、迭代求根应注意的事项 (10) 七、参考文献 (11) 八附录.c语言代码 (13) 题目: 牛顿法---插值方法 摘要: 牛顿迭代法(Newton's method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时线性收敛,但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。牛顿迭代法是一个重要的计算方法和思想。牛顿迭代法的主要功能:计算方程时可以比较快速方便的计算出来结果但并不影响计算出来结果的精确度,运用于多种工业设计和数学设计方面. 关键字: 牛顿迭代方程根算法 一 .牛顿迭代法简介 1.1 牛顿迭代法的产生背景 牛顿迭代法(Newton's method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时线性收敛,但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。 1.2 牛顿迭代法的概述 牛顿迭代法(Newton's method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。设r是f(x) = 0的根,选取x0作为r初始近似值,过点(x0,f(x0))做曲线y = f(x)的切线L,L的方程为y = f(x0) f'(x0)(x-x0),求出L与x轴交点的横坐标 x1 = x0-f(x0)/f'(x0),称x1为r的一次近似值。过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x轴的横坐标 x2 = x1-f(x1)/f'(x1),称x2为r的二次近似值。重复以上过程,得r的近似值序列,其中x(n+1)=x(n)-f(x(n))/f'(x(n)),称为r的n+1次近似值,上式称为牛顿迭代公式。解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种近似方法。把f(x)在x0点附近展开成泰勒级数 f(x) = f(x0)+(x-x0)f'(x0)+(x-x0)^2*f''(x0)/2! +…取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f'(x0)(x-x0)=f(x)=0 设f'(x0)≠0则其解为x1=x0-f(x0)/f'(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f'(x(n))。 1.3 牛顿迭代法的优点 迭代法是求方程近似根的一个重要方法,也是计算方法中的一种基本方法,它的算法简单,是用于求方程或方程组近似根的一种常用的算法设计方法。牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具 第十三章 药动学数据的曲线拟合以及常用软件 计算药动学参数,是药代动力学进一步应用的基础。如何测定有关的动力学参数呢?常用的方法是:首先在用药后的若干不同时间,采取血样(或尿样),测定其血药浓度值或尿中药量(这些数值称为实测值或观察值,用C i 表示),这样就有了药物浓度经时曲线数据;然后,依据半对数坐标图,选定一种模型方程 (是时间t 的曲线函数)计算理论估算值(用i C )表示),按照观察值和理论估算值之 差的平方和(即残差平方和)或加权残差平方和(均用Re 表示)最小的原则,采用适当的算法,求出有关的动力学参数。这种方法,在数学上称为曲线拟合(fitting a curve)。由于所采用的线性药代动力学的模型方程是多指数项之和的函数形式,并且是所含动力学参数的非线性函数,所以这种曲线拟合方法称为非线性最小二乘法。 一、最小二乘法的一般原理 设y 是变量x 的函数,含有m 个待定参数a 1,a 2,…,a m 。记为 y =f (x ;a 1,a 2,…,a m ) 若对x 和y 作n 次观察,测得观察值(x 1,y 1),(x 2,y 2),…,(x n ,y n )。根据这样一组二维数据,即平面上的若干点,要求确定这个一元函数y =f (x ;a 1,a 2,…,a m );(i=1,2,…,n),即一条曲线,使这些点与曲线总体来说尽量接近。并使y 的观察值y i 与理论估算值=i y )f (x i ;a 1,a 2,…,a m ) ;(i=1,2,…,m)的误差平方和,即残差平方和21 ()n e i i i y y ==?∑)2121((,,,,)n i i m i y f x a a a ==?…∑R )i 取得最小值, 或者加权残差平方和21()/n e i i i R y y w ==?∑)2121 ((,,,,))/n i i m i i y f x a a a w ==?…∑ 取得 最小值。其中w i 称为权重系数,在后面的段落会详细讲解。这时Re 有时候也称为目标函数。这就是数据拟合成曲线的思想,简称为曲线拟合。曲线拟合的目的是根据实验获得的数据去建立因变量和自变量之间有效的函数关系,这个函数关系对于药动学来讲就是通过房室模型推导出来的药时曲线公式。根据观察值求出待 311 牛顿迭代法(简写)就是一种近似求解实数域与复数域求解方程的数学方法。那么这个方法是具体是什么原理呢? 牛顿迭代如何迭代? 直接看数学公式描述如何迭代不直观,先来看动图就很容易理解牛顿迭代法为什么叫迭代法以及怎样迭代的: 牛顿迭代法是原理是根据一个初始点在该点做切线,切线与X轴相交得出下一个迭代点的坐标,再在处做切线,依次类推,直到求得满足精度的近似解为止。 由前面描述知道,牛顿迭代法是用来近似求解方程的,这里有两个点需要说明:?为啥要近似求解?很多方程可能无法直接求取其解 ?迭代法非常适合计算机编程实现,实际上计算机编程对于牛顿迭代法广为应用来看看,数学上如何描述的? 其中为函数在处的一阶导数,也就是该点的切线。 来简单推一推上面公式的由来,直线函数方程为: 知道一个直线的一个坐标点以及斜率则该直线的方程就很容易可以得知: 那么该直线与轴的交点,就是y=0也即等式x 的解: 啥时候停止迭代呢? 1.计算出 2.给出一个初始假定根值x0,利用上面迭代式子进行迭代 3.计算绝对相对迭代近似误差 4.将绝对相对近似误差与预定的相对误差容限进行比较。如果,则迭 代步骤2,否则停止算法。另外,检查迭代次数是否已超过允许的最大迭代次数。如果是这样,则需要终止算法并退出。另一个终止条件是: 如何编码呢? 由于牛顿迭代法主要目的是解方程,当然也有可能用于某一个数学函数求极值,所以无法写出通用的代码,这里仅仅给出一个编代码的思路。相信掌握了思路,对于各种实际应用应该能很快的写出符合实际应用的代码。 假定一函数为 其波形图如下: 其一阶导数为: 那么对于该函数的根: 从图上大致可以知道有两个根,如果直接解方程,则很难求出其根,可以编个代码试试: #include 用牛顿迭代法求近似根
非线性方程组的牛顿迭代法的应用
非线性回归预测法——高斯牛顿法(詹学朋)
数值分析练习第五套
数值分析编程及运行结果(高斯顺序消元法)
牛顿迭代法及其应用教学提纲
数值分析版试题及答案
非线性方程组的牛顿迭代法的应用
非线性回归预测法——高斯牛顿法(詹学朋)知识分享
高斯—牛顿迭代法
牛顿迭代法论文
第十三章 曲线拟合以及常用的药代动力学软件
牛顿-拉夫逊迭代法原理及其实现
