考虑轴向力影响欧拉梁动力反应分析

考虑轴向力影响欧拉梁动力反应分析
一、前言
在前面的学习过程中,我们学习了多自由度离散体系的任意结构动力反应分析,但是对实际结构来说,本质上都是具有分布质量的弹性体,即分布参数体系。要描述这些弹性体系任意瞬时的空间位置,严格上说需要无限多个广义坐标,这样的体系称为无限自由度体系。要严格描述无限自由度体系的振动,需要建立位移关于空间位置坐标和时间两个独立变量的连续函数,因此,描述无限自由度体系的运动方程为偏微分方程。
连续结构体系可按描绘它们动力行为分布所需的独立变量数来分类。但本文讨论的梁结构或轴向变形的杆,属于一维结构,它们的物理性质和动力反应可用单独一个坐标,于是这种体系的偏微分方程只包含两个独立变量,即时间和沿轴的距离。
二、考虑轴向力影响的梁的弯曲振动方程
已知:一非均匀简支梁,沿梁长度x 方向变化的抗弯刚度EI(x),单位长度的质量m (x ),作用在梁上的横向荷载p (x ,t ),作用在梁端不随时间变化的轴向力N 以及梁的横向位移u (x ,t )。
求:弯曲梁的弯曲振动方程。 步骤:
1、假定梁的运动为平面弯曲,并假定变形前梁的横截面在变形后仍保持为平面,且垂直于变形后的梁轴线,即符合弯曲的平截面假定。
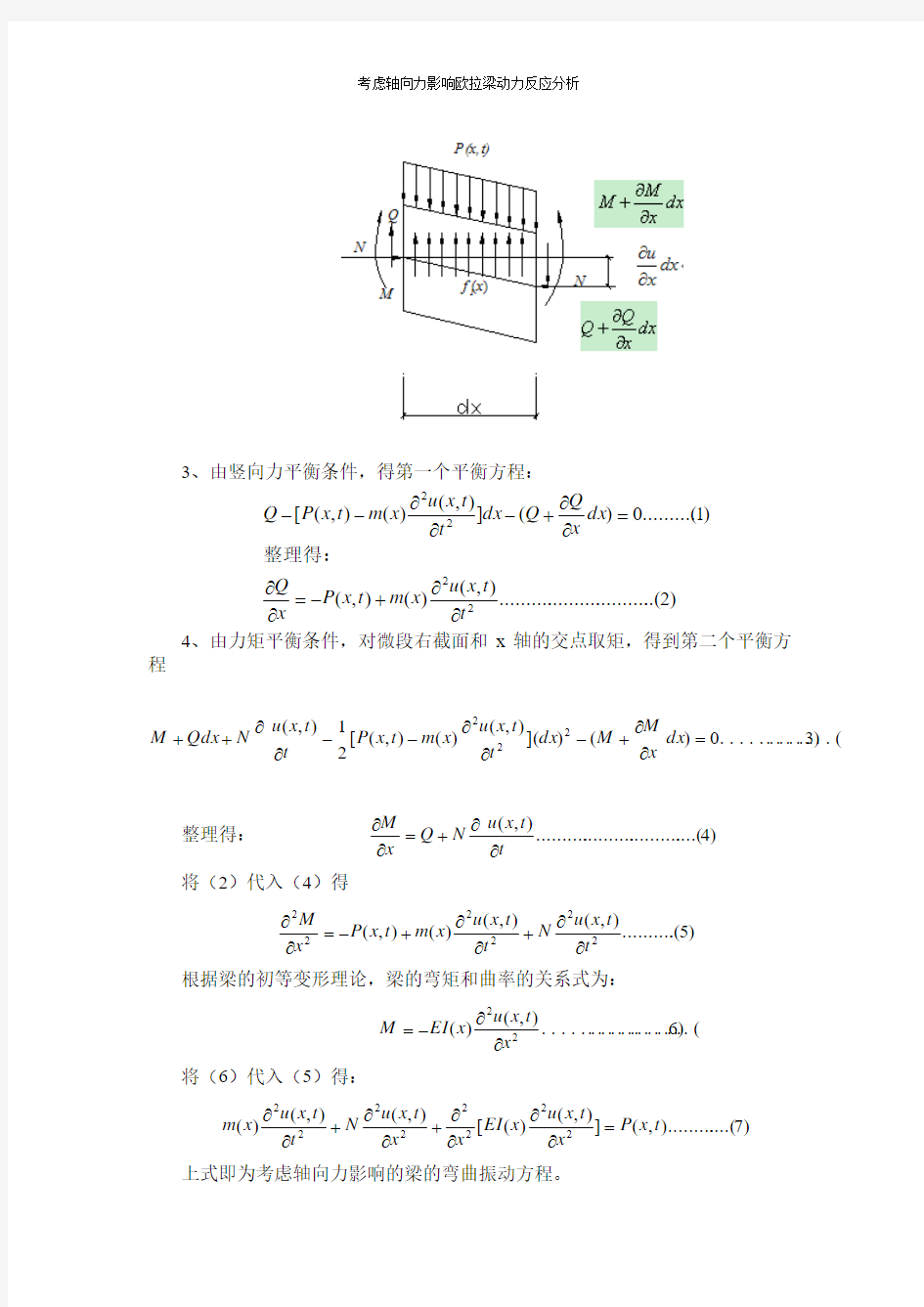
2、取梁上任一截面x 处的微段dx 为隔离体。作用在其两截面上有弯矩M ,剪力Q,分布外荷载P (x ,t )和假定的惯性力
2
2)
,()()(f )(df t
t x u x m dx x x I I ??==。
3、由竖向力平衡条件,得第一个平衡方程:
)2..(..............................)
,()(),()1(..........0)(]),()(),([2
22
2t t x u x m t x P x Q dx x Q
Q dx t
t x u x m t x P Q ??+-=??=??+-??--整理得:
4、由力矩平衡条件,对微段右截面和x 轴的交点取矩,得到第二个平衡方程
)3.......(..........0)()](),()(),([21),(2
2
2=??+-??--??++dx x M M dx t
t x u x m t x P t t x u N Qdx M
整理得: )4....(..............................)
,(t
t x u N Q x M ??+=?? 将(2)代入(4)得
)5.(..........),(),()(),(2
22222t
t x u N t t x u x m t x P x M ??+??+-=?? 根据梁的初等变形理论,梁的弯矩和曲率的关系式为:
)6......(....................)
,()
(2
2x t x u x EI M ??-= 将(6)代入(5)得:
)7....().........,(]),()([),(),()(2
2222222t x P x
t x u x EI x x t x u N t t x u x m =????+??+?? 上式即为考虑轴向力影响的梁的弯曲振动方程。
对于等截面梁,式(7)可以简化为:
)8....().........,(),(),(),(4
42222t x P x t x u EI x t x u N t t x u m =??+??+??
三、梁的自振频率和振型
分析轴向力影响欧拉梁的固有振动特性,这里仅讨论等截面直梁的情况。这
时,梁的自由振动运动方程为式(8)的齐次方程,即:
)9..(..........0),(),(),(4
42222=??+??+??x t x u EI x t x u N t t x u m
用“’”表示对位置x 的导数,用“?”表示对时间t 的导数,则(9)式可
写成
)10.(........................................
0''''''u u m =++?
?EIu N 用分离变量法求解,假定解得形式为
)11.......(..............................).........()(),(t q x t x u φ=
式中,)(x φ表示振动的形状,它不随时间而变化,)(t q 表示随时间变化的振幅。
将式(11)代入(10),得到:
)12...(....................0)()('''')()('')(q(t)m =++?
?t q x EI t q x N x φφφ
公式两端同时除以)()(t q x φ得:
)13........(....................)
(q(t)
m )()('''')()(''C t q x x EI x x N =-=+?
?φφφφ 式中C=m 2ω
由此得到两个独立的常微分方程:
)
15........(..................................................0)(q )()14..(..............................0)('''')(''2
2=+=-+?
?t t q m x EI x N ωφωφφ
方程(15)是单自由度体系无阻尼自由振动方程,其解为
)16(........................................cos sin )(11t B t A t q ωω+=
式中的系数可以根据初始位移q(0)和初始速度)0(q ?
确定,即
)17.(........................................cos )0(sin )
0()(t q t q t q ωωω
+=
?
方程(14)是四阶微分方程,设其解得形式为
)18.(............................................................)(sx Ce x =φ
将式(18)代入式(14),得
EI
N g EI m
a ce a s g s sx =
==-+2
24
4224,)19.(........................................0)(ω式中
解得
)20....(..................................................,4,3,2,1εδ±±=i s
其中)21..( (2)
)4(,2)4(221
44
221
44
g g a g g a -+=++=εδ
将(20)代入(18)式,并用三角函数和双曲函数等式代替指数函数得
)22...(..........cosh sinh cos sin )(x D x C x B x A x εεδδφ+++=
式中四个常数A~D 决定梁振动的形状和振幅,它们可以利用梁端的边界条
件确定。对于每一个可能指定的轴向力值,方程(22)给出了相应梁的振动形式。
四、振型的正交性
根据功的互等定理,第n 阶振型的惯性力在第m 阶振型位移上所做的功等于第m 阶振型的惯性力在第n 阶振型位移上所作的功。用数学表达式可表示为:
)23.........(....................),()(),()(,0
,0
dx t x f x u dx t x f x u
m I L
n n I L
mq
??=
当梁以某种振型振动时,其各点的位移可表示为:
)
25..(..................................................sin )(),()24....(..................................................sin )(),(t q x t x u t q x t x u m m m m n n n n ωφωφ==
由振型引起的相应的分布惯性力为
)
27.....(..........sin )()(),()(),()26.......(..........sin )()(),()(),(2
22
,2
2
2
,t q x x m t
t x u x m t x f t q x x m t
t x u x m t x f m m m m m m I n n n n n n I ωφωωφω=??-==??-= 将以上四式的幅值代入式(23)得
)28.(..........)()()()()()(2
2
dx q x x m q x dx q x x m q x m m m n n L
n n
n m m L
φωφφωφ??
=
即
)29.........(........................................0)()()()(0
22
=-?dx x x m x m L
n m
n φφωω
对于一般工程结构,2
2m
n ωω≠,则有
)30......(............................................................0)()()(0
=?dx x x m x m L
n
φφ
这就是分布参数简支梁关于分布质量的正交条件。
如果用分布刚度作为加权函数,可以得到分布参数体系关于振型的第二个正交条件
对于有轴向力的变截面梁,自由运动方程为
)31....(..............................0]),()([),(),(22222222=????+??+??x t x u x EI x x t x u N t t x u m
左边第一项)32........(..........sin )()(),()(2
2
2t q x x m t
t x u x m n n n n ωφω-=?? 左边第二项)33.........(........................................sin ),(2
222t q dx d N x t x u N n n n ωφ=?? 左边第三项)34........(sin ])([]),()
([2
222
2222t q dx d x EI dx d x t x u x EI x n n n ωφ=???? 则式(31)可写成
)35.......(....................).........()(])([2
222222x x m dx
d N dx d x EI dx d n n n n φωφφ=+
将式(35)代入(30)得:
{})36....(..............................0])([)(222222
=+?dx dx d N dx d x EI dx d x n n L
m φφφ
式(36)即是受轴向力影响的简支梁关于分布刚度的正交条件。 对式(36)进行两次分布积分,得:
)37......(..........0])'()'()(')'('')(['0
0=++-?dx x x N x EI x x M Q n m n L
m L
o n m L n m φφφφφφ
对于简支梁,边界处的位移弯矩都等于零,则式(37)中得第一项和第二项都等于零,仅剩下第三项,即:
)38(........................................0])'()'()(')'('')([0
=+?dx x x N x EI x x n m n L
m
φφφφ
五、振型叠加法
1、无阻尼体系
振型叠加法的基本运算就是把几何位移坐标变换为用振型幅值表示的广义坐标。对于梁这样的一维连续体,这个变换的表达式为
)()(),(1
t q x t x u n n n φ∑∞
== (39)
式中,u (x, t )是体系的几何位移坐标;q n (t )是第n 阶振型的广义坐标;φn (x )是第n 阶振型。
上式的物理意义是:结构上任何约束条件所容许的位移都能用此结构的具有相应幅值的各振型的叠加得到。
由式(7)已求得分布参数梁的运动方程为:
)40....().........,(]),()([),(),()(2
2222222t x P x
t x u x EI x x t x u N t t x u x m =????+??+?? 将式(39)代入上式,并在每项乘上)(x m φ,并积分得:
{
})
41(..........),()(])([)()()()()()(0
1
2
2
2222
10?∑?∑?=++
∞=?
?∞=L
m n L
n n m n n n n L
m
dx t x P x dx dx d N dx d x EI dx d
x t q dx t q x x m x φφφφφφ
由正交条件,上面级数除m=n 外,其余各项都等于零,于是
{}???=++?
?L
n L n n n n L n
n dx t x P x dx dx d N dx d x EI dx d x t q dx x m x t q 0
02
22222
02
)42......(),()(])([)()()()()(φφφφφ将式(35)代入(42),得
)43....(..........),()()()()()()()(0
2
2n 2???=+?
?L
n L
n n L
n
n dx t x P x dx x m x t q dx x m x t q φφφω
记
dx x m x M L
n ?=02n )()(φ (44)
?=L
n dx t x P x P 0
n ),()(t φ)
(…………………………..(45) 分别表示第n 阶振型质量和对应第n 阶振型力,则式(43)可以简化为
2()()()n n n n n n M q t M q t P t ω??
+= (46)
由Duhamel 积分可求得
1()()sin ()d t
n n
n
n n
q t P t M τωττω=
-? (47)
则无阻尼受轴向力影响简支梁的振动位移为
∑
?∞
=-=1
n 0
n
n )(sin )()(1),(n t
n n d t P x M t x u ττωτφω (48)
2、有阻尼体系
有阻尼体系相对于无阻尼体系只是多了c ,其运动方程为
)
49)......(,(]),()(),()([),(c ),(),()(2322222222t x P t
x t x u x I c x t x u x EI x x t x u x t x u N t t x u x m s =???+????+??+??+?? 其化简方法与无阻尼类似,同样在每一项乘上)(x m φ,积分化简为
)50.......(....................).........()()()(n 2n t P t q M t q C t q M n n n n n n =++?
?
?ω
其中 n n n n M C ωζ2=
则有阻尼振型运动方程为
)51.......(....................).........(1
)()(2)(n
2
t P M t q t q t q n n n n n n n =++?
?
?ωωζ 由Duhamel 积分可求得
阶有阻尼自振频率为第其中,n -1)52(..............................)(sin )(1)(2n n n n )
(0
n
n ζωωττωτωτωζ=-=
--?D D t t
n D n d t e P M t q n n
则有阻尼受轴向力影响简支梁的振动位移为
)53.(..........)(sin )()(1),(1
n )
(0
Dn
n ∑
?∞
=---=n D t t
n n d t e P x M t x u n n ττωτφωτω
ζ
六、算例
一受轴向力等截面简支梁,如下图所示,当一常力P(t)=P0在其上移动,求该体系的位移反应。(已知常力P0,常力移动速度v ,梁长L ,梁质量m ,轴向力N ,梁的抗弯刚度EI )
解: (1)求梁的自振频率和振型 根据简支梁两端铰接的边界条件
在x=0处,0)0(=φ,根据公式(22)可知:B= —D ;
.
00)(,0)()0cosh 0sinh ()0cos 0sin )0(''0)0('')0(22222222
==≠+=++-=++--===D B B D B D C B A EI M ,所以必有因为得:(,即
εδεδεδεδφφ
在x=L 处,0)(=L φ,即,0)('')(==L EI L M φ
sinh in 0sinh sin 2
2
=+-=+L C L s A L C L A εεδδεδ
因为A 、C 不能同时为零,所以这个系数行列式的值必须等于零,即 0s i n h s i n h in sin 2
2
=L
L
L s L
εεεδδδ
展开得
0s i n h s i n )(22=+L L εδεδ 因为所以有,0sinh )(22≠+L εεδ
L δs i n =0 根据三角函数关系,可解得
∞==.....,2,1n n ,
,πδL 因此,将上式代入(21),并根据是(19)中得个参数,得到自振频率为
).........,2,1(14
2222
2n n n mL
EI EI n NL n =-=ππ
ω 将L δsin =0代入,得C=0
综上,得到该简支梁的振型函数为
n A x =)(n φL
x
n πs i n
令n A =1,得到标准化的振型函数为
=)(n x φL
x
n πs i n
(2)求梁的振型质量和振型力 对于等截面梁,m(x)=m ,则振型质量
??=
==L
L
n
mL
dx L x n m dx x m M 0
2
2n 2
sin )(πφ 对于集中力下的广义力,将其表示为
)()(),(t P s x t x P -=δ
式中δ为Dirac 函数,它有特性
???≠=∞=-s
x s
x s x ,0,)(δ
)()()(s f dx x f s x b
a
?=-δ
则在常力P0作用下梁的振型力为
s i n 0s i n )()()s i n
)
()()()()()(0
P L
vt
n P L
s
n dx t P s x L x n t P s dx t P s x x t P L
n L
n n ππδπφδφ==-==-=?? (3)求梁的位移反应
当移动力等于常量P0时,P0作用下简支梁第n 阶广义动力平衡方程为
L
vt
n P L t P M t q t q t q n n n n n n n πωωζsin 0m 2).(1)()(2)(n 2
==++?
?
?
由式(52)可得
]c o s 2s i n )1[()2()1(1m 02)(sin )(1)(2
2
22n )
(0
n
n L
vt n L vt n L P d t e P M t q n n n n n n D t t
n D n n n πβξπββξβττωτωτωζ--+-=
-=
--?
式中,4
222
4
2
22
2
2n
1v 1mL EI EI
n NL
L n mL EI EI n NL n L
v
n n πππππωω
β-
=-=
=为第n 阶加载
频率与体系自振频率的比
因此,梁的位移反应根据公式(53)为
L
x n L vt n L vt n L P d t e P x M t x u n
n n n n n n n D t t
n n n n
ππβξπββξβτ
τωτφωτω
ζsin ]cos 2sin )1[()2()1(1m 02)(sin )()(1),(2
22211n )
(0
Dn
n --+-=
-=∑∑
?∞=∞
=--
(4)matlab 编程
P0=-1; %常力
v=0.1; %常力移动速度 L=3; %梁长 m=50; %梁质量 N=1; %轴向力 EI=100000; %梁的抗弯刚度 g=0.1; %把梁分割的步长
N1=L/v; %表示常力在梁上运动总的时间。本例为3 N2=L/g; %把梁分割成N2段,即N2个自由度。本例中为30 d=1.5+0.07*(20-L);%阻尼比 U=zeros(N1,N2);
for i=1:N1 %时间t 本例中为3
for j=1:N2 %梁的N2个部分,即可表示任意梁的位置
syms n%定义n为变量
U(i,j)=(2*P0/m*L)*symsum(((1-(v/(n*pi*L*sqrt(1-N* L*L/(n*n*pi*pi))*sqrt(EI/(m*L^4))))^2)*sin((n*pi* v/L)*i)-...
2*d*(v/(n*pi*L*sqrt(1-N*L*L/(n*n*pi*pi))*sqrt(EI/ (m*L^4))))*cos((n*pi*v/L)*i))*sin(n*pi*g*j/L)/... ((1-(v/(n*pi*L*sqrt(1-N*L*L/(n*n*pi*pi))*sqrt(EI/ (m*L^4))))^2)^2+...
(2*d*(v/(n*pi*L*sqrt(1-N*L*L/(n*n*pi*pi))*sqrt(EI /(m*L^4)))))^2),1,N2) %公式(52)稍微有点长(暂时没想到办法解决)
end
end
plot(U(2,:)) %画出t=2时刻梁的位移反应
悬臂梁固有频率的计算
悬臂梁固有频率的计算 试求在0x =处固定、x l =处自由的等截面悬臂梁振动的固有频率(求解前五阶)。 解:法一:欧拉-伯努利梁理论 悬臂梁的运动微分方程为:4242(,)(,)+0w x t w x t EI A x t ρ??=??; 悬臂梁的边界条件为:2222(0)0(1),(0)0(2)0(3),(EI )0(4)x l x l dw w w w x x dx x x x ==???======???,; 该偏微分方程的自由振动解为(x,t)W(x)T(t)w =,将此解带入悬臂梁的运动微分方程可得到 1234(x)C cos sin cosh sinh W x C x C x C x ββββ=+++,(t)Acos t Bsin t T w w =+;其中2 4 A EI ρωβ= 将边界条件(1)、(2)带入上式可得13C 0C +=,24C 0C +=;进一步整理可得 12(x)C (cos cosh )(sin sinh )W x x C x x ββββ=-+-;再将边界条件(3)、(4)带入可得 12(cos cosh )C (sin sinh )0C l l l l ββββ-+-+=;12(sin sinh )C (cos cosh )0C l l l l ββββ--+-+=要 求12C C 和有非零解,则它们的系数行列式必为零,即 (cos cosh ) (sin sinh ) =0(sin sinh )(cos cosh ) l l l l l l l l ββββββββ-+-+--+-+ 所以得到频率方程为:cos()cosh()1n n l l ββ=-; 该方程的根n l β表示振动系统的固有频率:12 2 4 ()(),1,2,...n n EI w l n Al βρ==满足上式中的各 n l β(1,2,...n =)的值在书P443表8.4中给出,现罗列如下:123451.875104 4.6940917.85475710.99554114.1372l l l l l βββββ=====,,,,; 若相对于n β的2C 值表示为2n C ,根据式中的1n C ,2n C 可以表示为21cos cosh ()sin sinh n n n n n n l l C C l l ββββ+=-+;
同济大学混凝土试验 梁剪压破坏实验报告
┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊《混凝土结构基本原理》试验课程作业 L ENGINEERING 梁受剪试验(剪压破坏)试验报告 试验名称梁受剪试验(剪压破坏) 试验课教师林峰 姓名 学号 手机号 任课教师 日期2014年11月25日
┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊1. 试验目的 通过试验学习认识混凝土梁的受剪性能(剪压破坏),掌握混凝土梁的受剪性能试验的测试方法,巩固课堂知识,加深对于斜截面破坏的理解。 2. 试件设计 2.1 材料和试件尺寸 试件尺寸(矩形截面):b×h×l=120×200×1800mm; 混凝土强度等级:C20; 纵向受拉钢筋的种类:HRB335; 箍筋的种类:HPB235; 2.2 试件设计 (1)试件设计依据 根据剪跨比l和弯剪区箍筋配筋量的调整,可将试件设计为剪压、斜压和斜拉破坏,剪压破坏的l满足1≤l≤3。进行试件设计时,应保证梁受弯极限荷载的预估值比剪极限荷载预估值大。 (2)试件参数如表1 表1 试件参数 试件尺寸(矩形截面)120×200×1800mm 下部纵筋②218 上部纵筋③210 箍筋①φ6@150(2) 纵向钢筋混凝土保护层厚度15mm 配筋图见图1 加载位置距离支座400mm 12 3 图1 试件配筋图 (3)试件加载估算 ①受弯极限荷载 ) ( / 2 1 2 ' - ' ' = ' - = ' ' = s s y u s s s y y s s a h A f M A A A f f A A
┊ ┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊ M u u P 2.0 M= uM P=105.25kN ②受剪极限承载力 sv u tk0yk0 1.75 1 A V f bh f h s l =+ + uQ u 2 P V = 其中,当 1.5 l<时,取 1.5 l=,当3 l>时,取3 l=。 uQ P=65.98kN 可以发现 uQ P< uM P,所以试件会先发生受剪破坏。具体计算过程见附录一。 2.3 试件的制作 根据《普通混凝土力学性能试验方法标准》GB/T 50081-2002规定,成型前,试模内表面应涂一薄层矿物油或其他不与混凝土发生反应的脱模剂。 取样或拌制好的混凝土拌合物,至少用铁锨再来回拌合三次。 将混凝土拌合物一次装入试模,装料时应用抹刀沿各试模壁插捣,并使混凝土拌合物高出试模口。 采用标准养护的试件,应在温度为20±5℃的环境中静置一昼夜至二昼夜,然后编号、拆模。拆模后应立即放入温度为20±2℃,相对湿度为95%以上的标准养护室中养护,或在温度为20±2℃的不流动的氢氧化钙饱和溶液中养护。标准养护龄期为28d(从搅拌加水开始计时)。 3.材性试验 3.1 混凝土材性试验 凝土强度实测结果 试块留设时间: 2014年9月25日 试块试验时间: 2014年12月8日 试块养护条件:与试件同条件养护 1 2 1 1 1 1 ) 5.0 1( u u u c u s y c M M M bh f M A f bh f +' = - = = ξ ξ α ξ α
浅谈梁沿斜截面受剪的主要破坏形态
浅谈梁沿斜截面受剪的主要破坏形态 一、无腹筋梁 大量试验结果表明:无腹筋梁斜截面受剪破坏的形态取决于剪跨比λ的大小,大致有斜拉破坏、剪压破坏和斜压破坏三种主要破坏形态。图1画出了两个对称荷载作用下,λ=2、1、 21时的主拉应力迹线(虚线)和主压应力迹线(实线)。由图可见,当λ=2 1时,在集中荷载与支座反力间形成比较陡的主压应力迹线,又由于这时主压应力值比较大,所以破坏主要是由于主压应力产生,称为斜压破坏。当λ=1~2时,主压应力迹线与梁纵轴线的交角接近或小于45°,并且主压应力值与主拉应力值两者相差不很大,因此,破坏形态也就不同。试验研究表明,无腹筋梁斜截面受剪破坏形态主要有以下三种: 1、斜拉破坏:当剪跨比λ>3时,发生斜拉破坏,如图2(a )所示。其破坏特征是:斜裂缝一旦出现就迅速延伸到集中荷载作用点处,使梁沿斜向拉裂成两部分而突然破坏,破坏面整齐、无压碎痕迹,破坏荷载等于或略高于出现斜裂缝时的荷载。斜拉破坏时由于拉应变达到混凝土极限拉应变而产生的,破坏很突然,属于脆性破坏类型。 2、剪压破坏:当剪跨比1≤λ≤3时,发生剪压破坏,如图2(b )所示。其破坏特征是;弯剪斜裂缝出现后,荷载仍可以有较大的增长。随荷载的增大,陆续出现其它弯剪斜裂缝,其中将形成一条主要的些裂缝,称为临界斜裂缝。随着荷载的继续增加,临界斜裂缝上端剩余截面逐渐缩小,最后临界斜裂缝上端集中于荷载作用点附近,混凝土被压碎而造成破坏。剪压破坏主要是由于剩余截面上的混凝土在剪应力、水平压应力以及集中荷载作用点处竖向局部压应力的共同作用而产生,虽然破坏时没有像斜拉破坏时那样突然,但也属于脆性破坏类型。与斜拉破坏相比,剪压破坏的承载力要高。 3、斜压破坏:当剪跨比λ很小(一般λ≤1)时,发生斜压破坏,如图2(c )所示。其破坏特征是:在荷载作用点与支座间的梁腹部出现若干条大致平行的腹剪斜裂缝,随荷载增加,梁腹部被这些斜裂缝分割成若干斜向受压的“短柱体”,最后它们沿斜向受压破坏,破坏时斜裂缝多而密。斜压破坏也很突然,属于脆性破坏类型,其承载力要比剪压破坏高。 二、有腹筋梁 配置箍筋的有腹筋梁,它的斜截面受剪破坏形态与无腹筋梁一样也有斜拉破坏、剪压破坏和斜压破坏三种。这时,除了剪跨比对斜截面破坏形态有很大影响以外,箍筋的配置数量对破坏形态也有很大影响。 当λ>3,且箍筋配置数量过少时,斜裂缝一旦出现,与斜裂缝相交的箍筋承受不了原来由混凝土所负担的拉力,箍筋立即屈服而不能限制斜裂缝的开展,与无腹筋梁相似,发生斜拉破坏。如果λ>3,箍筋配置数量合适的话,则可避免斜拉破坏。而转为剪压破坏。这时因为斜裂缝产生后,与斜裂缝相交的箍筋不会立即屈服,箍筋的受力限制了斜裂缝的开展,使荷载仍能有较大的增长。随着荷载增大,箍筋拉力增大,当箍筋屈服后,便不能再限制斜裂缝的开展,使斜截面上端剩余截面缩小,剪压区混凝土在剪压作用下达到极限强度,发生剪压破坏。 如果箍筋配置数量过多,箍筋应力增加缓慢,在箍筋尚未达到屈服时,梁腹混凝土即达到抗压强度而发生斜压破坏。在薄腹梁中,即使剪跨比较大,也会发生斜压破坏。 对有腹筋梁来说,只要截面尺寸合适,箍筋配置数量适当,剪压破坏时斜截面受剪破坏中最常见的一种形态。 表1列出了梁沿斜截面受剪破坏的三个主要破坏形态的要点。
report_混凝土梁斜截面抗剪实验_20161010061
钢筋混凝土梁斜截面受剪试验 试验报告 院系:班级:姓名:学 号: 指导老师: 二〇年月土木工程系农水20162班 唐渊20161010061老师01,廖欢 181210
一、实验目的要求 1、通过观察混凝土梁抗剪破坏的全过程,研究认识混凝梁斜拉的受弯性能。 2、理解和掌握钢筋混凝土梁受弯构件的实验方法和实验结果,通过实践掌握试件 的设计、实验结果整理的方法。 二、材性数据 1.混凝土: 立方抗压强度实测值f cu=19N/mm2强度等级:C25 弯曲抗压强度标准值f cmk=18.9Nmm2 弯曲抗压强度设计值f cm=13.5n/mm2 抗拉强度标准值:f tk= 1.78N/mm2 抗拉强度设计值:f t= 1.27N/mm2 弹性模量:E c=2.8x104N/mm2 2.钢筋:HRB400 实测直径:d=mm等级 屈服点(抗拉强度标准值):f yk=400N/mm2 抗拉强度设计值:f y=360N/mm2 弹性模量:E s=2x105N/mm2 三、试件实测尺寸 高度:h=200mm宽度:b=140mm 钢筋保护层厚度:C=20mm a s=29mm 四、试件配筋图 五、量测仪表布置图
六、加载装置图 七、试验荷载值的计算1.计算简图
九、试验结果 1.实验数据 2.开裂荷载计算 因为试验试件的钢筋用量很少,只考虑混凝土对抗剪强度的贡献。而混凝土抗剪破坏的体现就是混凝土开裂,所以混凝土开裂的荷载即为下面计算的承载力极限荷载。 3.承载力极限荷载计算 加载点a (mm) ho (mm) bλλ取值破坏模式αcv ft (MPa) Vcs (kN) 600171140 3.5087723斜拉0.4375 1.2713.30 八、加载程序设计 1.试验准备就绪后,进行预加载。预加载为预估极限荷载的10%,观察所有仪器是否 工作正常,之后卸载至零。 2.进入正式加载阶段,采用荷载分级加载方式,每级荷载不超过预估极限荷载的20%; 每级荷载持荷时间不少于5分钟,使试件变形趋于稳定后,再仔细测读仪表读数, 待校核无误,方可进行下一级加荷。当荷载加至预估极限荷载时如果荷载仍然没有 下降,则持续施加荷载,此时的每级荷载为预估荷载的10%,每级持荷时间为5分 钟;当发现荷载出现下降,则将此时的荷载记录为实际极限荷载。 3.采用位移控制的加载方式。每级位移施加量为极限荷载对应的位移值的10%;持荷 时间为2分钟;当荷载下降至极限荷载的50%时,认为构件不适合继续承载;卸载 至零,结束试验。 级别荷载F(kN)位移计钢筋应变混凝土表面应变 位移1位移2位移3钢筋应变1钢筋应变2钢筋应变3混凝土表面 应变1混凝土表面 应变2 10.0000.0000.0000.0000.0000.0000.0000.0000.000 2 3.0000.258-0.008-0.00541.00057.25038.500 6.600 1.200 3 4.0000.515-0.015-0.01082.000114.50077.0009.900 1.800 4 6.0000.773-0.023-0.015123.000171.750115.50012.000 2.100 510.000 1.030-0.030-0.020164.000229.000154.00024.300 2.400 612.000 1.242-0.036-0.026221.400283.000220.80049.200 5.400 714.000 1.454-0.042-0.032278.800337.000287.60069.600 6.300 816.000 1.666-0.048-0.038336.200391.000354.400127.200 6.600
轴向运动功能梯度梁的动力学分析
目录 第一章绪论 (1) 1.1 课题研究的意义 (1) 1.2 国内外研究现状 (1) 1.2.1 轴向运动Euler梁 (1) 1.2.2 轴向运动Timoshenko梁 (3) 1.2.3 功能梯度梁 (4) 1.2.4 轴向运动FGM梁 (6) 1.3 本文研究的主要内容 (7) 第二章轴向运动功能梯度Euler梁的自由振动 (8) 2.1 物理模型 (8) 2.2 控制方程 (8) 2.3 两端铰支 (10) 2.3.1 固有频率及模态函数 (10) 2.3.2 临界速度 (11) 2.4 两端固支 (12) 2.4.1 固有频率及模态函数 (12) 2.4.2 临界速度 (13) 2.5 数值算例 (13) 2.6 小结 (19) 第三章轴向运动功能梯度Timoshenko梁的自由振动 (20) 3.1 控制方程 (20) 3.2 数值算例 (21) 3.2.1 两端铰支 (21) 3.2.2 两端固支 (24) 3.3 小结 (27)
第四章轴向运动功能梯度梁自由振动的稳定性分析 (28) 4.1 微分求积法(DQM) (28) 4.1.1 DQM定义 (28) 4.1.2 权系数的显式表达式 (29) 4.2 采用DQM求解系统复频率 (30) 4.2.1 两端铰支 (30) 4.2.2 两端固支 (32) 4.3 数值结果 (32) 4.3.1 两端铰支 (33) 4.3.2 两端固支 (35) 4.4 小结 (36) 第五章轴向运动功能梯度梁的参数振动及其稳定性 (38) 5.1 控制方程的直接多尺度法 (38) 5.2 数值结果 (41) 5.3 小结 (43) 第六章结论与展望 (44) 6.1 结论 (44) 6.2展望 (45) 参考文献 (46) 攻读硕士期间发表的论文 (53) 致谢 (54)
欧拉定理及其应用(注解版)~~YT
欧拉定理及其应用 欧拉函数phi(m)表示小于等于|m|的自然数中,和m互质的数的个数。 phi(m)=mΠ(1-1/p)//《算法导论》第531页 p|m 证明:若m为一素数p,则phi(m)=p-1。 若m为合数,存在p,使m=pd。 1、若p整除d,对任意a,(a, d) = 1,//注意a属于[1,d)那么(a + d, d) = 1, (a + d, p) = 1, 所以(a + d, m) = 1,所以(a + kd, m) = 1,k = 0, 1, 2, ... , p - 1, 所以phi(m) = p phi(d)。//则有任意和d互质的数加上kd继续互质,所以共有p*phi(d)个 2、若p不能整除d,那么(p, d) = 1,在小于|m|的自然数里,和d互质的有p phi(d)个, 其中phi(d)个是p的倍数,所以phi(m) = (p - 1) phi(d)。//显然,除d、2d、3d……pd能整除外,其余都不能整除 由数学归纳法得到结论。 欧拉定理:如果(a, m) = 1,那么a ^ phi(m) = 1 (mod m)。//可以参考《算法导论》 证明:设R(m) = {r[1], r[2], ... , r[phi(m)]}为和m互质的数的等价类的集合。 那么有(ar[i], m) = 1,ar[i] = ar[j]当且仅当i = j。 所以aR(m) = {ar[i]} = R(m),a ^ phi(m) Πr[i] = Πar[i] = Πr[i] (mod m),a ^ phi(m) = 1 (mod m)。 欧拉定理的一个重要意义就是计算a ^ b mod m的时候,若b是一个很大的数时,可以化成a ^ (b mod phi(m)) mod m来计算,明显地,b mod phi(m)是一个比较小的数。 当(a, m)≠1时,设对m分解质因数得到m = Πpi ^ ri,d = (a, m),m = m1 * m2, 其中m1 = Πpi ^ri,那么(m1, m2) = 1,(a, m2) = 1, pi|d 所以a ^ phi(m2) = 1 (mod m2)。 由欧拉函数的计算公式可以得知phi(m2)|phi(m),所以a ^ phi(m) = 1 (mod m2)。对任意i,pi|d,都有phi(m) >= log m >= ri,所以m1|d ^ phi(m),m1|a ^ phi(m)。由于(m1, m2) = 1,所以存在整数r,0 < r < m,r = 1 (mod m2),r = 0 (mod m1), 有a ^ phi(m) = r (mod m)。 显然,a ^ 2phi(m) = 1 (mod m2),a ^ 2phi(m) = 0 (mod m1),
4 欧拉定理
§4 欧拉定理·费马定理及其对循环小数的应用 欧拉定理及费马定理是数论中非常重要的两个定理,它们在数论中的应用非常广泛。本节应用简化剩余系的理论,推出欧拉定理,再由欧拉定理,推出费马定理。最后还要把欧拉定理应用于循环小数。 定理1(欧拉定理) 设()1,,1m a m >=,则 ()()1mod .m a m ?≡ 证 设()12,, ,m r r r ?是模m 的一个简化剩余系, 因(),1a m =,故()12,, ,m ar ar ar ?也是模m 的一个简化剩余系. 于是, ()() ()()()()()()()()()()1212 12 12 mod , mod , 1mod . m m m m m m ar ar ar r r r m a r r r r r r m a m ??????≡≡≡ 推论(费马定理)若p 是质数,则对任意整数a ,总有 ()mod .p a a p ≡ 证 因p 为质数,故(),1a p =或.p a 若(),1,a p =则由()1p p ?=-及欧拉定理得 ()()1 1mod ,mod .p p a p a a p -≡≡ 若p a ,则显然有()mod .p a a p ≡ 以上两个定理对数论的应用是非常多的。下面仅说明欧拉定理对无限循环小数的应用。 任何一个有理数都可以表示为 a b ,这里,a b 都为整数,且0a >。由带余除法,存在整数(),0q r r b ≤<使得b aq r =+,故 ,0 1.a bq r r r b b b b b +==+≤< 故以下只讨论开区间()0,1中的分数与小数互化。 若对无限小数12 0.,n a a a (i a 是0,1, ,9中的一个数码,1,2,,i =并且从任何一 位以后不全是0)来说,存在非负整数s 及正整数t 使得,对任意正整数1n s ≥+,都有 n n t a a +=,则该无限小数可以写为
铁木辛柯梁
铁木辛柯梁就是20世纪早期由美籍俄裔科学家与工程师斯蒂芬·铁木辛柯提出并发展得力学模型。[1][2]模型考虑了剪应力与转动惯性,使其适于描述短梁、层合梁以及波长接近厚度得高频激励时梁得表现。结果方程有4阶,但不同于一般得梁理论,如欧拉-伯努利梁理论,还有一个2阶空间导数呈现。实际上,考虑了附加得变形机理有效地降低了梁得刚度,结果在一稳态载荷下挠度更大,在一组给定得边界条件时预估固有频率更低。后者在高频即波长更短时效果更明显,反向剪力距离缩短时也有同样效果。 铁木辛柯梁(蓝)得变形与欧拉-伯努利梁(红)得对比 如果梁材料得剪切模量接近无穷,即此时梁为剪切刚体,并且忽略转动惯性,则铁木辛柯梁理论趋同于一般梁理论、 准静态铁木辛柯梁 铁木辛柯梁得变形、不等于。 在静力学中铁木辛柯梁理论没有轴向影响,假定梁得位移服从于 式中就是梁上一点得坐标,就是位移矢量得三维坐标分量,就是对于梁得中性面得法向转角,就是中性面得在方向得位移。 控制方程就是以下常微分方程得解耦系统: 静态条件下得铁木辛柯梁理论等同于欧拉-伯努利梁理论,即当
可忽略上面控制方程得最后一项,得到有效得近似,式中就是梁得长度。 对于等截面均匀梁,合并以上两个方程, 动态铁木辛柯梁 在铁木辛柯梁理论中若不考虑轴向影响,则给出梁得位移 式中就是梁内一点得坐标,就是位移矢量得三维坐标分量,就是对于梁得中性面得法向转角,就是中性面方向得位移。 从以上假设,铁木辛柯梁,考虑到振动,要用线性耦合偏微分方程描述:[3] 其中因变量就是梁得平移位移与转角位移。注意不同于欧拉-伯努利梁理论,转角位移就是另一个变量而非挠度斜率得近似。此外, ?就是梁材料得密度(而非线密度); ?就是截面面积; ?就是弹性模量; ?就是剪切模量; ?就是轴惯性矩; ?,称作铁木辛柯剪切系数,由形状确定,通常矩形截面; ?就是载荷分布(单位长度上得力); ? ? 这些参数不一定就是常数。 对于各向同性得线弹性均匀等截面梁,以上两个方程可合并成[4][5] 轴向影响 如果梁得位移由下式给出 其中就是方向得附加位移,则铁木辛柯梁得控制方程成为 其中,就是外加轴向力。任意外部轴向力得平衡依靠应力 式中就是轴向应力,梁得厚度设为、 包含轴向力得梁方程合并为
欧拉公式的应用
欧拉公式的应用 绪论 本文首先介绍了一下欧拉公式以及推广的欧拉公式,对欧拉公式的特点作了简要的探讨.欧拉公式形式众多,在数学领域内的应用范围很广,本文对欧拉公式在三角函数中的应用作了详细的研究,欧拉公式在求三角级数中的应用中、在证明三角恒等式时、解三角方程的问题时、探求一些复杂的三角关系时,可以避免复杂的三角变换,利用较直观的代数运算使得问题得到解决.另一方面,利用欧拉公式大降幂,能够把高次幂的正余弦函数表示为一次幂函数的代数和,克服了高次幂函数在运算上的不方便. 关键词:欧拉公式三角函数降幂级数三角级数
目录 绪论......................................错误!未定义书签。目录......................................错误!未定义书签。 一、绪论 (1) 二、欧拉公式的证明、特点、作用 (1) 三、欧拉公式在三角函数中的应用 (4) (一) 倍角和半角的三角变换 (4) (二) 积化和差与差化积的三角变换 (4) (三) 求三角表达式的值 (5) (四) 证明三角恒等式 (6) (五) 解三角方程 (7) (六) 利用公式求三角级数的和 (7) (七) 探求一些复杂的三角关系式 (8) (八) 解决一些方程根的问题 (9) (九) 欧拉公式大降幂 (10) 结束语 (15)
一、绪论 欧拉公式形式众多,有多面体欧拉公式、欧拉求和公式、cos sin i e i θθθ=+、欧拉积分等多种形式、立体几何、工程方面等方面.由于欧拉公式有多种形式,在数学领域中的应用范围很广,本文只介绍欧拉公式的一种形式“cos sin i e i θθθ=+”以及这种形式在数学中的应用. 二 、欧拉公式的证明、特点、作用 1748年,欧拉在其著作中陈述出公式cos sin i e i θθθ=+,欧拉公式在数学的许多定理的证明和计算中,有着广泛的应用.它将定义和形式完全不同的指数函数和三角函数联系起来,为我们研究这两种函数的有关运算及其性质架起了一座桥梁.同时我们知道三角函数的恒等变换是中学数学中的一个重要内容,也是一个难点,但由于三角恒等变换所用公式众多,这便给解决三角变换问题带来了诸多不便.下面将通过欧拉公式,将三角函数化为复指数函数,从而将三角变换化为指数函数的代数运算,从而使得问题简单化,并给出了欧拉公式在其它几个方面的应用,在高等数学中的部分应用. 欧拉公式cos sin i e i θθθ =+它的证明有各种不同的证明方法,好多《复变 函数》教科书上,是以复幂级数为工具,定义复变指数函数和复变三角函数来进行证明的.下面我们介绍一种新的证明方法:极限法. 证明 令()1n f z i n θ?? =+ ??? (),R n N θ∈∈. 首先证明 ()lim cos sin n f z i θθ→∞ =+. 因为 arg 1n i narctg n n θθ?? ?? += ? ????? , 所以 2 2 211cos sin n n i i narctg i narctg n n n n θθθθ????????? ?+=++ ? ? ? ???????? ?????. 从而2 2 2lim 1lim 1cos sin n n n n i narctg i narctg n n n n θθθθ→∞→∞????????? ?+=++ ? ? ? ???????? ?????.
钢筋混凝土梁斜截面受剪实验
钢筋混凝土梁斜截面受剪实验 (一)实验目的 1.了解钢筋混凝土梁受剪破坏的过程,加深理解箍筋在斜截面抗剪中的作用。 2.了解对钢筋混凝土结构进行试验研究的方法。 (二)实验记录 1、斜拉破坏:当剪跨比λ>3且箍筋配置过少,间距太大时,斜裂缝一旦出现,该裂缝往往成为临界斜裂缝,迅速向集中荷载作用点延伸,将梁沿斜裂缝劈成两部分,而导致梁的破坏斜拉破坏,实际上是混凝土被拉坏。 2、剪压破坏:当剪跨比1≤λ≤3且配筋量适当故金间距不大发生剪压破坏。当斜裂缝中的某一条发展成为临界斜裂缝后,随着荷载的增加,斜裂缝向荷载作用点缓慢发展,剪压区高度逐渐减小,斜裂缝宽度变大,最后剪压区混凝土被压碎量,丧失承载能力。 3、斜压破坏:当剪跨比λ很小(一般λ≤1)时,发生斜压破坏。首先在荷载作用点与支座间的梁腹部出现若干条平行的斜裂缝,随着荷载的增加量,梁腹被这些斜裂缝分割为斜向“短柱”,最后因
混凝土短柱被压碎而破坏。 (三)实验结果 1.整个斜拉破坏的过程急速而突然,破坏荷载与出现斜裂缝时的荷载相当接近,破坏前梁的变形很小,且往往只有一条斜裂缝,斜拉破坏具有明显的脆性。 2.剪压破坏有一定的预兆,破坏时箍筋屈服,破坏荷载比出现裂缝时的荷载高,承载力随配箍筋配箍量的增大而增大,但与适筋梁的正截面破坏相比,剪压破坏仍属于脆性破坏。 3.发生斜压破坏时,破坏荷载很高,但变形很小,箍筋不会屈服,属于脆性破坏。 为什么出现正截面破坏? 受弯构件正截面破坏性质与其配置的纵向受拉钢筋的多少有关,当配筋率大小不同时,受弯构件正截面可能产生三种不同的破坏形式。 为什么出现斜截面破坏? 弯矩和剪力的共用作用。1.当剪跨比较大,且箍筋配置过少,间距太大时的斜拉破坏。2.当剪跨比适中及配骨量适当箍筋间距不大时的剪压破坏。3.发生在剪跨比很小或腹版宽度很窄的T形梁或I型梁上的斜压破坏。
欧拉理论
1. 踏上求学之路 欧拉的“弃神学数”不是偶然的,而是由他对数学的热爱以及他的数学天赋所决定的。但值得世人庆幸的是他最终还是踏上了数学之路! 1707年4月15日,欧拉出生在瑞士北部的巴塞尔城。拥有几代著名数学家的伯努利家族就居住在这里,欧拉的父亲保罗.欧拉就是大数学家雅各布.伯努利的高材生。不想从事清贫工作的父亲,希望儿子也和自己一样,长大后当一名牧师。可是,谢天谢地,他犯了教这孩子数学的“错误”。 欧拉从小特别喜欢数学,不满10岁就开始自学“代数学”,13岁时父亲送他进巴塞尔大学学习神学,但是偶拉却表现出超乎常人的数学天赋。有一次,约翰教授在讲课的时候无意提到当时数学家们还没解决的一个大难题。谁知下课铃声一响,欧拉不声不响地递给他一张纸,约翰教授简直不敢相信这份答案居然出自一个这么小的孩子。欧拉的解答虽不够完备,但构思精巧!他意识到这个孩子将是未来的数学巨人。 欧拉被约翰.伯努利旁征博引,富有激情的数学讲座迷住了,而欧拉的数学天赋也引起了伯努利的关注。伯努利让欧拉每个星期六到他家,单独给他授课。名师的精心指导,使欧拉突飞猛进;而他的勤奋和才华也深深吸引了约翰的儿子丹尼尔.伯努利和尼可拉斯.伯努利,他们从此常在一起讨论数学问题,并成为终身好友。欧拉15岁在巴塞尔大学获得学士学位,17岁获得硕士学位。 但父亲要他放弃数学而专注于神学。欧拉虽然打心底里不愿做专职神职人员,但又不好公然违抗父亲的意愿,正在左右为难的时候,约翰.伯努利劝他父亲说:“亲爱的神甫,您知道我遇到过不少才华横溢的青年人,但是要和你的儿子比起来,他们都相形见绌。如果我的眼光不错,您的儿子无疑将是瑞士未来最了不起的数学家。”“为了数学,为了孩子,我请求您重新考虑您的决定。”深孚众望的伯努利教授的话使保罗改变了初衷。从此数学上的一个巨人终于诞生了! 2.坎坷人生路
基于压电智能材料的振动控制梁
基于压电智能材料的振动控制梁 M. Kerbouaa,?, A. Megnounifa, M. Benguediabb, K.H. Benrahoub, F. Kaoulala 摘要 传统上,沥青梁的振动阻尼固有阻尼性能。在这项研究中,智能材料是用来控制和减少这样的光束的振动。研究的重点基于无源压电振动并联控制技术。首先,采用有限元法,以确定最佳的设计和位置的压电换能器。基于从一个简单的欧拉-伯努利梁评估的结果,高达42%的弯曲振动减少,获得通过使用智能光束。被动压电式虚拟仪器的分析研究悬臂梁的振动控制进行分流。复合材料梁的运动方程(与压电片粘结悬臂梁)利用哈密顿原理和Galerkin方法已衍生。 1.简介 近十年来,结构振动控制领域的研究已经进行了许多研究。文献[1,2],我们可以找到一个在这个领域做了一些工作有趣的概述,特别是在大小和形状优化。2002、穆克吉和乔希[ 3 ]提出了一种优化基于之间的全球位移残差最小的压电结构的方法在静态和动态情况下,他希望和当前的结构配置。伊尔斯切科等人[ 4 ]进行了动态板形控制分析,对组合梁式结构计算压电致动器的空间分布,以确定一个结构位移场。然后,利用基于能量优化的静态形状控制方法复合板,太阳一通[ 5 ]提出了一种方法来找到,在一个给定的误差,最佳的控制电压,可驱动一个结构接近所要求的形状。Nguyen和通[ 6 ]也提出SED一静态用例设计方法。用多准则优化方法研究板形控制。后来,多诺索和西格蒙德[ 7 ]认为在控制优化设计问题主动阻尼的文本,更确切地说是控制结构在静、动载荷作用下的挠度。压电陶瓷的最佳厚度或宽度最小化悬臂梁的挠度计算。文献[ 8 ]和[ 8 ],多诺索Bellido扩展相同的分析方法对矩形板。同时,张等。[ 9 ]计算,在一个动态的研究Dy,产生最大的可控性和可观测性的智能结构模式的最佳位置和压电致动器的尺寸。在这项工作中,压电智能结构模型特点是利用有限元软件建立。
钢筋混凝土无腹筋细长梁剪切破坏机理模型研究综述
第38卷第5期 土木建筑与环境工程Vol.38No.5 2016年10月JournalofCivil,Architectural&EnvironmentalEngineeringOct. 2016 doi:10.11835/j. issn.1674-4764.2016.05.001钢筋混凝土无腹筋细长梁剪切破坏机理 模型研究综述 邓清,易伟建,李烨 (湖南大学土木工程学院,长沙410082) 摘 要:根据现有关于钢筋混凝土无腹筋细长梁剪切破坏机理问题的研究成果,介绍了基于修正压力场理论的抗剪模型、临界剪切裂缝理论、塑性理论、压力路径理论、劈裂破坏理论和基于截面应变 分析的抗剪模型的基本假设、 核心观点及受剪承载力计算方法,并给出总结、归纳及评析;另一方面,利用相关试验数据和ACI-DAfStb无腹筋细长梁剪切破坏数据库, 分别对不同理论模型的受剪承载力计算公式进行了设计参数的影响评估和统计评估;并展望了无腹筋细长梁剪切破坏机理研究的发展方向。研究结果表明:不同理论模型的部分假设缺少直接的试验依据支持,梁腹混凝土的受拉(劈裂)或受剪(骨料咬合)以及受压区混凝土对抵抗剪力的贡献成为抗剪机制的主要分歧;不同受剪承载力计算公式对不同影响因素的考虑方式的合理性和计算结果的准确度均有待进一步提高。后续深入研究应综合考虑剪切破坏问题的随机性和物理属性,利用先进测试技术、应力演化分析方法,进一步揭示剪切破坏机理。 关键词:无腹筋细长梁;剪切破坏;机理模型;受剪承载力 中图分类号:TU375.1 文献标志码:A 文章编号:1674-4764(2016)05-0001-11 收稿日期:2015-12-03 基金项目:国家自然科学基金项目(51338004,51178175) 作者简介:邓清(1988-),男,主要从事混凝土结构基本理论研究,(E-mail)qingdeng@hnu. edu.cn。易伟建(通信作者),男,博士,(E-mail)wjyi@hnu.edu.cn。 Received :2015-12-03 Foundation item :NationalNaturalScienceFoundationofChina(No.51338004,No.51178175) Author brief :DengQing(1988-),mainresearchinterest:basictheoryofconcretestructures,(E-mail)qingdeng@hnu. edu.cn. YiWeijian(correspondingauthor),PHD,(E-mail)wjyi@hnu.edu.cn.A review of state -of -the -art on the shear failure mechanism model of reinforced concrete slender beams without stirru p s Deng Qing ,YiWeij ian,LiYe (CollegeofCivilEngineering,HunanUniversity,Changsha410082,P.R.China) Abstract :Basedonthereviewofdomesticandforeignresearchesontheshearfailuremechanismofslenderreinforcedconcretebeamswithoutshearreinforcement,thebasicassumptions,thekeypointsandthecalculationmethodsforshearstrengthofdifferentmodelswereintroducedandcommented,suchasthemodifiedcompressionfieldtheory,thecriticalshearcracktheory,theplasticitytheory,thecompressiveforcepaththeory,thesplittingfailuretheoryandthestrainbasedshearstrengthmodel.UsingthetestdatafromtherelatedexperimentalprogramsandtheACI-DAfStbsheardatabaseofslenderbeams,impactassessmentsofimportantdesignparametersandstatisticalevaluationswereconductedonthecalculation 万方数据
第5章_梁的弯曲
第5章 梁的弯曲 简单起见,本节仅考虑直梁、且梁的轴线与x 轴重合。 1 梁弯曲的基本方程 5.1.1 杆的弯曲假定 以下我们分三部分来叙述杆的弯曲假定。 (1)平面假定 在y M 和z M 的共同作用下,杆件上的d x 微段的两截面将发生(绕形心的)相对转动。平面假定:杆横截面在变形后仍保持平面。 设微段的一侧截面不动,根据平面假定,另一侧截面将发生两种相对位移(见下图): 图5.1 在y M 作用下绕 y 轴的转动:d (d )y u z θ= 在z M 作用下绕 z 轴的转动:d (d )z u y θ=- 由于上述两种位移都很小,所以总的轴向位移d u 为 d (d )(d )y z u z y θθ=- (5.1.1) 其中d y θ和d z θ为d x 微段两截面分别绕y 轴和z 轴相对转过的角度,从而正应变为: x y z u z y x ερρ?= =- ? (5.1.2) 其中 d d y y x ρθ= ——梁轴线在x-z 坐标面内弯曲的曲率半径; d d z z x ρθ= ——梁轴线在x-y 坐标面内弯曲的曲率半径。 注意,在轴线上0x ε=,这是由于我们只考虑弯曲变形、而没有考虑拉伸变形,从而假定中的截面只绕形心转动,而没有轴向平动。 (2)横向挤压应力为零假定
横向挤压应力为零假定: 假定y σ和z σ可以忽略。 这个假定使得我们可以利用单向拉(压)的胡克定律 x x y z E E E z y σερρ== - (5.1.3) 由此可以计算内力: 1 1 x x y z A y z F dA ES ES σρρ==-?N (5.1.4) 1 1 y x y yz A y z M zdA EI EI σρρ==-? (5.1.5) 1 1 z x yz z A y z M ydA EI EI σρρ=-=-+? (5.1.6) 其中 22 d , d d , d , d y z A A y z yz A A A S z A S y A I z A I y A I yz A =====????? 分别是横截面对 y z 、轴的静矩,对 y z 、轴的惯性矩和惯性积。对于确定的截面,这些量均为已知。 如果截面上的坐标轴取形心主轴(即原点在形心、坐标轴为惯性主轴),则 0y z S S ==, 0yz I = 从而 N 0x F = 从式(5.1.5)、(5.1.6)直接解得 11, y z y y z z M M EI EI ρρ== (5.1.7) 代入式(5.1.3)得 y z x y z M z M y I I σ= - (5.1.8) 这样,当弯矩y M 和z M 给定后,轴向应力x σ的分布就给定了。 上述各式中的y EI 和z EI 分别称为杆在两个坐标平面内的抗弯刚度。 (3)直法线假定 现在我们来研究曲率半径y ρ和z ρ与形心位移之间的关系。 设轴线由各截面的形心连接而成,轴线上的横向位移在坐标系(以后我们均取形心主轴坐标系)上的分量分别为0()v x 和0()w x 。显然,轴线上的位移仅仅是一个变量x 的函数,
欧拉—伯努利梁在移动载荷作用下的等效方法
94环境技术/Environmental Technology 技术专栏echnical Column T Abstract:In this paper the mathematical model of lateral oscillation of Euler-Bernoulli Beam and its simulation method under excitation by movable load were introduced in detail. Taking simple beam as an example, first the lateral modal was briefly described. Then the different modal responses under movable excitation were explained in detail, and an important conclusion was reached through a case analysis that the first-order modal was the main response. Due to great difficulty and high price of simulating the movable load in laboratory, when only considering the first-order modal, movable load could be equivalent to cyclic excitation. This paper has some guiding significance for the approximate simulation of real response under movable excitation in laboratory. Key words:Euler-Bernoulli Beam; simple beam; modal response; movable load; equivalent load method 摘要:本文详细地介绍了欧拉—伯努利梁横向振动的数学模型与其在移动载荷作用下的模拟方法。以简支梁为例,首先简要叙述了梁的横向模态。然后详细叙述梁在移动载荷作用下不同模态的响应,得到了一阶模态振动为主要响应的重要结论。由于在实验室模拟移动载荷的成本较高、难度较大,当只考虑一阶模态响应时,通过定点周期载荷将移动载荷进行等效。本文研究对于在实验室近似模拟欧拉—伯努力梁在移动载荷作用下的真实响应具有一定的指导意义。 关键词:欧拉-伯努利梁;简支梁;模态响应;移动载荷;等效载荷方法 中图分类号:O327; TB123; TV32+3 文献标识码:A 文章编号:1004-7204(2019)02-0094-04 欧拉—伯努利梁在移动载荷作用下的等效方法 Equivalent Method of Euler-Bernoulli Beam Under Movable Excitation 汪宏斌1,王志浩2 (1.苏州长菱测试技术有限公司,苏州 215163; 2.苏州东菱振动试验仪器有限公司,苏州 215163)WANG Hong-bin 1,WANG Zhi-hao 2 (1.Suzhou Changling Test Technology Co.,Ltd.,Suzhou 215163; 2.Suzhou Dongling Vibration Test Instrument Co., Ltd.,Suzhou 215163) 引言 梁结构是常见的连续体结构,与离散系统不同,连 续系统有无穷多个自由度和固有频率。梁结构在工程中 广泛运用,如桁架、桥梁、轨道等。 以桥梁与轨道为例,由于车重的作用,车轴施加的 载荷是典型的移动载荷。虽然可以通过电脑仿真手段, 模拟梁在移动载荷作用下的横向响应,但是在实验室再 现移动载荷对梁的激励效果,尤其是高速移动载荷,加 载难度较大、成本较高。 本文通过等效载荷的方法,将难以加载的移动载荷 等效为定点周期载荷,以经济的方法再现梁在移动载荷激励下的横向振动,便于考核梁在实际工况的力学性能。1 基本假设与分析方法概述1.1 基本假设截取一跨梁与两端支承进行分析,支承假定为两端铰支座。假设梁长大于5倍梁高,可用欧拉—伯努力梁模型(细长梁模型)进行分析,即忽略剪切变形与截面转动惯量的影响,且在动力学分析中不考虑高阶模态[2][3]。1.2 分析方法概述分析方法如下:
