概率初步统计初步

概率初步
一、学习要求:
(1)理解什么是必然发生事件、不可能发生事件,什么是随机事件.
(2)在具体情境中了解概率的意义,体会概率是描述不确定事件发生可能性大小的数学概率,理解概率取值范围的意义.
(3)能够运用列举法(包括列表、画树状图)计算简单事件发生的概率.
(4)能够通过试验,获得事件发生的频率,知道大量重复试验时频率可作为事件发生概率的估计值,理解频率与概率的区别与联系.
(5)通过实例进一步丰富对概率的认识,并能解决一些实际问题.
(6)了解进行模拟试验的必要性,能根据问题的实际背景设计合理的模拟试验.
二、例题分析
1、概率的有关概念
1、下列事件中是必然事件的是()
A、小婷上学一定坐公交车
B、买一张电影票,座位号正好是偶数
C、小红期末考试数学成绩一定得满分
D、将豆油滴入水中,豆油会浮在水面上
2、下列说法正确的是()
A、一颗质地均匀的骰子已连续抛掷了2000次,其中,抛掷出5点的次数最少,则第2001次一定抛掷出
5点
B、某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖
C、天气预报说明天下雨的概率是50%.所以明天将有一半时间在下雨
D、抛掷一枚图钉,钉尖触地和钉尖朝上的概率不相等
2、用列举法求概率
(1)直接列举法
3、四张不透明的卡片为,除正面的数不同外,其余都相同.将它们背面朝上洗匀后,从中随机抽取一张卡片,抽到写有无理数卡片的概率为_______.
(2)两步、三步试验的问题:列表和树状图
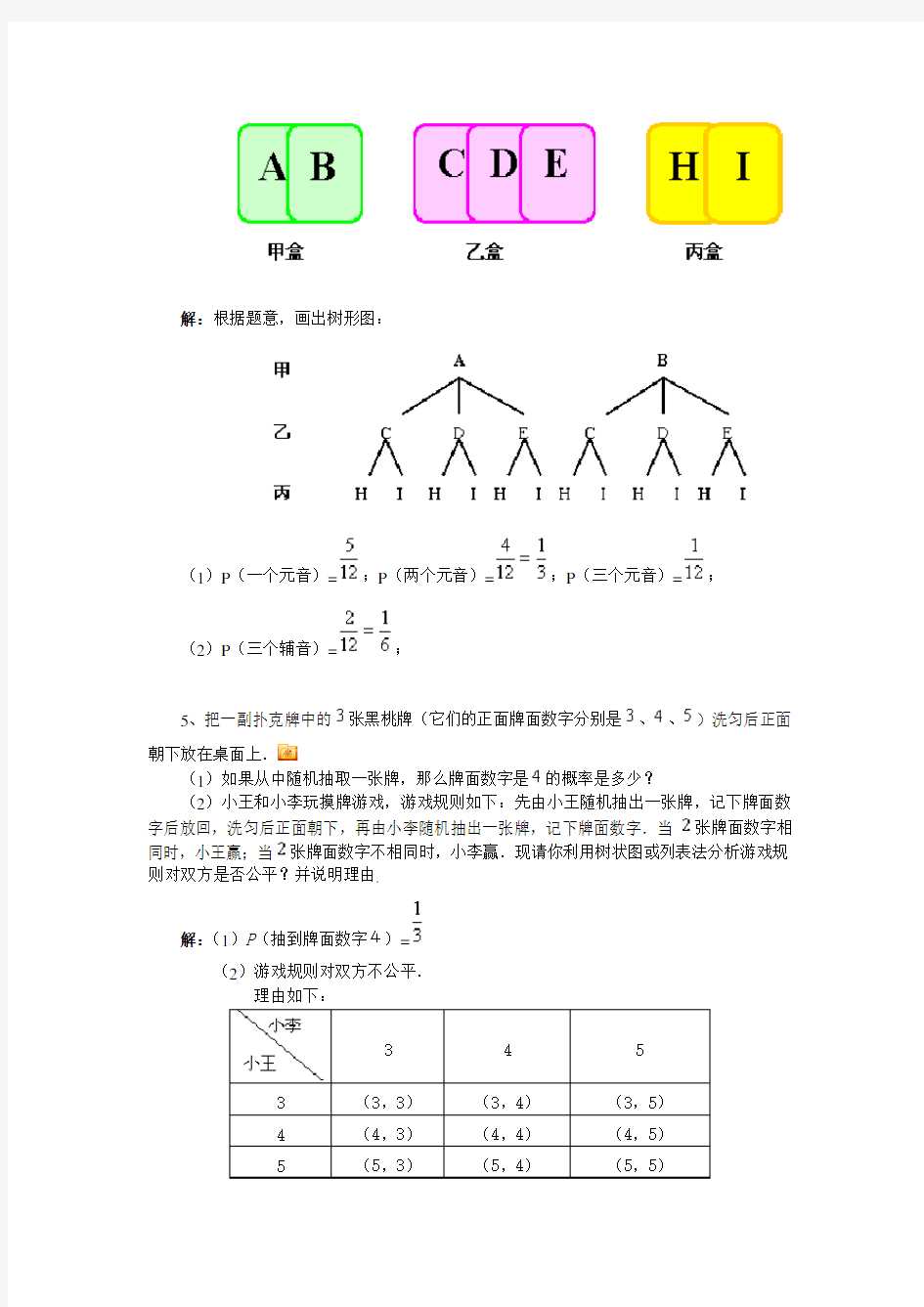
4、甲盒中装有2张相同的卡片,它们分别写有字母A和B;乙盒中装有3张相同的卡片,它们分别写有字母C、D和E;丙盒中装有2张相同的卡片,它们分别写着字母H和I,从3个盒中各随机取出一张卡片.
(1)取出的3张卡片上恰好有1个,2个,3个元音字母的概率是多少?
(2)取出的3张卡片上全是辅音字母的概率是多少?
解:根据题意,画出树形图:
(1)P(一个元音)=;P(两个元音)=;P(三个元音)=;
(2)P(三个辅音)=;
5、把一副扑克牌中的张黑桃牌(它们的正面牌面数字分别是、、)洗匀后正面
朝下放在桌面上.
(1)如果从中随机抽取一张牌,那么牌面数字是的概率是多少?
(2)小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽出一张牌,记下牌面数字.当张牌面数字相同时,小王赢;当张牌面数字不相同时,小李赢.现请你利用树状图或列表法分析游戏规则对双方是否公平?并说明理由.
解:(1)P(抽到牌面数字4)=
(2)游戏规则对双方不公平.
3 4 5
3 (3,3)(3,4)(3,5)
4 (4,3)(4,4)(4,5)
5 (5,3)(5,4)(5,5)
或
由上述表格或树状图知:所有可能出现的结果共有9种.
P(抽到牌面数字相同)=,
P(抽到牌面数字不相同)=.
∵,∴此游戏不公平,小李赢的可能性大.
3、用频率估计概率
1、通过实例让学生体会有频率估计概率的必要性和科学性.强调“同样条件,大量试验”
2、蒙特卡罗方法:有些事情是动态的,或者很难将每一个一一数出,这时可用试验频率来估计总数.
其思想依据是:理论概率=试验概率.常用方法是:先做记号,再数记号
6、为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记的鱼有10条,则估计池塘里有鱼______________条.
7、一个密封不透明的盒子里有若干个白球, 在不允许将球倒出来的情况下, 为估计白球的个数, 小刚向其中放入8个黑球, 摇匀后从中随机摸出一个球记下颜色, 再把它放回盒中, 不断重复, 共摸球400次, 其中88次摸到黑球. 估计盒中大约有白球( )
A、28个
B、30个
C、36个
D、42个
一、本章知识结构框图
二、学习目标:
1.理解什么是必然发生的事件、不可能发生的事件,什么是随机事件;
2.在具体情境中了解概率的意义,体会概率是描述不确定现象的规律的数学模型,理解概率的取值范围的意义,发展随机观念。能够运用列举法(包括列表、画树形图)计算简单事件发生的概率;
3.能够通过试验,获得事件发生的频率;知道大量重复试验时频率可作为事件发生概率的估计值,理解频率与概率的区别与联系。通过实例进一步丰富对概率的认识,并能解决一些实际问题。了解进行模拟试验的必要性,能根据问题的实际背景设计合理的模拟试验。
三、知识要点:
1.随机事件:在一定条件下,可能发生也可能不发生的事件,称为随机事件(random event)。
阅读:确定事件与随机事件:
在现实世界中,有许多现象我们是可以事先预言其结果的,如下雨必有云;同性电荷相斥;在中,若AB=AC,则;因为,所以。以上事实的反面,下雨而无云;同性电荷相吸;,而等。这种在一定条件下必然发生或必
然不发生的现象称为确定性事件(或现象)。确定性事件的特点是:当条件给定时,其结果可以事先确切地预言或推算。代数、几何都是研究这类现象的工具。
然而,在现实世界中还存在着许多现象,我们无法事先断定其结果。例如,向上抛出一枚硬币,落地时其结果是正面向上,还是背面向上?事先是无法准确断言的。又如新生儿的体重,在出生之前也无法准确断言是多少。某一路段,在一定时间段内有多少车辆通过,也是无法事先断定的。这类事件很多。它们的共同特点是:在相同的条件下,重复同一试验(或观察)时,会得到不同的结果,就一次或少数几次试验来看,其结果是不确定的、无规律的,但当大量重复试验(或观察)时,其结果就整体来说呈现出某种固有规律性。例如,将上述的抛硬币试验大量重复时,就可以发现正面朝上或反面朝上的次数总是大致相等的。通过大量统计新生婴儿的体重时,也会发现这些数字绝大多数集中在某一点附近,离开这点越远数字越少,呈现出一种确定的分布。这种大量重复试验(或观察)时所呈现出的规律性,称为统计规律。这类在个别试验中呈现出不确定性,而在大量重复试验中,又具有某种统计规律的现象,这就是随机事件。
2.概率:一般地,在大量重复试验中,如果事件A发生的频率会稳定在某个常数附近,那么这个常数就叫做事件A的概率(probability),记为。
可理解为:
(1)求一个事件的概率的基本方法是通过大量的重复试验;
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A的概率;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5),必然事件的概率为,不可能事件的概率为,
随机事件时。
理解概率与频率的内在联系与区别:
概率这一概念是建立在频率这一统计量的稳定性基础之上的,而统计也离不开概率的理论支撑。相同条件下,一个事件发生的概率是一个常数,是由事件固有的属性决定的,但是如果用概率试验的方法,频率会随着样本空间的变化而变化,但随着样本的增加,频率会越来越集中于一个常数,这个数就是概率。所以用频率估计出来的概率通常是不精确的,要有误差。这就是所说的“试验概率稳定于理论概率而又不等于理论概率”。
四、例题解析:
例1.在一个不透明的口袋中,装有10个除颜色外其他完全相同的球,其中5个红球,3个蓝球,2个白球,它们已经在口袋中搅匀了。下列事件中,哪些是必然发生的?哪些是不可能发生的?哪些是可能发生的?
(1)从口袋中任取出一个球,它恰是红球;
(2)从口袋中一次性任意取出2个球,它们恰好全是白球;
(3)从口袋中一次性任意取出5个球,它们恰好是1个红球,1个蓝球,3个白球。
例2.指出下列事件中,哪些是不可能事件?哪些是必然事件?哪些是随机事件?
(1)若a、b、c都是实数,则a(bc)=(ab)c;
(2)没有空气,动物也能生存下去;
(3)在标准大气压下,水在90℃时沸腾;
(4)直线y=k(x+1)过定点(-1,0);
(5)某一天内电话收到的呼叫次数为0;
(6)一个袋内装有形状大小完全相同的一个白球和一个黑球,从中任意摸出1个球则为白球。
例3.同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)两个骰子的点数和是12;
(2)两个骰子的点数和至少是9点;
(3)两个骰子的点数相同;
(4)两个骰子的点数都是偶数;
(5)两个骰子的点数和为1;
(6)两个骰子的点数和小于13。
例4.“石头、剪刀、布”是一个广为流传的游戏,游戏时甲乙双方每次做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛.假定甲乙两人每次做这三种手势都是等可能的,那么一次比赛时两人做同种手势(即不分胜负)的概率是多少?
解:所有机会均等的结果有9个,其中的3个——(石头,石头)、(剪刀,剪刀)、(布,布)是我们关注的结果,所以.
注意:使用树状图要注重“机会均等”.
例5.一个袋中装有2个黄球和2个红球,任意摸出一个球后放回,再任意摸出一个球,求两次都摸到红球的概率.
分析:方法1:列举法:先摸一次,放回后再摸一次,两次摸球是独立的,互不影响的,可能摸出的情况有(红,红),(红,黄),(黄,红),(黄,黄),所以概率为.方法2:树状图法
解:概率为.
例6.某射手在同一条件下进行射击,结果如下表所示:
射击次数(n)10 20 50 100 200 500
击中靶心次数(m)9 19 44 91 178 451
击中靶心频率()......
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约是多少?
例7.某种油菜籽在相同条件下的发芽试验结果如下表:
每批粒数 2 5 10 70 130 310 700 1500 2000 3000 发芽的粒数 2 4 9 60 116 282 639 1339 1806 2715
发芽的频率
..........
(1)计算表中每批油菜籽发芽的频率;
(2)油菜籽发芽的频率在左右摆动,油菜籽发芽的概率约为。
课后练习:
1.指出下列事件中,哪些是必然发生的,哪些是不可能发生的,哪些是随机事件:
(1)导体通电时,发热;
(2)抛一块石头,下落;
(3)在常温下,焊锡熔化;
(4)在标准大气压下且温度低于时,冰融化;
(5)掷一枚硬币,出现正面;
(6)某人射击一次,中靶。
2.必然事件的概率为_________,不可能事件的概率为_________,随机事件的概率范围是_________.
3. 同时掷两个质地均匀的骰子一次,共有_________种不同的结果.
4.随意从放有4个红球和1个蓝球的口袋中摸出一个球,再放回袋中搅匀后再摸出一个球,求两次摸到的球都为红球的概率。
5.“神舟六号”的成功发射凝聚了航天人无数的心血与汗水,仅就回归着陆是否能在预定
2
(1)填写表中的频率(精确到0.01);
(2)根据表中反映的规律,回答理想着陆的概率.
6.小明对小红说:“我们来做一个游戏,我向空中扔3个硬币。如果它们落地后全是正面朝上,你就得10分。如果它们全是反面朝上,你也得10分。但是,如果它们落地时是其他情况,我就得5分,得分多者获胜,好不好?”
小红说,“让我考虑一分钟,至少有两枚硬币必定情况相同,因为如果有两枚情况不同,则第三枚一定会与这两枚硬币之一情况相同。而如果两枚情况相同,则第三枚与其他两枚情况相同或情况不同的可能性一样。因此,3枚硬币情况完全相同或情况不完全相同的可能性是一样的。但是小明是用5分来赌它们的不完全相同,这分明对我有利,好吧,小明,我和你做这个游戏!”
请问:小红的推理正确吗?
概率初步单元测试
一、选择题(每题4分,共48分)
1.下列事件是必然事件的是( )
A.明天天气是多云转晴
B.农历十五的晚上一定能看到圆月
C.打开电视机,正在播放广告
D.在同一月出生的32名学生,至少有两人的生日是同一天
2.下列说法中正确的是( )
A.可能性很小的事件在一次实验中一定不会发生
B.可能性很小的事件在一次实验中一定会发生
C.可能性很小的事件在一次实验中有可能发生
D.不可能事件在一次实验中也可能发生
3.下列模拟掷硬币的实验不正确的是( )
A.用计算器随机地取数,取奇数相当于下面朝上,取偶数相当于硬币正面朝下
B.袋中装两个小球,分别标上1和2,随机地摸,摸出1表示硬币正面朝上
C.在没有大小王的扑克中随机地抽一张牌,抽到红色牌表示硬币正面朝上
D.将1、2、3、4、5分别写在5张纸上,并搓成团,每次随机地取一张,取到奇数号表示硬币正面朝上
4.在10000张奖券中,有200张中奖,如果购买1张奖券中奖的概率是( )
A. B. C. D.
5.有6张背面相同的扑克牌,正面上的数字分别是4、5、6、7、8、9,若将这六张牌背面向上洗匀后,从中任意抽取一张,那么这张牌正面上的数字是3的倍数的概率为( )
A. B. C. D.
6.一个袋子中有4个珠子,其中2个是红色,2个蓝色,除颜色外其余特征均相同,若在这个袋中任取2个珠子,都是红色的概率是( )
A. B. C. D.
7.有5条线段的长分别为2、4、6、8、10,从中任取三条能构成三角形的概率是( )
A. B. C. D.
8.一个均匀的立方体六个面上分别标有1,2,3,4,5,6,下图是这个立方体表面的展
开图,抛掷这个立方体,则朝上一面的数恰好等于朝下一面的数的的概率是( )
A. B. C. D.
9.四张完全相同的卡片上,分别画有圆、矩形、等边三角形、等腰梯形,现从中随机抽取一张,卡片上画的恰好是中心对称图形的概率为( )
A. B. C. D.
10.把一个沙包丢在如图所示的某个方格中(每个方格除颜色外完全一样),那么沙包落在黑色格中的概率是( )
A. B. C. D.
11.如果小明将飞镖随意投中如图所示的圆形木板,那么镖落在小圆内的概率为( )
A. B. C. D.
12.中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖.参加这个游戏的观众有三次翻牌的机会,某观众前两次翻牌均得若干奖金,已经翻过的牌不能再翻,那么这位获奖的概率是( )
A. B. C. D.
二、填空题(每题4分,共24分)
13.“抛出的篮球会下落”,这个事件是事件.(填“确定”或“不确定”)
14.10张卡片分别写有0至9十个数字,将它们放入纸箱后,任意摸出一张,则P(摸到数字2)=______,P(摸到奇数)=_______.
15.一只布袋中有三种小球(除颜色外没有任何区别),分别是2个红球,3个黄球和5个蓝球,每一次只摸出一只小球,观察后放回搅匀,在连续9次摸出的都是蓝球的情况下,第10次摸出黄球的概率是_______.
16.有五张卡片,每张卡片上分别写有1,2,3,4,5,洗匀后从中任取一张,放回后再抽一张,两次抽到的数字和为_______的概率最大,抽到和大于8的概率为_______.
17.某口袋中有红色、黄色、蓝色玻璃共72个,小明通过多次摸球试验后,发现摸到红球、黄球、蓝球的频率为35%、25%和40%,估计口袋中黄色玻璃球有个.
18.口袋里有红、绿、黄三种颜色的球,其中红球4个,绿球5个,任意摸出一个绿球的
概率是,则摸出一个黄球的概率是_______.
三、解答题(每题7分,共28分)
19.一个口袋中有10个红球和若干个白球,请通过以下实验估计口袋中白球的个数,从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程,实验中共摸200次,其中50次摸到红球.
20.一张椭圆形桌旁有六个座位,A、E、F先坐在如图所示的座位上,B、C、D三人随机坐到其他三个座位,求A与B不相邻而座的概率.
21.你喜欢玩游戏吗?现请你玩一个转盘游戏.如图所示的两个转盘中指针落在每一个数字上的机会均等,现同时自由转动甲乙两个转盘,转盘停止后,指针各指向一个数字,用所指的两个数字作乘积.
请你:⑴列举(用列表或画树状图)所有可能得到的数字之积
⑵求出数字之积为奇数的概率.
22.请你依据右面图框中的寻宝游戏规则,探究“寻宝游戏”的奥秘:
⑴用树状图表示出所有可能的寻宝情况;
⑵求在寻宝游戏中胜出的概率.
答案与解析
一、选择题
1.D
2.C
3.D
4.A
5.D
6.D
7.D
8.A
9.B 10.B 11.D 12.B
二、填空题
13.确定 14.; 15. 16.6; 17. 18 18.
三、解答题
19.设口袋中有个白球,,口袋中大约有30个白球 20.
21.解:⑴ 用列表法来表示所有得到的数字之积
乙
1 2 3 4 5 6
积
甲
1 1×1=12×1=23×1=34×1=45×1=56×1=6
2 1×2=22×2=43×2=64×2=85×2=106×2=12
3 1×3=32×3=63×3=94×3=125×3=156×3=18
4 1×4=42×4=83×4=124×4=165×4=206×4=24
⑵由上表可知,两数之积的情况有24种,所以P(数字之积为奇数)=.
22.解:⑴树状图如下:
⑵由⑴中的树状图可知:P(胜出).
概率初步单元复习与巩固
一、知识框图
二、目标认知
学习目标
1.理解并掌握确定事件和不确定事件,必然发生的事件和不可能发生的事件.知道必然发生的事件概率
为1,不可能发生事件的概率为0,随机事件发生的概率在0和1之间;
2.会用列表法和树形图法解决随机事件的概率,并注意二者的区别与联系;
3.用频率去估计实际概率要注意试验的次数必须足够多.
重点
1.随机事件、必然事件、不可能事件等的判断;
2.用列举法求概率;
3.利用稳定后的频率值来估计概率的大小.
难点
1.用试验得出概率;
2.列表法与树形图法的选择使用;
3.利用稳定后的频率值来估计概率的大小.
三、知识要点梳理
(一)概率的有关概念
1.概率的定义:
某种事件在同一条件下可能发生,也可能不发生,但可以知道它发生的可能性的大小,我们把刻划事件发生的可能性的大小的量叫做概率.
2.概率论:
研究概率的科学叫概率论.概率主要研究不确定现象,概率论作为一门科学,和人们的日常生活有着紧密的联系,比如:各种彩票、抽奖等等.人们用概率知识解决了许多生产实际问题.
3.必然事件:
有些事情我们事先肯定它一定发生,这些事情称为必然事件.
4.不可能事件:
有些事情我们事先肯定它一定不会发生,这些事情称为不可能事件.
5.不确定事件:
许多事情我们无法确定它会不会发生,这些事情称为不确定事件.
必然事件、不可能事件都是在事先能肯定它们会发生,或事先能肯定它们不会发生的事件,因此它们也可以称为确定性事件.
(二)概率的计算:
概率的计算有理论计算和实验计算两种方式,根据概率获得的方式不同,它的计算方法也不同.
当试验次数很大时,一个事件发生的频率也稳定在相应的概率附近.因此,我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.
对于某些特殊类型的试验,实际上不需要作大量重复的试验,而通过列举法进行分析就能得到事件的概率.例如掷一个骰子(骰子的构造相同,质地均匀),向上的一面的点数有6种
可能,即1,2,3,4,5,6.因此每种结果的可能性相等,都是.或从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根(纸签的形状,大小相同),抽出的签上的号码有5种可
能,即1,2,3,4,5.因此每个号被抽到的可能性相等,都是.
以上两个试验的共同特点是:
1.一次试验中,可能出现的结果有限多个;
2.一次试验中,各种结果发生的可能性相等.
具有这些特点的试验称为古典概型.
如何求具有上述特点的随机事件的概率呢?
如果一次试验中共有n种可能出现的结果,而且这些结果出现的可能性都相同,其中事
件A包含的结果有m种,那么事件A发生的概率P(A)=,可以利用列表法或树状图来球
其中的m、n,从而得到事件A的概率.
由此我们可以得到:
不可能事件发生的概率为0,即P(不可能事件)=0;
必然事件发生的概率为1,即P(必然事件)=1;
如果A为不确定事件,那么0 四、规律方法指导 1.生活中的随机事件分为确定事件和不确定事件,确定事件又分为必然事件和不可能事件,其中, ①必然事件发生的概率为1,即P(必然事件)=1; ②不可能事件发生的概率为0,即P(不可能事件)=0; ③如果A为不确定事件,那么0 2.随机事件发生的可能性(概率)的计算方法: ①理论计算又分为如下两种情况: 第一种:只涉及一步实验的随机事件发生的概率,如:根据概率的大小与面积的关系,对一类概率模型 进行的计算; 第二种:通过列表法、列举法、树状图来计算涉及两步或两步以上实验的随机事件发生的概率, 如:配紫色,对游戏是否公平的计算. ②实验估算又分为如下两种情况: 第一种:利用实验的方法进行概率估算.要知道当实验次数非常大时,实验频率可作为事件发生的概率 的估计值,即大量实验频率稳定于理论概率. 第二种:利用模拟实验的方法进行概率估算.如,利用计算器产生随机数来模拟实验. 综上所述,目前掌握的有关于概率模型大致分为三类;第一类问题没有理论概率,只能借助实验模拟获得其估计值;第二类问题虽然存在理论概率但目前尚不可求,只能借助实验模拟获得其估计值;第三类问题则是简单的古典概型,理论上容易求出其概率. 这里要引起注意的是,虽然我们可以利用公式计算概率,但在学习这部分知识时,更重要的是要体会概率的意义,而不只是强化练习套用公式进行计算. 3.你知道概率有哪些应用吗? 通过设计简单的概率模型,在不确定的情境中做出合理的决策;概率与实际生活联系密切,通过理解什么是游戏对双方公平,用概率的语言说明游戏的公平性,并能按要求设计游戏的概率模型,以及结合具体实际问题,体会概率与统计之间的关系,可以解决一些实际问题.
