同角三角函数基本关系及诱导公式

§4.2同角三角函数基本关系及诱导公式
1.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1.
(2)商数关系:sinα
cosα=tanα.
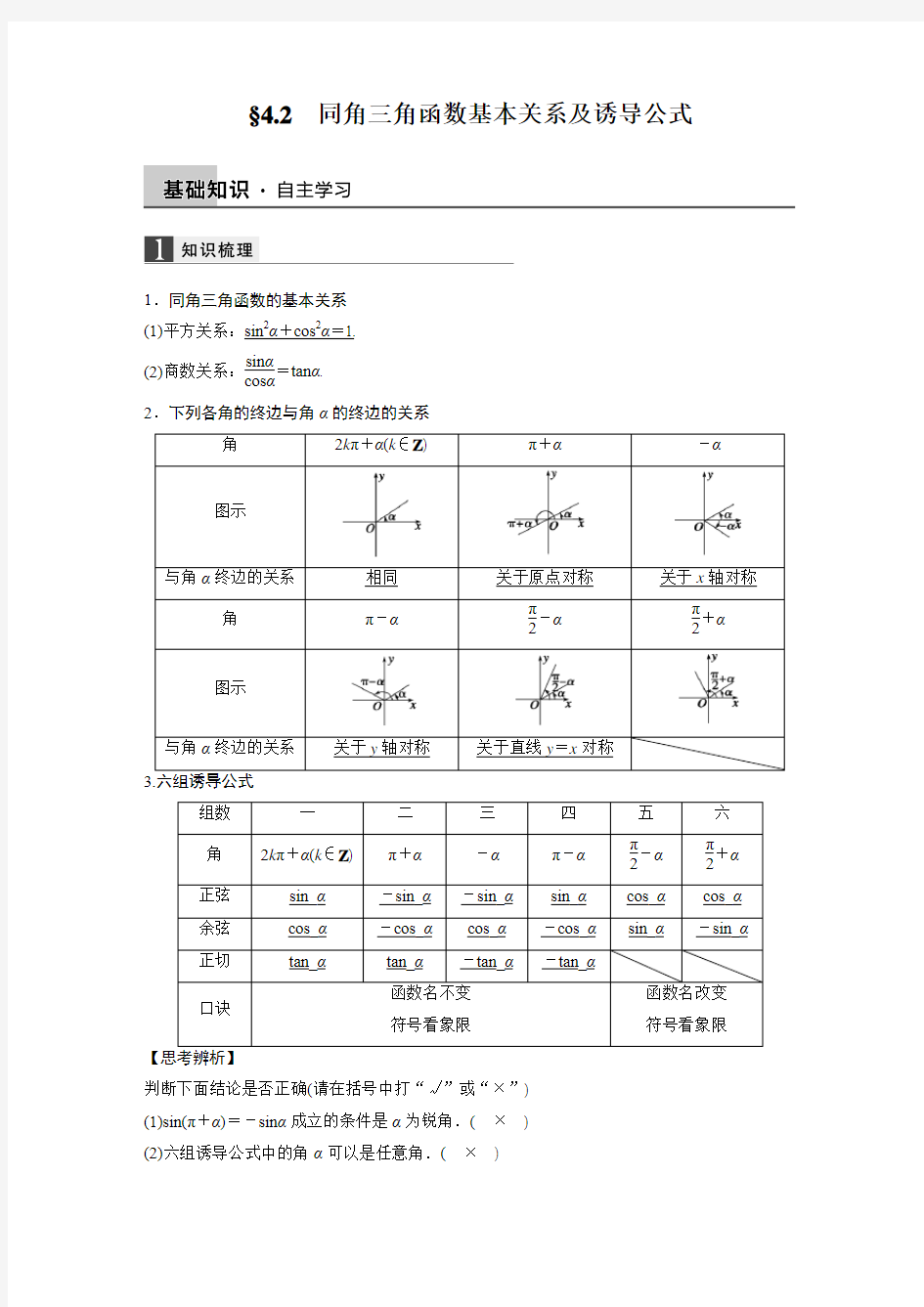
2.下列各角的终边与角α的终边的关系
判断下面结论是否正确(请在括号中打“√”或“×”)
(1)sin(π+α)=-sinα成立的条件是α为锐角.(×)
(2)六组诱导公式中的角α可以是任意角.(×)
(3)若cos(n π-θ)=13(n ∈Z ),则cos θ=1
3
.( × )
(4)已知sin θ=m -3m +5,cos θ=4-2m m +5,其中θ∈[π
2,π],则m <-5或m ≥3.( × )
(5)已知θ∈(0,π),sin θ+cos θ=
3-12,则tan θ的值为-3或-3
3
.( × ) (6)已知tan α=-12,则1+2sin αcos αsin 2α-cos 2α
的值是-1
3.( √ )
1.已知α是第二象限角,sin α=5
13
,则cos α等于( ) A .-513
B .-1213
C.513
D.1213
答案 B
解析 ∵sin α=5
13
,α是第二象限角,
∴cos α=-
1-sin 2α=-12
13
.
2.已知sin(π-α)=log 814,且α∈(-π
2,0),则tan(2π-α)的值为( )
A .-25
5
B.255
C .±255
D.52
答案 B
解析 sin(π-α)=sin α=log 814=-2
3,
又α∈(-π
2
,0),
得cos α=
1-sin 2α=
53
, tan(2π-α)=tan(-α)=-tan α
=-sin αcos α=255
.
3.已知cos ????π6-α=23,则sin ????α-2π
3=________. 答案 -2
3
解析 sin ? ????α-2π3=sin ??????-π2-? ????π6-α
=-sin ????
??π2+? ????π6-α
=-cos ? ??
??π6-α=-23. 4.已知函数f (x )=?????
2cos π3x ,x ≤2 000,
x -15,x >2 000,则f [f (2 015)]=________.
答案 -1
解析 ∵f [f (2 015)]=f (2 015-15)=f (2 000), ∴f (2 000)=2cos 2 000π3=2cos 2
3
π=-1.
题型一 同角三角函数关系的应用
例1 (1)已知cos(π+x )=3
5,x ∈(π,2π),则tan x =________.
(2)已知tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ等于( ) A .-43B.54C .-34D.45
答案 (1)4
3
(2)D
解析 (1)∵cos(π+x )=-cos x =35,∴cos x =-3
5.
又x ∈(π,2π),
∴sin x =-
1-cos 2x =-
1-(-35)2=-45
,
∴tan x =sin x cos x =4
3
.
(2)sin 2θ+sin θcos θ-2cos 2θ=sin 2θ+sin θcos θ-2cos 2θ
sin 2θ+cos 2θ
=sin 2θcos 2θ+sin θcos θ
cos 2
θ-2sin 2θ
cos 2+1=tan 2θ+tan θ-2tan 2θ+1=22+2-222+1
=4
5
. 思维升华 (1)利用sin 2α+cos 2α=1可以实现角α的正弦、余弦的互化,利用
sin α
cos α
=tan α可以实现角α的弦切互化.
(2)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.
(3)注意公式逆用及变形应用:1=sin 2α+cos 2α,sin 2α=1-cos 2α,cos 2
α=1-sin 2α.
(1)已知1+sin x cos x =-12,那么cos x
sin x -1
的值是( )
A.12B .-1
2
C .2
D .-2 (2)已知tan θ=2,则sin θcos θ=________. 答案 (1)A (2)25
解析 (1)由于1+sin x cos x ·sin x -1cos x =sin 2x -1
cos 2x =-1,
故
cos x
sin x -1=12
.
(2)sin θcos θ=sin θ·cos θ
sin 2θ+cos 2θ
=
tan θ
tan 2θ+1=222+1=25
.
题型二 诱导公式的应用
例2 (1)已知cos ????π6+α=3
3,求cos ???
?5π6-α的值; (2)已知π<α<2π,cos(α-7π)=-3
5,求sin(3π+α)·tan ????α-72π的值. 思维点拨 (1)将π6+α看作一个整体,观察π6+α与5π
6-α的关系.
(2)先化简已知,求出cos α的值,然后化简结论并代入求值.
解 (1)∵? ????π6+α+? ??
??5π6-α=π, ∴5π6-α=π-? ??
??π6+α. ∴cos ? ????5π6-α=cos ????
??π-? ????π6+α =-cos ? ????π6+α=-33,
即cos ?
??
??5π6-α=-33.
(2)∵cos(α-7π)=cos(7π-α) =cos(π-α)=-cos α=-3
5,
∴cos α=3
5
.
∴sin(3π+α)·tan ? ????α-72π =sin(π+α)·????
?
?-tan ? ????72π-α
=sin α·tan ? ????π2-α =sin α·sin ? ??
??π2-αcos ? ??
??π2-α
=sin α·cos αsin α=cos α=3
5
.
思维升华 熟练运用诱导公式和同角三角函数基本关系,并确定相应三角函数值的符号是
解题的关键.另外,切化弦是常用的规律技巧.
(1)已知sin ????α+π12=1
3,则cos ???
?α+7π12的值为________. (2)已知sin α是方程5x 2-7x -6=0的根,α是第三象限角,则sin (-α-32π)cos (3
2
π-α)
cos (π2-α)sin (π2+α)
·tan 2(π
-α)=__________________________________. 答案 (1)-13 (2)-9
16
解析 (1)cos ? ????α+7π12=cos ??????? ????α+π12+π2 =-sin ? ??
??α+π12=-13.
(2)∵方程5x 2-7x -6=0的根为-3
5或2,
又α是第三象限角,∴sin α=-3
5
,
∴cos α=-
1-sin 2α=-4
5
,
∴tan α=sin α
cos α=-35-45
=34
,
∴原式=cos α(-sin α)
sin α·cos α·tan 2α=-tan 2α=-9
16.
题型三 三角函数式的求值与化简
例3 (1)已知α为锐角,且有2tan(π-α)-3cos(π
2+β)+5=0,tan(π+α)+6sin(π+β)-1=0,
则sin α的值是( ) A.355
B.377
C.31010
D.13
(2)已知α是三角形的内角,且sin α+cos α=1
5,则tan α=________.
答案 (1)C (2)-4
3
解析 (1)2tan(π-α)-3cos(π
2+β)+5=0化简为
-2tan α+3sin β+5=0,①
tan(π+α)+6sin(π+β)-1=0化简为
tan α-6sin β-1=0.②
由①②消去sin β,
解得tan α=3.
又α为锐角,根据sin 2α+cos 2α=1, 解得sin α=310
10.
(2)因为sin α+cos α=1
5
,
所以(sin α+cos α)2=1+2sin α·cos α=(1
5
)2,
即2sin α·cos α=-24
25
,
所以(sin α-cos α)2=1-2sin α·cos α=1+2425=49
25,
又2sin α·cos α=-24
25
<0,0<α<π,
所以sin α>0,cos α<0,即sin α-cos α>0,
故sin α-cos α=
4925=75
, 由?????
sin α+cos α=1
5,sin α-cos α=7
5,得?????
sin α=45,cos α=-3
5
,
所以tan α=-43
.
思维升华 在三角函数式的求值与化简中,要注意寻找式子中的角,函数式子的特点和联
系,可以切化弦,约分或抵消,减少函数种类,对式子进行化简.
(1)若α为三角形的一个内角,且sin α+cos α=2
3
,则这个三角形是( )
A .正三角形
B .直角三角形
C .锐角三角形
D .钝角三角形
(2)已知tan α=2,sin α+cos α<0, 则
sin (2π-α)·sin (π+α)·cos (π+α)
sin (3π-α)·cos (π-α)
=________.
答案 (1)D (2)-25
5
解析 (1)∵(sin α+cos α)2=1+2sin αcos α=4
9,
∴sin αcos α=-5
18
<0,∴α为钝角.故选D.
(2)原式=-sin α·(-sin α)·(-cos α)
sin α·(-cos α)
=sin α,
∵tan α=2>0,∴α为第一象限角或第三象限角.
又sin α+cos α<0,∴α为第三象限角, 由tan α=sin α
cos α
=2,
得sin α=2cos α代入sin 2α+cos 2α=1, 解得sin α=-
25
5
.
分类讨论思想在三角函数求值化简中的应用
典例:(1)已知A =sin (k π+α)sin α+cos (k π+α)
cos α(k ∈Z ),则A 的值构成的集合是( )
A .{1,-1,2,-2}
B .{-1,1}
C .{2,-2}
D .{1,-1,0,2,-2}
(2)在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),则C =________. 思维点拨 (1)角中含有整数k ,应对k 是奇数还是偶数进行讨论;(2)利用同角三角函数基
本关系式的平方关系时,要对开方的结果进行讨论. 解析 (1)当k 为偶数时,A =sin αsin α+cos α
cos α=2;
k 为奇数时,A =-sin α
sin α-cos α
cos α=-2.
∴A 的值构成的集合是{2,-2}.
(2)由已知得错误!
①2+②2得2cos 2A =1,即cos A =±2
2,
当cos A =
22时,cos B =32
, 又A 、B 是三角形的内角, ∴A =π4,B =π
6,
∴C =π-(A +B )=712π.
当cos A =-
22时,cos B =-32
. 又A 、B 是三角形的内角,∴A =34π,B =5
6π,不合题意.
综上,C =7
12π.
答案 (1)C (2)7
12
π
温馨提醒 (1)本题在三角函数的求值化简过程中,体现了分类讨论思想,即使讨论的某种情况不合题意,也不能省略讨论的步骤;(2)三角形中的三角函数问题,要注意隐含条件的挖掘及三角形内角和定理的应用.
方法与技巧
同角三角函数基本关系是三角恒等变形的基础,主要是变名、变式.
1.同角关系及诱导公式要注意象限角对三角函数符号的影响,尤其是利用平方关系在求
三角函数值时,进行开方时要根据角的象限或范围,判断符号后,正确取舍.
2.三角求值、化简是三角函数的基础,在求值与化简时,常用方法有:(1)弦切互化
法:主要利用公式tan x =
sin x
cos x
化成正弦、余弦函数;(2)和积转换法:如利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化;(3)巧用“1”的变换:1=sin 2θ+cos 2θ=cos 2θ(1+tan 2θ)=sin 2θ? ????1+1tan 2θ=tan π4=….
失误与防范
1.利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其步
骤:去负—脱周—化锐.
特别注意函数名称和符号的确定.
2.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号.
3.注意求值与化简后的结果一般要尽可能有理化、整式化.
A 组 专项基础训练 (时间:45分钟)
1.α是第四象限角,tan α=-5
12,则sin α等于( )
A.15B .-15C.513D .-513 答案 D
解析 ∵tan α=sin αcos α=-512,∴cos α=-125sin α,
又sin 2α+cos 2α=1,
∴sin 2α+14425sin 2α=169
25
sin 2α=1.
又sin α<0,∴sin α=-5
13
.
2.若sin ????π6-α=13,则cos ????2π
3+2α等于( ) A .-79B .-13C.13D.7
9
答案 A
解析 ∵? ????π3+α+? ????π6-α=π2,
∴sin ? ????π6-α=sin ??????π2-? ????π3+α =cos ? ????π3+α=13
.
则cos ?
????2π3+2α=2cos 2? ??
??π3+α-1=-79.
3.已知sin(π-α)=-2sin(π
2+α),则sin α·cos α等于( )
A.25B .-25C.25或-25D .-15 答案 B
解析 由sin(π-α)=-2sin(π
2+α)得sin α=-2cos α,
所以tan α=-2,
∴sin α·cos α=sin α·cos αsin 2α+cos 2α=tan α1+tan 2α
=-2
5
,故选B.
4.已知f (α)=sin (π-α)·cos (2π-α)cos (-π-α)·tan (π-α),则f ????-25π
3的值为( ) A.12B .-12C.32D .-3
2 答案 A
解析 ∵f (α)=sin αcos α-cos α·(-tan α)
=cos α,
∴f ? ????-25π3=cos ? ??
??-25π3
=cos ?
????8π+π3=cos π3=12. 5.函数y =3cos(x +φ)+2的图象关于直线x =π
4对称,则φ的可能取值是( )
A.3π4B .-3π4C.π4D.π2 答案 A
解析 ∵y =cos x +2的对称轴为x =k π(k ∈Z ),
∴x +φ=k π(k ∈Z ),即x =k π-φ(k ∈Z ),令π4=k π-φ(k ∈Z )得φ=k π-π
4(k ∈Z ),在四个选项
中,只有
3π
4
满足题意. 6.如果sin α=1
5,且α为第二象限角,则sin ????3π2+α=______________________________. 答案
26
5
解析 ∵sin α=1
5
,且α为第二象限角,
∴cos α=-
1-sin 2α=-
1-125=-265
,
∴sin ?
??
??3π2+α=-cos α=265.
7.已知α为钝角,sin(π4+α)=34,则sin(π
4-α)=________.
答案 -
7
4
解析 有题意可得cos(π4+α)=±74,由因为α为钝角,所以cos(π4+α)=-74,所以sin(π
4-
α)=cos[π2-(π4-α)]=cos(π4+α)=-7
4
.
8.化简:sin 2(α+π)·cos (π+α)·cos (-α-2π)
tan (π+α)·sin 3(π2+α)·sin (-α-2π)=________.
答案 1
解析 原式=sin 2α·(-cos α)·cos α
tan α·cos 3
α·(-sin α)=sin 2αcos 2α
sin 2αcos 2α=1.
9.已知sin θ=45,π
2<θ<π.
(1)求tan θ的值;
(2)求sin 2θ+2sin θcos θ3sin 2θ+cos 2θ
的值.
解 (1)∵sin 2θ+cos 2θ=1,∴cos 2θ=9
25.
又π2<θ<π,∴cos θ=-35. ∴tan θ=sin θcos θ=-43
.
(2)由(1)知,sin 2θ+2sin θcos θ3sin 2θ+cos 2θ=tan 2θ+2tan θ
3tan 2θ+1
=-8
57
.
10.已知sin θ,cos θ是关于x 的方程x 2-ax +a =0(a ∈R )的两个根,求cos 3(π2-θ)+sin 3(π
2-θ)
的值.(已知:a 3+b 3=(a +b )(a 2-ab +b 2))
解 由已知原方程的判别式Δ≥0,即(-a )2-4a ≥0,
∴a ≥4或a ≤0.
又∵?????
sin θ+cos θ=a ,
sin θcos θ=a ,
∴(sin θ+cos θ)2=1+2sin θcos θ,
则a 2-2a -1=0,从而a =1-2或a =1+2(舍去),
因此sin θ+cos θ=sin θcos θ=1- 2.
∴cos 3(π2-θ)+sin 3(π
2-θ)=sin 3θ+cos 3θ
=(sin θ+cos θ)(sin 2θ-sin θcos θ+cos 2θ) =(1-2)[1-(1-2)]=2-2.
B 组 专项能力提升 (时间:20分钟)
11.已知sin θ=-13,θ∈(-π2,π2),则sin(θ-5π)sin(3
2π-θ)的值是( )
A.229B .-229C .-19D.1
9
答案 B
解析 ∵sin θ=-13,θ∈(-π2,π2
),
∴cos θ=
1-sin 2θ=223
.
∴原式=-sin(π-θ)·(-cos θ)=sin θcos θ =-13×223=-229
.
12.已知2tan α·sin α=3,-π2<α<0,则sin α等于( )
A.32
B .-
32
C.12 D .-12
答案 B
解析 由2tan α·sin α=3得,2sin 2α
cos α=3,
即2cos 2α+3cos α-2=0, 又-π
2
<α<0,
解得cos α=1
2(cos α=-2舍去),
故sin α=-
32
. 13.已知角θ的顶点在坐标原点,始边与x 轴正半轴重合,终边在直线2x -y =0上,则sin (3π
2
+θ)+cos (π-θ)
sin (π
2-θ)-sin (π-θ)等于( )
A .-2
B .2
C .0 D.2
3
答案 B
解析 由题意可得tan θ=2, 原式=-cos θ-cos θcos θ-sin θ=-2
1-tan θ
=2.
14.已知cos ????π6-θ=a (|a |≤1),则cos ????5π6+θ+sin ????2π
3-θ的值是________. 答案 0
解析 cos ? ????5π6+θ=cos ??????π-? ????π6-θ =-cos ? ??
??π6-θ=-a . sin ? ????2π3-θ=sin ??????π2+? ????π6-θ=cos ? ????π6-θ=a , ∴cos ? ????5π6+θ+sin ? ??
??2π3-θ=0. 15.已知f (x )=cos 2(n π+x )·sin 2(n π-x )cos 2[(2n +1)π-x ](n ∈Z ).
(1)化简f (x )的表达式; (2)求f (π2014)+f (503π
1007
)的值.
解 (1)当n 为偶数,即n =2k (k ∈Z )时,
f (x )=cos 2(2k π+x )·sin 2(2k π-x )cos 2
[(2×2k +1)π-x ]
=cos 2x ·sin 2(-x )cos 2(π-x )
=cos 2x ·(-sin x )2(-cos x )2
=sin 2x ;
当n 为奇数,即n =2k +1(k ∈Z )时,
f (x )=cos 2[(2k +1)π+x ]·sin 2[(2k +1)π-x ]cos 2
{[2×(2k +1)+1]π-x }
=cos 2[2k π+(π+x )]·sin 2[2k π+(π-x )]cos 2[2×(2k +1)π+(π-x )]
=cos 2(π+x )·sin 2(π-x )cos 2
(π-x )
=(-cos x )2sin 2x (-cos x )2
=sin 2x ,
综上得f (x )=sin 2x . (2)由(1)得f (π2014)+f (503π
1007
)
=sin 2π2014+sin 21006π2014 =sin 2π2014+sin 2(π2-π
2014) =sin 2
π2014+cos 2π
2014
=1.
同角三角函数与诱导公式
同角三角函数基本关系 1,平方关系:sin 2α+cos 2α=1; 2,商数关系:tan α=α αcos sin 3,同角三角函数的关系式的基本用途: 根据一个角的某一个三角函数值,求出该角的其他三角函数值;化简同角三角函数式;证明同角的三角恒等式. 题型一,同角间的计算 利用基本关系计算,开方时注意正负 1,若sin α=45 ,且α是第二象限角,则tan α的值等于( ) A .-43 B.34 C .±34 D .±43 2,化简1-sin 2160°的结果是( ) A .cos160° B .-cos160° C .±cos160° D .±|cos160°| 3,若cos α=-817 ,则sin α=________,tan α=________ 4,若α是第四象限的角,tan α=-512 ,则sin α等于( ) A.15 B .-15 C.315 D .-513 5,若α为第三象限角,则cos α1-sin 2α+2sin α1-cos 2α 的值为( ) A .3 B .-3 C .1 D .-1 6,计算1-2sin40°·cos40°sin40°-1-sin 240° =________。 7,已知8 1cos sin =?αα,则ααsin cos -的值等于( ) A .±34 B .±23 C .23 D .-2 3
8,已知 2cos sin cos sin =-+θθθθ,求θθcos sin ?的值。 9,已知sin α·cos α= 81,且24παπ<<,则cos α-sin α的值是多少? 10,已知sin θ +cos θ=51,θ∈(0,π),求值: (1)tan θ; (2)sin θ-cos θ;(3)sin 3θ+cos 3θ。 11,求证: ()x x x x x x x x cos sin 1sin cos 2cos 1sin sin 1cos ++-=+-+。
高中常用三角函数公式大全
高中常用三角函数公式 两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+ 倍角公式 tan2A =A tan 12tanA 2- Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 半角公式 sin(2A )=2 cos 1A - cos(2A )=2 cos 1A + tan(2A )=A A cos 1cos 1+- cot( 2A )=A A cos 1cos 1-+ tan(2 A )=A A sin cos 1-=A A cos 1sin + 诱导公式 sin(-a) = -sina cos(-a) = cosa sin( 2 π-a) = cosa cos(2 π-a) = sina sin(2π+a) = cosa
cos( 2 π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =a a cos sin 万能公式 sina=2 )2 (tan 12tan 2a a + cosa=2 2 )2 (tan 1)2(tan 1a a +- tana=2 )2 (tan 12tan 2a a - 其它公式 a?sina+b?cosa=)b (a 22+×sin(a+c) [其中tanc= a b ] a?sin(a)-b?cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2 a )2 1-sin(a) = (sin 2a -cos 2 a )2 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanα cot (2kπ+α)= cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinα cos (π+α)= -cosα tan (π+α)= tanα cot (π+α)= cotα 公式三: 任意角α与 -α的三角函数值之间的关系:
三角函数诱导公式、万能公式、和差化积公式、倍角公式等公式总结及其推导
三角函数诱导公式: 诱导公式记忆口诀:“奇变偶不变,符号看象限”。 “奇、偶”指的是π/2的倍数的奇偶,“变与不变”指的是三角函数的名称的变化:“变”是指正弦变余弦,正切变余切。(反之亦然成立)“符号看象限”的含义是:把角α看做锐角,不考虑α角所在象限,看n?(π/2)±α是第几象限角,从而得到等式右边是正号还是负号。 符号判断口诀: “一全正;二正弦;三两切;四余弦”。这十二字口诀的意思就是说:第一象限内任何一个角的四种三角函数值都是“+”;第二象限内只有正弦是“+”,其余全部是“-”;第三象限内只有正切和余切是“+”,其余全部是“-”;第四象限内只有余弦是“+”,其余全部是“-”。 “ASCT”反Z。意即为“all(全部)”、“sin”、“cos”、“tan”按照将字母Z反过来写所占的象限对应的三角函数为正值。 三角函数诱导公式- 其他三角函数知识 同角三角函数的基本关系式 倒数关系 tanα?cotα=1 sinα?cscα=1 cosα?secα=1 商的关系 sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα 平方关系 sin^2(α)+cos^2(α)=1
1+tan^2(α)=sec^2(α) 1+cot^2(α)=csc^2(α) 同角三角函数关系六角形记忆法 构造以"上弦、中切、下割;左正、右余、中间1"的正六边形为模型。 倒数关系 对角线上两个函数互为倒数; 商数关系 六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。(主要是两条虚线两端的三角函数值的乘积,下面4个也存在这种关系。)。由此,可得商数关系式。 平方关系 在带有阴影线的三角形中,上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。 两角和差公式 sin(α+β)=sinαcosβ+cosαsinβ sin(α-β)=sinαcosβ-cosαsinβ cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ tan(α+β)=(tanα+tanβ )/(1-tanα ?tanβ) tan(α-β)=(tanα-tanβ)/(1+tanα ?tanβ) 二倍角的正弦、余弦和正切公式 sin2α=2sinαcosα
三角函数公式的推导及公式大全
诱导公式 目录·诱导公式 ·诱导公式记忆口诀 ·同角三角函数基本关系 ·同角三角函数关系六角形记忆法 ·两角和差公式 ·倍角公式 ·半角公式 ·万能公式 ·万能公式推导 ·三倍角公式 ·三倍角公式推导 ·三倍角公式联想记忆 ·和差化积公式 ·积化和差公式 ·和差化积公式推导 诱导公式 ★诱导公式★ 常用的诱导公式有以下几组: 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三: 任意角α与 -α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα
tan(-α)=-tanα cot(-α)=-cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五: 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα 公式六: π/2±α及3π/2±α与α的三角函数值之间的关系: sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα (以上k∈z) 诱导公式记忆口诀 ※规律总结※
同角三角函数基本关系式与诱导公式
第2节同角三角函数基本关系式与诱导公式 最新考纲 1.理解同角三角函数的基本关系式:sin2α+cos2α=1,sin α cos α =tan α;2.能利用单位圆中的三角函数线推导出π 2± α,π±α的正弦、余弦、正 切的诱导公式. 知识梳理1.同角三角函数的基本关系 (1)平方关系:sin2α+cos2α=1. (2)sin α cos α =tan__α. 2.三角函数的诱导公式 [常用结论与微点提醒] 1.诱导公式的记忆口诀:奇变偶不变,符号看象限. 2.同角三角函数基本关系式的常用变形: (sin α±cos α)2=1±2sin αcos α. 3.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号. 诊断自测 1.思考辨析(在括号内打“√”或“×”)
(1)sin(π+α)=-sin α成立的条件是α为锐角.( ) (2)六组诱导公式中的角α可以是任意角.( ) (3)诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的奇、偶是指π 2的奇数倍和偶数倍,变与不变指函数名称的变化.( ) (4)若sin(k π-α)=13(k ∈Z ),则sin α=1 3.( ) 解析 (1)对于α∈R ,sin(π+α)=-sin α都成立. (4)当k 为奇数时,sin α=1 3, 当k 为偶数时,sin α=-1 3. 答案 (1)× (2)√ (3)√ (4)× 2.(2018·成都诊断)已知α为锐角,且sin α=4 5,则cos (π+α)=( ) A.-35 B.35 C.-45 D.45 解析 因为α为锐角,所以cos α=1-sin 2α=3 5,所以cos(π+α)=-cos α =-3 5,故选A. 答案 A 3.已知sin ? ????5π2+α =1 5,那么cos α=( ) A.-25 B.-15 C.15 D.25 解析 ∵sin ? ????5π2+α=sin ? ???? π2+α=cos α,∴cos α=15.故选C. 答案 C 4.(必修4P22B3改编)已知tan α=2,则 sin α+cos α sin α-cos α 的值为________. 解析 原式=tan α+1tan α-1=2+1 2-1 =3. 答案 3 5.已知sin θ+cos θ=43,θ∈? ? ???0,π4,则sin θ-cos θ的值为________. 解析 ∵sin θ+cos θ=43,∴sin θcos θ=7 18.
常用的三角函数公式大全
三角函数公式 两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+ 倍角公式 tan2A = A tan 12tanA 2- Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A =2Cos 2A-1=1-2sin 2A 三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3 π-a) 半角公式 sin(2A )=2 cos 1A - cos(2A )=2 cos 1A + tan(2A )=A A cos 1cos 1+- cot( 2A )=A A cos 1cos 1-+
tan( 2 A )=A A sin cos 1-=A A cos 1sin + 和差化积
sina+sinb=2sin 2b a +cos 2 b a - sina-sinb=2cos 2b a +sin 2 b a - cosa+cosb = 2cos 2b a +cos 2 b a - cosa-cosb = -2sin 2b a +sin 2 b a - tana+tanb=b a b a cos cos )sin(+ 积化和差 sinasinb = - 2 1[cos(a+b)-cos(a-b)] cosacosb = 2 1[cos(a+b)+cos(a-b)] sinacosb = 2 1[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 万能公式 sina=2 )2 (tan 12tan 2a a + cosa=2 2 )2 (tan 1)2(tan 1a a +- tana=2 )2(tan 12tan 2a a - 其它公式 a?sina+b?cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a?sin(a)-b?cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2 a )2 1-sin(a) = (sin 2a -cos 2 a )2
三角函数公式大全81739
三角函数公式大全三角函数定义 函数关系 倒数关系: 商数关系: 平方关系: . 诱导公式 公式一:设为任意角,终边相同的角的同一三角函数的值相等: 公式二:设为任意角,与的三角函数值之间的关系:
公式三:任意角与的三角函数值之间的关系: 公式四:与的三角函数值之间的关系: 公式五:与的三角函数值之间的关系: 公式六:及与的三角函数值之间的关系: 记背诀窍:奇变偶不变,符号看象限.即形如(2k+1)90°±α,则函数
名称变为余名函数,正弦变余弦,余弦变正弦,正切变余切,余切变正切。形如2k×90°±α,则函数名称不变。 诱导公式口诀“奇变偶不变,符号看象限”意义: k×π/2±a(k∈z)的三角函数值.(1)当k为偶数时,等于α的同名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号; (2)当k为奇数时,等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号。 记忆方法一:奇变偶不变,符号看象限: 其中的奇偶是指的奇偶倍数,变余不变试制三角函数的名称变化若变,则是正弦变余弦,正切变余切------------------奇变偶不变 根据教的范围以及三角函数在哪个象限的争锋,来判断三角函数的符号-------------符号看象限 记忆方法二:无论α是多大的角,都将α看成锐角. 以诱导公式二为例: 若将α看成锐角(终边在第一象限),则π十α是第三象限的角(终 边在第三象限),正弦函数的函数值在第三象限是负值,余弦函数的函数 值在第三象限是负值,正切函数的函数值在第三象限是正值.这样,就得 到了诱导公式二. 以诱导公式四为例: 若将α看成锐角(终边在第一象限),则π-α是第二象限的角(终 边在第二象限),正弦函数的三角函数值在第二象限是正值,余弦函数的 三角函数值在第二象限是负值,正切函数的三角函数值在第二象限是负 值.这样,就得到了诱导公式四. 诱导公式的应用:运用诱导公式转化三角函数的一般步骤: 特别提醒:三角函数化简与求值时需要的知识储备:①熟记特殊角 的三角函数值;②注意诱导公式的灵活运用;③三角函数化简的要求是项 数要最少,次数要最低,函数名最少,分母能最简,易求值最好。
1.2.2同角的三角函数的基本关系 教案
1. 2.2同角的三角函数的基本关系 一、教学目标: ⒈掌握同角三角函数的基本关系式,理解同角公式都是恒等式的特定意义; 2 通过运用公式的训练过程,培养学生解决三角函数求值、化简、恒等式证明的解题技能,提高运用公式的灵活性; 3 注意运用数形结合的思想解决有关求值问题;在解决三角函数化简问题过程中,注意培养学生思维的灵活性及思维的深化;在恒等式证明的教学过程中,注意培养学生分析问题的能力,从而提高逻辑推理能力. 二、教学重、难点 重点:公式1cos sin 2 2=+αα及 αα α tan cos sin =的推导及运用: (1)已知某任意角的正弦、余弦、正切值中的一个,求其余两个;(2)化简三角函数式;(3)证明简单的三角恒等式. 难点: 根据角α终边所在象限求出其三角函数值;选择适当的方法证明三角恒等式. 三、学法与教学用具 利用三角函数线的定义, 推导同角三角函数的基本关系式: 1cos sin 2 2 =+αα及 αα α tan cos sin =,并灵活应用求三角函数值,化减三角函数式,证明三角恒等式等. 教学用具:圆规、三角板、投影 四、教学过程 【创设情境】 与初中学习锐角三角函数一样,本节课我们来研究同角三角函数之间关系,弄清同角各不同三角函数之间的联系,实现不同函数值之间的互相转化. 【探究新知】 探究:三角函数是以单位圆上点的坐标来定义的,你能从 圆的几何性质出发,讨论一 下同一个角不同三角函数之间的关系吗? 如图:以正弦线MP ,余弦线OM 和半径OP 三者的长构成直角三角形,而且1OP =.由勾股定理由2 2 1MP OM +=, 因此2 2 1x y +=,即22 sin cos 1αα+=. 根据三角函数的定义,当()2a k k Z π π≠+ ∈时,有 sin tan cos α αα =. 这就是说,同一个角α的正弦、余弦的平方等于1,商等于角α的正切. 【例题讲评】 例1化简: 440sin 12- 解:原式 80cos 80cos 80sin 1)80360(sin 122 2 ==-=+-= 例2 已知α α αααsin 1sin 1sin 1sin 1+---+是第三象限角,化简
三角函数诱导公式专项练习(含答案)
三角函数诱导公式专项练习 学校:___________姓名:___________班级:___________考号:___________ 一、单选题 1.() A. B. C. D. 2.的值为() A. B. C. D. 3.已知,则cos(60°–α)的值为 A. B. C. D.– 4.已知,且,则()A. B. C. D. 5.已知sin(π-α)=-,且α∈(-,0),则tan(2π-α)的值为( ) A. B.- C.± D. 6.已知,则=( ) A. B. C. D. 7.已知,,则() A. B. C. D. 8.已知,则() A. B. - C. D. - 9.如果,那么 A. - B. C. 1 D. -1 10.已知,则() A. B. C. D. 11.化简的值是()
A. B. C. D. 12.的值是() A. B. C. D. 13.已知角的终边经过点,则的值等于 A. B. C. D. 14.已知,则() A. B. C. D. 15.已知的值为()A. B. C. D. 16.已知则() A. B. C. D. 17.已知,且是第四象限角,则的值是( ) A. B. C. D. 18.已知sin=,则cos=( ) A. B. C.- D.- 19.已知cos α=k,k∈R,α∈,则sin(π+α)=( ) A.- B. C.± D.-k 20.=( ) A. sin 2-cos 2 B. sin 2+cos 2 C.±(sin 2-cos 2) D. cos 2-sin 2 21.的值为 A. B. C. D. 22.() A. B. C. D.
三角函数公式及记忆方法
三角函数公式 诱导公式的本质 所谓三角函数诱导公式,就是将角απ ±?)2 (n 的三角函数转化为角α的三角函数。 常用的诱导公式Z k ∈ 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: ααπs i n )2s i n (=+k ααπcos )2cos(=+k ααπt a n )2t a n (=+k ααπcot )2cot(=+k ααπs e c )2s e c (=+k ααπcsc )2csc(=+k 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: ααπs i n )s i n (-=+ ααπcos )cos(-=+ ααπt a n )t a n (=+ ααπcot )cot(=+ ααπs e c )s e c (-=+ ααπcsc )csc(-=+ 公式三: 任意角α与 -α的三角函数值之间的关系: ααs i n )s i n (-=- ααcos )cos(=- ααt a n )t a n (-=- ααcot )cot(-=- ααs e c )s e c (=- ααcsc )csc(-=- 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: ααπs i n )s i n (=- ααπcos )cos(-=- ααπt a n )t a n (-=- ααπcot )cot(-=- ααπs e c )s e c (-=- ααπcsc )csc( =- 公式五: 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: ααπs i n )2 s i n (-=- ααπcos )2cos(=- ααπt a n )2 t a n (-=- ααπcot )2cot(-=- ααπs e c )2s e c (=- ααπcsc )2csc(-=-
(完整版)三角函数诱导公式一览表(打印)
三角函数有关诱导公式一览表 公式 ) ( tan ) 2 tan( cos ) 2 cos( sin ) 2 sin( .1Z k k k k ∈ ? ? ? ? ? = + = + = + α α π α α π α α π ? ? ? ? ? = + - = + - = + α α π α α π α α π tan ) tan( cos ) cos( sin ) sin( .2 ? ? ? ? ? - = - = - - = - α α α α α α tan ) tan( cos ) cos( sin ) sin( .3 ? ? ? ? ? - = - - = - = - α α π α α π α α π tan ) tan( cos ) cos( sin ) sin( .4 ? ? ? ? ? = - = - α α π α α π sin ) 2 cos( cos ) 2 ( sin .5 ? ? ? ? ? - = + = + α α π α α π sin ) 2 cos( cos ) 2 ( sin .6 ? ? ? ? ? - = - - = - α α π α α π sin ) 2 3 cos( cos ) 2 3 ( sin .7 口诀函数名不变,符号看象限函数名改变,符号看先象限 图形 简记结合图形,7组公式可用口诀概括为:“奇变偶不变,符号看象限” 说明①公式的推导思路:前面4组通过找角的终边位置关系—坐标关系—三角函数关系而得出(后面3组通过角的变换,进而借助前面的有关公式转化得到)②各组诱导公式都可用含角度的形式
③在应用诱导公式解题时,基本思路是:“负化正,大化小,化成锐角再求值”。 一定要记清特殊角的三角函数值,根据问题做到准确应用,正确求解。
考研必备三角函数公式
三角函数诱导公式 常用的诱导公式有以下几组: 公式一: 设α为人意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三: 任意角α与-α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα
公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五: 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα 公式六: π/2±α与α的三角函数值之间的关系: sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π/2-α)=cosα cos(π/2-α)=sinα
tan(π/2-α)=cotα cot(π/2-α)=tanα 诱导公式记忆口诀 ※规律总结※ 上面这些诱导公式可以概括为: 对于k·π/2±α(k∈Z)的个三角函数值, ①当k是偶数时,得到α的同名函数值,即函数名不改变; ②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan. (奇变偶不变) 然后在前面加上把α看成锐角时原函数值的符号。 (符号看象限) 例如: sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。 当α是锐角时,2π-α∈(270°,360°),sin(2π-α)<0,符号为“-”。 所以sin(2π-α)=-sinα 上述的记忆口诀是: 奇变偶不变,符号看象限。 公式右边的符号为把α视为锐角时,角k·360°+α(k∈Z),-α、180°±α,360°-α 所在象限的原三角函数值的符号可记忆
同角三角函数公式的转化
同角三角函数公式的转化 同角三角函数的基本关系式十分重要,主要运用于三角函数的求值和恒等变形中各函数间的相互转化.在解答时,若能根据函数式的结构特点,适时灵活地选用公式,往往能获得简捷、迅速的解答. 一、“1”的代换 例1 证明:66441sin cos 31sin cos 2 x x x x --=--. 证明:∵22sin cos 1x x +=, ∴2231(sin cos )x x =+,2221(sin cos )x x =+, ∴662236644222441sin cos (sin cos )sin cos 1sin cos (sin cos )sin cos x x x x x x x x x x x x --+--=--+-- 424222223sin cos 3cos sin 3(sin cos )32sin cos 22 x x x x x x x x ++===··. 评注:本题在证明过程中,充分利用了三角函数的平方关系,对“1”进行了巧妙的代换,使问题迎刃而解.同学们要注意掌握和灵活运用“1”的代换. 二、化切为弦 例2 化简:tan (cos sin )sin (tan cot )θ θθθθθ-++··. 解:原式sin sin cos (cos sin )sin cos cos sin θθθθθθθθθ??=-++ ??? ·· 22sin sin sin cos sin cos cos cos θθθθθθθθ =-++=+ 例3 求证:2212sin 2cos21tan 2cos 2sin 21tan 2x x x x x x --=-+. 证明:右边sin 211tan 2cos 2sin 2cos 2sin 21tan 2cos 2sin 2cos 2x x x x x x x x x x - --===++ 2 (cos 2sin 2)(cos 2sin 2)(cos 2sin 2) x x x x x x -=+- 2222cos 2sin 22cos sin cos 2sin 2x x x x x x +-=- 2212sin cos2cos 2sin 2x x x x -==-左边.故原式成立. 评注:三角中的化简及三角恒等式的证明问题常常采用“化切为弦”,即利用商数关系把切函数化为弦函数,以达到统一名称之目的. 三、化弦为切 例3 已知tan 2α=,求下列各式的值: (1)sin 3cos sin cos αααα -+; (2)222sin sin cos cos αααα-+. 解:由已知tan 2α=.
同角三角函数基本关系及诱导公式(经典)
§4.2 同角三角函数基本关系及诱导公式 1. 同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1. (2)商数关系:sin αcos α =tan α. 2. 下列各角的终边与角α的终边的关系 3.
1. 判断下面结论是否正确(请在括号中打“√”或“×”) (1)sin(π+α)=-sin α成立的条件是α为锐角. ( × ) (2)六组诱导公式中的角α可以是任意角. ( × ) (3)若cos(n π-θ)=13(n ∈Z ),则cos θ=1 3 . ( × ) (4)已知sin θ=m -3m +5,cos θ=4-2m m +5,其中θ∈[π 2,π],则m <-5或m ≥3. ( × ) (5)已知θ∈(0,π),sin θ+cos θ=3-12,则tan θ的值为-3或-3 3 . ( × ) (6)已知tan α=-12,则1+2sin αcos αsin 2α-cos 2α 的值是-1 3. ( √ ) 2. 已知sin(π-α)=log 814,且α∈(-π 2,0),则tan(2π-α)的值为 ( ) A .-25 5 B.255 C .±25 5 D. 52 答案 B 解析 sin(π-α)=sin α=log 814=-2 3, 又α∈(-π 2,0), 得cos α=1-sin 2α= 53, tan(2π-α)=tan(-α)=-tan α=-sin αcos α=25 5. 3. 若tan α=2,则2sin α-cos α sin α+2cos α 的值为________. 答案 34
常用三角函数公式和口诀
常用三角函数公式及口诀 常用的诱导公式有以下几组: 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)=sinα (k∈Z) cos(2kπ+α)=cosα (k∈Z) tan(2kπ+α)=tanα (k∈Z) cot(2kπ+α)=cotα (k∈Z) 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三: 任意角α与 -α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五:
利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα 公式六: π/2±α及3π/2±α与α的三角函数值之间的关系: sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα (以上k∈Z) 注意:在做题时,将a看成锐角来做会比较好做。 诱导公式记忆口诀 规律总结 上面这些诱导公式可以概括为: 对于π/2*k ±α(k∈Z)的三角函数值,
(完整版)三角函数诱导公式总结
三角函数诱导公式与同角的三角函数 【知识点1】诱导公式及其应用 公式一: sin()-sin αα-=; cos()cos αα-= ; tan()tan αα-=- 公式二: ααπ-sin sin(=+); ααπ-cos cos(=+); ααπtan tan(=+). 公式三: ααπsin sin(=-); ααπ-cos cos(=-); ααπtan tan(-=-) 公式四: sin(2sin παα-=-); cos(2cos παα-=); tan(2tan παα-=-) 公式五: sin( 2π-α) = cos α; cos(2π -α) = sin α. 公式六: sin(2π+α) = cos α; cos(2π +α) =- sin α. 公式七: sin(32π-α)=- cos α; cos(32π -α) = -sin α. 公式八: sin(32π+α) = -cos α; cos(32 π +α) = sin α. 公式九:απαsin )2sin(=+k ; απαcos )2cos(=+k ; απαtan )2tan(=+k .(其中Z ∈k ). 方法点拨: 把α看作锐角 一、前四组诱导公式可以概括为:函数名不变,符号看象限 公式(五)到公式(八)总结为一句话:函数名改变,符号看象限(原函数所在象限) 二、奇变偶不变,符号看象限 将三角函数的角度全部化成απ +?2 k 或是απ-? 2 k ,符号名该不该变就看k 是奇数还是偶数,是奇数就改变函 数名,偶数就不变
例1、求值(1)29cos( )6π= __________. (2)0tan(855)-= _______ ___. (3)16 sin()3 π-= __________. 的值。 求:已知、例)sin(2)4cos() 3sin()2cos( , 3)tan( 2απααπαπαπ-+-+--=+ 例3、 )2cos()2sin(21++-ππ【 】 A .sin2-cos2 B .cos2-sin2 C .±(sin2-cos2) D .sin2+cos2 例4、下列各式不正确的是【 】 A . sin (α+180°)=-sin α B .cos (-α+β)=-cos (α-β) C . sin (-α-360°)=-sin α D .cos (-α-β)=cos (α+β) 例5、若sin (π+α)+sin (-α)=-m ,则sin (3π+α)+2sin (2π-α)等于【 】 A .-23 m B .-32 m C .23 m D .3 2 m 例6、已知函数1tan sin )(++=x b x a x f ,满足.7)5(=f 则)5(-f 的值为【 】 A .5 B .-5 C .6 D .-6 例7、试判断 sin(2)cos() (9tan (5) 2αππαα παπα-+??+- ??? ··cos 为第三象限角)符号 例8、化简3 sin(3)cos()cos(4) 25 tan(3)cos()sin() 22 πααππαπαπααπ-?-?+-?+?- 例9、已知方程sin(α - 3π) = 2cos(α - 4π),求 ) sin()2 3sin(2) 2cos(5)sin(α--α-π α-π+α-π 例10、若1sin()3 πθ-= ,求 []cos() cos(2) 3 3 cos()1cos sin()cos()sin() 22 πθθππθθ θπθπθπ+-+ --?-?--+的值. 提示:先化简,再将1sin 3 θ=代入化简式即可.
三角函数诱导公式大全
三角函數誘導公式大全 三角函数诱导公式 常用的诱导公式有以下几组: 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三: 任意角α与 -α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα 公式四:
利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五: 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα 公式六: π/2±α与α的三角函数值之间的关系: sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα 诱导公式记忆口诀 ※规律总结※ 上面这些诱导公式可以概括为:
对于k2π/2±α(k∈Z)的个三角函数值, ①当k是偶数时,得到α的同名函数值,即函数名不改变; ②当k是奇数时,得到α相应的余函数值,即 sin→cos;cos→sin;tan→cot,cot→tan. (奇变偶不变) 然后在前面加上把α看成锐角时原函数值的符号。 (符号看象限) 例如: sin(2π-α)=sin(42π/2-α),k=4为偶数,所以取sinα。 当α是锐角时,2π-α∈(270°,360°),sin(2π-α)<0,符号为“-”。 所以sin(2π-α)=-sinα 上述的记忆口诀是: 奇变偶不变,符号看象限。 公式右边的符号为把α视为锐角时,角k2360°+α(k∈Z),-α、180°±α,360°-α 所在象限的原三角函数值的符号可记忆 水平诱导名不变;符号看象限。 各种三角函数在四个象限的符号如何判断,也可以记住口诀“一全正;二正弦;三为切;四余弦”. 这十二字口诀的意思就是说: 第一象限内任何一个角的四种三角函数值都是“+”; 第二象限内只有正弦是“+”,其余全部是“-”; 第三象限内切函数是“+”,弦函数是“-”; 第四象限内只有余弦是“+”,其余全部是“-”. 上述记忆口诀,一全正,二正弦,三正切,四余弦
角函数的概念同角三角函数的基本关系式诱导公式重难点分析与出题角度归纳
Xx 学校学科教师辅导讲义 一)一、定义:角可以看作成平面内一条射线绕着端点从一个位置到另一个位置所称的图形。旋转开始时的射线、终止时 的射线分别叫作_______、_______,射线的端点O 叫做_________.按逆时针方向旋转形成的角叫做_______,顺时针方向旋转形成的角叫做_______,若一条射线没有作任何旋转,称它形成了一个_______。 二、在直角坐标系内讨论角: (1)角的顶点在原点,始边与x 轴的非负半轴重合,角的终边(除端点外)在第几项先,就说这个角是第几象限角(或 者说这个角属于第几象限); 例如:30°、390°、-330°等都是第一象限角;120°、480°、-240°等都是第二象限角;240°、600°、-120°等 都是第三象限角;-30°、-390°、330°等都是第四象限角。 注意:锐角_____第一象限角,但第一象限角_______锐角;钝角______第二象限角,但第二象限角________钝角。(填 “都是”或者“不都是”) (2)若角的终边在坐标轴上,就说这个角不属于任一象限。 例如:直角、周角、平角都不属于任一象限。 三、终边相同的角(重点) 所有与角α终边相同的角,连同角α在内,可构成一个集合S={Z k k ∈?+=?,360/αββ },即任一与角α终 边相同的角都可以表示为角α与整个周角的和。 四、1弧度角的定义:我们把等于半径长的圆弧所对的圆心角叫做1弧度的角。单位符号是 rad,读作弧度。2、弧度 数:在单位圆中,当圆心角为周角时,它所对的弧长为2π,所以周角的弧度数为2π,周角是2πrad 的角. 任意一个0°~360°的角的弧度数必然适合不等式 0≤x<2π. 任一正角的弧度数都是一个正实数;,任一负角的弧度数都是一个负实数; 零角的弧度数是0. 五、弧度制与角度制的换算 360°=2πrad ;180°=πrad ;1°= 180πrad ≈;1rad=π 180 ≈°≈57°18′。
同角三角函数的基本关系与诱导公式
同角三角函数的基本关系与诱导公式 [A 级 基础题——基稳才能楼高] 1.(2019·新疆普通高中学业水平考试)已知x ∈? ????-π2,0,cos x =45,则tan x 的值为( ) A.3 4 B .-34 C.43 D .-43 解析:选B 因为x ∈? ????-π2,0,所以sin x =-1-cos 2 x =-35,所以tan x = sin x cos x =-3 4 .故选B. 2.(2019·淮南十校联考)已知sin ? ????α-π3=13,则cos ? ????α+π6的值是( ) A .-1 3 B.13 C.22 3 D .-223 解析:选A ∵sin ? ????α-π3=13,∴cos ? ????α+π6=cos ??????π2+? ????α-π3=-sin ? ????α-π3=-1 3 ,故选A. 3.(2019·重庆一模)log 2? ????cos 7π4的值为( ) A .-1 B .-12 C.1 2 D.22 解析:选B log 2? ????cos 7π4=log 2? ????cos π4=log 222=-12.故选B. 4.(2019·遵义模拟)若sin ? ????π2+α=-35,且α∈( π2,π ),则sin(π-2α) =( ) A .-24 25 B .-1225 C.1225 D.2425
解析:选A ∵sin ? ????π2+α=cos α=-35,α∈? ????π2,π,∴sin α=45,∴sin(π-2α)=sin 2α=2sin αcos α=2×45×? ????-35=-24 25 .故选A. 5.(2019·沈阳模拟)若1+cos α sin α=2,则cos α-3sin α=( ) A .-3 B .3 C .-95 D.95 解析:选C ∵1+cos αsin α=2,∴cos α=2sin α-1,又sin 2α+cos 2 α=1, ∴sin 2α+(2sin α-1)2=1,5sin 2 α-4sin α=0,解得sin α=45或sin α=0(舍 去), ∴cos α-3sin α=-sin α-1=-9 5 .故选C. 6.(2019·庄河高中期中)已知sin ? ????α-π12=13,则cos ? ????α+17π12等于( ) A.1 3 B.22 3 C .-13 D .-223 解析:选A cos ? ????α+17π12=cos ??????3π2+? ????α-π12=sin ? ????α-π12=13.故选A. [B 级 保分题——准做快做达标] 1.(2019·宝鸡金台区质检)已知sin 2α=23,则tan α+1 tan α=( ) A. 3 B. 2 C .3 D .2 解析:选C tan α+1tan α=sin αcos α+cos αsin α=1sin αcos α=2sin 2α=2 2 3=3.故选 C. 2.(2019·常德一中月考)已知α∈R ,sin α+2cos α=10 2 ,则tan 2α=( ) A.43 B.34
