R语言与机器学习(4)支持向量机

算法四:支持向量机
说到支持向量机,必须要提到july大神的《支持向量机通俗导论》,个人感觉再怎么写也不可能写得比他更好的了。这也正如青莲居士见到崔颢的黄鹤楼后也只能叹“此处有景道不得”。不过我还是打算写写SVM的基本想法与libSVM中R的接口。
一、SVM的想法
回到我们最开始讨论的KNN算法,它占用的内存十分的大,而且需要的运算量也非常大。那么我们有没有可能找到几个最有代表性的点(即保留较少的点)达到一个可比的效果呢?
要回答这个问题,我们首先必须思考如何确定点的代表性?我想关于代表性至少满足这样一个条件:无论非代表性点存在多少,存在与否都不会影响我们的决策结果。显然如果仍旧使用KNN算法的话,是不会存在训练集的点不是代表点的情况。那么我们应该选择一个怎样的“距离”满足仅依靠代表点就能得到全体点一致的结果?
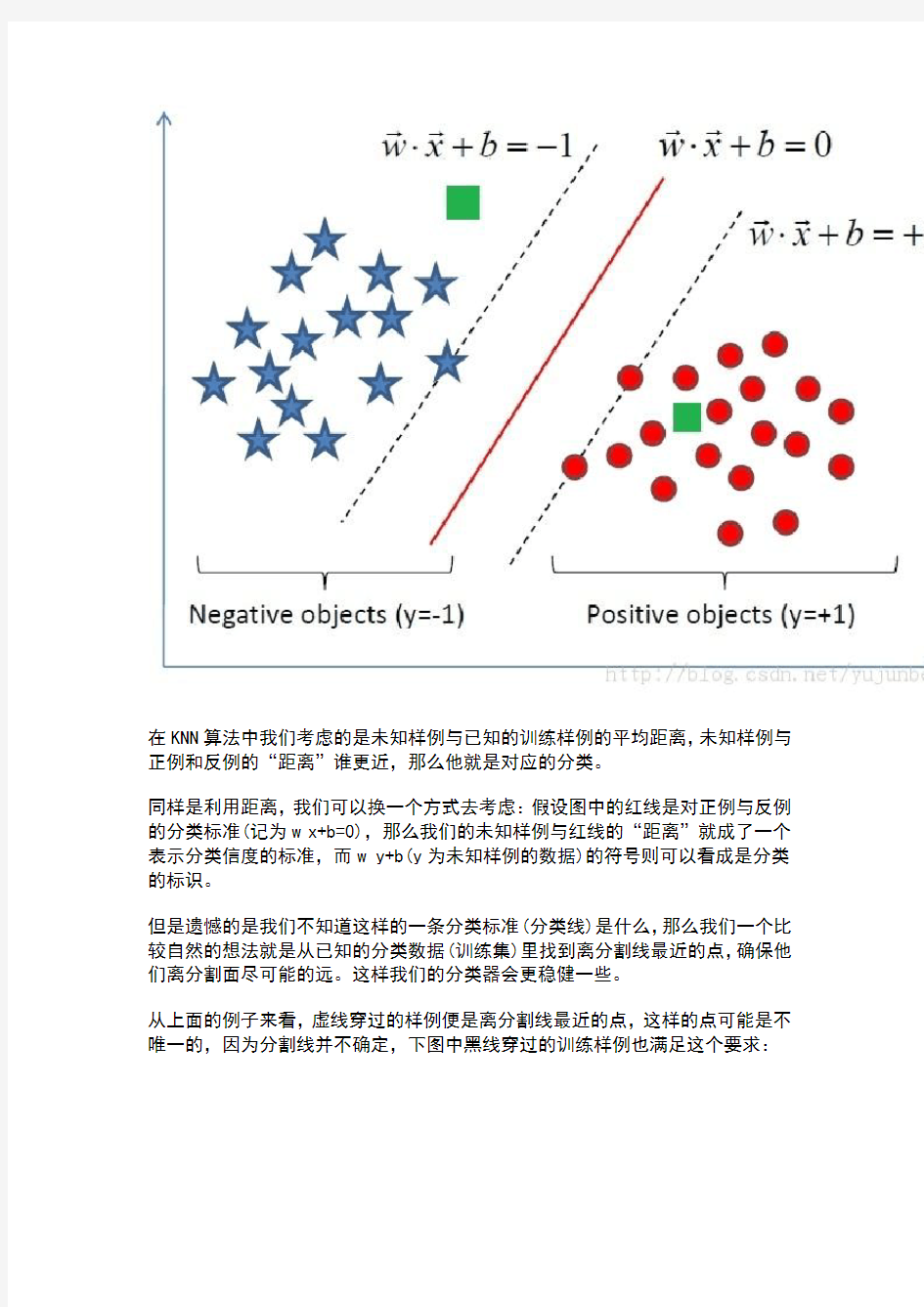
我们先看下面一个例子:假设我们的训练集分为正例与反例两类,分别用红色的圆圈与蓝色的五角星表示,现在出现了两个未知的案例,也就是图中绿色的方块,我们如何去分类这两个例子呢?
在KNN算法中我们考虑的是未知样例与已知的训练样例的平均距离,未知样例与正例和反例的“距离”谁更近,那么他就是对应的分类。
同样是利用距离,我们可以换一个方式去考虑:假设图中的红线是对正例与反例的分类标准(记为w x+b=0),那么我们的未知样例与红线的“距离”就成了一个表示分类信度的标准,而w y+b(y为未知样例的数据)的符号则可以看成是分类的标识。
但是遗憾的是我们不知道这样的一条分类标准(分类线)是什么,那么我们一个比较自然的想法就是从已知的分类数据(训练集)里找到离分割线最近的点,确保他们离分割面尽可能的远。这样我们的分类器会更稳健一些。
从上面的例子来看,虚线穿过的样例便是离分割线最近的点,这样的点可能是不唯一的,因为分割线并不确定,下图中黑线穿过的训练样例也满足这个要求:
所以“他们离分割面尽可能的远”这个要求就十分重要了,他告诉我们一个稳健的超平面是红线而不是看上去也能分离数据的黄线。
这样就解决了我们一开始提出的如何减少储存量的问题,我们只要存储虚线划过的点即可(因为在w x+b=-1左侧,w x+b=1右侧的点无论有多少都不会影响决策)。像图中虚线划过的,距离分割直线(比较专业的术语是超平面)最近的点,我们称之为支持向量。这也就是为什么我们这种分类方法叫做支持向量机的原因。
至此,我们支持向量机的分类问题转化为了如何寻找最大间隔的优化问题。
二、SVM的一些细节
支持向量机的实现涉及许多有趣的细节:如何最大化间隔,存在“噪声”的数据集怎么办,对于线性不可分的数据集怎么办等。
我这里不打算讨论具体的算法,因为这些东西完全可以参阅july大神的《支持向量机通俗导论》,我们这里只是介绍遇到问题时的想法,以便分析数据时合理调用R中的函数。
几乎所有的机器学习问题基本都可以写成这样的数学表达式:
给定条件:n个独立同分布观测样本(x1 , y1 ), (x2 , y2 ),……,(xn , yn )
目标:求一个最优函数f (x,w* )
最理想的要求:最小化期望风险R(w)
不同的是我们如何选择f,R。对于支持向量机来说,f(x,w*)=w x+b,最小化风险就是最大化距离|w x|/||w||,即arg max{min(label (w x+b))/||w||} (也就是对最不confidence 的数据具有了最大的 confidence)
这里的推导涉及了对偶问题,拉格朗日乘子法与一堆的求导,我们略去不谈,将结果叙述如下:
(完整word版)支持向量机(SVM)原理及应用概述分析
支持向量机(SVM )原理及应用 一、SVM 的产生与发展 自1995年Vapnik (瓦普尼克)在统计学习理论的基础上提出SVM 作为模式识别的新方法之后,SVM 一直倍受关注。同年,Vapnik 和Cortes 提出软间隔(soft margin)SVM ,通过引进松弛变量i ξ度量数据i x 的误分类(分类出现错误时i ξ大于0),同时在目标函数中增加一个分量用来惩罚非零松弛变量(即代价函数),SVM 的寻优过程即是大的分隔间距和小的误差补偿之间的平衡过程;1996年,Vapnik 等人又提出支持向量回归 (Support Vector Regression ,SVR)的方法用于解决拟合问题。SVR 同SVM 的出发点都是寻找最优超平面(注:一维空间为点;二维空间为线;三维空间为面;高维空间为超平面。),但SVR 的目的不是找到两种数据的分割平面,而是找到能准确预测数据分布的平面,两者最终都转换为最优化问题的求解;1998年,Weston 等人根据SVM 原理提出了用于解决多类分类的SVM 方法(Multi-Class Support Vector Machines ,Multi-SVM),通过将多类分类转化成二类分类,将SVM 应用于多分类问题的判断:此外,在SVM 算法的基本框架下,研究者针对不同的方面提出了很多相关的改进算法。例如,Suykens 提出的最小二乘支持向量机 (Least Square Support Vector Machine ,LS —SVM)算法,Joachims 等人提出的SVM-1ight ,张学工提出的中心支持向量机 (Central Support Vector Machine ,CSVM),Scholkoph 和Smola 基于二次规划提出的v-SVM 等。此后,台湾大学林智仁(Lin Chih-Jen)教授等对SVM 的典型应用进行总结,并设计开发出较为完善的SVM 工具包,也就是LIBSVM(A Library for Support Vector Machines)。LIBSVM 是一个通用的SVM 软件包,可以解决分类、回归以及分布估计等问题。 二、支持向量机原理 SVM 方法是20世纪90年代初Vapnik 等人根据统计学习理论提出的一种新的机器学习方法,它以结构风险最小化原则为理论基础,通过适当地选择函数子集及该子集中的判别函数,使学习机器的实际风险达到最小,保证了通过有限训练样本得到的小误差分类器,对独立测试集的测试误差仍然较小。 支持向量机的基本思想:首先,在线性可分情况下,在原空间寻找两类样本的最优分类超平面。在线性不可分的情况下,加入了松弛变量进行分析,通过使用非线性映射将低维输
【原创】R语言支持向量机svm实践案例报告附代码数据
支持向量机(support vector machine)第一次见到这个词可能难以理解这个奇怪的名字,这是一个90年代产生在深度学习出来之前逼格满满的算法,被认为是适应性最广的分类器之一。SVM是一个基于严格的数学推导的算法(但本文不推导),本文只大概介绍基本思想和简单原理及实践过程。 最大间隔分类器 在二维平面上,一条直线可以把平面分成两边;在三维空间中,一个平面可以把空间分成两块……那么同理,在p+1的高维空间中,一个p维的超平面也可以将其成本两部分,超平面的定义: 超平面的定义 根据高中空间几何的知识可知,把一个点代入上式,如果等于0说明正好在超平面上;大于0在其上方,小于0在其下方。 那么就可以根据这个特点来映射二分类问题。只要我们可以构建出超平面方程,再把样本点代入,根据结果的正负就可以进行分类。 超平面分隔 实际上,能把不同类别样本分隔开来的超平面并不止一个,有无数个。如图中蓝色和橙色虚线都能把两类样本分开,那么你认为这两个哪一个分隔效果更好? 如果用蓝色分隔超平面,那上面的白球就被分成橙色,下面的白球则被分成蓝色;如果用橙色分隔超平面,则结果完全相反。可是根据KNN的思想,很容易看出上面的白球应该被分成蓝色,下面的白球应该被分成橙色。
可以观察到,橙色超平面总体上距离两边的球都比蓝色的远,这就是涉及到最大间隔超平面的概念。对于任一个超平面(以实线表示),把它往两边平移,直至与两边的样本相交(以虚线表示,相交点就叫支持向量,现在知道支持向量机这个名字的由来了吧~),如果两边的虚线的距离最大,这个超平面就是最大间隔超平面。因为最大间隔超平面总体上把不同类别的样本分得最大,所以泛化性能最好。 最大间隔超平面 那么SVM算法的优化实际上就是对超平面间距的最大值优化,以数字公式来表达是这样的: SVM的约束条件及优化目标 其中M是超平面间隔,也是优化目标。β是归一化参数,y取1或-1表示二分类。 优化过程涉及到复杂的数学推导就不细说了。 线性不可分情况 上面的例子中,不同样本之间本来就分隔得挺好,所以很容易被线性超平面分隔开来。但现实中的数据往往不太可能自动地分离得这么好,甚至存在着线性不可分,比如请用一条直线把下面两种类别的点完全区分开来:
支持向量机及支持向量回归简介
3.支持向量机(回归) 3.1.1 支持向量机 支持向量机(SVM )是美国Vapnik 教授于1990年代提出的,2000年代后成为了很受欢迎的机器学习方法。它将输入样本集合变换到高维空间使得其分离性状况得到改善。它的结构酷似三层感知器,是构造分类规则的通用方法。SVM 方法的贡献在于,它使得人们可以在非常高维的空间中构造出好的分类规则,为分类算法提供了统一的理论框架。作为副产品,SVM 从理论上解释了多层感知器的隐蔽层数目和隐节点数目的作用,因此,将神经网络的学习算法纳入了核技巧范畴。 所谓核技巧,就是找一个核函数(,)K x y 使其满足(,)((),())K x y x y φφ=,代 替在特征空间中内积(),())x y φφ(的计算。因为对于非线性分类,一般是先找一个非线性映射φ将输入数据映射到高维特征空间,使之分离性状况得到很大改观,此时在该特征空间中进行分类,然后再返会原空间,就得到了原输入空间的非线性分类。由于内积运算量相当大,核技巧就是为了降低计算量而生的。 特别, 对特征空间H 为Hilbert 空间的情形,设(,)K x y 是定义在输入空间 n R 上的二元函数,设H 中的规范正交基为12(),(),...,(), ...n x x x φφφ。如果 2 2 1 (,)((),()), {}k k k k k K x y a x y a l φφ∞ == ∈∑ , 那么取1 ()() k k k x a x φφ∞ ==∑ 即为所求的非线性嵌入映射。由于核函数(,)K x y 的定义 域是原来的输入空间,而不是高维的特征空间。因此,巧妙地避开了计算高维内 积 (),())x y φφ(所需付出的计算代价。实际计算中,我们只要选定一个(,)K x y ,
R语言-支持向量机
支持向量机 一、SVM的想法 回到我们最开始讨论的KNN算法,它占用的内存十分的大,而且需要的运算量也非常大。那么我们有没有可能找到几个最有代表性的点(即保留较少的点)达到一个可比的效果呢? 我们先看下面一个例子:假设我们的训练集分为正例与反例两类,分别用红色的圆圈与蓝色的五角星表示,现在出现了两个未知的案例,也就是图中绿色的方块,我们如何去分类这两个例子呢? 在KNN算法中我们考虑的是未知样例与已知的训练样例的平均距离,未知样例与正例和反例的“距离”谁更近,那么他就是对应的分类。 同样是利用距离,我们可以换一个方式去考虑:假设图中的红线是对正例与反例的分类标准(记为w x+b=0),那么我们的未知样例与红线的“距离”就成了一个表示分类信度的标准,而w y+b(y为未知样例的数据)的符号则可以看成是分类的标识。 但是遗憾的是我们不知道这样的一条分类标准(分类线)是什么,那么我们一个比较自然的想法就是从已知的分类数据(训练集)里找到离分割线最近的点,确保他们离分割面尽可能的远。这样我们的分类器会更稳健一些。 从上面的例子来看,虚线穿过的样例便是离分割线最近的点,这样的点可能是不唯一的,因为分割线并不确定,下图中黑线穿过的训练样例也满足这个要求:
所以“他们离分割面尽可能的远”这个要求就十分重要了,他告诉我们一个稳健的超平面是红线而不是看上去也能分离数据的黄线。 这样就解决了我们一开始提出的如何减少储存量的问题,我们只要存储虚线划过的点即可(因为在w x+b=-1左侧,w x+b=1右侧的点无论有多少都不会影响决策)。像图中虚线划过的,距离分割直线(比较专业的术语是超平面)最近的点,我们称之为支持向量。这也就是为什么我们这种分类方法叫做支持向量机的原因。 至此,我们支持向量机的分类问题转化为了如何寻找最大间隔的优化问题。 二、SVM的一些细节 支持向量机的实现涉及许多有趣的细节:如何最大化间隔,存在“噪声”的数据集怎么办,对于线性不可分的数据集怎么办等。 我这里不打算讨论具体的算法,因为这些东西完全可以参阅july大神的《支持向量机通俗导论》,我们这里只是介绍遇到问题时的想法,以便分析数据时合理调用R中的函数。 几乎所有的机器学习问题基本都可以写成这样的数学表达式: 给定条件:n个独立同分布观测样本(x1 , y1 ), (x2 , y2 ),……,(xn , yn )
SVM支持向量机白话入门
(一)SVM的八股简介 支持向量机(Support Vector Machine)是Cortes和Vapnik于1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中[10]。 支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度,Accuracy)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷,以期获得最好的推广能力[14](或称泛化能力)。 以上是经常被有关SVM 的学术文献引用的介绍,有点八股,我来逐一分解并解释一下。 Vapnik是统计机器学习的大牛,这想必都不用说,他出版的《Statistical Learning Theory》是一本完整阐述统计机器学习思想的名著。在该书中详细的论证了统计机器学习之所以区别于传统机器学习的本质,就在于统计机器学习能够精确的给出学习效果,能够解答需要的样本数等等一系列问题。与统计机器学习的精密思维相比,传统的机器学习基本上属于摸着石头过河,用传统的机器学习方法构造分类系统完全成了一种技巧,一个人做的结果可能很好,另一个人差不多的方法做出来却很差,缺乏指导和原则。 所谓VC维是对函数类的一种度量,可以简单的理解为问题的复杂程度,VC 维越高,一个问题就越复杂。正是因为SVM关注的是VC维,后面我们可以看到,SVM解决问题的时候,和样本的维数是无关的(甚至样本是上万维的都可以,这使得SVM很适合用来解决文本分类的问题,当然,有这样的能力也因为引入了核函数)。 结构风险最小听上去文绉绉,其实说的也无非是下面这回事。
支持向量机原理及应用(DOC)
支持向量机简介 摘要:支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷,以求获得最好的推广能力 。我们通常希望分类的过程是一个机器学习的过程。这些数据点是n 维实空间中的点。我们希望能够把这些点通过一个n-1维的超平面分开。通常这个被称为线性分类器。有很多分类器都符合这个要求。但是我们还希望找到分类最佳的平面,即使得属于两个不同类的数据点间隔最大的那个面,该面亦称为最大间隔超平面。如果我们能够找到这个面,那么这个分类器就称为最大间隔分类器。 关键字:VC 理论 结构风险最小原则 学习能力 1、SVM 的产生与发展 自1995年Vapnik 在统计学习理论的基础上提出SVM 作为模式识别的新方法之后,SVM 一直倍受关注。同年,Vapnik 和Cortes 提出软间隔(soft margin)SVM ,通过引进松弛变量i ξ度量数据i x 的误分类(分类出现错误时i ξ大于0),同时在目标函数中增加一个分量用来惩罚非零松弛变量(即代价函数),SVM 的寻优过程即是大的分隔间距和小的误差补偿之间的平衡过程;1996年,Vapnik 等人又提出支持向量回归 (Support Vector Regression ,SVR)的方法用于解决拟合问题。SVR 同SVM 的出发点都是寻找最优超平面,但SVR 的目的不是找到两种数据的分割平面,而是找到能准确预测数据分布的平面,两者最终都转换为最优化问题的求解;1998年,Weston 等人根据SVM 原理提出了用于解
R语言与机器学习(4)支持向量机
算法四:支持向量机 说到支持向量机,必须要提到july大神的《支持向量机通俗导论》,个人感觉再怎么写也不可能写得比他更好的了。这也正如青莲居士见到崔颢的黄鹤楼后也只能叹“此处有景道不得”。不过我还是打算写写SVM的基本想法与libSVM中R的接口。 一、SVM的想法 回到我们最开始讨论的KNN算法,它占用的内存十分的大,而且需要的运算量也非常大。那么我们有没有可能找到几个最有代表性的点(即保留较少的点)达到一个可比的效果呢? 要回答这个问题,我们首先必须思考如何确定点的代表性?我想关于代表性至少满足这样一个条件:无论非代表性点存在多少,存在与否都不会影响我们的决策结果。显然如果仍旧使用KNN算法的话,是不会存在训练集的点不是代表点的情况。那么我们应该选择一个怎样的“距离”满足仅依靠代表点就能得到全体点一致的结果? 我们先看下面一个例子:假设我们的训练集分为正例与反例两类,分别用红色的圆圈与蓝色的五角星表示,现在出现了两个未知的案例,也就是图中绿色的方块,我们如何去分类这两个例子呢?
在KNN算法中我们考虑的是未知样例与已知的训练样例的平均距离,未知样例与正例和反例的“距离”谁更近,那么他就是对应的分类。 同样是利用距离,我们可以换一个方式去考虑:假设图中的红线是对正例与反例的分类标准(记为w x+b=0),那么我们的未知样例与红线的“距离”就成了一个表示分类信度的标准,而w y+b(y为未知样例的数据)的符号则可以看成是分类的标识。 但是遗憾的是我们不知道这样的一条分类标准(分类线)是什么,那么我们一个比较自然的想法就是从已知的分类数据(训练集)里找到离分割线最近的点,确保他们离分割面尽可能的远。这样我们的分类器会更稳健一些。 从上面的例子来看,虚线穿过的样例便是离分割线最近的点,这样的点可能是不唯一的,因为分割线并不确定,下图中黑线穿过的训练样例也满足这个要求:
【原创】r语言SVM-in-R代码
> ## SVM in R > ## classify cats into male / female by heart and body weight > library(e1071) > data(cats, package="MASS") > inputData <- data.frame(cats[, c (2,3)], + response = as.factor(cats$Sex)) > ## linear kernel > svmfit <- svm(response ~ ., data = inputData, kernel = "linear", + cost = 10, scale = FALSE) > plot(svmfit, inputData) > compareTable <- table (inputData$response, predict(svmfit)) > mean(inputData$response != predict(svmfit)) [1] 0.1944444 > compareTable F M F 33 14 M 14 83 > ## radial kernel > svmfit <- svm(response ~ ., data = inputData, kernel = "radial", + cost = 10, scale = FALSE) > plot(svmfit, inputData) > compareTable <- table (inputData$response, predict(svmfit)) > mean(inputData$response != predict(svmfit)) [1] 0.1875 > ## radial kernel > svmfit <- svm(response ~ ., data = inputData, kernel = "radial", + cost = 10, scale = FALSE) > plot(svmfit, inputData) > compareTable <- table (inputData$response, predict(svmfit)) > mean(inputData$response != predict(svmfit)) [1] 0.1875 > > ## Prepare training and test data > set.seed(100) > rowIndices <- 1 : nrow(inputData) > sampleSize <- 0.8 * length(rowIndices) > trainingRows <- sample (rowIndices, sampleSize) > trainingData <- inputData[trainingRows, ] > testData <- inputData[-trainingRows, ] > ## tune to select best gamma and cost > tuned <- tune.svm(response ~., data = trainingData, + gamma = 10^(-6:1), cost = 10^(-1:2)) > summary(tuned) Parameter tuning of 'svm': - sampling method: 10-fold cross validation - best parameters: gamma cost 0.01 100 - best performance: 0.2439394 - Detailed performance results: gamma cost error dispersion 1 0.000001 0.1 0.3325758 0.16269565 2 0.000010 0.1 0.3325758 0.16269565 3 0.000100 0.1 0.3325758 0.16269565 4 0.001000 0.1 0.3325758 0.16269565 5 0.010000 0.1 0.3325758 0.16269565 6 0.100000 0.1 0.3325758 0.16269565
随机森林与支持向量机分类性能比较
随机森林与支持向量机分类性能比较 黄衍,查伟雄 (华东交通大学交通运输与经济研究所,南昌 330013) 摘要:随机森林是一种性能优越的分类器。为了使国内学者更深入地了解其性能,通过将其与已在国内得到广泛应用的支持向量机进行数据实验比较,客观地展示其分类性能。实验选取了20个UCI数据集,从泛化能力、噪声鲁棒性和不平衡分类三个主要方面进行,得到的结论可为研究者选择和使用分类器提供有价值的参考。 关键词:随机森林;支持向量机;分类 中图分类号:O235 文献标识码: A Comparison on Classification Performance between Random Forests and Support Vector Machine HUANG Yan, ZHA Weixiong (Institute of Transportation and Economics, East China Jiaotong University, Nanchang 330013, China)【Abstract】Random Forests is an excellent classifier. In order to make Chinese scholars fully understand its performance, this paper compared it with Support Vector Machine widely used in China by means of data experiments to objectively show its classification performance. The experiments, using 20 UCI data sets, were carried out from three main aspects: generalization, noise robustness and imbalanced data classification. Experimental results can provide references for classifiers’ choice and use. 【Key words】Random Forests; Support Vector Machine; classification 0 引言 分类是数据挖掘领域研究的主要问题之一,分类器作为解决问题的工具一直是研究的热点。常用的分类器有决策树、逻辑回归、贝叶斯、神经网络等,这些分类器都有各自的性能特点。本文研究的随机森林[1](Random Forests,RF)是由Breiman提出的一种基于CART 决策树的组合分类器。其优越的性能使其在国外的生物、医学、经济、管理等众多领域到了广泛的应用,而国内对其的研究和应用还比较少[2]。为了使国内学者对该方法有一个更深入的了解,本文将其与分类性能优越的支持向量机[3](Support Vector Machine,SVM)进行数据实验比较,客观地展示其分类性能。本文选取了UCI机器学习数据库[4]的20个数据集作为实验数据,通过大量的数据实验,从泛化能力、噪声鲁棒性和不平衡分类三个主要方面进行比较,为研究者选择和使用分类器提供有价值的参考。 1 分类器介绍 1.1 随机森林 随机森林作为一种组合分类器,其算法由以下三步实现: 1. 采用bootstrap抽样技术从原始数据集中抽取n tree个训练集,每个训练集的大小约为原始数据集的三分之二。 2. 为每一个bootstrap训练集分别建立分类回归树(Classification and Regression Tree,CART),共产生n tree棵决策树构成一片“森林”,这些决策树均不进行剪枝(unpruned)。在作者简介:黄衍(1986-),男,硕士研究生,主要研究方向:数据挖掘与统计分析。 通信联系人:查伟雄,男,博士,教授,主要研究方向:交通运输与经济统计分析。 E-mail: huangyan189@https://www.360docs.net/doc/3913649965.html,.
R语言学习
#层次聚类 Data=iris[,-5]; Means=sapply(data,mean);SD=sapply(data,sd); dataScale=scale(data,center=means,scale=SD); Dist=dist(dataScale,method=”euclidean”); heatmap(as.matrix(Dist),labRow=FALSE,labCol=FALSE); clusteModel=hclust(Dist,method=”ward”); result=cutree(clusteModel,k=3); table(iris[,5],result); plot(clusteModel); library(fastcluster); # kuaisu cengcijulei clusteModel=hclust(Dist,method=”ward”); library(proxy); res=dist(data,method=”cosine”); x=c(0,0,1,1,1,1); y=c(1,0,1,1,0,1); dist(rbind(x,y),method=”Jaccard”); x=c(0,0,1.2,1,0.5,1,NA); y=c(1,0,2.3,1,0.9,1,1); d=abs(x-y); Dist=sum(d[!is.na(d)])/6; # k-means聚类 clusteModel=kmeans(dataScale,centers=3,nstart=10); class(clusteModel); library(proxy); library(cluster); clustModel=pam(dataScale,k=3,metric=”Mahalanobis”); clustModel$medoids table(iris$Species,clustModel$clustering); par(mfcol=c(1,2)); plot(clustModel,which.plots=2,main=””); Plot(clustModel,which.plots=1,main=””); library(devtools); install_github(“lijian13/rinds”);
支持向量机
第四章 支持向量机(SVM ——Support Vector Machine ) §4-1. 线性分类问题的支持向量机 一、 分类问题与机器学习 设有两类模式1C 和2C ,() () (){}N 221y ,y ,y ,N X X X T 1 =是从模式1 C 和2C 中抽样得到的训练集,其中M n R X ∈、{}1- ,1∈n y 。若n X 属于1C 类,则对应有1=n y ;若n X 属于2C 类,则对应有1-=n y ;。寻求M R 上的一个实函数()X g ,对于任给的未知模式,有 ()()1 20, 0, g C g C >∈?? <∈? X X X X 或者 (){}(){}12s g n 1, s g n 1, g C g C ?=∈?? =-∈??X X X X (4-1) 式中()sgn 为符号函数,()X g 称为决策(分类)函数。 前两章学过的前向神经元网络和径向基网络,都可以用来解决此类问题。这一章,我们称解决上述问题的方法为“分类机”。当()X g 为线性函数时,称为线性分类机;当()X g 为非线性函数时,称为非线性分类机。 举例:患有心脏病与年龄和胆固醇水平密切相关。对大量病人进行调查,得到表4-1所示数据,图4-1是数据的分布示意图。 根据数据{}21x x =X 分布以及所对 应的y 值,我们可以目测获得一条分类线()X g 。()X g 不仅可以将两类模式分开,并且具有最宽的“边带(Margin )” 。以后,对任意一个被观察者进行检验,得到 图4-1.样本分布
其数据{}21x x =X 后,若X 处于()X g 上边,即可判定为心脏病疑似;处于() X g 下边,则认为没有患有心脏病。 以上仅用年龄和胆固醇水平来判定是否患有心脏病显然是极其不可靠的。也就是说仅凭1x 和2x 两个参数不足以判别一个人是否患有心脏病,还必须考虑更多的参数,{}N x x x 21 =X 的维数很高。 这种情况下已无法人为直观地确定判别函数()X g 了。于是,我们需要一种根据给定的大量样本确定判别函数的方法,即需要一个能够由经验数据学会对某些模式进行分类的“学习机”。 二、 两类可分问题的线性分类机 实际上,以前讲过的“采用硬限幅函数的单个神经元”就是一个线性分类机。这里,我们从最大分类间隔角度,导出另外一种线性分类机。 仍以图4-1为例,对于这个二维问题,线性分类机的作用就是要在1C 和2C 之间寻找一条分类线l ,其表达式为()X g 。我们已经熟知,在高维情况下()X g 是一个超平面。 对于线性可分的两类模式1C 和2C 而言,能够准确将其分开的直线不是唯一的。假设有直线l 可以无误地将1C 和2C 两类模式分开,另有直线1l 和直线2l 与l 之间的间距为k , 1l 与2l 之间形成一个没有学习样本的带状区域,不妨称该带状区域为“边带(Margin )”,而l 是边带的中分线。显然,最合理的分类线应该具有最宽的边带。 假设,已知分类线l 的法线矢量为0W ,则分类线的表达式为: ()000g b =?+=X W X (4-2) 式中?表示矢量点积。显然, ()X g 到原点距离为 b W 。 对于给定的所有N 个学习样本(){}N n n n y 1 ,=X ,()X g 应满足:
r语言基于SVM模型的文本分类研究 附数据代码
基于SVM模型的文本分类研究 1 Perceptron与SVM概念介绍 1.1 感知机(Perceptron) 感知机(perceptron)1957年由Rosenblatt提出,是神经网络与支持向量机的基础? 感知机,是二类分类的线性分类模型,其输入为样本的特征向量,输出为样本的类别出为样本的类别,取+1和‐1二值,即通过某样本的特征即通过某样本的特征,就可以准确判断该样本属于哪一类。感知机能够解决的问题首先要求特征空间是线性可分的,再者是二类分类,即将样本分为{+1, ‐1}两类。由输入空间到输出空间的符号函数: 其中,w和b为感知机参数,w为权值(weight),b为偏置(bias)。 在感知机的定义中,线性方程对应于问题空间中的1个超平面(二维空间中为直线)S,位于这个超平面两侧的样本分别被归为两类,例如下图,红色作为一类(正类),蓝色作为另一类(负类),它们的特征很简单,就是它们的坐标。 作为有监督学习的一种方法,感知机学习由训练集,求得感知机模型,即求得模型参数w,b,这里x和y分别是特征向量和类别(也称为目标)。基于此,感知机模型可以对新的输入样本进行分类。 1.2支持向量机(SVM) 感知机学习算法会因采用的初值不同而得到不同的超平面。而SVM试图寻找一个最佳的超平面来划分数据,怎么算最佳呢?我们自然会想到用最中间的超平面就是最好的。如下图 :
显然在SVM中我们不能在使用函数距离γ^(i)来作为损失函数了,当我们试图使上图虚线之间的”gap”,最大自然要用几何距离。 我们期望目标函数是一个凸函数,这样优化起来就比较方便了。所以上面的优化问题可以化成: maxγ,w,bs.t.1||w||?minγ,w,b12||w||2y(i)(wTx(i)+b)?1,i=1,...,m 这样SVM模型就转化为了一个二次规划问题(Quadratic Programming)。此时我们可以用R的一些工具来处理这个优化问题了。 1.3感知机与支持向量机的区别: 感知机是支持向量机的基础,由感知机误分类最小策略可以得到分离超平面(无穷多个),支持向量机利用间隔最大化求得最优分离超平面(1个)。间隔最大化就是在分类正确的前提下提高确信度。比如,A离超平面远,若预测点就是正类,就比较确信是正确的。点C离超平面近,就不那么确信正确。 同时SVM具有核函数,线性支持向量机解决线性分类问题。对于非线性分类问题,可以采用非线性支持向量机解决。具体为: 采取一个非线性变换,将非线性问题转变为线性问题。再通过线性支持向量机解决,这就是核技巧。
【原创】R语言svm决策树模型分析空气质量附代码数据
data=read.csv("air.csv",skip =1) head(data) ## label X1 X2 X3 X4 X5 X6 X7 Y1 Y2 X8 X9 X10 ## 1 北京 14 50 102 81 46965 3.6 203 186 124 23014.60 16410.54 2170. 50 ## 2 天津 29 42 117 70 94867 3.1 142 216 104 16538.19 11946.88 1547. 00 ## 3 石家庄 47 51 147 89 88167 4.3 148 180 123 5440.60 15848.00 1028. 84 ## 4 太原 71 38 114 62 79456 3.1 131 230 94 2735.34 6999.00 367. 39 ## 5 呼和浩特 34 39 103 43 55970 3.2 145 276 87 3090.52 17224.00 238. 58 ## 6 沈阳 66 48 115 72 98871 2.2 155 207 107 7280.49 12948.00 730. 41 ## X11 X12 X13 X14 X15 ## 1 561.90 342.40 0.26 4542.64 0.20 ## 2 273.62 229.03 0.18 7704.22 0.47 ## 3 219.53 138.52 0.21 2452.40 0.45 ## 4 113.30 161.88 0.31 1020.18 0.37 ## 5 85.39 49.58 0.36 867.08 0.28 ## 6 181.70 140.33 0.25 3474.18 0.48 # 分析分为两个部分 # 第一部分: ###################################################################### ##### 数据导入与处理 ###################################################################### data$Y1<-ifelse(data$Y1>365*0.8,'空气好','空气差') ## 构建因变量 data$Y1<-as.factor(data$Y1) ## 将因变量格式转为因子型 ###################################################################### ##### 构建训练集、测试集 ##### 分层抽样,70%作为训练集,30%作为测试集 ###################################################################### # library(sampling) trainindex=sample(1:nrow(data),nrow(data)*0.7) train<-data[trainindex, ] ## 去除price变量的训练集 test<-data[-trainindex, ] ## 去除price变量的测试集
R中SVM的实现
一、R中svm介绍 R的函数包e1071提供了libsvm的接口。使用e1071包中svm函数可以得到与libsvm相同的结果。write.svm()更是可以把R训练得到的结果写为标准的Libsvm格式,以供其他环境下libsvm的使用。下面我们来看看svm()函数的用法。有两种格式都可以。 svm(formula,data=NULL,…,subset,na.action=na.omit,sacle=TRUE) 或者 svm(x, y = NULL, scale = TRUE, type = NULL, kernel = "radial", degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x), coef0 = 0, cost = 1, nu = 0.5, class.weights = NULL, cachesize = 40, tolerance = 0.001, epsilon = 0.1, shrinking = TRUE, cross = 0, probability = FALSE, fitted = TRUE, ..., subset, na.action = na.omit) 主要参数说明如下: formula:分类模型形式,在第二个表达式中可以理解为y~x 即y相当于标签,x相当于特征(变量) data:数据框。 subset:可以指定数据集的一部分作为训练数据。 na.cation:缺失值处理,默认为删除缺失数据。 scale:将数据标准化,中心化,使其均值为0,方差为1,将自动执行。
type:s vm的形式。为:C-classification ,nu-classification, one-classification (for novelty detection) ,eps-regression, nu-regression 五种形式。后面两者为做回归时用到。默认为C分类器。kernel:在非线性可分时,我们引入核函数来做。R中提供的核函数如下 线性核: u'*v 多项式核: (gamma*u'*v + coef0)^degree 高斯核: exp(-gamma*|u-v|^2) sigmoid核: tanh(gamma*u'*v + coef0) 默认为高斯核。顺带说一下,在kernel包中可以自定义核函数。degree:多项式核的次数,默认为3 gamma:除去线性核外,其他核的参数,默认为1/数据维数 coef0:多项式核与sigmoid核的参数,默认为0. cost:C分类中惩罚项c的取值 nu:Nu分类,单一分类中nu的值 cross:做k折交叉验证,计算分类正确性。
支持向量机在分类和回归中的应用研究_冼广铭
ComputerEngineeringandApplications计算机工程与应用2008,44(27) 1引言 模式分类和回归分析是知识发现中的重要内容,也是处理其它问题的核心。虽然分类和回归具有许多不同的研究内容,但它们之间却具有许多相同之处,简单地说,它们都是研究输入输出变量之间的关系问题,分类的输出是离散的类别值,而回归的输出是连续的数值。用于分类和回归的方法很多,如传统的统计学和神经网络方法和最近刚刚兴起的支持向量机等[1]。 现有机器学习方法的重要理论基础之一是统计学。当人们面对数据而又缺乏理论模型时,统计分析方法是最先采用的方法。然而传统的统计方法只有在样本数量趋于无穷大时才能有理论上的保证,现有学习方法也多是基于此假设。而在实际应用中样本数目通常都是有限的,甚至是小样本,对此基于大数定律的传统统计方法难以取得理想的效果[2]。 ANN(ArtificialNeuralNetwork,人工神经网络)[3]等经验非线性方法利用已知样本建立非线性模型,克服了传统参数估计方法的困难。同时设计者在设计过程中利用了自己的经验和先验知识,取得了许多成功的应用。但是在实际工程应用中,有很多数据建模问题属于数学中的小样本、不适定问题,而人工神经网络等方法忽略了这一特点,将其作为无穷样本、适定问题来求解。所以神经网络具有局部极小点、过学习以及结构和类型的选择过分依赖于经验等固有的缺陷,降低了其应用和发展的效果。 作为分类、回归等问题来说,很可能在低维样本空间无法线性处理的样本集,在高维特征空间却可以通过一个线性超平面实现线性划分(或回归),而与特征空间的线性划分(或回归)相对应的却是样本空间的非线性分类(或回归)。但是采用升维的方法,即向高维空间做映射,一般只会增加计算的复杂性,甚至会引起“维数灾难”。 SVM通过核函数实现到高维空间的非线性映射,所以适合于解决本质上非线性的分类、回归等问题。同时,SVM方法巧妙地解决了如何求得非线性映射和解决算法的复杂性这两个难题:由于应用了核函数的展开定理,所以根本不需要知道非线性映射的显式表达式;由于是在高维特征空间中应用线性学习机的方法,所以与线性模型相比几乎不增加计算的复杂性,这在某种程度上避免了“维数灾难”[2]。 近年来SVM在许多领域的分类和回归方面起了越来越重要的作用,显示了它的优势,成为继模式识别和神经网络研究之后机器学习领域的一个新颖而有发展前途的研究方向。随着研究的进一步深入,SVM的应用将更加广泛。 国际上对SVM算法及其应用的研究日益广泛和深入,而我国在此领域的研究才刚起步不久[4]。因此,加强这一方面的研究工作,使我国在这一领域的研究和应用能够尽快赶上国际先 ◎数据库、信号与信息处理◎ 支持向量机在分类和回归中的应用研究 冼广铭1,曾碧卿1,冼广淋2 XIANGuang-ming1,ZENGBi-qing1,XIANGuang-lin2 1.华南师范大学南海校区计算机工程系,广东佛山528225 2.广东轻工职业技术学院计算机系,广州510300 1.DepartmentofComputerEngineering,NanhaCampus,SouthChinaNormalUniversity,Foshan,Guangdong528225,China 2.DepartmentofComputerEngineering,GuangdongIndustryTechnicalCollege,Guangzhou510300,China E-mail:Xgm20011@163.com XIANGuang-ming,ZENGBi-qing,XIANGuang-lin.ApplicationresearchofSVMinclassificationandregression.ComputerEngineeringandApplications,2008,44(27):134-136. Abstract:SVMplayamoreandmoreimportantroleinclassificationandregression.Becauseofexcellentperformanceinappli-cation,alotofSVMmethodisproposedinrecentyears.InthispaperaseriesofissueaboutSVMinclassificationandregres-sionisproposed.Itismagnificantforustocatchupwithinternationaladvancelevel. Keywords:SupportVectorMachine(SVM);classification;regression 摘要:SVM在许多领域的分类和回归方面起了越来越重要的作用,显示了它的优势。由于SVM方法较好的理论基础和它在一些领域的应用中表现出来的与众不同的优秀的泛化性能,近年来,许多关于SVM方法的应用研究陆续提了出来。围绕支持向量机在分类和回归中的问题进行了阐述,使我国在这一领域的研究和应用能够尽快赶上国际先进水平具有十分重要的意义。 关键词:支持向量机;分类;回归 DOI:10.3778/j.issn.1002-8331.2008.27.043文章编号:1002-8331(2008)27-0134-03文献标识码:A中图分类号:TP311 作者简介:冼广铭,男,博士,讲师,研究方向为数据挖掘和软件工程等。 收稿日期:2008-01-08修回日期:2008-07-14 134
