关于最小费用最大流的解题
关于最小费用最大流的解题
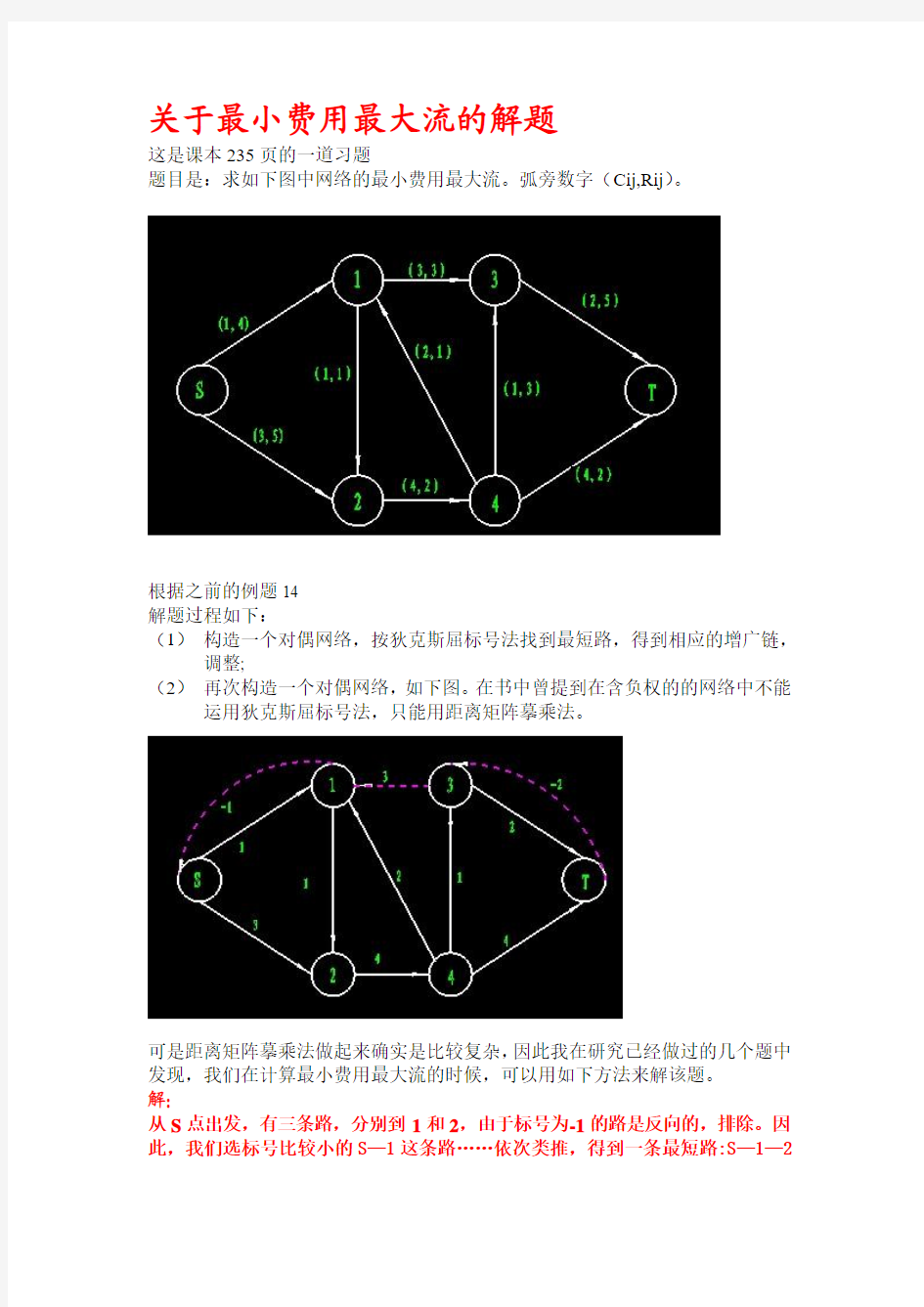
这是课本235页的一道习题
题目是:求如下图中网络的最小费用最大流。弧旁数字(Cij,Rij)。
根据之前的例题14
解题过程如下:
(1)构造一个对偶网络,按狄克斯屈标号法找到最短路,得到相应的增广链,调整;
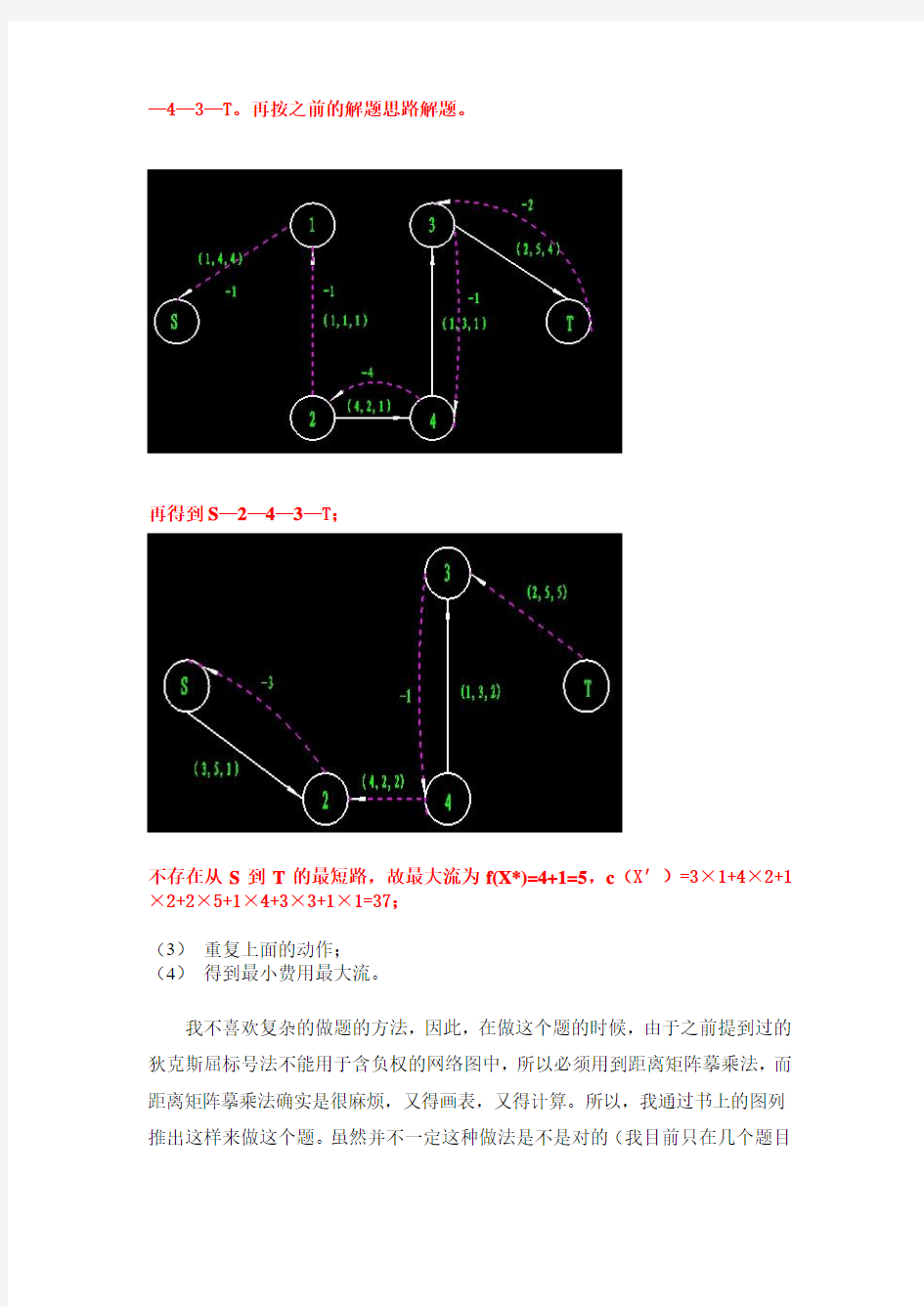
(2)再次构造一个对偶网络,如下图。在书中曾提到在含负权的的网络中不能运用狄克斯屈标号法,只能用距离矩阵摹乘法。
可是距离矩阵摹乘法做起来确实是比较复杂,因此我在研究已经做过的几个题中发现,我们在计算最小费用最大流的时候,可以用如下方法来解该题。
解:
从S点出发,有三条路,分别到1和2,由于标号为-1的路是反向的,排除。因此,我们选标号比较小的S—1这条路……依次类推,得到一条最短路:S—1—2
—4—3—T。再按之前的解题思路解题。
再得到S—2—4—3—T;
不存在从S到T的最短路,故最大流为f(X*)=4+1=5,c(X′)=3×1+4×2+1×2+2×5+1×4+3×3+1×1=37;
(3)重复上面的动作;
(4)得到最小费用最大流。
我不喜欢复杂的做题的方法,因此,在做这个题的时候,由于之前提到过的狄克斯屈标号法不能用于含负权的网络图中,所以必须用到距离矩阵摹乘法,而距离矩阵摹乘法确实是很麻烦,又得画表,又得计算。所以,我通过书上的图列推出这样来做这个题。虽然并不一定这种做法是不是对的(我目前只在几个题目
中运用,结果是对的),但我相信这样一个方向是对的,以前的运筹学方法也是前辈们研究出来的。
另外,我还在维普中文网上看到了一篇题为《含负权最短路问题的一个改进标号法》的论文,载要:在不出现负回路的情况下,给出了在赋权的网络图中求两点之间的最短路问题的一个改进标号法,该方法对于网络图中出现负权的情况也有效。最后给出了该算法的数值实验结果。
这篇文章中,提到了对狄克斯屈标号法的在负权网络不能运用的缺陷的改进。
这让我体会到了运筹学学习当中的另一个重要方面:我们不能拘泥于课本上一层不变的解题方法,应多了解运筹学发展的最新动态,掌握有关运筹学的最新知识。通过对其的研究,从而找到更好的方法来解决相关的问题。
这是我在这次作业当中,所获得的心得体会。
实验三:使用matlab求解最小费用最大流算问的题目
北京联合大学 实验报告 项目名称:运筹学专题实验报告 学院:自动化专业:物流工程 班级:1201B 学号:2012100358081 姓名:管水城成绩:
2015 年 5 月 6 日 实验三:使用matlab求解最小费用最大流算问题 一、实验目的: (1)使学生在程序设计方面得到进一步的训练;,学习Matlab语言进行程序设计求解最大流最小费用问题。 二、实验用仪器设备、器材或软件环境 计算机, Matlab R2006a 三、算法步骤、计算框图、计算程序等 1.最小费用最大流问题的概念。 在网络D(V,A)中,对应每条弧(vi,vj)IA,规定其容量限制为cij(cij\0),单位流量通过弧(vi,vj)的费用为dij(dij\0),求从发点到收点的最大流f,使得流量的总费用d(f)为最小,即mind(f)=E(vi,vj)IA 2.求解原理。 若f是流值为W的所有可行流中费用最小者,而P是关于f的所有可扩充链中费用最小的可扩充链,沿P以E调整f得到可行流fc,则fc是流值为(W+E)的可行流中的最小费用流。 根据这个结论,如果已知f是流值为W的最小费用流,则关键是要求出关于f 的最小费用的可扩充链.为此,需要在原网络D的基础上构造一个新的赋权有向图E(f),使其顶点与D的顶点相同,且将D中每条弧(vi,vj)均变成两个方向相反的弧(vi,vj)和(vj,vi)1新图E(f)中各弧的权值与f中弧的权值有密切关系,图E(f)中各弧的权值定义为:
新图E(f)中不考虑原网络D中各个弧的容量cij.为了使E(f)能比较清楚,一般将长度为]的弧从图E(f)中略去.由可扩充链费用的概念及图E(f)中权的定义可知,在网络D中寻求关于可行流f的最小费用可扩充链,等价于在图E(f)中寻求从发点到收点的最短路.因图E(f)中有负权,所以求E(f)中的最短路需用Floyd算法。 1.最小费用流算法的框图描述。 图一 2.计算最小费用最大流MATLAB源代码,文件名为mp_mc.m function[Mm,mc,Mmr]=mp_mc(a,c) A=a; %各路径最大承载流量矩阵 C=c; %各路径花费矩阵 Mm=0; %初始可行流设为零 mc=0; %最小花费变量 mcr=0; mrd=0;
最大流的增广路算法(KM算法).
1459:Power Network Time Limit: 2000MS Memory Limit: 32768K Total Submissions: 17697 Accepted: 9349 Description A power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be supplied with an amount s(u) >= 0 of power, may produce an amount 0 <= p(u) <= p max(u) of power, may consume an amount 0 <= c(u) <= min(s(u),c max(u)) of power, and may deliver an amount d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0 for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for any dispatcher. There is at most one power transport line (u,v) from a node u to a node v in the net; it transports an amount 0 <= l(u,v) <= l max(u,v) of power delivered by u to v. Let Con=Σu c(u) be the power consumed in the net. The problem is to compute the maximum value of Con. An example is in figure 1. The label x/y of power station u shows that p(u)=x and p max(u)=y. The label x/y of consumer u shows that c(u)=x and c max(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and l max(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6. Input There are several data sets in the input. Each data set encodes a power network. It starts with four integers: 0 <= n <= 100 (nodes), 0 <= np <= n (power stations), 0 <= nc <= n (consumers), and 0 <= m <= n^2 (power transport lines). Follow m data triplets (u,v)z, where u and v are node identifiers (starting from 0) and 0 <= z <= 1000 is the value of l max(u,v). Follow np doublets (u)z, where u is the identifier of a power station and 0 <= z <= 10000 is the value of p max(u). The data set ends with nc doublets (u)z, where u is the identifier of a consumer and 0 <= z <= 10000 is the value of
算法分析与设计(最大流问题)
算法分析与设计题目:最大流算法 院系:软件工程 班级:软件11-2班 :慕永利 学号: 23 号
目录 1算法提出背景........................................................... - 3 - 2 问题实例及解决......................................................... - 3 - 3算法论述............................................................... - 4 - 3.1、可行流.......................................................... - 4 - 3.2 最大流.......................................................... - 5 - 3.3最大流算法....................................................... - 6 - 3.3.1 增广路径................................................. - 6 - 3.3.2沿增广路径增广............................................. - 7 - 3.3.3样例:..................................................... - 8 - 3.3.4定理:.................................................... - 13 - 3.3.5算法的实现:.............................................. - 13 - 3.3.6 优化...................................................... - 16 - 4算法应用.............................................................. - 18 -
最大和最小费用流问题模型
最大流和最小费用流的作业 1.在下图中A 、B 为发点,分别有50和40单位物资往外发送,D 和E 是为收点,分别需要物资30和60单位,C 为中转站,各弧旁数字为(Cij ,Bij ),求满足上述收发量要求的最小费用流。 解:把问题转化为网络图: (20,90) (50,40) ( 10,20 ) (30,20) (10,30) (40,30) (80,10) 决策变量:设A 运到B 为L1, A 运到C 为L2, A 运到D 为L3,B 运到C 为L4, C 到E 为L5 D 到E 为L6, E 到D 为L7。 目标函数: Min Z=L1×20+L2×40+L3×90+L4×30+L5×10+L6×30+L7×20 约束条件: L1<=10,L2<=50,L3<=20,L4<=40,L5<=80,L6<=30,L7<=20 L1+L2+L3=50 L4=40+L1 L2+L4=L5 L3+L7=30 L5+L6=60 Li 为整数(i=1,2,3,4,5,6,7); A D B E C
结果如下: 解得L1=0 L2=40 L3=10 L4=40 L5=80 L6=0 L7=20 Min Z=4900 2、下图是描述一个水渠系统,其中R1,R2,R3,代表三个水库,A,B,C,D,E,F,代表水渠的交汇点,T 表示水渠终点的一个城市,水渠各段每日允许通过的最大流量(1000m 3)分别见表6-10和6-11.城市水资源管理部门希望制定一个方案,使每天输送到城市的水流量为最大,请将此问题归结为求最大流问题。 表6-10 到 从 A B C R1 73 65 _ R2 40 50 60 R3 _ 80 70 R1 R2 R3 A D B E T C F
图论算法 最大流算法和最大匹配算法
最大流算法 clc,clear,M=1000; c(1,2)=3;c(1,4)=3; c(2,3)=1;c(2,4)=20; c(3,6)=3; c(4,5)=10; c(5,1)=4;c(5,3)=2;c(5,6)=13; n=length(u); list=[]; maxf=zeros(1:n);maxf(n)=1; while maxf(n)>0 maxf=zeros(1,n);pred=zeros(1,n); list=1;record=list;maxf(1)=M; while (~isempty(list))&(maxf(n)==0) flag=list(1);list(1)=[]; index1=(find(u(flag,:)~=0)); label1=index1(find(u(flag,index1)... -f(flag,index1)~=0)); label1=setdiff(label1,record); list=union(list,label1); pred(label1(find(pred(label1)==0)))=flag; maxf(label1)=min(maxf(flag),u(flag,label1)... -f(flag,label1)); record=union(record,label1); label2=find(f(:,flag)~=0); label2=label2'; label2=setdiff(label2,record); list=union(list,label2); pred(label2(find(pred(label2)==0)))=-flag; maxf(label2)=min(maxf(flag),f(label2,flag)); record=union(record,label2); end if maxf(n)>0 v2=n; v1=pred(v2); while v2~=1 if v1>0
最小费用最大流问题matlab程序
下面的最小费用最大流算法采用的是“基于Floyd最短路算法的Ford和Fulkerson迭加算法”,其基本思路为:把各条弧上单位流量的费用看成某种长度,用Floyd求最短路的方法确定一条自V1至Vn的最短路;再将这条最短路作为可扩充路,用求解最大流问题的方法将其上的流量增至最大可能值;而这条最短路上的流量增加后,其上各条弧的单位流量的费用要重新确定,如此多次迭代,最终得到最小费用最大流。本源码由GreenSim团队原创,转载请注明 function [f,MinCost,MaxFlow]=MinimumCostFlow(a,c,V,s,t) %%MinimumCostFlow.m %最小费用最大流算法通用Matlab函数 %% 基于Floyd最短路算法的Ford和Fulkerson迭加算法 % GreenSim团队原创作品,转载请注明 %% 输入参数列表 %a单位流量的费用矩阵 %c链路容量矩阵 %V最大流的预设值,可为无穷大 %s源节点 %t目的节点 %% 输出参数列表 %f链路流量矩阵 %MinCost最小费用 %MaxFlow最大流量 %% 第一步:初始化 N=size(a,1);%节点数目 f=zeros(N,N);%流量矩阵,初始时为零流 MaxFlow=sum(f(s,:));%最大流量,初始时也为零 flag=zeros(N,N);%真实的前向边应该被记住 for i=1:N for j=1:N if i~=j&&c(i,j)~=0 flag(i,j)=1;%前向边标记 flag(j,i)=-1;%反向边标记 end if a(i,j)==inf a(i,j)=BV; w(i,j)=BV;%为提高程序的稳健性,以一个有限大数取代无穷大 end end end if L(end) 关于最小费用最大流的解题 这是课本235页的一道习题 题目是:求如下图中网络的最小费用最大流。弧旁数字(Cij,Rij)。 根据之前的例题14 解题过程如下: (1)构造一个对偶网络,按狄克斯屈标号法找到最短路,得到相应的增广链,调整; (2)再次构造一个对偶网络,如下图。在书中曾提到在含负权的的网络中不能运用狄克斯屈标号法,只能用距离矩阵摹乘法。 可是距离矩阵摹乘法做起来确实是比较复杂,因此我在研究已经做过的几个题中发现,我们在计算最小费用最大流的时候,可以用如下方法来解该题。 解: 从S点出发,有三条路,分别到1和2,由于标号为-1的路是反向的,排除。因此,我们选标号比较小的S—1这条路……依次类推,得到一条最短路:S—1—2 —4—3—T。再按之前的解题思路解题。 再得到S—2—4—3—T; 不存在从S到T的最短路,故最大流为f(X*)=4+1=5,c(X′)=3×1+4×2+1×2+2×5+1×4+3×3+1×1=37; (3)重复上面的动作; (4)得到最小费用最大流。 我不喜欢复杂的做题的方法,因此,在做这个题的时候,由于之前提到过的狄克斯屈标号法不能用于含负权的网络图中,所以必须用到距离矩阵摹乘法,而距离矩阵摹乘法确实是很麻烦,又得画表,又得计算。所以,我通过书上的图列推出这样来做这个题。虽然并不一定这种做法是不是对的(我目前只在几个题目 中运用,结果是对的),但我相信这样一个方向是对的,以前的运筹学方法也是前辈们研究出来的。 另外,我还在维普中文网上看到了一篇题为《含负权最短路问题的一个改进标号法》的论文,载要:在不出现负回路的情况下,给出了在赋权的网络图中求两点之间的最短路问题的一个改进标号法,该方法对于网络图中出现负权的情况也有效。最后给出了该算法的数值实验结果。 这篇文章中,提到了对狄克斯屈标号法的在负权网络不能运用的缺陷的改进。 这让我体会到了运筹学学习当中的另一个重要方面:我们不能拘泥于课本上一层不变的解题方法,应多了解运筹学发展的最新动态,掌握有关运筹学的最新知识。通过对其的研究,从而找到更好的方法来解决相关的问题。 这是我在这次作业当中,所获得的心得体会。 从一道题目的解法试谈网络流的构造与算法 福建师大附中江鹏 1. 引论 A. 对网络流算法的认识 网络流算法是一种高效实用的算法,相对于其它图论算法来说,模型更加复杂,编程复杂度也更高,但是它综合了图论中的其它一些算法(如最短路径),因而适用范围也更广,经常能够很好地解决一些搜索与动态规划无法解决的,看似NP的问题。 B. 具体问题的应用 网络流在具体问题中的应用,最具挑战性的部分是模型的构造。这没用现成的模式可以套用,需要对各种网络流的性质了如指掌(比如点有容量、容量有上下限、多重边等等),并且归纳总结一些经验,发挥我们的创造性。 2. 例题分析 【问题1】项目发展规划(Develop) Macrosoft?公司准备制定一份未来的发展规划。公司各部门提出的发展项目汇总成了一张规划表,该表包含了许多项目。对于每个项目,规划表中都给出了它所需的投资或预计的盈利。由于某些项目的实施必须依赖于其它项目的开发成果,所以如果要实施这个项目的话,它所依赖的项目也是必不可少的。现在请你担任Macrosoft?公司的总裁,从这些项目中挑选出一部分,使你的公司获得最大的净利润。 ●输入 输入文件包括项目的数量N,每个项目的预算Ci和它所依赖的项目集合Pi。格式如下:第1行是N; 接下来的第i行每行表示第i个项目的信息。每行的第一个数是Ci,正数表示盈利,负数表示投资。剩下的数是项目i所依赖的项目的编号。 每行相邻的两个数之间用一个或多个空格隔开。 ●输出 第1行是公司的最大净利润。接着是获得最大净利润的项目选择方案。若有多个方案,则输出挑选项目最少的一个方案。每行一个数,表示选择的项目的编号,所有项目按从小到大的顺序输出。 ●数据限制 0≤N≤1000 -1000000≤Ci≤1000000 ●输入输出范例 最小费用流问题的研究 摘要 本文主要研究的是最小费用流问题。在给出一些定义定理的基础上进一步求解最小费用流问题从而得到更好的算法。 关键字 最小费用流问题 剩余网络 容许网络 算法 复杂度 1最小费用流问题的概述 给定一个有向网络),(A N G =。其中},...,,...,3,2,1{n i N =表示顶点集合,A 表示G 中的所有弧构成的一个集合。任意的弧A j i ∈),(,用ij c 表示弧),(j i 上单位流量的费用,用ij u 表示弧),(j i 上的最大流量,任意的N i ∈用)(i b 表示在i 这一点处所提供的流量或所需要的流量。当0)(>i b 时,表示在i 这一点处所提供的流量为)(i b ,当0)( 求最小费用最大流算法的MATLAB 程序代码如下(算例): n=5; C=[0 15 16 0 0 0 0 0 13 14 0 11 0 17 0 0 0 0 0 8 0 0 0 0 0]; %弧容量 b=[0 4 1 0 0 0 0 0 6 1 0 2 0 3 0 0 0 0 0 2 0 0 0 0 0]; %弧上单位流量的费用 wf=0;wf0=Inf; %wf 表示最大流量, wf0 表示预定的流量值 for(i=1:n)for(j=1:n)f(i,j)=0;end;end %取初始可行流f 为零流 while(1) for(i=1:n)for(j=1:n)if(j~=i)a(i,j)=Inf;end;end;end%构造有向赋权图 for(i=1:n)for(j=1:n)if(C(i,j)>0&f(i,j)==0)a(i,j)=b(i,j); elseif(C(i,j)>0&f(i,j)==C(i,j))a(j,i)=-b(i,j); elseif(C(i,j)>0)a(i,j)=b(i,j);a(j,i)=-b(i,j);end;end;end for(i=2:n)p(i)=Inf;s(i)=i;end %用Ford 算法求最短路, 赋初值 for(k=1:n)pd=1; %求有向赋权图中vs 到vt 的最短路 for(i=2:n)for(j=1:n)if(p(i)>p(j)+a(j,i))p(i)=p(j)+a(j,i);s(i)=j;pd=0;end;end;end if(pd)break;end;end %求最短路的Ford 算法结束 if(p(n)==Inf)break;end %不存在vs 到vt 的最短路, 算法终止. 注意在求最小费用最大流时构造有 向赋权图中不会含负权回路, 所以不会出现k=n dvt=Inf;t=n; %进入调整过程, dvt 表示调整量 while(1) %计算调整量 if(a(s(t),t)>0)dvtt=C(s(t),t)-f(s(t),t); %前向弧调整量 elseif(a(s(t),t)<0)dvtt=f(t,s(t));end %后向弧调整量 if(dvt>dvtt)dvt=dvtt;end if(s(t)==1)break;end %当t 的标号为vs 时, 终止计算调整量 t=s(t);end %继续调整前一段弧上的流f pd=0;if(wf+dvt>=wf0)dvt=wf0-wf;pd=1;end%如果最大流量大于或等于预定的流量值 t=n;while(1) %调整过程 if(a(s(t),t)>0)f(s(t),t)=f(s(t),t)+dvt; %前向弧调整 elseif(a(s(t),t)<0)f(t,s(t))=f(t,s(t))-dvt;end %后向弧调整 if(s(t)==1)break;end %当t 的标号为vs 时, 终止调整过程 t=s(t);end if(pd)break;end %如果最大流量达到预定的流量值 wf=0; for(j=1:n)wf=wf+f(1,j);end;end %计算最大流量 zwf=0;for(i=1:n)for(j=1:n)zwf=zwf+b(i,j)*f(i,j);end;end %计算最小费用 f %显示最小费用最大流 wf %显示最小费用最大流量 zwf %显示最小费用, 程序结束 综合性、设计性实验报告格式 桂林电子科技大学 数学与计算科学学院综合性、设计性实验报告 实验室: 实验日期:2014年12月13日 院(系) 数学与计算科学 年级、专业、班 姓名 成绩 课程 名称 运筹学实验 实验项目 名 称 最小费用最大流(综合实验) 指导 教师 南江霞 教师 评语 教师签名: 年 月 日 一 ,实验目的 1. 掌握最大流及最小费用最大流问题的数学建模; 2. 掌握最大流问题的WinQSB 软件求解和Lingo 软件求解; 3. 掌握最小费用最大流问题问题的的WinQSB 软件求解和Lingo 软件求解。 二,实验原理 1、熟悉建立最大流问题的数学模型; 2、熟悉建立最小费用最大流问题的数学模型; 3、熟悉WinQSB 软件的基本操作。 4、熟悉Lingo 软件建模。 三,使用仪器,材料 WinQSB 软件 Lingo 软件 四,实验内容与步骤 求最大流: 五,实验过程原始记录(数据,图表,计算等) 用WinQSB 软件进行求解 S A B C D T (7,2) (10,10) (5,3) (7,7) (5,1) (8,4) (10,9) (5,3) 用Lingo 软件进行求解 建立数学模型 ()()()(),max max ,,min ,..0,0,,ij ij i j A ij ji j V j V i j A j i A ij ij e f f i S s t f f f i T i S T f c i j A ∈∈∈∈∈=??-=-=??≠?≤≤∈∑∑∑ model : sets : nodes/S,A,B,C,D,T/; arcs(nodes,nodes)/ S,A S,B A,B,A,C B,C,B,D C,D,C,T D,T/:C,f; endsets data: C=7 10 5 7 5 8 7 10 5; enddata max=flow; @for(nodes(i)|i#ne#1#and#i#ne#@size(nodes): @sum(arcs(i,j):f(i,j))-@sum(arcs(j,i):f(j,i))=0); @sum(arcs(i,j)|i#eq#1:f(i,j))=flow; @sum(arcs(i,j)|j#eq#@size(nodes):f(i,j))=flow; @for(arcs:@bnd(0,f,C)); end Global optimal solution found. Objective value: 15.00000 Infeasibilities: 0.000000 Total solver iterations: 4 Variable Value Reduced Cost FLOW 15.00000 0.000000 C( S, A) 7.000000 0.000000 C( S, B) 10.00000 0.000000 C( A, B) 5.000000 0.000000 C( A, C) 7.000000 0.000000 C( B, C) 5.000000 0.000000 C( B, D) 8.000000 0.000000 C( C, D) 7.000000 0.000000 C( C, T) 10.00000 0.000000 C( D, T) 5.000000 0.000000 F( S, A) 7.000000 0.000000 F( S, B) 8.000000 0.000000 F( A, B) 0.000000 0.000000 F( A, C) 7.000000 0.000000 F( B, C) 3.000000 0.000000 F( B, D) 5.000000 0.000000 F( C, D) 0.000000 0.000000 F( C, T) 10.00000 -1.000000 F( D, T) 5.000000 -1.000000 S到T的最大流=15 六,实验结果分析或总结 网络最大流算法算法拓展 一、网络最大流的算法分类: 一、Ford-Fulkerson增广路方法 1、Ford-Fulkerson标号算法(最简单的实现) 分别记录这一轮扩展过程中的每个点的前驱与到该节点的增广最大流量,从源点开始扩展,每次选择一个点(必须保证已经扩展到这个点),检查与它连接的所有边,并进行扩展,直到扩展到t。 2、最大容量增广路算法 每次找一条容量最大的增广路来增广,找的过程类似Dijkstra,实现起来相当简单。 3、Edmonds-Karp,最短路增广算法的BFS实现 每次找一条最短的增广路,BFS是一个可以很方便的实现思想。 4、距离标号算法 最短路增广的O(n)寻找实现,使用距离函数d:d[t]=0;d<=d[j]+1若存在(i,j)∈E;只有路径上满足d=d[i+1]+1的增广路才为满足要求的,一开始我们初始化使标号恰好满足要求,之后不断更改标号使其可以使增广继续。 5、Dinic,分层思想 对网络分层(按照距t的距离),保留相邻层之间的边,然后运用一次类似于距离标号的方法(其实质是DFS)进行增广。 二、预留与推进算法 1、一般性算法 随便找个点,要么将他的盈余推出去,要么对他进行重标记,直至无活跃点为止。 2、重标记与前移算法 维护一个队列,对一个点不断进行推进与重标记操作,直至其盈余为0,若过程中他没有被重标记过,则可出列,否则加入队头,继续等待检查。 3、最高标号预留与推进算法 记录d值,然后优先处理d值较高的,直至没有盈余。 二、网络最大流的算法实现 一、Edmonds-Karp(EK)算法 就是用广度优先搜索来实现Ford-Fulkerson方法中对增广路径的计算,时间复杂度为O(VE2),Shortest Augmenting Path (SAP) 是每次寻找最短增广路的一类算法,Edmonds - Karp 算法以及后来著名的Dinic 算法都属于此。SAP 类算法可统一描述如下: Shortest Augmenting Path { x <-- 0 while 在残量网络Gx 中存在增广路s ~> t do { 找一条最短的增广路径P delta <-- min{rij:(i,j) 属于P} 从一个可行流f 开始, 求最大流的Ford--Fulkerson 标号算法的基本步骤: ⑴ 标号过程 ① 给发点 v s 以标号(+, +∞) , d s = +∞. ② 选择一个已标号的点 x, 对于x 的所有未给标号的邻接点y, 按下列规则处理: 当 yx∈E, 且f yx >0 时, 令d y = min { f yx , d x }, 并给y 以标号 ( x ? , d y ). 当 xy∈E, 且f xy<C xy 时, 令d y = min {C xy ? f xy , d x }, 并给y 以标号 ( x +, d y ). ③ 重复②直到收点v t 被标号或不再有点可标号时为止. 若v t 得到标号, 说明存在一条 可增广链, 转⑵调整过程; 若v t 未得到标号, 标号过程已无法进行时, 说明f 已经是最大流. ⑵ 调整过程 ④ 决定调整量d =d vt , 令u = v t . ⑤ 若 u 点标号为( v +, d u ), 则以f vu + d 代替 f vu ; 若u 点标号为( v ?, d u ), 则以f vu ? d 代替 f vu. ⑥ 若 v = v s, 则去掉所有标号转⑴重新标号; 否则令u = v, 转⑤. 算法终止后, 令已有标号的点集为S, 则割集(S, S c )为最小割, 从而W f = C (S, S c ). 例1 求图 6-19 所示网络的最大流. 利用 Ford--Fulkerson 标号法求最大流算法的MATLAB 程序代码如下: n=8;C=[0 5 4 3 0 0 0 0 0 0 0 0 5 3 0 0 0 0 0 0 0 3 2 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0]; %弧容量 for(i=1:n)for(j=1:n)f(i,j)=0;end;end %取初始可行流f 为零流 for(i=1:n)No(i)=0;d(i)=0;end %No,d 记录标号 while(1) No(1)=n+1;d(1)=Inf; %给发点vs 标号 while(1)pd=1; %标号过程 for(i=1:n)if(No(i)) %选择一个已标号的点vi for(j=1:n)if(No(j)==0&f(i,j) %最大流算法源程序 clc,clear,M=1000; u(1,2)=1;u(1,3)=1;u(1,4)=2; u(2,3)=1;u(2,5)=2; u(3,5)=1; u(4,3)=3;u(4,5)=3; f(1,2)=1;f(1,3)=0;f(1,4)=1; f(2,3)=0;f(2,5)=1; f(3,5)=1; f(4,3)=1;f(4,5)=0; n=length(u); list=[]; maxf=zeros(1:n);maxf(n)=1; while maxf(n)>0 maxf=zeros(1,n);pred=zeros(1,n); list=1;record=list;maxf(1)=M; while (~isempty(list))&(maxf(n)==0) flag=list(1);list(1)=[]; index1=(find(u(flag,:)~=0)); label1=index1(find(u(flag,index1)... -f(flag,index1)~=0)); label1=setdiff(label1,record); list=union(list,label1); pred(label1(find(pred(label1)==0)))=flag; maxf(label1)=min(maxf(flag),u(flag,label1)... -f(flag,label1)); record=union(record,label1); label2=find(f(:,flag)~=0); label2=label2'; label2=setdiff(label2,record); list=union(list,label2); pred(label2(find(pred(label2)==0)))=-flag; maxf(label2)=min(maxf(flag),f(label2,flag)); record=union(record,label2); end if maxf(n)>0 v2=n; v1=pred(v2); while v2~=1 if v1>0 f(v1,v2)=f(v1,v2)+maxf(n); else v1=abs(v1); f(v2,v1)=f(v2,v1)-maxf(n);关于最小费用最大流的解题
从一道题目的解法试谈网络流的构造与算法
最小费用流问题的研究
求最小费用最大流算法的MATLAB程序代码
运筹学实验之最小费用最大流(综合实验)
最大流算法拓展
最大流算法MATLAB
最大流算法源程序
