第十二章 双正交小波及小波包

346

第12章 双正交小波及小波包

我们在上一章给出了正交小波的构造方法。正交小波有许多好的性质，如

)()(),('

,,'

k k t t k j k j -=δφφ，)()(),('

,,'

k k t t k

j k

j -=δψ

ψ

，0)(),('

,,=t t k

j k j ψ

φ ，此

外，尺度函数和小波函数都是紧支撑的，有着高的消失矩等等。Daubechies 给出的正交小波的构造方法可以方便的构造出所需要的小波(如DBN ，SymN ，CoifN)。但是，正交小波也有不足之处，即)(t φ和)(t ψ都不是对称的，尽管SymN 和CoifN 接近于对称，但毕竟不是真正的对称，因此，这在实际的信号处理中将不可避免地带来相位失真。)(t φ和)(t ψ的不对称性来自所使用的共轭正交滤波器组)(0z H 和)(1z H 的不对称性。我们已在7.8节讨论了具有线性相位的双正交滤波器组的基本概念，给出了可准确重建的双正交滤波器组的设计方法。本章，我们把这些内容引入到小波分析，给出适合小波变换的双正交滤波器组准确重建的条件，给出双正交条件下的多分辨率分析及双正交小波的构造方法，最后简要讨论小波包的基本概念

12.1 双正交滤波器组

现在，我们结合小波变换的需要来研究双正交滤波器组的内在关系及实现准确重建

的条件。所谓“小波变换的需要”是指在用)(0z H 对)(0z a 分解时需要将)(0z H 和)(1z H 的

系数作时间上的翻转，即用的是)(10-z H 及)(11-z H ，或)()(00n h n h -=,)()(11n h n h -=，

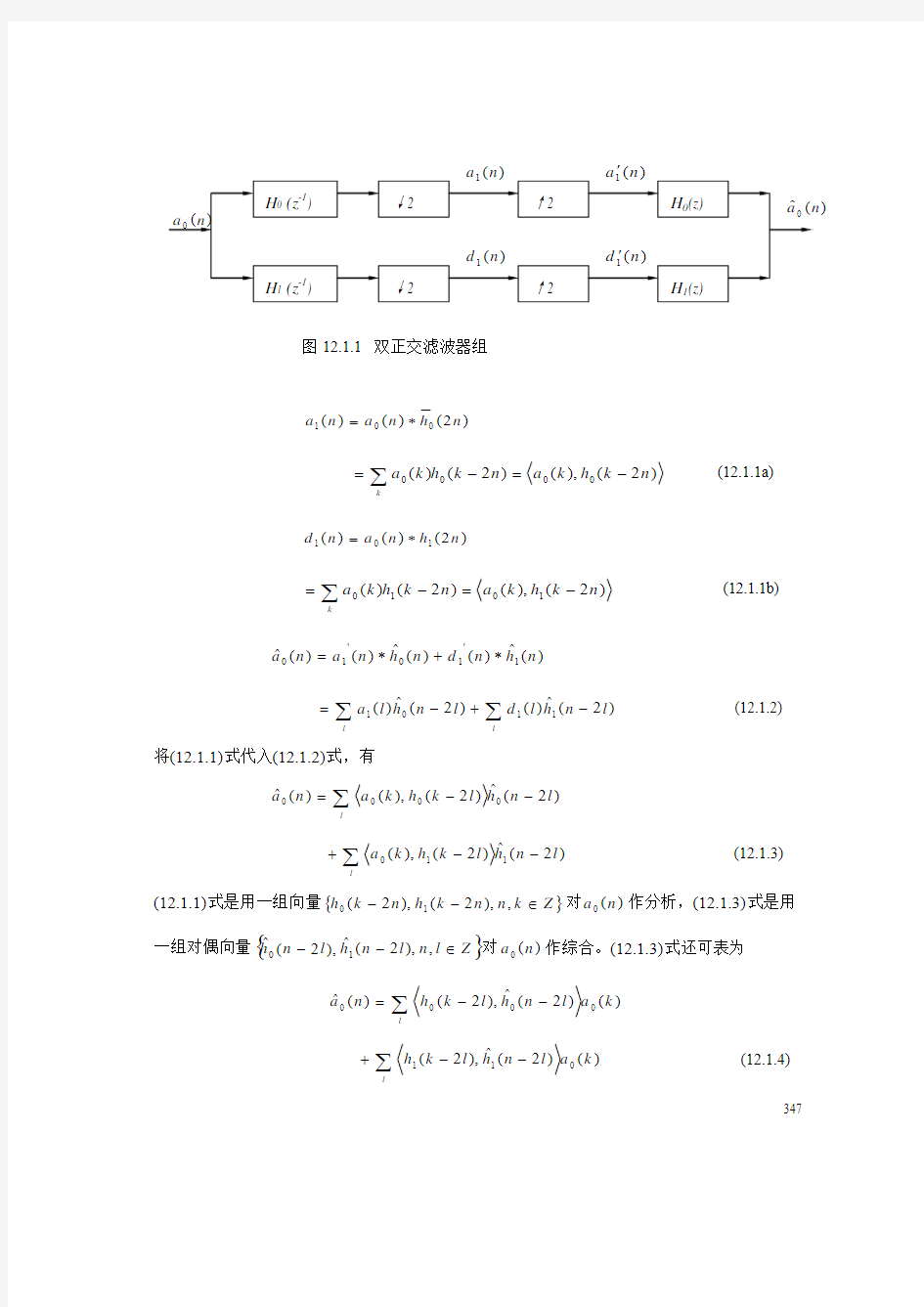
见(10.6.1)式及图10.6.2。将图10.6.2的正变换和图10.6.3的反变换结合起来，我们可得到如图12.1.1所示的一级分解和重建的类似于两通道滤波器组的信号流图。注意，图中用于重建的滤波器不再是图10.6.3中的)(0z H 和)(1z H ，而是)(?0

z H 和)(?1z H ，它们分别是)(0z H 和)(1z H 的对偶滤波器。有关“对偶”的概念见1.6节，在下面的讨论中将涉及对

偶滤波器的作用。

现在我们来分析该图中各信号之间的关系及实现PR 的条件。由第七章关于两通道滤波器组的理论，我们有

347

图12.1.1 双正交滤波器组

)2()()(001n h n a n a *=

)2(),()2()(0000

n k h k a n k h k a

k

-=-=

∑ (12.1.1a)

)2()()(101n h n a n d *= )2(),()2()(1010

n k h k a n k h k a

k

-=-=

∑ (12.1.1b)

)(?)()(?)()(?1

'10'10n h n d n h n a n a *+*= ∑∑-+-=

l

l

l n h l d

l n h l a

)2(?)()2(?)(1

1

1

(12.1.2)

将(12.1.1)式代入(12.1.2)式，有

)2(?)2(),()(?0000l n h l k h k a n a

l

--=∑

)2(?)2(),(1

10l n h l k h k a l

--+

∑

(12.1.3)

(12.1.1)式是用一组向量{}Z k n n k h n k h ∈--,),2(),2(10对)(0n a 作分析，(12.1.3)式是用一组对偶向量{}

Z l n l n h l n h ∈--,),2(?),2(?1

0对)(0n a 作综合。(12.1.3)式还可表为 )()2(?),2()(?0

000k a l n h l k h n a

l

∑

--=

)()2(?),2(0

11k a l n h l k h l

∑

--+

(12.1.4)

)

348

显然，如果

)()2(?),2(00k n l n h l k h -=--δ (12.1.5a)

)()2(?),2(1

1k n l n h l k h -=--δ (12.1.5b)

则

)(2)(?00n a n a

= 从而实现了准确重建。(12.1.5)式的含意是，在图12.1.1中，同一条支路上的两个滤波器)(?),(0

0n h n h 或)(?),(11n h n h 的偶序号位移之间是正交的。但是该式没有涉及上下支路两个滤波器之间的关系。我们更关心的是这些滤波器系数的移位可否构成小波分析中的基函数。下面的两个定理清楚地回答了该问题。

定理12.1

对图12.1.1所示的两通道滤波器组，对任意的输入信号)(0n a ，其准确

重建的充要条件是：

0)(?)()(?)(1

*10*

0=+++ωπωωπωH H H H (12.1.6a) 及

2)(?)()(?)(1

*10*

0=+ωωωωH H H H

(12.1.6b)

证明：仿照(7.1.5)式的导出，有

[]

)()(?)()(?)(2

1)(?01110100z A z H z H z H z H z A --+= []

)()(?)()(?)(2

10

11101

z A z H z H z H z

H

--+-+

-- (12.1.7)

式中)(0z A 、)(?0

z A 分别是)(0n a 和)(?0n a 的z 变换，)(0z A -是混迭分量。因此，为消除混迭失真，应有

0)(?)()(?)(1

11010=-+---z H z H z H z H (12.1.8a)

为保证系统的准确重建，应有

k cz z H z H z H z H ---=+2)(?)()(?)(1

11010 (12.1.8b)

式中c 和k 均为常数。令1=c ，0=k ，(12.1.8)式对应的频率表示是：

0)(?)()(?)(1

*10*

0=+++ωπωωπωH H H H

349

2)(?)()(?)(1

*10*

0=+ωωωωH H H H 于是定理得证。

对比图7.1.1的两通道滤波器组，其对应的PR 条件是（见(7.1.5)式）： 0)()()()(1100=-+-z G z H z G z H

(12.1.9a)

2)()()()(1100=+z G z H z G z H

(12.1.9b)

将(12.1.9)和(12.1.8)式相比较可以看出，在双正交滤波器组的情况下，我们分别用)(?0

z H 、)(?1z H 代替了)(0z G 和)(1z G ，并在分析滤波器组中，用)(10-z H 、)(11-z H 分别代替了)(0z H 和)(1z H 。其实，(12.1.8)式导出的原理和(12.1.9)式是完全一样的。 由(12.1.6a)式，有

??????=??????????

??++*

*02)(?)(?)()

()

()

(10

1010ωωπωπωωωH H H H H H (12.1.10)

可求出

??

?

???+-+=?

?????**)()()

(det 2)(?)(?0110

πωπωωωωH H H H H (12.1.11)

式中

)()()()()(d e t 0110πωωπωωω+-+=H H H H H

(12.1.12)

显然，为了保证对偶滤波器)(?0z H 和)(?1z H 是稳定的，)(det ωH 在ππω~-=的范围内应该非零。为了保证)(?0

z H 和)(?1z H 是FIR 的，)(det ωH 应取纯延迟的形式。 仿照(7.2.16)式对)(0z G 和)(1z G 的定义，我们可给出在双正交条件下对偶滤波器和分析滤波器之间的关系：

)(?)(0

)12(1πωωω

+=*+-H e

H l j (12.1.13a)

)()(?0

)12(1πωωω+=*+-H e H l j (12.1.13b)

或

)(?)(10

)

12(1-+--=z H z

z H l (12.1.14a)

350

)()(?10

)12(1-+--=z H z z H l (12.1.14b)

假定0=l ，它们对应的时域关系是 )1(?)

1()(0

1

1n h n h n --=+ (12.1.15a)

)1()1()(?0

11n h n h n --=+

(12.1.15b)

注意，上述时域、频域关系均是在图12.1.1中的交叉方向上给出的，它正好反映了双正交滤波器组的特点。

将(12.1.13)式代入(12.1.6)式，我们可得到如下的关系：

2)(?)()(?)(0

000=+++**

πωπωωωH H H H (12.1.16a) 或

2)(?)()(?)(1

111=+++**

πωπωωωH H H H

(12.1.16b)

及

0)(?)()(?)(1

010=+++**

πωπωωωH H H H (12.1.17a) 或

0)(?)()(?)(0

101=+++**

πωπωωωH H H H

(12.1.17b)

至此，我们给出了在双正交滤波器组中的若干基本关系，即

(1) 去除混迭条件：(12.1.6a)式； (2) PR 条件

：(12.1.6b)式；

(3) 保证PR 条件和滤波器均为FIR 的情况下，四个滤波器在时域和频域的关系：

(12.1.13)式～(12.1.17)式。

回顾在共轭正交滤波器组的情况下，我们经常用到的功率互补关系，即

2)

()

(2

02

0=++πωωH H ，

或

2)()()()(0000=+++*

*

πωπωωωH H H H

(12.1.18)

显然，若)()(?0

0z H z H =，则(12.1.16a)式即变成(12.1.18)式，也即双正交滤波器组变成了正交滤波器组。

有了以上讨论的基础，我们可给出在小波分析中要用到的“基”的概念。

351

定理12.2[8] 如果图12.1.1中的四个滤波器)(0z H ，)(1z H ，)(?0

z H 和)(?1z H 满足准确重建条件，且它们的傅里叶变换均是有界的，则

Z l l n h l n h ∈--)},2(?),2(?{1

0 和 Z l l n h l n h ∈--)},2(),2({10 是)(2R L 中的双正交Riesz 基。

证明：为证明0h 、1h 、0?h 及1

?h 的偶序号项移位是双正交的，我们需要证明如下三个关系成立：

)()2(),(?00n n k h k h δ=- (12.1.19a)

)()2(),(?1

1n n k h k h δ=- (12.1.19b)

及

0)2(),(?)2(),(?0

110=-=-n k h k h n k h k h (12.1.19c)

由(12.1.16a)式，有

[]

1)(?)()(?)(2

10

000=+++**πωπωωωH H H H

该式对应的时域关系是

)()2()(?

)2(?00

0n n k h k h n h h k δ=-=*∑∞

-∞

=

(12.1.20)

于是(12.1.19a)式得证。同理，由(12.1.16b)式可证明(12.1.19b)式，而(12.1.17)式对应的时域关系即是(12.1.19c)式。这样，(12.1.19)式给出了三组正交关系。

若0h ，0?h ，1

h ，1?h 的偶序号位移能够构成)(2

R L 中的双正交Riesz 基，它们还需满足如下的条件：

[]ππω,-∈?，有

A

k B

k 1)

2(?12

≤

+≤

∑

∞

-∞

=πωθ (12.1.21)

此即(10.2.11)式。式中0>A ，0>B ，)(?ωθ是θ的傅里叶变换，此处θ代表0h ，0?h ，1h 或1

?h 。由本定理所给的条件，即它们的傅里叶变换都是有界的，所以(12.1.21)式满足，因

352

此0h ，0?h ，1

h 及1?h 的偶序号移位构成)(2R L 中的双正交Riesz 基。于是定理得证。 我们之所以说这些序列为“双正交”基，是因为在图12.1.21中的滤波器组中，上下支

路各自是正交的，即0h 和其对偶0?h 正交，1h 和其对偶1?h 正交；同时，上下支路交叉正交，即0h 正交于 1?h ，1

h 正交于0?h 。注意，在双正交滤波器中，我们并没有强调)(0z H 和)(1z H 之间的正交关系，而这一正交关系是共轭正交滤波器组中的基本关系。由此读者可搞清正交和双正交的区别。总之，在小波的多分辨率分析中，使用正交滤波器组时，分解滤波器和重建滤波器是相同的，而在双正交小波分析中，分析滤波器是0H 和1H ，而综合滤波器

是它们的对偶，即0?H 和1

?H 。 此外，(12.1.19a)和 (12.1.19b)的双正交关系与本章开头所给出的(12.1.5)式的关系是一致的，只不过(12.1.19)式更简洁。

12.2 双正交小波

上一节我们讨论了双正交滤波器的基本概念、PR 条件及各滤波器时域、频域的关系。本节，我们将把双正交滤波器组的概念引入双正交小波变换，给出类似第十章的多分辨率分析。

由(9.8.18)和 (9.8.19)式，信号)(t x 的离散小波变换是：

Z k j t t x dt t t x k j WT k

j k

j x ∈==

?,,)(),()()(),(,,ψ

ψ

(12.2.1)

令),()(k j WT k d x j =，则)(k d j 称为小波系数，也即)(t x 的DWT 。我们可由)(k d j 重建

)(t x 。由(9.8.20)式，有

∑∑∑∑

∞

=∞

-∞

=∞

=∞

-∞

==

=

00,,,)(?)(),()(?)()(j k j k k

j k

j k

j j

t t t x t k d

t x ψ

ψ

ψ

(12.2.2)

式中)(?,t k j ψ是)(,t k

j ψ

的对偶小波。由以上两式可以看出，小波)(,t k

j ψ

用于信号的分析，

对偶小波)(?,t k j ψ用于信号的综合。在正交小波的情况下，)()(?,,t t k

j k j ψ

ψ=。

我们在第十章详细讨论了离散小波变换的多分辨率分析，引出了尺度函数)(t φ，证明

353

了在)(2R L 中存在正交基)(,t k j φ和)(,t k

j ψ

，给出了)(,t k

j φ

、)(,t k

j ψ

和正交滤波器组的关

系，即二尺度差分方程和(10.4.7)和(10.4.8)式的频域关系。在双正交滤波器组的情况下，分解滤波器(0H ，1H )和重建滤波器(0?H ，1?H )将产生两个尺度函数(φ，φ?)和两个小波函数(ψ，ψ?)。其中φ和ψ对应信号的分解，而φ?和ψ?对应信号的重建。它们和0H ，0

?H ，1H 及1

?H 相应的时域和频域的关系是： ∑∞

-∞

=-=n n t n h

t )2()(2

)(0

φφ (12.2.3a)

∑∞

-∞=-=

n n t n h t )2(?)(?

2

)(?0

φφ

(12.2.3b)

∑∞

-∞=-=

n n t n h

t )2()(2

)(1

φψ (12.2.4a)

∑∞

-∞

=-=n n t n h t )2(?)(?2

)(?1

φψ

(12.2.4b)

及

)()(2

1)2(0ωωωΦ=

ΦH

(12.2.5a)

)(?)(?21)2(?0ωωωΦ=ΦH

(12.2.5b)

)()(2

1)2(1ωωωΦ=

ψH

(12.2.6a)

)(?)(?2

1)2(?1

ωωωΦ=ψH

(12.2.6b)

定理10.3给出了在正交滤波器组情况下)(0ωH 和)(1ωH 的关系，即(10.5.1)式。对应双正交滤波器组，这一关系变成：

2)(?)()(?)(0

*00*

0=+++πωπωωωH H H H (12.2.7)

此即(12.1.6a)式。由(12.1.13)式，令0=l ，则分解和重建滤波器之间有如下关系：

)(?)(10

11---=z H z z H ，或)(?)(01πωωω+=*

-H e H j (12.2.8a)

354

)()(?1011---=z H z z H ，或)()(?0

1πωωω+=*-H e H j (12.2.8b)

同正交小波时一样，我们要求)(t φ和)(?t φ都是低通的，)(t ψ和)(?t ψ都是带通的。对应的，要求)(0z H 和)(?0

z H 是低通的，)(1z H 和)(?1z H 是高通的，即

0)(?)(00===π

ωωωH H (12.2.9a)

0)(?)(0

1

1===ωωωH H

(12.2.9b)

??==

1)(?

)(dt

t dt t φφ (12.2.10a)

??==0)(?)(dt t dt

t ψ

ψ

(12.2.10b)

由(12.1.16)式，有 2)(?)(0

00==ωωωH H ，及 2)(?)(0

00===ωωωH H (12.2.11a)

2)(?)(1

1==πωωωH H ，及 2)(?)(1

1===π

ωωωH H

(12.2.11b)

类似(10.4.14)式，可由(12.2.5)式导出

∏

∞

==

Φ1

02

)

2()(j j

H ωω (12.2.12a)

∏

∞

==Φ

1

2

)2(?)(?j j H ωω (12.2.12b)

类似(10.4.15)式，可由(12.2.6)式导出

∏

∞

==

ψ2

012

)

2(2

)

2/()(j j

H H ωωω (12.2.13a)

∏

∞

==ψ2

1

2

)2(?2

)2/(?)(?j j H H ωωω (12.2.13b)

由上面的讨论可知，在“双正交”的情况下，我们在第七章及第十章所讨论的滤波器

组及两尺度差分方程各增加了一套“对偶”，即0H ，0?H ；1

H ，1?H ；φ，φ和ψ，ψ?。上面各节给出了它们所应满足的时域及频域关系。下面的定理将给出双正交小波基的存在

355

性。

定理12.3[42,5,8] 假定存在两个恒正的三角多项式)(ωp 和)(?ωp ，使得

)(2)2

(

)2

(

)2

(

)2

(

2

02

0ωπωπωωωp p H p H =+++ (12.2.14a)

)(?2)2

(?)2

(?)2

(

)2

(?2

2

ωπω

πω

ω

ω

p p

H p H =+++ (12.2.14b)

并假定

)(0ωH 、)(?0

ωH 在2

~2ππ-内非零，则 1． 由(12.2.12)式定义的)(t φ和)(?t φ属于)(2R L ，且满足双正交关系

)()(?),(n n t t δφφ=-

(12.2.15)

2． 两个小波函数序列)(,t k j ψ

和)(?,t k

j ψ

是)(2R L 中的双正交Riesz 基，即

)()()(?),('

',,''k k j j t t k

j k j --=δδψψ

(12.2.16)

该定理的证明见文献[42]。有了)(2R L 中的双正交基，我们可对)(t x 作如下的分解：

)(?)(),()(,0,t t t x t x k

j j k k

j ψ

ψ

∑∑

∞

=∞

-∞==

)()(?),(,0,t t t x k

j j k k

j ψ

ψ

∑∑

∞

=∞

-∞

==

(12.2.17)

既然)(,t k

j ψ，)(?,t k

j ψ

是)(2R L 中的Riesz 基，则必然存在常数0>A ，0>B ，使得

2

2

,,2

)()(),()

(t x B t t x t x A k

j k

j ≤≤

∑

ψ

(12.2.18a)

2

2

,,2

)(1)(?),()(1t x A

t t x t x B

k

j k

j ≤

≤

∑

ψ

(12.2.18b) 由上面的讨论可知，在双正交的情况下，我们并不要求}{,k

j ψ

和}{'

,k

j ψ

之间是正交的，

也不要求}{,k j φ和}{,k

j ψ

之间，以及其对偶函数}?{,k j φ和}?{,'

k

j ψ

之间是正交的，仅要求

}{,k

j φ

和}?

{'

,k

j φ之间以及}{,k

j ψ

和}?{'

',k

j ψ

之间是正交的，也即(12.2.15)和(12.2.16)式。正交

356

性的放宽是使)(0z H 及)(1z H 具有线性相位，从而使)(t φ和)(t ψ更具有对称性，从而减小了相位失真。

在第十章的多分辨率分析中，我们假定

},,{close ,Z k j V k j j ∈=φ

(12.2.19a)

},,{close ,Z k j W k

j j ∈=ψ

(12.2.19b)

并有

11++⊕=j j j W V V ，j j V W ⊥

(12.2.19c)

在双正交情况下，尺度函数k j ,φ及其对偶k j ,?φ将产生两个空间。除了(12.2.19a)和(12.2.19b)式的关系外，还有

},,?{c l o s e ?,Z k j V k j j ∈=φ (12.2.20a) 及

},,?{c l o s e ?,Z k j W k j j

∈=ψ

(12.2.20b)

j V 和j

V ?的嵌套关系是

1101+-?????j j V V V V V

(12.2.21a)

1

101?????+-?????j j V V V V V (12.2.21b)

此时，j W 不再是j V 的正交补空间，但j V ，j V ?，j W 和j

W ?之间有如下关系： j j W V ?⊥， j

j W V ⊥? (12.2.22a)

j j j W V V ⊕=-1，j

j j W V V ???1⊕=- (12.2.22b)

由1.7节关于正交基的性质，有

0)2(?)2(=+Φ

+Φ*∞

-∞=∑πωπω

k k k (12.2.23a)

0)2(?)2(=+ψ

+ψ*∞

-∞

=∑

πωπωk k k (12.2.23b)

357

双正交小波下的快速算法和正交基小波下的快速算法基本相同，区别是在重建时使用的是对偶滤波器)(?0

z H 和)(?1z H 。具体的分解方程和重建方程是： ∑∞

-∞=---=*=k j j j n k h k a

n h n a n a )2()()2()()(01

01 （12.2.24a ）

∑∞

-∞

=---=

*=k j j j n k h k a

n h n a n d )2()()2()()(11

11 (12.2.24b)

)(?)()(?)()(1

'0'1n h n d n h n a n a j j j *+*=- ∑∑∞

-∞

=∞

-∞

=-+-=

k j

k j

k n h k d

k n h k a

)2(?)()2(?)(1

(12.2.25) 式中)('n a j ，)('

n d j 分别是)(n a j ，)(n d j 作二插值得到的序列，见图12.1.1。

12.3 双正交小波的构造

双正交小波的构造包括)(t ψ，)(?t ψ

，)(t φ及)(?t φ的构造，而它们又都源于分解滤波器)(0z H 、)(1z H 及用于重建的对偶滤波器)(?0z H 和)(?1z H 。(12.1.14)式给出了)(1z H 、)(?1z H 和)(?0z H 及)(0z H 的关系，因此，双正交小波构造的核心问题是)(0z H 和)(?0

z H 的构造，这和正交小波的构造过程是一样的。如同第十一章关于正交小波的讨论，在具体给出双正交小波的构造方法之前，先讨论一下有关支撑范围、消失矩等有关的有关问题。

1． 支撑范围

如果)(0n h 和)(?0

n h 都是FIR 滤波器，由(12.2.3)和(12.2.4)式，)(t φ，)(?t φ，)(t ψ及)(?t ψ将都具有有限支撑。若)(0n h 和)(?0

n h 的支撑范围分别是21N n N ≤≤，21??N n N ≤≤，则)(t φ和)(?t φ的支撑范围分别是[]21,N N 和[]

2

1?,?N N ，而小波函数)(t ψ和)(?t ψ的支撑范围分别是

[8]

358

??????+-+-21?,21?1221N N N N 和??

????+-+-21?,21?1

2

21N N N N

它们的长度都是2/)??(1

212N N N N -+- 2． 消失矩

)(t ψ和)(?t ψ消失矩的数目取决于)(0ωH 和)(?0

ωH 在πω=处零点的数目。由定理11.1，若)(0ωH 在πω=处有p 阶零点，则)(t ψ有p 阶消失矩。同理，若)(?0ωH 在πω=处有p ?阶零点，则)(?t ψ有p ?阶消失矩。因此，在构造)(0z H 和)(?0

z H 时，应尽量让它们在πω=处有高阶的重零点。

3． 规则性

此处不再详细讨论，其一般结论是：

a) 由(12.2.4a)式，)(t φ和)(t ψ有着相同的规则性；

b) )(t φ和)(t ψ的规则性随着)(0ωH 在πω=处零点数的增加而增加； c)

)(?t φ和)(?t ψ的规则性也是随着)(?0

ωH 在πω=处零点数的增加而增加； d) 如果)(0ωH 和)(?0

ωH 在πω=处有不同的零点数，则)(t ψ和)(?t ψ的规则性也不相同。

4． 对称性

之所以使用双正交小波，其目的是使)(0z H ，)(1z H 及其对偶滤波器具有线性相位，同时也使)(t φ和)(t ψ都具有对称性。除Haar 小波外，在正交小波的情况下，上述对称性是不可能实现的。如果)(0n h ，)(?0n h 具有奇数长且以0=n 为对称，则)(t φ和)(?t φ是以0=t 为对称的，而)(t ψ和)(?t ψ是相对位移位中心为对称的。如果)(0n h ，)(?0

n h 具有偶数长且以2/1=n 为中心作对称，则)(t φ和)(?t φ是以2/1=t 为中心作对称，而)(t ψ和

)(?t ψ

以其位移中心作反对称。

359

显然，若)(0n h ，)(1n h 是对称的，

则图12.1.1中的)(10-z H ，)(1

1-z H 都可改记为)(0z H 和)(1z H ，也即在对)(n a j 作分解时无需再将)(0n h 和)(1n h 翻转。

5.

)(0z H 及)(?0

z H 的构造 由于要求)(0z H 及)(?0

z H 具有线性相位，因此，它们的频率响应可表为：

)()(00ωωω

H e

H jk =

(12.3.1a)

)(?)(?0

?0ωωωH e H k j = (12.3.1b)

这是和Daubechies 正交小波的一个主要区别。在实际工作中，我们总选取)(0n h 和)(?0

n h 为实值序列。因此，又有

)()(00ωω-=H H ，)(?)(?0

0ωω-=H H (12.3.2)

由(12.2.12)式，必有)()(ωω-Φ=Φ。同理，我们总是选择)(t φ为实函数，因此又有

)()(t t -=φφ，即尺度函数)(t φ以0=t 为对称。同样的结论适用于)(?t φ。

若)(t φ和)(?t φ以2/1=t 为对称，例如，Haar 小波的尺度函数即是如此。此时要求)(0ωH 、)(?0

ωH 仍是偶对称，但要增加一个移位因子，即

)()(00ωωω

H e

H j =-，)(?)(?0

ωωω

H e H j =- (12.3.3)

现在的问题是，如何找到合适的)(0z H 及)(?0

z H ，使其所形成的滤波器组为双正交滤波器组，也即保证)(t φ、)(?t φ及)(t ψ，)(?t ψ

的双正交条件，即满足：

2)(?)()(?)(0

000=+++**

πωπωωωH H H H 也即(12.1.16a)式。习惯上将该式两边取共轭，即

360

2)(?)()(?)(0

000=+++**πωπωωωH H H H (12.3.4)

Cohen ，Daubechies 给出了不同类型的双正交小波的结构方法[42, 5]

，其要点是：

(1). 令)(0ωH 固定，假定)(?0

ωH 是(12.3.4)式的解，若)()(00ωω-=H H ，则 []

)(?)(?2

1)(0

00ωωω-+='H H H 也是(12.3.4)式的解。将该式代入(12.3.4)式即可验证。

(2). 因为)(0n h 、)(?0n h 是实序列，)(0ωH 、)(?0

ωH 满足(12.3.2)式，所以)(0ωH 、)(?0

ωH 均应是实系数的三角多项式，它们可分别写成

)(cos 2cos 2)(020ωωωP H l

???

?

?

=

(12.3.5a)

和

)(cos ?2cos 2)(?0?

20

ωωωP H l ??? ?

?

=

(12.3.5b)

的形式。

若)(0ωH 、)(?0

ωH 按(12.3.3)式的形式对称，则它们可表为

)(cos 2cos 2)(01

22

/0ωωωωP e

H l j +-?

?? ??=

(12.3.6a)

)(cos ?2cos 2)(?0

1

?22

/0

ωωωωP e

H l j +-?

??

?

?= (12.3.6b)

的形式。

(3). 将(12.3.5)和(12.3.6)式分别代入(12.3.4)式，有

2)cos (?)cos (2sin )(cos ?)(cos 2cos 0

020

02=--???

?

?+?

??

?

?

ωωωωωωP P P P k

k

(12.3.7)

对应(12.3.5)式，l l k ?+=；对应(12.3.6)式，1?++=l l k 。

由于2/)cos 1(2sin 2

ωω-=??? ?

?，所以)(cos 0ωP ，)(cos ?0

ωP 均可以表示为2sin 2ω的

361

函数，再令

??

?

?

???

? ?

?=???

?

?2sin ?2sin 2sin 202

02

ωωωP P P

(12.3.8)

则(12.3.7)式可表示为：

2)2

(cos

2sin )2(sin

2cos 2

22

2=??

? ??

+?

?? ??

ωωω

ωP P k

k

(12.3.9)

(4). 令2

sin 2

ω

=y ，则(12.3.9)式又可表为如下的Bezout 方程：

1)1()()1(=-+-y P y y P y k k

(12.3.10)

该方程和(11.4.5)式是一样的，区别只是)(y P 所表示的内容。只要能求出)(y P ，由(12.3.8)式，即可得到)(0y P 和)(?0y P ，从而可按(12.3.5)或(12.3.6)式构造出)(0z H 和)(?0

z H 。 (5). (12.3.10)式的解由下式给出：

)21(1)(1

0y R y y m m k y P k

m k m -+???

? ??+-=

∑-= (12.3.11)

这和(11.4.7)式的结果是一样的，式中)(y R 是一奇对称多项式，即)1()(y R y R --=。

当 l l k ?+=时， )(0z H 、)(?0

z H 以0=n 为对称

1?++=l l k 时，)(0z H 、)(?0

z H 以2/1=n 为对称 选用不同的R ，对)(?)()(0

0y P y P y P =作不同的分解可得到不同类型的双正交小波。Daubechies 重点给出了基于样条函数的双正交小波的构造方法，同时也给出了)(0z H 、)(?0

z H 长度接近相等的基于样条函数的双正交小波的构造方法，现分别给以讨论。

12.4 双正交样条小波

样条函数是分段光滑且在连结点处具有一定光滑性的一类函数，它在数值逼近方面获得了广泛的应用。其中基数B 样条(Cardinal B-Spline)函数具有最小的支撑范围且又容易在计算机上实现，因此被认为是构造小波函数的最佳候选者之一。

m 次B 样条函数)(t N m 是一阶B 样条函数)(1t N 自身作1-m 次卷积所得到的，而

)(1t N 正是Haar 小波的尺度函数，即

362

???=0

1

)(1t N

其它

10<≤t (12.4.1)

所以

??

?

??-=*=02)()()(112t t t N t N t N

其它

2110<≤<≤t t (12.4.2)

????

?

????---*0)3(21)2/3(4

32/)()()(2

2

2

123t t t t N t N t N ＝＝ 其它

322110<≤<≤<≤t t t (12.4.3)

依次类推，有 )()()()()()(11211t N t N t N t N t N t N m m m **=*=--

)()()(111t N t N t N ***=

(12.4.4)

Battle 和Lemarie 用上述的样条函数构造了小波[8]，其思路是令尺度函数)(?t φ等于

)(t N m 。考虑到)(?t φ往往以0=t 为对称，所以令

1=m

)()(?1t N t =φ

(12.4.5)

2=m

??

?-=+=0

1)1()(?2t t N t φ

其它

1≤t (12.4.6)

3=m

???

?

???----+=0)

2(2/1)21(4/3)1(5.0)1()(?22

2

3t t t t N t ＝＋φ 其它21100

1<≤<≤<≤-t t t (12.4.7) 3,2,1=m 时的)(?t φ如图12.4.1所示。由该图可以看出，)(1t N 是不连续的，)(2t N 连续但

一阶导数不连续，而)(3t N 的一阶导数是连续的，曲线已比较光滑。当m 增大时，)(t N m 会变得更光滑。

363

图12.4.1 由)1(+t N m 得到尺度函数

很容易证明(12.4.4)式所决定的)(t N m 的傅里叶变换是

m

m j m

j e

j e ??

????=???

?

?

?---2/2/sin 12/ωωωωω

(12.4.8)

而对移位后的)1()(?+=t N t m φ，其傅里叶变换为

m

j e ?

?

?

???=Φ

-2/2/sin )(?2

/ωωωεω (12.4.9)

如果m 为偶数，式中0=ε，若m 为奇数，则式中1=ε。

分析(12.4.6)式，我们发现

)12(?2

1

)2(?)12(?21)1()(?2-+++=

+=t t t t N t φφφφ (12.4.10)

满足我们在第十章所讨论的二尺度差分方程。同时，可求出

364

2

cos

3

23

1)2(?2

2

ω

πω+

=

+Φ

∑

∞

-∞

=l l (12.4.11)

是有界的。当3=m 时，

)22(?4

1

)12(?43)2(?43)12(?41)1()(?3-+-+++=

+=t t t t t N t φφφφφ (12.4.12)

同样也满足二尺度差分方程，同理可求出

ωωπω2

2

cos 30

1cos 30

1315

8)2(?+

+

=

+Φ

∑

∞

-∞

=l l

(12.4.13)

因此，在3,2,1=m 时不同的)(?t φ可构成一个多分辨率分析。由1.7节关于正交基频域的性质，由于(12.4.11) 和(12.4.13)式的右边不等于1，因此)(?t φ的整数移位之间不构成正交基。由(9.8.40)式，我们可将)(?t φ“正交化”，即令

21

2)2(?

)(?)(???

????+ΦΦ

=Φ

∑∞-∞=⊥k l πωωω (12.4.14)

对)(?ω⊥Φ

作反变换，得尺度函数)(?t φ，则)(?n t -φ，Z n ∈可形成一族正交基。再由第十章的方法可得到正交归一的小波函数。

在双正交的情况下，我们可不必对)(?t φ作(12.4.14)式的正交化，而直接用)(t N m 作适当移位后的)(?t φ作为尺度函数，如(12.4.5)～(12.4.7)式所示。这样选定)(?t φ后，Daubechies 令(12.3.11)式中的)21(y R -等于零，并令1)(?0=y P 。)()(0y P y P =，从而得到了在双正交条件下样条小波分析滤波器)(0z H 和重建滤波器)(?0

z H 的系数，即

N

H ?0

2cos 2)(???? ?

?=ωω，l N

?2?= (12.4.15a)

365

N

j e

H ?2

/0

2cos 2)(???? ?

?=-ωωω，1?2?+=l N

(12.4.15b)

m

l l m N m m l l H ??

?

??

???? ??+-+?

?? ?

?

=

∑-+=2sin 1?2cos 2)(2

1

?00ωωω，l N 2=

(12.4.16a)

m

l l m N j m m l l e

H ??

?

?

????? ??++?

?? ?

?=

∑+=-2sin ?2cos 2)(2

?

02

/0ωωωω，12+=l N

(12.4.16b)

(12.4.15a)和 (12.4.15b)分别对应(12.3.5b)式和 (12.3.6b)式，而(12.4.16)式是(12.3.5a)式、(12.3.6a)式和(12.3.11)式的结合。

由(12.4.15)式可以看出，)(?0

ωH 仅和l ?有关，而和l 无关；由(12.4.16)式，)(0ωH 不但和l 有关，而且还和l ?有关，也即)(0ωH 取决于N 和N

?。给定不同的N 和N ?，就可求出一对)(0ωH 和)(?0ωH 。将(12.4.15)式和(12.4.8)及(12.4.9)式相比较可以看出，尺度函数)(t φ的傅里叶变换的“阶次m ”和)(?0

ωH 中的N ?等价，也即1?-N 即是得到)(t φ时由)(1t N 卷积的次数，或称之为)(t φ的“阶次”

。 现给出不同N 和N ?组合情况下)(0z H 、)(?0z H 、)(t φ、)(?t φ、)(t ψ和)(?t ψ的系数。 情况1. 令1?=N

，则必有0?=l ，由(12.4.15b)式，有 []

ω

ωωωωj j j j e e e e

H ---+=?

?

????+=

12222)(2/2/2

/0 所以[]注，

)1(2

2)(?1

-+=z z H

即

{}707.0,707.0)(?0

=n h

令1=N ，则必有0=l ，由(12.4.16b)式，有