全等三角形模型总结及经典练习题

全等三角形模型及习题练习
第一部分全等模型图
一、平移模型
特征:可看成是三角形在一边所在直线上移动构成的,故在同一直线上的对应边的相等关系一般可由加(减)公共边证得,对应角的相等关系可由平行线的性质证得。
二、平行模型(X型)
特征:平行线所形成的同位角、内错角相等
三、折叠轴对称模型(翻转型,部分X型)
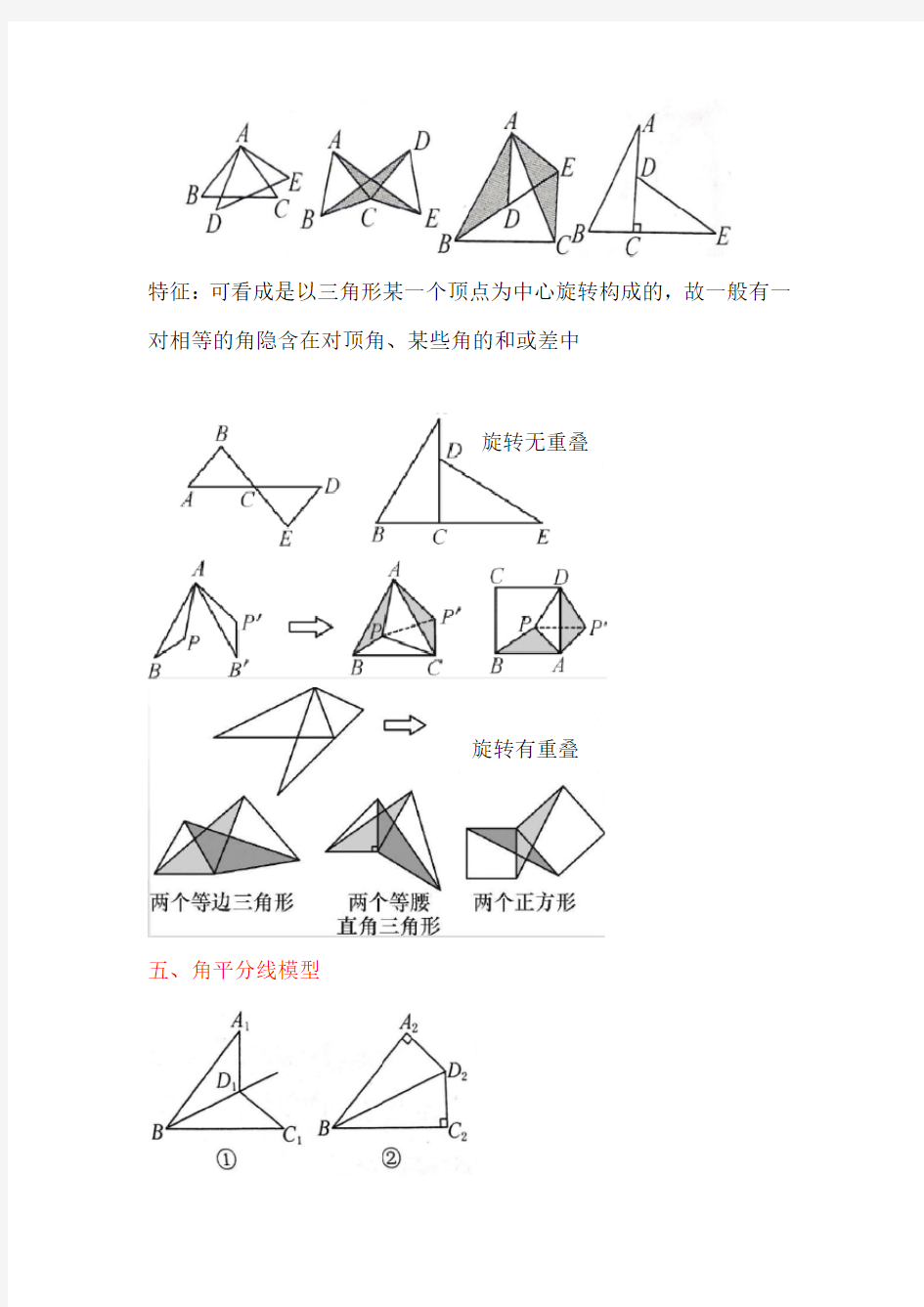
特征:图形关于某一条直线对称,则这条直线两边的部分能完全重合,重合的顶点就是全等三角形的对应点。图①中有公共角∠A;图②中对顶角相等(∠AOC=∠BOD);图③④中分别有公共边AB,BD
四、旋转模型
七年级全等三角形证明经典题
七年级数学下册《全等三角形》专题练习 1、已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C(做AB=AE交AC于E点) 6、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE(做AD=AF交AB于F点) 8. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。求 证:BC=AB+DC。 C D B A
9、已知:AB 知:如图所示,AB = AD ,BC =DC ,E 、F 分别是DC 、BC 的中点,求证: AE =AF 。 35.在△ABC 中,?=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ?≌CEB ?;②BE AD DE +=; (2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗若成立,请给出证明;若不成立,说明理由. A B C D D C B A F E P E D C B A D C B A M F E C B A F E D C B A F D C B F E D C B A D B C A F E
46. 如图, AB=12, CA⊥AB于A, DB⊥AB于B, 且AC=4m, P点从B向A运动, 每分钟走1m, Q 点从B向D运动, 每分钟走2m,P、Q两点同时出发, 运动几分钟后△CAP≌△PQB 试说明理由. 47、如图(1), 已知△ABC中, ∠BAC=900, AB=AC, AE是过A的一条直线, 且B、C在A、E的异侧, BD⊥AE于D, CE⊥AE于E. (图1) (图2) (图3) (1)试说明: BD=DE+CE. (2) 若直线AE绕A点旋转到图(2)位置时(BD
全等三角形证明经典题(含答案)
全等三角形证明经典题(含答案) 1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADCBD=DC ∴△ACD ≌△BDE ∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE ∵AB=4即 4-2<2AD <4+21<AD <3∴AD=2 2. 已知:D 是AB 中点,∠ACB=90°,求证:12 CD AB 延长CD 与P ,使D 为CP 中点。连接AP,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB 3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 4. 5. 证明:连接BF 和EF ∵BC=ED,CF=DF,∠BCF=∠EDF ∴三角形BCF 全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF 连接BE 在三 角形BEF 中,BF=EF ∴∠EBF=∠BEF 。 ∵∠ABC=∠AED 。∴∠ABE=∠AEB 。∴AB=AE 。在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴三角形ABF 和三角形AEF 全等。∴∠BAF=∠ EAF(∠1=∠2)。 6. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC A D B C
过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGD DE =DC ∠FDE =∠GDC (对顶角)∴△EFD ≌△CGD EF =CG ∠CGD =∠EFD 又EF ∥AB ∴∠EFD =∠1∠1=∠2 ∴∠CGD =∠2∴△AGC 为等腰三角形,AC =CG 又EF =CG ∴EF =AC 7. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C 证明:延长AB 取点E ,使AE =AC ,连接DE ∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD ∴△AED ≌△ACD (SAS ) ∴∠E =∠C ∵AC =AB+BD ∴AE =AB+BD ∵AE =AB+BE ∴BD =BE ∴∠BDE =∠E ∵∠ABC =∠E+∠BDE ∴∠ABC =2∠E ∴∠ABC =2∠C 8. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF ∵CE ⊥AB ∴∠CEB =∠CEF =90° ∵EB =EF ,CE =CE ,∴△CEB ≌△CEF ∴∠B =∠CFE ∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC ∴△ADC ≌△AFC (SAS ) ∴AD =AF ∴AE =AF +FE =AD +BE 9. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。求证:BC=AB+DC 。 在BC 上截取BF=AB ,连接EF ∵BE 平分∠ABC ∴∠ABE=∠FBE 又∵BE=BE ∴⊿ABE ≌⊿FBE (SAS ) ∴∠A=∠BFE ∵AB//CD ∴∠A+∠D=180o ∵∠BFE+∠CFE=180o ∴∠D=∠CFE 又∵∠DCE=∠FCECE 平分∠BCDCE=CE ∴⊿DCE ≌⊿FCE (AAS )∴CD=CF ∴BC=BF+CF=AB+CD 10. 已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C AB ‖ED ,得:∠EAB+∠AED=∠BDE+∠ABD=180度, ∵∠EAB=∠BDE , B A C D F 2 1 E D C B A F E A
专题训练(三) 全等三角形的基本模型
专题训练(三)全等三角形的基本模型 ?模型一平移模型 常见的平移模型: 图3-ZT-1 1.如图3-ZT-2,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:∠A=∠E. 图3-ZT-2 2.如图3-ZT-3,点A,B,C,D在同一条直线上,AB=CD,AE∥BF,CE∥DF.求证:AE=BF. 图3-ZT-3 ?模型二轴对称模型 常见的轴对称模型: 图3-ZT-4 3.如图3-ZT-5,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由. 图3-ZT-5 4.如图3-ZT-6,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD. 图3-ZT-6 5.如图3-ZT-7,A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF.求证:DE=CF. 图3-ZT-7 6.如图3-ZT-8,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC. 图3-ZT-8 ?模型三旋转模型 常见的旋转模型: 图3-ZT-9
7.如图3-ZT-10,已知AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:AD=AE. 图3-ZT-10 ?模型四一线三等角模型 图3-ZT-11 8.如图3-ZT-12,B,C,E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B. (1)求证:BC=DE; (2)若∠A=40°,求∠BCD的度数. 图3-ZT-12 ?模型五综合模型 平移+对称模型:平移+旋转模型: 图3-ZT-13 图3-ZT-14 9.如图3-ZT-15,点B,F,C,E在同一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF. 3-ZT-15 10.如图3-ZT-16,AB=BC,BD=CE,AB⊥BC,CE⊥BC.求证:AD⊥BE. 图3-ZT-16 详解详析
初中全等三角形模型总结—全面完整版2018.5.23
初中全等三角形模型总结——全面完整版 (模型总结+精选例题+优选练习题) 第一部分 模型总结 一、公共边模型 △ABD ≌△ABC , △EFD ≌△ABC △ABD ≌△ABC △ABE ≌△FDC △ABD ≌△ACD 二、公共角模型 △ABE ≌△ABD 三、平行X 型 △ABO ≌△OCD 四、非平行X 型 △ABE ≌△ABD B D C
五、母子等腰三角形 △ABD ≌△AEC ,△ABE ≌△ACD 六、旋转模型 △ ABC ≌△AB`C 第二部分 精选例题 例1.如图,已知AB ∥CD ,AD ∥BC ,F 在DC 的延长线上,AM =CF ,FM 交DA 的延长线上于E .交BC 于N,求证:AE=CN. 思路分析:欲证AE=CN.看它们在哪两个三角形中, 设法证这两个三角形全等即可.结合图形可发现 △AME ≌△FCN 可证. 题设告知AM=CF,AD ∥BC,AB ∥CD.由两平行条件, 可找两对角相等. ∵∠1=∠2(对顶角相等) ∴∠2=∠E(等量代换) ∴AE=CN (全等三角形的对应边相等) 例2.△ABC 中,∠ACB =90°,AC =BC ,过C 的一条直线CE ⊥AE 于E ,BD ⊥CE 的延长线于D ,求证:AE =BD +DE . 思路分析:从本例的结论知是求线段和的问题, 由此入手,很难找到突破口.此时可迅速调整思维角 度,可仔细观察图形,正确的图形是证题的“向导”,由 此可发现△ACE 与△CBD 好像(猜测)全等.那么 AE =CD =CE +DE .又BD =CE .那么,此时已水落石出. B C E D B'A 'B '
全等三角形证明经典50题(含答案)
全等三角形证明经典50题(含答案) 1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 2. 已知:D 是AB 中点,∠ACB=90°,求证:12 CD AB 延长CD 与P ,使D 为CP 中点。连接AP ,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90 ∴平行四边形ACBP 为矩形 A D B C
∴AB=CP=1/2AB 3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。 ∵ ∠ABC=∠AED 。 ∴ ∠ABE=∠AEB 。 ∴ AB=AE 。 在三角形ABF 和三角形AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。 ∴ ∠BAF=∠EAF (∠1=∠2)。 4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC ∠FDE =∠GDC (对顶角) B A C D F 2 1 E
全等三角形证明经典50题(含答案)
1、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE 2、已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC 3、如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC . 4.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N . 求证:∠OAB =∠OBA 5.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线 交AP 于D .求证:AD +BC =AB . P E D C B A F A E D C B
6.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F , 若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF (2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立 请给予证明;若不成立请说明理由. 7.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积 相等的三角形.(直接写出结果,不要求证明): 8.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线 垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE . O E D C B A F E D C B A
初中数学三角形全等常用几何模型及构造方法大全(初二)
初二数学三角形全等 常用几何模型及构造方法大全 掌握它轻松搞定全等题! 全等是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握~ 全等变换类型: (一)平移全等:平行等线段(平行四边形) (二)对称全等模型:角平分线或垂直或半角 1:角平分线模型; 2:对称半角模型; (三)旋转全等模型:相邻等线段绕公共顶点旋转 1. 旋转半角模型 2. 自旋转模型 3. 共旋转模型 4. 中点旋转
如图,在△ABC的边上取两点D、E,且BD=CE,求证:AB+AC>AD+AE 分析:将△ACE平移使EC与BD重合。B\D,上方交点,左右两个三角形,两边和大于第三边!
1:角平分线模型: 说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。 2:对称半角模型 说明:上图依次是45°、30°、45+ 22.5°、对称(翻折)15°+30°直角三角形对称(翻折)30+60+90直角三角形对称(翻折) 翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
1. 半角:有一个角含1/2角及相邻线段 2. 自旋转:有一对相邻等线段,需要构造旋转全等 3. 共旋转:有两对相邻等线段,直接寻找旋转全等(共顶点) 4. 中点旋转:倍长中点相关线段转换成旋转全等问题(专题七) 1、旋转半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。 2、自旋转模型 构造方法: 遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角 遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称
全等三角形常见的几何模型
全等三角形常见的几何 模型 集团文件版本号:(M928-T898-M248-WU2669-I2896-DQ586-M1988)
1、绕点型(手拉手模型) (1)自旋转:???????,造中心对称遇中点旋全等 遇等腰旋顶角,造旋转,造等腰直角 旋遇,造等边三角形 旋遇自旋转构造方法0000 018090906060 (2)共旋转(典型的手拉手模型) 例1、在直线ABC 的同一侧作两个等边三角形△ABD 和 △ BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC (2) A E=DC (3) A E 与DC 的夹角为60。 (4) △AGB ≌△DFB (5) △EGB ≌△CFB (6) B H 平分∠AHC (7) G F ∥AC 变式练习1、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC (2) A E=DC (3) A E 与DC 的夹角为60。 (4) A E 与DC 的交点设为H,BH 平分∠AHC 变式练习2、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1)△ABE ≌△DBC (2)AE=DC (3)AE 与DC 的夹角为60。 (4)AE 与DC 的交点设为H,BH 平分∠AHC
3、(1)如图1,点C是线段AB上一点,分别以AC,BC为边在AB的同侧作等边△ACM和△CB N,连接AN,BM.分别取BM,AN的中点E,F,连接CE,CF,EF.观察并猜想△CEF的形状,并说明理由. (2)若将(1)中的“以AC,BC为边作等边△ACM和△CBN”改为“以AC,BC为腰在AB的同侧作等腰△ACM和△CBN,”如图2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理由. 例4、例题讲解: 1. 已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B,C重合),以AD为边作菱形ADEF(按A,D,E,F逆时针排列),使∠DAF=60°,连接CF. (1)?如图1,当点D在边BC上时,求证:①?BD=CF???②AC=CF+CD. (2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由; ? (3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD 之间存在的数量关系。 2、半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。 例1、如图,正方形ABCD的边长为1,AB,AD上各存在一点P、Q,若△APQ的周长为2, 求PCQ 的度数。
最新全等三角形经典模型总结
全等三角形相關模型總結 一、角平分線模型 (一)角平分線の性質模型 輔助線:過點G作GE⊥射線AC A、例題 1、如圖,在△ABC中,∠C=90°,AD平分∠CAB,BC=6cm,BD=4cm,那麼點D到直線AB の距離是cm. 2、如圖,已知,∠1=∠2,∠3=∠4,求證:AP平分∠BAC. B、模型鞏固 1、如圖,在四邊形ABCD中,BC>AB,AD=CD,BD平分∠ABC,求證:∠A+∠C=180°.
(二)角平分線+垂線,等腰三角形必呈現 A、例題 輔助線:延長ED交射線OB於F 輔助線:過點E作EF∥射線OB 例1、如圖,在△ABC中,∠ABC=3∠C,AD是∠BACの平分線,BE⊥AD於F . 求證: 1 () 2 BE AC AB =-.
例2、如圖,在△ABC中,∠BACの角平分線AD交BC於點D,且AB=AD,作CM⊥AD交 ADの延長線於M. 求證: 1 () 2 AM AB AC =+. (三)角分線,分兩邊,對稱全等要記全 兩個圖形飛輔助線都是在射線ON上取點B,使OB=OA,從而使△OAC≌△OBC . A、例題 1、如圖,在△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC於P,BQ平分∠ABC 交AC於Q,求證:AB+BP=BQ+AQ .
2、如圖,在△ABC中,AD是∠BACの外角平分線,P是AD上異於點Aの任意一點,試比較PB+PC與AB+ACの大小,並說明理由.
B、模型鞏固 1、在△ABC中,AB>AC,AD是∠BACの平分線,P是線段AD上任意一點(不與A重合). 求證:AB-AC>PB-PC . 2、如圖,△ABC中,AB=AC,∠A=100°,∠Bの平分線交AC於D, 求證:AD+BD=BC . 3、如圖,△ABC中,BC=AC,∠C=90°,∠Aの平分線交BC於D, 求證:AC+CD=AB .
八年级全等三角形证明经典题
全等三角形证明经典题 1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 2. 已知:D 是AB 中点,∠ACB=90°,求证:12 CD AB = 3. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 4. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C 5. 已知:D 是AB 中点,∠ACB=90°,求证:12 CD AB = A D B C C D B B A C D F 2 1 E A
6. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 7. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 8. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C 一:如果abc=1,求证 11++a ab +11++b bc +11 ++c ac =1 二:已知a 1+b 1= )(29b a +,则a b +b a 等于多少? B B A C D F 2 1 E C D B A
9. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证: AE=AD+BE 13. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。求证:BC=AB+DC 。 14.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C 14. 已知:AB=CD ,∠A=∠D ,求证:∠B=∠C 15. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB 作弊? 漫画释义 三角形9级 全等三角形的经典模型(二) 三角形8级 全等三角形的经典模型(一) 三角形7级 倍长中线与截长补短 满分晋级 3 全等三角形的 经典模型(一) D C B A 45°45° C B A 等腰直角三角形数学模型思路: ⑴利用特殊边特殊角证题(AC=BC 或904545??°,,).如图1; ⑵常见辅助线为作高,利用三线合一的性质解决问题.如图2; ⑶补全为正方形.如图3,4. 图1 图2 图3 图4 思路导航 知识互联网 题型一:等腰直角三角形模型 A B C O M N A B C O M N 【例1】 已知:如图所示,Rt △ABC 中,AB =AC ,90BAC ∠=°,O 为BC 的中点, ⑴写出点O 到△ABC 的三个顶点A 、B 、C 的距离的关系(不要 求证明) ⑵如果点M 、N 分别在线段AC 、AB 上移动,且在移动中保持 AN =CM .试判断△OMN 的形状,并证明你的结论. ⑶如果点M 、N 分别在线段CA 、AB 的延长线上移动,且在移动中保持AN =CM ,试判断⑵中结论是否依然成立,如果是请给出证明. 【解析】 ⑴OA =OB =OC ⑵连接OA , ∵OA =OC 45∠=∠=BAO C ° AN =CM ∴△ANO ≌△CMO ∴ON =OM ∴∠=∠NOA MOC ∴90∠+∠=∠+∠=?NOA BON MOC BON ∴90∠=?NOM ∴△OMN 是等腰直角三角形 ⑶△ONM 依然为等腰直角三角形, 证明:∵∠BAC =90°,AB =AC ,O 为BC 中点 ∴∠BAO =∠OAC =∠ABC =∠ACB =45°, ∴AO =BO =OC , ∵在△ANO 和△CMO 中, AN CM BAO C AO CO =?? ∠=∠??=? ∴△ANO ≌△CMO (SAS ) ∴ON =OM ,∠AON =∠COM , 又∵∠COM -∠AOM =90°, ∴△OMN 为等腰直角三角形. 【例2】 两个全等的含30,60角的三角板ADE 和三角板ABC ,如 图所示放置,,,E A C 三点在一条直线上,连接BD ,取BD 的 中点M ,连接ME ,MC .试判断EMC △的形状,并说明理由. 【解析】EMC △是等腰直角三角形. 典题精练 A B C O M N M E D C B A 1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 的长. 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 2. 已知:BC=ED ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠ 2 证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。 ∵ ∠ABC=∠AED 。 ∴ ∠ABE=∠AEB 。 ∴ AB=AE 。 在三角形ABF 和三角形AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。 ∴ ∠BAF=∠EAF (∠1=∠2)。 A D B C 3. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC ∠FDE =∠GDC (对顶角) ∴△EFD ≌△CGD EF =CG ∠CGD =∠EFD 又,EF ∥AB ∴,∠EFD =∠1 ∠1=∠2 ∴∠CGD =∠2 ∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC 4. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C 证明:延长AB 取点E ,使AE =AC ,连接DE ∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD ∴△AED ≌△ACD (SAS ) ∴∠E =∠C ∵AC =AB+BD ∴AE =AB+BD ∵AE =AB+BE ∴BD =BE ∴∠BDE =∠E B A C D F 2 1 E A 全等三角形证明经典试题50道 1. (已知:如图,E,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B . 求证:AE =CF . 【答案】∵AD ∥CB ∴∠A=∠C 又∵AD=CB ,∠D=∠B ∴△ADF ≌△CBE ∴AF=CE ∴AF+EF=CE+EF 即AE=CF 2. 已知:如图,∠ABC =∠DCB ,BD 、C A 分别是∠ABC 、∠DCB 的平分线.求证:AB =DC 证明:在△ABC 与△DCB 中 (ABC DCB ACB DBC BC BC ∠=∠?? ∠=∠??=? 已知)(公共边)(∵AC 平分∠BCD ,BD 平分∠ABC ) ∴△ABC ≌△DCB ∴AB =DC 3. 如图,点D ,E 分别在AC ,AB 上. (1) 已知,BD=CE,CD=BE,求证:AB=AC; (2) 分别将“BD=CE”记为①,“CD=BE”记为②,“AB=AC”记为③.添加条件①、③,以②为结论构成命题1,添加条件②、③以①为结论构成命题2.命题1是命题2的命题,命题2是命题.(选择“真”或“假”填入空格). 【答案】 (1) 连结BC,∵ BD=CE,CD=BE,BC=CB. ∴△DBC≌△ECB (SSS) ∴∠DBC =∠ECB ∴ AB=AC (2) 逆,假; 4. 如图,在□ABCD中,分别延长BA,DC到点E,使得AE=AB,CH=CD,连接EH,分别交AD,BC于点F,G。求证:△AEF≌△CHG. 【答案】证明:∵□ABCD ∴ AB=CD,∠BAD=∠BCD AB∥CD ∴∠EAF=∠HCG ∠E=∠H ∵ AE=AB,CH=CD ∴ AE=CH 1绕点型(手拉手模型) 遇600旋60°,造等边三角形 遇90°旋90°,造等腰直角遇等腰旋 顶角,造旋转全等遇中点旋1800,造中 心对称 (2)共旋转(典型的手拉手模型) 例1、在直线ABC的同一侧作两个等边三角形△ (1)△ ABE ◎△ DBC (2)AE=DC (3)AE与DC的夹角为60。 (4)△ AGB ◎△ DFB (5)△ EGB ◎△ CFB (6)BH 平分/ AHC (7)GF // AC 变式练习2、如果两个等边三角形△ ABD和厶BCE,连接AE与CD,证明: ("△ ABE ◎△ DBC (2)AE=DC (3)AE与DC的夹角为60。 (4) AE与DC的交点设为H,BH平分/ AHC [D山3 Vi壮-U (I) ? 变式练习1、如果两个等边三角形△ABD和厶BCE,连接AE与CD,证明 (1) △ ABE ◎△ DBC (2) AE=DC (3) AE与DC的夹角为60。 (4) AE与DC的交点设为H,BH 平分/ AHC (1自旋转:自旋转构造方法 ABD和厶BCE,连接AE与CD,证明: 3、(1)如图1,点C是线段AB上一点,分别以AC, BC为边在AB的同侧作等边△ ACM和厶CBN ,连接AN , BM .分别取BM, AN的中点E, F,连接CE, CF, EF.观察并猜想△ CEF的形状,并说明理由. (2)若将(1)中的“以AC , BC为边作等边△ ACM和厶CBN”改为“以AC, BC为腰在AB的同侧作等腰△ ACM和△ CBN,”如图2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理由. B 例4、例题讲解: 1.已知△ ABC为等边三角形,点D为直线BC上的一动点(点D不与B,C重合),以AD为边作菱形ADEF(按A,D,E,F 逆时针排列),使/ DAF=60 ° ,连接CF. (1)如图1,当点D在边BC上时,求证:① BD=CF 宓AC=CF+CD. (2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、 CD之间存在的数量关系,并说明理由; ⑶如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系。 2、半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起, 成对称全等。 D A D A M x N rt B D 例1、如图,正方形ABCD的边长为1, AB,AD上各存在一点P、0,若厶APQ的周长为2, A P 【最新整理,下载后即可编辑】 全等三角形之手拉手模型专题 基本图形1、图(1)中,C 点为线段AB 上一点,△ACM,△CBN 是等边三角形,AN 与BM 相等吗?说明理由; 如图(2)C 点为线段AB 上一点,等边三角形ACM 和等边三角形CBN 在 AB 的异侧,此时AN 与BM 相等吗?说明理由; 如图(3)C 点为线段AB 外一点,△ACM,△CBN 是等边三角形,AN 与BM 相等吗? 说明理由. 分析:题中三问均是对等边三角形性质的考查以及全等三角形的证明,由 已知条件,利用等边三角形的性质可找出对应边及夹角相等,证明全等, 即可得到线段相等. 解:(1)相等. 证明如下:∵△ACM,△CBN 是等边三角形, ∴AC=CM,CN=BC, 又∠ACN=∠MCN+60°∠MCB=∠MCN+60°, ∴∠ACN=∠MCB, ∴△ACN≌△MCB,∴AN=BM. (2)相等. 证明如下:∵△ACM,△CBN 是等边三角形, ∴AC=CM,CN=BC 又∠ACN=∠MCB, ∴△ACN≌△MCB, ∴AN=BM. (3)相等. 证明如下:∵△ACM,△CBN 是等边三角形, ∴AC=CM,CN=BC, 又∠ACN=∠MCN+60°∠MCB=∠MCN+60°, ∴∠ACN=∠MCB, ∴△ACN≌△MCB, ∴AN=BM. 点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可围 绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,证得三 角形全等是正确解答本题的关键. 变形2、(1)如图1,点C 是线段AB 上一点,分别以AC,BC 为边在AB 的同侧 作等边△ACM 和△CBN,连接AN,BM.分别取BM,AN 的中点E,F,连接 CE,CF,EF.观察并猜想△CEF 的形状,并说明理由. (2)若将(1)中的“以AC,BC 为边作等边△ACM 和△CBN”改为“以 AC,BC 为腰在AB 的同侧作等腰△ACM 和△CBN,”如图2,其他条件不变, 那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理 1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD 2.已知:D是AB中点,∠ACB=90°,求证: 1 2 CD AB = 3.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2 4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC 5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C 6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证: AE=AD+BE 7.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD 8.已知:D是AB中点,∠ACB=90°,求证: 1 2 CD AB = 9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2 10.已知:∠1=∠2,CD=DE,EF//AB,求证: EF=AC A D B C B B A C D F 2 1 E C D B A A D B C 11.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C 12.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证: AE=AD+BE 12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD 上。求证:BC=AB+DC。 13.已知:AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证:∠F=∠C 14.已知:AB=CD,∠A=∠D,求证:∠B=∠C 15.P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB 专项练习(二)全等三角形的基本模型?基本模型一平移模型 常见的平移模型: 图2-ZT-1 1.如图2-ZT-2,点B在线段AD上,BC∥DE,AB=ED,BC=D B. 求证:∠A=∠E. 图2-ZT-2 2.如图2-ZT-3,点A,B,C,D在一条直线上,AB=CD,AE∥BF,CE∥DF. 求证:AE=BF. 图2-ZT-3 ?基本模型二轴对称模型 常见的轴对称模型: 图2-ZT-4 3.如图2-ZT-5,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由. 图2-ZT-5 4.如图2-ZT-6,BD⊥AC于点D,CE⊥AB于点E,AD=AE. 求证:BE=CD. 图2-ZT-6 5.如图2-ZT-7,A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF. 求证:DE=CF. 图2-ZT-7 6.如图2-ZT-8,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC. 图2-ZT-8 ?基本模型三旋转模型 常见的旋转模型: 图2-ZT-9 7.如图2-ZT-10,O是线段AB和线段CD的中点.求证:(1)△A OD≌△BOC; (2)AD∥BC. 图2-ZT-10 8.:如图2-ZT-11,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:AD=AE. 图2-ZT-11 ?基本模型四一线三等角模型 图2-ZT-12 9.如图2-ZT-13,B,C,E三点在同一条直线上,AC∥DE,AC =CE,∠ACD=∠B. (1)求证:BC=DE; (2)假设∠A=40°,求∠BCD的度数. 图2-ZT-13 ?基本模型五综合模型 平移+对称模型: 图2-ZT -14 10.如图2-ZT-15,点B,F,C,E在一条直线上,FB=CE,AB ∥ED,AC∥FD.求证:AC=DF. 图2-ZT-15 平移+旋转模型: 图2-ZT-16 11.:如图2-ZT-17,AB=BC,BD=EC,AB⊥BC,EC⊥BC.求证:AD⊥BE. 图2-ZT-17 详解详析 全等三角形与角平分线 全等图形:能够完全重合的两个图形就是全等图形. 全等多边形: 能够完全重合的多边形就是全等多边形. 相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角. 全等多边形的对应边、对应角分别相等. 如下图,两个全等的五边形,记作:五边形ABCDE ≌五边形'''''A B C D E . 这里符号“≌”表示全等,读作“全等于”. A' B'C' D' E' E D C B A 全等三角形:能够完全重合的三角形就是全等三角形. 全等三角形的对应边相等,对应角分别相等; 反之,如果两个三角形的边和角分别对应相等,那么这两个三角形全等. 全等三角形对应的中线、高线、角平分线及周长面积均相等. 全等三角形的概念与表示:能够完全重合的两个三角形叫作全等三角形.能够相互重合的顶点、边、角分别叫作对应顶点、对应边、对应角.全等符号为“≌”. 全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等. 寻找对应边和对应角,常用到以下方法: (1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边. (2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角. (3)有公共边的,公共边常是对应边. (4)有公共角的,公共角常是对应角. (5)有对顶角的,对顶角常是对应角. 全等三角形的判定方法: (1) 边角边定理(SAS ):两边和它们的夹角对应相等的两个三角形全等. (2) 角边角定理(ASA ):两角和它们的夹边对应相等的两个三角形全等. (3) 边边边定理(SSS ):三边对应相等的两个三角形全等. (4) 角角边定理(AAS ):两个角和其中一个角的对边对应相等的两个三角形全等. (5) 斜边、直角边定理(HL ):斜边和一条直角边对应相等的两个直角三角形全等. 判定三角形全等的基本思路: SAS HL SSS →?? →??→? 找夹角已知两边 找直角 找另一边 ASA AAS SAS AAS ?? ?? ?? ?? ?? ?? 边为角的对边→找任意一角→ 找这条边上的另一角→已知一边一角 边就是角的一条边 找这条边上的对角→ 找该角的另一边→ ASA AAS →??→? 找两角的夹边已知两角 找任意一边 全等三角形的图形归纳起来有以下几种典型形式: ⑴ 平移全等型 全等三角形证明经典题(含答案) 1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE < AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 2. 已知:D 是AB 中点,∠ACB=90°,求证:12 CD AB 延长CD 与P ,使D 为CP 中点。连接AP,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90 ∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB 3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠ CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。 ∵ ∠ABC=∠AED 。 ∴ ∠ABE=∠AEB 。 ∴ AB=AE 。在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。∴ A D B C ∠BAF=∠EAF (∠1=∠2)。 4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC ∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又EF∥AB ∴∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形,AC =CG 又 EF =CG ∴EF =AC 5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C 证明:延长AB 取点E ,使AE =AC ,连接DE ∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD ∴△AED ≌△ACD (SAS ) ∴∠E =∠C ∵AC =AB+BD ∴AE =AB+BD ∵AE =AB+BE ∴BD =BE ∴∠BDE =∠E ∵∠ABC =∠E+∠BDE ∴∠ABC =2∠E ∴∠ABC =2∠C 6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF ∵CE ⊥AB ∴∠CEB =∠CEF =90° ∵EB =EF ,CE =CE , ∴△CEB ≌△CEF ∴∠B =∠CFE ∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC ∴△ADC ≌△AFC (SAS ) ∴AD =AF ∴AE =AF +FE =AD +BE 7. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。求证: BC=AB+DC 。 在BC 上截取BF=AB ,连接EF ∵BE 平分∠ABC ∴∠ABE=∠FBE 又∵BE=BE ∴⊿ABE ≌⊿FBE (SAS ) ∴∠A=∠BFE ∵AB//CD ∴∠A+∠D=180o∵∠BFE+∠CFE=180o ∴∠D=∠CFE 又∵∠DCE=∠FCE CE 平分∠BCD CE=CE ∴⊿DCE ≌⊿FCE (AAS )∴CD=CF B A C D F 2 1 E A全等三角形的经典模型(一)
全等三角形证明经典40题(含答案)
全等三角形证明经典试题50道
全等三角形常见的几何模型
全等三角形之手拉手模型专题(完整资料).doc
全等三角形证明经典50题
专项练习(二) 全等三角形的基本模型
(完整版)全等三角形几种类型总结
全等三角形证明经典题(含答案解析)
