自相关函数与偏自相关函数

自相关函数与偏自相关函数
上一节介绍了随机过程的几种模型。实际中单凭对时间序列的观察很难确定其属于哪一种模型,而自相关函数和偏自相关函数是分析随机过程和识别模型的有力工具。
1、自相关函数定义
在给出自相关函数定义之前先介绍自协方差函数概念。由第一节知随机过程{t x }中的每一个元素t x ,t = 1, 2, … 都是随机变量。对于平稳的随机过程,其期望为常数,用μ表示,即
()t E x μ=,1,2,
t =
随机过程的取值将以 μ 为中心上下变动。平稳随机过程的方差也是一个常量
2
()t x V a r x σ=,
1,2,t =
2x σ用来度量随机过程取值对其均值μ的离散程度。
相隔k 期的两个随机变量t x 与t k x -的协方差即滞后k 期的自协方差,定义为:
(,)[()()]k
t t k
t
t k
C o v x x E x x γμμ--==--
自协方差序列:k γ,0
,1,2,k =
称为随机过程{t x }的自协方差函数。当k = 0 时,2
0()t x V a rx γσ==。
自相关系数定义:(,)()()t tk k
t tk C o v x x V a r x V a r x ρ
-
-
=
因为对于一个平稳过程有:2
()()t t k x
V a r x V a r x σ
-== 所以
220
(,)t tk k k
k
x
x
C o v x x γγρσσγ
-
===,当 k = 0 时,有0
1ρ=。
以滞后期k 为变量的自相关系数列k ρ(0,1,2,k =)称为自相关函数。因为k k ρρ-=,
即(,)t k t C o v x x -= (,)t t k C o v x x +,自相关函数是零对称的,所以实际研究中只给出自相关
函数的正半部分即可。
2、自回归过程的自相关函数 (1)平稳AR(1)过程的自相关函数
AR(1) 过程:11t t t x x u φ-=+,|φ1| < 1。
已知()0t E x =(why?)。用t k x -同乘上式两侧
t x t k x -11t t k t t k x x u x φ---=+
上式两侧同取期望:k γ11k φγ-=
其中()0t t k Eux -=(why?)(由于x t = u t + φ1 u t -1 + φ12 u t -2 +… ,所以x t-k = u t-k + φ1 u t-k-1 +
φ12 u t-k-2 +…,而u t 是白噪音与其t - k 期及以前各项都不相关)。
两侧同除 γ0 得:
2
1112
10
k
k
k k ρφρφρφρ--====
因为ρo = 1,所以有k ρ=1k
φ(0k ≥)
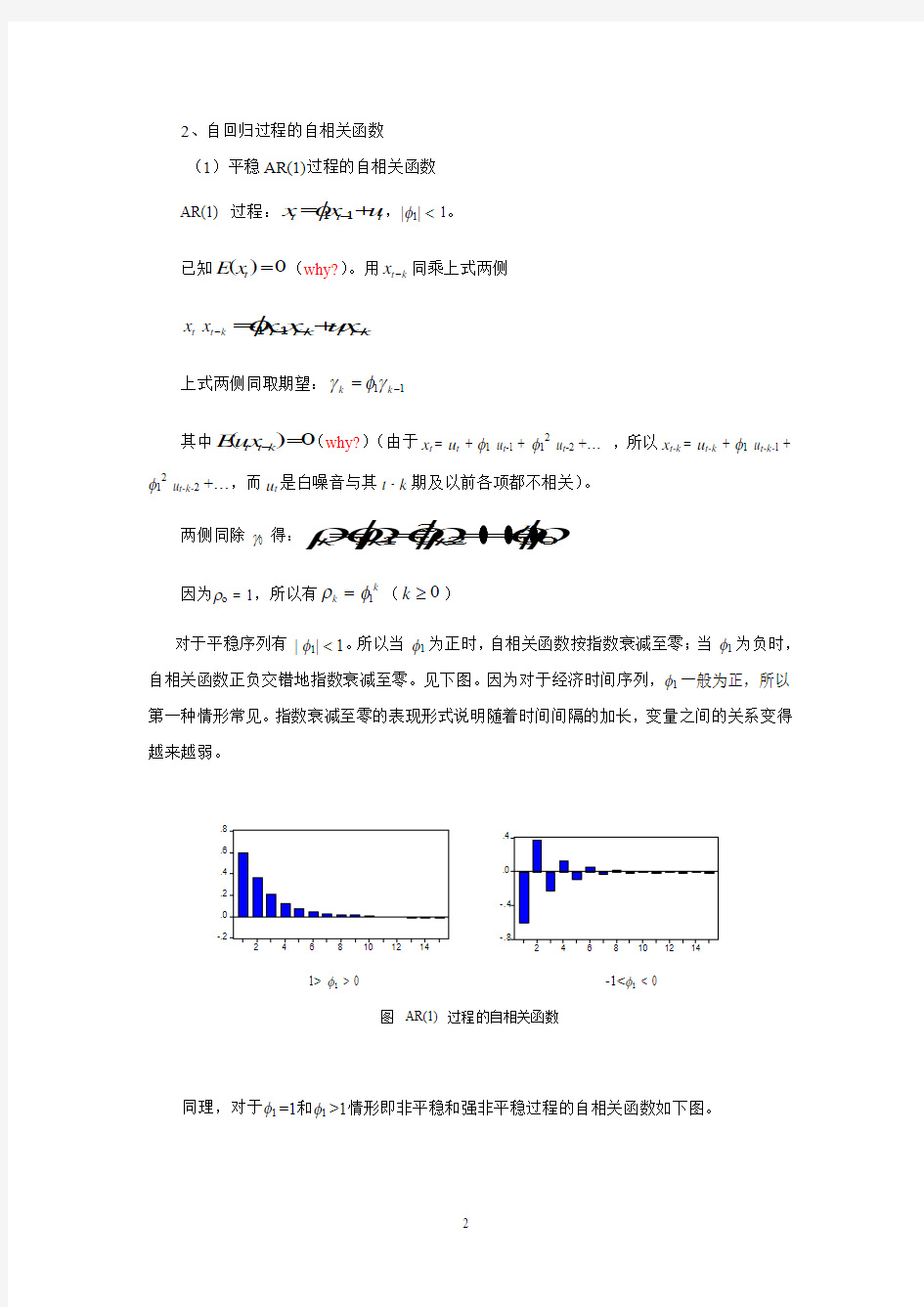
对于平稳序列有 | φ1| < 1。所以当 φ1为正时,自相关函数按指数衰减至零;当 φ1为负时,自相关函数正负交错地指数衰减至零。见下图。因为对于经济时间序列,φ1一般为正,所以第一种情形常见。指数衰减至零的表现形式说明随着时间间隔的加长,变量之间的关系变得越来越弱。
-.2
.0.2
.4.6.82
4
6
8
10
12
14
-.8
-.4.0.4
2468101214
1> φ1 > 0 -1<φ1 < 0
图 AR(1) 过程的自相关函数
同理,对于φ1 =1和φ1 >1情形即非平稳和强非平稳过程的自相关函数如下图。
-4
-3-2-1012342
4
6
8
10
12
14
-1.5
-1.0-0.50.00.51.01.5
2468101214
φ1 = 1.1(强非平稳过程) φ1 = 1(随机游走过程)
(2)AR(p ) 过程的自相关函数
用t k x -(k > 0) 同乘平稳的 p 阶自回归过程1122t t t p tp t
x x x x u φφ
φ
---=++++ 的两侧,得:1122t k t t k t t k t p t k t p t k t
x x x x x x x x x u φφφ
--------=++++ 对上式两侧分别求期望得:k γ1122k k p k p
φγφγ
φγ
---=+++,k > 0 用 γ0分别除上式的两侧得Yule-Walker 方程:
ρk = φ1 ρk -1 + φ2 ρk -2 + … + φp ρk -p , k > 0
令2
12
1
()1(1- )p
p p
i
i L L L L G L φφφ=Φ=----=∏
,其中L 为k 的滞后算子,这里1
i G -, i = 1, 2, …, p 是特征方程()0L Φ=的根。为保证随机过程的平稳性,要求1i G <。则:
121210p i i p i GG G φφ
φ-------=,也即1212k k k k p
i i i p i G G G G φφφ
---=+++。
可证:
11
22
k
k
k k
pp
A G A G A G ρ=+++(*)
其中A i , i = 1, … ,p 为待定常数。(提示:可把(*)式代入到Yule-Walker 方程中证明) 由(*)式知道会遇到如下几种情形。
① 当i G 为实数时,(*)式中的k
i i AG 将随着k 的增加而几何衰减至零,称为指数衰减。
② 当i G 和j G 表示一对共轭复数时,设i G a b i =+,j G a b i =-,2
2b a += R ,则i G ,
j G 的极座标形式是:
(
c o s s i n )i GR i θθ=+ (c o s s i n )j G R i θθ=
-
若AR(p ) 过程平稳,则1i G <,所以必有R <1。那么随着k 的增加,
(c o s s i n)k k i
GR k i k θθ=+ (
c o s s i n)k k j GR k i k θθ=- 自相关函数(*)式中的相应项k
i G , k
j G 将按正弦振荡形式衰减。
注意:实际中的平稳自回归过程的自相关函数常是由指数衰减和正弦衰减两部分混合而成。
③ 从(*)式可以看出,当特征方程的根取值远离单位圆时,k 不必很大,自相关函数就会衰减至零。
④ 有一个实数根接近1时,自相关函数将衰减的很慢,近似于线性衰减。当有两个以上的根取值接近1时,自相关函数同样会衰减的很慢。
-.4
.0
.4
2
4
6
8
10
12
14
-.4
-.2.0
.2
.4.6
2468101214
两个特征根为实根 两个特征根为共轭复根图
AR(2) 过程的自相关函数
3、移动平均过程的自相关函数 (1)MA(1) 过程的自相关函数。
对于MA(1)过程11t t t x u u θ-=+,有:
1111
()[()()]k
t t k
t
t t k t k E x x E u u u u γθθ-----==++
当k = 0时,
1111
()[()()]t t t t t t E x x E u u u u γθθ--==++2
2
11
1
(2)t
t t t E u u u u θ--=++
2
2
1(1)
θσ=+ 当k = 1时,
1
1
11112
()[()()]
t t t
t t t E x x E u u u u γθθ----==++
22
11112112
()t t t t t t t E u u u u u u u θθθ
-----=+++21θσ= 当 k > 1 时,
1111
()[()()]k
t t k
t
t t k t k E x x E u u u u γθθ-----==++
2
1111111
()t t k t t k t t k t t k E u u u u u u u u θθθ--------=+++0=
综合以上三种情形,MA(1)过程自相关函数为
ρk =
γγk
= 1
21, 1
10, 1
k k θθ?=?+??
>? -.4
-.2.0.2.42
4
6
8
10
12
14
-.4
-.2.0.2.42468101214
θ1 > 0 θ1 < 0
图 MA(1)过程的自相关函数
可见MA(1) 过程的自相关函数具有截尾特征。当k > 1时,ρk = 0。
(2) MA(q ) 过程的自相关函数 MA(q ) 过程的自相关函数是
ρk = 1122222
12...,1,2,,1...0,k k k q k q
q
k q k q θθθθθθθ
θθθ
++-++++?=?++++??>?
当k > q 时,ρk = 0,说明 ρk , k = 0, 1, … 具有截尾特征。
例如,对于MA(2) 过程,自相关函数是
ρ1=22212111θθθθθ+++, ρ2=22
212
1θθθ++, ρk = 0, k > 2。
4、 ARMA (1, 1) 过程的自相关函数
ARMA (1, 1) 过程的自相关函数ρk 从 ρ1开始指数衰减。ρ1的大小取决于 φ1和 θ1, ρ1
的符号取决于 (φ1 -θ1 )。若 φ1 > 0,指数衰减是平滑的,或正或负。若 φ1 < 0,相关函数为正负交替式指数衰减。
对于ARMA (p , q ) 过程,p , q ≥ 2时,自相关函数的表现形式比较复杂,可能是指数衰减、正弦衰减或二者的混合衰减。
5、相关图(correlogram ,或估计的自相关函数,样本自相关函数) 对于一个有限时间序列(x 1, x 2, …, x T )用样本平均数 x =
T
1∑=T
t t
x
1
估计总体均值 μ,用样本方差
s 2
= 21
)(1
∑
=-T
t t x x T 估计总体方差σx 2。
当用样本矩估计随机过程的自相关函数,则称其为相关图或估计的自相关函数,记为
r k =
0C C k
, k = 0, 1 , 2, …, K , ( K < T ) .
r k 是对ρk 的估计。其中
C k =
1
T k
-1
()(),Tk t
t k
t x x x x -+=--∑
k = 0, 1, 2, …, K , 是对γk 的估计。
C 0 =21
)(1
∑
=-T
t t x x T 是对γ0的估计。T 是时间序列数据的样本容量。实际中T 不应太小,最好能大于60。
注意:C k 为有偏估计量。但在小样本条件下更有效。
相关图是对自相关函数的估计。由于MA 过程和ARMA 过程中的MA 分量的自相关函数具有截尾特性,所以通过相关图可以估计MA 过程的阶数q 。相关图是识别MA 过程阶数和ARMA 过程中MA 分量阶数的一个重要方法。对于年度时间序列数据,相关图一般取k = 15就足够了。
k r 的方差近似为1T -。所以在观察相关图时,若k r 的绝对值超过212T -(2个标准差),就被认为是显著地不为零。当T 充分大时,近似有:12
(0)k r T --
=k r 12T ~ N (0, 1)
第五节 偏自相关函数
偏自相关函数是描述随机过程结构特征的另一种方法。用 φkj 表示k 阶自回归过程中第j 个回归系数,则k 阶自回归模型表示为:
1122t k t kt k k t k t
x x x x u φφφ
---=++++ 其中kk φ是最后一个回归系数。若把kk φ看作是滞后期k 的函数,则称
kk φ,1
,2,k =
为偏自相关函数。它由下式中的红项组成。
1111t t t x x u φ-=+
2112222t t t t x x x u φφ--=++
1122t k t kt k k t k k t
x x x x u φφφ
---=++++ 因偏自相关函数中每一个回归系数kk φ恰好表示t x 与t k x -在排除了其中间变量1t x -,
2t x -,,1t k x -+ 影响之后的相关系数,
112211t k t k t k k t k k k t k k t
xx x x x u φφφφ
----+-----=+ 所以偏自相关函数由此得名。 用kj φ表达Yule-Walker 方程
1122
k
k k p k p
ρφρφρφρ---=+++,得
1122
j
k j k j k kj k
ρφρφρφρ---=+++
用矩阵形式表示上式,
????
??
??????k
ρρρ (2)
1= ???????
????
?-----1.....................1 (13)
2121
11
2
1
k k k k k ρρρρρρρρρ????
?
?
?
?????kk k k φφφ...21 或
ρ = P φ. 则
φ = P -1ρ,
将k = 1, 2 , … 代入上式连续求解,可求得偏自相关函数 φ 11 = ρ1,
??????2221φφ=1
1
111-??
????ρρ??
????21ρρ=
1
1
111
1
2111ρρρρρ
ρ??
?
????????
?--=2
1
2122111ρρρρρρ-???
?
??--
其中
φ 22 = 2
1
2
1
21ρρρ-- …
对于AR(1)过程,t x = φ11 x t -1 +t u ,当k = 1时,φ11 ≠ 0;当k > 1时,0kk φ=。所以AR(1)过程的偏自相关函数特征是在k = 1出现峰值(φ11 = ρ1)然后截尾。
-0.8
-0.6-0.4-0.20.00.20.40.60.82
4
6
8
10
12
14
-0.8
-0.6-0.4-0.20.00.20.40.60.82
4
6
8
10
12
14
φ11 > 0 φ11 < 0
AR(1) 过程的偏相关图
对于AR(2)过程,当k ≤ 2时,0kk φ≠;当k >2时,0kk φ=。偏自相关函数在滞后期2以后有截尾特性。
对于AR(p )过程,当k ≤ p 时,0kk φ≠;当k > p 时,0kk φ=。偏自相关函数在滞后期p 以后有截尾特性,因此可用此特征识别AR(p )过程的阶数。
对于MA(1)过程t x =t u + θ1 u t -1,有 [1/ (1+ θ1 L )]t x =t u , (1- θ1 L + θ12 L 2 - … )t x =t u ,
t x = θ1 x t -1 - θ12 x t -2 +θ13 x t -3 - … +t u
当θ1 > 0时,自回归系数的符号是正负交替的;当θ1 < 0时,自回归系数的符号全是负的。
因为MA(1) 过程可以转换为无限阶的AR 过程,所以MA(1) 过程的偏自相关函数呈指数衰减特征。
-0.8
-0.6-0.4-0.20.00.20.40.60.82
4
6
8
10
12
14
-0.8
-0.6-0.4-0.20.00.20.40.60.82
4
6
8
10
12
14
θ1 > 0 θ1 < 0
MA(1) 过程的偏自相关函数
对于MA(2) 过程,若Θ (L ) = 0的根是实数,偏自相关函数由两个指数衰减形式叠加而成。若Θ (L ) = 0的根是复数,偏自相关函数呈正弦衰减形式。
因为任何一个可逆的MA(q ) 过程都可以转换成一个无限阶的系数按几何递减的AR 过程,所以MA(q ) 过程的偏自相关函数呈缓慢衰减特征。
ARMA( p , q ) 过程的偏自相关函数也是无限延长的,其表现形式与MA(q )过程的偏自相关函数相类似。根据模型中移动平均部分的阶数q 以及参数θi 的不同,偏自相关函数呈指数衰减和(或)正弦衰减混合形式。
对于时间序列数据,偏自相关函数通常是未知的。可以用样本计算 φ11, φ22, … 的估计
量 11?φ, 22?φ, …。估计的偏自相关函数
kk φ?, k = 1, 2, …, K ,
称为偏相关图。因为AR 过程和ARMA 过程中AR 分量的偏自相关函数具有截尾特性,所以可利用偏相关图估计自回归过程的阶数p 。实际中对于偏相关图取k = 15就足可以了。
kk φ?的方差近似为T -1。当T 充分大时,近似有 (kk φ?- 0) / T -1/2 = T 1/2kk φ? ~ N (0, 1)
所以在观察偏相关图时,若kk φ?的绝对值超过2 T
-1/2(2个标准差),就被认为是显著地不为零。
注:2个标准差 = 2 T -1/2 = 2(1/7)= 0.286。图中虚线表示到中心线2个标准差宽度。
补充知识:检验过程是否为白噪声的Q 统计量
在介绍Q 统计量之前,先介绍序列y t 的估计的自相关函数(相关图)的定义,
r k =
∑
∑
=+=-----T t t t T k t t k t t t y y T y y y y k T 1
2
1
)(1)
)((1, k = 1, 2, ….
其中r k 表示y t 与y t-k 估计的自相关系数,是对自相关系数ρk 的估计。
定义k t y -= (∑k t y -)/ (T -k ),t y = (∑y t )/ T 。
模型残差序列是否为白噪声的检验是用Box-Pierce (1970) 提出的Q 统计量完成的。Q 检验的零假设是
H :ρ1 = ρ2 = … = ρK = 0
即序列是一个白噪声过程。其中ρi 表示自相关系数。Q 统计量定义为
Q = T
∑=K
k k
r
1
2
(k r 是用残差序列计算的自相关系数的估计值)
随着T →∞,Q 渐近服从2
(
)K p q χ--分布,其中T 表示样本容量,K 表示自相关系数的
个数,p 表示模型自回归部分的最大滞后值,q 表示移动平均部分的最大滞后值。
Ljung 和Box 认为定义的Q 统计量的分布与2
(
)K p q χ--分布存在差异(相应值偏小),于是提出修正的Q 统计量。
Q = T (T +2)∑
=-K
k k
k T r 1
2
其中r k ,K ,p ,q 的定义如上式。修正的Q 统计量渐近服从2
(
)K p q χ--分布。且它的近似性比原Q 统计量的近似性更好。(注意:EViews 中给出的Q 统计量就是按修正的Q 统计量定义的。)
用残差序列计算Q 统计量的值。显然若残差序列不是白噪声,残差序列中必含有其他成份,自相关系数不等于零。则Q 值将很大,反之Q 值将很小。判别规则是:
若Q 2
(
)K p q αχ≤--,则接受H 0。 若Q >2
(
)K p q αχ--,则拒绝H 0。 其中α 表示检验水平;p ,q 分别表示时间序列模型中自回归和移动平均滞后项的个数。 实际检验中,K 取15左右即可。
自相关函数与互相关函数 不错的材料
2.4.3 相关函数 1.自相关函数 自相关函数是信号在时域中特性的平均度量,它用来描述信号在一个时刻的取值与另一时刻取值的依赖关系,其定义式为 (2.4.6) 对于周期信号,积分平均时间T为信号周期。对于有限时间内的信号,例如单个脉冲,当T趋于无穷大时,该平均值将趋于零,这时自相关函数可用下式计算 (2.4.7) 自相关函数就是信号x(t)和它的时移信号x(t+τ)乘积的平均值,它是时移变量τ的函数。 例如信号的自相关函数为 若信号是由两个频率与初相角不同的频率分量组成,即 ,则
对于正弦信号,由于,其自相关函数仍为 由此可见,正弦(余弦)信号的自相关函数同样是一个余弦函数。它保留了原信号的频率成分,其频率不变,幅值等于原幅值平方的一半,即等于该频率分量的平均功率,但丢失了相角的信息。 自相关函数具有如下主要性质: (1)自相关函数为偶函数,,其图形对称于纵轴。因此,不论时移方向是导前还是滞后(τ为正或负),函数值不变。 (2)当τ=0时,自相关函数具有最大值,且等于信号的均方值,即 (2.4.8)(3)周期信号的自相关函数仍为同频率的周期信号。 (4)若随机信号不含周期成分,当τ趋于无穷大时,趋于信号平均值的平方,即 (2.4.9) 实际工程应用中,常采用自相关系数来度量其不同时刻信号值之间的相关程
度,定义式为 (2.4.10) 当τ=0时,=1,说明相关程度最大;当τ=∞时,,说明信号x(t)与 x(t+τ)之间彼此无关。由于,所以。值的大小表示信号相关性的强弱。 自相关函数的性质可用图2.4.3表示。 图2.4.3 自相关函数的性质 常见四种典型信号的自相关函数如图2.4.4所示,自相关函数的典型应用包括:(1)检测信号回声(反射)。若在宽带信号中存在着带时间延迟的回声,那么该信号的自相关函数将在处也达到峰值(另一峰值在处),这样可根据确定反射体的位置,同时自相关系数在处的值将给出反射信号相对强度的度量。 时间历程自相关函数图形
自相关函数和互相关函数的利用MATLAB计算和作图
互相关函数,自相关函数计算和作图 1.自相关和互相关的概念。 ●互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1,t2间的相关程度。 ●自相关函数是描述随机信号x(t)在任意两个不同时刻t1,t2间的相关程度。 互相关函数是在频域内两个信号是否相关的一个判断指标,把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号,对修正测量中接入噪声源而产生的误差非常有效。 -----------------------------------------------------------------------------------事实上,在图象处理中,自相关和互相关函数的定义如下:设原函数是f(t),则自相关函数定义为R(u)=f(t)*f(-t),其中*表示卷积;设两个函数分别是f(t)和g(t),则互相关函数定义为R(u)=f(t)*g(-t),它反映的是两个函数在不同的相对位置上互相匹配的程度。 2.利用matlab中实现这两个相关并用图像显示: 自相关函数: dt=.1; t=[0:dt:100];x=cos(t); [a,b]=xcorr(x,'unbiased'); plot(b*dt,a)
互相关函数:把[a,b]=xcorr(x,'unbiased');改为[a,b]=xcorr(x,y,'unbiased');便可。 3.实现过程: 在Matalb中,求解xcorr的过程事实上是利用Fourier变换中的卷积定理进行的,即 R(u)=ifft(fft(f)×fft(g)),其中×表示乘法,注:此公式仅表示形式计算,并非实际计算所用的公式。当然也可以直接采用卷积进行计算,但是结果会与xcorr的不同。事实上,两者既然有定理保证,那么结果一定是相同的,只是没有用对公式而已。下面是检验两者结果相同的代码: dt=.1; t=[0:dt:100]; x=3*sin(t); y=cos(3*t); subplot(3,1,1); plot(t,x); subplot(3,1,2); plot(t,y); [a,b]=xcorr(x,y); subplot(3,1,3); plot(b*dt,a); yy=cos(3*fliplr(t));%or use:yy=fliplr(y); z=conv(x,yy); pause; subplot(3,1,3); plot(b*dt,z,'r'); 即在xcorr中不使用scaling。
正弦函数、余弦函数的图象和性质教案
正弦函数、余弦函数的图象和性质 一、学情分析: 1、学习过指数函数和对数函数; 2、学习过周期函数的定义; 3、学习过正弦函数、余弦函数[]π2,0上的图象。 二、教学目标: 知识目标: 1、正弦函数的性质; 2、余弦函数的性质; 能力目标: 1、能够利用函数图象研究正弦函数、余弦函数的性质; 2、会求简单函数的单调区间; 德育目标: 渗透数形结合思想和类比学习的方法。 三、教学重点 正弦函数、余弦函数的性质 四、教学难点 正弦函数、余弦函数的性质的理解与简单应用 五、教学方法 通过引导学生观察正弦函数、余弦函数的图象,从而发现正弦函数、余弦函数的性质,加深对性质的理解。(启发诱导式)
六、教具准备 多媒体课件 七、教学过程 1、复习导入 (1) 我们是从哪个角度入手来研究指数函数和对数函数的? (2) 正弦、余弦函数的图象在[]π2,0上是什么样的? 2、讲授新课 (1)正弦函数的图象和性质(由教师讲解) 通过多媒体课件展示出正弦函数在[]ππ2,2-内的图象,利用函数 图象探究函数的性质: ⅰ 定义域 正弦函数的定义域是实数集R ⅱ 值域 从图象上可以看到正弦曲线在[]1,1-这个范围内,所以正弦函数的值域是[]1,1- ⅲ 单调性 结合正弦函数的周期性和函数图象,研究函数单调性,即: ⅳ 最值 观察正弦函数图象,可以容易发现正弦函数的图象与虚线的交点,都是函数的最值点,可以得出结论: 上是增函数;在)(22,22Z k k k ∈??????+-ππππ上是减函数;在)(232,22Z k k k ∈????? ?++ππππ1,22max =∈+=y Z k k x 时,当ππ1,2 2min -=∈-=y Z k k x 时,当ππ
自相关和互相关
1. 首先说说自相关和互相关的概念。 这个是信号分析里的概念,他们分别表示的是两个时间序列之间和同一个时间序列在任意两个不同时刻的取值之间的相关程度,即互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1,t2的取值之间的相关程度,自相关函数是描述随机信号x(t)在任意两个不同时刻t1,t2的取值之间的相关程度。 自相关函数是描述随机信号X(t)在任意两个不同时刻t1,t2的取值之间的相关程度;互相关函数给出了在频域内两个信号是否相关的一个 判断指标,把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号,对修正测量中接入噪声源而产生的误差非常有效. 事实上,在图象处理中,自相关和互相关函数的定义如下:设原函数是f(t),则自相关函数定义为R(u)=f(t)*f(-t),其中*表示卷积;设两个函数分别是f(t)和g(t),则互相关函数定义为R(u)=f(t)*g(-t),它反映的是两个函数在不同的相对位置上互相匹配的程度。 那么,如何在matlab中实现这两个相关并用图像显示出来呢? dt=.1; t=[0:dt:100]; x=cos(t); [a,b]=xcorr(x,'unbiased'); plot(b*dt,a) 上面代码是求自相关函数并作图,对于互相关函数,稍微修改一下就可以了,即把[a,b]=xcorr(x,'unbiased');改为[a,b]=xcorr(x,y,'unbiased');便可。 2. 实现过程: 在Matalb中,求解xcorr的过程事实上是利用Fourier变换中的卷积定理进行的,即R(u)=ifft(fft(f)×fft(g)),其中×表示乘法,注:此公式仅表示形式计算,并非实际计算所用的公式。当然也可以直接采用卷积进行计算,但是结果会与xcorr的不同。事实上,两者既然有定理保证,那么结果一定是相同的,只是没有用对公式而已。下面是检验两者结果相同的代码: dt=.1; t=[0:dt:100]; x=3*sin(t); y=cos(3*t); subplot(3,1,1); plot(t,x); subplot(3,1,2); plot(t,y); [a,b]=xcorr(x,y); subplot(3,1,3); plot(b*dt,a); yy=cos(3*fliplr(t)); % or use: yy=fliplr(y); z=conv(x,yy); pause;
正弦函数的图像和性质
1 定义编辑数学术语 正弦函数是三角函数的一种. 定义与定理 定义:对于任意一个实数x 都对应着唯一的角(弧度制中等于这个实数) ,而这个角又对应 着唯一确定的正弦值Sin X ,这样,对于任意一个实数X都有唯一确定的值Sin X与它对应, 按照这个对应法则所建立的函数,表示为f(x)=sin X ,叫做正弦函数。 正弦函数的定理:在一个三角形中,各边和它所对角的正弦的比相等,即a/Sin A=b/Sin B=c/Sin C 在直角三角形ABC中,/ C=90 ,y为一条直角边,r为斜边,X为另一条直角边(在坐标 系中,以此为底),贝U Sin A=y∕r,r= √( x^2+y^2) 2 性质 编辑图像 图像是波形图像(由单位圆投影到坐标系得出) ,叫做正弦曲线(Sine curve) 正弦函数X∈& 定义域 实数集R 值域 [-1,1] (正弦函数有界性的体现) 最值和零点 ①最大值:当X=2k ∏+ ( ∏/2) , k ∈Z 时,y(max)=1 ②最小值:当X=2k ∏+ (3∏/2), k∈Z 时,y(min)=-1 零值点:( kπ ,0) ,k∈Z 对称性 既是轴对称图形,又是中心对称图形。 1) 对称轴:关于直线X= ( π /2) +kπ , k∈Z 对称 2) 中心对称:关于点(k ∏ , 0), k∈Z对称 周期性最小正周期:y=SinX T=2 π 奇偶性 奇函数(其图象关于原点对称) 单调性 在[-∏∕2+2k ∏ , ∏∕2+2k ∏], k∈Z 上是单调递增. 在[∏∕2+2k ∏ , 3∏∕2+2k ∏], k ∈Z 上是单调递减. 3 正弦型函数及其性质 编辑 正弦型函数解析式:y=Asin (ω x+ φ )+h
正弦函数的图像和性质(一)
正弦函数的图像和性质(一) 【使用说明】1.课前认真完成预习学案的问题导学及例题、深化提高; 2.认真限时完成,规范书写,课上小组合作探讨,答疑解惑。 【重点难点】重点:正弦函数的图像 难点:图像的画法 一、学习目标 1.了解正弦曲线的画法,能用五点法画出正弦函数的图像; 2.能通过函数图像对函数的性质做简单分析; 3.通过从单位圆和图像两个不同的角度去观察和研究正弦函数的变化规律,培养学生从不同角度观察、研究问题的思维习惯。 二、问题导学 1、函数的图像的画法: 描点法 步骤:列表→描点→连线 补全上述表格,并根据表格中数据在直角坐标系中画出的图像。 几何法 阅读教材25—26页内容,试借助于单位圆,利用正弦函数的定义画出的图像。 五点法
观察的图像,发现有五个点起着关键的作用,它们是图像与轴的交点和图像的最高点及最低点: ______,________,_________,________,__________. 因此,在精度要求不高的情况下,我们通常在直角坐标系中描出这起关键作用的五个点,然后用光滑的曲线连接,做出图像的简图。 请同学们用五点法画出的图像。 2、 因为正弦函数是以为周期的周期函数,所以函数在区间上的图像与在区间上的图像形状完全一样,只是位置不同,因此我们只需将函数的图像向左、向右平行移动(每次移动个单位)就可以得到的图像,正弦函数的图像叫做___________ 请同学们在几何法做出的图像的基础上,画出正弦曲线。 3、 合作探究 例1、用五点法画出下列函数在区间上的简图。 (1) (2) 例2、在上,利用的图像求满足下列不等式的的取值范围。 (1) (2)
自相关与互相关函数
相关函数 1.自相关函数 自相关函数是信号在时域中特性的平均度量,它用来描述信号在一个时刻的取值与 另一时刻取值的依赖关系,其定义式为 (2.4.6) 对于周期信号,积分平均时间T为信号周期。对于有限时间的信号,例如单个脉 冲,当T趋于无穷大时,该平均值将趋于零,这时自相关函数可用下式计算 (2.4.7) 自相关函数就是信号x(t)和它的时移信号x(t+τ)乘积的平均值,它是时移变量τ的函数。 例如信号的自相关函数为 若信号是由两个频率与初相角不同的频率分量组成,即 ,则
对于正弦信号,由于,其自相关函数仍为 由此可见,正弦(余弦)信号的自相关函数同样是一个余弦函数。它保留了原信号的频率成分,其频率不变,幅值等于原幅值平方的一半,即等于该频率分量的平均功率 ,但丢失了相角的信息。 自相关函数具有如下主要性质: (1)自相关函数为偶函数,,其图形对称于纵轴。因此,不论时移方向是导前还是滞后(τ为正或负),函数值不变。 (2)当τ=0时,自相关函数具有最大值,且等于信号的均方值,即 (2.4.8)(3)周期信号的自相关函数仍为同频率的周期信号。 (4)若随机信号不含周期成分,当τ趋于无穷大时,趋于信号平均值的平方,即 (2.4.9)实际工程应用中,常采用自相关系数来度量其不同时刻信号值之间的相关程度,定义式为 (2.4.10)
当τ=0时,=1,说明相关程度最大;当τ=∞时,,说明信号x(t)与x(t+τ)之间彼此无关。由于,所以。值的大小表示信号相关性的强弱。 自相关函数的性质可用图2.4.3表示。 图2.4.3 自相关函数的性质 常见四种典型信号的自相关函数如图2.4.4所示,自相关函数的典型应用包括: (1)检测信号回声(反射)。若在宽带信号中存在着带时间延迟的回声,那么该 信号的自相关函数将在处也达到峰值(另一峰值在处),这样可根据确定 反射体的位置,同时自相关系数在处的值将给出反射信号相对强度的度量。 时间历程自相关函数图形 正 弦 波
Matlab自相关函数和互相关函数的计算和作图
自相关函数(Autocorrelation function,缩写ACF)是信号处理、时间序列分析中常用的数学工具,反映了同一序列在不同时刻的取值之间的相关程度。 自相关函数在不同的领域,定义不完全等效。在某些领域,自相关函数等同于自协方差(autocovariance)。 信号处理 在信息分析中,通常将自相关函数称之为自协方差方程。用来描述信息在不同时间τ的,信息函数值的相关性。 ,其中“*”是卷积算符,为取共轭 自相关函数的性质 以下以一维自相关函数为例说明其性质,多维的情况可方便地从一维情况推广得到。 ?对称性:从定义显然可以看出R(i) = R(?i)。连续型自相关函数为偶函数当f为实函数时,有: 当f是复函数时,该自相关函数是厄米函数,满足: 其中星号表示共轭。 ?连续型实自相关函数的峰值在原点取得,即对于任何延时τ,均有 。该结论可直接有柯西-施瓦茨不等式得到。离散型自相关函数亦有此结论。 ?周期函数的自相关函数是具有与原函数相同周期的函数。 ?两个相互无关的函数(即对于所有τ,两函数的互相关均为0)之和的自相关函数等于各自自相关函数之和。 ?由于自相关函数是一种特殊的互相关函数,所以它具有后者的所有性质。
?连续时间白噪声信号的自相关函数是一个δ函数,在除τ = 0 之外的所有点均为0。 ?维纳-辛钦定理(Wiener–Khinchin theorem)表明,自相关函数和功率谱密度函数是一对傅里叶变换对: ?实值、对称的自相关函数具有实对称的变换函数,因此此时维纳-辛钦定理中的复指数项可以写成如下的余弦形式: 白噪声的自相关函数为δ函数: 自相关函数和偏相关函数的问题 在时间序列分析的研究中,首先是判别时间序列的稳定性,如果时间序列是平稳的就可以计算这些数据的自相关函数和偏相关函数。 如果自相关函数是拖尾的,偏相关函数是截尾的,那麽数据符合AR(P)模型。 如果自相关函数是截尾的,偏相关函数是拖尾的,那麽数据复合MA( Q )模型 如果自相关函数和偏相关函数都是拖尾的,那麽数据复合ARMA( P,Q )模型。 自相关函数和互相关函数的matlab计算和作图 1. 首先说说自相关和互相关的概念。 这个是信号分析里的概念,他们分别表示的是两个时间序列之间和同一个时间序列在任意两个不同时刻的取值之间的相关程度,即互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1,t2的取值之间的相关程度,自相关函数是描述随机信号x(t)在任意两个不同时刻t1,t2的取值之间的相关程度。互相关函数给出了在频域内两个信号是否相关的一个判断指标,把两测点之间信号的互谱与
正弦函数的图像和性质(一)
x y 等分圆 平移三角函数线作正弦函数的图像 三角函数线 圆 O O 正弦函数的图像和性质(一) 【使用说明】1.课前认真完成预习学案的问题导学及例题、深化提高; 2.认真限时完成,规范书写,课上小组合作探讨,答疑解惑。 【重点难点】重点:正弦函数的图像 难点:x y sin =图像的画法 一、学习目标 1.了解正弦曲线的画法,能用五点法画出正弦函数x y sin =的图像; 2.能通过函数图像对函数的性质做简单分析; 3.通过从单位圆和图像两个不同的角度去观察和研究正弦函数的变化规律,培养学生从不同 角度观察、研究问题的思维习惯。 二、问题导学 1、函数] 2,0[ sinπ ∈ =x x y,的图像的画法: 补全上述表格,并根据表格中数据在直角坐标系中画出] 2,0[ sinπ ∈ =x x y,的图像。 ②几何法阅读教材25—26页内容,试借助于单位圆,利用正弦函数的定义画出 ] 2,0[ sinπ ∈ =x x y,的图像。 ③五点法 观察] 2,0[ sinπ ∈ =x x y,的图像,发现有五个点起着关键的作用,它们是图像与x轴的 交点和图像的最高点及最低点:______,________,_________,________,__________. 因此,在精度要求不高的情况下,我们通常在直角坐标系中描出这起关键作用的五个点,然 后用光滑的曲线连接,做出图像的简图。 请同学们用五点法画出] 2,0[ sinπ ∈ =x x y,的图像。 2、因为正弦函数是以π2为周期的周期函数,所以函数x y sin =在区间 )0 ] )1 2, 2[≠ ∈ +k Z k k k且 ( (π π上的图像与在区间] 2,0[π上的图像形状完全一样,只是位置 不同,因此我们只需将函数] 2,0[ sinπ ∈ =x x y,的图像向左、向右平行移动(每次移动π2 个单位)就可以得到R sin∈ =x x y,的图像,正弦函数的图像叫做___________ 请同学们在几何法做出的图像的基础上,画出正弦曲线。 三、合作探究 例1、用五点法画出下列函数在区间] 2,0[π上的简图。 (1)x y sin 3 =(2)x y sin -1 =
自相关函数
自相关函数在不同的领域,定义不完全等效。在某些领域,自相关函数等 同于自协方差(autocovariance)。 统计学 R(k) = \frac{E[(X_i - \mu)(X_{i+k} - \mu)]}{\sigma^2} 信号处理 R_f(\tau) = f(\tau) * f^*(-\tau)= \int_{-\infty}^{\infty} f(t+\tau)f^*(t)\, dt = \int_{-\infty}^{\infty} f(t)f^*(t-\tau)\, dt,其中“*”是卷积算符,(\cdot)^*为取共轭。 同一时间函数在瞬时t和t+a的两个值相乘积的平均值作为延迟时间t 的函数,它是信号与延迟后信号之间相似性的度量。延迟时间为零时,则 成为信号的均方值,此时它的值最大。 编辑本段 自相关函数的性质 以下以一维自相关函数为例说明其性质,多维的情况可方便地从一维 情况推广得到。 对称性:从定义显然可以看出R(i) = R(?i)。连续型自相关函数为偶 函数 当f为实函数时,有: R_f(-\tau) = R_f(\tau)\, 当f是复函数时,该自相关函数是厄米函数,满足: R_f(-\tau) = R_f^*(\tau)\, 其中星号表示共轭。 连续型实自相关函数的峰值在原点取得,即对于任何延时τ,均有 |R_f(\tau)| \leq R_f(0)。该结论可直接有柯西-施瓦兹不等式得到。离 散型自相关函数亦有此结论。 周期函数的自相关函数是具有与原函数相同周期的函数。 两个相互无关的函数(即对于所有τ,两函数的互相关均为0)之和 的自相关函数等于各自自相关函数之和。 由于自相关函数是一种特殊的互相关函数,所以它具有后者的所有性质。 连续时间白噪声信号的自相关函数是一个δ函数,在除τ = 0 之外 的所有点均为0。 维纳-辛钦定理(Wiener–Khinchin theorem)表明,自相关函数和功 率谱密度函数是一对傅里叶变换对: R(\tau) = \int_{-\infty}^\infty S(f) e^{j 2 \pi f \tau} \, df
自相关函数和互相关函数计算和作图的整理之欧阳家百创编
自相关函数和互相关函数计算和作图的整理 欧阳家百(2021.03.07) 1. 首先说说自相关和互相关的概念。 --[转版友gghhjj]------------------------------------------------------------------------------------- 这个是信号分析里的概念,他们分别表示的是两个时间序列之间和同一个时间序列在任意两个不同时刻的取值之间的相关程度,即互相关函数是描述随机信号 x(t),y(t)在任意两个不同时刻t1,t2的取值之间的相关程度,自相关函数是描述随机信号x(t)在任意两个不同时刻t1,t2的取值之间的相关程度。 ---------------------------------------------------------------------------------------------------------------------------------------------- --[转版友hustyoung]----------------------------------------------------------------------------------- 自相关函数是描述随机信号X(t)在任意两个不同时刻t1,t2的取值之间的相关程度;互相关函数给出了在频域内两个信号是否相关的一个判断指标,把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号,对修正测量中接入噪声源而产生的误差非常有效。 ---------------------------------------------------------------------------------------------------------------------------------------------- 事实上,在图象处理中,自相关和互相关函数的定义如下:设原函数是f(t),则自相关函数定义为R(u)=f(t)*f(-t),其中*表示卷积;设两个函数分别是f(t)和g(t),则互相关函数定义为R(u)=f(t)*g(-t),它反映的是两个函数在不同的相对位置上互相匹配的程度。 那么,如何在matlab中实现这两个相关并用图像显示出来呢?这个问题happy教授给出了完整答案: -----------[转happy教授]--------------------- dt=.1; t=[0:dt:100]; x=cos(t); [a,b]=xcorr(x,'unbiased'); plot(b*dt,a) ----------------------------------------------------- 上面代码是求自相关函数并作图,对于互相关函数,稍微修改一下就可以了,即把[a,b]=xcorr(x,'unbiased');改为[a,b]=xcorr(x,y,'unbiased');便可。 2. 实现过程: 在Matalb中,求解xcorr的过程事实上是利用Fourier变换中的卷积定理进行的,即R(u)=ifft(fft(f)×fft(g)),其中 ×表示乘法,注:此公式仅表示形式计算,并非实际计算所用的公式。当然也可以直接采用卷积进行计算,但是结果会与xcorr的不同。事实上,两者既然有定理保证,那么结果一定是相同的,只是没有用对公式而已。下面是检验两者结果相同的代码: dt=.1; t=[0:dt:100]; x=3*sin(t); y=cos(3*t); subplot(3,1,1); plot(t,x); subplot(3,1,2); plot(t,y); [a,b]=xcorr(x,y); subplot(3,1,3); plot(b*dt,a); yy=cos(3*fliplr(t)); % or use: yy=fliplr(y); z=conv(x,yy); pause; subplot(3,1,3); plot(b*dt,z,'r'); 即在xcorr中不使用scaling。 3. 其他相关问题: 1) 相关程度与相关函数的取值有什么联系? -------------[转版友gghhjj]------------------------------------------------------------------------------------- 相关系数只是一个比率,不是等单位量度,无什么单位名称,也不是相关的百分数,一般取小数点后两位来表示。 相关系数的正负号只表示相关的方向,绝对值表示相关的程度。因为不是等单位的度量,因而不能说相关系数0.7是0.35两倍,只能说相关系数为0.7的二列变量相关程度比相关系数为0.35的二列变量相关程度更为密切和更高。也不能说相关系数从0.70到0.80与相关系数从0.30到0.40增加的程度一样大。 对于相关系数的大小所表示的意义目前在统计学界尚不一致,但通常按下是这样认为的: 相关系数相关程度 0.00-±0.30 微相关 ±0.30-±0.50 实相关 ±0.50-±0.80 显著相关 ±0.80-±1.00 高度相关 ---------------------------------------------------------------------------------------------------------------------------------------------- 2) 功率,能量,自相关函数的关系: ---[转happy教授]------------------------------------------------------------------------------------------- 参见https://www.360docs.net/doc/a817093656.html,/jingpinke/xhst/final/XiTongJiaoCai/chap6/chap6_3/chap6_3_3.htm 需要指出的是,相关和相关函数的概念原本是为描述随机过程的统计特征而引入的,称之为统计相关函数。按照随机过程的理论,要获得一个实际随机过程的统计相关函数是相当困难的,但对于满足各态历经性(遍历性)或广义平稳的随机过程,它们的统计相关函数等于其一个样本函数的时间相关函数。从确定性信号引出相关的概念,是为后续课程的学习打下一个基础。 两信号互相关函数的傅里叶变换等于其中第一个信号变换与第二个信号变换取共轭二者之乘积,这就是相关定理。对于自相关函数,它的傅里叶变换等于原信号幅度谱的平方。 周期余弦信号和它的自相关函数具有相同的角频率,即周期信号的自相关函数仍然是同周期的周期信号。 在实际应用中,有些信号无法求它的傅里叶变换,但是可以用求自相关函数的方法求得信号的功率谱。
互相关函数自相关函数计算和作图
互相关函数-自相关函数计算和作图
————————————————————————————————作者: ————————————————————————————————日期: ?
互相关函数,自相关函数计算和作图 1.自相关和互相关的概念。 ●互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1,t2间的相关程度。 ●自相关函数是描述随机信号x(t)在任意两个不同时刻t1,t2间的相关程度。 互相关函数是在频域内两个信号是否相关的一个判断指标,把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号,对修正测量中接入噪声源而产生的误差非常有效。 ----------------------------------------------------------------------------------- 事实上,在图象处理中,自相关和互相关函数的定义如下:设原函数是f(t),则自相关函数定义为R(u)=f(t)*f(-t),其中*表示卷积;设两个函数分别是f(t)和g(t),则互相关函数定义为R(u)=f(t)*g(-t),它反映的是两个函数在不同的相对位置上互相匹配的程度。 2.利用matlab中实现这两个相关并用图像显示: 自相关函数:? dt=.1; t=[0:dt:100];x=cos(t); [a,b]=xcorr(x,'unbiased'); plot(b*dt,a) ?
互相关函数:把[a,b]=xcorr(x,'unbiased');改为[a,b]=xcorr(x,y,'unbia sed');便可。 ?3. 实现过程: 在Matalb中,求解xcorr的过程事实上是利用Fourier变换中的卷积定理进行的,即R(u)=ifft(fft(f)×fft(g)),其中×表示乘法,注:此公式仅表示形式计算,并非实际计算所用的公式。当然也可以直接采用卷积进行计算,但是结果会与xcorr的不同。事实上,两者既然有定理保证,那么结果一定是相同的,只是没有用对公式而已。下面是检验两者结果相同的代码:??dt=.1; t=[0:dt:100];?x=3*sin(t);?y=cos(3*t);?subplot(3,1,1); plot(t,x); subplot(3,1,2);?plot(t,y); [a,b]=xcorr(x,y); subplot(3,1,3);?plot(b*dt,a);?yy=cos(3*fliplr(t)); % or use:yy=fliplr(y); z=conv(x,yy); pause; subplot(3,1,3); plot(b*dt,z,'r');??即在xcorr中不使用scaling。 ?4. 其他相关问题:?1) 相关程度与相关函数的取值有什么联系?
互相关函数的应用
苏州大学《机械工程测试技术基础》课程作业 题目:互相关函数的应用——测量钢带速度、确定输油管裂损位置 姓名:王臻 学号:1442404033 年级:_14 级 专业:车辆工程 2017年04月03日
互相关函数的应用——测量钢带速度、确定输油管裂损位置 一、实验目的 1、理解相关性原理,掌握信号的互相关函数的求法以及互相关函数的特性。 2、利用互相关函数知识,探索测量钢带速度、确定输油管裂损位置的方法。 二、实验原理 1、相关的概念 相关是指客观事物变化量之间的相依关系,当两个随机变量之间具有某种关系时,随着某个变量数值的确定,另一变量却可能去许多值,但取值有一定的概率统计规律,这时称两个随机变量存在着相关关系。在统计学中是用相关系数来描述两个变量x ,y 之间的相关性,相关系数的公式为: y x y x y x E σσμμρ)] )([(xy --= 注: E 为数学期望; x μ为随机变量x 的均值,x μ=E[x]; y μ为随机变量y 的均值,y μ=E[y]; x σ,y σ为随机变量x ,y 的标准差; 2x σ =E[(x- x μ)2] 2y σ=E[(y-y μ)2 ] 利用柯西—许瓦兹不等式: E[(x-x μ)(y-y μ)]2≦E[(x-x μ)2]E[(y-y μ)2] 式中 xy ρ是两个随机变量波动量之积的数学期望,称之为协方差或相关性, 表征了x 、y 之间的关联程度;x σ、y σ 分别为随机变量x 、y 的均方差,是随机变量波动量平方的数学期望。 故知| xy ρ|≤1,当 xy ρ的绝对值越接近1,x 和y 的线性相关程度越好,当 xy ρ
自相关函数和互相关函数的matlab计算和作图
自相关函数和互相关函数的matlab计算和作图 1. 首先说说自相关和互相关的概念。 这个是信号分析里的概念,他们分别表示的是两个时间序列之间和同一个时间序列在任意两个不同时刻的取值之间的相关程度,即互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1,t2的取值之间的相关程度,自相关函数是描述随机信号x(t)在任意两个不同时刻t1,t2的取值之间的相关程度。 自相关函数是描述随机信号X(t)在任意两个不同时刻t1,t2的取值之间的相关程度;互相关函数给出了在频域内两个信号是否相关的一个 判断指标,把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号,对修正测量中接入噪声源而产生 的误差非常有效. 事实上,在图象处理中,自相关和互相关函数的定义如下:设原函数是f(t),则自相关函数定义为 R(u)=f(t)*f(-t),其中*表示卷积;设 两个函数分别是f(t)和g(t),则互相关函数定义为R(u)=f(t)*g(-t),它反映的是两个函数在不同的相对位置上互相匹配的程度。 那么,如何在matlab中实现这两个相关并用图像显示出来呢? dt=.1; t=[0:dt:100]; x=cos(t); [a,b]=xcorr(x,'unbiased'); plot(b*dt,a) 上面代码是求自相关函数并作图,对于互相关函数,稍微修改一下就可以了,即把[a,b]=xcorr(x,'unbiased');改为[a,b]=xcorr (x,y,'unbiased');便可。 2. 实现过程: 在Matalb中,求解xcorr的过程事实上是利用Fourier变换中的卷积定理进行的,即 R(u)=ifft(fft(f)×fft(g)),其中×表示乘法,注:此 公式仅表示形式计算,并非实际计算所用的公式。当然也可以直接采用卷积进行计算,但是结果会与xcorr的不同。事实上,两者既然有定理保证 ,那么结果一定是相同的,只是没有用对公式而已。下面是检验两者结果相同的代码: dt=.1; t=[0:dt:100]; x=3*sin(t);
正弦函数的图像和性质教学设计
正弦函数的图象和性质 教师行为 学生学习活动 设计意图 (一) 提出问题,引入新课 教师引导学生复习:1、三角函数的定义及实质;2、三角函数线的作法和作用。 提问:根据以往学习函数的经验,你准备采取什么方法作出正弦函数的图象? 在作图过程中有什么困难? 学生根据教师的提问,思考并回答问题。根据经验,画函数的图象,应该列表、描点。可是,感觉到困难。 把问题作为教学的出发点,引起学生的好奇,激发学生求知欲,为发现新知识创设一个最佳的心理和认识环境,关注学生动手能力培养。 (二) 初步探索,展示内涵 提出问题一:你是如何精确描出点 呢? 问题二:什么是正弦线?我们怎样找的正弦线? 学生讨论,问题一引导他们想到 的正弦值是 学生回答问题二:由单位圆的正弦线知识,只要已知角x 的大小,就可以由几何法作出相应的正弦值 来。 由浅入深、由易到难,帮助学生体会从三角函数线出发,“以已知探求未知”的数学思想方法,培养 学生的思维能力。 通过对正弦线的复习,来发现几何作图与描点作图之间的本质区别,以培养运用已有数学知识解决新问题的能力。 数形结合,扫清了学生的思维障 碍,更好地突破了教学的重难点。 (三) 合作交流,联想探究 1、 介绍正弦函数图象的几何作 图法 学生分组讨论研究,总结交流成果。一方面分组合作探究,展示动手结果,上台板演,同时回答同学们提出的问题。 使学生掌握探究问题的方法,发展他们分析问题和解决问题的能力,老师的点拨,学生探究实践,进一步加深学生对几何法作正弦函数图象的理解。
2、介绍“五点作图法” 让学生亲自动手实践,体会数与形的完美结合。 (四) 循序渐进,延伸探究 例1 画出函数 的 简图 思考:若从函数 的图像变换分析 的图象可由的图象怎 样得到? 大家是否能用同样方法来解决变式题呢? 变式:画出函数 的简 图 逐步掌握“五点法”作图。 学生思考、小结。 归纳得到,函数y=1+sinx 的图象可由y=sinx 的图象向上平移1个单位得到。 学生独立完成,上台板演,进一 步巩固“五点法”作图。 突出学生的主体性,通过协作讨论区,同学之间互相配合、互相帮助、各种观点互相补充,增强合作意识。 (五) 归纳总结,内化知识 1、正弦曲线 2、注意与三角函数线等知识的联系 3、思想方法:“以已知探求未知”、类比、从特殊到一般 学生讨论,相互补充后进行回答。 让学生自己小结,不仅仅总结知识更重要地是总结数学思想方法。这是一个重组知识的过程,是一个 多维整合的过程,是一个高层次的自我认识过程,这样可帮助学生自行构建知识体系,理清知识脉络, 养成良好的学习习惯
互相关函数求相位差.doc
互相关函数求相位差 法一、利用互相关函数的性质:对于单频信号而言,时移相当于相移,相关系数从初始值变成最大值的时候,说明相位差也从初始相位差变为零。 法二、利用互相关函数的两同频正弦信号的互相关函数零时刻值与其相位差的余弦值成正比的原理获得相位差。 比较两种方法可知:第二种方法的计算精度较高。可见如果只是简单的求取互相关函数,用
第一种方法即可(直接调用xcorr),但是如果要求取延迟时间,则可以按照互相关的具体公式编写函数! 具体程序如下: n=512;%设定每周期数据采集点数 T=5;%采样周期数 fen=60;%将度转化为分:1度=60分 hs=360/(2*pi);%弧度转化为度数 t=0:2*pi/(n-1):2*T*pi;%采样数 N=length(t);%采样长度 y1=4*sin(t);%信号1 y2=4*sin(t+pi/(180*6));%信号2 Cc=xcorr(y1);%求互相关函数 %用互相关函数数学表达式求相位差:rm(n)=Rxy(n)/sqrt(Rxx(0)*Ryy(0)) C0=sum(y1.*y2);%y1和y2互相关 A0=sum(y1.*y1);%y1自相关 B0=sum(y2.*y2);%y2自相关 a=sqrt(A0); b=sqrt(B0); zhunquezhi=(pi/(180*6))*hs*fen jiaocha=acos(C0/(a*b))*hs*fen%相位差计算公式 jdwucha=jiaocha-zhunquezhi%绝对误差 xdwucha=((jiaocha-zhunquezhi)/zhunquezhi)*100%相对误差 %用有效值计算比值差 youxiaoy1=sqrt((1/(N-1))*sum(y1.^2)) %计算y1有效值 youxiaoy2=sqrt((1/(N-1))*sum(y2.^2)) %计算y2有效值 bizhicha=abs((youxiaoy1-youxiaoy2)/youxiaoy1)*100 %计算比值差 %作图 m=(-N+1):(N-1); subplot(311); plot(t,y1); grid; subplot(312); plot(t,y2); grid; subplot(313); plot(m,Cc); grid;
自相关函数和互相关函数的利用MATLAB计算和作图
《 互相关函数,自相关函数计算和作图 1.自相关和互相关的概念。 互相关函数是描述随机信号x(t),y(t)在任意两个不同时刻t1,t2间的相关程度。 自相关函数是描述随机信号x(t)在任意两个不同时刻t1,t2间的相关程度。 互相关函数是在频域内两个信号是否相关的一个判断指标,把两测点之间信号的互谱与各自的自谱联系了起来。它能用来确定输出信号有多大程度来自输入信号,对修正测量中接入噪声源而产生的误差非常有效。 -----------------------------------------------------------------------------------事实上,在图象处理中,自相关和互相关函数的定义如下:设原函数是f(t),则自相关函数定义为R(u)=f(t)*f(-t),其中*表示卷积;设两个函数分别是f(t)和g(t),则互相关函数定义为R(u)=f(t)*g(-t),它反映的是两个函数在不同的相对位置上互相匹配的程度。 】 2.利用matlab中实现这两个相关并用图像显示: 自相关函数: dt=.1; t=[0:dt:100];x=cos(t); [a,b]=xcorr(x,'unbiased'); plot(b*dt,a)
互相关函数:把[a,b]=xcorr(x,'unbiased');改为[a,b]=xcorr(x,y,'unbiased');便可。 ? 3. 实现过程: 在Matalb中,求解xcorr的过程事实上是利用Fourier变换中的卷积定理进行的,即 R(u)=ifft(fft(f)×fft(g)),其中×表示乘法,注:此公式仅表示形式计算,并非实际计算所用的公式。当然也可以直接采用卷积进行计算,但是结果会与xcorr的不同。事实上,两者既然有定理保证,那么结果一定是相同的,只是没有用对公式而已。下面是检验两者结果相同的代码: dt=.1; t=[0:dt:100]; x=3*sin(t); y=cos(3*t); subplot(3,1,1); plot(t,x); subplot(3,1,2); plot(t,y); [a,b]=xcorr(x,y); subplot(3,1,3);
自相关与互相关函数
相关函数 1.自相关函数? 自相关函数就是信号在时域中特性得平均度量,它用来描述信号在一个时刻得取值与 另一时刻取值得依赖关系,其定义式为? (2、4、6)??对于周期信号,积分平均时间T为信号周期。对于有限时间内得信号,例如单个脉 ?冲,当T趋于无穷大时,该平均值将趋于零,这时自相关函数可用下式计算 (2、4、7)? 自相关函数就就是信号x(t)与它得时移信号x(t+τ)乘积得平均值,它就是时移变量τ得函 ?数。??例如信号得自相关函数为 ? 若信号就是由两个频率与初相角不同得频率分量组成,即 ,则? ?对于正弦信号,由于,其自相关函数仍为??? 由此可见,正弦(余弦)信号得自相关函数同样就是一个余弦函数。它保留了原信号 ?得频率成分,其频率不变,幅值等于原幅值平方得一半,即等于该频率分量得平均功率 ?,但丢失了相角得信息。??自相关函数具有如下主要性质: ? (1)自相关函数为偶函数,,其图形对称于纵轴。因此,不论时移 方向就是导前还就是滞后(τ为正或负),函数值不变。 (2)当τ=0时,自相关函数具有最大值,且等于信号得均方值,即 (2、4、8) ?(3)周期信号得自相关函数仍为同频率得周期信号。 (4)若随机信号不含周期成分,当τ趋于无穷大时,趋于信号平均值得平方 ?,即? (2、4、9) 实际工程应用中,常采用自相关系数来度量其不同时刻信号值之间得相关程? 度,定义式为? (2、4、10) ?当τ=0时,=1,说明相关程度最大;当τ=∞时,,说明信号x(t)与 x(t+τ)之间彼此无关。由于,所以.值得大小表示信号相 关性得强弱。??自相关函数得性质可用图2、4、3表示.
