mov在系统中直接生成缩略图
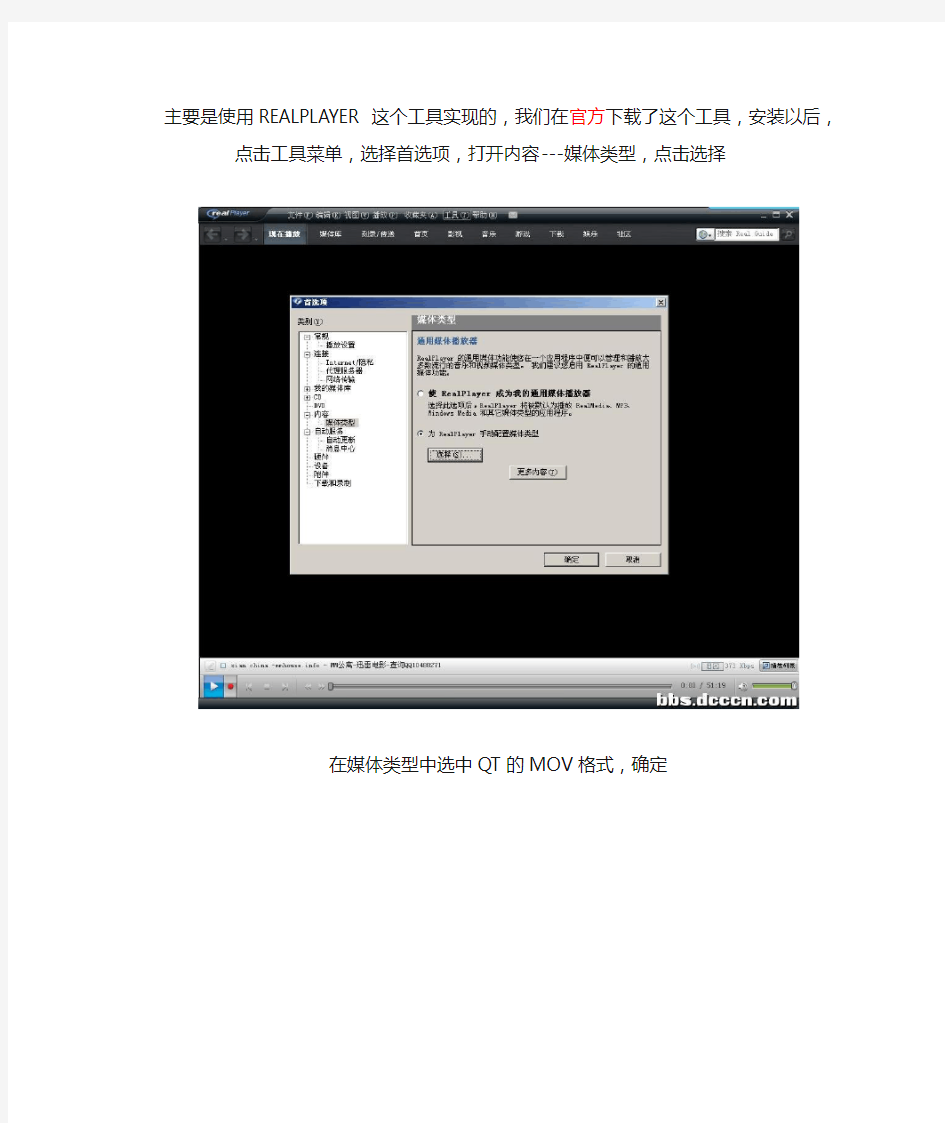
主要是使用REALPLAYER这个工具实现的,我们在官方下载了这个工具,安装以后,点击工具菜单,选择首选项,打开内容---媒体类型,
点击选择
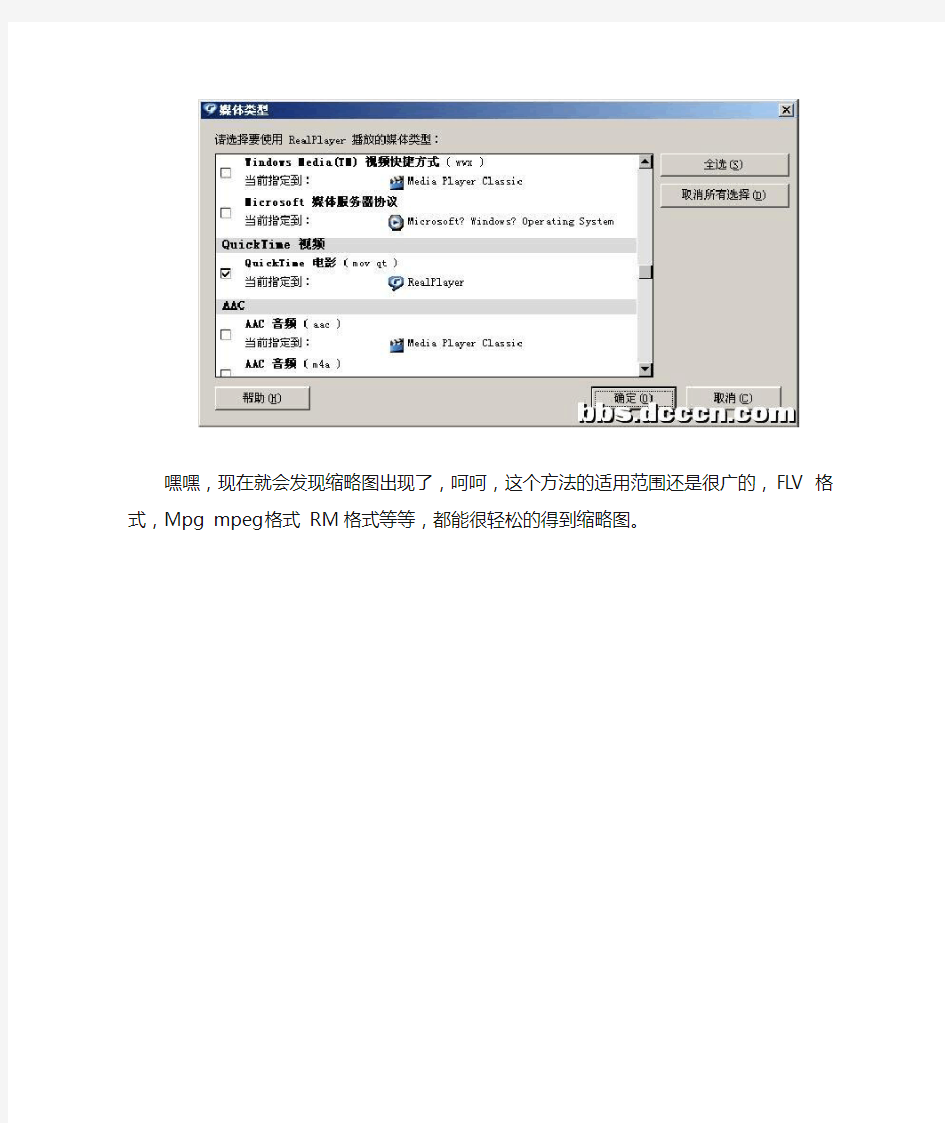
在媒体类型中选中QT的MOV格式,确定
嘿嘿,现在就会发现缩略图出现了,呵呵,这个方法的适用范围还是很广的,FLV格式,Mpg mpeg格式RM格式等等,都能很轻松的得到缩略图。
基于分形几何的分形图绘制与分析
基于分形几何的分形图绘制与分析 摘要:基于分形几何的分形图绘制方法源于l系统、迭代函数系统ifs、复动力系统等。在运用分形原理及算法编程绘制多种分形图的基础上,重点对ifs参数进行实验分析,ifs吸引集实现了对原图形的几何变换。分形图的演变具有渐变性。 关键词:分形几何迭代函数系统分形图绘制渐变 1 分形几何学 现代数学的一个新的分支——,它是由美籍法国数学家曼德勃罗(b.b.mandelbrot)1973年在法兰西学院讲课时,首次提出了分形几何的设想。分形(fractal)一词,是曼德勃罗创造出来的,其原意具有不规则、支离破碎等意义,分形几何学是一门以非规则几何形态为研究对象的几何学。由于不规则现象在自然界是普遍存在的,因此分形几何又称为描述大自然的几何学。分形几何的诞生无论是在理论上还是在实践上都具有重要价值。 2 分形的定义 目前分形还没有最终的科学定义,曼德勃罗曾经为分形下过两个定义: (1)分形是hausdorff-besicovitch维数严格大于拓扑维数的集合。因为它把许多hausdorff维数是整数的分形集合排除在外,例如,经典分形集合peano曲线分形维数 (2)局部与整体以某种方式自相似的形,称为分形。 然而,经过理论和应用的检验,人们发现这两个定义很难包括分形
如此丰富的内容。实际上,对于什么是分形,到目前为止还不能给出一个确切的定义,正如生物学中对“生命”也没有严格明确的定义一样,人们通常是列出生命体的一系列特征来加以说明。对分形的定义也可同样的处理。 (ⅰ) 分形集合在任意小尺度下,它总有复杂的细节,或者说它具有精细的结构。 (ⅱ) 分形集合是非常不规则的,用传统的几何语言无法来描述它的局部和整体,它既不是满足某些条件的点的轨迹,也不是某些简单方程的解集。 (ⅲ) 分形集具有某种自相似形式,可能是近似的自相似或者统计的自相似。 (ⅳ) 以某种方式定义的分形集合的“分形维数”,严格大于它相应的拓扑维数。 (ⅴ) 在大多数令人感兴趣的情形下,分形集合是以非常简单的递归的方法产生的。 3 分形研究的对象 几何学的研究对象是物体的形状,在自然界中,许多物体的形状是极不规则的,例如:弯弯曲曲的海岸线,起伏不平的山脉,变化无偿的浮云,以及令人眼花缭乱的满天繁星,等等。这些物体的形状有着共同的特点,就是极不规则,极不光滑。但是,所有的经典几何学都是以规则而光滑的形状为其研究对象的,例如:初等平面几何的主要研究对象是直线与圆;平面解析几何的主要研究对象是一
如何能让Java生成复杂Word文档(1)
先用office2003或者2007编辑好word的样式,然后另存为xml,将xml翻译为FreeMarker 模板,最后用java来解析FreeMarker模板并输出Doc。经测试这样方式生成的word文档完全符合office标准,样式、内容控制非常便利,打印也不会变形,生成的文档和office中编辑文档完全一样。 AD:客户要求用程序生成标准的word文档,要能打印,而且不能变形,以前用过很多解决方案,都在客户严格要求下牺牲的无比惨烈。 POI读word文档还行,写文档实在不敢恭维,复杂的样式很难控制不提,想象一下一个20多页,嵌套很多表格和图像的word文档靠POI来写代码输出,对程序员来说比去山西挖煤还惨,况且文档格式还经常变化。 iText操作Excel还行。对于复杂的大量的word也是噩梦。 直接通过JSP输出样式基本不达标,而且要打印出来就更是惨不忍睹。 Word从2003开始支持XML格式,用XML还做就很简单了。 大致的思路是先用office2003或者2007编辑好word的样式,然后另存为xml,将xml 翻译为FreeMarker模板,最后用java来解析FreeMarker模板并输出Doc。经测试这样方式生成的word文档完全符合office标准,样式、内容控制非常便利,打印也不会变形,生成的文档和office中编辑文档完全一样。 看看实际效果 首先用office【版本要2003以上,以下的不支持xml格式】编辑文档的样式,图中红线的部分就是我要输出的部分:
将编辑好的文档另存为XML 再用Firstobject free XML editor将xml中我们需要填数据的地方打上FreeMarker标记
PHP使用imagick读取PDF生成png缩略图的两种方法
这篇文章主要介绍了PHP使用imagick读取PDF第一页生成png缩略图的两种方法,使用了PHP扩展php_imagick,需要的朋友可以参考下 一、ImageMagick是什么 ImageMagick是一套功能强大、稳定而且免费的工具集和开发包,可以用来读、写和处理超过185种基本格式的图片文件,包括流行的TIFF, JPEG, GIF, PNG, PDF以及PhotoCD 等格式。利用ImageMagick,你可以根据web应用程序的需要动态生成图片, 还可以对一个(或一组)图片进行改变大小、旋转、锐化、减色或增加特效等操作,并将操作的结果以相同格式或其它格式保存。 二、php_imagick什么 一个可以供PHP调用ImageMagick功能的PHP扩展。使用这个扩展可以使PHP具备和ImageMagick相同的功能。 三、PDF生成png缩略图的两种方法 第一种: 代码如下:/** * PDF2PNG * @param $pdf 待处理的PDF文件 * @param $path 待保存的图片路径 * @param $page 待导出的页面-1为全部0为第一页1为第二页 * @return 保存好的图片路径和文件名 */ function pdf2png($pdf,$path,$page=0) { if(!is_dir($path)) { mkdir($path,true); } if(!extension_loaded('imagick')) { echo '没有找到imagick!' ; return false; } if(!file_exists($pdf)) { echo '没有找到pdf' ; return false; } $im = new Imagick(); $im->setResolution(120,120); //设置图像分辨率 $im->setCompressionQuality(80); //压缩比 $im->readImage($pdf."[".$page."]"); //设置读取pdf的第一页 //$im->thumbnailImage(200, 100, true); // 改变图像的大小 $im->scaleImage(200,100,true); //缩放大小图像
分形(一种别样的数学美丽)
分形(一种别样的数学美丽) 从海螺和螺旋星云到人类的肺脏结构,我们身边充满各种各样的混沌图案。分形(一种几何形状,被以越来越小的比例反复折叠而产生不能被标准几何所定义的不标准的形状和表面)是由混沌方程组成,它包含通过放大会变的越来越复杂的自相似图案。要是把一个分形图案分成几小部分,结果会得到一个尺寸缩小,但形状跟整个图案一模一样的复制品。 分形的数学之美,是利用相对简单的等式形成无限复杂的图案。它通过多次重复分形生成等式,形成美丽的图案。我们已经在我们的地球上搜集到一些这方的天然实例,下面就让我看一看。 1.罗马花椰菜:拥有黄金螺旋 罗马花椰菜 这种花椰菜的变种是最重要的分形蔬菜。它的图案是斐波纳契数列,或称黄金螺旋型(一种对数螺旋,小花以花球中心为对称轴,螺旋排列)的天然代表。 2.世界最大盐沼——天空之镜
盐沼
坚硬的盐层上呈现非常一致的不规则图案 过去一个世纪,上图里的旧金山海湾盐沼一直被用来进行工业盐生产。下图显示的是位于玻利维亚南部的世界最大盐沼——天空之镜(Salar de Uyuni)。坚硬的盐层上呈现非常一致的不规则图案,这是典型的分形。 3.菊石缝线 菊石的外壳还生长成一个对数螺旋型
大约6500万年前灭绝的菊石 在大约6500万年前灭绝的菊石,是制作分成许多间隔的螺旋形外壳的海洋头足纲动物。这些间隔之间的壳壁被称作缝线,它是分形复曲线。美国著名古生物学家史蒂芬·杰伊·古尔德依据不同时期的菊石缝线的复杂性得出结论说,进化并没驱使它们变得更加复杂,我们人类显然是“一个例外”,是宇宙里独一无二的。菊石的外壳还生长成一个对数螺旋型,很显然,自然界经常会出现这种图案,例如罗马花椰菜。 4.山脉 山脉 山脉是构造作用力和侵蚀作用的共同产物,构造作用力促使地壳隆起,侵蚀作用导致一些地壳下陷。这些因素共同作用的产物,是一个分形。上图显示的是喜马拉雅山脉,它
经典的分形算法 (1)
经典的分形算法 小宇宙2012-08-11 17:46:33 小宇宙 被誉为大自然的几何学的分形(Fractal)理论,是现代数学的一个新分支,但其本质却是一种新的世界观和方法论。它与动力系统的混沌理论交叉结合,相辅相成。它承认世界的局部可能在一定条件下,在某一方面(形态,结构,信息,功能,时间,能量等)表现出与整体的相似性,它承认空间维数的变化既可以是离散的也可以是连续的,因而拓展了视野。 分形几何的概念是美籍法国数学家曼德布罗(B.B.Mandelbrot)1975年首先提出的,但最早的工作可追朔到1875年,德国数学家维尔斯特拉斯(K.Weierestrass)构造了处处连续但处处不可微的函数,集合论创始人康托(G.Cantor,德国数学家)构造了有许多奇异性质的三分康托集。1890年,意大利数学家皮亚诺(G.Peano)构造了填充空间的曲线。1904年,瑞典数学家科赫(H.von Koch)设计出类似雪花和岛屿边缘的一类曲线。1915年,波兰数学家谢尔宾斯基(W.Sierpinski)设计了象地毯和海绵一样的几何图形。这些都是为解决分析与拓朴学中的问题而提出的反例,但它们正是分形几何思想的源泉。1910年,德国数学家豪斯道夫(F.Hausdorff)开始了奇异集合性质与量的研究,提出分数维概念。1928年布利干(G.Bouligand)将闵可夫斯基容度应用于非整数维,由此能将螺线作很好的分类。1932年庞特里亚金(L.S.Pontryagin)等引入盒维数。1934年,贝塞考维奇(A.S.Besicovitch)更深刻地提示了豪斯道夫测度的性质和奇异集的分数维,他在豪斯道夫测度及其几何的研究领域中作出了主要贡献,从而产生了豪斯道夫-贝塞考维奇维数概念。以后,这一领域的研究工作没有引起更多人的注意,先驱们的工作只是作为分析与拓扑学教科书中的反例而流传开来。 真正令大众了解分形是从计算机的普及肇始,而一开始,分形图的计算机绘制也只是停留在二维平面,但这也足以使人们心驰神往。近来,一个分形体爱好者丹尼尔?怀特(英国一钢琴教师)提出一个大胆的方法,创造出令人称奇的3D分形影像,并将它们命名为芒德球(mandelbulb)。
Visual C++茱莉亚分形图形绘制
1.绘制茱莉亚图 (1)绘制窗口 首先在VC中建一个新的Projects,选择项目类型为MFC AppWizard(exe),在项目名称中键入DrawJulial,按下OK。 在随后的窗口中选择Single Document,选中Document/View architecture support,在语言中选中中文。 在Step 2 of 6窗口中不要数据库支持(None)。 在Step 3 of 6窗口中选中不要复合文档支持(None),将Automation的ActiveX Controls 选项都取消 在Step 4 of 6窗口中将默认选项中的Printing and print preview 和Docking toolbar去除,接下Next。 对Step 5 of 6窗口和Step 6 of 6窗口不作修改,按下Finish。 此时VC已经自动将我们想要的程序框架建立完毕。 然后将VC框架建立的菜单中的编辑菜单完全删去,将文件菜单中除退出一项外全部删去,在查看后面加入一个菜单项,去掉其Pop-up属性,命其ID号为ID_DRAWJULIAL,Caption为绘制茱莉亚图。 (2)定义消息映射函数 在Class Wizard中选择Message Maps栏,在Class Name 栏中选择CDrawJulialView,在Object IDs中选择
ID_DRAWJULIAL,为其COMMAND消息建立一个消息映射函数。 (3)建立代码 1.类CBaseDraw是一个基本的绘图函数,可以作为基类使用。CJulial类就是从CBaseDraw继承下来的类。由于在CBaseDraw的成员函数sleep中调用了系统函数timeGetTime(),因此要做以下工作: 选择主菜单的Project项中的Setting,在弹出的对话框中选择Link页,在Object/library modules项中加入“winmm.lib”。 源程序BaseDraw.h代码如下: //BaseDraw.h: interface for the CBaseDraw class #if !defined(AFX_BASEDRAW_H__CB43CA20_175A_11D4_81F F_94DCC6655E1C__INCLUDED_) #define AFX_BASEDRAW_H__CB43CA20_175A_11D4_81FF_94DCC6655E1 C__INCLUDED_ #if _MSC_VER > 1000 #pragma once # endif //_MSC_VER >1000 #define pi 3.141592654 //基本绘图类 class CBaseDraw
图片缩略图和原图不一样
图片缩略图和原图不一样 在正常情况下一个图片和它的缩略图应该是一样的,但是在有的时候会出现图片和缩 略图完全不一样的情况。也就是说用Windows自带的图片查看器看到的图片是一个样子,而 这些图片在文件夹中“预浏览”或者“缩略图”看到的却是完全另一个样子。 出现这种情况是因为在Windows缩略图中有一个Bug,利用这个Bug,Exifer就能够轻松 制作图片和缩略图不同的图片。 一、缩略图原理 这是什么原理呢?因为现在JPEG的文件采用了压缩的方式,其过程比较复杂。为了能 让大家快速查看其缩略图,JPEG标准在文件中记录了一些EXIF 信息。数码照相机拍出的图 片带有相机的很多参数,这都属于EXIF信息,其中缩略图也是一部分。缩略图是一幅较小 的JPEG图片,存储在EXIF信息段。支持EXIF信息内嵌缩略图数据库的片格式的图片除了JP EG格式(.jpg、.jpeg、.jpe),还有PSD、PDD、EPS、TIF、TIFF 等格式。 而Windows在第一次显示缩略图时先读当前目录中的“Thum
bs.db”这个文件,其实这 是一个缩略图数据库,从而来判断是否有该图片的缩略图。如果不存在“Thumbs.db”文件 或者该库中不存在该图片的缩略图,那么Windows会尝试取图片中的EXIF信息,判断是否存 在缩略图数据。如果图片中EXIF信息中不存在缩略图信息或信息错误,那么Windows就会用 插值的方法重新生成缩略图(如果可能则保存到当前目录中的“Th umbs.db”缩略图数据库 中)。 二、如何制作缩略图 了解了这些,既然知道原理,那么我们能否也做出这样的图片呢?其实很简单,只需 通过修改EXIF信息中的缩略图信息达到上面那种奇异的效果了。那么用什么软件能够修改 EXIF信息呢?这里笔者给大家介绍一款名字为Exifer 软件,通过它就可以很轻松的修改E XIF信息。 第一步:首先打开Exifer,选择要进行添加要修改的图片(图1)。 第二步:图片添加好之后,会在右边EXIF thumbnail中看到图片的缩略图,这时候按鼠标
分形之Julia集及其算法实现
成绩:课程名称:智能信息处理概论 分形之Julia集及其算法实现 摘要:本文从自然界的几何现象引出分形的概念,再从其定义、几何特征和分形维的计算这三个方面来加以介绍。以Julia集和Mandelbort集为例来具体描述分形。本文主要从Julia集的特点和算法实现来描述分形以及其实现的方法。 关键词:分形、分数维、Julia集、Mandelbort集、算法实现 引言 大自然是个很伟大的造物者,它留给我们一大笔美丽景观:蜿蜒曲折的海岸线、起伏不定的山脉,变幻无常的浮云,粗糙不堪的断面,袅袅上升的烟柱,九曲回肠的河流,纵横交错的血管,令人眼花缭乱的满天繁星……那么,我们又能从这些美妙的自然现象中得到什么有趣的结论呢? 正文 分形概述 分形的英文单词为fractal,是由美籍法国数学家曼德勃罗(Benoit Mandelbrot)创造出来的。其取自拉丁文词frangere(破碎、产生无规则碎片)之头,撷英文之尾所合成,本意是不规则的、破碎的、分数的。他曾说:分形就是通过将光滑的形状弄成多个小块,反复的碎弄。1975年,曼德勃罗出版了他的法文专著《分形对象:形、机遇与维数》,标志着分形理论正式诞生。【1】 两种定义 其一:具有自相似性结构的叫做分形; 其二:数学定义:豪斯道夫维Df>=拓扑维Dt。 若一有界集合,包含N个不相重叠的子集,当其放大或缩小r倍后,仍与原集合叠合,则称为自相似集合。自相似集合是分形集。具有相似性的系统叫做分形。 当放大或缩小的倍数r不是一个常数,而必须是r(r1,r2,….)的各种不同放大倍数去放大或缩小各子集,才能与原集合重合时,称为自仿射集合。具有自仿射性的系统叫做分形。【2】 特征 1.自相似性:局部与整体的相似,是局部到整体在各个方向上的等比例变换的结果; 2.自仿射性:是自相似性的一种拓展,是局部到整体在不同方向上的不等比例变换的结果; 3.精细结构:即使对该分形图放大无穷多倍,还是能看到与整体相似的结构,表现出无休止的重复; 4.分形集无法用传统几何语言来描述,它不是某些简单方程的解集,也不是满足某些条件的点的轨 迹; 5.分形集一般可以用简单的方法定义和产生,如递归、迭代;分形其实是由一些简单的图形,经过 递归或者迭代产生的复杂、精细的结构; 6.无确定的标度且具有分数维数。【3】
Java 图片处理 格式转换
Java 图片处理(包括 Jmagick 的应用) 图片处理( 的应用)
作者: 佚名, 出处:IT 专家网,
2010-10-29 08:30
责任编辑: 谢妍妍,
近期有使用到图片的压缩处理,由于在之前用 Java 处理时,在低像素的情况下, Java 处理的效果确实很差,然后尝试了用网上推荐的免费开源的第三方软件,利用 Java 的 jni 调用 dll 文件进行处理,效果还可以。在此记录下,方便以后继续积累。
近期有使用到图片的压缩处理, 由于在之前用 Java 处理时, 在低像素的情况下, Java 处理的效果确实很差,然后尝试了用网上推荐的免费开源的第三方软件,利用 Java 的 jni 调用 dll 文件进行处理,效果还可以。在此记录下,方便以后继续积累。
1、纯 Java 类处理图片代码
Java 代码
以下是代码片段: 以下是代码片段: /** * 转换图片大小,不变形 * * @param img * 图片文件 * @param width * 图片宽 * @param height * 图片高 */ public static void changeImge(File img, int width, int height) { try { Image image = ImageIO.read(img); //图片尺寸的大小处理, 如果长宽都小于规定大小, 则返回, 如果有一个大于规定大小, 则等比例缩放 int srcH = image.getHeight(null); int srcW = image.getWidth(null); if (srcH <= height && srcW <= width) { return;
分形图程序
(1)Koch曲线程序koch.m function koch(a1,b1,a2,b2,n) %koch(0,0,9,0,3) %a1,b1,a2,b2为初始线段两端点坐标,n为迭代次数 a1=0;b1=0;a2=9;b2=0;n=3; %第i-1次迭代时由各条线段产生的新四条线段的五点横、纵坐标存储在数组A、B中 [A,B]=sub_koch1(a1,b1,a2,b2); for i=1:n for j=1:length(A)/5; w=sub_koch2(A(1+5*(j-1):5*j),B(1+5*(j-1):5*j)); for k=1:4 [AA(5*4*(j-1)+5*(k-1)+1:5*4*(j-1)+5*(k-1)+5),BB(5*4*(j-1)+5*(k-1)+1:5*4*(j-1)+5*(k-1)+5)]=sub_koch1(w(k,1),w(k,2),w(k,3),w(k,4)); end end A=AA; B=BB; end plot(A,B) hold on axis equal %由以(ax,ay),(bx,by)为端点的线段生成新的中间三点坐标并把这五点横、纵坐标依次分别存%储在数组A,B中 function [A,B]=sub_koch1(ax,ay,bx,by) cx=ax+(bx-ax)/3; cy=ay+(by-ay)/3; ex=bx-(bx-ax)/3;
ey=by-(by-ay)/3; L=sqrt((ex-cx).^2+(ey-cy).^2); alpha=atan((ey-cy)./(ex-cx)); if (ex-cx)<0 alpha=alpha+pi; end dx=cx+cos(alpha+pi/3)*L; dy=cy+sin(alpha+pi/3)*L; A=[ax,cx,dx,ex,bx]; B=[ay,cy,dy,ey,by]; %把由函数sub_koch1生成的五点横、纵坐标A,B顺次划分为四组,分别对应四条折线段中 %每条线段两端点的坐标,并依次分别存储在4*4阶矩阵k中,k中第i(i=1,2,3,4)行数字代表第%i条线段两端点的坐标 function w=sub_koch2(A,B) a11=A(1);b11=B(1); a12=A(2);b12=B(2); a21=A(2);b21=B(2); a22=A(3);b22=B(3); a31=A(3);b31=B(3); a32=A(4);b32=B(4); a41=A(4);b41=B(4); a42=A(5);b42=B(5); w=[a11,b11,a12,b12;a21,b21,a22,b22;a31,b31,a32,b32;a41,b41,a42,b42];
分形图形与分形的产生
分形图形 分形理论是非线性科学的主要分支之一,它在计算机科学、化学、生物学、天文学、地理学等众多自然科学和经济学等社会科学中都有广泛的应用。分形的基本特征是具有标度不变性。其研究的图形是非常不规则和不光滑的已失去了通常的几何对称性;但是,在不同的尺度下进行观测时,分形几何学却具有尺度上的对称性,或称标度不变性。研究图形在标度变换群作用下不变性质和不变量对计算机图形技术的发展有重大的意义。 说到分形(fractal),先来看看分形的定义。分形这个词最早是分形的创始人曼德尔布诺特提来的,他给分形下的定义就是:一个集合形状,可以细分为若干部分,而每一部分都是整体的精确或不精确的相似形。分形这个词也是他创造的,含有“不规则”和“支离破碎”的意思。分形的概念出现很早,从十九世纪末维尔斯特拉斯构造的处处连续但处处不可微的函数,到上个世纪初的康托三分集,科赫曲线和谢尔宾斯基海绵。但是分形作为一个独立的学科被人开始研究,是一直到七十年代曼德尔布诺特提出分形的概念开始。而一直到八十年代,对于分形的研究才真正被大家所关注。 分形通常跟分数维,自相似,自组织,非线性系统,混沌等联系起来出现。它是数学的一个分支。我之前说过很多次,数学就是美。而分形的美,更能够被大众所接受,因为它可以通过图形化的方式表达出来。而更由于它美的直观性,被很多艺术家索青睐。分形在自然界里面也经常可以看到,最多被举出来当作分形的例子,就是海岸线,源自于曼德尔布诺特的著名论文《英国的海岸线有多长》。而在生物界,分形的例子也比比皆是。 近20年来,分形的研究受到非常广泛的重视,其原因在于分形既有深刻的理论意义,又有巨大的实用价值。分形向人们展示了一类具有标度不变对称性的新世界,吸引着人们寻求其中可能存在着的新规律和新特征;分形提供了描述自然形态的几何学方法,使得在计算机上可以从少量数据出发,对复杂的自然景物进行逼真的模拟,并启发人们利用分形技术对信息作大幅度的数据压缩。它以其独特的手段来解决整体与部分的关系问题,利用空间结构的对称性和自相似性,采用各种模拟真实图形的模型,使整个生成的景物呈现出细节的无穷回归的性质,丰富多彩,具有奇妙的艺术魅力。分形对像没有放大极限,无论如何放大,总会看到更详细的结构。借助于分形的计算机生成,从少量的数据生成复杂的自然景物图形,使我们在仿真模拟方面前进了一大步。在分形的诸多研究课题中,分形的计算机生成问题具有明显的挑战性,它使传统数学中无法表达的形态(如山脉、花草等)得以表达,还能生成一个根本“不存在”的图形世界。分形在制造以假乱真的景物方面的进展和潜在的前途,使得无论怎样估计它的影响也不过分。可以肯定,分形图案在自然界真实物体模拟、仿真形体生成、计算机动画、艺术装饰纹理、图案设计和创意制作等具有广泛的应用价值。 分形图形简介一、关于分形与混沌 关于分形的起源,要非常准确的找出来是非常困难的。研究动态系统、非线形数学、函数分析的科学家,已数不胜数。尽管分形的早期线索已非常古老,但这一学科却还很年轻。比如关于动态系统和细胞自动机的大部分工作可以追溯到冯-诺依曼;但是,直到Mandelbrot 才如此清楚地将自然现象和人工现象中的混沌及分形同自相似性联系在一起。大家如果对此感兴趣,可进一步查阅有关资料。下面我们看一看分形的概念。 什么是分形呢?考虑到此文的意图,我们无意给出它严格的定义,就我们的目的而言,一个分形就是一个图象,但这个图象有一个特性,就是无穷自相似性。什么又是自相似呢?在自然和人工现象中,自相似性指的是整体的结构被反映在其中的每一部分中。比如海岸线,常举的例子,你看它10公里的图象(曲线),和一寸的景象(曲线)是相似的,这就是自相似性。 与分形有着千差万屡的关系的,就是混沌。混沌一词来源与希腊词汇,原意即“张开咀”,但是在社会意义上,它又老爱和无序联系在一起。解释分形和混沌的联系,要注意到分形是
java实现将图片和缩略图存储到数据库中
public class PicCreateCtrl extends HttpServlet{ public PicCreateCtrl(){ super(); } public void destroy(){ super.destroy();//Just puts"destroy"string in log //Put your code here } public void doGet(HttpServletRequest request,HttpServletResponse response) throws ServletException,IOException{ doPost(request,response); } public void doPost(HttpServletRequest request,HttpServletResponse response) throws ServletException,IOException{ response.setContentType("text/html;charset=gb2312"); PrintWriter out=response.getWriter(); SmartUpload mySmartUpload=new SmartUpload();//creat new SmartUpload object long file_size_max=10000000;//the bigest size of file String fileExt=""; String url="temp/";//the path of save upload file mySmartUpload.initialize(this.getServletConfig(),request,response); try{ mySmartUpload.setAllowedFilesList("png,emf,bmp,jpg,gif,BMP,JPG,GIF,PN G,EMF"); //上载文件 mySmartUpload.upload(); }catch(Exception e){ e.printStackTrace(); out.print(""); } try{ BaseduManager manager=new BaseduManager(); File myFile=mySmartUpload.getFiles().getFile(0); String xh=mySmartUpload.getRequest().getParameter("xcxh"); if(myFile.isMissing()){ out.print("
