天津市部分区2019届高三质量调查试卷(二)数学(理)试题+Word版含解析

合集下载

天津市河西区2019高三二模数学试题(理科)有答案(已审阅)

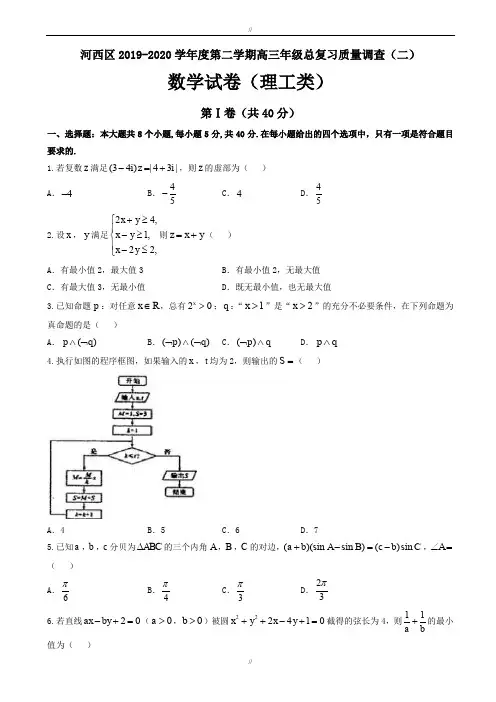
河西区2019-2020学年度第二学期高三年级总复习质量调查（二）数学试卷（理工类）第Ⅰ卷（共40分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若复数z 满足(34)|43|i z i -=+，则z 的虚部为（） A ．4-B ．45-C ．4D ．452.设x ，y 满足24,1,22,x y x y x y +≥⎧⎪-≥⎨⎪-≤⎩则z x y =+（）A ．有最小值2，最大值3B ．有最小值2，无最大值C ．有最大值3，无最小值D ．既无最小值，也无最大值3.已知命题p ：对任意x R ∈，总有20x >；q ：“1x >”是“2x >”的充分不必要条件，在下列命题为真命题的是（） A ．()p q ∧⌝B ．()()p q ⌝∧⌝C ．()p q ⌝∧D ．p q ∧4.执行如图的程序框图，如果输入的x ，t 均为2，则输出的S =（）A ．4B ．5C ．6D ．75.已知a ，b ，c 分贝为ABC ∆的三个内角A ，B ，C 的对边，()(sin sin )()sin a b A B c b C +-=-，A ∠=（） A ．6πB ．4π C ．3π D ．23π 6.若直线20ax by -+=（0a >，0b >）被圆222410x y x y ++-+=截得的弦长为4，则11a b+的最小值为（）A．32+BC ．14D．32+7.在平面直角坐标系xOy 中，已知双曲线1C ：2221x y -=，过1C 的左顶点引1C 的一条渐进线的平行线，则该直线与另一条渐进线及x 轴围成的三角形的面积（） ABCD8.已知()|21|xf x =-，当a b c <<时，有()()()f a f c f b >>，则必有（） A ．0a <，0b <，0c < B ．0a <，0b >，0c > C ．22a c -<D ．1222a c <+< 第Ⅱ卷（共110分）二、填空题（每题5分，满分30分，将答案填在答题纸上）9.设U R =，集合{}2|320A x x x =++=，{}2|(1)0B x x m x m =+++=，若()U A B =∅ð，则m = ．10.若8(x 的展开式中4x 的系数为7，则实数a = ． 11.一个多面体的三视图如图所示，则该多面体的体积是．12.如图，在ABC ∆中，H 为BC 上异于B ，C 的任一点，M 为AH 的中点，若AM AB AC λμ=+，则λμ+= ．13.在平面直角坐标系xOy 中，以原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，曲线1C 的极坐标方程为(cos sin )2ρθθ+=-，曲线2C的参数方程为2x ty ⎧=⎪⎨=⎪⎩（t 为参数），则1C 与2C 的公共点的直角坐标为． 14.已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数(())1y f f x =+的所有零点构成的集合为．三、解答题（本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.） 15.已知向量1(cos ,)2a x =-，(3sin ,cos 2)b x x =，x R ∈，设函数()f x a b =⋅．（Ⅰ）求()f x 的最小正周期；（Ⅱ）求()f x 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值． 16.盒内有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球．规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得1-分，现从盒内任取3个球．（Ⅰ）求取出的3个球中至少有一个红球的概率；（Ⅱ）求取出的3个球得分之和恰为1分的概率；（Ⅲ）设ξ为取出的3个球中白色球的个数，求ξ的分布列及期望．17.如图，已知梯形ABCD 中，//AD BC ，AD AB ⊥，22AB BC AD ===，四边形EDCF 为矩形，CF =EDCF ⊥平面ABCD ．（Ⅰ）求证：//DF 平面ABE ；（Ⅱ）求平面ABE 与平面EFB 所成锐二面角的余弦值；（Ⅲ）在线段DF 上是否存在点P ，使得直线BP 与平面ABE 若存在，求出线段BP 的长；若不存在，请说明理由．18.数列{}n a 的前n 项和为n S ，且(1)n S n n =+（*n N ∈）．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）若数列{}n b 满足：3122331313131n n n b b b ba =++++++++…，求数列{}nb 的通项公式；（Ⅲ）令4n nn a b c =（*n N ∈），求数列{}n c 的前n 项和n T ． 19.在直角坐标系xOy 中，已知中心在原点，离心率为12的椭圆E 的一个焦点为圆C ：22420x y x +-+=的圆心．（Ⅰ）求椭圆E 的方程；（Ⅱ）设P 是椭圆E 上一点，过P 作两条斜率之积为12的直线1l ，2l ，当直线1l ，2l 都与圆C 相切时，求P 的坐标．20.设k R ∈，函数()ln f x x kx =-．（Ⅰ）若2k =，求曲线()y f x =在1x =处的切线方程；（Ⅱ）若()f x 无零点，求实数k 的取值范围；（Ⅲ）若()f x 有两个相异零点1x ，2x ，求证：12ln ln 2x x +>．河西区2019-2020学年度第二学期高三年级总复习质量调查（二）数学试卷（理工类）答案一、选择题1-5:DBADC 6-8: ACD 二、填空题 9.1或2 10.12 11.233 12.12 13.(2,4)-14.113,,24⎧--⎨⎩三、解答题15.解：（Ⅰ）1()cos cos 22f x a b x x x =⋅=-1sin 2cos 222x x =-sin(2)6x π=-，最小正周期为T π=．（Ⅱ）当0,2x π⎡⎤∈⎢⎥⎣⎦时，52,666x πππ⎡⎤-∈-⎢⎥⎣⎦，由sin y x =图象可知,62x ππ⎡⎤∈-⎢⎥⎣⎦时单调递增，5,26x ππ⎡⎤∈⎢⎥⎣⎦时单调递减，所以当266x ππ-=-，即0x =时，()f x 取最小值12-；当262x ππ-=，即3x π=时，()f x 取最大值1．16.解：（Ⅰ）37397112C P C =-=．（Ⅱ）记“取出1个红色球，2个白色球”为事件B ，“取出2个红色球，1个黑色球”为事件C ，则1221232433995()()()42C C C C P B C P B P C C C +=+=+=．（Ⅲ）ξ可能的取值为0,1,2,3．36395(0)21C P C ξ===，12363945(1)84C C P C ξ===，2136393(2)14C C P C ξ===，33391(3)84C P C ξ===． ξ的分布列为：ξ 0 1 2 3P521 4584 314 18454531()0123121841484E ξ=⨯+⨯+⨯+⨯=． 17.（Ⅰ）证明：取D 为原点，DA 所在直线为x 轴，DE 所在直线为z 轴建立空间直角坐标系，如图，则(1,0,0)A ，(1,2,0)B，E，(1,F -，∴(1,BE =--，(0,2,0)AB =，设平面ABE 的法向量(,,)n x y z =，∴20,20,x y y ⎧--=⎪⎨=⎪⎩不妨设(3,0,1)n =，又(1,DF =-，∴30DF n ⋅=-=， ∴DF n ⊥，又∵DF ⊄平面ABE ， ∴//DF 平面ABE ．（Ⅱ）解：∵(1,BE =--，(BF =-，设平面BEF 的法向量(,,)m x yz =，∴20,20,x y x ⎧--=⎪⎨-+=⎪⎩不妨设(23,4)m =，∴|cos |||31||||2m n m n θ⋅===⋅⋅， ∴平面ABE 与平面EFB所成锐二面角的余弦值为31．（Ⅲ）设(1,DP DF λλ==-(,2)λλ=-，[]0,1λ∈，∴(,2)P λλ-，∴(1,2)BP λλ=---，又∵平面ABE 的法向量(3,0,1)n =，∴sin |cos ,|4BP n θ=<>==， ∴28610λλ-+=， ∴12λ=或14λ=．当12λ=时，3(,1,22BP =--，∴||2BP =；当14λ=时，53(,,424BP =--，∴||2BP =．综上，||2BP =．18.解：（Ⅰ）当1n =时，112a S ==；当2n ≥时，12n n n a S S n -=-=，知12a =满足该式， ∴数列{}n a 的通项公式为2n a n =．（Ⅱ）31223(1)31313131n n n b b b ba n =++++≥++++…，① 3+112+123+13131313131n n n n n b b b b ba =++++++++++…，② ②-①得111231n n n n b a a +++=-=+，112(31)n n b ++=+，而18b =，故2(31)nn b =+（*n N ∈）．（Ⅲ）∵(31)34n n n nn a b c n n n ==+=⋅+， ∴123n n T c c c c =++++…23(1323333)(12)nn n =⨯+⨯+⨯++⨯++++……，令231323333nn H n =⨯+⨯+⨯++⨯…，③则234131323333n n H n +=⨯+⨯+⨯++⨯…，④③-④得，231233333n n n H n +-=++++-⨯…13(13)313n n n +-=-⨯-，1(21)334n n n H +-⋅+=，∴数列{}n c 的前n 项和1(21)33(1)42n n n n n T +-⋅++=+．19.解：（Ⅰ）由C ：22420x y x +-+=，得22(2)2x y -+=，故圆C 的圆心为点(2,0)，从而可设椭圆E 的方程为22221(0)x y a b a b+=>>，其焦距为2c ，由题设知2c =，12e =，所以24a c ==，22212b a c =-=，故椭圆E 的方程为2211612x y +=．（Ⅱ）设点P 的坐标为00(,)x y ，1l ，2l 的斜率分别为1k ，2k ，则1l ，2l 的方程分别诶1l ：010()y y k x x -=-，2l ：020()y y k x x -=-，且1212k k =，由1l 与圆C ：22(2)2x y -+=相切，=222010010(2)22(2)20x k x y k y ⎡⎤--+-+-=⎣⎦，同理可得222020020(2)22(2)20x k x y k y ⎡⎤--+-+-=⎣⎦，从而1k ，2k 是方程2220000(2)22(2)20x k x y k y ⎡⎤--+-+-=⎣⎦的两个实根，于是202200(2)20,8(2)20,x x y ⎧--≠⎪⎨⎡⎤∆=-+->⎪⎣⎦⎩① 且20122021(2)22y k k x -==--，由220020201,161221,(2)22x y y x ⎧+=⎪⎪⎨-⎪=⎪--⎩得20058360x x --=解得02x =-或0185x =．由02x =-，得03y =±；由0185x =，得0y =，它们满足①式，故点P 的坐标为(2,3)-或(2,3)--或18(5或18(,5．20.解：（Ⅰ）函数的定义域为(0,)+∞，11'()kxf x k x x-=-=，当2k =时，'(1)1f =-，则切线方程为(2)(1)y x --=--，即10x y ++=．（Ⅱ）①若0k <时，则'()0f x >，()f x 是区间(0,)+∞上的增函数， ∵(1)0f k =->，()(1)0kkkf e k ke k e =-=-<， ∴(1)()0kf f e ⋅<，函数()f x 在区间(0,)+∞有唯一零点； ②若0k =，()ln f x x =有唯一零点1x =； ③若0k >，令'()0f x =，得1x k=，在区间1(0,)k上，'()0f x >，函数()f x 是增函数；在区间1(,)k+∞上，'()0f x <，函数()f x 是减函数；故在区间(0,)+∞上，()f x 的最大值为11()ln1ln 1f k k k=-=--，由于()f x 无零点，须使1()ln 10f k k =--<，解得1k e>，故所求实数k 的取值范围是1(,)e+∞．（Ⅲ）设()f x 的两个相异零点为1x ，2x ，设120x x >>， ∵1()0f x =，2()0f x =，∴11ln 0x kx -=，22ln 0x kx -=， ∴1212ln ln ()x x k x x -=-，1212ln ln ()x x k x x +=+，∵212x x e >w ，要证12ln ln 2x x +>，只需证12()2k x x +>，只需121212ln ln 2x x x x x x ->-+，等价于1122122()ln x x x x x x ->+，设121x t x =>上式转化为2(1)ln 1t t t ->+（1t >），设2(1)()ln 1t g t t t -=-+，22(1)'()0(1)t g t t t -=>+， ∴()g t 在(1,)+∞上单调递增， ∴()(1)0g t g >=，∴2(1)ln 1t t t ->+， ∴12ln ln 2x x +>．。

天津市和平区2019届高三下学期二模考试数学(理)试题Word版含答案

1
b f ( log 5 2), c f (e 2 ), 则 a, b, c 的大小关系是
(A) b c a
(7) 已知双曲线 C : x2 a2
(B) a b c
(C) c b a (D) a c b
y2 b2
1 (a
0,b
0) 的右焦点为 F (c,0) ，直线 x
a2 与一条渐近
c
线交于点 P ， POF 的面积为 a 2 (O 为原点），则抛物线 y 2 2b x 的准线方程为
x 1 x 1 (D) x x 1
(2) 已知 x, y 满足约束条件
x 2y 4
2x y 4 则 z 2x y 的最小值为 x1
y0
开始
i 2,S 0
(A) 2 (B) 4 (C)
1 (D)
2
2
5
(3) 执行如图所示的程序框图 , 若输入的 n 6 ，
则输出 S
(A) 5 (B)
1 (C)
27 (D)
2. 本卷共 12 小题，共 110 分。
二、填空题：本大题共 6 小题 , 每小题 5 分 , 共 30 分. 把答案填在答题卷上 .
(9) 如果 2 1 mi （ m R, i 表示虚数单位），那么 m
.
1i
(10) 若直线 y
x 2 与曲线 x 1 2cos (
y 2 2sin
为参数 ) 交于两点 A, B ，则
( Ⅱ) 在 ABC 中， a, b, c分别是角 A, B,C 的对边， A 为锐角，若 f (A) sin( 2A ) 1 ，
6
且 ABC 的面积为 2 3 ，求 b c 的最小值 .

【区级联考】天津市和平区2019届高三第二学期第二次质量调查数学(理)试题(原卷版)

三、解答题：本大题共 6 小题 , 共 80 分 . 解答应写出文字说明 , 证明过程或演算步骤 .
15. 已知函数 ( Ⅰ)求在上的单调递增区间；
(Ⅱ)在
中，
分别是角
的对边，为锐角，若
，且
的面积为，
求
的最小值 .
16. 某中学图书馆举行高中志愿者检索图书的比赛，从高一、高二两个年级各抽取
10 名志愿者参赛。在规定
1.设全集
，集合
,
,则
A.
B.
C.
D.
2.已知满足约束条件
则
的最小值为
A. 2
B. 4
C.
D.
3.执行如图所示的程序框图 , 若输入的
，则输出
A.
B.
C.
D.
4.下列结论错误的是
A. 命题：“若
，则
”的逆否命题是“若
，则
”
B. “
”是“
”的充分不必要条件
C. 命题：“
，
”的否定是“
，
”
D. 若“
12. 一个四棱柱的各个顶点都在一个直径为形，侧棱与底面垂直，则该四棱柱的表面积为
的球面上，如果该四棱柱的底面是对角线长为 ___________ .
的正方
13. 若不等式
对任意实数都成立 , 则实数的最大值为 ________.
的 14.已知函数
且函数
在
内有且仅有两个不同
的零点，则实数的取值范围是 ___________.
天津市和平区 2018-2019 学年度第二学期高三年级第二次质量调查数
学（理）学科试卷
第Ⅰ卷选择题（共 40 分）
注意事项 :

天津市和平区2019届高三下学期二模考试数学(理)试卷含答案

注意事项 :
1. 用钢笔或圆珠笔直接答在答题卷上，答在本试卷上的无效。 2. 本卷共 12 小题，共 110 分。二、填空题：本大题共 6 小题 , 每小题 5 分 , 共 30 分 . 把答案填在答题卷上 .2 Nhomakorabea(9) 如果
1 mi （ m R,i 表示虚数单位），那么 m
.
1i
x 1 2 cos
(12) 一个四棱柱的各个顶点都在一个直径为
2 cm 的球面上，如果该四棱柱的底面是对角线长为
2 cm 的正方形，侧棱与底面垂直，则该四棱柱的表面积为
.
(13) 若不等式 x 2
x
2
1 3a
2 对任意实数
x 都成立 , 则实数 a 的最大值为
.
(14) 已知函数 f ( x)
1 3，x ( 1，0]，
求 X 的分布列和数学期望 .
E
(17) ( 本小题满分 13 分 )
F
M
如图 , 正方形 ADEF 与梯形 ABCD 所在的平面互相垂直，
1
AD CD, AB // CD ， AB AD CD 1, 点 M 在线段 EC 上 .
2
D C
(Ⅰ ) 若点 M 为 EC 的中点，求证： BM // 平面 ADEF ；
…………… (5 分 )
P( X
0)
C16 C82
12
C10 C10
168 450
84 ，
225
12
111
P( X
1)
C4C8 C6 C2C8
C
1 10
C120
208 450
104 ， 225
P( X
2)
C

天津市河北区2019届高三数学总复习质量检测试题(二)理(含解析)

4.已知，则的大小关系为（）
A. B. C. D。
【答案】A
【解析】
【分析】
容易得出，再根据对数函数的性质将b化为与c同底的对数,即可比较出大小。
【详解】解：，，，所以 .
故选A。
【点睛】本题考查指数与对数大小的比较，考查对数换底公式以及对数函数的单调性,属于基础题。
5。已知双曲线的左、右焦点分别为，以线段为直径的圆与双曲线渐近线的一个交点为，则双曲线的方程为
【答案】808
【解析】
【分析】
由甲社区抽取人数和总人数计算可得抽样比，从而可根据抽取的人数计算得到驾驶员总人数.
【详解】由题意可得抽样比为：
本题正确结果：
【点睛】本题考查分层抽样中抽样比、总体数量的计算,属于基础题.
10.阅读如图的程序框图，运行相应的程序，则输出的值为______．
【答案】4
【平面
平面
由此可将四面体放入边长为的正方体中,如下图所示:
正方体的外接球即为该四面体的外接球
正方体外接球半径为体对角线的一半，即
球的表面积：
本题正确选项：
【点睛】本题考查多面体的外接球表面积的求解问题，关键是能够通过线面之间的位置关系，将所求四面体放入正方体中，通过求解正方体外接球来求得结果。
12。在平面直角坐标系中,直线的参数方程为（为参数），以坐标原点为极点, 轴的非负半轴为极轴建立极坐标系，圆的极坐标方程为，若直线与圆交于，两点，则线段的长度为__________．
【答案】
【解析】
分析】
将的参数方程化为普通方程; 的极坐标方程化为直角坐标方程，确定圆心和半径；根据直线被圆截得的弦长等于求得结果。

2019年天津市高考理科数学试卷及答案解析【word版】

绝密 ★ 启用前2019年普通高等学校招生全国统一考试（天津卷）数学（理工类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

第Ⅰ卷1至2页，第Ⅱ卷3至5页。

答卷前，考生务必将自己的姓名、准考号填写在答题卡上，并在规定位置粘贴考试用条形码。

答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效。

考试结束后，将本试卷和答题卡一并交回。

祝各位考生考试顺利！第Ⅰ卷注意事项：1.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

2本卷共8小题，每小题5分，共40分。

参考公式：•如果事件A ，B 互斥，那么 •如果事件A ，B 相互独立，那么()()()P A B P A P B =+()()()P AB P A P B =.•圆柱的体积公式V Sh =. •圆锥的体积公式13V Sh =. 其中S 表示圆柱的底面面积，其中S 表示圆锥的底面面积，h 表示圆柱的高. h 表示圆锥的高.一、选择题：在每小题给出的四个选项中只有一项是符合题目要求的.（1）i 是虚数单位，复数734i i（）（A ）1i （B ）1i （C ）17312525i （D ）172577i （2）设变量x ，y 满足约束条件0,20,12,y x y y x +-⎧≥--≤≥⎪⎨⎪⎩则目标函数2z x y =+的最小值为（）（A ）2 （B ）3 （C ）4 （D ）5（3）阅读右边的程序框图，运行相应的程序，输出的S 的值为（）（A ）15 （B ）105 （C ）245 （D ）945FED CBA （4）函数212log 4f x x 的单调递增区间是（）（A ）0, （B ）,0（C ）2,（D ）,2（5）已知双曲线22221x y a b 0,0ab 的一条渐近线平行于直线l ：210y x ，双曲线的一个焦点在直线l 上，则双曲线的方程为（）（A ）221520x y （B ）221205x y （C ）2233125100x y （D ）2233110025x yD ，交（6）如图，ABC 是圆的内接三角形，BAC 的平分线交圆于点BC 于点E ，过点B 的圆的切线与AD 的延长线交于点F .在上述条件下，给出下列四个结论：①BD 平分CBF ；②2FB FD FA ；③AE CEBE DE ；④AF BD AB BF .则所有正确结论的序号是（）（A ）①② （B ）③④ （C ）①②③ （D ）①②④ （7）设,a bR ，则|“a b ”是“a a b b ”的（）（A ）充要不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充要也不必要条件（8）已知菱形ABCD 的边长为2，120BAD，点,E F 分别在边,BC DC 上，BE BC ，DFDC .若1AE AF ，23CE CF，则（）（A ）12 （B ）23 （C ）56 （D ）712第Ⅱ卷注意事项： 1．用黑色墨水钢笔或签字笔将答案写在答题卡上。

天津市河西区2019届高三下学期总复习质量调查(二)数学(理)试题(二模)Word版含答案

（Ⅱ）若 B 是钝角，且 cos A
3 ， sin B
12 ，求 sin C 的值 .
5
13
B ) 和 a ， b 的值；
（ 16）（本小题满分 13 分）
0
1
2
3
甲，乙，丙三
位学生独立地解同
一道题，甲做对的
P
1 4
a
1
b
24
1
概率为，乙，丙
2
做对的概率分别为 m ， n ( m ＞ n ) ，且三位学生是否做对相互独立 . 记为这三位学生中做
河西区 2018—2019学年度第二学期高三年级总复习质量调查（二）
数学试卷（理工类）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共
150 分，考试用时 120 分
钟。第Ⅰ卷 1 至 3 页，第Ⅱ卷 4 至 7 页。
答卷前，考生务必将自己的姓名、准考号填写在答题卡上，并在规定位置粘贴考试用条
2 sin t
原点为极点 , x 轴的正半轴为极轴建立极坐标系 , 则 l 的极坐标方程为 _____________.
(13 ）若 log 4 3a 4b log 2 ab ，则 a b 的最小值为 _____________.
（ 14）已知函数 f x 满足， f x
kx k , x 0 ，其中 k 0 ，若函数 y f f x 1 有 4
（ D）既不充分也不必要条件
（ 5）设 a （ A） b
0.5
3 ,b
4 ac
0.4
4 ，c
3
log3 log3 4 ，则
4
（ B） c a b
（ C） c b a
（ D） a c b

天津市和平区2019届高三下学期第二次质量调查数学(理)试卷 Word版含解析

天津市和平区2018-2019学年度第二学期高三年级第二次质量调查数学（理）学科试卷第Ⅰ卷选择题（共40分）注意事项:1. 答第Ⅰ卷前，考生务必将自己的姓名、准考号、科目涂写在答题卡上。

2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

答在试卷上的无效。

3. 本卷共8小题，每小题5分，共40分。

参考公式：如果事件互斥,那么如果事件相互独立,那么.柱体的体积公式. 锥体的体积公式.其中表示柱体的底面积, 其中表示锥体的底面积,表示柱体的高. 表示锥体的高.一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.1.设全集，集合,,则A. B. C. D.【答案】B【解析】【分析】由集合或，先求解，再由集合能够求出答案.【详解】因为全集,集合或，所以，所以，故选B.【点睛】本题主要考查了集合的混合运算，属于基础题，其中解答中准确计算集合和集合的交集、补集的运算是解答的关键，着重考查了推理与运算能力.2.已知满足约束条件则的最小值为A. 2B. 4C.D.【答案】C【解析】【分析】首先绘制出可行域，注意到目标函数取最小值时直线系方程在y轴的截距有最大值，据此结合直线方程确定目标函数取得最小值时点的坐标，然后代入目标函数确定其最小值即可. 【详解】绘制不等式组表示的平面区域如图所示，目标函数即：，其中z取得最小值时，其几何意义表示直线系在y轴上的截距最大，据此结合目标函数的几何意义可知目标函数在点A处取得最大值，联立直线方程：，可得点A的坐标为：，据此可知目标函数的最小值为：.故选：C.【点睛】求线性目标函数z＝ax＋by(ab≠0)的最值，当b＞0时，直线过可行域且在y轴上截距最大时，z值最大，在y轴截距最小时，z值最小；当b＜0时，直线过可行域且在y轴上截距最大时，z值最小，在y轴上截距最小时，z值最大.3.执行如图所示的程序框图,若输入的，则输出A. B. C. D.【答案】B【解析】【分析】首先确定流程图所实现的功能，然后利用裂项求和的方法即可确定输出的数值.【详解】由流程图可知，程序输出的值为：，即.故选：B.【点睛】本题主要考查流程图功能的识别，裂项求和的方法等知识，意在考查学生的转化能力和计算求解能力.4.下列结论错误的是A. 命题：“若，则”的逆否命题是“若，则”B. “”是“”的充分不必要条件C. 命题：“，”的否定是“，”D. 若“”为假命题，则均为假命题【答案】B【解析】【分析】由逆否命题的定义考查选项A，由不等式的性质考查选项B，由全称命题的否定考查选项C，由真值表考查选项D，据此确定所给的说法是否正确即可.【详解】逐一考查所给命题的真假：A. 同时否定条件和结论，然后以原来的条件为结论，以原来的结论为条件即可得到原命题的逆否命题，故命题：“若，则”的逆否命题是“若，则”B. 若“”，当时不满足“”，即充分性不成立，反之，若“”，则一定有“”，即必要性成立，综上可得，“”是“”的必要不充分条件C. 特称命题的否定是全称命题，命题：“，”的否定是“，”，D. 由真值表可知：若“”为假命题，则均为假命题.即结论错误的为B选项.故选：B.【点睛】当命题真假容易判断时，直接判断命题的真假即可.否则，可利用以下结论进行判断：①一个命题的否定与原命题肯定一真一假;②原命题与其逆否命题同真假.5.的图象向右平移个单位，所得到的图象关于轴对称，则的值为A. B. C. D.【答案】A【解析】【分析】由题意首先确定函数平移之后的函数解析式，所得到的图象关于轴对称，则时函数取得最大值或最小值，据此确定的值即可.【详解】的图象向右平移个单位后的解析式为：，图象关于轴对称，则当时函数取得最大值或最小值，即：，故，令可得：.【点睛】本题主要考查三角函数的平移变换，三角函数的对称性等知识，意在考查学生的转化能力和计算求解能力.6.已知是定义在R上的偶函数，且在上是增函数，设则的大小关系是A. B. C. D.【答案】D【解析】【分析】首先比较自变量的大小，然后结合函数的奇偶性确定函数在区间上的单调性，最后利用单调性比较函数值的大小即可.【详解】注意到，，且，据此可得：，函数为偶函数，则：，由偶函数的性质可知：函数在区间上单调递减，故，即.故选：D.【点睛】本题主要考查函数的单调性，函数的奇偶性，实数比较大小的方法等知识，意在考查学生的转化能力和计算求解能力.7.已知双曲线的右焦点为，直线与一条渐近线交于点，的面积为为原点），则抛物线的准线方程为A. B. C. D.【解析】【分析】首先联立双曲线的渐近线方程和直线确定点P的坐标，然后求解的面积得到a,b 的关系，最后由抛物线方程确定其准线方程即可.【详解】不妨取双曲线的渐近线方程为，与直线联立可得：，即,由题意可得，，抛物线方程为，其准线方程为.故选：C.【点睛】本题主要考查双曲线的渐近线方程，抛物线准线方程的求解等知识，意在考查学生的转化能力和计算求解能力.8.在中，，，点是所在平面内的一点，则当取得最小值时，A. B. C. D.【答案】B【解析】【分析】由题意结合平面向量的定义可得，建立平面直角坐标系，结合平面向量的坐标运算法则确定当取得最小值时点P的坐标，然后求解的值即可.【详解】，，，，以A为坐标原点建如图所示的平面直角坐标系，则，设，则，所以当x=2，y=1时取最小值，此时.故选：B.【点睛】本题主要考查平面向量的数量积运算法则，平面向量的坐标运算，二次函数最值的求解等知识，意在考查学生的转化能力和计算求解能力.第Ⅱ卷非选择题（共110分）注意事项:1. 用钢笔或圆珠笔直接答在答题卷上，答在本试卷上的无效。

【k12高考数学模拟】2019届天津市部分区高三质量调查试题(二)数学(理)试题(解析版)

2019届天津市部分区高三质量调查试题（二）数学（理）试题一、单选题1．已知全集，集合，，则=（）A．{0，4} B．{0，1，4} C．{1，4} D．{0，1}【答案】B【解析】先求全集，再求交集，最后根据补集得结果.【详解】因为，,所以= {0，1，4}，选B.【点睛】本题考查交集与补集概念，考查基本求解能力，属基础题.2．设变量x，y满足约束条件，则目标函数最小的值为（）A．4 B．3 C．2 D．1【答案】D【解析】先作可行域，再根据目标函数表示的直线，结合图象确定最优解，即得结果.【详解】作可行域，则直线过点A(1,0)时取最小值1，选D.【点睛】本题考查线性规划求最值，考查基本分析求解能力，属基础题.3．阅读下面的程序框图，运行相应的程序，则输出的值为（）A．3 B．1 C．0 D．-1【答案】C【解析】解：当i=1时，；当i=2时，；当i=3时，，当i=4时，，故选C。

4．若，，，则a，b，c的大小关系为（）A．B．C．D．【答案】A【解析】根据对数函数与指数函数单调性确定大小.【详解】因为，，所以，选A.【点睛】本题考查利用对数函数与指数函数单调性比较大小，考查基本分析求解能力，属基础题.5．已知双曲线的左、右焦点分别为，以线段为直径的圆与双曲线渐近线的一个交点的坐标为(4，3)，则此双曲线的方程为（）A．B．C．D．【答案】A【解析】根据坐标原点到交点距离等于半径得c，再根据交点在渐近线可得关系，解得即可. 【详解】因为以线段为直径的圆与双曲线渐近线的一个交点的坐标为(4，3)，所以坐标原点到交点(4，3)距离等于半径c，即因为(4，3)在双曲线渐近线上，所以，因为,所以，即双曲线的方程为，选A.【点睛】本题考查双曲线渐近线与标准方程，考查基本分析求解能力，属基础题.6．在ABC中，内角A，B，C所对的边分别为a，b，c.则“”是“”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【答案】C【解析】由正弦定理得，所以“”是“”的充要条件，选C. 7．如图，AB，CD是半径为1的圆O的两条直径，，则的值是（）A．B．C．D．【答案】B【解析】根据向量表示化简数量积，即得结果.【详解】,选B.【点睛】本题考查向量数量积，考查基本分析求解能力，属基础题.8．已知函数，若关于x的方程恰有三个不同的实数根a，b，c，则的取值范围是（）A．B．C．D．【答案】D【解析】先作图，再确定关系以及范围，即得结果.【详解】作图可得，，所以，选D.【点睛】本题考查函数与方程，考查基本分析求解能力，属中档题.二、填空题9．已知i是虚数单位，则________________.【答案】【解析】根据复数除法运算法则求解.【详解】.【点睛】本题考查复数除法运算法则，考查基本分析求解能力，属基础题.10．某工厂生产A，B，C三种不同型号的产品，产量分别为400，800，600件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取90件进行检验，则应从C种型号的产品中抽取________件.【答案】【解析】根据分层抽样确定抽取数.【详解】由题意得从C种型号的产品中抽取件.【点睛】本题考查分层抽样，考查基本分析求解能力，属基础题.11．已知四棱锥的底面是边长为2的正方形，侧棱长均为，则四棱锥的体积为________.【答案】【解析】试题分析：正四棱锥的底面边长为2，底面面对角线的一半为，所以棱锥的高为【考点】棱锥的体积12．在平面直角坐标系xOy中，直线l的方程为，在以坐标原点O为极点，x轴的非负半轴为极轴的极坐标系中，圆C的方程为，则直线l与圆C的位置关系为___________.【答案】相交【解析】先将圆极坐标方程化为直角坐标方程，再根据圆心到直线距离与半径大小关系确定位置关系. 【详解】因为圆C的方程为，所以，因此圆心到直线距离为，所以直线与圆C相交.【点睛】本题考查极坐标方程化为直角坐标方程以及直线与圆位置关系，考查基本分析求解能力，属基础题. 13．ABC的内角A，B，C的对边分别为a，b，c，，，则ABC周长的最大值是_______.【答案】【解析】根据余弦定理以及基本不等式求最值.【详解】因为，所以，当且仅当时取等号，因此，即ABC周长的最大值是【点睛】本题考查余弦定理以及基本不等式求最值，考查基本分析求解能力，属基础题.14．四个不同的小球放入编号为1，2，3，4的四个盒子中，则恰有两个空盒的不同放法共有__________种.【答案】84【解析】分析：先选两个空盒子，再把4个小球分为，两组，分到其余两个盒子里，即可得到答案.详解：先选两个空盒子，再把4个小球分为，两组，故有.故答案为：84.点睛：本题考查的是排列、组合的实际应用，考查了计数原理，注意这种有条件的排列要分两步走，先选元素再排列.三、解答题15．已知函数，.(1)求的最小正周期和最大值；(2)讨论在区间上的单调性.【答案】(1) ，其最大值为. (2)见解析【解析】（1）先根据二倍角公式、配角公式将函数化为基本三角函数形式，再根据正弦函数性质求周期与最值，（2）根据正弦函数性质求单调性.【详解】解：（1）由题意，得.所以的最小正周期，其最大值为.（2）令则函数的单调递增区间是.由,得设，易知.所以，当时,在区间上单调递增；在区间上单调递减.【点睛】本题考查二倍角公式、配角公式以及正弦函数性质，考查基本分析求解能力，属基础题.16．某闯关游戏共有两关，游戏规则：先闯第一关，当第一关闯过后，才能进入第二关，两关都闯过，则闯关成功，且每关各有两次闯关机会.已知闯关者甲第一关每次闯过的概率均为，第二关每次闯过的概率均为.假设他不放弃每次闯关机会，且每次闯关互不影响.(1)求甲恰好闯关3次才闯关成功的概率；(2)记甲闯关的次数为，求随机变量的分布列和期望.。

2019年天津市高考理科数学试卷及答案解析【word版】

高考数学精品复习资料2019.5绝密 ★ 启用前普通高等学校招生全国统一考试（天津卷）数学（理工类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

第Ⅰ卷1至2页，第Ⅱ卷3至5页。

答卷前，考生务必将自己的姓名、准考号填写在答题卡上，并在规定位置粘贴考试用条形码。

答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效。

考试结束后，将本试卷和答题卡一并交回。

祝各位考生考试顺利！第Ⅰ卷注意事项：1.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

2本卷共8小题，每小题5分，共40分。

参考公式：•如果事件A ，B 互斥，那么 •如果事件A ，B 相互独立，那么()()()P A B P A P B =+()()()P AB P A P B =.•圆柱的体积公式V Sh =. •圆锥的体积公式13V Sh =. 其中S 表示圆柱的底面面积，其中S 表示圆锥的底面面积，h 表示圆柱的高. h 表示圆锥的高.一、选择题：在每小题给出的四个选项中只有一项是符合题目要求的.E D CBA （1）i 是虚数单位，复数734ii+=+（）（A ）1i - （B ）1i -+ （C ）17312525i + （D ）172577i -+ （2）设变量x ，y 满足约束条件0,20,12,y x y y x +-⎧≥--≤≥⎪⎨⎪⎩则目标函数2z x y =+的最小值为（）（A ）2 （B ）3 （C ）4 （D ）5（3）阅读右边的程序框图，运行相应的程序，输出的S 的值为（）（A ）15 （B ）105 （C ）245 （D ）945（4）函数()()212log 4f x x =-的单调递增区间是（）（A ）()0,+¥ （B ）(),0-¥ （C ）()2,+¥（D ）(),2-?（5）已知双曲线22221x y a b-=()0,0a b >>的一条渐近线平行于直线l ：210y x =+，双曲线的一个焦点在直线l 上，则双曲线的方程为（）（A ）221520x y -= （B ）221205x y -= （C ）2233125100x y -= （D ）2233110025x y -= （6）如图，ABC D 是圆的内接三角形，BAC Ð的平分线交圆于点D ，交BC 于点E ，过点B 的圆的切线与AD 的延长线交于点F .在上述条件下，给出下列四个结论：①BD 平分CBF Ð；②2FB FD FA =?；③AE CE BE DE ??；④AF BDAB BF ??.则所有正确结论的序号是（）（A ）①② （B ）③④ （C ）①②③ （D ）①②④ （7）设,a b R Î，则|“a b >”是“a a b b >”的（）（A ）充要不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充要也不必要条件（8）已知菱形ABCD 的边长为2，120BAD?，点,E F 分别在边,BC DC 上，BE BC l =，DF DC m =.若1AE AF?，23CE CF?-，则l m +=（）（A ）12 （B ）23 （C ）56 （D ）712第Ⅱ卷注意事项： 1．用黑色墨水钢笔或签字笔将答案写在答题卡上。

天津市和平区2019届高三下学期二模考试数学(理)试卷(含答案)

天津市和平区2019届高三下学期二模考试理科数学试题温馨提示：本试卷包括第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。

考试时间120分钟。

祝同学们考试顺利！第Ⅰ卷选择题（共40分）注意事项:1. 答第Ⅰ卷前，考生务必将自己的姓名、准考号、科目涂写在答题卡上。

2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

答在试卷上的无效。

3. 本卷共8小题，每小题5分，共40分。

参考公式：如果事件B A ，互斥,那么如果事件B A ，相互独立,那么)()()(B P A P B A P += )()()(B P A P AB P =. 柱体的体积公式Sh V =. 锥体的体积公式Sh V 31=.其中S 表示柱体的底面积, 其中S 表示锥体的底面积, h 表示柱体的高. h 表示锥体的高.一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. (1) 设全集R U =，集合})1lg({2-==x y x M ,{02}N x x =<<,则=N M C R )((A) {}12≤≤-x x (B) {}10≤<x x (C) {}11≤≤-x x (D) {}1<x x(2) 已知y x ,满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+014242y x y x y x 则y x z -=2的最小值为(A) 2 (B) 4 (C)21(D) 52 (3) 执行如图所示的程序框图,若输入的6=n ，则输出=S (A) 145 (B) 31 (C) 5627 (D) 103(4) 下列结论错误的是(A) 命题：“若0232=+-x x ，则2=x ”的逆否命题是“若2≠x ，则0232≠+-x x ” (B) “b a >”是“22bc ac >”的充分不必要条件(C) 命题：“R x ∈∃， 02>-x x ”的否定是“R x ∈∀， 02≤-x x ” (D) 若“q p ∨”为假命题，则q p ,均为假命题(5) )2()2sin()(πϕϕ<+=x x f 的图象向右平移12π个单位，所得到的图象关于y 轴对称，则ϕ的值为 (A) 3π-(B) 4π- (C) 3π (D) 6π- (6) 已知)(x f 是定义在R 上的偶函数，且在]0,(-∞上是增函数，设),(ln πf a =),2log (5-=f b ),(21-=ef c 则c b a ,,的大小关系是(A)a c b << (B)c b a << (C)a b c << (D)b c a <<(7) 已知双曲线1:2222=-by a x C )0,0(>>b a 的右焦点为)0,(c F ，直线c a x 2=与一条渐近线交于点P ，POF ∆的面积为2a O (为原点），则抛物线x aby 22=的准线方程为 (A) 21=y (B) 1=x (C) 1-=x (D) 2=x (8) 在ABC ∆中，62==AC AB ，2=⋅，点P 是ABC ∆所在平面内的一点，则当222++取得最小值时，=⋅(A)53 (B) 9- (C) 7 (D) 52- 第Ⅱ卷非选择题（共110分）注意事项:1. 用钢笔或圆珠笔直接答在答题卷上，答在本试卷上的无效。

【精品高考数学试卷】2019年天津市高考数学二模试卷(理科)+答案

2019年天津市高考数学二模试卷（理科）一、选择题：本大题共8小题，每小题5分，满分40分．1．（5分）已知集合A ＝{﹣1，1}，B ={x||x +12|＜32，x ∈Z}，则A ∪B ＝（） A ．{﹣1}B ．{﹣1，1}C ．{﹣1，0，1}D ．{﹣1，0，1，2}2．（5分）设变量x ，y 满足约束条件{x +2≥0x −y +3≥02x +y −3≤0，则目标函数z ＝3x +2y 的最大值为（）A ．﹣4B ．92C ．6D ．83．（5分）执行如图所示的程序框图，若输入k 的值为9，则输出的结果S 为（）A ．109B ．48C ．19D ．64．（5分）设x ∈R ，则“x 3＜27”是“log 13x ＞−1”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件5．（5分）已知△ABC 为直角三角形，AC ＝BC ＝2，点D 为斜边AB 的中点，点P 是线段CD 上的动点，则PA →⋅PB →的最小值为（） A ．﹣2B ．−14C ．−12D ．06．（5分）已知函数f （x ）＝e |x |，令a =f(sin 3π4)，b =f(2−3)，c =f(log 123)，则a ，b ，c的大小关系为（）A ．b ＜a ＜cB ．c ＜b ＜aC ．b ＜c ＜aD ．a ＜b ＜c7．（5分）已知抛物线C 1：y 2＝2px （p ＞0）的焦点F 为双曲线C 2：x 2−y 23=1的顶点，过点F 的直线与抛物线C 1相交于M 、N 两点，点A 在x 轴上，且满足|MN |＝8，若|AM |＝|AN |，则△AMN 的面积为（） A ．3√6B ．6√3C ．6√2D ．8√28．（5分）已知函数f(x)=2sin(ωx +φ)(ω＞0，|φ|＜π2)的图象过点B(0，√3)，且在(π12，5π12)上单调，把f （x ）的图象向右平移π个单位之后与原来的图象重合，当x 1，x 2∈(2π3，4π3)且x 1≠x 2时，f （x 1）＝f （x 2），则f （x 1+x 2）＝（） A ．−√3 B ．√3 C ．﹣1 D ．1二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡中的相应横线上. 9．（5分）i 是虚数单位，复数−3+2i 1+i= ．10．（5分）在(√x 3−1x)n 的二项式展开式中，所有项的二项式系数之和为256，则展开式中常数项等于．11．（5分）已知圆锥的高为3，底面半径长为4，若某球的表面积与此圆锥侧面积相等，则该球的体积为．12．（5分）在直角坐标系xOy 中，曲线C 1的参数方程为{x =−1+√2cosαy =√2sinα（α为参数），以坐标原点为极点，以x 轴的正半轴为极轴，建立极坐标系，曲线C 2的极坐标方程为ρsin （θ+π4）＝2√2．设点P 在C 1上，点Q 在C 2上，则|PQ |的最小值为．13．（5分）若log 4(a +4b)=log 22√ab ，则a +b 的最小值是．14．（5分）已知函数f(x)={xlnx −2x ，x ＞0x 2+32x ，x ≤0，函数g （x ）＝f （x ）﹣kx +1有四个零点，则实数k 的取值范围是．三、解答题：本大题6小题，共80分．解答应写出必要的文字说明，证明过程或演算步骤． 15．（13分）在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且atanA=b 2sinB．（Ⅰ）求角A 的值；（Ⅱ）若a ＝6，b ＝2c ，求△ABC 的面积．16．（13分）为响应党中央号召，学校以“我们都是追梦人”为主题举行知识竞赛．现有10道题，其中6道甲类题，4道乙类题，王同学从中任取3道题解答．（Ⅰ）求王同学至少取到2道乙类题的概率；（Ⅱ）如果王同学答对每道甲类题的概率都是23，答对每道乙类题的概率都是35，且各题答对与否相互独立，已知王同学恰好选中2道甲类题，1道乙类题，用X 表示王同学答对题的个数，求随机变量X 的分布列和数学期望．17．（13分）如图，在多面体ABCDEF 中，四边形ABCD 为平行四边形，平面ADE ⊥平面CDEF ，∠ADE ＝60°，DE ∥CF ，CD ⊥DE ，AD ＝2，DE ＝DC ＝3，CF ＝4，点G 是棱CF 上的动点．（Ⅰ）当CG ＝3时，求证EG ∥平面ABF ；（Ⅱ）求直线BE 与平面ABCD 所成角的正弦值；（Ⅲ）若二面角G ﹣AE ﹣D 所成角的余弦值为√2211，求线段CG 的长．18．（13分）设S n 是等差数列{a n }的前n 项和，满足a 2＝5，S 5＝35，T n 是数列{b n }的前n 项和，满足T n ＝2b n ﹣1（n ∈N *）．（Ⅰ）求数列{a n }，{b n }的通项公式；（Ⅱ）令c n ={2S n ，n =2k −1a nb n ，n =2k(k ∈N ∗)，设数列{c n }的前n 项和P n ，求P 2n 的表达式．19．（14分）已知椭圆C 的方程为x 2a 2+y 2b 2=1(a ＞b ＞0)，离心率为√22，它的一个顶点恰好是抛物线x 2=−4√3y 的焦点．（Ⅰ）求椭圆C 的方程；（Ⅱ）过动点M （0，m ）（0＜m ＜b ）的直线交x 轴的负半轴于点N ，交C 于点A ，B （A 在第一象限），且M 是线段AN 的中点，过点A 作x 轴的垂线交C 于另一点D ，延长线DM 交C 于点G ．（i ）设直线AM ，DM 的斜率分别为k ，k ′，证明：3k +k ′＝0；（ii）求直线BG的斜率的最小值．20．（14分）已知函数f（x）＝（ax2+x+a）e﹣x（a∈R）．（Ⅰ）当a＝0时，求f（x）在点（0，f（0））处的切线方程；（Ⅱ）若a≥0，求函数f（x）的单调区间；（Ⅲ）若对任意的a≤0，f（x）≤bln（x+1）在x∈[0，+∞）上恒成立，求实数b的取值范围．2019年天津市高考数学二模试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，满分40分． 1．【解答】解：集合A ＝{﹣1，1}，B ={x||x +12|＜32，x ∈Z}={x |﹣2＜x ＜1，x ∈Z }＝{﹣1，0}， ∴A ∪B ＝{﹣1，0，1}．故选：C ．2．【解答】解：由变量x ，y 满足约束条件{x +2≥0x −y +3≥02x +y −3≤0，作可行域如图．由z ＝3x +2y ，结合图形可知，当直线分别经过可行域内的点A ，B 时，目标函数取得最值，由：{x −y +3=02x +y −3=0，可得A （0，3），分别为z max ＝3×0+2×3＝6，目标函数的最大值为6．故选：C ．3．【解答】解：模拟程序的运行，可得 k ＝9，n ＝1，S ＝1不满足判断框内的条件n ＞k ，执行循环体，n ＝4，S ＝6 不满足判断框内的条件n ＞k ，执行循环体，n ＝7，S ＝19 不满足判断框内的条件n ＞k ，执行循环体，n ＝10，S ＝48 此时，满足判断框内的条件n ＞k ，退出循环，输出S 的值为48．故选：B ．4．【解答】解：由x 3＜27得x ＜3，由log 13x ＞−1得0＜x ＜3，则“x 3＜27”是“log 13x ＞−1”的必要不充分条件，故选：B ．5．【解答】解：根据题意，以C 为坐标原点，CB 为x 轴，CA 为y 轴建立坐标系，如图：则B （2，0），A （0，2），D 为AB 的中点，则D （1，1），点P 是线段CD 上的动点，设P （m ，m ），（0≤m ≤1）；则PA →=（﹣m ，2﹣m ），PB →=（2﹣m ，﹣m ），则PA →⋅PB →=（﹣m ）（2﹣m ）+（2﹣m ）（﹣m ）＝2m 2﹣4m ＝2（m ﹣1）2﹣2，又由0≤m ≤1，则当m ＝1时，PA →⋅PB →取得最小值﹣2；故选：A ．6．【解答】解：根据题意，函数f （x ）＝e |x |，有f （﹣x ）＝e |﹣x |＝e |x |＝f （x ），即函数f （x ）为偶函数，则有c ＝f （log 123）＝f （﹣log 23）＝f （log 23），又由当x ＞0时，f （x ）＝e x ，易得f （x ）为[0，+∞）上为增函数，又由log 23＞1＞sin 3π4=√22＞12＞2﹣3，则有f （log 23）＞f （sin 3π4）＞f （2﹣3），则有b ＜a ＜c ；故选：A ．7．【解答】解：由题意可知，抛物线C 1：y 2＝2px （p ＞0）的焦点F （1，0），则p2=1，p ＝2．∴抛物线方程为y 2＝4x ．如图，设MN 所在直线方程为y ＝k （x ﹣1），联立{y =k(x −1)y 2=4x ，得k 2x 2﹣（2k 2+4）x +k 2＝0．设M （x 1，y 1），N （x 2，y 2）．则x 1+x 2=2k 2+4k2，由|MN |＝x 1+x 2+2＝8，得2k 2+4k 2=6，解得k ＝±1．∴x 1+x 2＝6，则MN 的中点坐标为（3，2），不妨取k ＝1，可得MN 的垂直平分线方程为y ﹣2＝﹣1×（x ﹣3），即y ＝﹣x +5．取y ＝0，得A （5，0）．此时A 到直线x ﹣y ﹣1＝0的距离d =2=2√2． ∴△AMN 的面积S =12×8×2√2=8√2．故选：D ．8．【解答】解：∵函数f(x)=2sin(ωx +φ)(ω＞0，|φ|＜π2)的图象过点B(0，√3)，∴2sin φ=√3，∴φ=π3．f （x ）在(π12，5π12)上单调，∴12•2πω≥5π12−π12，∴0＜ω≤3．把f （x ）的图象向右平移π个单位之后与原来的图象重合，∴k •2πω=π，k ∈Z ，∴ω＝2，f （x ）＝2sin （2x +π3）．当x 1，x 2∈(2π3，4π3)且x 1≠x 2时，2x +π3∈（5π3，3π），若 f （x 1）＝f （x 2），则x 1+x 2＝2•5π2=5π，f （x 1+x 2）＝2sin （10π+π3）＝2sin π3=√3，故选：B ．二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡中的相应横线上. 9．【解答】解：−3+2i 1+i =(−3+2i)(1−i)(1+i)(1−i)=−1+5i 2=−12+52i ．故答案为：−12+52i ．10．【解答】解：由在(√x 3−1x)n 的二项式展开式中，所有项的二项式系数之和为256，可得：2n ＝256，解得：n ＝8，又（√x 3−1x ）8的二项式展开式的通项为T r +1=C 8r （√x 3）8﹣r （−1x ）r ＝（﹣1）r C 8r x8−4r 3，令8−4r 3=0，则r ＝2，即展开式中常数项等于（﹣1）2C 82=28，故答案为：28．11．【解答】解：∵圆锥的底面半径r ＝4，高h ＝3， ∴圆锥的母线l ＝5， ∴圆锥侧面积S ＝πrl ＝20π，设球的半径为r ，则4πr 2＝20π， ∴r =√5，∴该球的体积为V =43•π•（√5）3=20√5π3．故答案为：20√5π3．12．【解答】解：由C 1的参数方程消去参数α得曲线C 1的普通方程为：（x +1）2+y 2＝2，由曲线C 2的极坐标方程以及互化公式可得C 2的普通方程为：x +y ﹣4＝0，依题意可得|PQ |的最小值等于圆心到直线的距离减去半径， ∴|PQ |min =2−√2=32√2．故答案为：32√2．13．【解答】解：∵log 4(a +4b)=log 22√ab =log 4（4ab ），∴a +4b ＝4ab ，{a +4b ＞04ab ＞0得{a ＞0b ＞0，得a+4b 4ab =1，即14b+1a=1，则a +b ＝（a +b ）（14b+1a）＝1+14+a 4b +b a ≥54+2√a 4b ⋅b a =54+1=94，当且仅当a4b=ba，即a ＝2b 时取等号，即a +b 的最小值为94，故答案为：9414．【解答】解：由g （x ）＝f （x ）﹣kx +1＝0得kx ＝f （x ）+1，当x ＝0时，0＝f （0）+1＝0+1不成立，即x ≠0，则k =f(x)+1x，若g （x ）有四个零点，则等价为k =f(x)+1x有四个不同的根，设h （x ）=f(x)+1x，则当x ＞0时，h （x ）=xlnx−2x+1x =lnx +1x−2， h ′（x ）=1x −1x 2=x−1x 2，则当x ＞1时，h ′（x ）＞0，函数为增函数，当0＜x ＜1时，h ′（x ）＜0，函数为减函数，即此时当x ＝1时，h （x ）取得极小值，极小值为h （1）＝﹣1，当x →+∞，f （x ）→+∞，当x ≤0时，h （x ）=x 2+32x+1x =x +1x +32，h ′（x ）＝1−1x 2=x 2−1x2，由h ′（x ）＞0得x ＞1（舍）或x ＜﹣1，此时函数为增函数，由h ′（x ）＜0得﹣1＜x ＜0，此时h （x ）为减函数，即当x ＝﹣1时，h （x ）取得极大值，极大值为h （﹣1）＝﹣1﹣1+32=−12，作出函数h （x ）的图象如图：要使k =f(x)+1x有四个根，则满足﹣1＜k ＜−12，即实数k 的取值范围是（﹣1，−12），故答案为：（﹣1，−12）三、解答题：本大题6小题，共80分．解答应写出必要的文字说明，证明过程或演算步骤． 15．【解答】（本小题满分13分）解：（Ⅰ）由已知得acosA sinA=b 2sinB，…………（2分）∵a sinA=b sinB ，∴cosA =12，…………（4分） ∵A ∈（0，π），∴A =π3．…………（6分）（Ⅱ）∵a ＝6b ＝2c ，∴a 2＝b 2+c 2﹣2bc cos A ，…………（8分）整理可得36＝4c 2+c 2﹣2c 2， ∴解得c =2√3，…………（10分）∴S △ABC =12bcsinA =12×4√3×2√3×√32=6√3．…………（13分） 16．【解答】（本小题满分13分）解：（Ⅰ）设“王同学至少取到2道乙类题”为事件A ……（1分） P(A)=C 61C 42+C 43C 103=13⋯⋯（5分）（列式（2分），结果2分）（Ⅱ）X 的所有可能取值为0，1，2，3 ……（6分）P(X =0)=C 20⋅(23)0⋅(13)2⋅(1−35)=245， P(X =1)=C 21⋅(23)⋅(13)⋅(1−35)+C 20⋅(23)0⋅(13)2⋅35=1145， P(X =2)=C 22⋅(23)2⋅(13)0⋅25+C 21⋅23⋅13⋅35=2045=49 P(X =3)=C 22⋅(23)2⋅(13)0⋅35=1245=415⋯⋯（10分）（每个结果一分） X 0123P245114549415E(X)=0×245+1×1145+2×49+3×415=2915⋯⋯（13分）（列式（1分），结果2分） 17．【解答】（Ⅰ）证明：由已知得CG ∥DE 且CG ＝DE ，故四边形CDEG 为平行四边形，∴CD ∥EG ， ∵四边形ABCD 为平行四边形，∴CD ∥AB ， ∴AB ∥EG ，又EG ⊄平面ABF ，AB ⊂平面ABF ， ∴EG ∥平面ABF ．（Ⅱ）过点A 作AO ⊥DE 交DE 于点O ，过点O 作OK ∥CD 交CF 于点K 由（1）知平面ADE ⊥平面CDEF ，平面ADE ∩平面CDEF ＝DE ，AO ⊂平面ADE ， ∴AO ⊥平面CDEF ， ∵CD ⊥DE ，∴OK ⊥DE ，以O 为原点建立如图的空间直角坐标系，则D （0，﹣1，0），E （0，2，0），C （3，﹣1，0），F （3，3，0），A(0，0，√3)，D （0，﹣1，0），∴DC →=(3，0，0)，DA →=(0，1，√3)，BE →=(−3，2，−√3)，设平面ABCD 的法向量为m →=(x ，y ，z)，则{m →⋅DC →=0m →⋅DA →=0，即{x =0y +√3z =0，令z ＝﹣1，则y =√3，m →=(0，√3，−1)， ∴cos ＜m →，BE →＞=m →⋅BE→|m →|⋅|BE →|=3√38，∴直线BE 与平面ABCD 所成角的正弦值为3√38，（Ⅲ）CG →=λCF →=λ(0，4，0)（0≤λ≤1）∴G （3，4λ﹣1，0）． ∴AE →=(0，2，−√3)，EG →=(3，4λ−3，0)，设平面AEG 的法向量为p →=(x ，y ，z)，则{p →⋅AE →=0p →⋅EG →=0，即{2y −√3z =03x +(4λ−3)y =0，令y ＝3，则z =2√3，x ＝3﹣4λ，∴p →=(3−4λ，3，2√3)，平面AED 的法向量为q →=(1，0，0)，|cos ＜p →，q →＞|=|p →⋅q →||p →|⋅|q →|=|4λ−3|√(4λ−3)+21=√2211，解得(4λ−3)2=143，∴4λ=3±√423，∴|CG |＝λ|CF |＝4λ=3±√423， ∵|CG |≤4，∴|CG|=3−√423．18．【解答】解：（Ⅰ）∵{a n }是等差数列S 5＝35 ∴S 5=5(a 1+a 5)2=35，a 3＝7， ∵a 2＝5， ∴d ＝2，∴a n ＝a 2+（n ﹣2）•2＝2n +1．当n ＝1时 T 1＝2b 1﹣1， ∴b 1＝1．当n ≥2时 T n ﹣1＝2b n ﹣1﹣1 又∵T n ＝2b n ﹣1， ∴b n ＝2b n ﹣2b n ﹣1b n ＝2b n ﹣1∴{b n }是以1为首项，2为公比的等比数列． ∴b n =2n−1．（Ⅱ）∵S n =n(a 1+a n )2=n(n +2)， ∴2S n=2n(n+2)=1n−1n+2设前2n 项中奇数项的和为A n ，偶数项的和为B n A n =1−13+13−15+15−⋯+12n−1−12n+1=1−12n+1=2n 2n+1．B n =a 2b 2+a 4b 4+⋯+a 2n b 2n =5×21+9×22+⋯+(4n +1)×22n−1①4B n =5×22+9×23+⋯+(4n +1)×22n+1②， ①﹣②得：−3B n =5×21+4×(23+25+⋯+22n−1)−(4n +1)×22n+1．−3B n =5×21+4×23−22n−1⋅41−4−(4n +1)×22n+1， −3B n =5×21+4×(−83+22n+13)−(4n +1)×22n+1−3B n =−23+(13−4n)⋅22n+1B n =(12n−1)⋅22n+19+29．∴P 2n=(12n−1)⋅22n+19+29+2n2n+1． 19．【解答】（Ⅰ）解：∵抛物线x 2=−4√3y 的焦点是(0，−√3)，∴b =√3⋯⋯（1分）． ∵ca =√22，a 2＝b 2+c 2∴a =√6，c =√3⋯⋯（2分）． ∴椭圆C 的方程x 26+y 23=1⋯⋯（3分）（Ⅱ）（i ）设A （x 0，y 0）那么D （x 0，﹣y 0）．∵M 是线段AN 的中点∴A （x 0，2m ）D （x 0，﹣2m ）……（4分）． ∴k =2m−m x 0=m x 0，k ′=−2m−m x 0=−3m x 0⋯⋯（5分）， ∴3k +k ′＝0……（6分）（ii ）根据题意得：直线AM 的斜率一定存在且k ＞0 设直线AM 为y ＝kx +m ，则直线DM 为y ＝k ′x +m ＝﹣3kx +m 由{y =kx +m x 26+y 23=1可得（1+2k 2）x 2+4kmx +2m 2﹣6＝0……（7分）利用韦达定理可知：x 0⋅x B =2m 2−61+2k2，∴x B =2m 2−6(1+2k 2)x 0⋯⋯（8分），∵3k +k ′＝0，∴同理可得x G =2m 2−6(1+2k ′2)x 0=2m 2−6(1+2(−3k)2)x 0=2m 2−6(1+18k 2)x 0⋯⋯（9分），∴k BG =y B −y G x B −x G =kx B +m−(−3kx G +m)x B −x G =kx B +3kx Gx B −x G=k 2m 2−6(1+2k 2)x 0+3k 2m 2−6(1+18k 2)x 02m 2−6(1+2k 2)x 0−2m 2−6(1+18k 2)x 0=k 1+2k 2+3k 1+18k211+2k 2−11+18k2=k+18k 3+3k+6k 31+18k 2−1−2k 2#/DEL/#=4k+24k 316k 2=14k +32k#/DEL/#∵k ＞0，∴k BG =14k +32k ≥2√14k ⋅32k =√62 当且仅当14k=32k 时即为k =√66时等号成立 ……（14分）（不求出k 值，不扣分）20．【解答】解：（Ⅰ）当a ＝0时，f （x ）＝x •e ﹣x ， ∴f ′（x ）＝e ﹣x ﹣x •e ﹣x ＝e ﹣x （1﹣x ）……（1分）∴f ′（0）＝1，f （0）＝0，∴函数f （x ）在点（0，f （0））处的切线方程为y ＝x ．……（2分）（Ⅱ）由题意，f '（x ）＝（2ax +1）e ﹣x ﹣（ax 2+x +a ）e ﹣x ＝﹣e ﹣x [ax 2+（1﹣2a ）x +a ﹣1]＝﹣e ﹣x （x ﹣1）（ax +1﹣a ）．……（3分）（ⅰ）当a ＝0时，f '（x ）＝﹣e ﹣x （x ﹣1），令f '（x ）＞0，得x ＜1；f '（x ）＜0，得x ＞1，所以f （x ）在（﹣∞，1）单调递增，（1，+∞）单调递减；……（4分）（ⅱ）当a ＞0时，1−1a ＜1，令f '（x ）＞0，得1−1a ＜x ＜1；f '（x ）＜0，得x ＜1−1a 或x ＞1，……（5分）所以f （x ）在(1−1a ，1)单调递增，在(−∞，1−1a )，（1，+∞）单调递减，………（6分）（Ⅲ）令g （a ）＝e ﹣x （x 2+1）a +xe ﹣x ，a ∈（﹣∞，0]，当x ∈[0，+∞）时，e ﹣x （x 2+1）≥0，g （a ）单调递增，则g(a)max =g(0)=xe −x ，………………（7分）则g （a ）≤bln （x +1）对∀a ∈（﹣∞，0]恒成立等价于bln （x +1）≥g （a ）max ＝g （0），即xe ﹣x ≤bln （x +1），对x ∈[0，+∞）恒成立．………（8分）（ⅰ）当b ≤0时，∀x ∈（0，+∞），bln （x +1）＜0，xe ﹣x ＞0，此时xe ﹣x ＞bln （x +1），不合题意，舍去．…………（9分）（ⅱ）当b＞0时，令h（x）＝bln（x+1）﹣xe﹣x，x∈[0，+∞），则ℎ′(x)=bx+1−(e−x−xe−x)=bex+x2−1(x+1)e x，……（10分）其中（x+1）e x＞0，∀x∈[0，+∞），令p（x）＝be x+x2﹣1，x∈[0，+∞），则p（x）在区间[0，+∞）上单调递增，……（11分）①当b≥1时，p（x）≥p（0）＝b﹣1≥0，所以对∀x∈[0，+∞），h'（x）≥0，则h（x）在[0，+∞）上单调递增，故对任意x∈[0，+∞），h（x）≥h（0）＝0，即不等式bln（x+1）≥xe﹣x在[0，+∞）上恒成立，满足题意．…………（12分）②当0＜b＜1时，由p（0）＝b﹣1＜0，p（1）＝be＞0及p（x）在区间[0，+∞）上单调递增，所以存在唯一的x0∈（0，1）使得p（x0）＝0，且x∈（0，x0）时，p（x）＜0．即h'（x）＜0，所以h（x）在区间（0，x0）上单调递减，则x∈（0，x0）时，h（x）＜h （0）＝0，即bln（x+1）＜xe﹣x，不符合题意．……（13分）综上所述，b≥1．…………（14分）。

天津市河西区2019届高三下学期总复习质量调查(二)数学试卷(二模)(理)附答案

天津市河西区2019届高三下学期总复习质量调查（二）数学（理）试题（二模）第Ⅰ卷参考公式：·如果事件A ，B 互斥，那么()()()P A B P A P B =+U·如果事件A ，B 相互独立，那么)()()(B P A P AB P ⋅=·柱体的体积公式Sh V = ·锥体的体积公式Sh V 31=其中S 表示柱（锥）体的底面面积 h 表示柱（锥）体的高一.选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．（1）设全集{}110U n N n =∈≤≤，{}1,2,3,5,8A =，{}1,3,5,7,9B =，则()U C A B =I （）A.{}6,9B.{}6,7,9C.{}7,9D.{}7,9,10（2）若变量满足约束条件则的最小值等于（）（A ）5-2（B ）（C ）（D ）2（3）如图所示,程序框图的输出结果是（）（A ）5 （B ）6 （C ）7,x y 20,0,220,x y x y x y +≥⎧⎪-≤⎨⎪-+≥⎩2z x y =-2-32-（D ）8（4）设{}n a 是公比为q 的等比数列，则“1>q ”是“{}n a 为递增数列”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件（5）设5.043⎪⎭⎫ ⎝⎛=a ,4.034⎪⎭⎫⎝⎛=b ，()334log log 4c =，则（）（A ）c a b << （B ）b a c << （C ）a b c <<（D ）b c a <<（6）已知函数()()ϕ+=x x f 2sin ，其中ϕ为实数，若()⎪⎭⎫⎝⎛≤6πf x f 对R x ∈恒成立，且()ππf f >⎪⎭⎫ ⎝⎛2，则()x f 的单调递增区间是（）（A ）()Z k k k ∈⎥⎦⎤⎢⎣⎡+-6,3ππππ（B ）()Z k k k ∈⎥⎦⎤⎢⎣⎡+2,πππ （C ）()Z k k k ∈⎥⎦⎤⎢⎣⎡++32,6ππππ （D ）()Z k k k ∈⎥⎦⎤⎢⎣⎡-πππ,2 （7）已知抛物线()220y px p =>与双曲线()222210,0x y a b a b-=>>有相同的焦点F ，点A 是两曲线的一个交点，若直线AF ）（A （B ）327+ （C （D （8）在平行四边形ABCD 中，2AD =uuu r ，4CD =uu u r， 60=∠ABC ，F E ,分别是CD BC ,的中点，DE 与AF 交于H ，则DE AH ⋅的值（）（A ）12（B ）16（C ）125（D ）165第Ⅱ卷二.填空题：本大题共6小题，每小题5分，共30分．（9）设1z i =-（i 是虚数单位），则2z z+= . （10）在三棱锥ABC P -中，E D ,分别为PC PB ,的中点，记三棱锥ABE D -的体积为1V ，三棱锥ABC P -的体积为2V ，则=21v v .（11）523x ⎛ ⎝的展开式中3x 的系数为 .（用数字作答）(12）已知曲线C 的参数方程为⎪⎩⎪⎨⎧==ty tx sin 2cos 2 (t 为参数), C 在点()1,1处的切线为l ,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,则l 的极坐标方程为_____________. (13）若()42log 34log a b +=，则a b +的最小值为_____________.（14）已知函数()x f 满足，()⎩⎨⎧>≤+=0,ln 0,x x x k kx x f ，其中0≥k ，若函数()()1+=x f f y 有4个零点，则实数k的取值范围是 .三.解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．（15）（本小题满分13分）在ABC ∆中，A ，B ，C 对应的边为a ，b ，c . （Ⅰ）若2c =，3C π=，且ABC △，求cos()A B +和a ，b 的值；（Ⅱ）若B 是钝角，且3cos 5A =，12sin 13B =，求sinC 的值.（16）（本小题满分13分）甲，乙，丙三位学生独立地解同一道题，甲做对的概率为1，乙，丙做对的概率分别为m，n(m＞n)，且三位2学生是否做对相互独立.记ξ为这三位学生中做对该题的人数，其分布列为：（Ⅰ）求至少有一位学生做对该题的概率；（Ⅱ）求m，n的值；（Ⅲ）求ξ的数学期望.（17）（本小题满分13分）如图，平面PAD ⊥平面ABCD ，PA PD =，四边形ABCD 为平行四边形，45ABC ∠=，2AB AC ==，M 为线段AD 的中点，点N 满足2PN ND =.（Ⅰ）求证：直线//PB 平面MNC ；（Ⅱ）求证：平面MNC ⊥平面PAD ；（Ⅲ）若平面PAB ⊥平面PCD ，求直线BP 与平面PCD 所成角的正弦值.（18）（本小题满分13分）数列{}n a 是等比数列，公比大于0，前n 项和nS ()n N *∈，{}nb 是等差数列，DB已知112a =，32114a a =+，3461a b b =+，45712a b b =+. （Ⅰ）求数列{}n a ，{}n b 的通项公式n a ，n b ；（Ⅱ）设{}n S 的前n 项和为n T ()n N *∈，（i ）求n T ；（ii ）证明：()21121311<⋅-∑=+++++ni i i i i i b b b b T .（19）（本小题满分14分）在平面直角坐标系xOy 中，设椭圆13222=+y a x ()3>a 的右焦点为F ，右顶点为A ，已知1=-OF OA ，其中O 为原点，e 为椭圆的离心率. （Ⅰ）求椭圆的标准方程及离心率e ；（Ⅱ）设过点A 的直线l 与椭圆交于点()轴上不在x B B ，垂直于l 的直线与l 交于点M ，与y 轴交于点H ，若HF BF ⊥，且MAO MOA ∠≤∠，求直线l 的斜率的取值范围.（20）（本小题满分14分）已知函数()ax x x f +=ln ，在点()()t f t ,处的切线方程为13-=x y ．（Ⅰ）求a 的值；（Ⅱ）已知2≤k ，当1>x 时，()1231-+⎪⎭⎫⎝⎛->x x k x f 恒成立，求实数k 的取值范围；（Ⅲ）对于在()1,0中的任意一个常数b ，是否存在正数0x ，使得()122023100<+--+x b ex x f ,请说明理由．【参考答案】一、选择题：本题考查基本知识和基本运算.每小题5分，满分40分.（1）C （2）A （3）C （4）D （5）B（6）C（7）B（8）C二、填空题：本题考查基本知识和基本运算.每小题5分，满分30分.（9）22i +（10）41 （11）270（12）24sin =⎪⎭⎫⎝⎛+πθρ （13）7+ （14）⎪⎭⎫⎢⎣⎡+∞,1e三、解答题：本大题共6小题，共80分. （15）本小题满分13分.（Ⅰ）解：因为A B C π++=,3C π=,所以A B C π+=-. 所以1cos()cos()cos cos 32A B C C ππ+=-=-=-=-.由余弦定理及已知条件得，224a b ab +-=，又因为ABC △，所以1sin 2ab C =4ab =．联立方程组2244a b ab ab ⎧+-=⎨=⎩，，解得2a =，2b =． ……………………7分（Ⅱ）解：因为B 是钝角，且3cos 5A =，12sin 13B =.所以234sin 5A ⎛⎫===5cos 13B ===-所以[]sin sin()sin()C A B A B π=-+=+sin cos cos sin A B A B =+ 453121651351365⎛⎫=⨯-+⨯= ⎪⎝⎭ ……13分（16）本小题满分13分.（Ⅰ）解：设“甲做对”为事件A ，“乙做对”为事件B ，“丙做对”为事件C ，由题意知，()()()12P A P B m P C n ,,===. 由于事件“至少有一位学生做对该题”与事件“”是对立的，所以至少有一位学生做对该题的概率是()1310144P ξ-==-=. ……………4分 0ξ=（Ⅱ）解：由题意知()()()()1101124PP ABC m n ξ===--=， ()()113224P P ABC mn ξ====，整理得，712m n +=. 由m n >，解得13m =，14n =. ……………8分（Ⅲ）解：由题意知()()()()1a PP ABC P ABC P ABC ξ===++()()()()11111111122224m n m n m n =--+-+-=， =14，所以ξ的数学期望为=1312. …………13分（17）本小题满分13分.（Ⅰ）证明：连接BD ，交MC 于点O ，连接NO在平行四边形ABCD 中，因为12MD BC =，所以12OD OB =，又因为2PN ND =，即12ND PN =，所以//ON PB ，112mn =(2)1(0)(1)(3)b P P P P ξξξξ===-=-=-=0(0)1(1)2(2)3(3)E P P P P ξξξξξ=⨯=+⨯=+=+=又因为ON ⊂平面MNC ，PB ⊄平面MNC ，所以直线//PB 平面MNC . ……………4分（Ⅱ）证明：因为PA PD =，M 为线段AD 的中点，所以PM AD ⊥，又因为平面PAD ⊥平面ABCD 于AD ，PM ⊂平面PAD 所以PM ⊥平面ABCD在平行四边形ABCD 中，因为45ABC ∠=，2AB AC ==，所以AB AC ⊥ 如图，以A 为原点，分别以,AB AC 所在直线为x 轴，y 轴，建立空间直角坐标系，则(2,0,0),(0,2,0)B C ，(2,2,0),(1,1,0)D M -- 因为PM ⊥平面ABCD 设(1,1,)P t -(0)t >，则(1,1,)AP t =-，(1,1,0)CM =--，(2,2,0)AD =- 所以2200CM AD ⋅=-+=，1100CM AP ⋅=-+= 所以,CM AD CM AP ⊥⊥，又因为APAD A =所以CM ⊥平面PAD ，又因为CM ⊂平面MNC所以平面MNC ⊥平面PAD . ……………8分（Ⅲ）解：因为(2,0,0)AB =，(1,1,)AP t =- 设(,,)x y z =m 为平面ABP 的一个法向量则0x x y tz =⎧⎨-++=⎩ 不妨设(0,,1)t =-m因为(2,0,0)DC =，(1,1,)DP t =- 设(,,)x y z =n 为平面DCP 的一个法向量则0x x y tz =⎧⎨-+=⎩ 不妨设(0,,1)t =n因为平面PAB ⊥平面PCD ，所以⊥m n ，所以210t ⋅=-=m n 以为0t > 所以1t =所以(3,1,1)BP =-，(0,1,1)=n ，所以sin cos ,11BP θ=<>==n所以直线BP 与平面PCD. ……………13分（18）本小题满分13分.（Ⅰ）解：设数列{}n a 的公比为q （0q >）121112114a a q a q ⎧=⎪⎪⎨⎪=+⎪⎩，21120q q --=，=-1q （舍）或=2q ，12n na = 设数列{}nb 的公差为d111182(4)1116316b d b d⎧=⎪+⎪⎨⎪=⎪+⎩ 114431616b d b d +=⎧⎨+=⎩ 101b d =⎧⎨=⎩，1n b n =-.……………6分（Ⅱ）解：112212(1)1112n n n S -==-- 211111(111)()(1)122222n n n nT n n =+++-+++=--=-+111132112()(2)()(2)(1)(1)2i i i i i i i i i i T b b i b b i i i i ++++++++-⋅+-⋅+==⋅⋅+⋅+⋅1112(1)2i i i i +=-⋅+⋅ 1132231112()111111()()()122222322(1)2ni i i n n i i i T b b b b n n ++++=++-⋅=-+-++-⋅⋅⋅⋅⋅⋅+⋅∑ 11112(1)22n n +=-<+⋅. ……………13分（19）本小题满分14分.（Ⅰ）解：由已知得1=-c a ，即132=--a a ，解得2=a ，所以1=c ，得21==a c e ，椭圆方程为13422=+y x . ……………………5分（Ⅱ）解：设直线l 的斜率为()0≠k k ，则直线l 的方程为()2-=x k y ，设()B B y x B ,由方程组()⎪⎩⎪⎨⎧=+-=134222y x x k y ，消去y ，整理得()0121616342222=-+-+k x k x k解得2=x 或346822+-=k k x ，所以B 点坐标为⎪⎪⎭⎫⎝⎛+-+-3412,3468222k k k k .由（Ⅰ）知，()0,1F ，设()H y H ,0，有()H y ,1-=，⎪⎪⎭⎫⎝⎛++-=3412,3449222k k k k ，由HF BF ⊥,则0=⋅，所以034123494222=+++-k ky k k H ，解得kk y H 12492-=，因此直线MH 的方程为kk x k y 124912-+-=，设()M M y x M ,，由方程组()⎪⎩⎪⎨⎧-+-=-=1249122k x k y x k y 消去y ，解得()11292022++=k k x M ，在MAO ∆中，MO MA MAO MOA ≤⇔∠≤∠，即()22222MMMM y x y x +≤+-，化简得1≥M x ，即()111292022≥++k k ，解得46-≤k ，或46≥k . 所以，直线l 的斜率的取值范围为⎪⎪⎭⎫⎢⎣⎡+∞⎥⎦⎤ ⎝⎛-∞-,4646, .………14分（20）本小题满分13分.（Ⅰ）解：函数()ax x x f +=ln 的导数为()a xx f +='1，在点()()t f t ,处的切线方程为13-=x y ，可得()a tt f +='1，所以函数的切线方程为()()t x a t at t y -⎪⎭⎫ ⎝⎛+=+-1ln ，即1ln 1-+⎪⎭⎫ ⎝⎛+=t x a t y ，所以⎪⎩⎪⎨⎧-=-=+11ln 31t a t ，解得2=a . ……………………3分（Ⅱ）证明：由（Ⅰ）可得()x x x f 2ln +=，因为()1231-+⎪⎭⎫⎝⎛->x x k x f ，所以131ln -⎪⎭⎫⎝⎛->x k x ，即为，()03ln >--+x k x x x 可令()()3ln --+=x k x x x x g ，()k x x g -+='ln 2，由1>x ，可得02,0ln ≥->k x ，即有()0>'x g ，()x g 在()+∞,1递增，可得()()0211≥+=>k g x g ，所以221≤≤-k ，故k 的取值范围为⎥⎦⎤⎢⎣⎡-2,21； ……………………7分（Ⅲ）解：对于在()1,0中的任意一个常数b ，假设存在正数0x ，使得：()122023100<+--+x b e x x f ．由()()201ln 20231220000x b e x b ex x x x f +=+-+--+()1212000<+⋅+=-x b e x x 成立，从而存在正数0x ，使得上式成立，只需上式的最小值小于0即可．令()()1212-+⋅+=-x b e x x H x ， ()()()x x x e b x bx e x e x H ----=++-='1令()0>'x H ，解得b x ln ->，令()0<'x H ，解得b x ln 0-<<，则b x ln -=为函数()x H 的极小值点，即为最小值点．故()x H 的最小值为()()1ln 21ln ln 2ln -+⋅+-=-b b e b b H b 1ln ln 22-+-=b b b b b，再令()1ln ln 22-+-=x x x x xx G ()10<<x()()()0ln 1ln 1ln 2ln 2122>=++-+='x x x x x G则()x G 在()1,0递增，可得()()01=<G x G ，则()0ln <-b H .故存在正数b x ln 0-=，使得()122023100<+--+x b e x x f . ……………………14分。

2019届天津市部分区(五区联考)高三下学期二模考试数学(理)试题Word版

天津市部分区2019年高三质量调查试卷（二）数学（理）试题参考答案与评分标准一、选择题：（本大题共8个小题，每小题5分，共40分）题号答案1 2 3 4 5 6 7 8 BDBAACBD二、填空题：（本大题共6个小题，每小题5分，共30分）1 2 8 39． - i 10．30 11．12．相交13．6 3 14．845 5 三、解答题：（本大题共6个小题，共80分） 15．解：（Ⅰ）由题意，得f (x ) cos x sin x3cos2x ………………………………1分13 (1cos2x ) …………………………………3分 2sin2x 2 13 cos2x 3 3 .…………5分sin(2x)3 2sin2x 22 2 2p = p ，其最大值为13 . …6分所以 f (x )的最小正周期T =22z 2x,（Ⅱ）令32则有函数 y = 2sin z 的单调递增区间是2k , 2k,k Z . ………7分22k 2x2k ,得k x 5k ,k Z . 由………9分23 2 12123 3 ,B xkx5设 A, k ,k Z ，12123 12 易知 A I B所以，当 x , . ………………………………………………………12分时, f (x )在区间上单调递增；, , 3 123 312 3在区间，上单调递减. ………………13分16．解：（Ⅰ）设事件 A 为“甲恰好闯关3次才闯关成功的概率”，则有12 2 1 2 5， P (A ) 1(1)……………………………4分 2 3 181 2 332 （Ⅱ）由已知得：随机变量的所有可能取值为 2,3,4， ……………………………5分1 2 1 1所以， P7 ， ………………………………………6分22 3 2 2 12P (3)1(1)1， ……………………8分1221 12 1 1 1 23 3 2 2 3 2 333 1 1 2 1. P 114 ……………………………………10分 2 2 3 12234从而7 1 3 1 P12 12…………………………………………………12分7 3? 1 4? 1 5所以， E (x ) = 2?.…………………………………13分12 3 12 217．解：（Ⅰ）证明：因为 P ,Q 分别是 AE , AB 的中点，1 所以， PQ //BE ,PQ = BE ，……2分21 又 D C//BE ,DC = BE ，2所以， PQ //DC ， PQ 平面 ACD ，DC 平面 ACD ，…………3分所以， PQ //平面 ACD . ……4分（Ⅱ）因为 DC 平面 ABC ，ACB 90.以点C 为坐标原点，分别以CD ,CA ,CB 的方向为 x , y ,z 轴的正方向建立空间直角坐标系. ……………………………………………………………………………5分，则得C (0,0,0),A (0,4,0),B (0,0,4),D (2,0,0),E (4,0,4) ………………………6分所以 AB (0,4,4),DE (2,0, 4)，……………………………………………7分 uuur uuur AB DE 105所以cos AB ,DE uuur uuur ， ………………………………………8分AB DE 所以异面直线 AB 与 DE 所成角的余弦值10 . …………………………………9分 5（Ⅲ）由（Ⅱ）可知 AB (0, 4,4)， AE (4,4,4)，设平面 ABE 的法向量为(n = x , y ,z ) ,n AB 0， 4y 4z 0则r uuur所以n =(0,1,1) . ………………………10分 4x 4y 4z 0n AE 0由已知可得平面 ACD 的法向量为以CB =(0,0,4)， r uuur n BC 2 . ………………………………………….……12分所以cos n ,BC r uuur2n BC 故所求平面 ACD 与平面 ABE 所成锐二面角的大小为45.......……….………13分18．解：（Ⅰ）设等比数列{a }的公比为，.……………………………………………1分na 2a 9 a (q22q ) 9，.......…………………………………………2分 4 3 2 由a 2 3 得a 3 2解得q =3或q = -1.......………………………………………………………………3分因为数列{a }为正项数列，所以 q =3，...………………………....………………4分na 2所以，首项a = q =1，..........………………………………………………………5分1 a =3n -1..........………………………………………………………6分n故其通项公式为 2n 1 log a 2n 2 (2n 1)(2n 1)，.......…………………8分（Ⅱ）由（Ⅰ）得bn3 11( 111b n (2n 1)(2n 1) 2 2n 1 2n 1)，.......………………………10分所以所以T1 1 L (1L 1 1 1 1 1 1 12n 1 2n 1)nb 1 b 2 b n 2 3 3 51 1 1 .......……………………………………………………13分2 4n 22 19．解：（Ⅰ）由椭圆的一个焦点为 F 1 1,0知:c =1，即a b 1.①....………2分2 2 b =3，所以b = 3 .……4分2又因为直线 B F 的方程为bx y b 0，即 1 1b +1 2由①解得 a = 4 .2故所求椭圆C 的标准方程为+ y x 2 23 =1....…………………………………………5分4（Ⅱ）假设存在过点 A 的直线l 适合题意，则结合图形易判断知直线l 的斜率必存在，于是可设直线l 的方程为y k x 2，...............…………………………………6分2 2x y 1由 4 3，得34k 2x 2 16k 2x 16k 2 12 0 .（*）.......………8分y k x 2因为点 A 是直线l 与椭圆C 的一个交点，且 x 2A16k 2 128k 2 6， 34k 2所以 x x B x ，所以BA 2 3 4k 8k 2 6 B12k34k2,即点所以 ....……………………………………………………10分34k 2 uuur uuur16k 2 OA OB34kuuur 12k 34k 14 16k 2 12k ,34k 34k2,，即OT . 2 2 7 22222 16k 12k 因为点T 在圆 x 2+ y 2 = 2上，所以2，……11分7 34k 234k 234 3 .48k 4 8k 2 210，解得k2= ，所以k ………………12分化简得 2经检验知，此时（*）对应的判别式0，满足题意. ………………………13分 3 故存在满足条件的直线l ，其方程为 yx 2 . ……………….……14分2 20．解：12x（Ⅰ）当a = 2时， f (x ) ln x 2x ，所以 f (x ) ...............………………1分f 11 21， ..........………………………………………….....……...……2分x 1 y 2则切线方程为，即x + y +1=0 . ………………....……………3分（Ⅱ）①当a =0时， f ( x ) =ln x 有唯一零点x =1；…………………............………4分 f x 0， f ( x )是区间 0,上的增函数，②当a <0时，则 a 0， f (e f 1a)= a - ae = a (1- ea a) <0，因为0，即函数 f ( x )在区间0,有唯一零点；所以 f 1 f e a ③当a >0时，令………6分1f x 0得 x= ， a 1 1 0, 所以，当 x0, 时， a f x 0，函数f ( x )在区间a 上是增函数；且 x 0, f (x )；1 当 x,时， f x 0，函数 a1，+f ( x )是在上是减函数，a且 x , f (x )；11 所以在区间 0, 上，函数 f ( x )的极大值为 fln 1ln a 1， …8分 aa 1a 1由 f0，即- ln a - 1<0，解得a >，e1 故所求实数a 的取值范围是,. …………………………………………9分e（Ⅲ）设 x > x >0，由 f( x ) =0，f ( x ) =0，可得ln x - ax =0 ln x - ax =0，，1 21 12 21 2 ln x ln x 2ln x - ln x =a x - x 2).所以a ( 11…........................…10分所以 1 2 x 2x 12要证 x +x >，只需证a (x +x ) >2 , 1 2 12 a ln x ln x 2x 1 2( x - x 2) .1 (x x )2，即 ln > 1 …………………11分即证x 21 2 x 2 x 1 +x x 1 22 x 1 x 2x 1 x 2ln t x >1，于是ln x 1 2 t 1令t = 1， …………………12分 x 2 x 2 t 1t 10，t t 12 22(t - 1)t +11 t t 14 设函数h (t ) =ln t -(t >1)，求导得h t 2 1,所以函数 h (t )是上的增函数，2(t - 1)成立， t +1h 1 0，即不等式ln t > h t所以故所证不等式x x 2成立.…………………………………………………14分12a。