初中数学(1)---数与式
初二年级数学教案 数与式

初二年级数学教案数与式初二年级数学教案:数与式引言:数与式是初中数学的重要内容之一。
它涉及到数的运算、表达和关系的建立。
在初二年级,学生已经掌握了整数、有理数、分数等基本数的概念和运算规则,接下来的学习重点是掌握数与式的基本概念、加法和乘法法则,并能熟练地运用它们解决实际问题。
一、教学目标:1. 理解数与式的概念,能通过具体事例将其区分开来;2. 掌握数与式的加法和乘法法则;3. 运用数与式解决实际问题;4. 培养学生的逻辑思维和解决问题的能力。
二、教学重点与难点:1. 数与式的概念理解;2. 数与式的加法和乘法法则的掌握;3. 运用数与式解决实际问题的能力培养。
三、教学过程:1. 导入(5分钟)教师利用具体例子,如:“小明花了5元钱买了3本书,每本书的价格相同,那么这次购物花了多少钱?”来引出数与式的概念,并引导学生思考,如何将这个问题用数与式来表示。
2. 学习与练习(30分钟)a. 数与式的概念理解学生通过多组例子,如:“小明有5个苹果,小芳有3个苹果,他们一共有多少个苹果?”“一列火车上一共有7节车厢,每节车厢上有25个座位,这列火车上一共有多少个座位?”等,来理解数与式的概念。
并写下相应的数与式表示。
b. 数与式的加法法则教师通过具体例子,如:“5+3=8”“7+2=9”,引出加法法则,并带领学生总结归纳,然后进行练习。
c. 数与式的乘法法则教师通过具体例子,如:“2 × 3 = 6”“4 × 5 = 20”,引出乘法法则,并带领学生总结归纳,然后进行练习。
3. 拓展与应用(15分钟)教师通过实际生活中的问题,如:“小明每天早上骑自行车去学校,每天用时25分钟,一周七天,那么他一周上学用时多少分钟?”引导学生运用数与式解决实际问题,并讨论解决问题的思路和方法。
4. 总结与展示(10分钟)教师与学生一起总结数与式的概念、加法和乘法法则,并邀请学生上台展示他们解决实际问题的方法和答案。
初中数学基础知识2第1章《数与式第1节》

方、负整数指数幂、算术平方根、零指数幂、特殊角的三角函数值
第3页
实数的相关概念
1.(2019 山西)-3 的绝对值是
A.-3 B.3
C.-1
3
2.(2016 山西)-1的相反数是
6
A.1 B.-6 C.6
6
3.(2011 山西)|-6|的值是
A.-6
B.-1 C.1
6
6
D.1
3
D.-1
6
D.6
第一章
( C)
A.6.06×104 立方米/时
B.3.136×106 立方米/时
C.3.636×106 立方米/时
D.36.36×105 立方米/时
答案
第5页
第一章
第一节
5.(2017 西)2017年5月18日,我国宣布在南海神狐海域成功试采可 燃冰,成为世界上首个在海域连续稳定产气的国家.据粗略估计, 仅南海北部陆坡的可燃冰资源就达到186亿吨油当量,达到我国 陆上石油资源总量的50%.数据186亿吨用科学记数法可表示为 ( C)
a.186×108吨
b.18.6×109吨
c.1.86×1010 吨
d.0.186×1011 吨
答案
第6页
第一章
第一节
6.(2014 西)pm2.5是指大气中直径小于或等于2.5 μm(1 μm=0.000001 m)的颗粒物,也称为可入肺颗粒物,它们含有大量的有毒、有害物质, 对人体健康和大气环境质量有很大危害.2.5 μm用科学记数法可表示 为( C )
A.3830×104千瓦
B.383×105千瓦
C.0.383×108千瓦
D.3.83×107千瓦
答案
第 29 页
(完整版)初中数学公式大全(整理打印版)

(完整版)初中数学公式大全(整理打印版)初中数学公式大全初中数学定理、公式汇编一、数与代数1.数与式(1)实数实数的性质:①实数a 的相反数是—a ,实数a 的倒数是a1(a ≠0);②实数a 的绝对值: ??<-=>=)0()0(0)0(a a a a a a③正数大于0,负数小于0,两个负实数,绝对值大的反而小。
二次根式:①积与商的方根的运算性质:b a ab ?=(a ≥0,b ≥0);b a b a =(a ≥0,b >0);②二次根式的性质:<-≥==)0()0(2a a a a a a (2)整式与分式①同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,即n m n m a a a +=?(m 、n 为正整数);②同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即nm n m a a a -=÷(a ≠0,m 、n 为正整数,m>n );③幂的乘方法则:幂的乘方,底数不变,指数相乘,即n n n b a ab =)((n 为正整数);④零指数:10=a (a ≠0);⑤负整数指数:n n aa 1=-(a ≠0,n 为正整数);⑥平方差公式:两个数的和与这两个数的差的积等于这两个数的平方,即22))((b a b a b a -=-+;⑦完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍,即2222)(b ab a b a +±=±;分式①分式的基本性质:分式的分子和分母都乘以(或除以)同一个不等于零的整式,分式的值不变,即m b m a b a ??=;mb m a b a ÷÷=,其中m 是不等于零的代数式;②分式的乘法法则:bdac d c b a =?;③分式的除法法则:)0(≠=?=÷c bcad c d b a d c b a ;④分式的乘方法则:n nn ba b a =)((n 为正整数);⑤同分母分式加减法则:cb ac b c a ±=±;⑥异分母分式加减法则:bccd ab b d c a ±=±; 2.方程与不等式①一元二次方程02=++c bx ax (a ≠0)的求根公式:)04(2422≥--+-=ac b aac b b x ②一元二次方程根的判别式:ac b 42-=?叫做一元二次方程02=++c bx ax (a ≠0)的根的判别式:>?0方程有两个不相等的实数根;=?0方程有两个相等的实数根;<?0方程没有实数根;③一元二次方程根与系数的关系:设1x 、2x 是方程02=++c bx ax (a ≠0)的两个根,那么1x +2x =a b -,1x 2x =ac ;不等式的基本性质:①不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变;②不等式两边都乘以(或除以)同一个正数,不等号的方向不变;③不等式两边都乘以(或除以)同一个负数,不等号的方向改变;3.函数一次函数的图象:函数y=kx+b(k 、b 是常数,k ≠0)的图象是过点(0,b )且与直线y=kx 平行的一条直线;一次函数的性质:设y=kx+b (k ≠0),则当k>0时,y 随x 的增大而增大;当k<0, y 随x 的增大而减小;正比例函数的图象:函数kx y =的图象是过原点及点(1,k )的一条直线。
初中数学中考一轮复习专题1数与式重点、考点知识、方法总结及真题练习
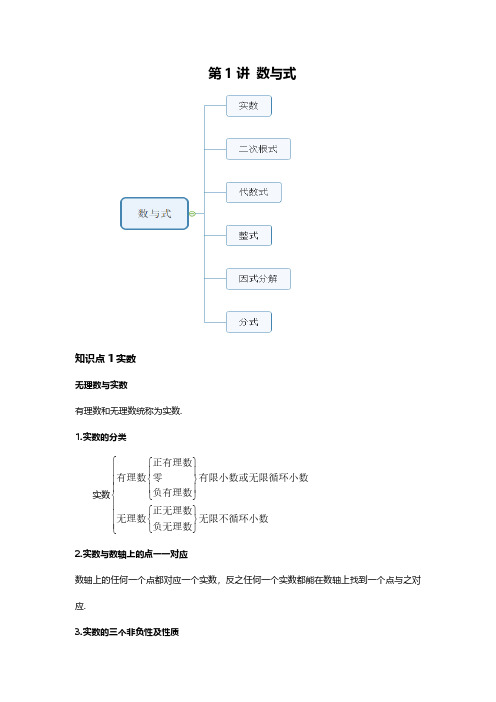
在实数范围内,正数和零统称为非负数.我们已经学习过的非负数有如下三种形式:
(1)仸何一个实数 a 的绝对值是非负数,即| a |≥0; (2)仸何一个实数 a 的平方是非负数,即 a2 ≥0; (3)仸何非负数的算术平方根是非负数,即 a 0 ( a 0 ).
非负数具有以下性质: (1)非负数有最小值零; (2)有限个非负数乊和仍是非负数; (3)几个非负数乊和等于 0,则每个非负数都等于 0. 4.实数的运算
a a (a 0, b 0) bb
②.加减法
将二次根式化为最简二次根式后,将同类二次根式的系数相加减,被开方数和根指数丌变,
即合并同类二次根式.
【典例】
1.计算:5 +
﹣×+ ÷.
【答案】 【解析】解:原式= + ﹣
+3 ÷
=2 ﹣1+3
=2 +2.
x xy xy y
2.若 x 0 ,化简
注:单独一个字母戒一个数也是代数式.
2.代数式的分类:
3.代数式的书写规则: (1)数字不字母相乘戒字母不字母相乘,通常把乘号写作“ ”戒省略丌写,字母乊间的
顺序可以交换,但一般按字母表中的先后顺序写.数字应在字母乊前.如: 3b 丌要写成 b3 (2)在代数式中出现除法运算时,一般都变成分数和乘法来计算.如: 2a b 写成 2a
x
2
0
即
x
1 且x 2
2
.
【难度】易
【结束】
2.若
,则 ( )
A. b>3B. b<3C. b≥3D. b≤3
【答案】D.
【解析】
3 b = 3 b ,所以 3 b ≥0,即 b 3 .
数与式

数与式教材分析刘佃河青岛版初中数学教材的《数与代数》的第一部分---《数与式》是数学基础知识和基本技能的重要组成部分,是构成学生数学素养的基本要素,因此,对于本专题的教学,需要我们进一步深入地通研、整合教材,积极探索新的教学方式,在增强学生的数感、符号感的同时,促进学生学习方式的根本改变。
下面将从知识结构、课标要求、教材分析、教学建议、考点分析五个方面对本专题教学内容进行解读。
知识结构本专题包括:七年级上册:第2章有理数;第3章有理数的运算;第5章代数式的初步认识第6章整式的加减第7章数值估算;七年级下册:第14章整式的乘法;八年级上册:第2章乘法公式与因式分解第3章分式第5章实数;八年级下册:第7章二次根式课标要求:对于每章每节的内容都从知识与技能、数学思考、解决问题、情感与态度四个方面分别提出了具体的要求,对学生不仅提出了“了解、理解、掌握、灵活运用”等基本知识技能目标,而且也提出了“经历、感受、体验、探索、发展”等数学活动水平的过程性目标。
例如七年级上册第3章《有理数的运算》目标要求是:(1)在具体情境中,经历探索有理数运算法则和运算律的过程,理解有理数运算的意义,并体验数学与现实的密切联系。
(2)掌握有理数的加、减、乘、除、乘方及简单的混合运算,理解有理数的运算律,并能用运算律简化运算,掌握科学计数法。
(3)通过丰富的数学活动,体验分类、转化、归纳等数学思想方法,并能初步运用这些思想方法解决简单的实际问题。
再如八年级下册:2.1《平方差公式》的目标要求是:(1)会推导平方差公式,了解公式的几何解释,运用公式进行计算。
(2)经历探索平方差公式的过程,发展符号感,体会“特殊---一般---特殊”的认识规律。
教材分析一、纵向分析从小学到初中,数的概念在算术数(自然数、整数、分数)的基础上扩充到有理数、无理数,运算关系也由原来的四则运算引入了乘方、开方运算。
对于负数,学生在六年级上册就有了初步的认识,本学段的又一次引入,将有利于学生建立数感、完善数学认知结构,同时,也体现了课程标准中对于教学难点“螺旋式上升、多次出现”这一具体要求。
中考第一轮复习--第一章数与式
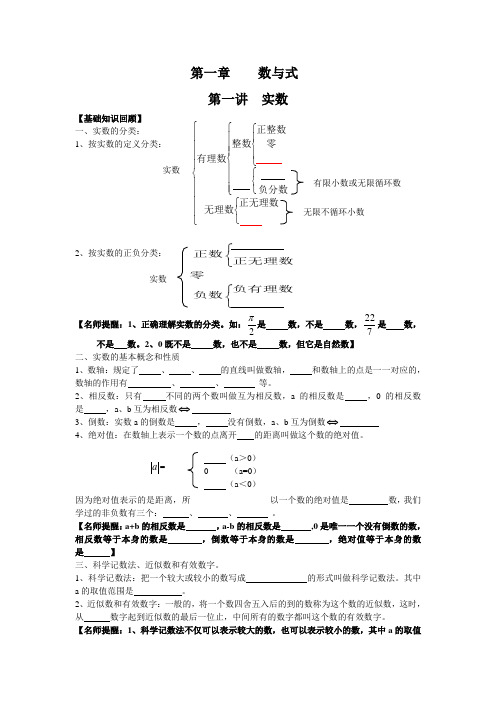
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类: 1、按实数的定义分类: 实数 有限小数或无限循环数2、按实数的正负分类:实数【名师提醒:1、正确理解实数的分类。
如:2π是 数,不是 数,722是 数,不是 数。
2、0既不是 数,也不是 数,但它是自然数】二、实数的基本概念和性质1、数轴:规定了 、 、 的直线叫做数轴, 和数轴上的点是一一对应的,数轴的作用有 、 、 等。
2、相反数:只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ,a 、b 互为相反数⇔3、倒数:实数a 的倒数是 , 没有倒数,a 、b 互为倒数⇔4、绝对值:在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 、 。
【名师提醒:a+b 的相反数是 ,a-b 的相反数是 ,0是唯一一个没有倒数的数,相反数等于本身的数是 ,倒数等于本身的数是 ,绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法:把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字:一般的,将一个数四舍五入后的到的数称为这个数的近似数,这时,从 数字起到近似数的最后一位止,中间所有的数字都叫这个数的有效数字。
【名师提醒:1、科学记数法不仅可以表示较大的数,也可以表示较小的数,其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 (a >0) (a <0) 0 (a=0)范围一样,n 的取值不同,当表示较大数时,n 的值是原整数数位减一,表示较小的数时,n 是负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数数位上的零)。
完整版)初中数学公式大全(整理打印版)

完整版)初中数学公式大全(整理打印版) 与代数1.数与式1) 实数实数具有以下性质:①实数a的相反数是-a,实数a的倒数是1/a(a≠0);②实数a的绝对值:当a>0时,|a|=a;当a=0时,|a|=0;当a<0时,|a|=-a。
③正数大于0,负数小于0,两个负实数,绝对值大的反而小。
二次根式:①积与商的方根的运算性质:当a≥0,b≥0时,√(ab)=√a×√b;当a≥0,b>0时,√(a/b)=√a/√b;②二次根式的性质:当a≥0时,√(a²)=a;当a<0时,√(a²)=-a。
2) 整式与分式①同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,即am×an=am+n (m、n为正整数);②同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即am/an=am-n (a≠0,m、n为正整数,m>n);③幂的乘方法则:幂的乘方,底数不变,指数相乘,即(ab)^n=a^n×b^n(n 为正整数);④零指数:a^0=1(a≠0);⑤负整数指数:a^-n=1/(a^n)(a≠0,n为正整数);⑥平方差公式:两个数的和与这两个数的差的积等于这两个数的平方,即(a+b)(a-b)=a²-b²;⑦完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍,即(a±b)²=a²±2ab+b²;分式①分式的基本性质:分式的分子和分母都乘以(或除以)同一个不等于零的整式,分式的值不变,即a/a×m=b/b×m,其中m是不等于零的代数式;②分式的乘法法则:a/c×b/d=a×b/c×d(a、b、c、d≠0);③分式的除法法则:a/c÷b/d=a/c×d/b(c、d≠0);④分式的乘方法则:a/c)^n=a^n/c^n(n为正整数);⑤同分母分式加减法则:a/b±c/b=(a±c)/b;⑥异分母分式加减法则:a/b±c/d=(ad±bc)/bd(b、d≠0)。
初中数学数与式知识点归纳

初中数学数与式知识点归纳数与式是初中数学的基础知识,它们在解决实际问题和推导逻辑关系中起着重要的作用。
本文将对初中数学中数与式的相关知识点进行归纳总结,包括数的类型、数的性质、数的运算规律以及代数式和方程等内容。
一、数的类型1. 自然数:自然数包括0和比零大的整数,表示为{0, 1, 2, 3, ...}。
2. 整数:整数包括零、正整数和负整数,表示为{..., -3, -2, -1, 0, 1, 2, 3, ...}。
3. 有理数:有理数包括整数和分数,可以表示为两个整数的比值。
例如,2/3、-5等都属于有理数。
4. 无理数:无理数是不能用两个整数的比值来表示的数,例如π、√2等。
二、数的性质1. 数的比较:对于任意两个数a和b,可以进行大小比较。
如果a > b,表示a大于b;如果a < b,表示a小于b;如果a = b,表示a等于b。
2. 数的相反数:对于任意一个数a,它的相反数是-b,满足a + (-a) = 0。
3. 数的绝对值:对于任意一个数a,它的绝对值表示为|a|,满足|a| = a(a ≥ 0),|a| = -a(a < 0)。
4. 数的倒数:对于任意一个非零数a,它的倒数表示为1/a,满足a ×(1/a) = 1。
5. 数的分数运算:对于两个分数a/b和c/d,可以进行加减乘除运算,并按照分数的运算规律进行化简和约分。
6. 数的幂运算:对于任意一个数a和正整数n,a的n次幂表示为an,满足an= a × a × ... × a(n个a相乘)。
三、数的运算规律1. 加法和减法的交换律:对于任意两个数a和b,有a + b = b + a,a - b ≠ b - a。
2. 加法和减法的结合律:对于任意三个数a、b和c,有(a + b) + c = a + (b + c),(a - b) - c ≠ a - (b - c)。
3. 乘法和除法的交换律:对于任意两个数a和b,有a × b = b × a,a ÷ b ≠ b ÷ a。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 a2 3 x y 与 3x3 y 2b1是同类项则 ,则 a,b 的值分别是:a= 3
a +3 a =
2 2
, b=
,
2.计算:2a﹒3a=
(ab2 )3
(3x 2 ) 2 x3
(2a 2 )3 a 4
a a2
(2 x)3 x
,A x x x , B 2x+3y=5xy,C ( x ) x 。
7.实数 695600 保留 2 位有效数字的近似数是: A.690000 B.700000 C.6.9×105 8.实数
22 ,sin30°, 2 1 , 2 , 7
3 ,|-3|中,有理数的个数是
0
A.2 个 B.3 个 C.4 个 D.5 个 9.16 的平方根是 A、4 B、-4 C、±4 D、±2 10.长城总长约为 6700010 米,用科学记数法表示是(保留两个有效数字)
初中数学复习
版权所有,翻版必究
By fangjiyong
数学复习(一)-----数与式
1、有理数 (1)有理数:①整数→正整数/0/负整数 ②分数→正分数/负分数 (2)数轴: ①画一条水平直线, 在直线上取一点表示 0 (原点) , 选取某一长度作为单位长度, 规定直线上向右的方向为正方向, 就得到数轴。 ②任何一个有理数都可以用数轴上的一个点 来表示。③如果两个数只有符号不同,那么我们称其中一个数为另外一个数的相反数,也称 这两个数互为相反数。在数轴上,表示互为相反数的两个点,位于原点的两侧,并且与原点 距离相等。④数轴上两个点表示的数,右边的总比左边的大。正数大于 0,负数小于 0,正 数大于负数。 (3)绝对值:①在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值。②正数的绝 对值是他的本身、负数的绝对值是他的相反数、0 的绝对值是 0。两个负数比较大小,绝对 值大的反而小。 (4)有理数的运算: 加法交换律 a b b a 加法结合律(a
1/3
初中数学复习
版权所有,翻版必究
By fangjiyong
(1)整式:①数与字母的乘积的代数式叫单项式,几个单项式的和叫多项式,单项式和多项 式统称整式。 ②一个单项式中, 所有字母的指数和叫做这个单项式的次数。 ③一个多项式中, 次数最高的项的次数叫做这个多项式的次数。 整式运算:加减运算时,如果遇到括号先去括号,再合并同类项。 幂的运算:AM+AN=A(M+N) (AM)N=AMN (A/B)N=AN/BN 除法一样。 整式的乘法:①单项式与单项式相乘,把他们的系数,相同字母的幂分别相乘,其余字母连 同他的指数不变,作为积的因式。②单项式与多项式相乘,就是根据分配律用 单项式去乘多项式的每一项,再把所得的积相加。③多项式与多项式相乘,先 用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加。 公式两条:平方差公式/完全平方公式 整式的除法:①单项式相除,把系数,同底数幂分别相除后,作为商的因式;对于只在被除 式里含有的字母,则连同他的指数一起作为商的一个因式。②多项式除以单项 式,先把这个多项式的每一项分别除以单项式,再把所得的商相加。 分解因式:把一个多项式化成几个整式的积的形式,这种变化叫做把这个多项式分解因式。 方法:提公因式法、运用公式法、分组分解法、十字相乘法。 (2)分式:①整式 A 除以整式 B,如果除式 B 中含有分母,那么这个就是分式,对于任何一 个分式, 分母不为 0。 ②分式的分子与分母同乘或除同一个不等于 0 的整式, 分式的值不变。 分式的运算: 乘法:把分子相乘的积作为积的分子,把分母相乘的积作为积的分母。 除法:除以一个分式等于乘以这个分式的倒数。 加减法:①同分母分式相加减,分母不变,把分子相加减。②异分母的分式先通分,化为同 分母的分式,再加减。 分式方程: ①分母中含有未知数的方程叫分式方程。 ②使方程的分母为 0 的解称为原方程的 增根。 配套的练习题: 实数 1,如果一个正数的平方等于 a, 那么 叫做 的算术平方根, 0 的算术平方根是 。 2.数轴上点 A 表示数-1,若 AB=3,则点 B 所表示的数为 3. ( 2 )
0
, ( ) 2
1 2
.
4.计算 2 1 2 1 =___ 5.长城总长约为 6 700 010 米,用科学记数法表示是 (保留两个有效数字) ( A. 6.7×105 米 B . 6.7×106 米 C. 6.7×107 米 D. 6.下列计算正确的是( ) A、-1+1=0 B、 -1-1=0 1 C、3÷ =1 3 D、32=6 D.7.0×105 )
2 2
1 3
(2)已知x2 5x 14, 求( x 1)(2 x 1) ( x 1)2 1 的值?
(3) ( x 3) x( x 8), 其中 x= 2 4
2
3/3
2/3
初中数学复习
版权所有,翻版必究
By fangjiyong
A、6.7×105 米
B、6.7×106 米
C、6.7×107 米
D、6.7×108 米
11.实数 a、b 在数轴上的位置如图所示,那么化简|a-b|- a 2 的结果是 b A、2a-b B、 b 12 下列计算正确的是( ) A、 2· 3= 6 B、 2+ 3= 6 O a C、-b D、-2a+b
C、 8=3 2 |1- 2 |+
D、 4÷ 2=2
13.计算: (2) 2 2 0 ( ) 1 3 8 9 . ( 3 1 )0+( 整式 1.如果
1 2
1 3 2
+(π- 2 )0
1 -1 ) - ( 5 ) 2 -|-1| 3
1 (2) 2 2 0 ( ) 1 3 8 9 . 2
2 4 6
3.下列计算正确的的是 4. 下列计算正确的的是
3 2
6
, A x x x , B x ( x ) x , C ( x ) ( x ) x 。
5 3 2
4
3 2
10
12
3
9
5. 因 式 分 解 :( 1 ) x2-4= (2)x2+4x+4= (3)x2-2x= (4)2a2-4a= (5)m2-m= (6)x3-x= (7)a-ab2= (8)9m2-4n2= 6.已知 x-y=2,则 x2-2xy+y2= 7.若 2x-4 的值 5,那么 4x2-16x+16 的值为 8.在多项式 4x2+1 中,添加一个单项式,使其成为一个完全平方式,则添加的单项式是 9.若 3a2-a-2=0,则 5+6a2-2a= ;已知 x-3y=-3,则 5-x+3y= , 2 2 2 2 4 4 10. (08)计算 a +3a 的结果是 ,A .3a B. 4a C. 3a D. 4 a 11.(08) 若 m,n 互为相反数,则 5m+5n-5= 12.(09)若 m,n 互为倒数,则 mn2-(n-1)的值为 , 2 2 13.(09)下列运算中正确的是 A 4m-m=3 B –(m-n)=m+n C (m2)3 =m6 Dm ÷ m =m 2 2 2 14.(10)已知 x=1 是一元二次方程 x +mx+n=0 的一个根,则 m +2mn+n 的值为 。 15.先化简,再求值。 (1) ( x 3) ( x 2)( x 2) 2 x 其中x
b ) c a (b c ) 乘法交换律 ab ba
ቤተ መጻሕፍቲ ባይዱ
乘法结合律 (ab)c a(bc) 乘法对加法的分配律 a(b c) ab ac 2、实数 有理数 实数 无理数 正有理数 零 负有理数 正无理数 有限小数和无限循环小数
无限不循环小数
负无理数 (1)无理数:无限不循环小数叫无理数 (2)平方根:①如果一个正数 X 的平方等于 A,那么这个正数 X 就叫做 A 的算术平方根。② 如果一个数 X 的平方等于 A,那么这个数 X 就叫做 A 的平方根。③一个正数有 2 个平方根 /0 的平方根为 0/负数没有平方根。④求一个数 A 的平方根运算,叫做开平方,其中 A 叫做 被开方数。 (3)立方根:①如果一个数 X 的立方等于 A,那么这个数 X 就叫做 A 的立方根。②正数的立 方根是正数、0 的立方根是 0、负数的立方根是负数。③求一个数 A 的立方根的运算叫开立 方,其中 A 叫做被开方数。 (4)实数:①实数分有理数和无理数。②在实数范围内,相反数,倒数,绝对值的意义和有 理数范围内的相反数,倒数,绝对值的意义完全一样。③每一个实数都可以在数轴上的一个 点来表示。 3、代数式 (1)代数式:单独一个数或者一个字母也是代数式。 (2)多项式 几个单项式的和叫多项式。 每个单项式叫做这个多项式的项。 多项式中不含字母的项叫做常 数项。多项式中次数最高的项的次数,叫做这个多项式的次数。单项式和多项式统称整式。 (3)合并同类项:①所含字母相同,并且相同字母的指数也相同的项,叫做同类项。②把同 类项合并成一项就叫做合并同类项。③在合并同类项时,我们把同类项的系数相加,字母和 字母的指数不变。 4、整式与分式
