2011-2012学年第二学期八年级数学第二次月考复习讲义
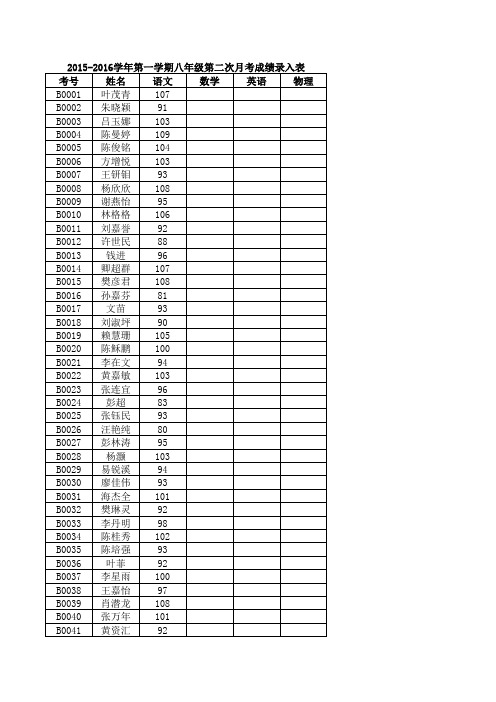
语文2015-2016学年第一学期八年级第二次月考成绩录入表
92 95 95 96 97 107 95 74 98 105 102 96 100 95 100 99 88 93 98 96 94 94 93 102 94 95 91 92 91 80 96 88 82 103 100 94 91 99 94 88 99 66 80
B0085 B0086 B0087 B0088 B0089 B0090 B0091 B0092 B0093 B0094 B0095 B0096 B0097 B0098 B0099 B0100 B0101 B0102 B0103 B0104 B0105 B0106 B0107 B0108 B0109 B0110 B0111 B0112 B0113 B0114 B0115 B0116 B0117 B0118 B0119 B0120 B0121 B0122 B0123 B0124 B0125 B0126 B0127
庄心怡 谷显雪 陈华 代芳 李晓敏 彭梦婷 张佳意 彭绘灵 王思琪 卞影影 方季声 陈丽丽 雷涛 贺惠琳 钟文婷 周梦瑶 杨静 王业 黎松坡 钟家业 刘嘉怡 曾津 蔡垸湘 叶绮琪 吴家明 劳湘雯 李文森 刘思诗 朱敏榕 劳小倩 谢赵棋 温心怡 朱晓宗 刘宝聪 郭凯旋 曾鑫 薛文娇 刘莉 刘 松 苏嘉豪 吴晨康 吴保良 刘奉琼
林铤 曾思源 庄晓威 吴俊豪 黄小红 吴佳雯 肖荟 钟惠娟 覃泰贤 王乾 黄配芩 林峻峰 罗贤裕 钟豪 郑秀敏 吴锦婷 张通 庄惠豪 钟锴城 叶尚智 赖雨珊 陈家龙 杨惠兰 叶杰雄 黄琦聪 胡灿佳 庄燕彬 古国荣 陈美婷 叶轩均 陈亚萍 张志壕 韩飞翔 宋恒易 叶稳 冯彪 曾珍珍 闫帅 李沛沛 李嘉耀 吕曼芳 黄孝冈 郑兴敏
周慧 洪妙宣 黄涛 邓智豪 翟智聪 黄钰梅 林淑婷 陈倩 周超 韦晓佳 范诗诗 张叶慧 梁淑仪 钟惠婷 张越 邓翔增 叶观婷 何芷仪 钟广源 黄锐洲 叶妙添 邓玉婷 廖文玉 田贤汶 叶凯欣 刘嘉城 黄秋云 廖滨滨 周子杰 赵晶晶 黎敬 魏怡鸿 刘庆 李美玲 谭广生 郑兴俊 徐昌浩 曾慧仪 赖倩柔 熊宇凤 叶永耿 朱磊 刘丽欢
永阳中学2011—2012学年度第二学期八年级下数学月考试卷

永阳中学2011—2012学年度第二学期八年级数学第一次月考试卷一、 选择题(每题3分,共39分)1、如果a >b ,那么下列各式中正确的是 ( )A 、a -2<b -2B 、22b a< C 、-2a <-2b D 、-a >-b 2、不等式组⎩⎨⎧-≤+001>x x 的解集为 ( )A 、x <-1B 、x <0C 、-1≤x <0D 、x ≤-13、下列各式从左到右,是因式分解的是 ( )A 、(y -1)(y +1)=2y -1B 、1)(122-+=-+y x xy xy y xC 、(x -2)(x -3)=(3-x )(2-x )D 、22)2(44-=+-x x x4、计算20032004)2(2-+的结果是 ( )A 、20042B 、20042-C 、20032D 、20032-5、下列多项式中,能用公式法进行因式分解的是 ( )A 、22y xy x +-B 、222y xy x -+C 、222y xy x -+-D 、22y xy x ++6、一次函数323+-=x y 的图象如图所示,当-3<y <3时,x 的 取值范围是( )A 、x >4B 、0<x <2C 、0<x <4D 、2<x <47、已知点A (2-a ,a +1)在第一象限,则a 的取值范围是 ( )A.a >2B.-1<a <2C.a <-1D.a <18、一个多项式分解因式的结果是)2)(2(33b b -+,那么这个多项式是 () A 、46-b B 、64b - C 、46+b D 、46--b9、下列各式是完全平方式的是 () A 、412+-x x B 、21x + C 、1++xy x D 、122-+x x 10、把多项式)2()2(2a m a m -+-分解因式等于 () A 、))(2(2m m a +- B 、))(2(2m m a --C 、m(a-2)(m-1)D 、m(a-2)(m+1)11、下列多项式中,含有因式)1(+y 的多项式是 () A 、2232x xy y --B 、22)1()1(--+y yC 、)1()1(22--+y yD 、1)1(2)1(2++++y y12、分解因式14-x 得 () A 、)1)(1(22-+x xB 、 )1)(1)(1(2++-x x xC 、 22)1()1(-+x xD 、3)1)(1(+-x x 13、如果不等式组434x x x n +<-⎧⎨>⎩的解集是4>x ,则n 的取值范围是 ( ) A 、4≤n B 、4≥n C 、4=n D 、4<n二、填空题(每题3分,共21分)14、不等式x -4<0的解集是______;不等式-2x -1<-1的解集是____。
2011-2012月考二

2011——2012学年度八年级上学期月考二数学试题第一章~第六章第4节(其中第四章第5节~第六章第4节占70%)一、选择题(本大题共8小题,每小题3分,共24分) 1.下列式子正确的是 ( )A .9)9(2-=- B .525±= C .1)1(33-=- D .2)2(2-=-2.观察下列图形,既是轴对称图形,又是中心对称图形的是( )A B C D3.点M (-3,2)向右平移2个单位,向下平移3个单位后得点N ,它的坐标是 ( ) A .(1,1) B .(-1,1) C .(-1,-1) D .(1,-1)4.如图,等边ΔABC 中,D 为BC 上一点,ΔABD 绕点A 旋转后到达ΔACE 的位置,如果∠BAD=18°,则旋转角等于( ) A .18° B . 32° C .60° D .72°5.已知菱形ABCD ,∠A=72°,将它分割成如图所示的四个等腰三角形,则∠1、∠2、∠3的度数分别是( ) A .36°,54°,36° B .18°,54°,54° C .54°,18°,72° D .18°,36°,36°6.函数y=kx+b 的图象经过一、三、四象限,则函数y=bx+k 的图象经过 ( ) A .二、三、四象限 B .一、二、三象限 C .一、三、四象限 D .一、二、四象限7.如图所示,在平面直角坐标系中,菱形MNPO 的顶点P 坐标是(3,4),则顶点M 、N 的坐标分别是( ) A .M (5,0),N (8,4) B .M (4,0),N (8,4) C .M (5,0),N (7,4) D .M (4,0),N (7,4)8.小高从家骑自行车去学校上学,先走上坡路到达点A ,再走下坡路到达点B ,最后走平路到达学校,所用的时间与路程的关系如图所示.放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是( ) A.14分钟 B.17分钟 C.18分钟 D.20分钟二、填空题(本大题共8小题,每小题3分,共24分)(第5题)EB (第4题))(第7题)9.在Rt △ABC 中,斜边AB=2,则AB 2+BC 2+AC 2= .10.已知点A (x ,2),B (-3,y ),若A ,B 关于x 轴对称,则x+y= . 11.如图,该一次函数图像的表达式为 .12.若凸n 边形的内角和为1260°,则从一个顶点出发引的对角线条数是__ . 13.已知等腰梯形ABCD 中,AD ∥BC ,∠B=60°,AD=3,BC=5,则梯形ABCD 的周长为 .14.如图,E 、F 分别是正方形ABCD 的边BC 、CD 上的点,BE=CF ,连接AE 、BF ,将△ABE绕正方形的中心按逆时针方向转到△BCF ,旋转角为a (0°<a <180°),则∠a =__ _. 15.如图,在直角坐标系中,O 是坐标原点,点A (3,-2),一次函数y=-2x+4的图象与y 轴的交点为B ,那么△AOB 面积为 .16.甲、乙两人同时沿着一条笔直的公路朝同一方向前行,开始时,乙在甲前2千米处,甲、乙两人行走的路程S (千米)与时间t (时)的函数图象(如图所示),下列说法不正确的是: .①乙的速度为4千米/时;②经过1小时,甲追上乙 ;③经过0.5小时,乙行走的路程约为2千米;④经过1.5小时,乙在甲的前面.三、解答题(本大题共3小题,每小题6分,共18分) 17(1+18. 实数a 、b 、c 在数轴上的位置如图所示,化简222)()()(b c a c b a --+++.19.如图,一艘轮船以16海里/时的速度离开港口向东南方向航行, 另一艘轮船同时以12海里/时的速度向东北方向航行,则它们离开港口半小时后相距多少海里?(请在图中标上必要的字母并解答) 四、(本大题共2小题,每小题8分,共16分)20.如图,平面直角坐标系中有一个等腰三角形ABC ,其腰长为5,底边BC 长为6. (1)直接写出A 、B 、C 三点的坐标;(第11题)(第15题))(第16题)(第14题)A BCDF(2)求出直线AC 、AB 的函数解析式.21.如图是以正八边形为“基本图形”构成的一种密铺图案.(1)图中间的四边形是什么四边形,请说说你的理由.(2)用两种不同的正多边形组成的密铺图案还有吗?发挥你的聪明才智,把它写出来.五、(本大题共2个小题,每小题9分,共18分) 22.△ABC 在平面直角坐标系中的位置如图所示.(1)作出△ABC 关于y 轴对称的△A 1B 1C 1,并写出△A 1B 1C 1各顶点的坐标;(2)将△ABC 向右平移6个单位,作出平移后的△A 2B 2C 2,并写出△A 2B 2C 2各顶点的坐标;(3)观察△A 1B 1C 1和△A 2B 2C 2,它们是否关于某直线对称?若是,请在图上画出这条对称轴.23.如图,已知一次函数2+-=x y 的图像与x 轴交于点A ,与y 轴交于点C . (1)求∠CAO 的度数;(2)若将直线2+-=x y 沿x 轴向右平移两个单位,试求出平移后直线的表达式;(3)若正比例函数)0(≠=k kx y 的图像与2+-=x y 的图像交于点B ,且∠ABO=30°,求AB 的长及点B 的坐标.六、(本大题共2小题,每小题10分,共20分) 24.【阅读】在平面直角坐标系中,以任意两点P (x 1,y 1)、Q (x 2,y 2)为端点的线段中点坐标为(x 1 +x 22,y 1 +y 22).【运用】(1)如图,矩形ONEF 的对角线交于点M ,ON 、OF 分别在x 轴和y 轴上,O 为坐标原点,点E 的坐标为(4,3),则点M 的坐标为______;(2)在直角坐标系中,有A (-1,2),B (3,1),C (1,4)三点,另有一点D 与点A 、B 、C 构成平行四边形的顶点,求点D 的坐标.25.如图,正方形ABCD 中,点O 是对角线AC 的中点,P 为对角线AC 上一动点,过P 点作PF ⊥DC 于点F .(1)如图1,当点P 与点O 重合时,证明:F 是DC 的中点; (2)如图2,若点P 在线段AO 上(不与点A 、O 重合),PE ⊥P B 且PE 交C D 于点E .①求证:PB =PE ;②写出线段PC 、PA 、CE 之间的一个等量关系式,并证明你的结论;(3)若点P 在线段OC 上(不与点O 、C 重合),PE ⊥PB 且PE 交直线CD 于点E ,请完成图3,并判断(2)中的结论①.②是否分别成立?若不成立,写出相应的结论(所写结论均不必证明).参考答案:1.C 2.D .A 3.C 4.C 5.D 6.D 7.A 8.D 9.8 10.-5 11.121+-=x y 12.6 13.12 14.90° 15.4 16.①③④ 17.18.0 19.10海里 20.(1)A (0,4) B (-3,0) C (3,0) (2)AC :434+-=x y AB :434+=x y 21.解:(1)是正方形,因为正八边形每一个内角是135°,故中间四边形的每一个内角为360°-2×135°=90°,又因为这个四边形的四条边是正八边形的边,故四条边也相等,所以中间的四边形是正方形.(2) 答案不唯一,如正方形和正三角形可以密铺、正六边形和正三角形可以密铺、正十二边形和正三角形等.22.(1)A 1(0,4) B 1(2,2) C 1(1,1)(2)A 2(6,4) B 2(4,2) C 2(5,1) (3)对称轴为x=1.23.(1)A(2,0) C(0,2),∠CAO=45° (2)4+-=x yABCDFO(P)图1ABCD F O图2PEABCDOP图3(3)①当直线kx y = 与2+-=x y 的交点在第四象限时,过点O 作OD ⊥AC 于点D ,AC=22,OD=2,OB=22,BD=6,AB=6-2,过点B作BE⊥x 轴于点E ,可知△ABE 为等腰直角三角形,设AE=BE=x ,x 2+x 2=(6-2)2,x=13-,OE =13+,B(13+,13-) ②当交点在第二象限时,同理可得AB=6+2, B (1-,31+3).24.解:(1)∵四边形ONEF 是矩形,∴点M 是OE 的中点.∵O (0,0),E (4,3),∴点M 的坐标为(2,32).(2)设点D 的坐标为(x ,y ).若以AB 为对角线,AC ,BC 为邻边构成平行四边形,则AB ,CD 的中点重合 ∴⎩⎨⎧1+x 2=-1+324+y 2=2+12,解得,⎩⎨⎧x =1y =-1.若以BC 为对角线,AB ,AC 为邻边构成平行四边形,则AD ,BC 的中点重合 ∴⎩⎨⎧-1+x 2=1+322+y 2=4+12,解得,⎩⎨⎧x =5y =3.若以AC 为对角线,AB ,BC 为邻边构成平行四边形,则BD ,AC 的中点重合 ∴⎩⎨⎧3+x 2=-1+121+y 2=2+42,解得,⎩⎨⎧x =-3y =5.综上可知,点D 的坐标为(1,-1)或(5,3)或(-3,5). 25.(1)连接OD ,四边形ABCD 为正方形,O 为对角线,则OD 为直角三角形 斜边上的中线,∴OD=OC=AC ,又OF ⊥CD ,∴△OFD ,△OFC 为直角三角形, 且OF =OF ,∴△ODF ≌△OCF ,∴CF=DF ,F 为CD 的中点.(2)如图,过P 作MG ⊥AD ,PN ⊥AB ,则四边形ANPM 也为正方形, AP =,2,222CF PC EF BG PN ===CF -EF =CE ,∴PC -PA =CE 2;(3)不成立,PA -PC=CE 2.A B CD F O图2P E M NGABCDF O图1。
八年级下册月考单元辅导资料

八年级下册月考单元辅导资料【导语】想要提高学习效率和成绩,第一要学会浓缩自己的学习时间,善于利用时间,并做到不拖沓,不浪费时间。
缩短了每件事的时间,才能留出更多的时间去学习更多的东西,这也是提高学习效率和成绩最直观的方式之一。
本篇文章是作者为您整理的《八年级下册月考单元辅导资料》,供大家鉴戒。
1.八年级下册月考单元辅导资料篇一一、通假字:1、才美不外见:“见”同“现”,显现。
2、食马者不知其能千里而食也:“食”同“饲”,豢养。
3、食之不能尽其材:“材”同“才”,才能。
4、其真无马邪:“邪”同“耶”,吗。
5、板印书籍:“板”同“版”,雕版。
6、若止印三二本:“止”同“只”,只,仅。
7、已后典籍皆为板本:“已”同“以”,以后。
8、舟首尾约八分有奇:“有”同“又”,表示零数。
9、诎右臂支船:“诎”同“屈”,曲折。
10、左手倚一衡木:“衡”同“横”,跟竖相对。
11、盖简桃核苗条者为之:“简”同“拣”,挑选。
12、满坐寂然:“坐”同“座”,座位。
13、四支僵劲:“支”同“肢”,肢体。
14、同舍生皆被绮绣:“被”同“披”,穿。
15、与之论辨:“辨”同“辩”,辩论。
16、裁如星点:“裁”同“才”,仅仅。
二、古今异义字1、一食或尽粟一石或:古义为“有时”,;今义为“或者”2、无丝竹之乱耳丝竹:古义为“管弦乐器”,文中指奏乐的声音;今义为“丝绸和竹子”3、无文案之劳形形::古义为“身体”;今义为“形状、样子”4、孔子云云::古义为“说”;今义为“云彩”5、其上以松脂、蜡和纸灰之类冒之冒:古义为“蒙、盖”;今义为“冒出”6、药稍熔药:文中指“松脂、蜡和纸灰”;今义为“治病的'药品”7、有布衣毕升布衣:古义为“平民”;今义为“衣服的一种”8、而计其长曾不盈寸曾:古义为“尚”;今义为“曾经”9、其两膝相比者比:古义为“挨着”;今义为“比较”10、高可二黍许许:古义为“左右、上下、光景”;今义为“答应或表猜测”11、尝贻余核舟一尝:古义为“曾经”;今义为“尝试”12、但闻屏障中抚尺一下但:古义为“只”;今义为“转折连词”13、微闻有鼠作作索索闻:古义为“听”;今义为“用鼻子嗅”14、虽人有百手虽:古义为“即便”;今义为“虽然”15、两股战战股:古义为“腿”;今义为“臀部”16、几欲先走走:古义为“跑”;今义为“行走”假:古义为“借”;今义为“与真相对”17、以是人多以书假余是;古义为“这”;今义为“判定动词”18、尝趋百里外从乡之先达趋:古义为“奔向”;今义为“趋向”19、不敢出一言以复复:古义为“辩解”;今义为“又、重复”20、主人日再食再:古义为“两次”;今义为“又一次”2.八年级下册月考单元辅导资料篇二【重点语法】一样将来时表示将要产生的动作或存在的状态。
2011-2012学年辽宁省沈阳市134中学八年级(下)月考数学试卷(含答案)

2011-2012学年辽宁省沈阳市134中学八年级(下)月考数学试卷一、选择题:1.若m<n,则下列不等式中正确的是()A.m﹣3>n﹣3B.3m>n C.﹣3m>﹣3n D.>2.当分式的值为零时,x的值为()A.3B.﹣3C.0D.3或﹣33.下列图形一定相似的是()A.两个矩形B.两个等腰梯形C.有一个内角相等的两个菱形D.对应边成比例的两个四边形4.如图,大正方形中有2个小正方形,如果它们的面积分别是S1、S2,那么S1、S2的大小关系是()A.S1>S2B.S1=S2C.S1<S2D.S1、S2的大小关系不确定5.已知△ABC的三边长分别为:6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF 的另两边长是下列哪一组时,这两个三角形相似()A.2cm,3cm B.4cm,5cm C.5cm,6cm D.6cm,7cm 6.已知点M将线段AB黄金分割(AM>BM),则下列各式中不正确的是()A.AM:BM=AB:AM B.AM=ABC.BM=AB D.AM≈0.618AB7.下列各组中的四条线段a,b,c,d成比例的是()A.a=,b=3,c=2,d=B.a=4,b=6,c=5,d=10C.a=2,b=,c=2,d=D.a=2,b=3,c=4,d=18.如图,AB是斜靠在墙壁上的长梯,梯脚B距墙1.6米,梯上点D距墙1.4米,BD长0.55米,则梯子长为()A.3.85米B.4.00米C.4.40米D.4.50米9.某市今年共有5万人参加研究生考试,为了了解5万名考生的成绩从中抽取1000名考生的英语成绩进行统计分析,以下说法正确的有()个.①5万名考生为总体②调查采用抽样调查方式③1000名考生是总体的一个样本④每名考生的英语成绩是个体.A.4B.3C.2D.110.下列任务中,适宜采用普查方式的是()A.调查某地的空气质量B.了解中学生每天的睡眠时间C.调查某电视剧在本地区的收视率D.了解某一天本校因病缺课的学生数二、填空题:11.分解因式:2(x+1)2﹣12(x+1)+18=.12.若,则=.13.已知关于x的不等式组无解,则a的取值范围是.14.在△ABC中,∠B=35°,AD是BC边上的高,并且AD2=BD•DC,则∠BCA的度数为.15.如图,△ABC中,∠ACB=90°,CD是斜边AB上的高,BD=9,AD=4,那么CD =;AC=.16.使分式方程产生增根的k的值为.17.两个相似三角形的相似比为2:3,它们面积的差是25,那么较大三角形的面积是.18.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为米.19.如图,在▱ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB 等于cm2.20.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,那么根据图的信息,估计小张和小李两人中新手是.21.亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D.然后测出两人之间的距离CD=1.25m,颖颖与楼之间的距离DN=30m(C,D,N在一条直线上),颖颖的身高BD=1.6m,亮亮蹲地观测时眼睛到地面的距离AC=0.8m.则住宅楼的高度为米.22.一组数据4,0,1,﹣2,2的标准差是.23.如图,在△ABC中,点D在AB上,请再添一个适当的条件,使△ADC∽△ACB,那么可添加的条件是.三、解答题:24.先化简再求值:,其中x=.25.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)求出△ABC与△A′B′C′的位似比;(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.26.矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM,E是垂足.①求△ABM的面积;②求DE的长;③求△ADE的面积.27.某城市平均每天处理垃圾700吨,有甲和乙两个处理厂处理,已知甲每小时可处理垃圾55吨,需要费用550元,乙厂每小时可处理垃圾45吨,需要费用495元.如果规定该城市每天用于处理垃圾的费用不得超过7370元,甲厂每天处理垃圾至少要多少吨?28.某广告公司将一块广告牌制作任务交给师徒两人,已知师傅单独完成时间是徒弟单独完成时间的,现由徒弟先做1天,师徒再合作2天完成.(1)师徒两人单独完成任务各需几天?(2)若完成后得到报酬540元,按各人完成的工作量计算报酬,该如何分配?29.为了让学生了解文明礼仪知识,增强文明意识,养成文明习惯.某中学在“文明日照,从我做起”知识普及活动中,举行了一次“文明礼仪知识”竞赛,共有3000名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行了统计.请你根据上面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:(1)求频率分布表中的m、n;(2)补全频率分布直方图;(3)你能根据所学知识确定“众数”、“中位数”在哪一组吗?(不要求说明理由)频率分布表:组别分组频数频率150.5~60.560.08260.5~70.590.12370.5~80.515m480.5~90.5240.32590.5~100.5n0.28合计频数分布直方图:2011-2012学年辽宁省沈阳市134中学八年级(下)月考数学试卷参考答案与试题解析一、选择题:1.若m<n,则下列不等式中正确的是()A.m﹣3>n﹣3B.3m>n C.﹣3m>﹣3n D.>【分析】根据不等式的性质分析判断.【解答】解:A、若m<n,根据不等式的基本性质,不等式两边加(或减)同一个数(或式子),不等号的方向不变,所以m﹣3>n﹣3不正确;B、3m>n中,m<n两边没有同时乘以3,所以不成立;C、不等式两边乘(或除以)同一个负数,不等号的方向改变,故﹣3m>﹣3n正确;D、不等式两边乘(或除以)同一个正数,不等号的方向不变,所以>不正确.故选:C.【点评】不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.2.当分式的值为零时,x的值为()A.3B.﹣3C.0D.3或﹣3【分析】根据分式的值为零的条件得到x2﹣9=0且x2﹣4x+3≠0,然后解方程,再把方程的解代入不等式进行检验.【解答】解:∵分式的值为零,∴x2﹣9=0且x2﹣4x+3≠0,解方程x2﹣9=0得x=3或﹣3,当x=3时,x2﹣4x+3=0,当x=﹣3时,x2﹣4x+3≠0,∴x=﹣3.故选:B.【点评】本题考查了分式的值为零的条件:当分式的分子为零,分母不为零时,分式的值为零.3.下列图形一定相似的是()A.两个矩形B.两个等腰梯形C.有一个内角相等的两个菱形D.对应边成比例的两个四边形【分析】根据相似图形的定义,四条边对应成比例,四个角对应相等,对各选项分析判断后利用排除法解答.【解答】解:A、两个矩形,对应角相等,都是直角,但四条边不一定对应成比例,故本选项不符合题意;B、两个等腰梯形,四个角不一定对应相等,边也不一定对应成比例,所以不一定相似,故本选项不符合题意;C、两个菱形,有一个角相等,则其它角也对应相等,而四条边都相等,所以对应成比例,所以相似,故本选项符合题意;D、对应边成比例,对应角不一定相等,所以不一定相似,故本选项不符合题意.故选:C.【点评】本题主要考查相似图形的定义,熟练掌握矩形、等腰梯形、菱形的性质是解题的关键.4.如图,大正方形中有2个小正方形,如果它们的面积分别是S1、S2,那么S1、S2的大小关系是()A.S1>S2B.S1=S2C.S1<S2D.S1、S2的大小关系不确定【分析】设大正方形的边长为x,根据等腰直角三角形的性质知AC、BC的长,进而可求得S2的边长,由面积的求法可得答案.【解答】解:如图,设大正方形的边长为x,根据等腰直角三角形的性质知,AC=BC,BC=CE=CD,∴AC=2CD,CD=,∴S2的边长为x,S2的面积为x2,S1的边长为,S1的面积为x2,∴S1>S2,故选:A.【点评】本题利用了正方形的性质和等腰直角三角形的性质求解.5.已知△ABC的三边长分别为:6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF 的另两边长是下列哪一组时,这两个三角形相似()A.2cm,3cm B.4cm,5cm C.5cm,6cm D.6cm,7cm【分析】根据三边对应成比例的三角形相似,即可求得.注意△DEF中为4cm边长的对应边可能是6cm或7.5cm或9cm,所以有三种情况.【解答】解:设△DEF的另两边为xcm,ycm,若△DEF中为4cm边长的对应边为6cm,则:,解得:x=5,y=6;若△DEF中为4cm边长的对应边为7.5cm,则:,解得:x=3.2,y=4.8;若△DEF中为4cm边长的对应边为9cm,则:,解得:x=,y=;故选:C.【点评】此题考查了相似三角形的判定:三边对应成比例的三角形相似.解此题的关键要注意△DEF中为4cm边长的对应边不确定,答案不唯一,要仔细分析,小心别漏解.6.已知点M将线段AB黄金分割(AM>BM),则下列各式中不正确的是()A.AM:BM=AB:AM B.AM=ABC.BM=AB D.AM≈0.618AB【分析】根据黄金分割的定义:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比,据此判断即可.【解答】解:∵点M将线段AB黄金分割(AM>BM),∴AM是较长的线段,根据黄金分割的定义可知:AB:AM=AM:BM,AM=AB≈0.618AB,BM=AB.故选:C.【点评】本题主要考查了黄金分割,应该识记黄金分割的公式:较短的线段=原线段的倍,较长的线段=原线段的倍,难度适中.7.下列各组中的四条线段a,b,c,d成比例的是()A.a=,b=3,c=2,d=B.a=4,b=6,c=5,d=10C.a=2,b=,c=2,d=D.a=2,b=3,c=4,d=1【分析】如果两条线段的乘积等于另外两条线段的乘积,我们就说这四条线段叫做成比例线段.【解答】解:A、×3≠×2,故错误;B、4×10≠5×6,故错误;C、2×=×,故正确;D、2×3≠1×4,故错误.故选:C.【点评】考查了比例线段的概念.注意相乘的时候,让最大的和最小的相乘,剩下的两条再相乘,看它们的积是否相等.8.如图,AB是斜靠在墙壁上的长梯,梯脚B距墙1.6米,梯上点D距墙1.4米,BD长0.55米,则梯子长为()A.3.85米B.4.00米C.4.40米D.4.50米【分析】根据梯子、墙、地面三者构成的直角三角形与梯子、墙、梯上点D三者构成的直角三角相似,利用相似三角形对应边成比例解答即可.【解答】解:因为梯子每一条踏板均和地面平行,所以构成一组相似三角形,即△ABC∽△ADE,则=设梯子长为x米,则=,解得,x=4.40.故选:C.【点评】本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.9.某市今年共有5万人参加研究生考试,为了了解5万名考生的成绩从中抽取1000名考生的英语成绩进行统计分析,以下说法正确的有()个.①5万名考生为总体②调查采用抽样调查方式③1000名考生是总体的一个样本④每名考生的英语成绩是个体.A.4B.3C.2D.1【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.【解答】解:①5万名考生的英语成绩是总体,故错误;②正确;③1000名考生的英语成绩是总体的一个样本,故错误;④正确.故选:C.【点评】解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.10.下列任务中,适宜采用普查方式的是()A.调查某地的空气质量B.了解中学生每天的睡眠时间C.调查某电视剧在本地区的收视率D.了解某一天本校因病缺课的学生数【分析】调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.【解答】解:A、调查某地的空气质量,由于范围广,应当使用抽样调查,故本选项错误;B、了解中学生每天的睡眠时间,由于人数多,不易全面掌握所有的人,故应当采用抽样调查;C、调查某电视剧在本地区的收视率,人数较多,不便测量,应当采用抽样调查,故本选项错误;D、了解某一天本校因病缺课的学生数,人数少,耗时短,应当采用全面调查的方式,故本选项正确.故选:D.【点评】此题考查了抽样调查和全面调查,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.二、填空题:11.分解因式:2(x+1)2﹣12(x+1)+18=2(x﹣2)2.【分析】首先提取公因式2,然后利用完全平方公式即可分解.【解答】解:原式=2[(x+1)2﹣6(x+1)+9],=2[(x+1)﹣3]2,=2(x﹣2)2.故答案是:2(x﹣2)2.【点评】本题主要考查提公因式法分解因式和利用完全平方公式分解因式,难点在于把(x+1)当作一个整体分解因式.12.若,则=.【分析】根据两内项之积等于两外项之积把比例式转化为乘积式,然后整理即可得解.【解答】解:∵=,∴3y=5(x﹣y),整理得,5x=8y,∴=.故答案为:.【点评】本题考查了比例的性质,熟记“据两内项之积等于两外项之积”,把比例式转化为乘积式是解题的关键.13.已知关于x的不等式组无解,则a的取值范围是a≥3.【分析】先求出不等式组的解集,利用不等式组的解集是无解可知,x应该是“大大小小找不到”,所以可以判断出a≥3.【解答】解:解关于x的不等式组,得,∵不等式组无解∴大大小小找不到,即a≥3.故答案为:a≥3.【点评】本题主要考查了已知一元一次不等式组的解集,求不等式中的字母的值,同样也是利用口诀求解,但是要注意当两数相等时,不等式组是x>3,x<3时没有交集,所以也是无解,不要漏掉相等这个关系.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到.14.在△ABC中,∠B=35°,AD是BC边上的高,并且AD2=BD•DC,则∠BCA的度数为55°或125°.【分析】分两种情况考虑:当∠BCA为锐角和钝角,将已知的积的恒等式化为比例式,再根据夹角为直角相等,利用两边对应成比例且夹角的相等的两三角形相似可得出△ADB∽△CDA,由相似三角形的对应角相等,利用直角三角形的两锐角互余及外角性质分别求出两种情况下∠BCA的度数即可.【解答】解:当∠BCA为锐角时,如图1所示,∵AD2=BD•DC,∴=,又AD⊥BC,∴∠ADB=∠CDA=90°,∴△ADB∽△CDA,又∠B=35°,∴∠CAD=∠B=35°,∠BCA=∠BAD,在Rt△ADB中,∠ADB=90°,∠B=35°,∴∠BAD=55°,则∠BCA=∠BAD=55°;当∠BCA为钝角时,如图2所示,同理可得△ADB∽△CDA,又∠B=35°,可得∠CAD=∠B=35°,则∠BCA=∠CDA+∠CAD=125°,综上,∠BCA的度数为55°或125°.故答案为:55°或125°【点评】此题考查了相似三角形的判定与性质,直角三角形的性质,以及外角的性质,利用了分类讨论的思想,其中相似三角形的判定方法有:两对对应角相等的两三角形相似;三边对应成比例的两三角形相似;两边对应成比例且夹角相等的两三角形相似.15.如图,△ABC中,∠ACB=90°,CD是斜边AB上的高,BD=9,AD=4,那么CD=6;AC=2.【分析】由于CD⊥AB,那么∠CDA=∠CDB=90°,根据直角三角形的性质可得∠A+∠ACD=90°,∠B+∠BCD=90°,而∠ACB=90°,那么∠A+∠B=90°,再根据同角的余角相等可得∠B=∠ACD,∠A=∠BCD,从而可证△ACD∽△CBD,于是=,易求CD,在Rt△ACD中,利用勾股定理可求AC.【解答】解:∵CD⊥AB,∴∠CDA=∠CDB=90°,∴∠A+∠ACD=90°,∠B+∠BCD=90°,∵∠ACB=90°,∴∠A+∠B=90°,∴∠B=∠ACD,∠A=∠BCD,∴△ACD∽△CBD,∴=,∴CD2=AD•BD,∵AD=4,BD=9,∴CD=6,在Rt△ACD中,AC2=AD2+CD2=52,∴AC=2.【点评】本题考查了相似三角形的判定和性质、勾股定理,解题的关键是证明△ACD∽△CBD,求出CD.16.使分式方程产生增根的k的值为±6.【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x+3)(x﹣3)=0,得到x=3或﹣3,然后代入整式方程算出k的值.【解答】解;方程两边都乘(x+3)(x﹣3),得x﹣3+x+3=k,∵原方程有增根,∴最简公分母(x+3)(x﹣3)=0,∴x=3或﹣3,当x=3时,k=6,当x=﹣3时,k=﹣6.【点评】增根问题可按如下步骤进行:①让最简公分母为0,确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.17.两个相似三角形的相似比为2:3,它们面积的差是25,那么较大三角形的面积是45.【分析】先根据相似三角形的性质求出其面积的比,再设较小的三角形的面积为4x,则较大的三角形的面积为9x,由它们面积的差是25即可求出x的值,进而得出结论.【解答】解:∵两个相似三角形的相似比为2:3,∴其面积的比等于4:9,设较小的三角形的面积为4x,则较大的三角形的面积为9x,∵它们面积的差是25,∴9x﹣4x=5x=25,解得x=5,∴较大三角形的面积=9×5=45.故答案为:45.【点评】本题考查的是相似三角形的性质,即相似三角形面积的比等于相似比的平方.18.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为10米.【分析】利用相似三角形对应线段成比例,求解即可.【解答】解:1米长的标杆测得其影长为1.2米,即某一时刻实际高度和影长之比为定值,所以墙上的2米投射到地面上实际为2.4米,即旗杆影长为12米,因此旗杆总高度为10米.【点评】本题考查的是相似形在投影中的应用,关键是利用相似比来解题.19.如图,在▱ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB 等于48cm2.【分析】根据相似三角形的性质,先证△DOE∽△BOA,求出相似比为,故面积比为,=4S△DOE.即可求S△AOB【解答】解:∵在▱ABCD中,E为CD中点,∴DE∥AB,DE=AB,在△DOE与△BOA中,∠DOE=∠BOA,∠OBA=∠ODE,∴△DOE∽△BOA,相似比为=,故面积比为,=4S△DOE=4×12=48cm2.即S△AOB故答案为:48.【点评】本题考查了平行四边形的性质,相似三角形的判定与性质.关键是明确相似三角形的面积比等于相似比的平方.20.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,那么根据图的信息,估计小张和小李两人中新手是小李.【分析】根据图形可知,小李的射击不稳定,可判断新手是小李.【解答】解:由图象可以看出,小李的成绩波动大,∵波动性越大,方差越大,成绩越不稳定,∴新手是小李.故填小李.【点评】考查了方差的意义:波动性越大,方差越大,成绩越不稳定.21.亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D.然后测出两人之间的距离CD=1.25m,颖颖与楼之间的距离DN=30m(C,D,N在一条直线上),颖颖的身高BD=1.6m,亮亮蹲地观测时眼睛到地面的距离AC=0.8m.则住宅楼的高度为20.8米.【分析】过A作CN的平行线交BD于E,交MN于F,由相似三角形的判定定理得出△ABE∽△AMF,再由相似三角形的对应边成比例即可得出MF的长,进而得出结论.【解答】解:过A作CN的平行线交BD于E,交MN于F.由已知可得FN=ED=AC=0.8m,AE=CD=1.25m,EF=DN=30m,∠AEB=∠AFM=90°.又∵∠BAE=∠MAF,∴△ABE∽△AMF.∴=,=,解得MF=20m.∴MN=MF+FN=20+0.8=20.8m.∴住宅楼的高度为20.8m.故答案为:20.8.【点评】本题考查的是相似三角形的应用,解答此题的关键是将实际问题转化为数学问题进行解答;此题需要转化为相似三角形的问题,利用相似三角形的判定与性质求解.22.一组数据4,0,1,﹣2,2的标准差是2.【分析】先算出平均数,再根据方差公式计算方差,求出其算术平方根即为标准差.【解答】解:数据4,0,1,﹣2,2的平均数为=[4+0+1﹣2+2]=1方差为S2=[(4﹣1)2+(0﹣1)2+(1﹣1)2+(﹣2﹣1)2+(2﹣1)2]=4∴标准差为2.故填2.【点评】计算标准差需要先算出方差,计算方差的步骤是:(1)计算数据的平均数;(2)计算偏差,即每个数据与平均数的差;(3)计算偏差的平方和;(4)偏差的平方和除以数据个数.标准差即方差的算术平方根,注意标准差和方差一样都是非负数.23.如图,在△ABC中,点D在AB上,请再添一个适当的条件,使△ADC∽△ACB,那么可添加的条件是∠ADC=∠ACB或∠ACD=∠B或AC2=AD•AB.【分析】已知△ADC和△ACB中有一个公共角,我们可以再添加一个角,从而利用有两组角对应相等的两个三角形相似来判定其相似.【解答】解:∵∠DAC=∠CAB,∴当∠ADC=∠ACB或∠ACD=∠B或AC2=AD•AB时,均可得出△ADC∽△ACB.故答案为:∠ADC=∠ACB或∠ACD=∠B或AC2=AD•AB【点评】这是一道开放性的题,答案不唯一.三、解答题:24.先化简再求值:,其中x=.【分析】先把括号里式子通分,再把除法转化为乘法,约分化为最简,最后代值计算.【解答】解:原式===﹣,当x=时,原式=﹣=﹣.【点评】本题主要考查分式的化简求值这一知识点,把分式化到最简是解答的关键.25.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)求出△ABC与△A′B′C′的位似比;(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.【分析】(1)位似图形对应点连线所在的直线经过位似中心,如图,直线AA′、BB′的交点就是位似中心O;(2)△ABC与△A′B′C′的位似比等于AB与A′B′的比,也等于AB与A′B′在水平线上的投影比,即位似比为3:6=1:2;(3)要画△A1B1C1,先确定点A1的位置,因为△A1B1C1与△ABC的位似比等于1.5,因此OA1=1.5OA,所以OA1=9.再过点A1画A1B1∥AB交O B′于B1,过点A1画A1C1∥AC交OC′于C1.【解答】解:(1)如图.(2)△ABC与△A′B′C′的位似比为1:2.(3)如图【点评】本题考查位似图形的意义及作图能力.画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.26.矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM,E是垂足.①求△ABM的面积;②求DE的长;③求△ADE的面积.【分析】①由M是BC的中点可得BM长度,那么△ABM的面积=×AB×BM,把相关数值代入即可求解;②由勾股定理易得AM长,可证得△ADE∽△MAB,那么利用对应边比等于相似比可求得DE长;③由相似可得AE的长,那么△ADE的面积=×AE×DE,把相关数值代入即可求解.【解答】解:①∵M是BC的中点,BC=6,∴MB=3,∵AB=4,∴△ABM的面积=×AB×BM=×4×3=6;②∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∴∠DAE=∠AMB,∵DE⊥AM,∴∠DEA=90°,∴△ADE∽△MAB,∵AB=4,BM=3,∴AM=5,∴AE:MB=AD:AM=DE:AB,∴AE=3.6,DE=4.8.③△ADE的面积=×AE×DE=×3.6×4.8=8.64.【点评】解决本题的关键是利用相似三角形对应边成比例的性质求得所求三角形的长与宽.27.某城市平均每天处理垃圾700吨,有甲和乙两个处理厂处理,已知甲每小时可处理垃圾55吨,需要费用550元,乙厂每小时可处理垃圾45吨,需要费用495元.如果规定该城市每天用于处理垃圾的费用不得超过7370元,甲厂每天处理垃圾至少要多少吨?【分析】设甲厂每天处理垃圾x吨,分别求出甲、乙两场分别处理1吨垃圾需要的费用,然后根据每天用于处理垃圾的费用不得超过7370元,可得出不等式,解出即可.【解答】解:设甲厂每天处理垃圾x吨,由题知:甲厂处理每吨垃圾费用为=10元,乙厂处理每吨垃圾费用为=11元.则有10x+11(700﹣x)≤7370,解得:x≥330,答:甲厂每天处理垃圾至少330吨.【点评】此题考查了一元一次不等式的知识,解题关键弄清题意,找出合适的不等关系,列出不等式,再求解,难度一般.28.某广告公司将一块广告牌制作任务交给师徒两人,已知师傅单独完成时间是徒弟单独完成时间的,现由徒弟先做1天,师徒再合作2天完成.(1)师徒两人单独完成任务各需几天?(2)若完成后得到报酬540元,按各人完成的工作量计算报酬,该如何分配?【分析】工作量常用的等量关系:工作时间×工效效率=工作总量.本题等量关系为:师工作量+徒工作量=1.【解答】解:(1)设徒弟单独完成任务需x天,则师需天,依题意得解得x=6经检验,x=6是原方程的解∴=4答:师傅需要4天,徒弟需要6天.(2)师傅完成的工作量=,∴徒弟完成的工作量为,故每人各得报酬270元,答:每人各得270元.【点评】本题考查工作量常用等量关系.分析题意,找到合适的等量关系是解决问题的关键.此题涉及的公式:工作总量=工作效率×工作时间.29.为了让学生了解文明礼仪知识,增强文明意识,养成文明习惯.某中学在“文明日照,从我做起”知识普及活动中,举行了一次“文明礼仪知识”竞赛,共有3000名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行了统计.请你根据上面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:(1)求频率分布表中的m、n;(2)补全频率分布直方图;(3)你能根据所学知识确定“众数”、“中位数”在哪一组吗?(不要求说明理由)频率分布表:。
八年级数学下册知识点复习专题讲练全套含解析

目录一、勾股定理的逆定理 (4)二、实际应用定理中的注意问题 (4)三、勾股定理逆定理的几种典型应用 (4)利用勾股定理计算角度 (5)开放性试题 (6)(答题时间:45分钟) (7)一、选择题 (7)二、填空题 (7)三、解答题 (8)函数中的动点问题 (12)利用动点形成的函数图象求解析式 (14)动点综合型问题 (15)(答题时间:45分钟) (16)一、选择题 (16)二、填空题: (18)三、解答题: (19)解析平方根和立方根 (24)1. 算术平方根 (24)(3)被开方数与算术平方根的关系 (24)当被开方数扩大时,它的算术平方根也扩大;当被开方数缩小时,它的算术平方根也缩小。
. 242. 平方根 (24)3. 立方根 (25)(3)被开方数与立方根的关系 (25)当被开方数扩大时,它的立方根也扩大;当被开方数缩小时,它的立方根也缩小。
(25)(答题时间:30分钟) (27)一、平行四边形的性质 (37)二、平行四边形的面积法使用 (37)平行四边形的面积问题 (39)平行四边形中的折叠 (40)(2)∵∠1=∠2,∴EG=GF,∵AB∥DC, (40)(答题时间:45分钟) (40)二、填空题 (42)三、解答题 (42)剖析不等式(组)的解集 (47)一、一元一次不等式(组)的解: (47)二、利用数轴求不等式组的解集分以下四种情况: (47)三、常考题型 (47)(答题时间:45分钟) (50)一、选择题(共8小题) (50)二、解答题(共4小题) (51)一、选择题(共8小题) (52)二、解答题(共4小题) (53)巧用勾股定理解决几何问题 (55)一、勾股定理在解决几何问题中的应用技巧 (55)二、特殊几何图形中的勾股定理计算规律 (56)分类讨论求值 (57)生活中的勾股定理方案设计 (58)(答题时间:45分钟) (58)一、选择题 (58)二、填空题: (59)三、解答题: (60)一次函数中的分段函数 (65)收费问题中的分段计算 (68)(答题时间:45分钟) (69)一、选择题 (69)二、填空题: (71)三、解答题: (71)图甲图乙 (72)用坐标表示旋转 (76)一、选择题 (78)二、填空题 (79)三、解答题 (80)一、选择题 (83)二、填空题 (83)三、解答题 (84)不等式组的解题技巧 (86)一、一元一次不等式组的解法 (86)二、用数轴表示不等式组的解集 (86)三、求不等式组的特殊解 (86)(答题时间:45分钟) (88)一、选择题 (88)二、填空题 (89)三、解答题 (89)一、选择题 (91)二、填空题 (91)三、解答题 (91)二次根式基本定义及其应用 (93)一、二次根式的定义 (93)二、二次根式的判定 (93)三、二次根式有意义的条件 (93)估算二次根式的值 (94)求最值问题 (94)(答题时间:45分钟) (95)一、选择题 (95)二、填空题: (96)三、解答题: (96)一、二次根式具有双重非负性 (99)二、二次根式整数部分、小数部分 (99)双重值非负性的应用 (100)特殊根式化简 (100)(答题时间:45分钟) (101)一、选择题 (101)二、填空题 (101)三、解答题 (102)勾股定理的综合使用 (105)一、勾股定理 (105)二、定理适用范围及应用 (105)分类讨论思想的应用 (107)图形变换的证明 (107)(答题时间:45分钟) (108)一、选择题 (108)二、填空题: (109)三、解答题: (110)勾股定理及逆定理的综合应用一、勾股定理的逆定理逆定理如果三角形三边长a,b,c满足222a b c+=,那么这个三角形是直角三角形,其中c为斜边。
八年级数学下册复习课件(人教版,整理版)

D
X=3 8-X=5
8-x
4
B 85-x S△BFD=5×4÷2=10
F3x
C
A′
考点七:与展开图有关的计算
1 、如图,在棱长为 1 的正方体 ABCD — A ’ B ’ C ’ D ’的表面上,求从顶点 A 到顶点 C ’ 的最短距离.
2 、 如图一个圆柱,底圆周长 6cm ,高 4cm ,一只蚂蚁沿外 壁爬行,要从 A 点爬到 B 点, 则最少要爬行 cm
考点一:利用勾股定理求面积
1 、求阴影部分面积:( 1 )阴影部分是正方形; ( 2 )阴影部分是长方形;( 3 )阴影部分是半 圆.
2. 如图,以 Rt △ ABC 的三边为直径分别向外 作三个半圆,试探索三个半圆的面积之间的关 系.
3 、如图所示,分别以直角三角形的三边向外作 三个正三角形,其面积分别是 S 1 、 S 2 、 S 3 , 则它们之间的关系是( )
由题意得
x 3
5 x
0, 0,
解得 - 5≤x<3.
考点二 二次根式的性质
例2 若 x 1 (3x y 1)2 0, 求 5x y2 的值. 【解析】根据题意及二次根式与完全平方式的非 负性可知 x 1和(3x y 1)2均为0. 解:∵ x 1 (3x y 1)2 0, ∴x-1=0,3x+y-1=0,解得x=1,y=-2. 则 5x y2 51 (2)2 3.
考点四: 应用勾股定理解决楼梯上铺地毯问题
某楼梯的侧面视图如图 3 所示,其中
米,
,
,
因某种活动要求铺设红色地毯,则在 AB 段楼梯所铺地毯的长度应为
.
考点五:利用列方程求线段的长(方程思想)
八年级数学第二次月考

明光三中2019-2019学年度第二学期第二次月考八年级数学试卷 (命题人:嘉禾)一、选择题(每小题4分,共40分)1、在下列长度的各组线段中,能组成直角三角形的是…………………………………( ). A .12,15,17 B .9,16,25 C .5a ,12a ,13a (a>0) D .2,3,42、若等腰三角形的腰长为10,底边长为12,则底边上的高为………………………( )A 、6B 、7C 、8D 、93、一块木板如图所示,已知AB =4,BC =3,DC =12,AD =13,∠B =90°,木板的面积为…………………………………………………………( ) A .60 B .30 C .24 D .124、下列二次根式中属于最简二次根式的是………………………( ) A .14 B .48 C .baD .44+a 5、已知三角形三边为a 、b 、c ,其中a 、b 两边满足0836122=-++-b a a ,那么这个三角形的最大边c 的取值范围是……………………………………………( ) A .8>c B .148<<c C .86<<c D .142<<c6、已知a <0,那么a a 22-可化简为…………………………………………………( )(A )-a (B )a (C )-3a (D )3a7、方程)3()3(+=+x x x 解是………………………………………………………………( ) A .x 1=1 B .x 1=0, x 2=-3 C .x 1=1,x 2=3 D .x 1=1, x 2=-3 8、要使根式3-x 有意义,则字母x 的取值范围是…………………………………( ) (A )x ≥3 (B )x >3 (C )x ≤3 (D )x ≠39、已知直角三角形的两条边长分别是3和4,则第三边为 ………………………( ) A.5 B.7 C.5或7 D. 不能确定10、若α、β是方程x 2+2x-2019=0的两个实数根,则α2+3α+β的值为…………( ) A 、2019 B 、2019 C 、-2019 D 、4010二、填空题(每小题5分,共20分)11、已知一个三角形的三边长分别为12、16、20,则这个三角形的面积是___________. 12、若关于x 的一元二次方程kx 2-2x+1=0有两个不相等的实数根,则k 的取值范围是_____________________ 13、若()()05422222=-+-+y x y x ,则=+22y x _________.14、.如右图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A ,B ,C ,D 的面积 之和为___________cm 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B169252011-2012学年第二学期八年级数学第二次月考复习课讲义第一、二课时一、细心选一选 (本题有10个小题, 每小题3分, 满分30分.)1.在式子22,2,,3,1y x xab b a c b a --π中,分式的个数为( )A .2个B .3个C .4个D .5个 2. 当分式13-x 有意义时,字母x 应满足( ). A. 0=x B. 0≠xC. 1=xD. 1≠x3.医学研究发现一种新病毒的直径约为0.000043毫米,•则这个数用科学记数法表示为( )毫米.A. 0.43×10-4B. 0.43×104C. 4.3×10-5D. 4.3×1054.已知反比例函数xky =的图象经过点(1,—2),则k 的值可确定为( ). A. -2 B. 21 C. 2 D. 21-5.如图,已知两正方形的面积分别是25和169,则字母B 所代表的正方形的面积是( ). A .12 B .13 C .144 D .194 6.根据分式的基本性质,分式aa b--可变形为( ). A .a a b-- B . a a b - C . -a a b - D . a a b +7.如果矩形的面积为6cm 2,那么它的长y cm 与宽xcm 之间的函数关系用图象表示大致是( ).A B C D8.某班抽取6名同学进行体育达标测试,成绩如下:80,90,75,80,75,80. 下列关于对这组数据的描述错误的是( )A .众数是80B .平均数是80C .中位数是75D .极差是15 9.在ABC ∆中,5=a ,12=b ,13=c .则=∆ABC S ( ) A 、60 B 、30 C 、78 D 、265 10.已知反比例函数y=xk的图象在第二、第四象限内,函数图象上有两点A (72-,y 1)、 B (5,y 2),则y 1与y 2的大小关系为( ). A .y 1>y 2B .y 1=y 2C .y 1<y 2D .无法确定yxOyxOyxOyxO二、耐心填一填 (本题有10个小题, 每小题3分, 共30分) 11.当x=__ __时,分式123+-x x 的值为零. 12.计算:2251235ab c c ab ∙= . 13.如图,学校有一块长方形花坛,有极少数人为了避开拐角走 “捷径”,在花坛内走出了一条“路”,他们仅仅少走了 m ,却踩伤了花草. 15.当x 时,分式23xx -的值大于0. 16.如图,反比例函数y=kx在第二象限内的图象如图,点M 是图象上一点,MP ⊥x 轴于点P ,如果S △MOP =2,则k=________.17.如图ABC ∆中,DE ∥BC ,DF ∥AC ,EF ∥AB ,图中共有_______个平行四边形, 如果ABC ∆是边长为3的等边三角形,那么连结各边中点所成的DEF ∆的周长为_______, ABC ∆的面积等于13题图 16题图 17题图18.如图,P 是四边形ABCD 的DC 边上的一个动点.当四边形ABCD 满足条件______时,△PBA 的面积始终保持不变(注:只需填上你认为正确的一种条件即可).19题图19.为了解用电量的多少,小明在四月初连续几天同一时刻观察电表显示的度数,记录如下表:估计小明家四月份(30天)的总用电量约为___________度.20.2132=--x m mx 的解是2,则m 的值是 .F_ x三、解答题(共90分,解答要求写出文字说明, 证明过程或计算步骤) 21.(本题满分满分20分)计算:(1)21233(2)(2)x y x y ---÷ (2) 11122-+--+a a a a a 22.(本题满分10分)解方程:32121---=-xxx 23.(本题满分10分)现要装配30台机器,在装配好6台以后,采用了新的技术,每天的工作效率提高了一倍,结果共用了3天完成任务,问原来每天装配机器有多少台? 24.(本题满分12分) 已知02=-y x ,求)(2222y x yxy x yx -∙+-+的值.25. (本题满分12分)如图,在正方形ABCD 中,E 是BC 的中点,F 为CD 上一点,且CF=41CD 。
求证:△AEF 是直角三角形。
26. (本题满分12分)如图,已知一次函数y=k 1x+b 的图象与反比例函数y=xk 2的图象交于A (1,-3),B (3,m )两点,连接OA 、OB . (1)求两个函数的解析式;(2)求△AOB 的面积.27.(本题满分12分)已知:如图,在△ABC 中,中线BE ,CD 交于点O ,F ,G 分别是OB ,OC 的中点.求证:四边形DFGE 是平行四边形.ABOxy第三、四课时一、细心选一选(本题有10个小题, 每小题3分, 满分30分.)1.用科学记数法表示0.0000071=().A.67.110-⨯ B.67.110⨯ C.57.110-⨯ D.77110-⨯2.下列计算正确的是().A.33x xy y+=+B.222()33b bc c=C.122a bb a÷= D.a ab b-=-3..某村的粮食总产量为a(a为常数)吨,设该村的人均粮食产量为y吨,人口数为x,则y与x之间的函数关系式的大致图象应为()(A) (B) (C) (D)4.若O是四边形ABCD对角线的交点,且OA=OB=OC=OD,则四边形ABCD是()(A)等腰梯形(B)矩形(C)正方形(D)菱形5.下列各命题都成立,而它们的逆命题不能成立的是().A.两直线平行,同位角相等 B.全等三角形的对应角相等C.四边相等的四边形是菱形 D.直角三角形中,斜边的平方等于两直角边的平方和6.某校八年级6个班级同学在“支援玉树灾区献爱心”活动中都捐了款,具体班级捐款情7.如图,过反比例函数2yx=(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设△AOC和△BOD的面积分别是S1、S2,比较它们的大小,可得()A、S1>S2B、S1=S2C、S1<S2D、大小关系不能确定8.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是()cm2(A) 28 (B) 49 (C) 98 (D) 147第8题图9.如图,在□ABCD中,对角线AC BD,相交于点O,2OA=,若要使□ABCD为矩形,则OB的长应该为().A.4 B.3 C.2 D.1A DOB C第9题第18题图第11题图10.如图,任意四边形ABCD 各边中点分别是E 、F 、G 、H ,若对角线AC 、BD 的长都为20cm ,则四边形EFGH 的周长是( )。
A 、80cmB 、40cmC 、20cmD 、10cm二、耐心填一填 (本题有10个小题, 每小题3分, 共30分)11.在□ABCD 中,50A ∠=,则C ∠=.12.在某校举行的艺术节的文艺演出比赛中,八位评委给其中一个表演节目现场打出的分数如下:9.3,8.9,9.3,9.1,8.9,8.8,9.3,9.5,则这组数据的众数是______. 13.已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 . 14.边长为1cm 的正方形的对角线长是 cm .15.已知反比例函数ky x=的图象过点(1,-2),则在图象的每一支上,y 随x 增大而 .(填‘增大’或‘减小’)16.如图,△ABC 中,D 为BC 上一点,且BD =3,DC =AB =5,AD =4,则AC = .17.在平面直角坐标系中,点A 、B 、C 的坐标分别是A (-2,5),B (-3,-1),C (1,-1),在第一象限内找一点D ,使四边形ABCD 是平行四边形,那么点D 的坐标是 。
18.如图,一棵树在离地面9米处断裂,树的顶部落在离底部12米处,树折断之前的高度是 米。
19.轮船顺水航行80千米和逆水航行60千米所用的时间相同.若水流的速度是3千米/时,轮船在静水中的速度是x 千米/时.则求x 所列的方程是 . 20.ABCD ,加一个条件______________,它就是菱形.三、解答题(共90分,解答要求写出文字说明, 证明过程或计算步骤)21. (本题满分10分) 先化简,再求值:2132446222--+-∙+-+a a a a a a a ,其中31=a .第16题22. (本题满分10分)如图,在等腰梯形ABCD 中,AD ∥BC ,AB ∥DE ,BC =8,AD =5,求EC 的长.23. (本题满分12分)(2)如图是一个外轮廓为矩形的机器零件平面示意图,根据图 中的尺寸(单位:mm ),计算两圆孔中心A 和B 的距离.24.(本题满分12分)已知经过闭合电路的电流I 与电路的电阻R 是反比例函数关系,请根据表格已知条件求出I 与R 的反比例函数关系式,并填写..表格中的空格.25.(本题满分12分)小青在本学期的数学成绩如下表所示(成绩均取整数):(1)计算小青本学期的平时平均成绩;(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x 至少为多少分才能保证达到总评成绩90分的最低目标?第20题 C 第22题 第18(2)题26.(本题满分12分)已知,如图,E、F分别为ΔABC的边BC、CA的中点,延长EF到D,使得DF=EF,连结DA,DC,AE.(1)求证:四边形ABED是平行四边形.(2)若AB=AC,试证明四边形AECD是矩形.27.(本题满分12分)已知:如图,AB=3,AC=4,AB⊥AC,BD=12,CD=13,(1)求BC的长度;(2)证明:BC⊥BD. 第21题第五、六课时一、选择题(本大题共10小题,每小题3分,满分30分) 1. 如图1,在等腰梯形ABCD 中,AD BC ∥,70B ∠=,则C =∠( ).(A )60(B ) 68(C )70(D )1102. 某校8年级(2)班的10名同学某天的早餐费用分别为(单位:元):2 、5、3、3 、4、5 、3 、6 、5、3, 在这组数据的众数是( ).(A )3 (B ) 3.5 (C )4 (D )6 3. 下列运算正确的是( ).(A )61233()b a b a-= (B )121231111R R R R ++==(C ) 51233()b a b a-= (D )1212112R R R R +=+ 4.如图3,已知□ABCD 的两条对角线AC 与BD 交于平面直角坐标系的原点,点A 的坐标为(-2,3),则点C 的坐标为( ).(A )(-3,2) (B)(-2,-3) (C )(3,-2) (D )(2,-3) 5. 下面命题中错误..的是( ). (A )梯形是轴对称图形(B )三角形的三条中线交于一点(C )菱形的四条边都相等 (D )有一个角是直角的菱形是正方形 6.已知广州市的土地总面积约为7434 km 2,人均占有的土地面积S (单位:km 2/人)随全市人口n (单位:人)的变化而变化,则S 与n 的函数关系式为( ).(A )7434S n = (B )7434S n=(C ) 7434n S = (D )7434nS =7. 如图5,函数y x m =+与(0)my m x=≠在同一坐标系内的图象可能是( ).A D CB图1图3xxx图5(B )(A) (C) (D)E B 8.已知:如图2在矩形ABCD 中,E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点.若AB =6,AD =8,则图中阴影部分的面积是( )A 、16B 、18C 、24D 、329.如图已知等腰梯形ABCD 中,AB ∥CD,AD=BC,对角线AC ⊥BD,AB=3,CD=7,那么梯形ABCD 的面积等于( ) A 、10.5 B 、21 C 、25 D 、10210.双曲线y=x6上有三点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),且x 1<x 2<0<x 3,用不等号把y 1,y 2,y 3,从小到大排列.....是___________________. 二、填空题(共10题,每题3分,共30分) 11.当_________x =时,分式11x x +-的值为0. 12.点(1,3)在反比例函数ky x=的图象上,则_________.k = 13.人体中成熟的红细胞的平均直径为0.00000077m ,用科学记数法表示0.00000077的结果为 .14.写出命题“直角三角形两直角边的平方和等于斜边的平方”的逆命题: . 15. 如图6,在菱形ABCD 中,对角线6AC cm =,5BC cm =,则菱形ABCD 的面积为 .16.如图7是甲、乙两地5月上旬的日平均气温统计图,则甲、乙两地这10天日平均气温的方差大小关系为:2S 甲 2S 乙.D图71 2 3 4 5 6 7 8 9 10ODCBA 图6HEFGDCB A17.若直角三角形的边长分别为3㎝,4㎝,则第三边长为.18.反比例函数3kyx+=的图象在二、四象限,则k的取值范围是 .19.在平行四边形ABCD中,∠B+∠D=130°,则∠C=___________度.20.已知∆ABC中,AB=10,BC=12,BC边上的中线AD=8,则△ABC的形状为___________。
