分数、百分数应用题(奥赛培训)第一讲
分数、百分数应用题(奥赛培训1)

分数、百分数应用题(奥赛培训1)分数.百分数应用题(一)例1:一篓苹果分给甲.乙.丙三人,甲分得全部苹果的加5个苹果,乙分得全部苹果的加7个苹果,丙分得其余苹果的,最后剩下的苹果正好等于一篓苹果的.这篓苹果有多少个?分析:丙分得苹果的也是总数的,其余为_2=,(5+7)÷=40(个)例2:甲数是乙数.丙数.丁数之和的,乙数是甲数.丙数.丁数之和的,丙数是甲数.乙数.丁数之和的.已知丁数是260,求甲数.乙数.丙数.丁数之和.分析:甲数为:(甲+乙+丙+丁)的,乙数为:(甲+乙+丙+丁)的丙数为:(甲+乙+丙+丁)的;甲+乙+丙+丁=〝1〞,丁数为:总数:260÷=1200(个).例3:有甲.乙两个粮库,原来甲粮库存粮的吨数是乙粮库的.如果从乙粮库调6吨粮食到甲仓库,甲仓库存粮的吨数就是乙仓库的.原来甲.乙粮库各存粮多少吨?解:设乙仓库存粮为_吨,甲仓库存粮为_吨.解之得 _=126例4:学校有皮球和足球共100个,皮球的个数的比足球个数的多16个.学校有皮球和足球各多少个?解:设皮球个数为_ 个,足球的个数为100-_,_=60,足球:100-_=100-60=40(个).例5:有红黄两种颜色的小球共140个,拿出红球的,再拿出7个黄球,剩下的红球和黄球正好一样多.原来红球和黄球各有多少个?解:设红球为_个,黄球为140-_个.(1-)_ =140-_-7 _=76 黄球=64(个)例6:金放在水里称,重量减轻;银放在水里称,重量减轻.一块合金重770克,放在水里称,共减轻了50克.这块合金含金含银各有多少克?解:方法(一):设金重为_克,银重为(770-_)克,解之得:_=570银重=770-570=200(克)方法(二):设金减轻_,银减轻50-_,_÷+(50-_)÷=770解之得: _=30 银减轻=50-30=20(克)金=30÷=570(克) 银=20÷=200(克)练习:1.桃树棵数的和梨树棵数相等.两种果树共有141棵,两种树各有多少棵?桃树: 梨树=:=20:27桃树:141_=60(棵)梨树:141_=81(棵)2.两个筑路队合修一条公路,甲队修的相当于乙队修的.甲队比乙队多修10千米,两队共修多少千米?甲:乙=:=5:410÷=90(千米)3.一堆砖,用去了它的后,又增加了340块,这时砖的总块数是原来设有用时的块数的.用去了多少块砖?340÷=540(块)4.甲.乙两个容器共有药水2000克.从甲容器里取出的药水,从乙容器里取出的药水,结果两个容器里共剩下1400克药水.甲.乙两个容器里原来各有多少克药水?解:设甲容器原来有_克药水,乙容器原来有(2000-_)克药水,=1400解之得:_=1200 乙容器原来有: (2000-_)=800.5.乙队原有人数是甲队的.现在从甲队派30人到乙队,则乙队人数是甲队的.甲.乙两队原来各有多少人?解:设甲队原来有_人,乙队原来有_人,解之得_=210乙队原来有: _=_210=90.6.图书馆新购进3种书,其中工具有180本,科技书占总数的,文艺书的本数是其它两种书本数的.购进的3种书共有多少本?180_(1+)÷(1--_)=360。
专题09:《分数和百分数—典型应用题(一)》小升初数学专题讲练(解析版)通用版
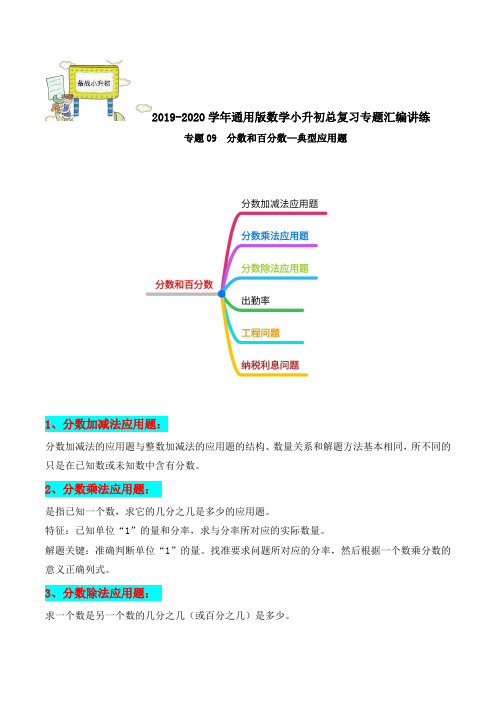
2019-2020学年通用版数学小升初总复习专题汇编讲练专题09 分数和百分数—典型应用题1、分数加减法应用题:分数加减法的应用题与整数加减法的应用题的结构、数量关系和解题方法基本相同,所不同的只是在已知数或未知数中含有分数。
2、分数乘法应用题:是指已知一个数,求它的几分之几是多少的应用题。
特征:已知单位“1”的量和分率,求与分率所对应的实际数量。
解题关键:准确判断单位“1”的量。
找准要求问题所对应的分率,然后根据一个数乘分数的意义正确列式。
3、分数除法应用题:求一个数是另一个数的几分之几(或百分之几)是多少。
特征:已知一个数和另一个数,求一个数是另一个数的几分之几或百分之几。
“一个数”是比较量,“另一个数”是标准量。
求分率或百分率,也就是求他们的倍数关系。
解题关键:从问题入手,搞清把谁看作标准的数也就是把谁看作了“单位一”,谁和单位一的量作比较,谁就作被除数。
甲是乙的几分之几(百分之几):甲是比较量,乙是标准量,用甲除以乙。
甲比乙多(或少)几分之几(百分之几):甲减乙比乙多(或少几分之几)或(百分之几)。
关系式(甲数减乙数)/乙数或(甲数减乙数)/甲数。
已知一个数的几分之几(或百分之几 ) ,求这个数。
特征:已知一个实际数量和它相对应的分率,求单位“1”的量。
解题关键:准确判断单位“1”的量把单位“1”的量看成x根据分数乘法的意义列方程,或者根据分数除法的意义列算式,但必须找准和分率相对应的已知实际数量。
4、出勤率发芽率=发芽种子数/试验种子数×100%小麦的出粉率= 面粉的重量/小麦的重量×100%产品的合格率=合格的产品数/产品总数×100%职工的出勤率=实际出勤人数/应出勤人数×100%5、工程问题:是分数应用题的特例,它与整数的工作问题有着密切的联系。
它是探讨工作总量、工作效率和工作时间三个数量之间相互关系的一种应用题。
解题关键:把工作总量看作单位“1”,工作效率就是工作时间的倒数,然后根据题目的具体情况,灵活运用公式。
分数百分数应用题的总复习公开课课件ppt

为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
1.求一个数是另一个数的几(百)分之几 的应用题
求一个数是另一个数的几(百) 分之几这类应用题是比较两个数量 之间关系的问题,并将两个数量间 的关系用分数或百分数的形式表示 出来。
3.已知一个数的几(百)分之几是多少,求 这个数的应用题 通俗的说就是已知单位“1”的几(百)分之几是多少, 求单位“1”。这类应用题通常单位“1” 是未知的, 解题以“除法的意义” 为依据。注意找准对应量与对 应分率。 用除法(或方程)解题!
已知量÷已知量的对应分率(百分率)=单位“1”的量
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
几?
分之几?
2、一批水果第一天卖出
3 8
,
这批水果重多少千克?
①刚好卖出40千克。
②第二天又卖出20千克,这时还剩下20千克。
③第二天卖出12.5%,两天共卖出40千克。
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
③彩电降价了百分之几?
(现价和原价比较,原价是单位“1”)
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
找单位“1”小窍门:
读题找准关键字,比、占、是、相当于, 后面的量就是单位“1” 单位“1”有时藏起来,就到问题中发现。 对应分率比“1”多(增加、提高、上 涨)就用“1+”,比“1”少(减少、降 低、便宜)就“1-”
小学六年级奥数教程题目

奥数教程(六年级)第一讲 分数的计算例1 计算:4.3695.3)5.3694.3(2009-⨯+⨯⨯ (提示:转化成分母相同) 例2 计算:1341321318428.44.22.113913313118628.106.32.1⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯ (提示:找分子分母共同点,变形)例3 计算:10241195121172561151281136411132191617815413211+++++++++(提示:先合并再相加) 例4 计算:)1099()988()877()766()655()544()433()322()211(-⨯-⨯-⨯-⨯-⨯-⨯-⨯-⨯-(提示:先求差)例5 计算:23191713111917132223171311132613117455⨯⨯+⨯⨯+⨯⨯+⨯⨯(分子分解质因数,约分) 例6 计算:()123...891098...32199...531)100...642(22222222++++++++++++++++-++++第二讲 分数的大小比较例1 分数75、1715、94、12440、309103中,哪一个最大?(提示:化简,统一分子)例2 在□内填上相同的自然数,使不等式3619613111>++++ 成立,此时□内的数的最大值是几?例3 若A=12009200912+-, B=2220082009200820091+⨯-,比较A 与B 的大小。
(提示:比较分母)例4 不求和,比较200520022004200420032005+与200520022003200420032006+的大小。
例5 在下列□内填两个相邻的整数,使不等式成立。
□<10191817161514131211+++++++++<□ 例6 已知A=21771 (21611216011)+++,求A 的整数部分是多少?第三讲 巧算分数的和例1 计算:50491...431321211⨯++⨯+⨯+⨯ 例2 计算:100981...861641421⨯++⨯+⨯+⨯ 例3 计算:10099981...43213211⨯⨯++⨯⨯+⨯⨯ 例4 计算:10099...3211...4321132112111++++++++++++++++例5 计算:2019...4321...54321432132121++++++++++++++++ 例6 计算:⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+++9911...311211991 (41131121141)3112113121121 第四讲 繁分数例1 计算:20072008200820091200920092009122⨯+-+-÷ 例2 计算:41322111+++例3 规定□表示选择两数中较大的数的运算,△表示选择两数中较小的数的运算。
分数百分数应用题-PPT课件

单 1、1某班有 女生20名,男生比女生
位 “
多4
,男生 有多少人?20 20 1 4
20 1 14
1 2、1某班有 男生25名,女生比男生
”
少 , 女生有多少人? 已
知
5
25 25 1 5
25
1
1 5
求 单 位
3、1某班有 男生25名,男生比女生
多 , 女生有多少人? 4
25
1
1 4
1 25
20
1
1 4
25 1 15
25
1
1 4
20 1- 15
20 1 25% 25 1 20%
25 1 25% 20 1- 20%
想一想:分数应用题 和百分数应用题数量 关系相同吗?解答方 法呢?
百分数应用题和分数 应用题的表现形式虽 然不同,但数量关系 相同,所以解答方法 也相同。
尝试练习:
1、男生比女生多几分之几?
1 (25-20)÷20=
4 2、女生比男生少几分之几?
1 (25-20)÷25= 5
1、男生比女生多 1
4
单位“1”:女生人
数 2、女生比男生少
1
5
单位“1”:男生人
数
你能把“某班男生25名,女生20名” 这两个条件 和 “女男生比男女生少多1 ”
编成单位“1”是已知的应用题吗?54
1.仓库里有15吨钢材,第一次用去总数的
20%,第二次用去总数的 1,还剩下多少吨
钢材?
2
15 ×(1-20%-
1 2
)
2.仓库里有一些钢材,第一次用去总数的20 %,第二次用去总数的 1 ,还剩下15吨,仓 库里有多少吨钢材? 2
六年级奥数十二.分数百分数应用题.教师版

六年级奥数十二.分数百分数应用题.教师版第一篇:六年级奥数十二.分数百分数应用题.教师版学远教育小六奥数资料小六奥数专题十二:分数百分数应用题一、知识点概述1.分析题目确定单位“1”2.准确找到量所对应的率,利用量÷对应率=单位“1”解题3.抓住不变量,统一单位“1”4.分数应用题是研究数量之间份数关系的典型应用题,一方面它是在整数应用题上的延续和深化,另一方面,它有其自身的特点和解题规律.在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键.二、解题技巧:分数应用题经常要涉及到两个或两个以上的量,我们往往把其中的一个量看作是标准量.也称为:单位“1”,进行对比分析。
在几个量中,关键也是要找准单位“1”和对应的百分率,以及对应量三者的关系例如:(1)a是b的几分之几,就把数b看作单位“1”.1,乙比甲少几分之几?819191方法一:可设乙为单位“1”,则甲为1+=,因此乙比甲少÷=.888891方法二:可设乙为8份,则甲为9份,因此乙比甲少1÷9=.9(2)甲比乙多三、怎样找准分数应用题中单位“1”(一)、部分数和总数在同一整体中,部分数和总数作比较关系时,部分数通常作为比较量,而总数则作为标准量,那么总数就是单位“1”。
例如:我国人口约占世界人口的几分之几?——世界人口是总数,我国人口是部分数,世界人口就是单位“1”。
解答题关键:只要找准总数和部分数,确定单位“1”就很容易了。
(二)、两种数量比较分数应用题中,两种数量相比的关键句非常多。
有的是“比”字句,有的则没有“比”字,而是带有指向性特征的“占”、“是”、“相当于”。
在含有“比”字的关键句中,比后面的那个数量通常就作为标准量,也就是单位“1”。
例如:六(2)班男生比女生多——就是以女生人数为标准(单位“1”),解题关键:在另外一种没有比字的两种量相比的时候,我们通常找到分率,看“占”谁的,“相当于”谁的,“是”谁的几分之几。
完整word版六年级奥数十二分数百分数应用题教师版

学远教育小六奥数资料小六奥数专题十二:分数百分数应用题一、知识点概述1.分析题目确定单位“1”2.准确找到量所对应的率,利用量÷对应率=单位“1”解题3.抓住不变量,统一单位“1”4.分数应用题是研究数量之间份数关系的典型应用题,一方面它是在整数应用题上的延续和深化,另一方面,它有其自身的特点和解题规律.在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键.二、解题技巧:分数应用题经常要涉及到两个或两个以上的量,我们往往把其中的一个量看作是标准量.也称为:单位“1”,进行对比分析。
在几个量中,关键也是要找准单位“1”和对应的百分率,以及对应量三者的关系例如:(1)a是b的几分之几,就把数b看作单位“1”.1,乙比甲少几分之几?(2)甲比乙多811919??1??1.,则甲为”方法一:可设乙为单位“,因此乙比甲少88988198??91.份,则甲为方法二:可设乙为份,因此乙比甲少9三、怎样找准分数应用题中单位“1”(一)、部分数和总数在同一整体中,部分数和总数作比较关系时,部分数通常作为比较量,而总数则作为标准量,那么总数就是单位“1”。
例如:我国人口约占世界人口的几分之几?——世界人口是总数,我国人口是部分数,世界人口就是单位“1”。
解答题关键:只要找准总数和部分数,确定单位“1”就很容易了。
(二)、两种数量比较分数应用题中,两种数量相比的关键句非常多。
有的是“比”字句,有的则没有“比”字,而是带有指向性特征的“占”、“是”、“相当于”。
在含有“比”字的关键句中,比后面的那个数量通常就作为标准量,也就是单位“1”。
例如:六(2)班男生比女生多——就是以女生人数为标准(单位“1”),解题关键:在另外一种没有比字的两种量相比的时候,我们通常找到分率,看“占”谁的,“相当于”谁的,“是”谁的几分之几。
这个“占”,“相当于”,“是”后面的数量——谁就是单位“!”。
《分数百分数应用题》课件

欢迎来到《分数百分数应用题》PPT课件!在这个课程中,我们将深入探讨分 数和百分数的各种应用,以及相关的概念和转换方法。
分数和百分数的概念
1 分数的定义
分数表示一个整体被平均分成若干等份的情况,由分子和分母组成。
2 百分数的定义
百分数表示某个数与100之间的关系,以百分号表示。
分数和百分数的转换
1 折扣和打折
在商业运算中,使用分数和百分数来计算折扣和打折等优惠。
2 销售增长率
分数和百分数可以用来计算销售增长率,帮助企业了解经营状况。
分数和百分数在生活中的应用
购物
在购物时,使用分数和百分数来 计算折扣价、优惠券抵扣等。
健康
财务管理
在健康管理中,使用分数和百分 数来记录体重、运动时间等指标。
分数转换为百分数
分子除以分母,再乘以100即可得到分数对应的百 分数。
百分数转换为分数
将百分数除以100,再化简即可得到百分数对应的 分数。
分数、百分数与小数的关系
1
分数和小数的关系
分数可以表示为小数,将分子除以分母
百分数和小数的关系
2
即可得到对应的小数。
百分数可以表示为小数,将百分数除以
100即可得到对应的小数。
3
分数和百分数的关系
分数可以表示为百分数,将分子除以分 母,再乘以100即可得到对应的百分数。
分数和百分数的四则运算
加法
分数和分数相加,或百分数和百分数相加,将分 母统一后进行运算。
乘法
分数和分数相乘,或百分数和百分数相乘,将分 子相乘,分母相乘。
减法
分数和分数相减,或百分数和百分数相减,将分 母统一后进行运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分数、百分数应用题(一)
例1:一篓苹果分给甲、乙、丙三人,甲分得全部苹果的5
1加5个苹果,乙分得全部苹果的41加7个苹果,丙分得其余苹果的2
1,最后剩下的苹果正好等于一篓苹果的8
1。
这篓苹果有多少个? 分析:丙分得苹果的21也是总数的81,其余为81×2=4
1, (5+7)÷⎪⎭
⎫ ⎝⎛---4151411=40(个) 例2:甲数是乙数、丙数、丁数之和的
21,乙数是甲数、丙数、丁数之和的31,丙数是甲数、乙数、丁数之和的
41。
已知丁数是260,求甲数、乙数、丙数、丁数之和。
分析:甲数为:(甲+乙+丙+丁)的31121=+,乙数为:(甲+乙+丙+丁)的4
1131=+ 丙数为:(甲+乙+丙+丁)的51;甲+乙+丙+丁=“1”,丁数为:60
135141311=⎪⎭⎫ ⎝⎛---总数:260÷60
13=1200(个)。
例3:有甲、乙两个粮库,原来甲粮库存粮的吨数是乙粮库的
75。
如果从乙粮库调6吨粮食到甲仓库,甲仓库存粮的吨数就是乙仓库的
5
4。
原来甲、乙粮库各存粮多少吨?
解:设乙仓库存粮为x 吨,甲仓库存粮为75x 吨。
4
567
56=+-x x 解之得 x=126 例4:学校有皮球和足球共100个,皮球的个数的31比足球个数的10
1多16个。
学校有皮球和足球各多少个?
解:设皮球个数为x 个,足球的个数为100-x ,
3
1610100x x =+- x=60,足球:100-x=100-60=40(个)。
例5:有红黄两种颜色的小球共140个,拿出红球的4
1,再拿出7个黄球,剩下的红球和黄球正好一样多。
原来红球和黄球各有多少个?
解:设红球为x 个,黄球为140-x 个。
(1-4
1)x =140-x -7 x=76 黄球=64(个) 例6:金放在水里称,重量减轻191;银放在水里称,重量减轻10
1。
一块合金重770克,放在水里称,共减轻了50克。
这块合金含金含银各有多少克? 解:方法(一):设金重为x 克,银重为(770-x )克,
5010
77019=-+x x 解之得:x=570 银重=770-570=200(克) 方法(二):设金减轻x ,银减轻50-x ,
x ÷191+(50-x )÷10
1=770 解之得: x=30 银减轻=50-30=20(克) 金=30÷191=570(克) 银=20÷10
1=200(克) 练习:
1、桃树棵数的53和梨树棵数9
4相等。
两种果树共有141棵,两种树各有多少棵?
桃树: 梨树=94:5
3=20:27 桃树:141×27
2020+=60(棵) 梨树:141×27
2027+=81(棵) 2、两个筑路队合修一条公路,甲队修的53相当于乙队修的4
3。
甲队比乙队多修10千米,两队共修多少千米?
甲:乙=43:53=5:4 10÷⎪⎭
⎫ ⎝⎛+-+454455=90(千米) 3、一堆砖,用去了它的
103后,又增加了340块,这时砖的总块数是原来设有用时的块数的9
8。
用去了多少块砖?
340÷10
3103198⨯⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=540(块) 4、甲、乙两个容器共有药水2000克。
从甲容器里取出3
1的药水,从乙容器里取出4
1的药水,结果两个容器里共剩下1400克药水。
甲、乙两个容器里原来各有多少克药水?
解:设甲容器原来有x 克药水,乙容器原来有(2000-x )克药水,
()x x -⨯⎪⎭
⎫ ⎝⎛-+⨯⎪⎭⎫ ⎝⎛-2000411311=1400 解之得:x=1200 乙容器原来有: (2000-x )=800。
5、乙队原有人数是甲队的7
3。
现在从甲队派30人到乙队,则乙队人数是甲队的3
2。
甲、乙两队原来各有多少人? 解:设甲队原来有x 人,乙队原来有7
3x 人, 2
3307
330=+-x x 解之得x=210 乙队原来有: 73x=73×210=90。
6、图书馆新购进3种书,其中工具有180本,科技书占总数的3
1,文艺书的本数是其它两种书本数的5
1。
购进的3种书共有多少本? 180×(1+51)÷(1-31-31×5
1)=360。
