采用Butterworth传递函数设计二自由度纯滞后控制系统
数字信号处理 Butterworth型二阶有源低通滤波器的设计
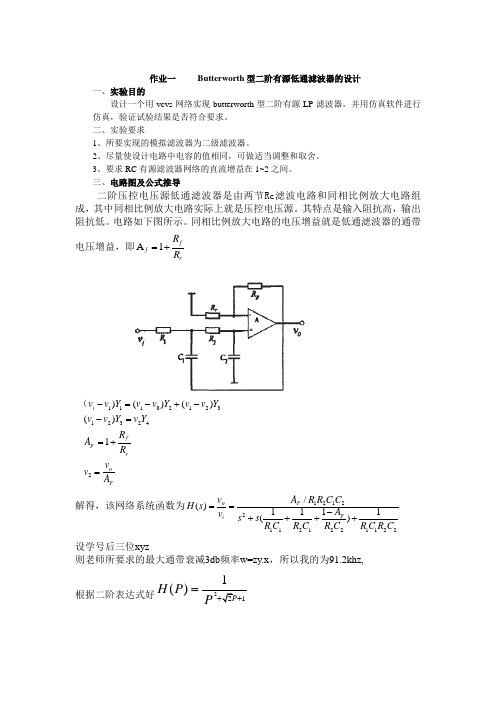
作业一 Butterworth 型二阶有源低通滤波器的设计一、实验目的设计一个用vcvs 网络实现butterworth 型二阶有源LP 滤波器,并用仿真软件进行仿真,验证试验结果是否符合要求。
二、实验要求1、所要实现的模拟滤波器为二级滤波器。
2、尽量使设计电路中电容的值相同,可做适当调整和取舍。
3、要求RC 有源滤波器网络的直流增益在1~2之间。
三、电路图及公式推导二阶压控电压源低通滤波器是由两节Rc 滤波电路和同相比例放大电路组成,其中同相比例放大电路实际上就是压控电压源。
其特点是输入阻抗高,输出阻抗低。
电路如下图所示。
同相比例放大电路的电压增益就是低通滤波器的通带电压增益,即rf f R R +=1AFo rf F i A v v R R A Y v Y v v Y v v Y v v Y v v =+==--+-=-242321321201111)()()()(解得,该网络系统函数为2211221211221211)111(/)(C R C R C R A C R C R s s C C R R A v v s H F F io +-+++==设学号后三位xyz则老师所要求的最大通带衰减3db 频率w=zy .x ,所以我的为91.2khz,根据二阶表达式好211()H P P+=而根据二阶巴特沃斯滤波器方程去归一化得2()HH s =比对系数,令12C C =,341000,R R ==Ω得12121000,2000 1.2R R C C nF ====,。
四、 分析验证用EWB 软件画出其电路图,代入参数,如下图所示此时选用5V ,1000Hz 的交流电源,用波特图示仪观察其衰减,输出如下图所示可以看出,当频率为91.2khz 时,为3db ,实验设计成功。
五、 实验总结 通过本次实验,让我们体会了将理论知识和实际设计过程中的差异。
这不仅仅巩固我们所学的知识,还提高了我的动手能力和思维的发散性。
butterworth滤波器 的matlab实现 -回复

butterworth滤波器的matlab实现-回复Butterworth滤波器的Matlab实现一、介绍Butterworth滤波器是一种常见的滤波器,它是模拟滤波器中最为基础的一种。
它的特点是具有平坦的幅频响应,在通带和阻带之间呈现出平滑的过渡。
在Matlab中,可以使用信号处理工具箱中的函数来实现Butterworth滤波器。
二、Butterworth滤波器的原理Butterworth滤波器的设计是基于将滤波器的传递函数表示为极点和零点的比值的形式。
其传递函数为:H(s) = 1 / ((s/a)^N + 1)其中,s是复变量,a是与滤波器的通带截止频率相关的常数,N是滤波器的阶数。
三、Butterworth滤波器的参数选择在实现Butterworth滤波器之前,我们需要选择一些参数来定义滤波器的特性。
这些参数包括采样率、通带截止频率、阻带截止频率和滤波器的阶数。
首先,采样率是指信号的采样频率,它决定了信号中可以表示的最高频率。
通常情况下,采样率应为信号中最高频率的两倍。
其次,通带截止频率是指滤波器在通带内的最高频率。
我们可以根据信号的频率范围来选择通带截止频率。
一般而言,通带截止频率应低于采样率的一半。
阻带截止频率是指滤波器在阻带内的最低频率。
我们可以根据信号的频率范围来选择阻带截止频率。
一般而言,阻带截止频率应高于通带截止频率。
最后,滤波器的阶数决定了滤波器的陡峭程度。
阶数越高,滤波器越陡峭。
但是,阶数过高可能导致滤波器的相位失真。
四、Matlab中的实现步骤在Matlab中,我们可以使用`butter`函数来设计Butterworth滤波器。
该函数的语法为:[b, a] = butter(阶数, [通带截止频率/采样率, 阻带截止频率/采样率], '滤波器类型')其中,阶数为滤波器的阶数,[通带截止频率/采样率, 阻带截止频率/采样率]为滤波器的截止频率与采样率的比值,'滤波器类型'为滤波器的类型,可以是'low'、'high'、'bandpass'或'bandstop'。
纯滞后控制实验报告

一、实验目的1. 理解纯滞后控制系统的概念及其在工业控制系统中的应用。
2. 掌握大林算法在纯滞后控制系统中的应用原理。
3. 通过实验验证大林算法在纯滞后控制系统中的控制效果。
二、实验原理1. 纯滞后控制系统:纯滞后控制系统是指被控对象具有纯滞后特性,即输入信号到输出信号的传递过程中存在一定的时间延迟。
这种时间延迟会使得控制作用不及时,从而影响系统的稳定性和动态性能。
2. 大林算法:大林算法是一种针对纯滞后控制系统的控制策略,其基本思想是在设计闭环控制系统时,采用一阶惯性环节代替最少拍多项式,并在闭环控制系统中引入与被控对象相同的纯滞后环节,以补偿系统的滞后特性。
三、实验设备1. MATLAB 6.5软件一套2. 个人PC机一台四、实验步骤1. 设计实验模型:根据实验要求,设计一个具有纯滞后特性的被控对象模型,并确定其参数。
2. 构建大林算法控制器:根据大林算法的原理,设计一个大林算法控制器,并确定其参数。
3. 进行仿真实验:在MATLAB软件中搭建实验平台,将设计的被控对象模型和大林算法控制器进行联接,进行仿真实验。
4. 分析实验结果:观察实验过程中系统的动态性能,分析大林算法在纯滞后控制系统中的应用效果。
五、实验结果与分析1. 实验结果(1)无控制策略:在无控制策略的情况下,被控对象的输出信号存在较大的超调和振荡,系统稳定性较差。
(2)大林算法控制:在采用大林算法控制的情况下,被控对象的输出信号超调量明显减小,振荡幅度减小,系统稳定性得到提高。
2. 分析(1)无控制策略:由于被控对象具有纯滞后特性,系统动态性能较差,导致输出信号存在较大超调和振荡。
(2)大林算法控制:大林算法通过引入与被控对象相同的纯滞后环节,有效补偿了系统的滞后特性,使得控制作用更加及时,从而提高了系统的动态性能和稳定性。
六、实验结论1. 纯滞后控制系统在实际工业生产中普遍存在,对系统的稳定性、动态性能和抗干扰能力具有较大影响。
采用一种新型的状态反馈设计方法实现纯滞后系统的控制

采用一种新型的状态反馈设计方法实现纯滞后系统的控制王伟;郑耀林【摘要】本文提出了一种采用最优状态反馈来实现对纯滞后对象的控制的方法.它将纯滞后环节进行非对称二阶伯德近似,然后按照Butterworth滤波器原理设计状态反馈系数矩阵从而实现对纯滞后对象的近似最优控制.仿真实验表明该系统具有较强的鲁棒性和抗扰性能.【期刊名称】《自动化与信息工程》【年(卷),期】2002(023)002【总页数】3页(P1-3)【关键词】纯滞后;Butterworth滤波器;状态反馈;鲁棒性【作者】王伟;郑耀林【作者单位】国立华侨大学机电及自动化学院;国立华侨大学机电及自动化学院【正文语种】中文【中图分类】TP27纯滞后是工业生产过程中一种最普遍而又最难控制的一类对象。
而在许多工业生产过程中,滞后现象又是普遍存在的,例如冶金、玻璃、造纸工业中板材厚度的控制,加热炉、炉窑的传热,化工、炼油生产中物料的传输,反应器的化学合成等系统都存在纯滞后环节。
目前工业控制中比较普遍采用Smith预估控制的方法,但smith预估控制系统又存在(1)随对象特性变化的鲁棒性差;(2)当存在外扰动时,不能很好地克服这两个主要的缺点。
虽然目前对纯滞后对象的控制方法还有内模控制、灰度控制或是模糊控制等设计方法,但是都存在着计算复杂或规则难以提取等困难,因此,本文提出了一种采用状态反馈来控制纯滞后对象的方法。
其基本原理是由于实际对象带有纯滞后环节,其状态无法直接提取,因此加入一个状态观测器,同时将纯滞后环节进行非对称二阶伯德近似,再按照Butterworth滤波器原理设计观测器和状态反馈系数从而实现对纯滞后对象的近似最优控制。
通过仿真试验发现其具有较高的鲁棒性和抗扰性。
对于纯滞后环节的近似可以采用对称或非对称的多种伯德近似方法。
文献[1]等在提出对IMC-PID(内模-PID)控制器的设计问题的同时对纯滞后分别采用零阶和一阶Pade近似,其控制效果较为理想。
Butterworth模拟低通滤波器设计

例:利用AF-BW filter及脉冲响应不变法设计一DF,满足
Wp=0.2p, Ws=0.6p, Ap2dB, As15dB 。
%determine the DF filter [numd,dend]=impinvar(numa,dena,Fs); %plot the frequency response w=linspace(0,pi,1024); h=freqz(numd,dend,w); norm=max(abs(h)); numd=numd/norm; plot(w/pi,20*log10(abs(h/norm))); xlabel('Normalized frequency'); ylabel('Gain,dB'); %computer Ap As of the designed filter w=[Wp Ws]; h=freqz(numd,dend,w); fprintf('Ap= %.4f\n',-20*log10( abs(h(1)))); fprintf('As= %.4f\n',-20*log10( abs(h(2))));
Ap=1.00dB, As=40dB
模拟高通滤波器的设计
MATLAB实现 [numt,dent] = lp2hp(num,den,W0)
例: 设计满足下列条件的模拟BW型高通滤波器 fp=5kHz, fs=1kHz, Ap1dB, As 40dB。
%高通滤波器的设计 wp=1/(2*pi*5000);ws=1/(2*pi*1000);Ap=1;As=40; [N,Wc]=buttord(wp,ws,Ap,As,'s'); [num,den] = butter(N,Wc,'s'); disp('LP 分子多项式'); fprintf('%.4e\n',num); disp('LP 分母多项式'); fprintf('%.4e\n',den); [numt,dent] = lp2hp(num,den,1); disp('HP 分子多项式'); fprintf('%.4e\n',numt); disp('HP 分母多项式'); fprintf(‘%.4e\n’,dent);
基于高阶Pade近似的纯滞后控制系统设计

基于高阶Pade近似的纯滞后控制系统设计姚婷梅【摘要】本文采用高阶的改进型butterworth传递函数作为目标函数,纯滞后因子采用高阶的对称pade近似进行逼近,设计出一高阶纯滞后控制系统。
通过仿真可以看出,采用这种方法所设计的控制系统具有良好的稳定性和鲁棒性。
【期刊名称】《电子制作》【年(卷),期】2015(000)004【总页数】1页(P58-58)【关键词】pade近似;纯滞后;传递函数【作者】姚婷梅【作者单位】华侨大学厦门工学院福建厦门 361021【正文语种】中文滞后现象在现在的工业过程中是比较常见的现象,纯滞后系统常采用传递函数进行控制。
文献[1]采用非对称二阶伯德近似逼近纯滞后因子,文献[2]采用高阶分时模型逼近纯滞后环节,以butterworth传递函数作为系统的理想传递函数来设计控制系统。
因此,本文采用高阶的pade近似替代滞后因子,并对传统的巴特沃斯传递函数进行改进,设计一滞后控制系统。
采用这种方法设计的纯滞后控制系统不但具有重要的理论意义,也有实用价值。
Pade近似技术由著名学者Pade提出,可用在滞后系统中。
MATLAB中的pade 函数可以实现滞后时间的近似,其调用格式为,此命令求出的近似多项式是同阶次的。
薛定语编写的paderm函数可以求出不同阶次的近似多项式。
所以若上式则称为对称pade近似,若不相等则为非对称pade近似。
在此控制系统中,为被控对象,为控制器,将改进型巴特沃斯传递函数作为此系统理想的闭环传递函数,因为巴特沃斯函数的特性,所以保证此系统的稳定性。
加入滞后,采用高阶pade近似来替代滞后时间,其传递函数为但上式进行等效变换后会导致系统不稳定。
所以,对式(4)进行处理,只对分母中的进行pade近似。
则闭环系统传递函数为设被控对象的传递函数为时的改进型巴特沃斯传递函数的分母系数,加入纯滞后对象,当时,进行Pade多项式近似,采用6阶改进后的巴特沃斯传递函数进行控制器设计,可得控制器传递函数为通过对纯滞后系统进行仿真研究,分别采用PID控制和高阶pade近似纯滞后因子设计的控制系统两种方法,系统的阶跃响应曲线如下:图2为纯滞后PID控制和改进后的对称pade近似的控制结果。
纯滞后控制系统设计

实验五 纯滞后控制系统设计一、实验目的1) 学习使用simulink 实现Dahlin 算法的设计方法。
2) 学习使用simulink 进行Smith 预估补偿控制的设计方法。
二、实验原理1. Dahlin 算法的设计已知被控对象传递函数:102()100s+1s G s e -=(1)采样周期为2s ,选择期望闭环传递函数中的时间常数分别为T τ=5s ,10s ,20s ,设计Dahlin 控制器。
基本原理参见课本P175 7.3节。
2. Smith 预估补偿控制的设计 已知被控对象传递函数:3023()2s +60s+1sG s e -= (2) 应用Smith 预估补偿算法设计控制系统,并采用PID 控制。
基本原理图参见课本P182 7.4节。
三、实验内容1) 按式(1)建立系统的Simulink 模型,设计Dahlin 控制器。
改变期望闭环传递函数中的时间常数,观察不同的仿真结果,记录实验曲线。
当T τ=5s 时,系统的Simulink 仿真图和响应曲线图如下:Simulink仿真图系统响应曲线图当Tτ=10s时,系统的Simulink仿真图和响应曲线图如下:Simulink仿真图系统响应曲线图当Tτ=20s时,系统的Simulink仿真图和响应曲线图如下:Simulink 仿真图系统响应曲线图2) 按式(2)建立系统的Simulink 模型,应用Smith 预估补偿算法设计控制系统,消除滞后时间的影响,并整定好PID 参数。
与同一PID 控制器对无滞后的被控对象控制结果相比较,记录实验曲线。
3023()2s +60s+1s G s e -= Smith 预估预估控制系统仿真框图如下图:Simulink仿真图PID控制器选取P=2,Ti=100,Td=0;响应曲线如下图:系统响应曲线图无滞后的仿真图为:Simulink仿真图响应曲线如下图:系统响应曲线图相比较后曲线几乎一样,只是带Smith预估补偿算法设计控制系统的曲线图为后者的向右平移30s。
butterworth滤波器 的matlab实现 -回复

butterworth滤波器的matlab实现-回复"butterworth滤波器的matlab实现"引言:滤波是信号处理中一个非常重要的步骤,它可以将信号中的噪声或干扰成分去除,同时保留信号的主要特征。
在滤波器设计中,Butterworth滤波器是一种经典的滤波器类型,它具有平滑的频率响应和无最大衰减的特性。
在本文中,我们将介绍Butterworth滤波器的原理,并使用MATLAB软件来实现它。
第一部分:Butterworth滤波器的原理Butterworth滤波器是一种基于最佳逼近理论的滤波器,它的频率响应函数具有平滑且无纹波的特点。
Butterworth滤波器的设计主要依赖于两个参数:阶数和截止频率。
阶数决定了滤波器的陡峭程度,截止频率决定了滤波器的截止特性。
在MATLAB中,我们可以使用"butter"函数来设计Butterworth滤波器。
第二部分:MATLAB中Butterworth滤波器的实现步骤1. 导入数据:首先,我们需要导入需要滤波的信号数据。
可以使用MATLAB的"load"函数来加载信号数据,或者手动输入信号。
2. 设计滤波器:使用MATLAB的"butter"函数来设计Butterworth滤波器。
该函数的参数包括滤波器的阶数、截止频率和滤波器类型。
示例代码如下:MATLABorder = 6; 指定滤波器阶数cutoff_freq = 100; 指定截止频率[b,a] = butter(order, cutoff_freq/(sampling_freq/2)); 设计Butterworth滤波器这里的"sampling_freq"表示数据的采样率。
3. 滤波信号:使用MATLAB的"filter"函数来对信号进行滤波。
示例代码如下:MATLABfiltered_signal = filter(b,a,signal);这里的"signal"表示需要滤波的信号数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 引 言
虽然 e 有 R =+O 0 的收敛半径 , 当 i 但 足够大
B t r o h滤 波 器 是 一 种 具 有 最 大 平 坦 幅 度 ue r tw t
过 程 控 制
化 动 及 表,0 ,74: ~1 工自 化 仪 20 3( 1 2 1 )9
Co to n nsr nr la d I tume t n Che c lI d ty n si mia n usr
采 用 B t r ot ut w rh传 递 函数 设 计 二 自 由度 e 纯 滞 后 控 制 系 统
响应 的低通 滤波 器 , 有本 质 的稳定性 , 的传 递 具 它 函数可作 为 系统 的最 优 传 递 函数 。文 献 [ ] 究 1研
了 B t rot 最 优 控 制 的 逆 问 题 , 开 B t rot ut w r e h 揭 ut w r e h
时, 也就变成无关紧要的小量了, 寺丁 因此, 用有
G( P
(靠+ 音 ) 1 r ( s ‘ 4 +s∑s ) ()
T 1
纯 滞后 对 象 G ()的 有 限 维状 态 空 间模 型 为 : s
f ()=A t “ t t X()+ ()
【 () = C t Yt X( ) () 5
能处理有限维的被控对象。纯滞后 对象的传递函数
李钟 慎
( 侨 大 学 机 电及 自动化 学 院 , 建 泉 州 32 2 ) 华 福 6 0 1
摘 要 : 采 用 B trot 传 递 函数 设 计 了纯滞 后 对 象 的状 态反 馈 控 制 系统 , 对 纯 滞 后 对 象 的状 态反 馈 控 制 ut w r e h 针 系统是 单 自由度 的 , 出一 种 采 用 B t rot 递 函数 设 计 二 自 由度 纯 滞 后 控 制 系统 的 方 法 。 用 m 阶模 型 逼 近 提 ut w r e h传 纯 滞后 因子 , 引入 状 态 观 测 器 , 构成 状 态反 馈 子 系统 , 串入 一 个 积 分 器 , 成 纯滞 后 过 程 的 串级 状 态反 馈 控 制 系 再 构
优 化 设 计 方 法 。本 文 将 纯 滞 后 因 子 用 m 阶模 型 逼
寺。 s ‘
对于很多实际工业 对象 , 以用二 阶加纯滞 后 可
环节来描述 , : 即
G )= ( 3)
近, 然后 以 /阶 B t rot 传 递 函数 为 目标 函数来 Z ut w r e h 协调优化 设 计状 态 反 馈 增 益 阵 和状 态 观 测 器 , 从 而实现对 纯 滞后 对 象 的 优 化控 制 , 过 仿 真 指 出 通 按 该方法 设 计 的纯 滞 后 控 制 系统 是 单 自由度 的 。 在 此基 础上 , 系统再 串人一 个 积分器 , 成 串级 给 构 状 态反馈 控制系统 , n+1阶 B t rot 递 函 以 ut w r e h传 数 为整个 系 统 的 目标 函 数 , 仍按 状 态 反 馈 增 益 阵 和状态观 测 器 的协 调 优 化设 计 状 态 反 馈 子 系统 , 通 过仿 真指 出按该 方 法设计 的纯 滞后 控制 系统 是
纯 滞 后 因子 e 的 马克 劳 林 展 开 式 为 :
一
:
() 1
一
・
窆
i 0 =
收稿 日期 :09 1-3 修改稿 ) 20 —22 ( 基金项 目: 福建省 自然科学 基金资助项 目( 0 10 8 ; E 70 1 ) 华侨
大 学 高 层 次人 才 科 研 启 动 费 资 助 项 目( 7 S 1 ) 0 B 5 0
统 , n +1阶 B tr o h传 递 函 数 为 整 个 系统 的 目标 函数 , 状 态反 馈 增 益 阵 和 状 态观 测 器 的 协 调 优 化 设 计 状 以 ut w r e t 按
态反 馈 子 系统 。仿 真 结果 表 明 了该 方 法设 计 的 系统 同 时获 得 良好 的给 定 值 跟 踪 特 性 和 干 扰 抑 制 特 性 。 关 键 词 : B t ro h传 递 函数 ; 滞 后 对 象 ; 态反 馈 ; u ew r t t 纯 状 串级控 制 ; 自由度 二
含 有 无 穷 维 因子 e , 用 马 克 劳 林 ( c ui) 应 Mal r 展 a n 开 式 将 纯 滞 后 因 子 e 用 有 限 维 数 学 模 型 来 逼 一
近 。
令 = m +2, 式 ( ) , 则 5中
==
[—二 一 . …] 。
一
( 6)
…
・
2 ・ 0
化 工 自 动 化 及 仪 表
第3 7卷
~
…
一
一
∑
( = 。 ) i 1 。 2 , n
B =l ‘I
() 7 3 2 仿 真
㈦
考 虑 纯 滞后 对 象 :
3 采 用 B tewo t u tr rh传 递 函 数 设 计 的 状 态 反 馈 系
二 自 由度 的 。 2 纯 滞 后 对 象 的 有 理 近 似 状 态 反 馈 控 制 理 论 是 基 于 有 理 函数 理 论 的 , 只
式 中: —— 对象静 态增益 ;。 —— 时间 常数 ; T、
— —
纯滞后时间 。
把式 ( ) 2 代入式 ( ) 得 : 3,
限维数学模型来逼近 e 是合 理 的, 以用 m 阶模 一 可
型近似 e , : ~ 即
e ~ — ( 2)
最优传递 函数与加 权矩阵 Q、 R的相 互关 系 。文 献
[ ] 择 B tr o h传 递 函数 作 为优 化 闭 环 传 递 2选 u ew r t t
函数 , 出一 种 纯滞 后 过 程 的串级 双环 状 态 反 馈 提
