中考《圆》有关的证明和计算
圆的相关证明与计算(复习讲义)(原卷版)-中考数学重难点题型专题汇总
题型五--圆的相关证明与计算（复习讲义）【考点总结|典例分析】考点01圆的有关概念1．与圆有关的概念和性质（1）圆：平面上到定点的距离等于定长的所有点组成的图形．（2）弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦．（3）弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧．（4）圆心角：顶点在圆心的角叫做圆心角．（5）圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角．（6）弦心距：圆心到弦的距离．考点02垂径定理及其推论1．垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形．2．推论（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧．考点03圆心角、弧、弦的关系1．定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．圆心角、弧和弦之间的等量关系必须在同圆等式中才成立．2．推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．考点04圆周角定理及其推论1．定理一条弧所对的圆周角等于它所对的圆心角的一半．2．推论（1）在同圆或等圆中，同弧或等弧所对的圆周角相等．（2）直径所对的圆周角是直角．考点05与圆有关的位置关系1．点与圆的位置关系设点到圆心的距离为d．(1)d<r⇔点在⊙O内；(2)d=r⇔点在⊙O上；(3)d>r ⇔点在⊙O 外．判断点与圆之间的位置关系，将该点的圆心距与半径作比较即可．2．直线和圆的位置关系位置关系相离相切相交图形公共点个数0个1个2个数量关系d>r d=r d<r考点06切线的性质与判定1．切线的性质（1）切线与圆只有一个公共点．（2）切线到圆心的距离等于圆的半径．（3）切线垂直于经过切点的半径．利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题．2．切线的判定（1）与圆只有一个公共点的直线是圆的切线（定义法）．（2）到圆心的距离等于半径的直线是圆的切线．（3）经过半径外端点并且垂直于这条半径的直线是圆的切线．切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直；②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径．考点07三角形与圆1.三角形外接圆外心是三角形三条垂直平分线的交点，它到三角形的三个顶点的距离相等．2．三角形的内切圆内心是三角形三条角平分线的交点，它到三角形的三条边的距离相等．1.如图，点,,,,A B C D E 在O 上，,42AB CD AOB =∠=︒，则CED ∠=（）A．48︒B．24︒C．22︒D．21︒2.如图，A，B，C 是半径为1的⊙O 上的三个点，若，∠CAB＝30°，则∠ABC 的度数为（）A．95°B．100°C．105°D．110°3.如图，AB 是⊙O 的直径，AC，BC 是⊙O 的弦，若20A ∠=︒，则B Ð的度数为（）A．70°B．90°C．40°D．60°4.如图，Rt ABC 中，90ACB ∠=︒，AC =3BC =．点P 为ABC ∆内一点，且满足22PA PC +2AC =．当PB 的长度最小时，ACP ∆的面积是（）A．3B．C．4D．25.如图，已知在⊙O 中， AB BCCD ＝＝，OC 与AD 相交于点E．求证：（1）AD∥BC（2）四边形BCDE 为菱形．6.如图，A，B 是O 上两点，且AB OA =，连接OB 并延长到点C，使BC OB =，连接AC．（1）求证：AC 是O 的切线．（2）点D，E 分别是AC，OA 的中点，DE 所在直线交O 于点F，G，4OA =，求GF 的长．7.如图，Rt ABC 中，90ABC ∠=︒，以点C 为圆心，CB 为半径作C ，D 为C 上一点，连接AD 、CD ，AB AD =，AC 平分BAD ∠．（1）求证：AD 是C 的切线；（2）延长AD 、BC 相交于点E，若2EDC ABC S S = ，求tan BAC ∠的值．8.如图，在O 中，AB 是直径，弦CD AB ⊥，垂足为H ，E 为 BC上一点，F 为弦DC 延长线上一点，连接FE 并延长交直径AB 的延长线于点G ，连接AE 交CD 于点P ，若FE FP =．（1）求证：FE 是O 的切线；（2）若O 的半径为8，3sin 5F =，求BG 的长．9.如图，ABC 是O 的内接三角形，AC 是O 的直径，点D 是 BC的中点，//DE BC 交AC 的延长线于点E ．（1）求证：直线DE 与O 相切；（2）若O 的直径是10，45A ∠=︒，求CE 的长．10.如图，已知点C 是以AB 为直径的圆上一点，D 是AB 延长线上一点，过点D 作BD 的垂线交AC 的延长线于点E ，连结CD ，且CD ED =．（1）求证：CD 是O 的切线；（2）若tan 2DCE ∠=，1BD =，求O 的半径．11.如图，AB 是⊙O 的直径，C 为⊙O 上一点，连接AC，CE⊥AB 于点E，D 是直径AB 延长线上一点，且∠BCE＝∠BCD．（1）求证：CD 是⊙O 的切线；（2）若AD＝8，BE CE=12，求CD的长．12.如图，△ABC内接于⊙O，AB为⊙O的直径，AB＝10，AC＝6，连结OC，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．（1）求证：∠CAD＝∠CBA．（2）求OE的长．13.如图，⊙O的半径OA＝6，过点A作⊙O的切线AP，且AP＝8，连接PO并延长，与⊙O 交于点B、D，过点B作BC∥OA，并与⊙O交于点C，连接AC、CD．（1）求证：DC∥AP；（2）求AC的长．=CD =DB ，连接AD，过点D作14.如图，AB为⊙O的直径，C、D为⊙O上的两个点，ACDE⊥AC交AC的延长线于点E．（1）求证：DE是⊙O的切线．（2）若直径AB＝6，求AD的长．15.如图，AB是半圆O的直径，C，D是半圆O上不同于A，B的两点，AD＝BC，AC与BD相交于点F．BE是半圆O所在圆的切线，与AC的延长线相交于点E．（1）求证：△CBA≌△DAB；（2）若BE＝BF，求证：AC平分∠DAB．16.如图，AB为⊙O的直径，C为⊙O上一点，AD与过C点的直线互相垂直，垂足为D，AC 平分∠DAB．（1）求证：DC为⊙O的切线．（2）若AD＝3，DC=3，求⊙O的半径．17.如图，在△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，过点D作⊙O的切线交AC于点E．（1）求证：DE⊥AC；（2）若⊙O的半径为5，BC＝16，求DE的长．。
2023年数学中考真题：圆的有关计算及证明精选(一)
圆的有关计算及证明2023年数学中考试题精选（一）1.（2023.营口23题）如图，在△ABC中，AB=BC，以BC为直径作圆O与AC将于点D，过点D作DE⊥AB，交CB延长线于点F，垂足为点E.（1）求证：DF为圆O的切线；，求BF的长。
（2）若BE=3，cosC=452.（2023.本溪铁岭辽阳24题）如图，AB是圆O的直径，点C，E在圆O上，∠CAB=2∠EAB，点F在线段AB的延长线上，且∠AFE=∠ABC.（1）求证：EF与圆O相切；，求BC的长。
（2）若BF=1，sin∠AFE=453.(2023.沈阳22题)如图，BE是圆O的直径，点A和点D是圆O上的两点，过点A作圆O的切线交BE延长线于点C.（1）若∠ADE=25°，求∠C的度数；（2）若AB=AC，CE=2，求圆O半径的长.4.(2023.大连市23题)如图1，在圆O中，AB为圆O的直径，点C为圆O上一点，AD为∠CAB的平分线交圆O于点D，连接OD交BC于点E.（1）求∠BED的度数；（2）如图2，过点A作圆O的切线BC延长线于点F，过点D作DG ∥AF交AB于点G.若AD=2√35,DE=4，求DG的长。
5.(2023.湖北省恩施州23题)如图，△ABC是等腰直角三角形，∠ACB=90°，点O为AB的中点，连接CO交圆O于点E，圆O与AC 相切于点D.（1）求证：BC是圆O的切线；（2）延长CO交圆O于点G，连接AC交圆O于点F，若AC=4√(2)，求FG的长.6.（2023.贵州省23题）如图，已知圆O是等边三角形ABC的外接圆，连接CO并延长交AB于点D，交圆O于点E，连接EA，EB.（1）写出图中一个度数为30°的角；____，图中与△ACD全等的三角形是______；（2）求证：△AED∽△CEB;（3）连接OA，OB，判断四边形OAEB的形状，并说明理由。
7.(2023.江苏省24题)如图，在△ABC中，AB=AC，以AB为直径的圆O交边AC于点D，连接BD，过点C作CE∥AB.（1）请用无刻度的直尺和圆规作图：过点B作圆O的切线，交CE 于点F；（不写作法，保留作图痕迹，标明字母）（2）在（1）的条件下，求证：BD=BF.8.(2023.江西省20题)如图，在△ABC中，AB=4,∠C=64°，以AB为直径的圆O与AC相交于点D，E为优弧ABD上一点，且∠ADE=40°.（1）求BE的长；（2）若∠EAD=76°，求证：CB为圆O的切线.9.(2023.沈阳22题)如图，AB是圆O的直径，点C是圆O上的一点（点C不与点A，B重合），连接AC，BC，点D是AB上的一点，AC=AD，BE交CD的延长线于点E，且BE=BC.（1）求证：BE是圆O的切线；（2）若圆O的半径为5，tanE=1，则BE的长为_____.210.(2023.扬州市25题)如图，在△ABC中，∠ACB=90°，点D是AB∠A，点O在BC上，以点O为圆心的圆经过C、上一点，且∠BCD=12D两点.（1）试判断直线AB与圆O的位置关系，并说明理由；，圆O的半径为3，求AC的长.（2）若sinB=3511.(2023.广西壮族自治区23题)如图，PO平分∠APD，PA与圆O相切于点A，延长AO交PD于点C，过点O作OB⊥PD，垂足为B.（1）求证：PB是圆O的切线；（2）若圆O的半径为4，OC=5，求PA的长.12.（2023.广东省22题）如图1，在矩形ABCD中（AB>AD），对角线AC，BD相交于点O，点A关于BD的对称点为A`，连接AA`交BD于点E，连接CA`.（1）求证：AA`⊥CA`；（2）以点O为圆心，OE为半径作圆.①如图2，圆O与CD相切，求证：AA`=√3CA`；②如图3，圆O与CA`相切，AD=1，求圆O的面积.13.(2023.安徽省20题)已知四边形ABCD内接于圆O，对角线BD是圆O的直径.（1）如图1，连接OA，CA，若OA⊥BD，求证：CA平分⊥BCD; （2）如图2，E为圆O内一点，满足AE⊥BC，CE⊥AB，若BD=3√3，AE=3.求弦BC的长.14.(2023.湖北黄冈市20题)如图，⊥ABC 中，以AB 为直径的圆O 交BC 于点D ，DE 是圆O 的切线 ，且DE⊥AC ，垂足为E ，延长CA 交圆O 于点F.（1）求证：AB=AC ；（2）若AE=3，ED=6，求AF 的长。
中考总复习正多边形与圆的有关的证明和计算--知识讲解
中考总复习正多边形与圆的有关的证明和计算--知识讲解【正多边形与圆的有关的证明和计算】一、正多边形的定义与性质：正多边形是指所有边相等、所有角相等的多边形。
正多边形的性质如下：1.所有边相等，所有角相等；2.任意两条边之间的夹角相等；3.对角线相等；4.中心角等于外角。
二、正多边形的内角与外角的关系：1.由正多边形的定义可知，正多边形的内角和为180°(n-2)，其中n 为正多边形的边数；2.正多边形的外角和为360°，由此可得正多边形的内角和与外角和之间的关系：内角和=外角和/2三、正多边形的周长和面积的计算：1.正多边形的周长为边长×边数；2.正多边形的面积为面积公式：面积=1/2×边长×边数×正弦(360°/边数)。
四、正多边形内接圆的半径和面积：2.正多边形内接圆的面积等于正多边形面积的一半。
五、正多边形外接圆的半径和面积：1.正多边形外接圆的半径等于正多边形的边长的一半乘以正弦(180°/边数)；2.正多边形外接圆的面积等于正多边形边长的平方乘以正弦(360°/边数)乘以1/2六、正多边形的对称轴：正多边形有旋转对称轴和镜像对称轴两类：1.正多边形的旋转对称轴有n条，其中n为正多边形的边数；2.正多边形的镜像对称轴有2n条，其中n为正多边形的边数。
七、圆的性质及计算：1.圆是由一个动点到一个定点的距离保持不变的动点集；2.圆的半径是动点到圆心的距离；3.圆的直径是通过圆心的一条线段，且长度等于半径的两倍；4.圆的周长等于直径的乘以π，即周长=2×半径×π；5.圆的面积等于半径的平方乘以π，即面积=半径×半径×π。
八、正多边形与圆的关系：1.正多边形的内接圆同时是这个正多边形的外接圆，即正多边形的内接圆与外接圆重合；3.正多边形的外接圆的半径等于正多边形的边长的一半乘以正弦(180°/边数)；4.正多边形的外接圆的面积等于正多边形边长的平方乘以正弦(360°/边数)乘以1/2；5.正多边形的内接圆和外接圆的关系可以用于计算正多边形的周长和面积。
2024年云南省人教版九年级中考数学二轮复习课件专题四 圆的证明与计算(35张PPT)
∴∠ODF=30°.∴∠DOF=60°.
∵AB⊥DC,∴DF=FC.
∵BF=OF,AB⊥DC,
∴S△CFB=S△CFO=S△DFO.
×
∴S 阴影部分=S 扇形 BOD=
= π.
[典型例题2] (2023北京)如图所示,圆内接四边形ABCD的对角线AC,BD
交于点E,BD平分∠ABC,∠BAC=∠ADB.
∵CP与☉O相切,∴OC⊥PC.∴∠PCB+∠OCB=90°.
∵AB⊥DC,∴∠PAD+∠ADF=90°.∴∠PCB=∠PAD.
(2)若☉O的直径为4,弦DC平分半径OB,求图中阴影部分的面积.
(2)解:如图②所示,连接 OD,
∵弦 DC 平分半径 OB,∴BF=OF.
在 Rt△ODF 中,OF= OD.
∵AC为☉O的直径,∴∠ABC=90°.
∵BD是∠ABC的平分线,∴∠ABD=∠DBE=45°.
∴∠DOC=2∠DBE=90°.
∵AC∥DE,∴∠ODE=90°,即OD⊥DE.
∵OD是☉O的半径,∴DE是☉O的切线
(2)探究线段BE,CE,DE之间有何数量关系?写出你的结论,并证明.
2
(2)解:DE =CE·BE.证明如下:
2
又∵
2
=
,∴ =
.解得 CE=
2
.
2
2.如图所示,☉O的半径为1,A,P,B,C是☉O上的四个点,
∠APC=∠CPB=60°.
(1)判断△ABC的形状,并说明理由.
解:(1)△ABC是等边三角形.理由如下:
∵∠APC=∠CPB=60°,
中考压轴题圆的切线证明与计算(中考真题)
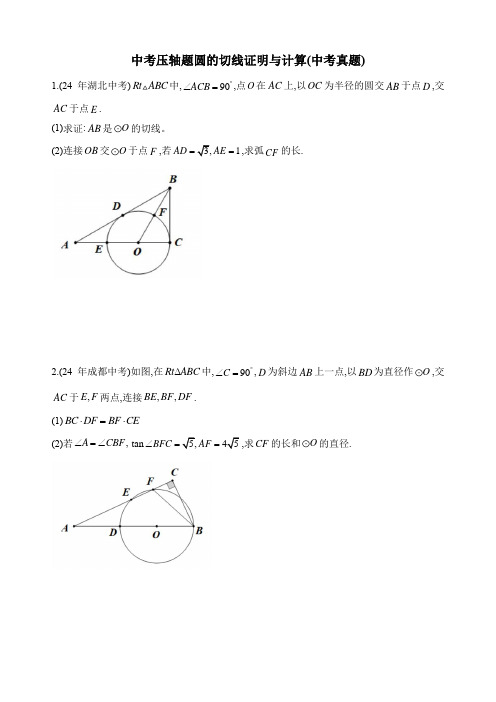
中考压轴题圆的切线证明与计算(中考真题)1.(24年湖北中考)Rt ABC 中,90ACB ︒∠=,点O 在AC 上,以OC 为半径的圆交AB 于点D ,交AC 于点E .(1)求证:AB 是O 的切线。
(2)连接OB 交O 于点F ,若1AD AE ==,求弧CF 的长.2.(24年成都中考)如图,在Rt ABC ∆中,90C ︒∠=,D 为斜边AB 上一点,以BD 为直径作O ,交AC 于,E F 两点,连接,,BE BF DF .(1)BC DF BF CE ⋅=⋅(2)若,A CBF ∠=∠tan BFC AF ∠==,求CF 的长和O 的直径.3.(24年浙江中考)如图,在圆内接四边形ABCD中,AD<AC,ADC BAD∠<∠,延长AD至点E,使AE=AC,延长BA至点F,连结EF,使AFE ADC∠=∠.(1)若60O∠的度数.∠=,CD为直径,求ABDAFE(2)求证:①EF∥BC ②EF=BD.4.(24年辽宁中考)如图,O是ABC的外接圆,AB是O的直径,点D在BC上,AC BD=,E ∠=∠．在BA的延长线上,CEA CAD(1)如图1,求证:CE是O的切线OA=,求BD的长．(2)如图2,若2CEA DAB∠=∠,85.(24年安徽中考)如图,O 是ABC ∆的外接圆,D 是直径AB 上一点,ACD ∠的平分线交AB 于点E ,交O 于另一点,.F FA FE =(1)求证:;CD AB ⊥(2)设FM AB ⊥,垂足为M ,若1OM OE ==,求AC 的长.6.(24年新疆中考)如图,在O 中,AB 是O 的直径,弦CD 交AB 于点E,AD BD =.(1)求证：△ACD ∽△ECB.(2)若AC=3,BC=1,求CE 的长.7.(24年江西中考)如图,AB 是半圆O 的直径,点D 是弦AC 延长线上一点,连接BD BC ，,60D ABC ∠=∠=︒．(1)求证:BD 是半圆O 的切线.(2)当3BC =时,求AC 的长．8.(24年呼伦贝尔中考)如图,在ABC 中,以AB 为直径的O 交BC 于点,D DE AC ⊥,垂足为E ． O 的两条弦,FB FD 相交于点,F DAE BFD ∠∠=．(1)求证:DE 是O 的切线;(2)若30,C CD ∠=︒=,求扇形OBD 的面积．9.(24年扬州中考)在综合实践活动中,“特殊到一般”是一种常用方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论．如图,已知ABC ,CA CB =, O 是ABC 的外接圆,点D 在O 上(AD BD >),连接AD ,BD ,CD ．【特殊化感知】(1)如图1,若60ACB ∠=︒,点D 在AO 延长线上,则AD BD -与CD 的数量关系为________【一般化探究】(2)如图2,若60ACB ∠=︒,点C ,D 在AB 同侧,判断AD BD -与CD 的数量关系并说明理由【拓展性延伸】(3)若ACB α∠=,直接写出AD ,BD ,CD 满足的数量关系．(用含α的式子表示)10.(24年赤峰中考)如图,ABC中,90ACB∠=︒,AC BC=,O经过B,C两点,与斜边AB交于点E,连接CO并延长交AB于点M,交O于点D,过点E作EF CD∥,交AC于点F．(1)求证:EF是O的切线;(2)若BM=,1tan2BCD∠=,求OM的长．11.(24年绥化中考)如图1,O是正方形ABCD对角线上一点,以O为圆心,OC长为半径的O 与AD相切于点E,与AC相交于点F．(1)求证:AB与O相切．(2)若正方形ABCD1,求O的半径．(3)如图2,在(2)的条件下,若点M是半径OC上的一个动点,过点M作MN OC⊥交CE于点N．当:1:4CM FM=时,求CN的长．12.(24年河北中考)已知O的半径为3,弦MN=ABC中.∠=︒==在平面上,先将ABC和O按图1位置摆放(点B与点N重90,3,ABC AB BC合,点A在O上,点C在O内),随后移动ABC,使点B在弦MN上移动,点A始终在O上=．随之移动,设BN x(1)当点B与点N重合时,求劣弧AN的长.(2)当OA MN∥时,如图2,求点B到OA的距离,并求此时x的值.(3)设点O到BC的距离为d．①当点A在劣弧MN上,且过点A的切线与AC垂直时,求d的值.①直接写出d的最小值．13.(24年滨州中考)【教材呈现】现行人教版九年级下册数学教材85页“拓广探索”第14题: 如图,在锐角ABC 中,探究sin a A ,sin b B ,sin c C之间的关系．(提示:分别作AB 和BC 边上的高．)【得出结论】sin sin sin a b c A B C==． 【基础应用】在ABC 中,75B ∠=︒,45C ∠=︒,2BC =,利用以上结论求AB 的长;【推广证明】进一步研究发现,sin sin sin a b c A B C==不仅在锐角三角形中成立,在任意三角形中均成立,并且还满足2sin sin sin a b c R A B C===(R 为ABC 外接圆的半径)． 请利用图1证明:2sin sin sin a b c R A B C ===．【拓展应用】如图2,四边形ABCD 中,2AB =,3BC =,4CD =,90B C ∠=∠=︒．求过A,B,D 三点的圆的半径．14.(24年苏州中考)如图,ABC 中,AB =为AB 中点,BAC BCD ∠=∠cos ADC ∠=. O 是ACD 的外接圆．(1)求BC 的长(2)求O 的半径．15.(24年乐山中考)如图,O 是ABC 的外接圆,AB 为直径,过点C 作O 的切线CD 交BA 延长线于点D,点E 为CB 上一点,且AC CE =．(1)求证:DC AE ∥;(2)若EF 垂直平分OB ,3DA =,求阴影部分的面积．16.(24年武汉中考)如图,ABC ∆为等腰三角形,O 是底边BC 的中点,腰AC 与半圆O 相切于点D ,底边BC 与半圆O 交于E ,F 两点．(1)求证:AB 与半圆O 相切(2)连接OA ．若4CD =,2CF =,求sin OAC ∠的值．17.(24年甘肃武威中考)如图,AB 是O 的直径,BC BD =,点E 在AD 的延长线上,且ADC AEB ∠=∠．(1)求证:BE 是O 的切线;(2)当O 的半径为2,3BC =时,求tan AEB ∠的值．18.(24年深圳中考)如图,在ABD △中,AB BD =,O 为ABD △的外接圆,BE 为O 的切线,AC 为O 的直径,连接DC 并延长交BE 于点E ．(1)求证:DE BE ⊥(2)若AB =5BE =,求O 的半径．19.(24年盐城中考)如图,点C 在以AB 为直径的O 上,过点C 作O 的切线l,过点A 作AD l ⊥,垂足为D,连接AC BC 、．(1)求证:ABC ACD △△∽;(2)若5AC =,4CD =,求O 的半径．20.(24年广西中考)如图,已知O 是ABC ∆的外接圆,AB AC =．点D,E 分别是BC ,AC 的中点,连接DE 并延长至点F,使DE EF =,连接AF ．(1)求证:四边形ABDF 是平行四边形(2)求证:AF 与O 相切(3)若3tan 4BAC ∠=,12BC =,求O 的半径． 21.(24年四川广安中考)如图,点C 在以AB 为直径的O 上,点D 在BA 的延长线上,DCA CBA ∠=∠．(1)求证:DC 是O 的切线;(2)点G 是半径OB 上的点,过点G 作OB 的垂线与BC 交于点F ,与DC 的延长线交于点E ,若4sin 5D =,2DA FG ==,求CE 的长．22.(24年四川南充中考)如图,在O 中,AB 是直径,AE 是弦,点F 是AE 上一点,AF BE =,,AE BF 交于点C,点D 为BF 延长线上一点,且CAD CDA ∠=∠．(1)求证:AD 是O 的切线．(2)若4,BE AD ==求O 的半径长．23.(24年四川泸州中考)如图,ABC ∆是O 的内接三角形,AB 是O 的直径,过点B 作O 的切线与AC 的延长线交于点D,点E 在O 上,AC CE =,CE 交AB 于点F ．(1)求证:CAE D ∠=∠;(2)过点C 作CG AB ⊥于点G,若3OA =,BD =求FG 的长．24.(24年四川德阳中考)已知O 的半径为5,B C 、是O 上两定点,点A 是O 上一动点,且60,BAC BAC ∠=︒∠的平分线交O 于点D ．(1)证明:点D 为BC 上一定点;(2)过点D 作BC 的平行线交AB 的延长线于点F ．①判断DF 与O 的位置关系,并说明理由;①若ABC 为锐角三角形,求DF 的取值范围．25.(24年四川宜宾中考)如图,ABC 内接于O ,10AB AC ==,过点A 作AE BC ∥,交O 的直径BD 的延长线于点E,连接CD ．(1)求证:AE 是O 的切线;(2)若1tan 2ABE ∠=,求CD 和DE 的长．26.(24年内蒙古通辽中考)如图,ABC 中,90ACB ∠=︒,点O 为AC 边上一点,以点O 为圆心,OC 为半径作圆与AB 相切于点D ,连接CD ．(1)求证:2ABC ACD ∠=∠;(2)若8AC =,6BC =,求O 的半径．27.(24年四川达州中考)如图,BD 是O 的直径．四边形ABCD 内接于O ．连接AC ,且AB AC =,以AD 为边作DAF ACD ∠=∠交BD 的延长线于点F ．(1)求证:AF 是O 的切线;(2)过点A 作AE BD ⊥交BD 于点E ．若3CD DE =,求cos ABC ∠的值．28.(24年四川遂宁中考)如图,AB 是O 的直径,AC 是一条弦,点D 是AC 的中点,DN AB ⊥于点E ,交AC 于点F ,连结DB 交AC 于点G ．(1)求证:AF DF =;(2)延长GD 至点M ,使DM DG =,连接AM ．①求证:AM 是O 的切线;①若6DG =,5DF =,求O 的半径．29.(24年包头中考)如图,AB 是O 的直径,,BC BD 是O 的两条弦,点C 与点D 在AB 的两侧,E 是OB 上一点(OE BE >),连接,OC CE ,且2BOC BCE ∠=∠．(1)如图1,若1BE =,CE =求O 的半径;(2)如图2,若2BD OE =,求证:BD OC ∥．(请用两种证法解答)30.(24年四川自贡中考)在Rt ABC △中,90C ∠=︒,O 是ABC 的内切圆,切点分别为D,E,F ．(1)图1中三组相等的线段分别是CE CF =,AF =________,BD =________;若3AC =,4BC =,则O 半径长为________;(2)如图2,延长AC 到点M,使AM AB =,过点M 作MN AB ⊥于点N ．求证:MN 是O 的切线．31.(24年山东枣庄中考)如图,在四边形ABCD 中,AD BC ∥,60DAB ∠=︒,22AB BC AD ===． 以点A 为圆心,以AD 为半径作DE 交AB 于点E ,以点B 为圆心,以BE 为半径作EF 所交BC 于点F ,连接FD 交EF 于另一点G ,连接CG ．(1)求证：CG 为EF 所在圆的切线(2)求图中阴影部分面积．(结果保留π)32.(24年青海中考) 如图,直线AB经过点C,且OA OB=．=,CA CB(1)求证:直线AB是O的切线;(2)若圆的半径为4,30∠=︒,求阴影部分的面积．B中考压轴题圆的切线证明与计算答案1.(24年湖北中考)【答案】(1)略 (2)弧CF 的长为3π2.(24年成都中考)【答案】(1)略(2)CF =;O 的直径为3.(24年浙江中考)【答案】(1)30o (2)证明略4.(24年辽宁中考)【答案】(1)见详解 (2)2π5.(24年安徽中考)【答案】(1)略 (2).6.(24年新疆中考)【答案】(1) 略 (2)CE =.7.(24年江西中考)【答案】(1)见解析 (2)2π8.(24年呼伦贝尔中考)【答案】(1)略 (2)43π 9.(24年扬州中考)【答案】(1)AD BD CD -=.(2)AD BD CD -=(3)当D 在BC 上时,2sin 2CD AD BD α⋅=-.当D 在AB 上时,2sin 2CD AD BD α⋅=+10.(24年赤峰中考)【答案】(1)略 (2)OM =11.(24年绥化中考)【答案】(1)证明略 (2)12.(24年河北中考)【答案】(1)π (2)点B 到OA 的距离为2;3 (3)①3d =2313.(24年滨州中考)【答案】教材呈现:见解析;基础应用:AB =;推广证明:见解析;拓展应用:6R =．14.(24年苏州中考)【答案】(1)4BC = (2)O 的半径为715.(24年乐山中考)【答案】(1)略 (2)3π-16.(24年武汉中考)【答案】(1)略 (2)4517.(24年甘肃武威中考)【答案】(1)略 (2)tan 3AEB ∠=18.(24年深圳中考)【答案】(1)略 (2)19.(24年盐城中考)【答案】(1)略 (2)25620.(24年广西中考)【答案】(1)略 (2)略 (3)1021.(24年四川广安中考)【答案】(1)略 (2)1422.(24年四川南充中考)【答案】(1)略 (2)23.(24年四川泸州中考)【答案】(1)证明略 (2)45 24.(24年四川德阳中考)【答案】(1)证明略(2)①DF 与O 相切,理由见解析;①DF 的取值范围为2DF <<25.(24年四川宜宾中考)【答案】(1)略 (2)CD =DE =． 26.(24年内蒙古通辽中考)【答案】(1)证明略 (2)327.(24年四川达州中考)【答案】(1)证明略 28.(24年四川遂宁中考)【答案】(1)证明略 (2)①证明略,①O 的半径为203． 29.(24年包头中考)【答案】(1)3 (2)略30.(24年四川自贡中考)【答案】(1)AD ;BE ;1 (2)略31.(24年山东枣庄中考)【答案】(1)略 3π32.(24年青海中考) 【答案】(1)详见解析 (2) 83S π=阴影。
突破中考之圆(解答题)专题训练
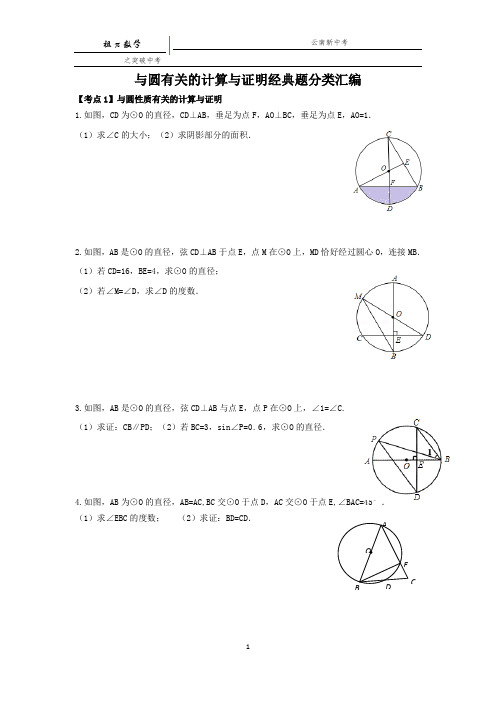
与圆有关的计算与证明经典题分类汇编【考点1】与圆性质有关的计算与证明1.如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，AO=1．（1）求∠C的大小；（2）求阴影部分的面积．2.如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB．（1）若CD=16，BE=4，求⊙O的直径；（2）若∠M=∠D，求∠D的度数．3.如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C.（1）求证：CB∥PD；（2）若BC=3，sin∠P=0.6，求⊙O的直径．4.如图，AB为⊙O的直径，AB=AC,BC交⊙O于点D，AC交⊙O于点E,∠BAC=45°．（1）求∠EBC的度数；（2）求证：BD=CD．AOECDB【考点2】与切线性质有关的证明与计算1.如图，PA、PB、EF分别与⊙O相切于点A、B、C，若△PEF的周长为18cm，且∠APB=60°,求⊙O的半径.2.如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB=18cm，BC=28cm，CA=26cm，求AF，BD，CE的长.3.如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点．（1）若∠ADE=25°，求∠C的度数；（2）若AB=AC，CE=2，求⊙O半径的长．4.如图，AB是⊙O的切线，B为切点，圆心在AC上，∠A=30°，D为弧BC的中点．（1）求证：AB=BC；（2）求证：四边形BOCD是菱形．5.如图，△ABC内接于⊙O，弦AD⊥AB交BC于点E，过点B作⊙O的切线交DA的延长线于点F，且∠ABF=∠ABC．（1）求证：AB=AC；（2）若AD=4，cos∠ABF=45，求DE的长．6.直线PD垂直平分⊙O的半径OA，交⊙O于点C、D，PE是⊙O的切线，E为切点，连结AE，交CD于点F．（1）若⊙O的半径为8，求CD的长；（2）证明：PE=PF；（3）若PF=13，sin A=513，求EF的长．【考点3】与切线的判定有关的证明与计算1.如图，已知⊙O的半径为1，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．（1）求AD的长；（2）证明BC是⊙O的切线．2.如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，若AC=FC．（1）求证：AC是⊙O的切线；（2）若BF=8，DF=40，求⊙O的半径r．3.如图，AB是⊙O的直径，点C在⊙O上，若∠BAC=∠CAM，过点C作直线L垂直于射线AM，垂足为点D．（1）试判断CD与⊙O的位置关系，并说明理由；（2）若直线L与AB的延长线相交于点E，⊙O的半径为3，并且∠CAB=30°，求CE的长．4.如图，△ABC是等边三角形，AO⊥BC，垂足为点O，⊙O与AC相切于点D，BE⊥AB交AC 的延长线于点E，与⊙O相交于G、F两点．（1）求证：AB与⊙O相切；（2）若等边三角形ABC的边长是4，求线段BF的长.【考点4】与阴影面积有关的计算与证明1.如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC．（1）求证：EF是⊙O的切线；（2）求证：AC2=AD•AB；（3）若⊙O的半径为2，∠ACD=30°，求图中阴影部分的面积．2.如图，在△ABC中，BE是它的角平分线，∠C＝90°，D在AB边上，以DB为直径的半圆O 经过点E，交BC于点F.(1)求证：AC是⊙O的切线；(2)已知cos A＝32，⊙O的半径为3，求图中阴影部分的面积．3.如图，在△ABC中，∠ACB=90°，E为BC上一点，以CE为直径作⊙O，AB与⊙O相切于点D，连接CD，若BE=OE=2．（1）求证：∠A=2∠DCB；（2）求图中阴影部分的面积．4.如图，BE是⊙O的直径，点A和点D是⊙O上的两点，连接AE，AD，DE，过点A作射线交BE的延长线于点C，使∠EAC＝∠EDA.(1)求证：AC是⊙O的切线；(2)若CE＝AE＝23，求阴影部分的面积．5.如图，在△BCE中，点A是边BE上一点，以AB为直径的⊙O与CE相切于点D，AD∥OC，点F为OC与⊙O的交点，连接AF.(1)求证：CB是⊙O的切线；(2)若∠ECB＝60°，AB＝6，求图中阴影部分的面积．6.如图，AB 是⊙O 的直径，∠BAC=90°，四边形EBOC 是平行四边形，EB 交⊙O 于点D ，连接CD 并延长交AB 的延长线于点F ． （1）求证：CF 是⊙O 的切线；（2）若∠F=30°，EB=4，求图中阴影部分的面积.【考点5】与圆有关的计算与证明综合1.如图，AE 为⊙O 的直径，D 是弧BC 的中点BC 与AD ，OD 分别交于点E ，F. （1）求证：OD ∥AC ；（2）求证：DE.DA=DC 2；（3）若tan ∠CAD=21,求tan ∠CDA 的值.2.如图，⊙O 与直线MN 相切于点A ，点B 是⊙O 上异于点A 的一点，∠BAN 的平分线与⊙O 交于点C ．(1)求证：△ABC 是等腰三角形；(2)①若∠CAN ＝15°，⊙O 的半径为23，则AB ＝ ；②当∠CAN ＝ 时，四边形OACB 为菱形．FEDOAC3.如图，PA为⊙O的切线，A为切点，直线PO交⊙O与点E，F过点A作PO的垂线AB垂足为D，交⊙O与点B，延长BO与⊙O交与点C，连接AC，BF．（1）求证：PB与⊙O相切；（2）试探究线段EF，OD，OP之间的数量关系，并加以证明；（3）若AC=12，tan∠F=12，求cos∠ACB的值．4.如图，△ABC 内接于⊙O ，AB 为直径，∠CBA 的平分线交AC 于点F ，交⊙O 于点D, DE ⊥AB 于点E ，且交AC 于点P ，连接AD.(1)求证：∠DAC ＝∠DBA ；(2)求证：P 是线段AF 的中点； (3)若⊙O 的半径为5, AD ＝6，求ADDB的值．5.如图1，⊙O 是△ABC 的外接圆，AB ＝AC ，BC ＝2，cos ∠ABC ＝1010.点D 为AC ︵上的动点，连接AD 并延长，交BC 的延长线于点E. (1)试求AB 的长；(2)试判断AD ·AE 的值是否为定值？若为定值；请求出这个定值；若不为定值，请说明理由； (3)如图2，连接BD ，过点A 作AH ⊥BD 于点H ，连接CD ，求证：BH ＝CD ＋DH.图1图2。
2020年中考数学考点聚焦(一)《与圆有关的证明及计算》
︵ (2)如图，点 A，B，C，D 是直径为 AB 的⊙O 上的四个点，是劣弧BD 的中点，AC 与 BD 交于点 E. ①求证：DC2＝CE·AC； ②若 AE＝2，EC＝1，求证：△AOD 是正三角形； ③在②的条件下，过点 C 作⊙O 的切线，交 AB 的延长线于点 H，求△ACH 的面积．
解：①证明：连接 AD，∵∠A＝∠BCD，∠AED＝∠CEB，∴△AED∽ △CEB，∴ACEE＝EEDB，∴AE·EB＝CE·ED ②解：∵⊙O 的半径为 3，∴OA＝OB＝OC＝3，∵OE＝2BE，∴OE＝2， BE＝1，AE＝5，∵DCEE＝95，∴设 CE＝9x，DE＝5x，∵AE·EB＝CE·ED，
[对应训练] 1．(1)如图，在Rt△ABC中，∠ACB＝90°，以AC为直径作⊙O交 AB于点D，E为BC的中点，连接DE并延长交AC的延长线于点F. ①求证：DE是⊙O的切线； ②若CF＝2，DF＝4，求⊙O直径的长．
解：①如图，连接OD，CD，∵AC为⊙O的直径，∴△BCD是直角三角 形，∵E为BC的中点，∴BE＝CE＝DE，∴∠CDE＝∠DCE，∵OD＝ OC，∴∠ODC＝∠OCD，∵∠ACB＝90°，∴∠OCD＋∠DCE＝90° ，∴∠ODC＋∠CDE＝90°，即OD⊥DE，∴DE是⊙O的切线 ②设 ⊙O的半径为r，∵∠ODF＝90°，∴OD2＋DF2＝OF2，即r2＋42＝(r＋ 2)2，解得r＝3，∴⊙O的直径为6
解：①如图 1 中，连接 OC.∵AB⊥CD，∴∠CHO＝90°，在 Rt△COH 中，
∵OC＝r，OH＝r－2，CH＝4，∴r2＝42＋(r－2)2，∴r＝5 ②如图 1 中，连
接 OD.∵AB⊥CD，AB 是直径，∴A︵D＝A︵C＝12C︵D，∴∠AOC＝12∠COD，
初中数学中考复习正多边形与圆的有关的证明和计算
初中数学中考复习正多边形与圆的有关的证明和计算正多边形与圆的关系是初中数学中重要的内容。
在中考复习中，我们需要掌握正多边形与圆的有关知识，并能够进行证明和计算。
一、正多边形的性质与计算：1.正多边形的定义：正多边形是指所有边相等，所有角也相等的多边形。
2.正多边形的计算：正n边形的内角和为180°(n-2)，每个内角为(180°(n-2))/n。
正n边形的外角和为360°，每个外角为360°/n。
正n边形的中心角为360°/n。
例题1：求正六边形的内角和。
解：内角和为180°(6-2)=720°。
例题2：求正五边形的每个内角大小。
解：每个内角为(180°(5-2))/5=108°。
二、正多边形与圆的关系：1.圆的定义：圆是平面上一组到一个固定点(圆心)距离相等的点的集合。
2.正多边形与圆的关系：正多边形的顶点均在圆上，且正多边形的外接圆和内切圆都满足以下性质：①外接圆：正多边形的外接圆的圆心与正多边形的中心重合。
②内切圆：正多边形的内切圆的圆心与正多边形的中心重合，且内接圆的半径等于正多边形的边长的一半。
3.正多边形与圆的证明：①外接圆的证明：由正多边形的定义可知，正多边形的每个顶点到圆心的距离都相等，即正多边形的顶点在圆上。
而圆心与正多边形的中心重合，所以正多边形的外接圆的圆心与正多边形的中心重合。
②内切圆的证明：首先，通过正多边形的定义，可以证明正多边形的每个顶点到圆心的距离都相等，即正多边形的顶点在圆上。
其次，由于正多边形的边长相等，所以正多边形的中心到各个顶点的距离也相等。
而内切圆的半径等于正多边形中心到任意一个顶点的距离，所以正多边形的内切圆的圆心与正多边形的中心重合，且内切圆的半径等于正多边形的边长的一半。
例题3：如图，正六边形ABCD中，O为外接圆的圆心，求AB的长。
解：由于正六边形的外接圆的圆心与正多边形的中心重合，所以O即为正六边形的中心。
陕西中考圆的证明与计算(2023版)
陕西中考圆的证明与计算（2023版）知识总结1．切线的性质：垂直于过切点的半径．（连半径，得垂直）2．切线的判定：（1）定义法：和圆只有一个交点的直线是圆的切线；（2）距离法：到圆心距离等于半径的直线是圆的切线；证明d =r 即可，常用于已知数据的计算，比如动圆相切问题．（3）判定定理：经过半径外端且垂直于这条半径的直线是圆的切线．换个说法：⎧⎨⎩有交点：连半径,证垂直无交点：作垂直,证半径，多用于几何证明．多数情况为有交点，重点考虑如何证垂直：①证明和已知垂线平行；②证明夹角为直角．3．常见相切图（1）角分+等腰得平行：点C 在以AB 为直径的圆O 上，AH ⊥CH ，且AC 平分∠HAB ．【证明】连接OC，则OC=OA，∴∠OCA=∠OAC，又∠OAC=∠HAC，∴∠OCA=∠HAC，∴OC∥AH，∴OC⊥CH，∴CH是圆O的切线．（2）证明和已知直角相等．证明△PCO≌△PAO，可得∠PCO=∠PAO=90°．（3）证明夹角为直角．（弦切角定理）如图，若∠BAC=∠D，则AB是圆O切线．如图，连接AO并延长交圆O于点P，则∠P=∠D=∠BAC，∵∠P+∠PAC=90°，∴∠BAC+∠PAC=90°，即AB⊥AP，∴AB是圆O的切线．1．如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，切线DE交AC 于点E．（1）求证：DE＝AE；（2）若AD＝8，DE＝5，求BC的长度．2．如图，在Rt△ABC中，∠ABC＝90°，以BC为直径的⊙O交AC于点E，⊙O的切线DE交AB于点D．（1）求证：DA＝DB；（2）连接BE，OD，交点为F，若cos A＝，BC＝6，求OF的长．3．如图，AB是⊙O的直径，经过⊙O上一点D，作⊙O的切线EF，交AB的延长线于点F，AE⊥EF，交BD的延长线于点C．（1）求证：AB＝AC．（2）若⊙O的半径为3，，求BF的长．4．如图，AB为⊙O的直径，C、E为⊙O上的两点，过点E的切线交CB的延长线于点D，且CD⊥DE，连接CE，AE．（1）求证：∠ABC＝2∠A；（2）若⊙O半径为，AB：BD＝5：1，求AE的长．5．已知：如图，AB为⊙O的直径，CD与⊙O相切于点C，交AB延长线于点D，∠D＝30°，连接AC、BC，CE平分∠ACB交⊙O于点E，过点B作BF⊥CE，垂足为F．（1）求证：CA＝CD；（2）若AB＝12，求线段BF的长．6．已知：如图，⊙O过正方形ABCD的顶点A，B，且与CD边相切于点E．点F是BC与⊙O的交点，连接OB，OF，AF，点G是AB延长线上一点，连接FG，且∠G+∠BOF＝90°．（1）求证：FG是⊙O的切线；（2）如果正方形边长为8，求⊙O的半径．7．如图，在△AOB中，以点O为圆心的⊙O与AB相切于点D，延长AO交⊙O于点C，连接CD，过点A作AF⊥BO，交BO的延长线于点H，交⊙O于点F，∠B＝∠C．求证：（1）AF∥CD；（2）AH2＝OH⋅BH．8．如图，AB是⊙O的直径，已知点D是弧BC的中点，连接DO并延长，在延长线上有一点E，连接AE，且∠E＝∠B．（1）求证：AE是⊙O的切线；（2）连接AC，若AC＝6，CF＝4，求OE的长．9．如图，AB是⊙O的直径，C在AB的延长线上，⊙O与CD相切于点D，过点A作AE ⊥CD，垂足为E．（1）求证：AD平分∠EAC．（2）若BC＝3，，求⊙O的半径以及线段ED的长．10．如图，AB是⊙O的直径，点D是直径AB上不与A，B重合的一点，过点D作CD⊥AB，且CD＝AB，连接BC交⊙O于点F，在CD上取一点E，使EF＝EC．（1）求证：EF是⊙O的切线；（2）当D是OA的中点时，AB＝4，求BF的长．11．如图，△ABC内接于⊙O，AB＝AC，过点A作BC平行线AM，连接BO并延长，交AM于点D，连接AO、CO．（1）求证：AM是⊙O的切线；（2）若BC＝10，AD＝8，求⊙O的半径．12．如图，已知△ABC的边AB所在的直线是⊙O的切线，切点为B，AC经过圆心O并与圆交于点D、C，E为AB延长线上一点，连接CE交⊙O于点F，且∠BCE＝∠ACB．（1）求证：CE⊥AB；（2）若⊙O的半径是6，AB＝8，求EF的长．13．如图，在△ABC中，∠C＝90°，以FB为直径作⊙O，⊙O与直角边AC相切，切点为E．（1）求证：∠DBE＝∠EBA；（2）若AB＝10，DB＝4，求EB的长．14．如图，已知AB是⊙O的直径，C是⊙O上一点，OD⊥BC，垂足为D，连接AD，过点A作⊙O的切线与DO的延长线相交于点E．（1）求证：∠B＝∠E；（2）若⊙O的半径为4，OE＝6，求AD的长．15．如图，AB是⊙O的直径，点D、E均在⊙O上，连接AD、BD、BE、DE，过点D作⊙O的切线，交AB的延长线于点C．（1）求证：∠DEB＝∠CDB；（2）若BD＝DE＝6，BE＝9.6，求⊙O的半径．16．如图，△ABC是⊙O的内接三角形，BC为⊙O的直径，点E是⊙O上一点，连接OE 并延长交过点C的切线CD于点D，∠B＝∠D．（1）求证：OD∥AC；（2）延长EO交AB于点F，AF＝2，⊙O的直径为2，求OD的长．17．如图，已知△ABC的外接圆直径是AB，点O是圆心，点D在⊙O上，且＝，过点D作⊙O的切线，与CA、CB的延长线分别交于点E、F．（1）求证：AB∥EF；（2）若⊙O的半径为5，BC＝8，求DF的长度．18．如图，AB为⊙O的直径，C为⊙O上一点，AD⊥CE，垂足为D，AC平分∠DAB．（1）判定直线CE与⊙O的位置关系，并说明你的理由；（2）若AD＝3，AC＝4，求圆的半径．19．如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点恰好为BC的中点D，与AC边的交点为F，过点D作DE⊥AC于点E．（1）求证：直线DE是⊙O的切线；（2）若AB＝5，tan∠ACB＝2，求弦AF的长度．20．如图，在△ABC中，AB＝AC，以AB为直径作⊙O交BC于点D．过点D作DE⊥AC，垂足为E，延长CA交⊙O于点F．（1）求证：DE是⊙O的切线；（2）若tan B＝，⊙O的半径为5，求线段CF的长．21．如图，AB为⊙O的直径，OD为⊙O的半径，⊙O的弦CD与AB相交于点F，⊙O的切线CE交AB的延长线于点E，EF＝EC．（1）求证：OD垂直平分AB；（2）若⊙O的半径长为3，且BF＝BE，求OF的长．22．如图，AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，BD⊥CD，DB的延长线与⊙O交于点E．（1）求证：∠ABE＝2∠A；（2）若，BD＝4，求BE的长．23．如图，在△ABC中，AC＝AB，以AB为直径的⊙O交BC于点D，过点D作ED⊥AC 点E，交AB延长线于点F．（1）求证：EF是⊙O的切线；（2）若DF＝4，tan∠BDF＝，求AC的长．24．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且∠DCF＝∠CAD．（1）求证：CF是⊙O的切线；（2）若直径AD＝10，cos B＝，求FD的长．25．如图，AB是⊙O的直径，AE是⊙O的切线，点C为直线AE上一点，连接OC交⊙O 于点D，连接BD并延长交线段AC于点E．（1）求证：∠CAD＝∠CDE；（2）若CD＝6，tan∠BAD＝，求⊙O的半径．26．如图，四边形ABCD是⊙O的内接四边形，且对角线BD为⊙O的直径，过点A作AE ⊥CD，与CD的延长线交于点E，且DA平分∠BDE．（1）求证：AE是⊙O的切线；（2）若⊙O的半径为5，CD＝6，求AD的长．27．如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是的中点，过点B的切线与AC的延长线交于点D．①求证：BD⊥AD；②若AC＝9，tan∠ABC＝，求⊙O的半径．28．如图，△ABC中，∠C＝90°，点O在AB上，⊙O经过点A，且与BC相切于点D．（1）求证：AD平分∠BAC；（2）若AC＝6，cos∠BAC＝，求⊙O的半径．29．如图，AB是⊙O的直径，点C为⊙O上一点，CD平分∠ACB，交AB于点E，交⊙O 于点D，延长BA到点P，使得PE＝PC．（1）求证：PC与⊙O相切；（2）若⊙O的半径3，PC＝4，求CD的长．30．如图，AB是⊙O的直径，点C、D是⊙O上两点，CE与⊙O相切，交DB延长线于点E，且DE⊥CE，连接AC，DC．（1）求证：∠ABD＝2∠A；（2）若DE＝2CE，AC＝8，求⊙O的半径．31．如图，AB是⊙O的直径，AC是弦，且OD⊥AC于点E，OD交⊙O于点F，连接CF、BF，若∠BFC＝∠ODA．（1）求证：AD是⊙O的切线：（2）若AB＝10，AC＝8，求AD的长．32．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，连接OD，过点D作⊙O的切线DE，交AC于点E，延长CA交⊙O于点F，连接BF．（1）求证：DE⊥AC；（2）若⊙O的直径为5，cos C＝，求CF的长．33．如图，在⊙O中，PA是直径，PC是弦，PH平分∠APB且与⊙O交于点H，过H作HB⊥PC交PC的延长线于点B．（1）求证：HB是⊙O的切线；（2）若HB＝4，BC＝2，求⊙O的半径．34．如图，AB是⊙O的直径，点D在直径AB上（D与A，B不重合），CD⊥AB，且CD＝AB，连接CB，与⊙O交于点F，在CD上取一点E，使得EF＝EC．（1）求证：EF是⊙O的切线；（2）若D是OA的中点，AB＝4，求CF的长．35．如图，四边形ABCD是⊙O的内接四边形，且对角线BD为直径，过点A作⊙O的切线AE，与CD的延长线交于点E，已知DA平分∠BDE．（1）求证：AE⊥DE；（2）若⊙O的半径为5，CD＝6，求AD的长．36．如图，在Rt△ACD中，∠ACD＝90°，点O在CD上，作⊙O，使⊙O与AD相切于点B，⊙O与CD交于点E，过点D作DF∥AC，交AO的延长线于点F，且∠OAB＝∠F．（1）求证：AC是⊙O的切线；（2）若OC＝3，DE＝2，求DF的长．37．如图，在Rt△ABC中，∠ACB＝90°，点D是AB的中点，以CD为直径作⊙O，与BC交于点E，过点E作⊙O的切线EF，交AB于点F．（1）求证：EF⊥AB；（2）若⊙O的半径是，cos∠ACD＝，求DF的长．38．如图，⊙O是△ABC的外接圆，＝，过点A作AD∥BC交⊙O于点D，连接CD，延长DA到点E，连接CE，∠D＝∠E．（1）求证：CE是⊙O的切线；（2）若CE＝8，AE＝5，求⊙O半径的长．39．如图，BD为⊙O的直径，∠ABE＝∠BCA，过点A的直线与⊙O分别交于点E，C，与BD交于点F，连接BE，BC．（1）求证：AB为⊙O的切线．（2）若∠A＝∠ABE，BE＝5，BC＝8，求⊙O的半径．40．如图，AB是⊙O的直径，AE是⊙O的切线，点C为直线AE上一点，连接OC交⊙O 于点D，连接BD并延长交线段AC于点E．（1）求证：∠CDE＝∠CAD；（2）若CD＝4，tan B＝，求⊙O的半径．。
中考数学压轴题提升训练圆中证明及计算问题含解析
圆中证明及计算问题【例1】如图,⊙O是△ABC的外接圆，点O在BC边上,∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．（1）求证：PD是⊙O的切线；（2）求证：AB•CP＝BD•CD；（3）当AB＝5 cm,AC＝12 cm时，求线段PC的长．【答案】见解析.【解析】（1）证明：连接OD．∵∠BAD＝∠CAD，∴弧BD=弧CD，∴∠BOD＝∠COD＝90°，∵BC∥PA，∴∠ODP＝∠BOD＝90°，即OD⊥PA，∴PD是⊙O的切线．(2）证明:∵BC∥PD，∴∠PDC＝∠BCD．∵∠BCD＝∠BAD，∴∠BAD＝∠PDC，∵∠ABD+∠ACD＝180°，∠ACD+∠PCD＝180°，∴∠ABD＝∠PCD,∴△BAD∽△CDP,∴AB BD,CD CP∴AB•CP＝BD•CD．（3）∵BC是直径，∴∠BAC＝∠BDC＝90°，∵AB＝5，AC＝12，由勾股定理得：BC＝13,由（1）知，△BCD是等腰直角三角形，∴BD＝CD＝∵AB•CP＝BD•CD．．∴PC＝16910【变式1-1】如图，△ABC内接于⊙O，且AB=AC,延长BC 到点D，使CD=CA，连接AD交⊙O于点E．(1）求证：△ABE≌△CDE；(2）填空：①当∠ABC的度数为时,四边形AOCE是菱形;②若AE=6，BE=8，则EF的长为．。
【答案】（1)见解析；（2）60；92【解析】（1）证明：连接CE，∵AB=AC，CD=CA,∴∠ABC=∠ACB,AB=CD，∵四边形ABCE是圆内接四边形,∴∠ECD+∠BCE=∠BAE +∠BCE=180°,∴∠ECD=∠BAE，同理，∠CED=∠ABC，∵∠ABC=∠ACB=∠AEB，∴∠CED=∠AEB，∴△ABE≌△CDE；（2）①60；连接AO、OC，∵四边形ABCE是圆内接四边形,∴∠ABC+∠AEC=180°,∵∠ABC =60，∴∠AEC =∠AOC =120°,∵OA =OC ,∴∠OAC =∠OCA =30°，∵AB =AC ，∴△ABC 是等边三角形，∴∠ACB =60°，∵∠ACB =∠CAD +∠D ，AC =CD ,∴∠CAD =∠D =30°，∴∠ACE =30°，∴∠OAE =∠OCE =60°，即四边形AOCE 是平行四边形，∵OA =OC ,∴四边形AOCE 是菱形；②由(1)得：△ABE ≌△CDE ，∴BE =DE =8，AE =CE =6，∠D =∠EBC ,由∠CED =∠ABC =∠ACB ，得△ECD ∽△CFB ， ∴CE CF DE BC==68, ∵∠AFE =∠BFC ，∠AEB =∠FCB ，∴△AEF ∽△BCF ， ∴EF CF AE BC=， 即668EF =，∴EF=9．2【例2】如图，AB为⊙O的直径,点C为AB上方的圆上一动点，过点C作⊙O的切线l，过点A作直线l的垂线AD，交⊙O于点D，连接OC，CD，BC，BD，且BD与OC交于点E．(1）求证：△CDE≌△CBE;（2）若AB＝4,填空：①当弧CD的长度是时，△OBE是等腰三角形；②当BC＝时，四边形OADC为菱形．;2．【答案】(1)见解析；（2)2【解析】（1）证明:延长AD交直线l于点F,∵AD垂直于直线l，∴∠AFC＝90°，∵直线l为⊙O切线，∴∠OCF＝90°,∴∠AFC＝∠OCF＝90°,∴AD∥OC,∵AB为⊙O直径,∴∠ADB ＝90°，∴∠OEB ＝90°，∴OC ⊥DB ,∴DE ＝BE ,∠DEC ＝∠BEC ＝90°，∵CE ＝CE ，∴△CDE ≌△CBE ；（2)①如图2，连接OD ，由（1）知∠OEB ＝90°,当△OBE 是等腰三角形时，则△OEB 为等腰直角三角形,∴∠BOE ＝∠OBE =45°，∵OD ＝OB ，OE ⊥BD ，∴∠DOC ＝∠BOE ＝45°,∵AB ＝4,∴OD ＝2，∴弧CD 的长=452180π⨯=2π;②当四边形OADC 为菱形时，则AD ＝DC ＝OC ＝AO ＝2，由(1）知，BC ＝DC ，∴BC ＝2.【变式2—1】(2019·河南南阳一模）如图,四边形ABCD 是⊙O 的内接四边形,⊙O 的半径为2，∠B =135°，则弧AC 的长为（ ）A. 2πB. π C 。
中考数学复习① 与圆的基本性质有关的计算与证明
类型①与圆的基本性质有关的计算与证明,备考攻略)1．圆的基本性质．(1)圆是轴对称图形，其对称轴是任意一条过圆心的直线．(2)垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．垂径定理的推论：平分弦(不是直径)的直径垂直于弦，并且平分弦对的弧．(3)圆具有旋转对称性，特别的圆是中心对称图形，对称中心是圆心．(4)圆心角定理：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．(5)圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半．圆周角定理推论1：在同圆或等圆中，同弧或等弧所对的圆周角相等．圆周角定理推论2：直径所对的圆周角是直角；90°的圆周角所对的弦是直径．2．圆中几个关键元素之间的相互转化：弧、弦、圆心角、圆周角等都可以通过相等来互相转化．这在圆中的证明和计算中经常用到．1．垂径定理及垂径定理推论混淆．2．圆的基本元素之间不会转化．3．计算错误．先找准与圆的哪些要素有关，然后选择对应的性质定理求解．计算圆中的线段长或线段比，通常与勾股定理、垂径定理与三角形的全等、相似等知识的结合，形式复杂，无规律性．注意圆中几个关键元素之间的相互转化：弧、弦、圆心角、圆周角等都可以通过相等来互相转化．,典题精讲)【例】(2017孝感中考)已知半径为2的⊙O中，弦AC＝2，弦AD＝22，则∠COD的度数为________．【解析】连接OC，过点O作OE⊥AD于点E，如图所示．∵OA ＝OC ＝AC ，∴∠OAC ＝60°，∵AD ＝22，OE ⊥AD ，∴AE ＝2，OE ＝OA 2－AE 2＝2，∴∠OAD ＝45°，∴∠CAD ＝∠OAC ＋∠OAD ＝105°或∠CAD ＝∠OAC －∠OAD ＝15°，∴∠COD ＝360°－2×105°＝150°或∠COD ＝2×15°＝30°.【答案】150°或30°1．(2017哈尔滨中考)如图，⊙O 中，弦AB ，CD 相交于点P ，∠A ＝42°，∠APD ＝77°，则∠B 的大小是( B )A ．43°B ．35°C ．34°D ．44°2．(达州中考)如图，半径为3的⊙A 经过原点O 和点C(0，2)，B 是y 轴左侧⊙A 优弧上一点，则tan ∠OBC 为( C )A .13B ．2 2C .24D .223,(第2题图)) ,(第3题图))3．(聊城中考)如图，四边形ABCD 内接于⊙O ，F 是CD ︵上一点，且DF ︵＝BC ︵，连接CF 并延长交AD 的延长线于点E ，连接AC.若∠ABC ＝105°，∠BAC ＝25°，则∠E 的度数为( B )A ．45°B ．50°C ．55°D ．60°4．(青岛中考)如图，AB 是⊙O 的直径，点C ，D 是⊙O 上的两点，若∠BCD ＝28°，则∠ABD ＝__62°__．,(第4题图)) ,(第5题图))5．(黔西南中考)如图，AB 是⊙O 的直径，CD 为弦，CD ⊥AB 于E ，若CD ＝6，BE ＝1，则⊙O 的直径为__10__.6．(安微中考)在⊙O 中，直径AB ＝6，BC 是弦，∠ABC ＝30°，点P 在BC 上，点Q 在⊙O 上，且OP ⊥PQ.(1)如图①，当PQ ∥AB 时，求PQ 的长度；(2)如图②，当点P 在BC 上移动时，求PQ 长的最大值．解：(1)连接OQ.∵PQ ∥AB ，OP ⊥PQ ，∴OP ⊥AB.在Rt △OBP 中，∵tan B ＝OPOB ，∴OP ＝3tan 30°＝ 3.在Rt △OPQ 中，∵OP ＝3，∴OQ ＝3，∴PQ ＝OQ 2－OP 2＝6；(2)连接OQ.在Rt △OPQ 中，PQ ＝OQ 2－OP 2＝9－OP 2，当OP 的长最小时，PQ 的长最大，此时OP ⊥BC ，则OP ＝OB·sin 30°＝OB 2＝32，∴PQ 长的最大值为9－⎝⎛⎭⎫322＝332.7．(鄂州中考)如图，在Rt △ABC 中，∠ACB ＝90°，AO 是△ABC 的角平分线．以O 为圆心，OC 为半径作⊙O.(1)求证：AB 是⊙O 的切线；(2)已知AO 交⊙O 于点E ，延长AO 交⊙O 于点D ，tan D ＝12，求AEAC 的值；(3)在(2)的条件下，设⊙O 的半径为3，求AB 的长．解：(1)作OF ⊥AB 于点F ，∵AO 是∠BAC 的平分线，∠ACB ＝90°， ∴OC ＝OF ， ∴AB 是⊙O 的切线；(2)连接CE ，∵ED 是⊙O 的直径， ∴∠ECD ＝90°，∴∠ECO ＋∠OCD ＝90°， ∵∠ACB ＝90°，∴∠ACE ＋∠ECO ＝90°， ∴∠ACE ＝∠OCD ， ∵OC ＝OD ，∴∠OCD ＝∠ODC ， ∴∠ACE ＝∠ODC ， ∵∠CAE ＝∠CAE ， ∴△ACE ∽△ADC ， ∴AE AC ＝CE CD， ∵tan D ＝12，∴CE CD ＝12，∴AE AC ＝12； (3)先在△ACO 中，设AE ＝x ，由勾股定理得(x ＋3)2＝(2x)2＋32，解得x ＝2， ∴AO ＝AE ＋OE ＝2＋3＝5， ∴AC ＝AO 2－OC 2＝4. ∴AF ＝AC ＝4.∵∠BFO ＝90°＝∠ACO ，易证Rt △BOF ∽Rt △BAC ，得BF BC ＝BO BA ＝OFAC ，设BO ＝y ，BF ＝z ，z 3＋y ＝y 4＋z ＝34，即⎩⎨⎧4z ＝9＋3y ，4y ＝12＋3z ，解得z ＝727，y ＝757，∴AB ＝727＋4＝1007.8．(2017株洲中考)如图所示AB 为⊙O 的一条弦，点C 为劣弧AB 的中点，E 为优弧AB 上一点，点F 在AE 的延长线上，且BE ＝EF ，线段CE 交弦AB 于点D.(1)求证：CE ∥BF;(2)若BD ＝2，且EA ∶EB ∶EC ＝3∶1∶5，求△BCD 的面积．(注：根据圆的对称性可知OC ⊥AB)解：(1)连接AC ，BE ，作直线OC ，如图所示： ∵BE ＝EF ，∴∠F ＝∠EBF.∵∠AEB ＝∠EBF ＋∠F ， ∴∠F ＝12∠AEB.∵C 是AB ︵的中点，∴AC ︵＝BC ︵， ∴∠AEC ＝∠BEC ，∵∠AEB ＝∠AEC ＋∠BEC ， ∴∠AEC ＝12∠AEB ，∴∠AEC ＝∠F ，∴CE ∥BF ；(2)∵∠DAE ＝∠DCB ，∠AED ＝∠CEB ， ∴△ADE ∽△CBE ， ∴AD CB ＝AE CE ，即AD CB ＝35. ∵∠CBD ＝∠CEB ，∠BCD ＝∠ECB ， ∴△CBE ∽△CDB ， ∴BD CB ＝BE CE ，即2CB ＝15， ∴CB ＝25， ∴AD ＝6， ∴AB ＝8，∵点C 为劣弧AB 的中点， ∴OC ⊥AB ，AG ＝BG ＝12AB ＝4，∴CG ＝CB 2－BG 2＝2，∴△BCD 的面积＝12BD·CG ＝12×2×2＝2.。
中考数学圆(上)圆的有关概念和性质
圆的有关概念和性质
考点聚焦
考查频率 考查题型 命题特点
方法点拨
有关概念
圆
圆的基本性质
圆心、半径、直径 弧、弦、弦心 等圆、同心圆 圆心角、圆周角
圆的轴对称性
中心对称性和旋转不 变性
垂径定理 圆周角定理 圆内接四边形的性质
平分弦（不是直径）的直径垂直于弦，并且平分 弦所对的两条弧．
C
·O
E
O
例3（2013贵州省黔西南州，3分）如图所示⊙O中，已知 ∠BAC=∠CDA=20°，则∠ABO的度数为 50°．
【解析】连结OA，由题意得
小试身手
（2013贵州省黔西南州，12分）如图，AB是⊙O的直径，
【解析】（1）证明：∵∠C=∠P．又∵∠1=∠C ∴∠1=∠P ．∴CB∥PD
（2）解：连接AC，∵AB为⊙O的直径，
A
B
D
几何语言表达
C
O
A
M
B
D
2．圆心角、弧、弦之间的关系
A
C
O
B
A' C'
B'
D
B E
●
O
A
C
C
A
●
B
O
B
A
C
●
O
D
【命题角度】本题考查的是垂径定理及勾股定理. 【方法点拨】根据题意作出辅助线，构造出直角三角形是解答此题的关键．
【解析】∵⊙O的半径OD⊥弦AB于点C，AB=8，∴AC=AB=4，
类型二：运用圆心角、弧、弦的关系解决问题
A
E
C
D
B
O
（1）证明：连接 OA、OB、OC，∵点 A 是弧 BC 的中点，
往年中考关于圆的证明汇总(有答案)
23 图
24 图
24、如图，⊙M 与 x 轴相切于点 C，与 y 轴的一个交点为 A。
（1）求证：AC 平分∠OAM；（2）如果⊙M 的半径等于 4，∠ACO=300，求 AM 所在直线的解析式．
25、如图，在直角三角形 ABC 中，∠ABC=90°．
1、如图，在⊙O 中，AB，CD 是直径，BE 是切线，B 为切点，连接 AD，BC，BD．
（1）求证：△ABD≌△CDB；
（2）若∠DBE=37°，求∠ADC 的度数．
1图
2图
2、如图，△ABC 中，∠ACB=90°，D 是边 AB 上的一点，E 是 BC 上的一点，以 EC 为直径的⊙O 经过点 D，OA⊥CD 于点
连接 AF． (1)证明：∠F＝∠CAD；(2)试判断直线 AF 与⊙O 的位置关系，并给出证明．
11 图
12 图
12、如图，AB 是半圆 O 的直径，点 C 是⊙O 上一点（不与 A，B 重合） ，连接 AC，BC，过点 O 作 OD∥AC 交 BC 于点 D，
在 OD 的延长线上取一点 E，连接 EB，使∠OEB=∠ABC．
那么图中两个扇形（即阴影部分）的面积之和
两等圆⊙A，⊙B外切， 为．
35 图
36 图
36、如图所示，AB 是⊙O 的直径，AE 是弦，C 是劣弧 AE 的中点，过 C 作 CD⊥AB 于点 D，CD 交 AE 于点 F，过 C 作 CG
∥AE 交 BA 的延长线于点 G．
（1）求证：CG 是⊙O 的切线． （2）求证：AF=CF． （3）若∠EAB=30°，CF=2，求 GA 的长．
33 图
圆的证明与计算 (基本图形)
圆的证明与计算(基本图形)圆的证明与计算是中考中的一类重要的问题，此题完成情况的好坏对解决后面问题的发挥有重要的影响，所以解决好此题比较关键。
一、考点分析：1.圆中的重要定理:(1)圆的定义:主要是用来证明四点共圆.(2)垂径定理:主要是用来证明——弧相等、线段相等、垂直关系，以及中点等等.(3)三者之间的关系定理: 主要是用来证明——弧相等、线段相等、圆心角相等.(4)圆周角性质定理及其推论: 主要是用来证明——直角、角相等、弧相等.(5)切线的性质定理:主要是用来证明——垂直关系.(6)切线的判定定理: 主要是用来证明直线是圆的切线.(7)切线长定理: 线段相等、垂直关系、角相等.2.圆中几个关键元素之间的相互转化:弧、弦、圆心角、圆周角等都可以通过相等来互相转化.这在圆中的证明和计算中经常用到.二、考题形式分析：主要以解答题的形式出现,近几年武汉市中考题的22题的第1问主要是判定切线；第2问主要是与圆有关的计算：①求线段长（或面积）；②求线段比；③求角度的三角函数值（实质还是求线段比）。
三、解题方法：1、判定切线的方法：（1）若切点明确，则“连半径，证垂直”。
常见手法有：全等转化；平行转化；直径转化；中线转化等；有时可通过计算结合相似、勾股定理证垂直；（2）若切点不明确，则“作垂直，证半径”。
常见手法：角平分线定理；等腰三角形三线合一，隐藏角平分线；（07武汉）22．(本题8分)如图，等腰三角形ABC中，AC＝BC＝10，AB＝12。
以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E。
(1)求证：直线EF是⊙O的切线；(2)求sin∠E的值。
(第22题图)（10武汉）22．(本题满分8分) 如图，点O 在∠APB 的平分线上，⊙O 与PA 相切于点C ． (1) 求证：直线PB 与⊙O 相切；(2) PO 的延长线与⊙O 交于点E ．若⊙O 的半径为3，PC=4．求弦CE 的长．2、与圆有关的计算：计算圆中的线段长或线段比，通常与勾股定理、垂径定理与三角形的全等、相似等知识的结合，形式复杂，无规律性。
中考数学解答题压轴题突破 重难点突破四 圆中的证明与计算
(1)求证：EF 是⊙O 的切线； 证明：连接 OE，∵AB 是⊙O 的直径，∴∠AEB＝90°， 即∠AEO＋∠OEB＝90°， ∵AE 平分∠CAB，∴∠CAE＝∠BAE， ∵∠BEF＝∠CAE，∴∠BEF＝∠BAE， ∵OA＝OE，∴∠BAE＝∠AEO， ∴∠BEF＝∠AEO，∴∠BEF＋∠OEB＝90°， ∴∠OEF＝90°，∴OE⊥EF， ∵OE 是⊙O 的半径，∴EF 是⊙O 的切线．
解：∵BD 为⊙O 的直径， ∴∠BCD＝∠DCE＝90°， ∵AC 平分∠BAD， ∴∠BAC＝∠DAC， BC＝DC＝2 2， ∴BD＝2 2× 2＝4.
(2)若 BE＝5 2，计算图中阴影部分的面积． 【分层分析】 ∵BC＝DC，∴阴影的面积等于三角形 CDE 的面积. 解：∵BE＝5 2，∴CE＝3 2 ∵BC＝DC，
2．(2022·宁波)如图①，⊙O 为锐角三角形 ABC 的外接圆，点 D 在B︵C上， AD 交 BC 于点 E，点 F 在 AE 上，满足∠AFB－∠BFD＝∠ACB，FG∥AC 交 BC 于点 G，BE＝FG，连接 BD，DG.设∠ACB＝α.
(1)用含α的代数式表示∠BFD. 解：∵∠AFB－∠BFD＝∠ACB＝α，① 又∵∠AFB＋∠BFD＝180°，② ②－①，得 2∠BFD＝180°－α，
1
1
∴S△ABC＝2BC·AC＝2×2×2 3＝2 3，
∴阴影部分的面积是12π×A2B2－2 3＝2π－2 3.
3．(2022·黔西南州第 23 题 14 分)如图，在△ABC 中，AB＝AC，以 AB 为 直径作⊙O，分别交 BC 于点 D，交 AC 于点 E，DH⊥AC，垂足为 H，连接 DE 并延长交 BA 的延长线于点 F.
α ∴∠BFD＝90°－ 2 .
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
半径，证垂直”，难点在于如何证明两线垂直例1 如图，在△ ABC中，AB=AC，以AB为直径的O O交BC于D，交AC于E, B为切点的切线交OD延长线于F.求证：EF与O O相切.例2 如图，AD是/ BAC的平分线，P为BC延长线上一点，且PA=PD.求证：PA与O O相切.证明一：作直径AE，连结EC.•/ AD是/ BAC的平分线，•••/ DAB= / DAC.•/ PA=PD ,•••/ 2=Z 1+ / DAC.•••/ 2=Z B+ / DAB ,•••/ 仁/ B.又•••/ B= / E,•••/ 仁/ E•/ AE是O O的直径，•AC 丄EC,/ E+ / EAC=90°.•••/ 1 + / EAC=90°.即OA丄PA.• PA与O O相切.证明二：延长AD交O O于E,连结OA , OE.•/ AD是/ BAC的平分线，•BE=C1E, c• OE 丄BC.•/ E+/ BDE=900.•/ OA=OE , • / E=/ 1.例5 如图，AB 是O O 的直径，CD 丄AB ，且 OA 2=OD • OP. 求证：PC 是O O 的切线.说明: 求证: •/ PA=PD , •••/ PAD= / PDA. 又•••/ PDA= / BDE, •••/ 1 + Z PAD=90 0即OA 丄PA. • PA 与O O 相切此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用如图，AB=AC , AB 是O O 的直径，O O 交BC 于D ,DM 与O O 相切.例4 如图，已知：AB 是O O 的直径，点 C 在O O 上，且/ CAB=30°, BD=OB , D 在AB 的延长线上 求证：DC 是O O 的切线例6如图，ABCD是正方形，G是BC延长线上一点, 求证：CE与厶CFG的外接圆相切.分析：此题图上没有画出△ CFG的外接圆，但△们取FG的中点0,连结0C,证明CE丄OC即可得解.证明：取FG中点0,连结0C.T ABCD是正方形，••• BC 丄CD , △ CFG 是Rt△•/ 0是FG的中点，•0是Rt △ CFG的外心.•/ 0C=0G ,•••/ 3= / G ,•/ AD // BC,•/ G=Z 4.•/ AD=CD , DE=DE ,/ ADE= / CDE=45°,•△ ADE ◎△ CDE (SAS)•••/ 4=Z 1,Z 1 = / 3./ / 0vZ 2+Z 3=90 ,•••/ 1 + Z 2=90°.即CE丄0C.AG交BD于E,交CD于F.CFG是直角三角形，圆心在斜边FG的中点，为此我••• CE与厶CFG的外接圆相切方法二：若直线l与O O没有已知的公共点，又要证明I是O O的切线，只需作OA丄I, A为垂足，证明OA是O O的半径就行了，简称：“作垂直；证半径”（一般用于函数与几何综合题）例1如图，AB=AC , D为BC中点，O D与AB切于E点.求证：AC与O D相切.分析：说明：证明一是通过证明三角形全等证明DF=DE的，证明二是利用角平分线的性质证明DF=DE的,这类习题多数与角平分线有关例2：已知：如图，AC , BD 与O O 切于A、B，且AC // BD，若/ COD=90求证：CD是O O的切线.证明一：连结OA , OB，作OE丄CD , E为垂足.•••AC , BD 与O O 相切，•AC 丄OA , BD 丄OB.•/ AC // BD ,•••/ 1+ / 2+Z 3+ / 4=180°.• / COD=90°,•/ 2+Z 3=90°,/ 1 + / 4=90°.•/ 4+Z 5=900.•Z 1 = / 5.•Rt△AOC s Rt△BDO.AC OC• __ __"OB OD .•/ OA=OB ,AC OC"OA OD.又•/ CAO= / COD=900,AB C• △ AOC ODC ,• / 1 = / 2.又• OA 丄AC , OE 丄CD,••• OE=OA. • E 点在O O 上. • CD 是O O 的切线.连结OA , OB ,作OE 丄CD 于E ,延长 DO 交CA 延长线于 F.••• AC ，BD 与O O 相切， • AC 丄 OA , BD 丄 OB. •/ AC // BD , • / F= / BDO. 又••• OA=OB ,• △ AOF ◎△ BOD (AAS ) • OF=OD. •••/ COD=9O °, • CF=CD ，/ 1 = / 2.又••• OA 丄 AC , OE 丄 CD , • OE=OA. • E 点在O O 上. • CD 是O O 的切线.连结AO 并延长，作 OE 丄CD 于E ,取CD 中点F ，连结OF.••• AC 与O O 相切， • AC 丄 AO. •/ AC // BD , • AO 丄 BD.••• BD 与O O 相切于B , • AO 的延长线必经过点 B. • AB 是O O 的直径.•/ AC // BD , OA=OB , CF=DF , • OF // AC , • / 1= / COF.•••/ COD=90 0, CF=DF ,1• OF = CD =CF .2• / 2= / COF.证明二: 证明三:•/ OA 丄AC , 0E 丄CD ,•OE=OA.•E点在O O上.•CD是O O的切线说明：证明一是利用相似三角形证明/ 1 = / 2，证明二是利用等腰三角形三线合一证明/是利用梯形的性质证明/ 1= / 2,这种方法必需先证明A、O、B三点共线.课后练习:BC丄AB, AD // OC交O O于D点，求证：CD为O O的切线;(2)如图，以Rt A ABC的直角边AB为直径作O O,交斜边DE是O O的切线•(3)如图，以等腰厶ABC的一腰为直径作O O,交底边BC于D，交另一腰于F，若DE丄AC于E (或E 为CF中点)，求证：DE是O O的切线•A 仁/2•证明三(1)如图，AB是O O的直径,求证:DE,(4)如图，AB是O O的直径，AE平分/ BAF，交O O于点E,过点E作直线ED丄AF，交AF的延长线于点D，交AB的延长线于点C，求证：CD是O O的切线.知识点二：与圆有关的计算计算圆中的线段长或线段比，通常与勾股定理、垂径定理与三角形的全等、相似等知识的结合，形式复杂，无规律性。
分析时要重点注意观察已知线段间的关系，选择定理进行线段或者角度的转化。
特别是要借助圆的相关定理进行弧、弦、角之间的相互转化，找出所求线段与已知线段的关系，从而化未知为已知，解决问题。
其中重要而常见的数学思想方法有：(1)构造思想：如：①构建矩形转化线段；②构建"射影定理”基本图研究线段(已知任意两条线段可求其它所有线段长)；射影定理：所谓射影，就是正投影。
其中，从一点到一条直线所作垂线的垂足，叫做这点在这条直线上的正投影。
一条线段的两个端点在一条直线上的正投影之间的线段，叫做这条线段在这直线上的正投影。
由三角形相似的性质：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
2公式Rt△ ABC 中，/ BAC=90° ,AD 是斜边BC 上的高,则有射影定理如下：：(1)(AD) ;=BD DC,2 2 ⑵(AB) ;=BD BC ,⑶(AC) ;=CD BC。
等积式(4)ABXAC=BCXAD(可用面积来证明)AB 0 C③构造垂径定理模型：弦长一半、弦心距、半径；④构造勾股定理模型(已知线段长度) ；⑤构造三角函数(已知有角度的情况)；©找不到，找相似(2)方程思想：设出未知数表示关键线段，通过线段之间的关系，特别是发现其中的相等关系建立方程, 解决问题。
(3)建模思想：借助基本图形的结论发现问题中的线段关系，把问题分解为若干基本图形的问题，通过基本图形的解题模型快速发现图形中的基本结论，进而找出隐藏的线段之间的数量关系。
典型基本图型：图形1 :如图1：AB是O O的直径，点E、C是O O上的两点，基本结论有：(1) 在“ AC平分/ BAE ”；“ AD丄CD ”；“ DC是O O的切线”三个论断中，知二推一。
(2) 如图2、3, DE等于弓形BCE的高；DC=AE的弦心距OF (或弓形BCE的半弦EF)。
（3） 如图（4）:若CK 丄AB 于K ，则： 1 ① C K=CD ; BK=DE ; CK= BE=DC ; AE+AB= 2BK= 2AD; 2 ② "ADC s" ACB 二 AC 2=AD?AB （4） 在（1）中的条件①、②、③中任选两个条件，当 BG 丄CD 于E 时（如图5）,则： ① DE=GB :② DC=CG :③ AD+BG=AB ; 1 2 2 ④ AD?BG= DG 2 =DC 24GO 交AC 于点E ,基本结图形 2:如图：Rt "ABC 中，/ ACB=90°。
点 论有： AO 是AC 上一点， 以oc 为半径作oA“BD=BC ”。
四个论断中，知一推三。
(1) 在“ BO 平分/ CBA ” ; “ BO // DE ” ; “ AB 是O O 的切线”(2) ① G 是"BCD 的内心；② C G=GD ；③"BCO s" CDE 二 BO?DE=CO?CE= CE 2 ； 2(3) (4) 在图（1 ）中的线段 BC 、CE 、AE 、AD 中，知二求四。
AE 1如图（3）,若① BC=CE ，则：②——=—=tan / ADE :③ BC : AC : AB=3: 4: 5 ;（在①、②、③中 AD 2知一推二）④设 BE 、CD 交于点H 「则BH=2EH 图形3：如图：Rt " ABC 中，/ ABC=90°，以AB 为直径作O O 交AC 于D ,基本结论有: 如右图：(1) DE 切O O= E 是BC 的中点；(2)若 DE 切O O ,则：① DE=BE=CE ; ② D 、O 、B 、E 四点共圆=/ CED=2 / A ③ CD-CA=4BE 2, DE = CD = BC R BD BAC EB图形特殊化：在（1 ）的条件下 如图1 : DE // AB= " ABC 、" CDE 是等腰直角三角形； 如图2 :若DE 的延长线交AB 的延长线于点F ，若AB=BF ，则:图形4：如图，"ABC 中，AB=AC ，以AB 为直径作O O ,交BC 于点D ，交AC 于点F ,基本结论有：(1) DE 丄AC= DE 切O O ;(2) 在DE 丄AC 或DE 切O O 下，有：①"DFC 是等腰三角形;②EF=EC :③D 是BF 的中点。