9.1 辐射角系数
合集下载
传热学-第九章 辐射计算

X1, 2
1,2 1,2 A 1,2 B
X1, 2i
i 1
n
A1 Eb1 X 1,2 A1 Eb1 X 1,2 A A1 Eb1 X 1,2 B X 1,2 X 1,2 A X 1,2 B
再来看一下2 对 1 的能量守恒情况: 2 ,1 2 A ,1 2 B ,1
X 1,2 X 2,1
1 A1 1 A2
A1
A2
X d 1, d 2 dA1 X d 2, d 1dA2
A
A1 1
1
cos 1 cos 2 dA1dA2
A2
A1
1 A2
A2
A1
r cos 1 cos 2 dA1dA2
2
(9-4a)
A2
r
2
(9-4b)
的电流、电位差和电阻比拟热辐射中的热流、热势差与热
阻,用电路来比拟辐射热流的传递路径。但需要注意的是, 该方法也离不开角系数的计算,所以,必须满足漫灰面、 物性均匀以及投入辐射均匀的条件。
热势差与热阻
上节公式(9-12):
J Eb ( 1)q
1
改写为:
Eb J q 1
1, 2 A1 Eb1 X 1, 2 A2 Eb 2 X 2,1 A1 X 1, 2 ( Eb1 Eb 2 ) 的热辐射 到达表面 2的部分 的热辐射 到达表面 1的部分
图9-13 黑体系统的 辐射换热
表面1发出 表面 2发出
例题9-4 一直径d=0.75m的圆筒形埋地式加热炉采用电加热。 在操作过程中需要将炉子顶盖移去一段时间,设此时筒身温 度为 500K ,筒底为 650K 。环境温度为 300K 。试计算顶盖移 去期间单位时间内的热损失。设筒身及底面均可作为黑体。
传热学 第九章 辐射换热的计算

灰体——多次反射、吸收
9-2 两表面之间的辐射换热过程
1. 黑体表面之间的辐射换热
任意位置的两个黑体表面1、2,从表面1发出并直接投射
到表面2上的辐射能为
1 2 A1 X 1,2 E b1
从表面2发出并直接投射到表面1上的辐射能为
21 A2 X 2 ,1 E b 2
两个表面之间的直接辐射换热量为
X 1,2 X 2 ,1 1
A2 a
A1
9-1 角系数
4. 角系数的计算方法
(2) 代数法
由三个垂直于纸面方向无限长的非凹表面构成的封闭空腔,
三个表面的面积分别为A1、A2、A3 。
X i ,i 0
根据角系数的完整性
角系数的相对性
A1 X 1, 2 A1 X 1, 3 A1
A1 X 1,2 A2 X 2 ,1
Eb1 cos 1 cos 2 dA1dA2
1d 1
dd11
2
2 Lb1 dA1 cos
2
r
Eb1
dA2 cos 2
Lb1
d1
r2
9-1 角系数
2. 角系数的定义式
12
cos 1 cos 2
cos 1 cos 2
dA1dA2
E b1
dA1dA2 E b1
2
2
A1 A2
A1 A2
r
r
表面1对表面2的角系数为
X 1,2
12
A1 Eb1
1
A1
cos 1 cos 2
A1 A2 r 2 dA1dA2
1
A2
cos 1 cos 2
9-2 两表面之间的辐射换热过程
1. 黑体表面之间的辐射换热
任意位置的两个黑体表面1、2,从表面1发出并直接投射
到表面2上的辐射能为
1 2 A1 X 1,2 E b1
从表面2发出并直接投射到表面1上的辐射能为
21 A2 X 2 ,1 E b 2
两个表面之间的直接辐射换热量为
X 1,2 X 2 ,1 1
A2 a
A1
9-1 角系数
4. 角系数的计算方法
(2) 代数法
由三个垂直于纸面方向无限长的非凹表面构成的封闭空腔,
三个表面的面积分别为A1、A2、A3 。
X i ,i 0
根据角系数的完整性
角系数的相对性
A1 X 1, 2 A1 X 1, 3 A1
A1 X 1,2 A2 X 2 ,1
Eb1 cos 1 cos 2 dA1dA2
1d 1
dd11
2
2 Lb1 dA1 cos
2
r
Eb1
dA2 cos 2
Lb1
d1
r2
9-1 角系数
2. 角系数的定义式
12
cos 1 cos 2
cos 1 cos 2
dA1dA2
E b1
dA1dA2 E b1
2
2
A1 A2
A1 A2
r
r
表面1对表面2的角系数为
X 1,2
12
A1 Eb1
1
A1
cos 1 cos 2
A1 A2 r 2 dA1dA2
1
A2
cos 1 cos 2
辐射换热·角系数及计算举例
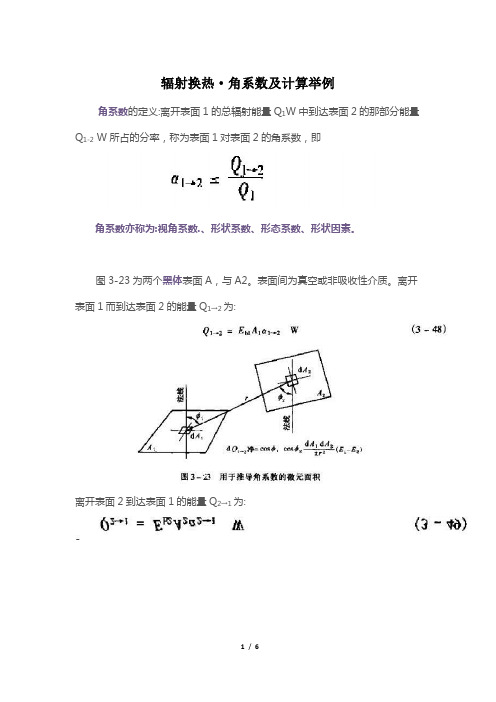
辐射换热·角系数及计算举例
角系数的定义:离开表面1的总辐射能量Q1W中到达表面2的那部分能量
Q1-2 W所占的分率,称为表面1对表面2的角系数,即
角系数亦称为:视角系数.、形状系数、形态系数、形状因素。
图3-23为两个黑体表面A,与A2。
表面间为真空或非吸收性介质。
离开表面1而到达表面2的能量Q1→2为:
离开表面2到达表面1的能量Q2→1为:
黑体表面能吸收全部的投射辐射,故两个表面的净换热量为:
对于黑体或灰体,属于扩散辐射,符合余弦定律,角系数纯粹是一项几何参数,仅取决于物体表面的形状及相对位置,而与各表面的温度,黑度无关。
这是因为当物体的温度、黑度改变时,其辐射能的绝对值虽然也发生变化,但这些能量在不同方向上分配的比例则是不变的,仍服从余弦定律。
因此当这两个表面的相对位置确定以后,从一个表面发出的能量到达另一表面的分率—角系数也就确定了。
在研究角系数时,为了方便起见,常用黑体表面间的换热作为对象。
角系数的推导。
图3-23为两个微元表面dA1和dA2之间的换热。
由于假定是扩散辐射(漫辐射),辐射强度在各个方向上是相同的,即Iφ不随φ而变,从而得知离开dA1的能量中投射到dA2的能量dQ2→1为:
例3一2
计算图3一盯中的面3对面4的角系数。
解:
由角系数的定义,可知。
辐射换热计算与规则

利用角系数的相对性、完整性及可加性,通过求解代数方程 而获得角系数的方法称为代数分析法。 (1)三个非凹表面组成的封闭系统
图8-5 三个非凹表面组成的封闭系统
辐射换热的计算和规则
由角系数完整性
X1,2 X1,3 1 X2,1 X2,3 1 X3,1 X3,2 1
A1
A2
由角系数相对性
A3
A1X1,2 A2X2,1
辐射换热的计算和规则
辐射换热的计算和规则
9.1 辐射换热的角系数
两个表面之间的辐射换热量与两个表面之间的相对位置 有很大关系
表面相对位置的影响
❖a图中两表面无限接近,相互间的换热量最大;
❖b图中两表面位于同一平面上,相互间的辐射换热量为零。 由图可以看出,两个表面间的相对位置不同时,一个表面
发出而落到另一个表面上的辐射能的百分数随之而异,从
两微元表面角系数的相对性表达式:
d A 1X d A 1 ,d A 2 d A 2X d A 2 ,d A 1
辐射换热的计算和规则
两个有限大小表面之间角系数的相对性
1 , 2 A 1 E b 1 X 1 ,2 A 2 E b 2 X 2 ,1
当 T1 时T2,净辐射换热量为零,即
Eb1 Eb2
则有限大小表面间角系数的相对性的表达式:
2表 面 A1的 断 面 长 度
两个非凹表面及假想面组
成的封闭系统
上述方法又被称为交叉线法。
注意:这里所谓的交叉线和不交叉线都是指虚拟 面断面的线,或者说是辅助线。
辐射换热的计算和规则
【例】求下列图形中的角系数
解: A1X1, 2A2X2, 1
X 1 ,2
X1,2
A2 A1
X 2,1
图8-5 三个非凹表面组成的封闭系统
辐射换热的计算和规则
由角系数完整性
X1,2 X1,3 1 X2,1 X2,3 1 X3,1 X3,2 1
A1
A2
由角系数相对性
A3
A1X1,2 A2X2,1
辐射换热的计算和规则
辐射换热的计算和规则
9.1 辐射换热的角系数
两个表面之间的辐射换热量与两个表面之间的相对位置 有很大关系
表面相对位置的影响
❖a图中两表面无限接近,相互间的换热量最大;
❖b图中两表面位于同一平面上,相互间的辐射换热量为零。 由图可以看出,两个表面间的相对位置不同时,一个表面
发出而落到另一个表面上的辐射能的百分数随之而异,从
两微元表面角系数的相对性表达式:
d A 1X d A 1 ,d A 2 d A 2X d A 2 ,d A 1
辐射换热的计算和规则
两个有限大小表面之间角系数的相对性
1 , 2 A 1 E b 1 X 1 ,2 A 2 E b 2 X 2 ,1
当 T1 时T2,净辐射换热量为零,即
Eb1 Eb2
则有限大小表面间角系数的相对性的表达式:
2表 面 A1的 断 面 长 度
两个非凹表面及假想面组
成的封闭系统
上述方法又被称为交叉线法。
注意:这里所谓的交叉线和不交叉线都是指虚拟 面断面的线,或者说是辅助线。
辐射换热的计算和规则
【例】求下列图形中的角系数
解: A1X1, 2A2X2, 1
X 1 ,2
X1,2
A2 A1
X 2,1
第九章 辐射传热的计算

Shanghai Jiao Tong University
(2)角系数的完整性
对于有n个表面组成的封闭系统, 据能量守恒
X1,1 X1, 2 X1,3 X1, n X1,i 1
i 1 n
( 3 )角系数的可加性
A1Eb1 X1,2A A1Eb1 X1,2B A 1 Eb1 X1,2
SJTU-OYH
Shanghai Jiao Tong University
Shanghai Jiao Tong University
据角系数相对性
X 3,1 A1 X1,3 A3
A3 X3,1 = A1 X1,3,故
(0.8cm)2 0.6 0.685 7 (r1 r2 ) L (0.8 0.6)cm 0.4cm
SJTU-OYH
9.2 组成封闭空间的两灰体之间的辐射换热计算
Shanghai Jiao Tong University
假设: ( 1)进行辐射换热的物体表面之间是不参与辐射的介质即透 明体或真空;
(2)每个表面都是漫灰体或黑体表面; (3)每个表面的温度、辐射特性及投入辐射分布均匀。
一、净热量法。 1. 黑体表面
SJTU-OYH
Shanghai Jiao Tong University
( 2 )三个非凹表面构成的封闭空腔
根据角系数的相对性和完整性
A1 X1,2 A1 X1,3 A1
A2 X 2,1 A2 X 2,3 A2
A3 X 3,1 A3 X 3,2 A3
A1 X1,2 A2 X 2,1 A1 X1,3 A3 X 3,1 A2 X 2,3 A3 X 3,2
SJTU-OYH
辐射换热的计算

若表面1为凹表面, X1,1 0
角系数的完整性
3、角系数的可加性
从表面1上发出而落到表面2上的总能量,等于落到表面2上 各部分的辐射能之和,于是有
A 1 E b 1 X 1 ,2 A 1 E b 1 X 1 ,2 a A 1 E b 1 X 1 ,2 b
X1,2X1,2aX1,2b
如把表面2进一步分成若干小块,则有
AX AX (1 2 ) (1 2 ) ( ,3 4 )(3 4 )( 3 4 ) ,(1 2 )
A X AX (1 2) (1 2),3 3 3 ,(1 2) A X AX 2 2 ,(3 4 ) (3 4 ) (3 4 ),2
A2X2,3A3X3,2
注:利用这样的分析方法,扩大线图的使用,可以得出很多几何结构简单的角系数
图8-5 三个非凹表面组成的封闭系统
由角系数完整性
X1,2 X1,3 1 X2,1 X2,3 1 X3,1 X3,2 1
由角系数相对性
A1X1,2 A2X2,1 A1X1,3 A3X3,1 A2X2,3 A3X3,2
A1
A2
A3
三表面封闭空间 角系数的确定
上述方程解得: X 1,2
A1 A2 2A1
A3
X 1,3
A1 A3 2A3
A2
X 2,3
A2 A3 2A2
A1
由于垂直纸面方向的长度相同,则有:
X 1,2
l1 l2 2 l1
l3
X 1,3
l1 l3 2 l1
l2
X
2 ,3
l2
l3 l1 2 l2
(2)任意两个非凹表面间的角系数 如图所示表面和假定在垂直于纸面的方向上表面的长度 是无限延伸的,只有封闭系统才能应用角系数的完整性, 为此作辅助线ac和bd,与ab、cd一起构成封闭腔。
角系数的完整性
3、角系数的可加性
从表面1上发出而落到表面2上的总能量,等于落到表面2上 各部分的辐射能之和,于是有
A 1 E b 1 X 1 ,2 A 1 E b 1 X 1 ,2 a A 1 E b 1 X 1 ,2 b
X1,2X1,2aX1,2b
如把表面2进一步分成若干小块,则有
AX AX (1 2 ) (1 2 ) ( ,3 4 )(3 4 )( 3 4 ) ,(1 2 )
A X AX (1 2) (1 2),3 3 3 ,(1 2) A X AX 2 2 ,(3 4 ) (3 4 ) (3 4 ),2
A2X2,3A3X3,2
注:利用这样的分析方法,扩大线图的使用,可以得出很多几何结构简单的角系数
图8-5 三个非凹表面组成的封闭系统
由角系数完整性
X1,2 X1,3 1 X2,1 X2,3 1 X3,1 X3,2 1
由角系数相对性
A1X1,2 A2X2,1 A1X1,3 A3X3,1 A2X2,3 A3X3,2
A1
A2
A3
三表面封闭空间 角系数的确定
上述方程解得: X 1,2
A1 A2 2A1
A3
X 1,3
A1 A3 2A3
A2
X 2,3
A2 A3 2A2
A1
由于垂直纸面方向的长度相同,则有:
X 1,2
l1 l2 2 l1
l3
X 1,3
l1 l3 2 l1
l2
X
2 ,3
l2
l3 l1 2 l2
(2)任意两个非凹表面间的角系数 如图所示表面和假定在垂直于纸面的方向上表面的长度 是无限延伸的,只有封闭系统才能应用角系数的完整性, 为此作辅助线ac和bd,与ab、cd一起构成封闭腔。
辐射传热的计算

X ab ,cd
(bc ad ) (ac bd ) 2ab
我们可以归纳出如下的一般关系:
ห้องสมุดไป่ตู้
X 1, 2
交叉线之和 不交叉线之和 2 表面A1的断面长度
图6 两个表面间的角系数
对于在一个方向上长度无限延伸的多个 表面组成的系统,该式为任意两个表面 之间的角系数的计算式,因此该方法又 称为交叉线法。
1. 二灰表面间的辐射换热
R1
1 1 A1 1
Rk
1 A1 X 1, 2
R2
1, 2
Eb1 Eb 2 1 1 1 1 2 A11 A1 X 1, 2 A2 2
2. 三灰表面间的辐射换热
应用电学中的基尔霍夫定律, 可列出节点的热流方程:
J1 :
Eb1 J1 J 2 J1 J 3 J1 0 1 1 1 1 1 A1 A1 X 1, 2 A1 X 1,3
i 1
此式表达的关系称为角系数的完整性。
图3 角系数的完整性
3. 角系数的可加性: 考虑如图4所示表面1对表面2的角系数。由于从表面1上发出而落到表 面2上的总能量,等于落到表面2上各部分的辐射能之和,于是有:
A1Eb1 X1, 2 A1Eb1 X1,2a A1Eb1 X1, 2b
故有 X1,2 X1,2a X1,2b 由于从表面2发出落到表面1上的总 辐射能,等于从表面2的各个组成部 分发出而落到表面1上的辐射能之和。 于是有:
9-1 辐射传热的角系数
一、定义
1.两个假定:1)所研究的表面是漫射的;2)在所研究表面的不同地点上 向外发射的辐射热流密度时均匀的。 * 两个表面之间的辐射换热量与两个表面之间的相对位置有很大关系.图 1示出了两个等温表面间的两种极端布置情况:图a中两表间无限接近, 相互间的换热量最大;图b中两表面位于同一表面上,相互间的辐射换 热量为零。由图可以看出,两个表面间的相对位置不同时,一个表面发 出而落到另一个表面上的 辐射能的百分数随之而异,从而 影响到换热量。 2.定义:我们把表面1发出的辐射能 中落到表面2上的百分数 称为表面1对表面2的角系数, 记为 X1, 2。同理也可以定义表面2 对表面l的角系数。 图1 表面相对位置的影响
传热学-学习课件-9-1 辐射传热的角系数

A1 A2
由角系数相对性
A1 X 1,2 A2 X 2,1 A1 X 1,3 A3 X 3,1 A2 X 2,3 A3 X 3,2
A3
三表面封闭空间 角系数的确定
传热学 Heat Transfer
上述方程解得: X1,2
A1
A2 2 A1
A3
X 1,3
A1
A3 2A3
传热学 Heat Transfer
从表面2上发出而落到表面1上的辐射能,等于从 表面2的各部分发出而落到表面1上的辐射能之和,于 是有
A 2 E b 2 X 2 ,1 A 2 a E b 2 X 2 a ,1 A 2 b E b 2 X 2 b ,1
A2 X 2,1 A2a X 2a,1 A2b X 2b,1
X 2,1
X 2a,1
A2a A2
X 2b,1
A2b A2
角系数的上述特性可以用来求解许多情况下 两表面间的角系数值。
传热学 Heat Transfer
9.1.3 角系数的计算方法
求解角系数的方法
直接积分法 代数分析法
传热学 Heat Transfer
1、直接积分法
• 按角系数的基本定义通过求解多重积分而获得角 系数的方法
2、代数分析法
利用角系数的相对性、完整性及可加性,通过求解代数方 程而获得角系数的方法称为代数分析法。 (1)三个非凹表面组成的封闭系统
图9-10 三个非凹表面组成的封闭系统
传热学 Heat Transfer
由角系数完整性
X1,2 X1,3 1 X 2,1 X 2,3 1 X 3,1 X 3,2 1
传热学 Heat Transfer
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
代入角系数的定义式
1
X i, j Ai
Aj
Ai
cos i cos j r2
dAi
dA j
1
X j,i A j
Ai
Aj
cos i cos j r2
dA j
dAi
• 角系数完全是一个几何量(有条件!)
• 角系数概念的前提条件:漫灰表面,或 者黑体;表面温度均匀,有效辐射均匀: 令 K1, 2=A1 X1, 2,由互换性, K1, 2= A2 X2, 1
K1,2 K1,2a K1,2b K 2,1 K 2a,1 K 2b,1
第九章 9.1节(12)
8
9.1.3 角系数的计算方法
(1)直接积分法 (2)数值计算方法 (3)图线方法 (4)代数方法 (5)几何投影方法(单位球法)
3
代入立体角的定义和 J 与 L 之间的关系式
d i j
Ji
cos i cos j r2
dAi dA j
离开有限表面Ai的辐射中到达Aj的部分
i j J i
Aj
Ai
cos i cos j r2
dAi
dA j
注意:这个写法本身已经附加了一项条件, 即 Ji 在 Ai上必须是常量。
第九章 9.1节(12)
5
• 微元面之间及微元对有限面的角系数是 定值,而有限面之间的角系数具有平均 的含义
1
X i j Ai Ai X di j dAi
X di j
di j
JidAi
cosi cos j
Aj
r2
dAj
第九章 9.1节(12)
6
9.1.2 角系数的基本性质
1. 互换性(相对性)
2. 完整性
Ai X i, j A j X j,i
第九章 9.1节(12)
9
第九章 9.1节(12)
10
三个无限长非凹表面构成的 封闭系统:
X 1,2 X 1,3 1, X 2,1 X 2,3 1, X 3,1 X 3,2 1,
A1 X 1,2 A2 X 2,1 A2 X 2,3 A3 X 3,2 A3 X 3,1 A1 X 1,3
X 1,2
A1
A2 A3 2 A1
第九章 9.1节(12)
11
上述结论可以延 伸到两个无限 长的非凹表面 之间的角系数 计算:
(bc ad) (ac bd)
X ab,cd
2ab
第九章 9.1节(12)
下一节
12
N
X i, j X i,1 X i,2 X i,i X i,N 1
j 1
• 包括假想面在内的空腔是封闭的
• Xi,I 表示离开表面i的有效辐射当中落到自 身上的能量份额
第九章 9.1节(12)
7
3. 分解性 X1,2 = X1,2a + X1,2b
X2,1 ?= X2a,1 + X2b,1
X i, j i j / ( Ai J i )
• 离开表面i 的所有辐射即有效辐射 • 到达或拦截均不能理解为被表面 j 吸收 • 表面j 可以是虚拟的假想面
第九章 9.1节(12)
2
离开微元面dAi的辐射中到达dAj的部分
d i j Li,er cos i dAi d ji
第九章 9.1节(12)
第 9 章 辐射换热计算
• 研究:处于真空状态,或者被不参与辐射 热交换的介质隔开的诸表面之间辐射换热 问题的计算方法
• 针对黑表面或者漫灰表面
• “封闭腔”条件
• 核心:角系数概念、辐射换热的网络方法
第九章 9.1节(12)
1
9.1 辐射角系数
9.1.1 角系数的定义 角系数 Xi, j :离开表面i的所有辐射中到达表面j, 或者说被表面j 拦截的百分数。
