初中数学—全等三角形解题方法、思路及技巧汇总
做全等三角形做题5技巧

做全等三角形做题5技巧《全等三角形做题的五大技巧,盘它就对啦!》嘿,各位小伙伴们!今天咱就来唠唠全等三角形做题的那五大技巧,这可是我在题海里摸爬滚打出来的经验之谈呀!第一个技巧,那就是瞪大眼睛找全等条件。
咱可别像没头苍蝇似的乱撞,得学会从题目里扒拉那些隐藏的全等线索。
边边角角都别放过,有时候一个小角度或者一条小线段就是全等的关键钥匙呢!就像侦探找线索一样,把那些能让三角形“重合”的证据都给揪出来。
然后吧,就是巧妙利用已知条件。
嘿呀,题目给的肯定有它的道理啊!别把那些已知条件当摆设,得让它们发挥出大作用。
比如说给了你一组对应边相等,那咱就得赶紧顺着这条线索去挖掘其他相等的东西,让全等triangle 慢慢浮出水面。
接着呢,要学会“乾坤大挪移”。
啥意思呢?就是把一个三角形移到另一个三角形旁边,好好观察它们到底哪里长得一样。
这招特别好使,有时候眼睛一花没看出来,这么一挪,嘿,全等就显而易见啦!还有啊,画图辅助那可太重要啦!别偷懒,动手画画,那感觉就像给全等三角形盖房子,一笔一划把它们的轮廓给勾勒出来。
画着画着,你就会发现那些隐藏的关系一下子就跳出来了。
最后一个技巧,就是保持耐心别烦躁。
全等三角形的题目有时候可真能绕晕你,但咱可不能趴下啊!要像小强一样顽强,一点点去分析,一点点去突破。
着急上火可没用,得冷静沉稳,仔细琢磨。
总之呢,做全等三角形题目就像是一场冒险,这五大技巧就是你的秘密武器。
拿着它们勇敢地去闯荡题目的世界吧!别害怕犯错,错了咱就改,改了继续冲!相信大家掌握了这些技巧,再遇到全等三角形题目就能轻松应对啦!加油吧,小伙伴们,让我们在全等的世界里畅游无阻!。
初中数学全等三角形解题思路

全等三角形解题思路全等是几何学中重要的概念之一,表示两个图形在形状和大小上完全相等。
在初中数学中,学习解决全等三角形的问题是非常重要的,下面将介绍解决全等三角形问题的一般思路。
1. 学习全等三角形的基本条件在解决全等三角形的问题之前,我们首先需要了解全等三角形的基本条件,即六ASA条件:•两角对应相等(Angle-Angle-Angle):如果两个三角形的三个内角相对应相等,那么这两个三角形全等。
•两边夹角和其对应边相等(Angle-Side-Angle):如果两个三角形的一对夹角和其对应的边相等,那么这两个三角形全等。
•两边对应相等(Side-Angle-Side):如果两个三角形的两边和夹角对应相等,那么这两个三角形全等。
熟练掌握这些基本条件是解决全等三角形问题的前提。
2. 观察图形特征,找出已知条件在解决全等三角形问题时,首先要仔细观察图形,找出已知条件。
通常,已知条件可以包括已知的边长、角度、直角等。
例如,题目可能给出两个三角形,已知它们的某个角相等、两个边长相等等。
我们需要将这些已知条件一一列出,以备后用。
3. 利用全等三角形的基本条件解题根据已知条件和全等三角形的基本条件,选择合适的方法进行推理和演算。
下面以几个常见的情况为例进行解析。
3.1 两角对应相等(Angle-Angle-Angle)已知两个三角形的三个内角相对应相等,我们可以得出这两个三角形全等。
例如,已知两个三角形的两个角相等(∠A = ∠A’,∠B = ∠B’),则可得出这两个三角形全等。
3.2 两边夹角和其对应边相等(Angle-Side-Angle)已知两个三角形的一对夹角和其对应的边相等,我们可以得出这两个三角形全等。
例如,已知两个三角形的一个夹角及其对边相等(∠A = ∠A’,AB = A’B’),则可得出这两个三角形全等。
3.3 两边对应相等(Side-Angle-Side)已知两个三角形的两边和夹角对应相等,我们可以得出这两个三角形全等。
全等三角形题型归纳经典完整
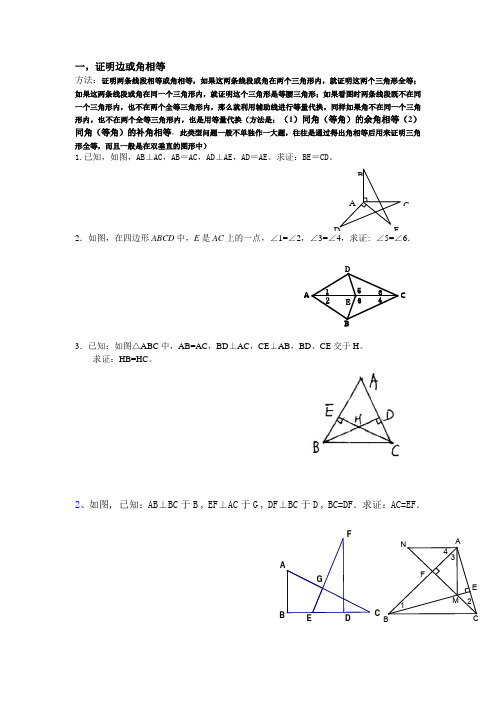
一,证明边或角相等方法:证明两条线段相等或角相等,如果这两条线段或角在两个三角形内,就证明这两个三角形全等;如果这两条线段或角在同一个三角形内,就证明这个三角形是等腰三角形;如果看图时两条线段既不在同一个三角形内,也不在两个全等三角形内,那么就利用辅助线进行等量代换,同样如果角不在同一个三角形内,也不在两个全等三角形内,也是用等量代换(方法是:(1)同角(等角)的余角相等(2)同角(等角)的补角相等,此类型问题一般不单独作一大题,往往是通过得出角相等后用来证明三角形全等,而且一般是在双垂直的图形中)1.已知,如图,AB ⊥AC ,AB =AC ,AD ⊥AE ,AD =AE 。
求证:BE =CD 。
2.如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6.3.已知:如图△ABC 中,AB=AC ,BD ⊥AC ,CE ⊥AB ,BD 、CE 交于H 。
求证:HB=HC 。
2、如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF .求证:AC=EF .A ED C B654321E DCBAFGE D CBAFMNE 1234EDC BA 二.证明线段和差问题 (形如:AB+BC=CD,AB=AD - CD)证明两条线段和等于另一条线段,常常使用截长补短法。
①截长法即为在这三条最长的线段截取一段使它等于较短线段中的一条,然后证明剩下的一段等于另一条较短的线段。
②补短法即为在较短的一条线段上延长一段,使它们等于最长的线段,然后证明延长的这一线段等于另一条较短的线段。
证明两条线段差等于另一条线段,只需把差化成和来解决即可。
1.如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .2、如图,已知:△ABC 中,∠BAC =90, AB =AC ,AE 是过A 一直线,且点B 、C 在AE 的异侧,BD ⊥AE 于D ,CE ⊥AE 于E . 求证:BD =DE +CE ;3、如图,AB ∥CD ,DE 平分∠ADC ,AE 平分∠BAD ,求证:AB=AD - CDP E D CB A三.证明线段的2倍或21关系 ( AB CE =2, MN BN =12) 1. 利用含30 角的直角三角形的性质证明例1. 已知,如图1,∆ABC 是等边三角形,在AC 、BC 上分别取点D 、E ,且AD =CE ,连结AE 、BD 交于点N ,过B 作BM AE ⊥,垂足为M ,求证:MN BN =12(提示:先证∠=BNE 60)2. 利用等线段代换(充分利用中点)例1.如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .3.转化为线段和问题,利用截长补短法例5. 已知:如图5,四边形ABCD 中,∠=D 90,对角线AC 平分∠BAD ,AC BC =,FE DCB A求证:AD AB12四.证明二倍角关系利用三角形外角和定理和等量代换如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠BD C BA。
12.1 全等三角形 解题技巧

12.1全等三角形技巧1全等三角形的性质运用1.利用全等三角形的性质求角度如图,△ABC≌△DEF,若AB=DE,∠B=50°,∠C=70°,∠E=50°,求∠D的度数.解析:由三角形的内角和定理易知∠A的度数,∠D与∠A是对应角.解:∵∠A+∠B+∠C=180°,∠B=50°,∠C=70°,∴∠A=180°-∠B-∠C=180°-50°-70°=60°.∵△ABC≌△DEF,∴∠D=∠A=60°.2.利用全等三角形的性质求线段如图已知CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,AB=10,AD=4,求线段CE的长.解析:由△ABE≌△ACD可求出AB,AD的对应边分别为AC,AE,然后由CE=AC-AE的关系求出CE.解:∵△ABE≌△ACD,AB=10,AD=4,∴AC=AB=10,AE=AD=4.∴CE=AC-AE=6.3.利用全等三角形的性质判断两线位置关系如图所示,△ADF≌CBE,且点E,B,D,F在同一条直线上.判断AD与BC的位置关系,并加以说明.解析:本题主要考查全等三角形的性质与平行线的综合应用.判断AD与BC的位置关系,可以初步判别AD和BC的位置关系是平行,欲说明AD//BC,需说明∠3=∠4,要说明∠3=∠4,可以利用三角形外角性质证明.解:AD与BC的位置关系是AD//BC.理由如下:∵△ADF≌△CBE,∴∠1=∠2,∠F=∠E.又∵点E,B,D,F在同一条直线上,∴∠3=∠1+∠F,∠4=∠2+∠E(三角形的外角的性质).∴∠3=∠4(等量代换).∴AD//BC(内错角相等,两直线平行).技巧2利用全等的基本图形解决几何问题1.利用基本图形求角度如图,△ABE和△ADC分别是△ABC沿着AB,AC边翻折形成的,若∠1:∠2:∠3=28:5:3,则∠α=.解析:翻折后,△ABE≌△ABC≌△ADC,由全等三角形的性质易得∠ABE=∠2,∠DCA=∠3.因为∠1:∠2:∠3=28:5:3,设∠1=28x,∠2=5x,∠3=3x,由三角形的内角和定理知:∠1+∠2+∠3=28x+5x+3x=36x=180°,解得x=5°,所以∠2=25°,∠3=15°,所以外角∠α=∠EBC+∠DCB=2(∠2+∠3)=80°.答案:80°.2.利用基本图形求面积如图所示,在Rt△ABC中,∠ACB=90°,且AC=BC=4 cm,已知△BCD≌△ACE,求四边形AECD的面积.解析:由于线段AC把四边形AECD分成两部分,通过观察我们可以把△ACE旋转到△BCD的位置,使之与△ACD恰好构成△ABC,从而可求面积.解:∵△BCD≌△ACE,∴S△BCD=S△ACE.又∵S四边形AECD=S△ACE+S△ACD,∴S四边形AECD=S△BCD+S△ACD=S△ABC=12×4×4=8(cm2).3.利用基本图形解决折叠问题如图所示,长方形ABCD沿AE折叠,使点D落在BC边上的点F处,若BC=8 cm,∠1=40°,求∠2的度数与AF的长度.解析:因为折叠后△AFE与△ADE完全重合,所以△AFE≌△ADE,可以得到AF=AD,∠F AE=∠DAE,又因为长方形的对边相等,每个角都是直角,所以可求出角度与线段长度.解:由题意可知:△AFE≌△ADE.∴AF=AD,∠3=∠2.在长方形ABCD中,AD=BC=8 cm,∠1+∠2+∠3=90°.∴AF=8 cm,∠2=12(90°-∠1)=25°.。
三角形全等解题方法及技巧

三角形全等的解题方法及技巧如下:1. 掌握全等三角形的判定条件:全等三角形的判定条件是全等三角形的基础知识,必须熟练掌握。
2. 学会利用已知条件寻找全等三角形:根据已知条件,通过构造或变换,使两个三角形满足全等条件,从而解决问题。
3. 掌握辅助线的构造方法:在解题过程中,有时需要添加辅助线来帮助解决问题。
常见的辅助线包括中线、高线、角平分线等。
4. 学会利用全等三角形的性质:全等三角形的性质是解题的重要依据,如对应边相等、对应角相等、对应高相等、对应中线相等等。
5. 掌握一些常见的解题技巧:如利用角平分线的性质、利用高线的性质、利用中线的性质等。
6. 理解并掌握全等三角形的不同类型:全等三角形有多种类型,如SSS、SAS、ASA、AAS等。
每种类型都有其特定的判定条件,理解并掌握这些类型有助于更灵活地解决全等三角形问题。
7. 注重解题步骤和思路:在解决全等三角形问题时,要注意解题步骤和思路的清晰。
要明确问题的需求,确定所使用的判定条件和辅助线,然后逐步推导并证明。
8. 练习大量的题目:通过大量的练习,可以加深对全等三角形判定条件和性质的理解,提高解题的速度和准确性。
同时,也可以掌握一些常见的解题技巧和方法。
9. 善于总结和归纳:在解决全等三角形问题时,要及时总结和归纳所使用的判定条件、辅助线、性质和技巧。
这样可以加深对全等三角形知识的理解和记忆,并为以后解决类似问题提供帮助。
10. 保持耐心和细心:全等三角形问题有时可能会比较复杂和繁琐,需要耐心和细心地推导和证明。
在解题过程中,要注意细节,避免因为粗心大意而犯错。
总之,三角形全等的解题方法及技巧需要多练习、多总结,通过不断的实践来提高自己的解题能力。
三角形全等证明的解题思路

三角形全等证明的解题思路关键信息项1、三角形全等的定义及性质定义:能够完全重合的两个三角形叫做全等三角形。
性质:全等三角形的对应边相等、对应角相等。
2、三角形全等的判定方法SSS(边边边):三边对应相等的两个三角形全等。
SAS(边角边):两边和它们的夹角对应相等的两个三角形全等。
ASA(角边角):两角和它们的夹边对应相等的两个三角形全等。
AAS(角角边):两角和其中一角的对边对应相等的两个三角形全等。
RHS(直角、斜边、边):在一对直角三角形中,斜边及另一条直角边相等的两个三角形全等。
3、常见的辅助线添加方法连接两点构造全等三角形。
作平行线构造全等三角形。
延长某边构造全等三角形。
作垂线构造全等三角形。
11 三角形全等的定义和性质的深入理解三角形全等是指两个三角形的形状和大小完全相同,这意味着它们的所有对应边长度相等,所有对应角的度数相等。
这是判断两个三角形是否全等的根本依据,也是在证明过程中需要最终证明的结论。
111 对应边和对应角的准确识别在给定的两个三角形中,正确找出对应边和对应角是至关重要的。
通常可以通过图形的位置关系、已知条件中的描述或者通过已经证明的相等关系来确定。
112 性质在解题中的应用一旦证明了两个三角形全等,就可以利用其对应边相等和对应角相等的性质来解决相关的问题,如求边长、角度大小、证明线段或角的相等关系等。
12 三角形全等的判定方法详解121 SSS(边边边)判定法当两个三角形的三条边分别对应相等时,可以判定这两个三角形全等。
在实际解题中,需要准确测量或通过已知条件推导出三边的长度,并进行比较。
122 SAS(边角边)判定法如果两个三角形的两条边及其夹角分别相等,那么这两个三角形全等。
这里的夹角必须是两条已知相等边的夹角。
123 ASA(角边角)判定法两角及其夹边分别相等的两个三角形全等。
需要注意的是,这里的夹边是两角之间的边。
124 AAS(角角边)判定法两角和其中一角的对边分别相等的两个三角形全等。
初中数学—全等三角形解题方法、思路及技巧汇总

初中数学—全等三角形解题方法、思路及技巧汇总全等三角形是初中数学中非常重要的内容,今天我们就把初二数学中,与全等三角形相关的方法、思路及技巧都来整理一下。
一、全等三角形的性质与判定。
五种判定方法:SSS,SAS,AAS,ASA,HL,其中HL是边边角(SSA的特例)。
全等三角形的对应边相等,对应角相等,一句话,凡是对应的,都相等。
二、寻找全等三角形常用方法1、直接从结论入手一般会有以下几种要求证的方向:•线段相等•角相等•度数•线段或者线段的和、差、倍、分关系然后根据题目要求证的方向,找到要证明的相关量分别在哪两个三角形中,再围绕这两个三角形进行研究。
2、从已知条件入手把所有能标注在图上的已经条件标注出来,注意用不同的标示进行区分,比如第一组相等的线段用一条短竖,第二组相等的线段用两条短竖,再比如第一组相等的角用一个小圆弧,第二组相等的角就用两个小圆弧等。
然后通过已知条件找到相关的两个三角形,再进行分析。
记住一句话:“充分利用已知条件”。
3、把已经条件和结论综合起来考虑找到所有的已知条件和隐藏条件,结合结论,找出可能全等的两个三角形,再进行分析。
4、如果上述方法都确定行不通,就考虑添加辅助线来构造全等三角形。
三、构造全等三角形的一般方法1、题目中出现角平分线(1)通过角平分线上的某个已知点,向两边作垂线,这是利用角平分线的性质定理或者逆定理来构造的全等三角形(2)在角平分线的某个已知点,作角平分线的垂线和两边相交,构造全等三角形。
(3)在该角的两边,距离角的顶点相等长度的位置上截取两点,分别连接这两点与角平分线上的某已知点,构造全等三角形2、题目中出现中点或者中线(中位线)(1)倍长中线法,把中线延长至二倍位置(2)过中点作某一条边的平行线3、题目中出现等腰或者等边三角形(1)找中点,倍长中线(2)过顶点作底边的垂线(3)过某已知点作一条边的平行线(4)三线合一4、题目中出现三条线段之间的关系通常用截长补短法,在某条线段上截取一段线段,使之与特定的线段相等,或者将某条线段延长,使之与特定线段相等。
全等三角形的解题思路

全等三角形是数学中的一个重要概念,它指的是两个三角形,形状相同,大小相等。
在解题过程中,我们可以利用全等三角形的性质来解决一些问题。
以下是一些关于全等三角形的解题思路:
1.寻找全等三角形:在题目中,如果有两个三角形,形状相同,大小相等,那么这两个三角形就是全等三角形。
我们需要找出这些全等三角形。
2.利用全等三角形的性质:全等三角形的性质包括:对应边相等,对应角相等。
我们可以利用这些性质来解决问题。
3.寻找证明全等三角形的方法:要证明两个三角形全等,我们需要找到一些方法。
其中,最常用的方法包括:SSS(边边边)、SAS(边角边)、ASA(角边角)、AAS(角角边)和HL(直角三角形中斜边和一条直角边分别相等的两个直角三角形全等)。
4.选择合适的方法证明:根据题目的条件和要求,选择合适的方法来证明全等三角形。
例如,在证明两个三角形全等时,我们可以按照以下步骤进行:
确定已知条件和要求;
根据已知条件画出图形;
根据全等三角形的性质,寻找可以应用的条件;
选择合适的方法进行证明;
得出结论。
总之,在解决与全等三角形相关的问题时,我们需要熟练掌握全等三角形的性质和证明方法,并能够灵活运用这些知识来解决问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学—全等三角形解题方法、思路及技巧汇总
全等三角形是初中数学中非常重要的内容,今天我们就把初二数学中,与全等三角形相关的方法、思路及技巧都来整理一下。
一、全等三角形的性质与判定。
五种判定方法:SSS,SAS,AAS,ASA,HL,其中HL是边边角(SSA的特例)。
全等三角形的对应边相等,对应角相等,一句话,凡是对应的,都相等。
二、寻找全等三角形常用方法
1、直接从结论入手
一般会有以下几种要求证的方向:
∙线段相等
∙角相等
∙度数
∙线段或者线段的和、差、倍、分关系
然后根据题目要求证的方向,找到要证明的相关量分别在哪两个三角形中,再围绕这两个三角形进行研究。
2、从已知条件入手
把所有能标注在图上的已经条件标注出来,注意用不同的标示进行区分,比如第一组相等的线段用一条短竖,第二组相等的线段用两条短竖,再比如第一组相等的角用一个小圆弧,第二组相等的角就用两个小圆弧等。
然后通过已知条件找到相关的两个三角形,再进行分析。
记住一句话:“充分利用已知条件”。
3、把已经条件和结论综合起来考虑
找到所有的已知条件和隐藏条件,结合结论,找出可能全等的两个三角形,再进行分析。
4、如果上述方法都确定行不通,就考虑添加辅助线来构造全等三角形。
三、构造全等三角形的一般方法
1、题目中出现角平分线
(1)通过角平分线上的某个已知点,向两边作垂线,这是利用角平分线的性质定理或者逆定理来构造的全等三角形
(2)在角平分线的某个已知点,作角平分线的垂线和两边相交,构造全等三角形。
(3)在该角的两边,距离角的顶点相等长度的位置上截取两点,分别连接这两点与角平分线上的某已知点,构造全等三角形
2、题目中出现中点或者中线(中位线)
(1)倍长中线法,把中线延长至二倍位置
(2)过中点作某一条边的平行线
3、题目中出现等腰或者等边三角形
(1)找中点,倍长中线
(2)过顶点作底边的垂线
(3)过某已知点作一条边的平行线
(4)三线合一
4、题目中出现三条线段之间的关系
通常用截长补短法,在某条线段上截取一段线段,使之与特定的线段相等,或者将某条线段延长,使之与特定线段相等。
这种方法,在证明多条线段的和、差、倍、分关系时,效果非常好。
5、题目中出现垂直平分线
把线段两端点与垂直平分线上的某点连接
6、某些特定题目中还可以使用旋转法、翻折法等。
四、补充一些常见的隐藏条件
1、等腰直角三角形,除了两腰相等、两底角相等外,很多同学都会忽略掉三个度数:45,45,90
2、等边三角形,同样除了三条边相等,三个角相等外,还要注意60度,通过三线合一,还能得到30度角
3、平角180度,这是最容易忽略的
4、外角,外角和,内角和
5、三角形的五心:重心(中线交点)、外心(中垂线交点)、内心(角平分线交点)、垂心(高线交点),旁心(旁切圆的圆心)
其实,成绩的好坏取决于每个人的学习能力,对于很多初中生而言,都缺乏一个良好的学习习惯,没有一个健全完整的的学习体系,所以,无论是贪玩的学生,还是苦学的学生,想要提高成绩,就要找出学习上的漏洞,精准突破,才能精准提分!。
