Fluent湍流模型
fluent湍流模型
第三节,
湍流模型
3.3.1 单方程(Spalart-Allmaras)模型 ~ ,表征出了近壁(粘性影响)区域以外的湍流运动粘 Spalart-Allmaras 模型的求解变量是ν ~ 的输运方程为: 性系数。ν
~ ~ ~ ∂ν Dν 1 ∂ ∂ν ~ − Yν ρ = Gν + 3-9 ( µ + ρν ) + Cb 2 ρ Dt σ ν~ ∂ x ∂ x ∂ x j j j 其中,Gν 是湍流粘性产生项;Yν 是由于壁面阻挡与粘性阻尼引起的湍流粘性的减少;σ ν ~
ρu y u = τ uτ µ ρuτ y u 1 = ln E µ uτ k
其中,k=0.419,E=9.793。
3-18
如果网格粗错不能用来求解层流底层,则假设与壁面近邻的网格质心落在边界层的对数 区,则根据壁面法则: 3-19
对流传热传质模型 在 FLUENT 中,用雷诺相似湍流输运的概念来模拟热输运过程。给出的能量方程为:
3-11
壁面的距离;S ≡
Ω ij =
∂u 1 j − ∂u i 2 ∂xi ∂x j
由于平均应变率对湍流产生也起到很大作用,FLUENT 处理过程中,定义 S 为:
S ≡ Ω ij + C prod min(0, S ij − Ω ij )
Байду номын сангаас其中, C prod = 2.0 , Ω ij ≡
率ε两个方程,湍流粘性系数用湍动能 k 和耗散率ε的函数。Boussinesq 假设的缺点是认为湍 流粘性系数 µ t 是各向同性标量,对一些复杂流动该条件并不是严格成立,所以具有其应用限 制性。 另外的方法是求解雷诺应力各分量的输运方程。这也需要额外再求解一个标量方程,通常 是耗散率ε方程。这就意味着对于二维湍流流动问题,需要多求解 4 个输运方程,而三维湍流 问题需要多求解 7 个方程,需要比较多的计算时间,对计算机内存也有更高要求。 在许多问题中,Boussinesq 近似方法可以得到比较好的结果,并不一定需要花费很多时间 来求解雷诺应力各分量的输运方程。但是,如果湍流场各向异性很明显,如强旋流动以及应力 驱动的二次流等流动中,求解雷诺应力分量输运方程无疑可以得到更好的结果。
中科大FLUENT讲稿_第三章_湍流模型

第三章,湍流模型第一节, 前言湍流流动模型很多,但大致可以归纳为以下三类:第一类是湍流输运系数模型,是Boussinesq 于1877年针对二维流动提出的,将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即:2121x u u u t ∂∂=''-μρ 3-1 推广到三维问题,若用笛卡儿张量表示,即有:ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3-2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目,可以分为零方程模型(代数方程模型),单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念,直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础,对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流,通过求解三维经过修正的Navier-Stokes 方程,得到大涡旋的运动特性,而对小涡旋运动还采用上述的模型。
实际求解中,选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高,应用简单,节省计算时间,同时也具有通用性。
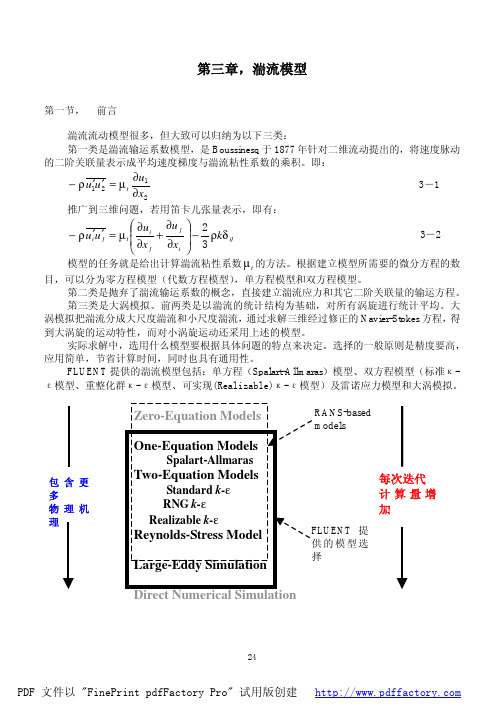
FLUENT 提供的湍流模型包括:单方程(Spalart-Allmaras )模型、双方程模型(标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型)及雷诺应力模型和大涡模拟。
湍流模型种类示意图包含更多 物理机理每次迭代 计算量增加提供RANS-based models第二节,平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度,有:i i i u u u '+= 3-3其中,i u 和i u '分别是平均速度和脉动速度(i=1,2,3)类似地,对于压力等其它标量,我们也有:φφφ'+= 3-4 其中,φ表示标量,如压力、能量、组分浓度等。
常用湍流模型及其在FLUENT软件中的应用

常用湍流模型及其在FLUENT软件中的应用常用湍流模型及其在FLUENT软件中的应用湍流是流体运动中不可避免的现象,它具有无规则、随机和混沌等特点,对于流体力学研究和工程应用具有重要影响。
为了更好地模拟流体运动中的湍流现象,并进行相关的工程计算和优化设计,科学家们提出了许多湍流模型。
本文将介绍一些常用的湍流模型,并探讨它们在流体动力学软件FLUENT中的应用。
1. 动力学湍流模型(k-ε模型)动力学湍流模型是最为经典和常用的湍流模型之一,主要通过求解湍流动能k和湍流耗散率ε来模拟湍流运动。
这一模型主要适用于较为简单的湍流流动,如外部流场和平稳湍流流动。
在FLUENT软件中,用户可以选择不同的k-ε模型进行计算,并对模型参数进行调整,以获得更准确的湍流模拟结果。
2. Reynolds应力传输方程模型(RSM模型)RSM模型是基于雷诺应力传输方程的湍流模型,它通过求解雷诺应力分量来描述湍流的速度脉动特性。
相比于动力学湍流模型,RSM模型适用于复杂的湍流流动,如边界层分离流动和不可压缩流动。
在FLUENT软件中,用户可以选择RSM模型,并对模型参数进行优化,以实现对湍流流动的更精确模拟。
3. 混合湍流模型混合湍流模型是将多个湍流模型相结合,以更好地模拟不同湍流流动。
常见的混合湍流模型有k-ε和k-ω模型的组合(k-ε/k-ω模型)和k-ε模型和RSM模型的组合(k-ε/RSM模型)等。
在FLUENT软件中,用户可以选择不同的混合模型,并根据具体的流动特征进行模型参数调整,以实现更准确的湍流模拟。
除了上述介绍的常用湍流模型外,FLUENT软件还提供了其他的湍流模型选择,如近壁函数模型(近壁k-ω模型、近壁k-ε模型)、湍流耗散模型(SD模型)、多场湍流模型(尺度能量模型)等。
这些模型针对不同的湍流现象和流动特性,提供了更加丰富和精确的模拟方法。
在FLUENT软件中,用户可以根据具体的工程问题和流动特性选择合适的湍流模型,并进行相应的设置和参数调整。
FLUENT常用的湍流模型及壁面函数处理

FLUENT常用的湍流模型及壁面函数处理本文内容摘自《精通CFD工程仿真与案例实战》。
实际上也是帮助文档的翻译,英文好的可直接参阅帮助文档。
FLUENT中的湍流模型很多,有单方程模型,双方程模型,雷诺应力模型,转捩模型等等。
这里只针对最常用的模型。
1、湍流模型描述2、湍流模型的选择有两种方法处理近壁面区域。
一种方法,不求解粘性影响内部区域(粘性子层及过渡层),使用一种称之为“wall function”的半经验方法去计算壁面与充分发展湍流区域之间的粘性影响区域。
采用壁面函数法,省去了为壁面的存在而修改湍流模型。
另一种方法,修改湍流模型以使其能够求解近壁粘性影响区域,包括粘性子层。
此处使用的方法即近壁模型。
(近壁模型不需要使用壁面函数,如一些低雷诺数模型,K-W湍流模型是一种典型的近壁湍流模型)。
所有壁面函数(除scalable壁面函数外)的最主要缺点在于:沿壁面法向细化网格时,会导致使数值结果恶化。
当y+小于15时,将会在壁面剪切力及热传递方面逐渐导致产生无界错误。
然而这是若干年前的工业标准,如今ANSYS FLUENT采取了措施提供了更高级的壁面格式,以允许网格细化而不产生结果恶化。
这些y+无关的格式是默认的基于w方程的湍流模型。
对于基于epsilon方程的模型,增强壁面函数(EWT)提供了相同的功能。
这一选项同样是SA模型所默认的,该选项允许用户使其模型与近壁面y+求解无关。
(实际上是这样的:K-W方程是低雷诺数模型,采用网格求解的方式计算近壁面粘性区域,所以加密网格降低y+值不会导致结果恶化。
k-e方程是高雷诺数模型,其要求第一层网格位于湍流充分发展区域,而此时若加密网格导致第一层网格处于粘性子层内,则会造成计算结果恶化。
这时候可以使用增强壁面函数以避免这类问题。
SA模型默认使用增强壁面函数)。
只有当所有的边界层求解都达到要求了才可能获得高质量的壁面边界层数值计算结果。
这一要求比单纯的几个Y+值达到要求更重要。
fluent中常见的湍流模型及各自应用场合

标题:深入探讨fluent中常见的湍流模型及各自应用场合在fluent中,湍流模型是模拟复杂湍流流动的重要工具,不同的湍流模型适用于不同的流动情况。
本文将深入探讨fluent中常见的湍流模型及它们各自的应用场合,以帮助读者更深入地理解这一主题。
1. 简介湍流模型是对湍流流动进行数值模拟的数学模型,通过对湍流运动的平均值和湍流运动的涡旋进行描述,以求解湍流运动的平均流场。
在fluent中,常见的湍流模型包括k-ε模型、k-ω模型、LES模型和DNS模型。
2. k-ε模型k-ε模型是最常用的湍流模型之一,在工程领域有着广泛的应用。
它通过求解两个方程来描述湍流场,即湍流能量方程和湍流耗散率方程。
k-ε模型适用于对流动场变化较为平缓的情况,如外流场和边界层内流动。
3. k-ω模型k-ω模型是另一种常见的湍流模型,在边界层内流动和逆压力梯度流动情况下有着良好的适用性。
与k-ε模型相比,k-ω模型对于边界层的模拟更加准确,能够更好地描述壁面效应和逆压力梯度情况下的流动。
4. LES模型LES(Large Ey Simulation)模型是一种计算密集型的湍流模拟方法,适用于对湍流细节结构和湍流的大尺度结构进行同时模拟的情况。
在fluent中,LES模型通常用于对湍流尾流、湍流燃烧和湍流涡流等复杂湍流流动进行模拟。
5. DNS模型DNS(Direct Numerical Simulation)模型是一种对湍流流动进行直接数值模拟的方法,适用于小尺度湍流结构的研究。
在fluent中,DNS模型常用于对湍流的微观结构和湍流的小尺度特征进行研究,如湍流能量谱和湍流的空间分布特性等。
总结与回顾通过本文的介绍,我们可以看到不同的湍流模型在fluent中各有其适用的场合。
从k-ε模型和k-ω模型适用于工程领域的实际流动情况,到LES模型和DNS模型适用于研究湍流细节结构和小尺度特征,每种湍流模型都有其独特的优势和局限性。
Fluent培训资料:8-湍流模型

T f ~
T
f
k
2
T
f k
3、Spalart-Allmaras 模型
• Spalart-Allmaras 是一种低耗的求解关于改进的涡粘输运方程的RANS 模型 • 主要用于空气动力学/涡轮机, 比如机翼上的超音速/跨音速流动, 边界层流动
等等 • 是一个相对新的一方程模型,不需求解和局部剪切层厚度相关的长度尺度 • 为气动领域设计的,包括封闭腔内流动
– RSM 对复杂的 3D湍流流动更有效,但是模型更加复杂, 计算强度 更大, 比涡粘模型更难收敛
2、 RANS 模拟
计算湍流粘性
• 基于量纲分析, μT 能够由 湍流时间尺度 (或速度尺度) 和空间尺度来决 定
– 湍流动能 [L2/T2] – 湍流耗散率 [L2/T3] – 比耗散率 [1/T]
Spalart-Allmaras 模型为单方程湍流模型:
湍流粘度:
湍流产生项
Spalart-Allmaras 模型默认常数
3、Spalart-Allmaras 模型
激活Spalart-Allmaras 模型的方法如下: 1)选择粘性模型面板中的 Spalart-Allmaras(1 equ); 2)选择Spalart-Allmaras模型中产生湍流 方法:Vorticity-Based; Strain/Vorticity-Based; 3)设置模型常数(Model Constants)
• 直接数值模拟 (DNS) – 理论上来说,所有的紊流流动能够由数值解出所有的N-S方程来模拟 – 解出尺寸频谱,不需要任何模型 – 花费太高! 对工程流动不实用 ,目前 DNS 在 Fluent中不可用。
• 现在没有一种简单而实用的湍流模型能够可靠的预测出具有充分精度的所有湍流流 动
fluent零方程湍流模型

fluent零方程湍流模型标题:湍流的魅力:探索Fluent零方程湍流模型导语:湍流是自然界中普遍存在的现象,它的复杂性使得我们对其理解充满了好奇与挑战。
在工程领域中,湍流对流体流动的影响不可忽视。
而Fluent零方程湍流模型为我们提供了一种研究湍流现象的有效工具。
本文将以人类的视角,探索这一模型的魅力,展示湍流的奥秘。
第一部分:湍流的定义与特性湍流是一种随机、不规则的流动现象,它在自然界中广泛存在。
与层流相比,湍流的特点是流速和压力的空间和时间波动较大。
湍流的复杂性使得其研究变得困难,但也正是这种复杂性使湍流显示出了一些令人惊叹的特性,比如能量耗散和涡旋结构的形成。
第二部分:Fluent零方程湍流模型的原理与应用Fluent零方程湍流模型是一种简化的湍流模型,它基于湍流的能量耗散理论。
该模型通过假设湍流的能量耗散率与流体的速度梯度成正比,从而实现了对湍流的模拟。
这种模型在工程领域中得到广泛应用,可以帮助工程师预测湍流对流体流动的影响,从而优化设计和提高效率。
第三部分:探索湍流的奥秘湍流的复杂性使得我们对其理解充满了挑战,但也正是这种挑战使得湍流的研究变得更加有趣。
从大气中的湍流到海洋中的湍流,从飞机机翼上的湍流到燃烧过程中的湍流,湍流无处不在。
通过Fluent零方程湍流模型,我们可以更好地理解湍流的形成机制和特性,进而应用于实际工程中。
结语:湍流是自然界中一种复杂而神奇的现象,它的研究对我们理解流体动力学以及优化工程设计具有重要意义。
Fluent零方程湍流模型为我们提供了一种有效的工具,可以帮助我们模拟和预测湍流对流体流动的影响。
通过深入研究湍流的特性和应用,我们可以更好地掌握湍流的奥秘,为工程实践提供更优化的解决方案。
让我们一同探索湍流的魅力,感受科学与工程的交融之美。
FLUENT培训教材05湍流模型

对NS方程进行平均,得到雷诺平均的NS方程 (RANS) :
Reynolds stress tensor, Rij
A Pera Global Company © PERA China
雷诺应力张量
Rij 对称二阶应力; 由对动量方程的输运加速度项平均得来
雷诺应力提供了湍流(随机脉动)输运的平均效应,是高度扩散的
outer layer
inner layer
A Pera Global Company © PERA China
近壁面网格尺寸预估
对平板流动,湍流摩擦系数的指数定律为:
壁面到第一层流体单元的中心点的距离 (Δy)可以通过估计壁面剪 切层的雷诺数来预估
(Bulk Reynolds number)
A Pera Global Company © PERA China
近壁面处理
在近壁面处,湍流边界层很薄,求解变量的梯度很大,但精确计算边 界层对仿真来说非常重要 可以使用很密的网格来解析边界层,但对工程应用来说,代价很大 对平衡湍流边界层,使用对数区定律能解决这个问题
– 由对数定律得到的速度分布和壁面剪切应力,然后对临近壁面的网格单 元设置应力条件 – 假设 k、ε、ω在边界层是平衡的 – 用非平衡壁面函数来提高预测有高压力梯度、分离、回流和滞止流动的 结果 – 对能量和组分方程也建立了类似的对数定律 – 优势:壁面函数允许在近壁面使用相对粗的网格,减少计算代价
类似的,对管流可以预估 Δy 为:
(Hydraulic diameter)
A Pera Global Company © PERA China
尺度化壁面函数
实际上,很多使用者难以保证 30 < y+ < 30–500 常规的壁面函数是精度的主要限制之一,壁面函数对近壁面网格尺寸 很敏感,而且随着网格加密,精度不一定总是提高。同时,加强的壁面 函数计算代价很高 Scalable Wall Functions – 对 k–ε 模型, 尺度化壁面函数假设壁面和粘性子层的边界是一致的, 因此,流体单元总是位于粘性子层之上,这样可以避免由于近壁面网格 加密导致的不连续性 (注意: k–ω, SST 和 S-A 模型的近壁面是自动处 理的,不能使用尺度化壁面函数) 通过 TUI 命令来运行
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Introductory FLUENT Training
© 2006 ANSYS, Inc. All rights reserved.
ANSYS, Inc. Proprietary
Introductory FLUENT Notes FLUENT v6.3 December 2006
Fluent User Services Center
Is the Flow Turbulent?
External Flows
Re x ≥ 500,000 along a surface
Re d ≥ 20,000 around an obstacle
Internal Flows
z
Boussinesq hypothesis – Reynolds stresses are modeled using an eddy (or turbulent) viscosity, µT. The hypothesis is reasonable for simple turbulent shear flows: boundary layers, round jets, mixing layers, channel flows, etc.
z z
Identifiable swirling patterns characterize turbulent eddies. Enhanced mixing (matter, momentum, energy, etc.) results Statistical averaging results in accountable, turbulence related transport mechanisms. This characteristic allows for turbulence modeling. The size/velocity of large eddies is on the order of mean flow.
6-5
ANSYS, Inc. Proprietary
© 2006 ANSYS, Inc. All rights reserved.
Introductory FLUENT Notes FLUENT v6.3 December 2006
Fluent User Services Center
Fluent User Services Center
RANS Modeling – Time Averaging
Ensemble (time) averaging may be used to extract the mean flow properties from the instantaneous ones:
Turbulence Models Available in FLUENT
One-Equation Models Spalart-Allmaras Two-Equation Models Standard k–ε RNG k–ε Realizable k–ε Standard k–ω SST k–ω Reynolds Stress Model Detached Eddy Simulation Large Eddy Simulation
where Re L =
ρU L µ L = x, d , d h , etc.
Re d h ≥ 2,300
Other factors such as free-stream turbulence, surface conditions, and disturbances may cause transition to turbulence at lower Reynolds numbers
Fluid properties and velocity exhibit random variations
z
z
Contains a wide range of turbulent eddy sizes (scales spectrum).
z
Large eddies derive energy from the mean flow In the smallest eddies, turbulent energy is converted to internal energy by viscous dissipation.
Natural Convection 2 3 3 ρ C β g L ∆T β g L ∆ T Ra p 9 ≥ 10 = where Ra = is the Rayleigh number να µk Pr ν µCp Pr = = is the Prandtl number k α
© 2006 ANSYS, Inc. All rights reserved.
RANS based models
Increase in Computational Cost Per Iteration
© 2006 ANSYS, Inc. All rights reserved.
6-6
ANSYS, Inc. Proprietary
Introductory FLUENT Notes FLUENT v6.3 December 2006
Large Eddy Simulation (LES)
z
z
Direct Numerical Simulation (DNS)
z
z z
There is not yet a single, practical turbulence model that can reliably predict all turbulent flows with sufficient accuracy.
z
∂ui µ ∂x j
∂ Rij + ∂x j
Rij = −ρui′u ′j
(Reynolds stress tensor)
The Reynolds stresses are additional unknowns introduced by the averaging procedure, hence they must be modeled (related to the averaged flow quantities) in order to close the system of governing equations.
The Closure Problem
The RANS models can be closed in one of the following ways (1) Eddy Viscosity Models (via the Boussinesq hypothesis)
∂ui ∂u j 2 ∂uk 2 − µT + Rij = −ρ ui′u′j = µT δij − ρ k δij ∂x ∂x 3 ∂x 3 i k j
1 ui (x, t ) = lim N →∞ N
∑
n =1
N
ui
(n )
(x, t )
ui (x, t )
ui′(x, t )
ui (x, t )
ui (x, t ) = ui (x, t ) + ui′(x, t )
Instantaneous component Time-average Fluctuating component component
Fluent User Services Center
Overview of Computational Approaches
Reynolds-Averaged Navier-Stokes (RANS) models
z z z
Solve ensemble-averaged (or time-averaged) Navier-Stokes equations All turbulent length scales are modeled in RANS. The most widely used approach for calculating industrial flows. Solves the spatially averaged N-S equations. Large eddies are directly resolved, but eddies smaller than the mesh are modeled. Less expensive than DNS, but the amount of computational resources and efforts are still too large for most practical applications. Theoretically, all turbulent flows can be simulated by numerically solving the full Navier-Stokes equations. Resolves the whole spectrum of scales. No modeling is required. But the cost is too prohibitive! Not practical for industrial flows - DNS is not available in Fluent.
Fluent User Services Center
What is Turbulence?
Unsteady, irregular (aperiodic) motion in which transported quantities (mass, momentum, scalar species) fluctuate in time and space
