第02章 变压器的运行分析(2)
第二章 变压器的运行原理

Electric Machinery
本章节重点和难点: 重点: (1)变压器空载运行时磁动势、电动势平衡关系,等值电路和相 量图; (2)变压器负载运行时磁动势、电动势平衡关系,等值电路和相 量图; (3)绕组折算前后的电磁关系; (4)变压器空载实验和短路实验,变压器各参数的物理意义; (5)变压器的运行特性。 难点: (1)变压器绕组折算的概念和方法; (2)变压器的等值电路和相量图; (3)励磁阻抗Zm与漏阻抗Z1的区别; (4)励磁电流与铁芯饱和程度的关系; (5)参数测定、标么值。
空载损耗约占额定容量的(0.2~1)%,随 容量的增大而减小。这一数值并不大,但因为 电力变压器在电力系统中用量很大,且常年接 在电网上,因而减少空载损耗具有重要的经济 意义。工程上为减少空载损耗,改进设计结构 的方向是采用优质铁磁材料:优质硅钢片、激 光化硅钢片或应用非晶态合金。
Electric Machinery
漏电动势 : E1
2 2
fN 1 1
2 fN 1 1
Electric Machinery
E 1 j 2 f
N 1 1
I 0 j 2 fL 1 I 0 j I 0 x 1
I0
x 1 2 f
N1
2
为一次侧漏抗,反映漏磁通的作用。
电机学:变压器第二章变压器的运行分析 04
用一台副绕组匝数等于原绕组匝数的假想变压器来模拟实际变压器,假想变压器与实际变压器在物理情况上是等效的。
2)3) 有功和无功损耗不变。
2I实际上的二次侧绕组各物理量称为实际值或折合前的值。
折合后,二次侧各物理量的值称为其折合到一次绕组的折合值。
当把副边各物理量归算到原边时,凡是单位为伏的物理量(电动势、电压等)的归算值等于其原来的数值乘以k;凡是单位为欧姆的物理量(电阻、电抗、阻抗等)的归算值等于其原来的数值乘以k2;电流的归算值等于原来数值乘以1/k。
参数意义220/110V,1R m E 0I 2I ′ U 2I简化等效电路R k 、X k 、Z k 分别称为短路电阻、短路电抗和短路阻抗,是二次侧短路时从简化等效电路一次侧端口看进去的电阻、电抗和阻抗。
R k =R 1+2R ′, X k =X 1+2X ′ Z k =R k +j X k应用基本方程式作出的相量图在理论上是有意义的,但实际应用较为困难。
因为,对已经制造好的变压器,很难用实验方法把原、副绕组的漏电抗x 1和x 2分开。
因此,在分析负载方面的问题时,常根据简化等效电路来画相量图。
短路阻抗的电压降落一个三角形ABC ,称为漏阻抗三角形。
对于给定的一台变压器,不同负载下的这个三角形,它的形状是相似的,三角形的大小与负载电流成正比。
在额定电流时三角形,叫做短路三角形。
讨论:变压器的运行分析感性负载时的简化相量图2U ′− 21I I ′−= 2ϕ 1kI r kx I j 1 1U ABC()()1111111121111210211220m2211P U I E I R jX I E I I RE I I I R I R E I I R =⎡⎤=−++⎣⎦=−+′=−−+′′=++ i i i i i()em 222222222222P E I U I R jX I U I I R ′′=′′′′′⎡⎤=++⎣⎦′′′′=+ i i i 有功功率平衡关系,无功功率平衡关系例题一台额定频率为60Hz的电力变压器,接于频率等于50Hz,电压等于变压器5/6倍额定电压的电网上运行,试分析此时变压器的磁路饱和程度、励磁电抗、励磁电流、漏电抗以及铁耗的变化趋势。
变压器的运行原理

变压器的运行原理
变压器是一种用来改变交流电压的电气设备,其运行原理主要基于电磁感应和法拉第电磁感应定律。
变压器主要由一个铁芯和两个绕组组成,分别是输入侧的初级绕组和输出侧的次级绕组。
首先,当交流电流通过变压器的初级绕组时,产生的磁场会使铁芯磁化,从而在次级绕组中感应出电动势。
根据法拉第电磁感应定律,感应电动势的大小与磁场的变化率成正比,因此变压器的初级和次级绕组匝数的比值决定了输出电压和输入电压的比值。
其次,由于铁芯的存在,可以大大增强磁场的传导效果,减小电磁泄漏,提高变压器的效率。
铁芯的磁化特性也对变压器的运行有重要影响,通常使用硅钢片制成的铁芯可以减小铁芯的磁滞和涡流损耗,提高变压器的效率和稳定性。
此外,变压器的运行还受到电阻、感抗和容抗等因素的影响。
电阻会导致变压器的损耗,感抗和容抗会影响变压器的电流和功率因数,需要在设计和运行过程中进行合理的补偿和控制。
总的来说,变压器的运行原理是利用电磁感应的原理,通过变压器的变压比和铁芯的磁化来改变输入和输出的电压。
在实际应用中,需要考虑电阻、感抗和容抗等因素,以确保变压器的稳定运行和高效率的电压变换。
变压器作为电力系统中的重要设备,承担着电压变换和电力传输的重要功能,对电力系统的运行和稳定性起着至关重要的作用。
浅谈变压器的不正常运行

浅谈变压器的不正常运行变压器是电力系统中不可或缺的设备,它在电力传输和分配中起着至关重要的作用。
正常运行的变压器也会出现一些不正常的情况,如过载、短路、温升过高等问题。
本文将对变压器的不正常运行进行浅谈,探讨其原因和解决方法。
一、过载变压器的过载是指变压器的负载电流超过了额定容量,导致变压器运行不正常。
过载可能是短期的或者长期的,这取决于过载的程度和持续时间。
过载会导致变压器的温升过高,影响其绝缘性能,甚至引发火灾。
过载的原因主要有以下几点:1.负载电流超过了变压器的额定容量;2.变压器安装环境温度过高,影响了变压器的散热性能;3.变压器内部绝缘老化或损坏,导致电气参数变化。
解决过载问题的方法有:1.提高变压器的额定容量,或者增加变压器的数量;2.改善变压器的散热条件,如增加散热设备或者改进变压器的安装位置;3.定期对变压器进行维护检查,及时发现并修复绝缘老化或损坏的问题。
二、短路变压器的短路是指变压器的一部分匝间发生了短路,导致变压器运行不正常。
短路会导致变压器的绝缘损坏,甚至造成变压器的报废。
短路的原因主要有以下几点:1.变压器内部绝缘老化或损坏;2.变压器的运行环境恶劣,如受到水汽侵蚀或者化学气体腐蚀;3.变压器的设计或制造缺陷,如绕组之间的绝缘距离不足等。
三、温升过高变压器的温升过高是指变压器在运行过程中温度超过了额定温升值,导致变压器运行不正常。
温升过高会导致变压器的绝缘老化加速,缩短变压器的使用寿命。
变压器作为电力系统中的重要设备,其不正常运行将对电网运行安全和供电质量产生一定影响。
对变压器的不正常运行进行及时的检测和处理,对保障电网的安全稳定运行具有重要意义。
加强变压器的日常维护和管理工作,提高变压器的可靠性和安全性,也是电力系统运行单位的重要任务。
第2章 变压器的工作原理和运行分析

SN SN ,I 2 N 3U 1 N 3U 2 N
注意!对于三相系统,额定值都是指线间值。
第二节 变压器空载运行
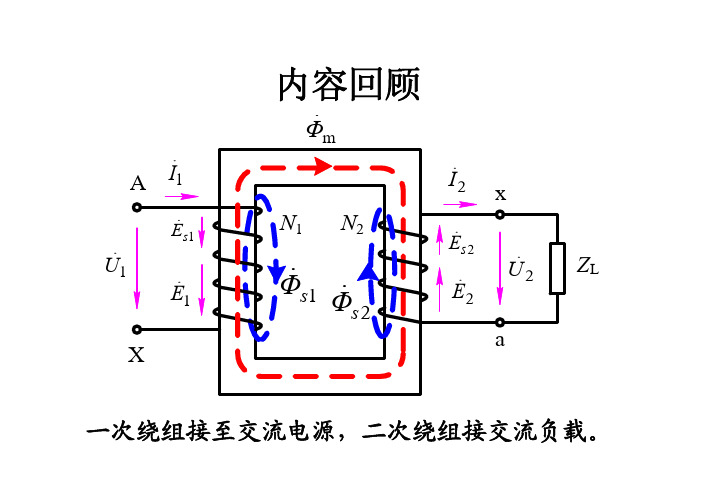
空载:一次侧绕组接到电源,二次侧绕组开路。 一、电磁现象
u1
Φm
i0
Φ 1σ
e1 e1σ
N1
N2
e2
u20
i
二、参考方向的规定
e
i i
e
e
三、变压原理、电压变比
对于变压器的原边回路,根据电路理论有:
u1 i0 r1 e1 e1
空载时 i0r1 和 e1σ 都很小,如略去不 计,则 u1 = - e1 。设外加电压 u1 按 正弦规律变化,则 e1 、Φ 和e2 也都 按正弦规律变化。 设主磁通 m sin t ,则:
u1
Φm
u1
Φm
e1
e2
ωt 0 180° 360°
现在的问题是,要产生上述大小的主磁通 Φm ,需 要多大(什么样)的激磁电流 Im ?
励磁电流的大小和波形受磁路饱和、磁滞及涡 流的影响。
1、磁路饱和对励磁电流的影响
mm mm
i0 tt
00
i0i0 tt
00
i0 i0
tt
tt
磁路不饱和时,i0 ∝φ,其波形为正弦波。
磁路饱和时,i0与φ 不成线性关系,φ越大,磁路 越饱和,i0/φ比值越大,励磁电流的波形为尖顶波。
六、漏抗 漏电势的电路模型与励磁特性的电路模型类似, 只是漏磁通所经路径主要为空气,磁阻大,磁通量 小,磁路不饱和,因此可以忽略漏磁路的铁耗,即 漏电势的电路模型中的等效电阻为零,即漏电势
第02章_变压器的基本理论

第 2 章 思考题与习题参考答案
2.1 试述变压器空载和负载运行时的电磁过程。
,建立磁动势 F ,由其产生主磁通 Φ 和 答:空载时,原边接交流电源,原绕组中流过交流电流 I 0 0 0
负载: R L = 3Ω , X L = 4Ω 。分别用 T 形等效电路、近似等效电路和简化等效电路计算 I 1 、 I 0 、 I 2 、
U 2 ,并比较三次计算的结果。
解:(1)用 T 形等效电路计算 根据已知参数可得: k =
U 1N 380 = = 1.7273 U 2 N 220
′ = k 2 R2 = 1.7273 2 × 0.035 = 0.104Ω R2 ′ = k 2 RL = 1.7273 2 × 3 = 8.951Ω RL
2.11 试说明变压器等效电路中各参数的物理意义,这些参数是否为常数?
′ 分别为副边一相绕组的电阻和漏电 ′和 X2 答: R1 和 X 1 分别为原边一相绕组的电阻和漏电抗, R2
′ 的大小分别反映了原、副绕组漏磁通的大小。 Rm 是 抗的折算值,上述四个参数为常数,其中 X 1 、 X 2
反映铁心损耗的等效电阻,称为励磁电阻, X m 是反映主磁通大小的电抗,称为励磁电抗,这两个参数 也是一相参数,当电源电压不变时, Rm 和 X m 近似为常数。 2.12 利用 T 形等效电路进行实际问题计算时,算出的一次和二次侧电压、电流、损耗、功率是否 均为实际值,为什么? 答: 一次各物理量数值均为实际值,二次电压、电流是折算值,二次损耗、功率是实际值。因为对 二次绕组进行折算时,是以等效为原则,其中,折算前、后的二次侧损耗、功率是保持不变的。 2.13 变压器空载实验一般在哪侧进行?将电源加在低压侧或高压侧所测得的空载电流、空载电流 百分值、空载功率、励磁阻抗是否相等? 答:空载实验一般在低压侧进行。空载电流不等,高压侧空载电流是低压侧的 1 / k ;空载电流百 分值相等;空载功率相等;励磁阻抗不等,高压侧励磁阻抗是低压侧的 k 倍。 2.14 变压器短路实验一般在哪侧进行?将电源加在低压侧或高压侧所测得的短路电压、短路电压 百分值、短路功率、短路阻抗是否相等? 答:短路实验一般在高压侧进行。短路电压不等,高压侧短路电压是低压侧的 k 倍;短路电压百分 值相等;短路功率相等;短路阻抗不等,高压侧短路阻抗是低压侧的 k 倍。 2.15 为什么可以把变压器的空载损耗看作铁耗?短路损耗看作额定负载时的铜耗? 答:空载试验时外加额定电压,空载损耗包括额定铁损耗和空载铜损耗,由于空载电流很小,空载 铜损耗远远小于额定铁损耗,可忽略,所以空载损耗可看作铁损耗。 短路试验时电流为额定电流,短路损耗包括额定铜损耗和短路时的铁损耗,由于短路电压很低,磁
飞机电气基础-第二章第2节变压器

03
绕组是变压器的电路, 通常由绝缘铜线或铝线 绕在铁芯上,起到转换 电压的作用。
04
绝缘材料用于绕组和铁 芯之间的绝缘,以及各 绕组之间的绝缘。
变压器的绕组
变压器的绕组分为初级绕组和 次级绕组,分别连接电源和负 载。
初级绕组的匝数较少,次级绕 组的匝数较多,通过改变匝数 比实现电压的转换
在飞机电气系统中,变压 器用于调节电压,以满足 不同设备对电压的不同需 求。
电磁干扰抑制
变压器具有电磁屏蔽功能, 能够抑制电磁干扰对飞机 电气系统的影响。
其他领域中的应用
通讯领域
变压器用于信号传输和处理,如电话、 电视信号的传输和卫星通信系统。
工业自动化
医疗器械
在医疗器械中,变压器用于提供稳定、 安全的电源,确保医疗设备的正常运 行。
详细描述
当交流电通过一次绕组时,会在一次绕组中产生交变磁场, 该磁场会在二次绕组中产生感应电动势,从而实现电压的变 换。同时,电流和阻抗的变换也是基于相同的原理。
02
变压器的结构
变压器的组成
01
变压器主要由铁芯、绕 组和绝缘材料组成。
02
铁芯是变压器的磁路, 通常由高磁导率的硅钢 片叠成,起到集中磁场 的作用。
变压器的分类
总结词
变压器可根据不同的分类标准进行分类,如变压器的相数、冷却方式、用途等。
详细描述
根据相数,变压器可分为单相和三相变压器;根据冷却方式,变压器可分为自然 冷却、强迫油循环冷却和强迫空气循环冷却;根据用途,变压器可分为电力变压 器、特种变压器和仪用变压器等。
变压器的工作原理
总结词
变压器的工作原理基于电磁感应定律,通过一次绕组和二次 绕组之间的电磁耦合实现电压、电流和阻抗的变换。
电机与拖动基础课后习题答案

第二章2 . 1 变压器能改变交流电的电压和电流,能不能改变直流电的电压和电流?为什么?答: 变压器能改变交流电的电压和电流,但不能改变直流电的电压和电流。
因为变压器是应用电磁感应原理而工作的,只有当一次绕组接交流电源时, 一次绕组才会流过交流电流,在铁心中产生变化的磁通,从而在二次绕组中产生感应电动势;如果一次绕组接直流电源,则一次绕组流过的是直流电流, 在铁心中产生的磁通是恒定不变的,不能在二次绕组中产生感应电动势,所以变压器只能改变交流电的电压和电流,不能改变直流电的电压和电流。
2 . 2 变压器的铁心为什么要用硅钢片叠成而不用整块钢制成?答: 变压器的绕组流过交流电流时会在铁心中产生磁滞损耗和涡流损耗,统称为铁损耗。
磁滞损耗与铁磁材料的磁滞回线面积有关, 硅钢片的磁滞回线较窄, 磁滞损耗较小。
涡流损耗与铁磁材料的电阻成反比,与钢片厚度的平方成正比, 硅钢片是在电工钢中加入少量的硅而制成, 电阻率较大, 用硅钢片叠成的铁心, 铁损耗较小,所以变压器的铁心要用硅钢片叠成而不用整块钢制成。
2 .3 一台变压器额定电压为220 /110 V ,若把二次绕组( 110 V )接在220 V交流电源上,主磁通和励磁电流将如何变化?答:若忽略变压器绕组漏阻抗压降,则绕组的端电压与感应电动势相等。
正常工作时铁心磁路处于饱和状态。
若把额定电压为110 V的二次绕组接在220 V交流电源上, 二次绕组感应电动势将增大一倍, 感应电动势与铁心磁通成正比,所以铁心磁通也将增大一倍,由于铁心磁路处于饱和状态, 励磁电流将不只是增大一倍,而将增大许多倍。
2 . 4 一台变压器一次绕组额定电压为220 V ,不小心把一次绕组接在220 V的直流电源上,会出现什么情况?答: 若把额定电压为交流220 V 的变压器一次绕组接在220 V 直流电源上时, 铁心中产生的磁通将是恒定不变的,不会在一次绕组中产生感应电动势, 一次绕组电流11R UI =,由于绕组电阻1R 比较小,则一次绕组电流会很大,大大超过其额定电流,很快会将变压器烧坏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Z L = 0.20 + j 0.07Ω
求:
①
I1 , I 2 ;
② U2 ;
③ P , P2 , Q1 , Q2 ; 1
④
η
ɺ 不变, ɺ 的变化。 保持 F2 不变,就不会影响 F1 的变化。
定义: ③ 定义:保持一个绕组的磁动势不变而改变其 电流和匝数的算法称为归算法(折合算法)。 电流和匝数的算法称为归算法(折合算法)。
定义:如果保持二次绕组磁动势不变, ④ 定义:如果保持二次绕组磁动势不变,而假想
它的匝数与一次绕组匝数相同的折合算法, 它的匝数与一次绕组匝数相同的折合算法,称为二 次绕组折合成一次绕组或简称二次向一次折合。 次绕组折合成一次绕组或简称二次向一次折合。
型等效电路可得: ㈢ 由“T”型等效电路可得: 型等效电路可得
ɺ I1 = ɺ U1 = I1∠ϕ1 ′ ′ Z1 + Z m || ( Z 2 + Z L )
ɺ′ ɺ ɺ ɺ ɺ 的夹角, ɺ ϕ1∠U1 I1 是 U1 、 I1 的夹角,进而可求出 I 2 Iɺ0 U 2′ 。 ɺ ɺ ɺ ɺ I 2 = I 2 ∠ϕ2 ϕ2∠U2 I2 是 U 、I 的夹角,是 Z L 的阻抗角, ɺ 的夹角, 的阻抗角, 2 2 因为求复数阻抗比较繁, 因为求复数阻抗比较繁,所以专业上常常把励磁支 路提前。 路提前。
1.1 一次侧电流
㈠能量的观点 ㈡用电磁关系来解释一次绕组的电流由 I 0 变成 I1
ɺ ɺ 1.2 磁动势 I1 N1 和 I 2 N 2
根据安培环路定律, 根据安培环路定律,此时一二次绕组的磁动势合 ɺ ɺ ɺ ɺ 成产生主磁通。 成产生主磁通。即 F1 + F2 = F0 ,其中 F0为合成磁 动势。 动势。
㈣ “一”字型等效电路 一
☆ “一”字型等效电路 一 不适用空载, 不适用空载,适用正常 负载运行和稳态短路。 负载运行和稳态短路。
ɺ I1
R1
jX 1
' R2
' jX 2
ɺ′ I2
ɺ U1
ɺ' U2
′ ZL
㈤ 简化等效电路
Rk
jX k' ɺ ɺ′ I1 = − I 2
′ Zk = Z1 + Z2 ′ X k = X1 + X 2 ′ Rk = R1 + R2
ɺ' ɺ ' ɺ′ ′ E2 = U 2 + I 2 Z 2
ɺ U1
ɺ jI1 X 1
ɺ I1 R1
ɺ − E1
ɺ' −I2
ϕ1
ϕ
ɺ I1
ɺ ɺ′ E1 = E2
ɺ ɺ I 0 = − E1 / Z m
ɺ I0
ɺ Φm
ɺ ɺ ɺ′ I1 = I 0 + ( − I 2 )
ɺ ɺ ɺ U1 = − E1 + I1Z1
ɺ U1
ɺ' U2
′ ZL
Z k 叫短路阻抗 , Rk 短路电阻, k 短路电抗 X 短路电阻,
★ 一般情况没给励磁阻抗 Z m ,只给短路阻抗 Z k 就用简化等值电路。 就用简化等值电路。
6、相量图
cos 已知: 已知: U 2 、I 2 、 ϕ 2 、k
ɺ ′ ɺ′ ′ U 2 = I2ZL
当仅考虑数量关系时, 当仅考虑数量关系时,一次磁动势等于二次磁 动势, 动势,即 I1 N1 = I 2 N 2 ,所以利用磁动势平衡的概 念来定性分析变压器负载运行时, 念来定性分析变压器负载运行时,可得如下结
kI 论:电流之比等于匝数之比, 1 = I 2 。 电流之比等于匝数之比,
2. 负载时二次电压、电流的关系 负载时二次电压、 ɺ ɺ ɺ ɺ U 2 = E2 + ES 2 − I 2 R2 ɺ ɺ ES 2 = − jI 2 X 2 ɺ ɺ ɺ U 2 = E2 − I 2 ( R2 + jX 2 ) ɺ ɺ U 2 = I2ZL
ɺ ɺ I1′ = k I1
R1 R1′ = 2 k
X1 X1′ = 2 k
Rm ′ Rm = 2 k
Xm ′ Xm = 2 k
5. 等效电路
折合后的六个基本方程式: ㈠ 折合后的六个基本方程式
ɺ ɺ ɺ U1 = − E1 + I1Z1 ɺ ɺ ɺ U ′ = E′ − I ′ Z ′
2 2 2 2
ɺ ɺ ɺ 1.3 空载一次绕组 U1 = −E1 + I0Z1
ɺ ɺ 负载一次绕组 U1 = − E1 + Iɺ1Z1
Zm << Z1
I1 > I 0
一次电流从空载到负载
ɺ I 0 Z1 << E1
时,有:
ɺ I1Z1 << E1
从大小关系来看,从空载到满载, 从大小关系来看,从空载到满载,因为电源 不变, 电压 U1不变,所以一次绕组的感应电动势 E1 变化不大, 变化不大, U1 ≈ E1 = 4.44 fN1Φ m 。所以 Φ m 基本 不变。 不变。
产生, ɺ 空载时主磁通是由励磁电流 Iɺ0 产生,F0 = Iɺ0 N1
ɺ ɺ ɺ F1 + F2 = F0
ɺ ɺ ɺ I1 N1 + I 2 N 2 = I 0 N1
Iɺ 2 Iɺ 2 ɺ ɺ Iɺ1 + = Iɺ 0 ⇒ Iɺ1 = Iɺ 0 + − = I 0 + I1L k k
ɺ' I2 ϕ 2
ɺ' U2 ɺ' ' I 2 R2
ɺ' ' jI 2 X 2
ɺ ɺ' E1 = E2
例2-1 (p30) -
已知: 已知
S N = 750 kVA , U1N / U 2 N = 10000 / 400 V,
x Y,y0联接, K = 1.4Ω , K = 6.48Ω ,副边Y接, r
折合值:二次向一次折合为例。 ⑤ 折合值:二次向一次折合为例。
ɺ ɺ′ ⑴ ∵ I 2 N 2 = I 2 N1 ∴
⑵电动势 ⑶阻抗
ɺ′ E2 = − j 4.44 fN1Φ m ɺ E = − j 4.44 fN Φ
2 2 m
ɺ′ ɺ E2 = kE2
′ Z2 = k 2Z2
′ ZL = k 2ZL
第二节 变压器的负载运行
ɺ Φm
ɺ I1
A
ɺ I2
*
−
ɺ Φ s1 ɺ Φ s2
x
+
ɺ U1
+
ɺ ɺ E2 E s 2 ɺ U2
ɺ E s1 E ɺ 1
ZL
−
X
+
N1 N2
−
*
a
一、负载时电压与电流的关系: 负载时电压与电流的关系: 一二次电流关系(磁动势平衡方程式) 1. 一二次电流关系(磁动势平衡方程式)
2 2 L
ɺ ɺ ɺ ɺ ɺ U1 = − E1 + I1Z1 = − E1 + I1 ( R1 + jX 1 )
ɺ ɺ ɺ′ I1 = I 0 + ( − I 2 )
ɺ I1
R1
jX 1
Iɺ0
.
Rm
R
' 2
jX
' 2
ɺ′ I2
ɺ U1
ɺ' ɺ E 1 = E2
ɺ' U2
′ ZL
jX m
变压器“ T ”型等值电路
3. 变压器的基本方程式
ɺ ɺ ɺ U1 = − E1 + I1Z1
ɺ ɺ U 2 = E2 − I 2 Z 2
ɺ Φ
m
ɺ ɺ U2 = I2ZL
Iɺ1
A
+
−
ɺ E1
*ɺ Φs1ɺ ΦIɺ 2
s2
x
+
ɺ E2
ɺ ɺ − E1 = I 0 Z m
ɺ I2 ɺ ɺ I1 + = I 0 k
ɺ U1
X −
ɺ ɺ′ E1 = E2 ɺ ɺ E = −I Z
1 0
ɺ ′ ɺ′ ′ U2 = I2ZL
ɺ ɺ ɺ′ I1 = I 0 + ( − I 2 )
m
㈡ “T”型等效电路 型等效电路
ɺ ɺ ɺ E1 = − I 0 Z m = − I 0 ( Rm + jX m )
ɺ ɺ' E1 = E2
' ɺ' ɺ ' ɺ′ ′ ɺ ' ɺ′ ' E2 = U 2 + I 2 Z 2 = U 2 + I 2 ( R2 + jX 2 ) ɺ ɺ U ′ = I ′Z ′
ɺ′ ɺ ⑷负载电压 U 2 = kU 2
说明: 说明:折合算法其结果不改变变压器运行的 物理本质,既不改变功率,不影响阻抗抗角。 物理本质,既不改变功率,不影响阻抗抗角。 如果
N1 k= N2
则一次向二次折合值为: 则一次向二次折合值为:
ɺ′ ɺ I0 = k I0
ɺ′ = 1U ɺ U1 1 k
N1 ——变压器变比 k= N2 ɺ I ——为一次电流的负载分量
1L
ɺ ɺ 由 I1L N1 + I 2 N 2 = 0 一次电流负载分量所建立 电流磁动势相平衡。 的磁动势与二次 电流磁动势相平衡。
ɺ ɺ I 当略去 I 0 时,1 N1 + Iɺ2 N 2 = 0
ɺ ɺ ɺ I 即一次电流达到满载时, 当 I1 = I1N 时,即一次电流达到满载时,2 = Iɺ2 N 也达到额定值 。
ɺ ɺ E s1 E s 2
ɺ U2
ZL
