三视图体积面积计算学生版
利用三视图求几何体的表面积与体积

圆锥的表面积:S圆锥 r(rl)
圆台的表面积: S(r 2 r '2 r l r 'l) 圆台
球的表面积:
S 4R2 球
柱体的体积:V Sh
柱
锥体的体积: V 1Sh
锥3
台体的体积:V1(S S'SS')h
台3
球的体积:
4R3
V
球
3
例1.已知一几何体的三视图如下图,试求其表面积与 体积.
1
1
长对正 高平齐 宽相等
正视图
侧视图
俯视图
(2)所求多面体的体积
V V 长 方 体 V 三 棱 锥 4 4 6 1 3 1 2 2 2 2 2 8 3 4 c m 3
长对正 高平齐 宽相等
练习
一个几何体的正视图为一个三角形,则这个几何体可能是下列 几何体中的_______(填入所有可能的几何体前的编号) ①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱 ⑤圆锥 ⑥圆柱 一个长方体去掉一个小长方体,所得几何体的正视图与侧(左) 视图分别如右图所示,则该几何体的俯视图为:
1
主视图
侧视图
2
2 236cm2, 3cm3
俯视图
直观图
长对正 高平齐 宽相等
练习 长对正 高平齐 宽相等
已知某个几何体的三视图如图(主视图中的弧线是半圆),
根据图中标出的尺寸(单位:cm),可得这个几何体的体积
A 是() Leabharlann m3 .1A.8
B.8 2
3
3 2
C.12
D.12 2
3
2 主视图
侧视图
2
俯视图
练习
如右图为一个几何体的三视图,尺寸如图所示,则该几何
山东省2014届理科数学一轮复习试题选编25:空间几何体的三视图、表面积与体积(学生版)
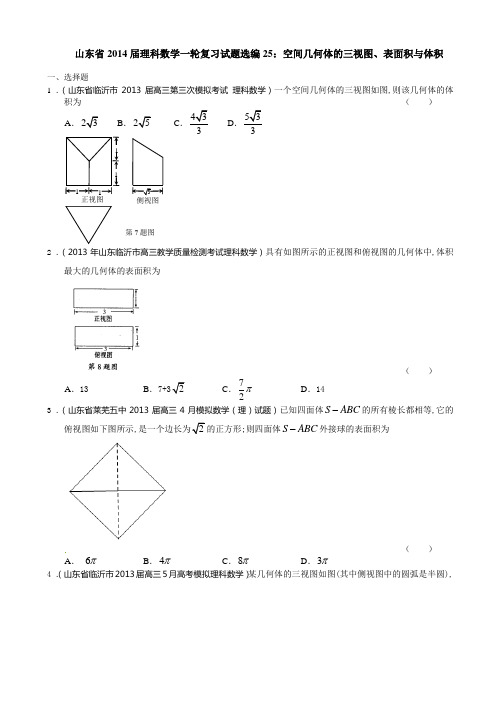
山东省2014届理科数学一轮复习试题选编25:空间几何体的三视图、表面积与体积一、选择题 1 .(山东省临沂市2013届高三第三次模拟考试 理科数学)一个空间几何体的三视图如图,则该几何体的体积为( )A.B.CD2 .(2013年山东临沂市高三教学质量检测考试理科数学)具有如图所示的正视图和俯视图的几何体中,体积最大的几何体的表面积为( )A .13B .C .72πD .143 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)已知四面体S ABC -的所有棱长都相等,它的俯视图如下图所示,的正方形;则四面体S ABC -外接球的表面积为( )A . 6πB .4πC .8πD .3π 4 .(山东省临沂市2013届高三5月高考模拟理科数学)某几何体的三视图如图(其中侧视图中的圆弧是半圆),第7题图( )A .9214+πB .8214+πC .9224+πD .8224+π5 .(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积、体积分别是 ( )A .12832,3ππ B .3216,3ππ C .1612,3ππ D .168,3ππ6 .(山东省潍坊市2013届高三第二次模拟考试理科数学)有一平行六面体的三视图如图所示,其中俯视图和左视图均为矩形,则这个平行六面体的表面积为( )A .B .6+C .30+D .42 7 .(山东省兖州市2013高三9月入学诊断检测数学(理)试题)如右图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t 变化的可能图象是第7题图8 .(山东省2013届高三高考模拟卷(一)理科数学)一个几何体的三视图如图所示,其正视图和侧视图都是底边长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是 ( ) A .π6 B .π12 C .π18 D .π249 .(山东省泰安市2013届高三上学期期末考试数学理)如图,若一个空间几何体的三视图中,正视图和侧视图都是直角三角形,其直角边均为1,则该几何体的体积为( )A .13B .12 C .16D .110.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的( )A.外接球的半径为3B1 CD .外接球的表面积为4π11.(山东省济南市2013届高三3月高考模拟理科数学)一个几何体的三视图如右图所示,则它的体积为( )A .203B .403C .20D .4012.(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)一个几何体的三视图如图所示,则该几何体的体积为( )A .1B .13 C.12D.32 13.(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)如图所示是以建筑物的三视图,现需将其外壁用油漆刷一遍,若每平方米用漆0.2k g,则共需油漆大约公斤数为(尺寸如图所示,单位:米 π取3)第11题图图图( )A .20B .22.2C .111D .11014.(山东省济宁市2013届高三4月联考理科数学)已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为1V ,直径为4的球的体积为2V ,则12:V V =( )A .1:2B .2:1C .1:1D .1:415.(2013届山东省高考压轴卷理科数学)右图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为的矩形.则该几何体的表面积是( )A.20+B.24+C .8D .1616.(山东省青岛市2013届高三第一次模拟考试理科数学)一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是( )A .16πB .14πC .12πD .8π17.(山东省枣庄市2013届高三3月模拟考试数学(理)试题)一个几何体的三视图如图所示,其中的长度单位为cm,则该几何体的体积为( )cm 3.正视图 俯视图左视图( )A .18B .48C .45D .54 18.(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)一个几何体的三视图如图所示,则该几何体的体积为( )A .2B .1C .23D .1319.(2011年高考(山东理))右图是长和宽分别相等的两个矩形.给定下列三个命题:① 存在三棱柱,其正(主)视图、俯视图如右图; ② 存在四棱柱,其正(主)视图、俯视图如右图; ③ 存在圆柱,其正(主)视图、俯视图如右图. 其中真命题的个数是 ( )A .3B .2C .1D .0 20.(山东省济南市2013届高三上学期期末考试理科数学)一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是21.(山东省潍坊市2013届高三上学期期末考试数学理 ( ) A .)一个几何体的三视图如图所示,其中主视图和左视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是 ( ) A .π12 B .π24 C .π32 D .π48 22.(山东省威海市2013届高三上学期期末考试理科数学)某几何体的三视图如右图所示,则该几何体的体积不可能是( )A .1B .1.5C .2D .323.(山东省烟台市莱州一中2013届高三第三次质量检测数学(理)试题)如图是某一几何体的三视图,则这个几何体的体积为【T 】1.( )A .4B .8C .16D .20 24.(山东省烟台市2013届高三上学期期末考试数学(理)试题)一个几何体的三视图如下所示,则该几何体的表面积是( )A .6+B .12+C .12+D .18+25.(山东师大附中2013届高三第四次模拟测试1月理科数学)已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )A .3242π-B .243π-C .24π-D .242π-26.(山东省泰安市2013届高三第二次模拟考试数学(理)试题)如右图,一个由两个圆锥组合而成的空间几何体的正视图和侧视图都是边长为1、一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的体积为( )AB .6ππC.12π D27.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))如图,正三棱柱ABC -111A B C 的各棱长均为2,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )A .22B .4C .3D .32 28.(2009高考(山东理))一空间几何体的三视图如图所示,则该几何体的体积为( )A .2ππ2π D .4π+侧(左)视图正(主)视图俯视图29.(山东省日照市2013届高三12月份阶段训练数学(理)试题)如右图,某几何体的主视图与左视图都是边长为1的正方形,且体积为12,则该几何体的俯视图可以是30.(山东省烟台市2013届高三3月诊断性测试数学理试题)如右图,某几何体的三视图均为边长为l 的正方形,则该几何体的体积是( )A .65B .32 C .1 D .21 31.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )A .1B .2C .3D .4 32.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)如图所示是一几何体的三视图,则该几何体外接球的表面积为 ( ) A .3π B .4π C .8π D .9π二、填空题 33.(山东省凤城高中2013届高三4月模拟检测数学理试题 )已知某几何体的三视图如图所示,其中正视图中半圆的直径为2,则该几何体的体积为____.34.(山东省文登市2013届高三3月二轮模拟考试数学(理))如图,已知球O 的面上有四点,,,A B C D ,DA ⊥平面ABC ,AB BC ⊥,2DA AB BC ===,则球O 的体积与表面积的比为__________.35.(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)已知矩形ABCD 的顶点都在半径为5的球O 的球面上,且8,23AB BC ==,则棱锥O ABCD -的体积为______. 36.(2012年山东理)(14)如图,正方体ABCD-A 1B 1C 1D 1的棱长为1,E,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1-EDF 的体积为____________.37.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )从如图所示的长方形区域内任取一个点M(x,y),则点M取自阴影部分的概率为 ____________;38.(山东省济南市2013届高三4月巩固性训练数学(理)试题)已知某几何体的三视图如图所示,则该几何体的体积为_________.39.(山东省德州市2013届高三3月模拟检测理科数学)一空间几何体的三视图如图所示,该几何体的体积为16π,则图中x的值为_______________.40.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)一个几何体的三视图如图所示,则这个几何体的表面积与其外接球面积之比为________.41.(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)一个几何体的三视图如右图所示,则该几何体的表面积为__________.42.(山东济南外国语学校2012—2013学年度第一学期高三质量检测数学试题(理科))一个几何体的三视图如图所示(单位:m),则该几何体的体积为__________________3m.正视图 侧视图俯视图山东省2014届理科数学一轮复习试题选编25:空间几何体的三视图、表面积与体积参考答案一、选择题1. D2. 【答案】D 由正视图和俯视图可知,该几何体可能是四棱柱或者是水平放置的三棱柱,或水平放置的圆柱.由图象可知四棱柱的体积最大.四棱柱的高为1,底面边长分别为1,3,所以表面积为2(131131)14⨯+⨯+⨯=,选D.3. A4. 【答案】A 由几何体的三视图,知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半. 长方体的中445EH HG GK ===,,,所以长方体的表面积为(去掉一个上底面)2(4445)45=92⨯+⨯+⨯.半圆柱的两个底面积为22=4ππ⨯,半圆柱的侧面积为25=10ππ⨯⨯,所以整个组合体的表面积为92+410=92+14πππ+,选A. . 5. C6. 【答案】C 由三视图可知该平行六面体的底面是个矩形,两个侧面和底面垂直.其中侧棱12AA =.底面边长3AD =,平行六面体的高为3.2BE =,又2222112(3)1AE AA A E =-=-=,所以123AB =+=.所以平行六面体的表面积为2(333332)=3063⨯+⨯+⨯+,选 C.7. B8. B 【解析】结合三视图可知该几何体是一个圆台,其上,下底面的半径分别为2,1,其直观图如图所示.则该几何的侧面积⨯=2(πS π12)414=⨯+.9. 【答案】A【解析】由三视图可知,该几何体是四棱锥,底面为边长为1的正方形,高为1的四棱锥,所以体积为1111133⨯⨯⨯=,选A. 10. B11. 【答案】B由三视图可知,该几何体是一个放到的四棱锥,其中四棱锥的底面是主视图,为直角梯形,直角梯形的上底为1,下底为4,高为 4.棱锥的高位4,所以四棱锥的体积为1144044323+⨯⨯⨯=,选 B.12. 【答案】B 由三视图可知,该几何体是四棱锥,以俯视图为底,高为1,俯视图的面积为11=1⨯,使用四棱锥的体积为111133⨯⨯=,选B. 13. 【答案】B 【解析】由三视图可知,该几何体上面是个圆锥,下面是个长方体.长方体的底面是边长为3的正方形,高为4,所以长方体的表面积(去掉上下两个底面)为24(34)=48()m ⨯⨯.圆锥的底面半径为3,母线为5,所以圆锥的侧面积为2351545()m ππ⨯⨯==,底面积(去掉一个正方形)为29339918()m ππ-⨯=-=,所以该几何体的总面积为2484518111()m ++=,所以共需油漆0.211122.2⨯=公斤,选B.14. A15. A.【解析】由已知俯视图是矩形,则该几何体为一个三棱柱,根据三视图的性质,俯视图的矩形宽为由面积4,则1+2=24+2S S S =⨯⨯⨯⨯侧底()2 =2820+.16. 【答案】A 由三视图可知,该几何体是一挖去12半球的球.其中两个半圆的面积为224ππ⨯=.34个球的表面积为2342124ππ⨯⨯=,所以这个几何体的表面积是12416πππ+=,选A. 17. 【答案】D由三视图可知,该几何体时底面是矩形的四棱柱,以俯视图为底,底面直角梯形的上底为4,下底为5,高为3.棱柱的高为4,所以四棱柱的体积为34534542cm +⨯⨯=,选D. 18. C19.解析:①②③均是正确的,只需①底面是等腰直角三角形的直四棱柱, 让其直角三角形直角边对应的一个侧面平卧;②直四棱柱的两个侧面是正方形或一正四棱柱平躺;③圆柱平躺即可使得三个命题为真,答案选A.20. 【答案】C【 解析】若俯视图为C,则俯视图的宽和左视图的宽长度不同,所以俯视图不可能是C.21. 【答案】D【解析】该几何体的直观图如图1所示,它是有一条侧棱垂直于底面的四棱锥.其中底面ABCD 是边长为4的正方形,高为CC 1=4,该几何体的所有顶点在同一球面上,则球的直径为12AC R ==,所以球的半径为R =所以球的表面积是224448R πππ=⨯=,选D.22. 【答案】D 由三视图可知,该几何体时一个侧面和底面垂直的的三棱锥,,其中底面三角形BAC 为直径三角形,PA ABC ⊥,2AB =,4PC =,设,04AC x x =<<,则PA ==,所以三棱锥的体积为111168232363x ⨯⨯=≤==,当且仅当x =即28,x x ===,此时体积有最大值82233=,所以该三棱锥的体积不可能是3,选D.23. C 【解析】由三视图可知,该几何体是一个四棱锥,四棱锥的高为4,底面为俯视图对应的矩形,俯视图的面积为2612⨯=,所以四棱锥的体积为1124163⨯⨯=,选C.24. 【答案】C 【解析】由三视图可知,该几何体是一个直三棱柱,三棱柱的底面是一个腰长为2,底面上的高是1的等腰三角形,侧棱长是3,所以该几何体的表面积为1213(22122⨯⨯+++=+,选C. 25. A 【解析】由三视图可知该几何体是一个长方体去掉一个半圆柱.长方体的长宽高分别为3,2,4.所以长方体的体积为32424⨯⨯=.半圆柱的高为3,所以半圆柱的体积为13322ππ⨯⨯=,所以几何体的体积为3242π-,选A. 26. A27. 【答案】D【解析】由正视图可知,此三棱柱的侧视图为,高为2,宽为3的矩形,所以面积为32,选D. 28. 【解析】:该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为2π,四棱锥的底面边长为2,高为3,所以体积为213⨯=所以该几何体的体积为2π. 答案:C 29. C 【解析】若俯视图为A,则该几何体为边长为1的正方体,体积为1,不成立.若俯视图为B,则该几何体为圆柱,体积为21()124ππ⨯=,不成立.若俯视图为C,则该几何体为三棱柱,体积为1111122⨯⨯⨯=,成立.若俯视图为D,则该几何体为14圆柱,体积为211144ππ⨯⨯=,不成立.所以只有C 成立,所以选C. 30. 【答案】A 由题意三视图对应的几何体如图所示, 所以几何体的体积为正方体的体积减去一个三棱锥的体积,即31151111326-⨯⨯⨯⨯=,选 A.31. 【答案】B 由题设及图知,此几何体为一个四棱锥,其底面为一个对角线长为2的正方形,故其底面积为141122⨯⨯⨯=.由三视图知其中一个侧棱为棱锥的高,其相对的侧棱与高及底面正方形的对角线组对角线长为2,3==.此棱锥的体积为12323⨯⨯=,选B.32. D二、填空题 33. 324π-34.35. 【答案】球心在矩形的射影为矩形对角线的交点上.所以对角线长为=,所以棱锥的高为=,所以棱锥的体积为183⨯=. 36.解析:61112113111=⨯⨯⨯⨯==--DE D F EDF D V V . 37. 31 38. 4163π+ 39. 【答案】3由三视图可知,该几何体下面是个圆柱,上面是个四棱锥.圆柱的体积为4416ππ⨯=,四棱锥的底面积为14482⨯⨯=,所以四棱锥的体积为18833h h ⨯⨯=,所以816163h ππ=+,所以四棱锥的高h =所以2222549x h =+=+=,即3x =.40.π3 41. 242π+ 【解析】由三视图可知,该组合体下部是底面边长为2,高为3的正四棱柱,上部是半径为2的半球,所以它的表面积为224322221224πππ⨯⨯+⨯+⨯=+.42. 4 【解析】由三视图可知,该组合体是由两个边长分别为2,1,1和1,1,2的两个长方体,所以体积之和为2111124⨯⨯+⨯⨯=。
三视图求体积面积学习资料

21.已知过球面上 A, B,C 三点的截面和球心的距离等于球半径的一半,且
AB BC CA 2 ,则球面积是( )
A. 16 9
B. 8 3
C. 64 9
D. 4
22.已知某空间几何体的三视图如图所示,则该几何体的体积是 ( )
A. 16 B. 32 C. 48 D. 144
23.某几何体的三视图如图所示,则其体积为( )
章算术》中,将底面是直角形的直三棱柱称之为“堑堵” ,已知某“堑堵”的
三视图如图所示,俯视图中虚线平分矩形的面积,则该 “堑堵”的侧面积为
()
A. 2 B. 4 2 2 C. 4 4 2 D. 4 6 2 30.已知一个几何体的三视图如图所示,则该几何体的体积为( )
精品文档
精品文档
A. 32 3
A. 8 B. 16 2 C. 10 D. 6 2 4.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为 1 的正方 形,则此四面体的外接球的体积为
精品文档
精品文档
A. 4
B. 3
C. 3
D.
3
2
5.若一个正四面体的表面积为 S1 ,其内切球的表面积为 S2 ,则
S1 S2
(
)
A. 6
A.
B.
C.
D.
36.如图,网格纸上小正方形的边长为 ,粗实线画出的是某几何体的三视图,若该几
精品文档
精品文档
A.
B.
C.
D.
34.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某
“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
A. 2 B. 4 C.
D.
专题由三视图求表面积和体积

由三视图求表面积与体积一、方法与技巧1.(括如下: 二(1)梭柱:两矩形和一多边形; —(2)棱锥:两三角形和一多边形; |_ (3)梭台:两梯形和两多边形(多 n 边形相似且顶点相连);—(4)圆柱:两矩形和一圆;(5)圆锥:两三角形和一个带有圆心的圆;务(6)圆台:两梯形和两同心圆;A.60 (7)球:三个大小相等的圆.【解1•技巧:根据几何体的三视图想 心;象其直观图时,可以从熟知的某 •故选一视图出发,想象出朮观图,再验2. 证其他視图是否正确.图如图P 视图知,三棱锥一条侧枝与底面垂克,结合其直观图判断三视图 的数据在克观图中对应的几何童. 解法阐释二:将三视图还原成直 观图是解决该类问题的关键•其 解题技巧是熟练学握一些简单几 何体的三视图,想象该几何体的 构成,或将三个方向获得的信息 综合,绘制儿何图形,然后检验其 三视图是否与已知相符合•确保 无误后再进行计算. 提醒:以三视图为栽体考查几何 体的表面积、体积,关键是能够对 给出的三视图进行恰当的分析, 小图所示从三视图中发现几何体中务元素A 的三视图也不一致. 【解答】解:由三视图可知,该几何体为放到得直四棱柱,且中间挖去半个圆柱,由三视图中得数据可得:四棱柱得高为3,底而为等腰梯形,梯形得上、下底边分别为2、4,高为2, 圆柱得高为3,圆柱底面得半径都就是1,几何体得体积V==,故选:B.4. (2016・广元二模)一个多而体得三视图分别就是正方形.等腰三角形与矩形,其尺寸如图,则该多而体得体积为()A. 4 8cm'B.2 4cm*C 。
32cm»D ・28cm'二、提醒:简单几何体的三视图可概 4.技巧:本題中根据正视图和侧2.技巧:根据几何体的直观图想 A 6 ;解 象其三视图时,若几何体是某一 其底熟悉的几何图形通过分割形成 故棱 的,可以将几何体还原后求解. 故选3.技巧:同一几何体的三视图,由 3,(2°于几何体放置位置不同,几何体间的位置关系及数量关系. :以俯视图为底面得四棱锥 ,图如图所示,则该几何体得体积为()I 而向下) ,4,斜【解答】解:由三视图可知该几何体就是平放得直三棱柱,高为4,底面三角形一边长为6,此边上得髙为4 体积V=S h == 4 8cnr故选A5. (20 1 6<江门模拟)一个几何体得三视图及其尺寸如下,则该几何体得表而积为()A. 12n B .1 5 H C. 24n D.36n【解答】解:由三视图可知该几何体为一个圆锥,底而直径为6,母线长为5, 底而圆得而积s i=nx () 2=9n・侧面积S 2=nx3x5=15n,表面积为S I+S?=24TI.故选C.6. (2016•安康二模)一空间几何体得三视图如图所示,则该几何体得体积为()Ao oBeCo D.【解答】解:三视图复原得几何体就是三棱锥,底面就是底边长为2,髙为2得等腰三角形,三棱锥得一条侧棱垂直底而,高为2。
三视图体积面积计算学生版汇总

高一直观图三视图及体积面积计算学校:___________姓名:___________班级:___________考号:___________一、选择题1.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为2.如图为某几何体的三视图,根据三视图可以判断这个几何体为()A.圆锥 B.三棱锥C.三棱柱 D.三棱台3.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是()4.如图所示,正方形O′A′B′C′的边长为1,它是水平放置的一个平面图形的直观图,则原图形的周长是()A.6 B.8 C.2+.2+5.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是()6.一个四面体的三视图如图所示,则该四面体的表面积是A .1+.2.1+.7.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A .18B .17C .16D .158.一个几何体的三视图如图所示,则该几何体的体积是( )A .64B .72C .80D .1129.已知某几何体的三视图如右图所示,则该几何体的外接球表面积为( )A .83πB .32πC .8πD . 10.一个几何体的三视图如图,则该几何体的体积为( )A .πB .2π C .3π D .6π 11. 三棱锥S ABC 及其三视图中的正视图和侧视图如图所示,则棱SB 的长为( )A .B .C .D .12.已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为 ( )A B 13.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是 ( )A .2B .4C .6D .12 14.一个棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是( )A 、13 B 、2 C 、3 D 、615.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为( )A .24-32π B .24-3π C .24-π D .24-2π16.一个体积为A .36B .8C .38D .1217.已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是( )A .31cm B .32cm C .33cm D .36cm 18.已知几何体的三视图(如图),则该几何体的体积为 ( )A .34 B .4 C .324 D .334 19.如图是一个四棱锥的三视图,则该几何体的体积为( )(A )403 (B )323 (C )163 (D )28320.已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( )A .108cm 3B .100 cm 3C .92cm 3D .84cm 321.一个几何体的三视图如图所示,已知这个几何体的体积为h =( )A.2B..22.某几何体的三视图如图所示,则它的体积是A .283π-B .83π-C .82π-D .23π 23.如图是正方体的平面展开图,则在这个正方体中N MFE DCB A①BM 与ED 平行②CN 与BE 是异面直线 ③CN 与BM 成︒60角 ④DM 与BN 是异面直线以上四个结论中,正确结论的序号是( )A .①②③B .②④C .③④D .①③④ 24.(2014•未央区二模)已知三棱锥的正视图与俯视图如图,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )A. B. C.D.二、填空题25.水平放置的某三角形的直观图是直角边为2的等腰直角三角形,如图,则原三角形的面积是.26.三棱柱的三视图如图所示,则该棱柱的体积等于.27.已知某几何体的三视图如右,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 cm3.m 28.设某几何体的三视图如下(尺寸的长度单位为m)则该几何体的体积为________329.如图是某几何体的三视图(单位:cm),则该几何体的表面积是__ ___cm2,体积为_ __ cm3.30.如图,网格纸上正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为.31.某三棱锥的主视图与俯视图如图所示,则其左视图的面积为___________.32.某几何体的三视图(单位:cm )如图所示,则该几何体最长棱的棱长为 cm .33.一个几何体的三视图如图所示,其中正视图中ABC 是边长为2的正三角形,俯视图为正六边形,那么该几何体的表面积为________________ .34.下图是一个几何体的三视图,根据图中数据可得 该几何体的表面积是_________;正(主)视图俯视图侧(左)视图三、解答题35.一个多面体的直观图及三视图如图所示,其中M ,N 分别是AF、BC 的中点(1)求证:MN∥平面CDEF;(2)求多面体A-CDEF的体积.36.如图,某多面体的直观图及三视图如图所示: E,F分别为PC,BD的中点(1)求证:PADEF平面//(2)求证:PADPDC平面平面(3)求此多面体的体积PCEFD1正视图侧视图俯视图。
三视图求体积面积

三视图求体积面积三视图求表面积体积1.一个三棱锥的三视图如下图所示,则该几何体的体积为A. 1B. 433 C. 2 D. 8332.一个三棱锥的三视图是三个直角三角形,如图所示,则该三棱锥的外接球表面积为()A. 30πB. 29πC. 292π D. 216π3.某四棱锥的三视图如图所示,该四棱锥的侧面积为A. 72πB. 4πC. 92πD. 5π9.某四棱锥的三视图如图所示,俯视图是一个等腰直角三角形,则该四棱锥的体积是( )A. 43B. 2323 D. 8310.某一简单几何体的三视图如图所示,该几何体的外接球的表面积是( )A. 13πB. 16πC. 25πD. 27π 11.一个几何体的三视图如图所示,该几何体的体积为( )A. 24π-B. 243π-C. 483π-D. 883π- 12.一个几何体的三视图如图所示,则该几何体的体积为( )A. 342 C. 44313.某几何体的三视图如图所示, 则其体积为( )3π B. 6π 3π3π14.三棱锥A BCD -内接于半径为2的球O , BC 过球心O ,当三棱锥A BCD -体积取得最大值时,三棱锥A BCD -的表面积为A. 643+B. 823+C. 463+D. 843+15.一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )A. 196B. 383C. 578D. 193 16.一个四面体的三视图如图所示,则该四面体的外接球的表面积为( )A. 43πB. 4πC. 23πD. 2π17.某棱锥的三视图如图所示,则该棱锥的外接球的表面积为( )A. πB. 2πC. 3πD. 4π18.一个几何体的三视图如图所示(其中正视图的弧线为四分之一圆周),则该几何体的表面积为()A. 726π+ C. 486π+ D.+ B. 724π+484π19.某几何体的三视图如图所示(在如图的网格线中,每个小正方形的边长为1),则该几何体的表面积为()A. 48B. 54C. 64D. 6020.某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则三棱锥的体积为A. 32B. 3277 D. 647 21.已知过球面上,,A B C三点的截面和球心的距离等于球半径的一半,且===,则球面积是()AB BC CA2A. 16π B. 83π C. 649π D. 4π922.已知某空间几何体的三视图如图所示,则该几何体的体积是()A. 16B. 32C. 48D. 14423.某几何体的三视图如图所示,则其体积为()A. 8B. 10C. 12D. 14 24.如图为某几何体的三视图,求该几何体的内切球的表面积为( )A. 4π B. 3π C. 4π D. 43π25.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )A. 25+B. 225+45 D. 526.如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )3 B. 3π43 D. 83π27.某几何体的三视图如图所示,则刻几何体的体积为()A. 23B. 43C. 53D. 7328.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( )A. 163πB. 3πC. 29πD. 169π29.(数学(文)卷·2017届福建省莆田六中高三上学期第二次月考第9题)《九章算术》中,将底面是直角形的直三棱柱称之为“堑堵” ,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该 “堑堵”的侧面积为( )A. 2B. 422+C. 442+D. 462+ 30.已知一个几何体的三视图如图所示,则该几何体的体积为( )A. 323 B. 163 C. 83 D. 4331.某几何体的三视图如图所示,则该几何体的体积为A. 883π+ B. 1683π+ C. 8163π+ D. 16163π+32.某几何体的三视图如图所示,则该几何体的体积为( )A. 2B. 1C. 13D. 16A. √2B. √3C. 2√3D. 4√3334.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为()A. 2B. 4C. 4+4√2D. 6+4√2 35.如图,在正方形网格纸上,粗实线画出的是某多面体的三视图及其部分尺寸.若该多面体的顶点在同一球面上,则该球的表面积等于()A. 8πB. 18πC. 24πD. 8√6π36.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为()A. 50πB. 25πC. 75πD. 100π参考答案1.C【解析】由三视图可得到如图所示几何体,该几何体是由正方体切割得到的,利用传统法或空间向量法可求得三棱锥的高为该几何体的体积为(21234⨯=.点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.2.B【解析】由三视图所提供的图形和数据可知:该几何体是一个底面是两直角边分别为2,4直角三角形,高为3的三棱锥,则其外接球的直径为d2429S ππ=⨯=⎝⎭,应选答案B。
由三视图确定几何体的面积或体积

2
HOMEWORK PRACTICE
练一练
1、学会根据物体的三视图描述出几何体的基本形状或实物原型,并计算表面积或
体积。
2、经历探索简单的几何体活动,培养动手实践能力,发展学生逆向思维能力。
02
练一练
根据物体的三视图描述物体的形状.
02
练一练
1.如图,是由一些棱长为1cm的小正方体构成的立体图形的三种视图,那么
3.在水平面内得到的由左向右观察物体
的视图,叫做左视图。
俯视图
左
视
图
01
三视图知识点回顾
将三个投影面展开在一个平面内,
得到这个物体的一张三视图.
主视图
高
投影规则:
主俯长对正、主左高平齐、俯左宽相等
长
左视图和俯视图的宽要相等。
宽
宽
即:主视图和俯视图的长要相等
主视图和左视图的高要相等
左视图
俯视图
01
01
三视图知识点回顾
我们用三个互相垂直的平面(例如:墙角处的三面墙面)作为投影面,
其中正对着我们的叫正面,正面下方的叫水平面,右边的叫做侧面.
对于一个物体(例如一个正方体)在三
个投影面内进行正投影,
1.在正面内得到的由前向后观察物体的
视图,叫主视图。
主视图
正面
2.在水平面内得到的由上向下观察物
体的视图,叫做俯视图。
定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
100mm
50mm
50mm
由展开图可知,密封罐由两个正六边形和6个正方形组成。
01
利用三视图计算实物面积
专训2根据物体的三视图计算其表面积和体积

∴AE= AB=3 cm,EG= CD=2 cm,
∴AG=AE-EG=3-2=1(cm).
在Rt△ACG中,
AC=
(cm).
∵CD∥AB,∴△OCD∽△OAB.
∴
,即
.
解得OF=10 cm.∴OE=OF+EF=10+5=15(cm).
由
,得OC=2AC=2 cm.
∴OA= OC=3 cm. ∴手电筒圆台部分的表面积为S1=π×
专训2根据物体的三视图 计算其表面积和体积
2020/9/3
在实际问题中,常常要求根据物体的三视图和尺 寸计算物体的表面积或体积.解决此类题型的方法是 先由三视图想象出几何体的形状,再根据图中的尺寸 利用相应的公式进行计算.
训练角度 1 利用三视图求几何体的表面积
1.如图是一个几何体的三视图. (1)写出此几何体的名称; (2)求此几何体的表面积S.
解:(1)圆锥. (2)由题图可知,圆锥高为8 cm,底面直径为12 cm, 易求得母线长为10 cm. ∴S=πr2+πrl=36π+60π=96π(cm2).
2.(1)图①是一个组合体,图②是它的两种视图,请在 横线上填写出两种视图的名称;
(2)根据两种视图中的尺寸(单位:cm),计算这个组 合体的表面积.(π取3.14)
解:(1)主;俯 (2)表面积=2×(11×7+ 11×2+7×2)+4×π× 6≈301.36(cm2).
(1)找到从正面和上面看所得到的图形即可得答 案.(2)根据题目所给尺寸,计算出下面长方体 的表面积+上面圆柱的侧面积即可得解.
训练角度 2 利用三视图求几何体的体积
3.某糖果厂想要为儿童设计一种新型的装糖果的不 倒翁,请你根据包装厂设计好的三视图(如图)的尺 寸计算其容积.(球的体积公式:V= πr3)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一直观图三视图及体积面积计算学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为
2.如图为某几何体的三视图,根据三视图可以判断这个几何体为()
A.圆锥 B.三棱锥
C.三棱柱 D.三棱台
3.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是()
4.如图所示,正方形O′A′B′C′的边长为1,它是水平放置的一个平面图形的直观图,则原图形的周长是()
A.6 B.8 C.2+.2+
5.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是()
6.一个四面体的三视图如图所示,则该四面体的表面积是
A .1+.2.1+.7.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
A .18
B .17
C .16
D .15
8.一个几何体的三视图如图所示,则该几何体的体积是( )
A .64
B .72
C .80
D .112
9.已知某几何体的三视图如右图所示,则该几何体的外接球表面积为( )
A .
83
π
B .32π
C .8π
D . 10.一个几何体的三视图如图,则该几何体的体积为( )
A .π
B .
2π C .3π D .6
π 11. 三棱锥S ABC 及其三视图中的正视图和侧视图如图所示,则棱SB 的长为( )
A .
B .
C .
D .
12.已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图
的面积为 ( )
A B 13.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是 ( )
A .2
B .4
C .6
D .12 14.一个棱锥的三视图如图所示,其中侧视图为正三角形,则该四棱锥的体积是( )
A 、
13 B 、2 C 、3 D 、6
15.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为( )
A .24-
32π B .24-3π C .24-π D .24-2
π
16.一个体积为
A .36
B .8
C .38
D .12
17.已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是( )
A .3
1cm B .3
2cm C .33cm D .3
6cm 18.已知几何体的三视图(如图),则该几何体的体积为 ( )
A .
34 B .4 C .324 D .3
3
4 19.如图是一个四棱锥的三视图,则该几何体的体积为( )
(A )
403 (B )323 (C )163 (D )28
3
20.已知某几何体的三视图(单位:cm )如图所示,则该几何体的体积是( )
A .108cm 3
B .100 cm 3
C .92cm 3
D .84cm 3
21
.一个几何体的三视图如图所示,已知这个几何体的体积为h =( )
A
.
2
B
.
.22.某几何体的三视图如图所示,则它的体积是
A .283π-
B .83π-
C .82π-
D .23
π 23.如图是正方体的平面展开图,则在这个正方体中
N M
F
E D
C
B A
①BM 与ED 平行
②CN 与BE 是异面直线 ③CN 与BM 成︒60角 ④DM 与BN 是异面直线
以上四个结论中,正确结论的序号是( )
A .①②③
B .②④
C .③④
D .①③④ 24.(2014•未央区二模)已知三棱锥的正视图与俯视图如图,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )
A. B. C.
D.
二、填空题
25.水平放置的某三角形的直观图是直角边为2的等腰直角三角形,如图,则原三角形的面积是.
26.三棱柱的三视图如图所示,则该棱柱的体积等于.
27.已知某几何体的三视图如右,根据图中标出的尺寸(单位:cm),可得这个几何体
的体积是 cm3.
m 28.设某几何体的三视图如下(尺寸的长度单位为m)则该几何体的体积为________3
29.如图是某几何体的三视图(单位:cm),则该几何体的表面积是__ ___cm2,体积为_ __ cm3.
30.如图,网格纸上正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的
各条棱中,最长的棱的长度为.
31.某三棱锥的主视图与俯视图如图所示,则其左视图的面积为___________.
32.某几何体的三视图(单位:cm )如图所示,则该几何体最长棱的棱长为 cm .
33.一个几何体的三视图如图所示,其中正视图中ABC 是边长为2的正三角形,俯视图为正六边形,那么该几何体的表面积为________________ .
34.下图是一个几何体的三视图,根据图中数据可得 该几何体的表面积是_________;
正(主)视图
俯视图
侧(左)视图
三、解答题
35.一个多面体的直观图及三视图如图所示,其中M ,N 分别是AF、BC 的中点
(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
36.如图,某多面体的直观图及三视图如图所示: E,F分别为PC,BD的中点(1)求证:PAD
EF平面
//
(2)求证:PAD
PDC平面
平面
(3)求此多面体的体积
P
C
E
F
D
1
正视图
侧视图
俯视图。
