2010年全国高中数学联赛福建赛区_5
2010福建省高考理科数学试卷及答案(文字版)

2010年普通高等学校招生全国统一考试(福建卷)数 学(理工农医类)第I 卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.计算sin 043cos 013-cos 043sin 013的结果等于A.12B.C.2 2.以抛物线24y χ=的焦点为圆心,且过坐标原点的圆的方程为A.2220y χχ++=B.220y χχ++=C.220y χχ+-=D.2220y χχ+-=3.设等差数列{}n a 的前n 项和为n s 。
若111a =-,466a a +=-,则当ns 取最小值时,n 等于A.6B.7C.8D.94.函数223,021,0(){n f χχχχχχ+-≤-+>=,的零点个数为 A.0 B.1 C.2 D.35.阅读右图所示的程序框图,运行相应的程序,输出的i 值等于A.2B.3C.4D.56.如图,若Ω是长方体ABCD-1111A B C D 被平面EFCH 截去几何体EFCH 11B C 后得到的几何体,其中E 为线段11A B 上异于1B 的点,F 为线段1BB 上异于1B 的点,且EH//11A D ,则下列结论中不正确...的是A.EH//FGB.四边开EFGH 是矩形C.Ω是棱柱D.Ω是棱台 7.若点O 和点F (-2,0)分别为双曲线()22210y a a χ-=>的中心和左焦点,点P 为双曲线右支上的任产电一点,则OP FP ⋅的取值范围为A.3⎡-⎣B.3⎡+⎣C.7,4⎡⎤-+∞⎢⎥⎣⎦D.7,4⎡⎤+∞⎢⎥⎣⎦8.设不等式组1,230χχγγχ≥⎧⎪-+≥⎨⎪≥⎩,所表示的平面区域是1Ω,平面区域2Ω与1Ω关于直线3490χγ+-=对称,对于1Ω中的任意A 与2Ω中的任意点B ,||AB 的最小值等于A.285B.4C. 125D.2 9.对于复数..a,b,c,d ,若集合{,,,}S a b c d =具有性质“对任意χ,S γ∈,必有S χγ∈”,则当221,1a b c b =⎧⎪=⎨⎪=⎩时,b c d ++等于A.1B.-1C.0D.i10.对于具有相同定义域D 的函数()f χ和()g χ,若存在函数()h k b χχ=+(,k b 为常数),对任给的正数m ,存在相应的0D χ∈,使得当D χ∈且0χχ>时,总有0()()0()()f h m h g m χχχχ<-<⎧⎨<-<⎩则称直线l:y =k χ+b 为曲线()y f χ=与()y g χ=的“分渐近线”。
福建省各地市2010年高考数学最新联考试题分类大汇编数列

A. 28
B. 33
C. 1 33
D. 1 28
12.( 福建省石狮石光华侨联合中学 2010 届高中毕业班 5 月份高考模拟文科 ) 若数列 a1, a2 , a3 , , a n, 是
公差不为零的等差数列,且 an 0 ,则下列四个数列
① lg a1, lg a2 , , lg an , ;
② 2 a1 ,2 a2 , ,2 an , ;
12 分)已知数列 { a n} 为等差
数列,且 a1 1 . {bn } 为等比数列,数列 { an bn } 的前三项依次为 3, 7,13。求
(1)数列 { a n } , { bn} 的通项公式; (2)数列 { an bn} 的前 n 项和 Sn 。
15.பைடு நூலகம்(本题12分) 解:①设公差为 d ,公比为 q
a2 , a3 ,…, an ,使得 k ak ( k =1,2, …, n )都是完全平方数,则称 n 为“好数”。若 n 分别取 4,5 ,
6,则这三个数中, “好数”的个数是(
)
A. 3
B. 2
C. 1 D . 0
3. ( 福建省龙岩市 2010 年高中毕业班第一次质量检查文) 已知等差数列 { a n}中, a2 a8 16, a4 1, 则 a6
18.(本小题满分 12 分)
解:( I ) a1 S1 3
…………………… 2 分
当 n 2时 , an Sn Sn 1 n 2 2n [( n 1)2 2(n 1)]
2n 1 ……………… 4 分
符合 n 1情况 , 所以 an
2n 1,(n
*
N)
……………… 6 分
( II )设等比数列 { bn} 的公比为 q,
2010年全国高中数学联赛福建赛区
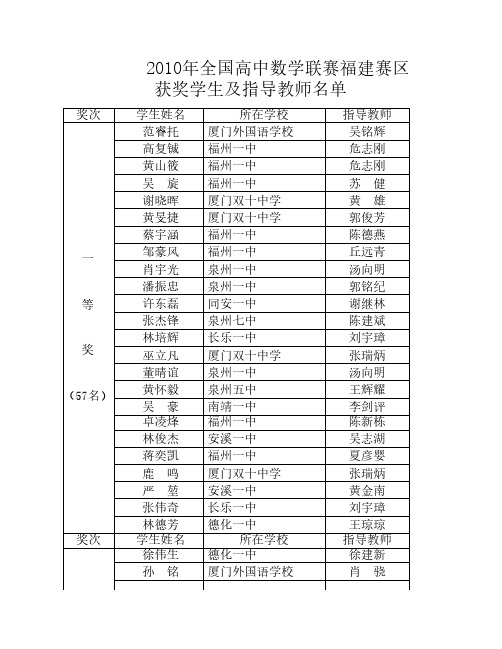
2010年全国高中数学联赛福建赛区获奖学生及指导教师名单奖次学生姓名所在学校指导教师 一等奖(57名)范睿托厦门外国语学校吴铭辉高复铖福州一中危志刚黄山筱福州一中危志刚吴 旋福州一中苏 健谢晓晖厦门双十中学黄 雄黄旻捷厦门双十中学郭俊芳蔡宇涵福州一中陈德燕邹豪风福州一中丘远青肖宇光泉州一中汤向明潘振忠泉州一中郭铭纪许东磊同安一中谢继林张杰锋泉州七中陈建斌林培辉长乐一中刘宇璋巫立凡厦门双十中学张瑞炳董晴谊泉州一中汤向明黄怀毅泉州五中王辉耀吴 豪南靖一中李剑评卓凌烽福州一中陈新栋林俊杰安溪一中吴志湖蒋奕凯福州一中夏彦婴鹿 鸣厦门双十中学张瑞炳严 堃安溪一中黄金南张伟奇长乐一中刘宇璋林德芳德化一中王琼琼奖次学生姓名所在学校指导教师徐伟生德化一中徐建新孙 铭厦门外国语学校肖 骁一等奖(57名)许有疆德化一中陈丽真杨 震莆田一中肖志强郑刘悦福州三中郑文祺陈恩俊莆田一中肖志强黄永招德化一中徐建新许若男厦门双十中学张瑞炳庄旭航泉州五中黄种生杨 洋福建师大附中林 峰何承玮福州三中张 军王经纬福安一中池水平陈若明厦门外国语学校吴铭辉林梦翔福州一中陈新栋林宇哲福州一中龚梅勇陈从翔连江一中陈志坚王文彬云霄立人学校林耀东谢 钧厦门双十中学张瑞炳张华林龙岩二中郭小峰陈水挺同安一中谢继林董张帆福州一中夏彦婴曾 林仙游一中陈凤龙陈彦哲厦门双十中学黄 雄林晨超福州一中苏 健林 煌福州一中危志刚曾祥桓平和正兴学校叶连雄周培聪厦门双十中学张瑞炳蔡期塬泉州五中庄晓玲奖次学生姓名所在学校指导教师一等奖蓝 捷上杭一中林文柱刘鸿辉厦门双十中学黄 雄黄国快晋江养正中学许贻旺陈振雄晋江季延中学陈 浩(57名)王 陶厦门双十中学张瑞炳 二等奖(45名)金 迪厦门双十中学黄 雄吴志煌晋江季延中学林笃锦张荣燊泉州五中黄种生曾大通惠安一中陈荣桂张志荣平和正兴学校叶连雄陈少峰晋江季延中学林笃锦胡丽婷福州一中吴 威张煜乾邵武一中高启长林一吾福州一中苏 健吴姗姗泉州五中王辉耀朱有基福鼎一中吴建文黄哲轩厦门双十中学黄 雄张昕玮厦门双十中学张瑞炳陈 隽永定一中包 喜柯佳鑫龙海一中洪小娇陈星炜长乐一中邱宇元许东南安溪一中吴志湖韩 超厦门双十中学张瑞炳洪少群晋江季延中学林笃锦郑启明南安一中廖国凤陈冠群莆田二中陈金亮廖世昌安溪一中黄金南刘必旭福州一中夏彦婴奖次学生姓名所在学校指导教师张剑华德化一中陈修周周 晔泉州五中黄种生曾嘉浩厦门双十中学张瑞炳郑喆斌莆田五中郑毓青傅家庆南安一中卓永宁林艺彬福州三中林 风 二等奖(45名)游志雄仙游私立一中李志明黄思荣龙海一中叶立平林 杰漳州一中李两火刘文章泉州七中林志敏肖跃坚安溪一中黄金南庄晨帆厦门双十中学张瑞炳庄佳威厦门外国语学校肖 骁胡致远厦门双十中学陈兆坚陈荔伟莆田二中林 伟陈 晓莆田一中林清利高扬乐平潭一中林玉生蒋家鑫泉州五中董少田赖 翔漳州一中林良斌李德欣上杭一中林文柱林晓明龙岩一中连亮曦郑细林莆田二中周伟强三等奖(52名)陈达兴泉州五中董少田陈建彬莆田一中苏玉蓉方子原福州一中苏 健林 灯福州一中吴 威林建和漳州一中林良斌施志国福安一中池水平郑昕烨福州一中陈 婷奖次学生姓名所在学校指导教师卓武仪南安一中林建源陈 龙福安一中游明霞黄文瀚福州三中杜重成林金勇同安一中黄献磅潘秋强三明一中李征宇朱晓琳泉州五中王辉耀黄境炀泉州现代中学陈永生三等奖(52名)庄少林晋江养正中学许贻旺蔡锐阳福州一中陈 婷林 森福州一中吴 威林弘杰永春一中李金进林文峰漳州一中林良斌田成锦泉州七中王雄伟涂炼祥龙岩一中连亮曦王施敏福州一中夏彦婴谢崇发龙岩一中连亮曦许灵达晋江养正中学许贻旺颜荣圻厦门双十中学黄 雄黄熹之福州一中王 欣施嘉察晋江养正中学许贻旺曾炜赫漳州一中张兵源高凌斌顺昌一中黄敬平林宇凯福州一中陈 婷张亚能泉州七中陈建彬刘英喆厦门双十中学黄 雄黄 晨莆田一中肖志强刘睿赟武夷山一中江丽华阮梦瑶龙岩一中陈木孙施佳宏福州一中李志勇奖次学生姓名所在学校指导教师三等张振宇仙游一中林宝坚王 薇龙海一中洪小娇郑辉煌仙游一中林宝坚陈正玮莆田二中陈金亮黄楚荧福州一中吴 威黄雅冠惠安一中陈荣桂金光宇厦门外国语学校吴铭辉林毅坤莆田一中肖志强奖杨 磊龙岩一中连亮曦陈正海永定一中包 喜丁晓娟顺昌一中何积仰邱佳霖同安一中谢继林王珍鑫晋江养正中学许贻旺吴 瑨厦门一中王淼生吴俊杰宁化一中赖国强卓 亮福州一中刘 鹏。
2010年福建高考数学(理科)含详细答案

2010年普通高等学校招生全国统一考试(福建卷)数学(理科)第I 卷(选择题 共60分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.cos13计算sin43cos 43 -sin13的值等于( )A.12B.3C.2D. 2【解析】∵sin43°cos13°-cos43°sin13°=sin(43°-13°)=21,∴选A . 【命题意图】本题考查三角函数中两角差的正弦公式以及特殊角的三角函数,考查基础知识,属保分题。
----------------------------------------------------------------------------------------------------------------------2.以抛物线24y x =的焦点为圆心,且过坐标原点的圆的方程为( )A.22x +y +2x=0B. 22x +y +x=0C. 22x +y -x=0D. 22x +y -2x=0【解析】∵由抛物线的方程x y 42=得其焦点坐标为(1,0),∴所求圆的圆心坐标为(1,0),半径为1,圆的方程为()1122=+-y x ,即0222=+-y x x ,故选D. 【命题意图】本题考查抛物线的几何性质以及圆的方程的求法,属基础题。
----------------------------------------------------------------------------------------------------------------------3.设等差数列{}n a 的前n 项和为n S ,若111a =-,466a a +=-,则当n S 取最小值时,n 等于A.6B.7C.8D.9【解析】设等差数列{}n a 的公差为d ,∵62,115641-==+-=a a a a ,∴2,35=-=d a ,∴()()366122211122--=-=⨯-+⨯-=n n n n n n s n .∴当n =6时,n s 有最小值.故选A.【命题意图】本题考查等差数列的通项公式以及前n 项和公式的应用,考查二次函数最值的求法及计算能力。
2010年全国高中数学联赛试题及答案

2010年全国高中数学联合竞赛一试 试题参考答案及评分标准(B 卷)说明:1. 评阅试卷时,请依据本评分标准. 填空题只设8分和0分两档;其他各题的评阅,请严格按照本评分标准的评分档次给分,不要增加其他中间档次.2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,解答题中第9小题4分为一个档次,第10、11小题5分为一个档次,不要增加其他中间档次。
一、填空题(本题满分64分,每小题8分) 1. 函数x x x f 3245)(---=的值域是 ]3,3[-.解:易知)(x f 的定义域是[]8,5,且)(x f 在[]8,5上是增函数,从而可知)(x f 的值域为]3,3[-. 2. 已知函数x x a y sin )3cos (2-=的最小值为3-,则实数a 的取值范围是 1223≤≤-a .解:令t x =sin ,则原函数化为t a att g )3()(2-+-=,即a att g )3()(3-+-=.由 3)3(3-≥-+-t a at , 0)1(3)1(2≥----t t at ,0)3)1()(1(≥-+--t at t 及01≤-t 知03)1(≤-+-t at 即 3)(2-≥+t t a (1)当1,0-=t 时(1)总成立; 对20,102≤+<≤<t t t ; 对041,012<+≤-<<-t t t . 从而可知 1223≤≤-a .3. 双曲线122=-y x 的右半支与直线100=x 围成的区域内部(不含边界)整点(纵横坐标均为整数的点)的个数是 9800 .解:由对称性知,只要先考虑x 轴上方的情况,设)99,,2,1( ==k k y 与双曲线右半支于k A ,交直线100=x 于k B ,则线段k k B A 内部的整点的个数为99k -,从而在x 轴上方区域内部整点的个数为991(99)99494851k k =-=⨯=∑.又x 轴上有98个整点,所以所求整点的个数为 98009848512=+⨯.4. 已知}{n a 是公差不为0的等差数列,}{n b 是等比数列,其中3522113,,1,3b a b a b a ====,且存在常数βα,使得对每一个正整数n 都有βα+=n n b a log ,则=+βα3.解:设}{n a 的公差为}{,n b d 的公比为q ,则 ,3q d =+ (1) 2)43(3q d =+, (2)(1)代入(2)得961292++=+d dd ,求得9,6==q d .从而有 βα+=-+-19log )1(63n n 对一切正整数n 都成立,即 βα+-=-9log )1(36n n 对一切正整数n 都成立.从而 βαα+-=-=9log3,69log,求得 3,33==βα, 333+=+βα.5. 函数)1,0(23)(2≠>-+=a a a a x f xx在区间]1,1[-∈x 上的最大值为8,则它在这个区间上的最小值是 41-.解:令,y a x =则原函数化为23)(2-+=y y y g ,)(y g 在3(,+)2-∞上是递增的.当10<<a 时,],[1-∈a a y ,211m ax 1()32822g y aaa a ---=+-=⇒=⇒=,所以 412213)21()(2min -=-⨯+=y g ;当>a 时,],[1a a y -∈,2823)(2max =⇒=-+=a a a y g ,所以 412232)(12min -=-⨯+=--y g .综上)(x f 在]1,1[-∈x 上的最小值为41-.6. 两人轮流投掷骰子,每人每次投掷两颗,第一个使两颗骰子点数和大于6者为胜,否则轮由另一人投掷.先投掷人的获胜概率是1217.解:同时投掷两颗骰子点数和大于6的概率为1273621=,从而先投掷人的获胜概率为+⨯+⨯+127)125(127)125(1274217121442511127=-⨯=.7. 正三棱柱111C B A ABC -的9条棱长都相等,P 是1CC 的中点,二面角α=--11B P A B ,则=αsin4.解一:如图,以AB 所在直线为x 轴,线段AB 中点O 为原点,OC 所在直线为y 轴,建立空间直角坐标系.设正三棱柱的棱长为2,则)1,3,0(),2,0,1(),2,0,1(),0,0,1(11P A B B -,从而,)1,3,1(),0,0,2(),1,3,1(),2,0,2(1111--=-=-=-=P B A B BP BA .设分别与平面P BA 1、平面P A B 11垂直的向量是),,(111z y x m =、),,(222z y x n =,则 ⎪⎩⎪⎨⎧=++-=⋅=+-=⋅,03,022111111z y x BP m z x BA m ⎪⎩⎪⎨⎧=-+-=⋅=-=⋅,03,022221211z y x P B n x A B n 由此可设 )3,1,0(),1,0,1(==n m ,所以cos m n m n α⋅=⋅,2cos cos 4αα=⇒=.所以 410sin =α.解二:如图,PB PA PC PC ==11, .设B A 1与1AB 交于点,O 则1111,,OA OB OA OB A B AB ==⊥ . 11,,PA PB PO AB =⊥因为 所以从而⊥1AB 平面B PA 1 .过O 在平面B PA 1上作P A OE 1⊥,垂足为E . 连结E B 1,则EO B 1∠为二面角11B P A B --的平面角. 设21=AA ,则易求得3,2,5111=====PO O B O A PA PB .在直角O PA 1∆中,OE P A PO O A ⋅=⋅11, 即 56,532=∴⋅=⋅OE OE .又 554562,222111=+=+=∴=OEO B E B O B .4105542sin sin 111===∠=EB O B EO B α.8. 方程2010=++z y x 满足z y x ≤≤的正整数解(x ,y ,z )的个数是 336675 .解:首先易知2010=++z y x 的正整数解的个数为 1004200922009⨯=C .把2010=++z y x 满足z y x ≤≤的正整数解分为三类:(1)z y x ,,均相等的正整数解的个数显然为1;(2)z y x ,,中有且仅有2个相等的正整数解的个数,易知为1003; (3)设z y x ,,两两均不相等的正整数解为k . 易知 100420096100331⨯=+⨯+k ,OEP1B 1A 1CBA110033*********-⨯-⨯=k200410052006123200910052006-⨯=-⨯+-⨯=, 3356713343351003=-⨯=k . 从而满足z y x ≤≤的正整数解的个数为 33667533567110031=++. 二、解答题(本题满分56分)9.(本小题满分16分)已知函数)0()(23≠+++=a d cx bx ax x f ,当10≤≤x 时,1)(≤'x f ,试求a 的最大值.解一: ,23)(2c bx ax x f ++='由 ⎪⎪⎩⎪⎪⎨⎧++='++='='cb a fc b a f c f 23)1(,43)21(,)0( 得(4分) )21(4)1(2)0(23f f f a '-'+'=. (8分)所以)21(4)1(2)0(23f f f a '-'+'=)21(4)1(2)0(2f f f '+'+'≤8≤, 38≤a . (12分)又易知当m x x x x f ++-=23438)((m 为常数)满足题设条件,所以a 最大值为38.(16分)解二:c bx ax x f ++='23)(2.设1)()(+'=x f x g ,则当10≤≤x 时,2)(0≤≤x g . 设 12-=x z ,则11,21≤≤-+=z z x . 14322343)21()(2++++++=+=c b a z ba z a z g z h . (4分)容易知道当11≤≤-z 时,2)(0,2)(0≤-≤≤≤z h z h . (8分) 从而当11≤≤-z 时,22)()(0≤-+≤z h z h ,即 21434302≤++++≤c b a z a ,从而0143≥+++c b a ,2432≤za ,由 102≤≤z 知38≤a . (12分)又易知当m x x x x f ++-=23438)((m 为常数)满足题设条件,所以a 最大值为38.(16分)10.(本小题满分20分)已知抛物线x y 62=上的两个动点1122(,)(,)A x y B x y 和,其中21x x ≠且421=+x x .线段AB 的垂直平分线与x 轴交于点C ,求ABC ∆面积的最大值.解一:设线段AB 的中点为),(00y x M ,则2,22210210y y y x x x +==+=,1221221212123666y y y yyy y x x y y k AB =+=--=--=.线段AB 的垂直平分线的方程是 )2(300--=-x y y y . (1)易知0,5==y x 是(1)的一个解,所以线段AB 的垂直平分线与x 轴的交点C 为定点,且点C 坐标为)0,5(. (5分)由(1)知直线AB 的方程为 )2(300-=-x y y y ,即 2)(300+-=y y y x . (2)(2)代入x y 62=得12)(2002+-=y y y y ,即 012222002=-+-y y y y .(3)依题意,21,y y 是方程(3)的两个实根,且1y 22200044(212)4480y y y ∆=--=-+>,32320<<-y .221221)()(y y x x AB -+-=22120))()3(1(y y y -+=]4))[(91(2122120y y y y y -++=))122(44)(91(202020--+=y y y)12)(9(322020y y -+=.定点)0,5(C 到线段AB 的距离 202029)0()25(y y CM h +=-+-==. (10分)2020209)12)(9(3121y y y h AB S ABC +⋅-+=⋅=∆)9)(224)(9(2131202020y y y +-+=3202020)392249(2131y y y ++-++≤ 7314=. (15分)当且仅当20202249y y -=+,即0y =,33A B 或33A B -++时等号成立.所以ABC ∆面积的最大值为7314. (20分)解二:同解一,线段AB 的垂直平分线与x 轴的交点C 为定点,且点C 坐标为)0,5(.(5分)设4,,,222121222211=+>==t t t t t x t x ,则161610521222121t t t t S ABC =∆的绝对值, (10分) 2222122112))656665(21(t t t t t t S ABC --+=∆221221)5()(23+-=t t t t)5)(5)(24(23212121++-=t t t t t t3)314(23≤,7314≤∆ABC S , (15分)当且仅当5)(21221+=-t t t t 且42221=+t t ,即,6571-=t 6572+-=t,33A B 或33A B -时等号成立.所以ABC ∆面积的最大值是7314. (20分)11.(本小题满分20分)数列{}n a 满足),2,1(1,312211 =+-==+n a a a a a n n nn .求证:nn n a a a 2212312131211-<+++<-- . (1)证明:由1221+-=+n n nn a a a a 知111121+-=+nnn a a a ,)11(1111-=-+nn n a a a . (2)所以211,111n nn n n nna a a a a a a ++==----即 1111n n n nn a a a a a ++=---. (5分)从而 n a a a +++ 21 1133222211111111++---++---+---=n n nn a a a a a a a a a a a a11111112111++++--=---=n n n n a a a a a a .所以(1)等价于nn n n a a 2112312112131211-<--<-++-,即 nn n n a a 21123131<-<++- . (3) (10分)由311=a 及 1221+-=+n nnn a a a a 知 712=a .当1n =时 ,2216a a -=,11122363<<- ,即1n =时,(3)成立.设)1(≥=k k n 时,(3)成立,即 kk k k a a 21123131<-<++-.当1+=k n 时,由(2)知kk k k k k k k a a a a a a a 2211111223)1()1(11>->-=-+++++++; (15分)又由(2)及311=a 知)1(1≥-n a a nn均为整数,从而由 kk k a a 21131<-++ 有131211-≤-++kk k a a 即kk a 2131≤+ ,所以122211122333111+<⋅<-⋅=-+++++k kkk k k k k a a a a a ,即(3)对1+=k n 也成立.所以(3)对1≥n 的正整数都成立,即(1)对1≥n 的正整数都成立. (20分)。
1高斯函数

第一讲:高斯函数 1第一讲:高斯函数高斯函数是数论中的重要函数,从小学、初中、高中,直到大学的各级、各类数学竞赛均有涉及,是数学竞赛极独特的内容.定义:[x]表示不超过实数x 的最大整数.则y=[x]称为高斯函数,也叫取整函数.由任一实数都能写成整数部分与非负纯小数之和,即x=[x]+α(0≤α<1),这里,[x]称为x 的整数部分,而α,即x-[x]称为x 的小数部分,记{x}=x-[x].函数性质:①高斯函数y=[x]的定义域是R,值域是Z;函数y={x}的定义域是R,值域是[0,1);②函数y=[x]与y=x-[x],即y={x}的图像分别为:③函数y=[x]是一个分段表达的不减的无界函数,即当x 1≤x 2时,有[x 1]≤[x 2];y={x}是一有界、周期为1的非单调函数;等式性质:①[n+x]=n+[x],{x+n}={x},其中x ∈R,n ∈Z;②[-x]=⎩⎨⎧∉--∈-)(1][)]([Z x x Z x x ;③若n ∈N +,x ∈R,则[n nx ][]=[x],特别地,[n x ][]=[n x],[nm x][]=[mn x ](证明:由x-1<[x]≤x<[x]⇒n[x]≤nx<n([x]+1)⇒[x]≤[n nx ][]>[x]+1⇒[n nx ][]=[x])不等性质:①若x ∈R,则x-1<[x]≤x<[x]+1;②若x,y ∈R,则[x+y]≥[x]+[y],且{x}+{y}≥{x+y},一般地,若x i ∈R,则[∑=ni i x 1]≥∑=ni i x 1][,特别地,[nx]≥n[x],[b na ]≥n[b a ];③若x,y ∈R +,则[xy]≥[x][y],特别地,][][y x ≥[yx],一般地,若x i ∈R +,则[∏=ni i x 1]≥∏=ni i x 1][,特别地,[x n ]≥[x]n ,[x]≥[n x ]n;厄米特恒等式:若x ∈R,n ∈N 6,则[x]+[x+n 1]+[x+n 2]+…+[x+nn 1-]=[nx]; 证明:引入辅助函数f(x)=[nx]-([x]+[x+n 1]+[x+n 2]+…+[x+n n 1-])⇒f(x+n 1)=[nx+1]-([x+n 1]+[x+n2]+…+[x+n n 1-]+[x+n 1+n n 1-])=[nx]+1-([x+n 1]+[x+n 2]+…+[x+n n 1-]+[x]+1)=f(x)⇒f(x)是一个以n1为周期的周期函数,而当x ∈[0,n1]时,直接计算知f(x)=0.故对任意x ∈R,厄米特等式成立. 1.函数性质:[例1]:(2010年全国高中数学联赛天津预赛试题)若关于x 的函数f(x)=|x-[x+a]|存在最大值M(a),则正实数a 的取值范是 (其中[x]表示不超过x 的最大整数).[解析]:设x+a=n+α,其中,n ∈Z,0≤α<1,则f(x)=|x-[x+a]|=|n+α-a-n|=|α-a|;①当0<a<21时,由-a ≤α-a<1-a,因|1-a|>|-a|⇒f(x)无最大值;②当a ≥21时,由-a ≤α-a<1-a,因|1-a|≤|-a|⇒f(x)有最大值.故a 的取值范是[21,+∞).[练习1]:2 第一讲:高斯函数1.(1994年全国高中数学联赛河北预赛试题)设f(x)=xa +11-21,且[m]表示不超过m 的最大整数,则[f(x)]+[f(-x)]的值域是 .2.(2012年全国高中数学联赛甘肃预赛试题)设f(x)=⎩⎨⎧>-≤-)0)(1()0]([x x f x x x ,其中[x]表示不超过x 的最大整数,若f(x)=kx+k(k>0)有三个不同的实数根,则实数k 的取值范围是 .3.(2008年全国高中数学联赛湖南预赛试题)某学校数学课外活动小组,在坐标纸上某沙漠设计植树方案如下:第k 棵树种植在点P k (x k ,y k )处,其中x 1=1,y 1=1,当k ≥2时,x k =x k-1+1-5[51-k ]+5[52-k ],y k =y k-1+[51-k ]-[52-k ].其中,[a]表示实数a 的整数部分,例如[206]=2,[0.6]=0.按此方案,第2008棵树种植点的坐标为 .2.求值问题:[例2]:(1993年全国高中数学联赛试题)整数[310103193+]的末两位数是_______.[解析]:由[310103193+]=[3103)310(313393+-+]=[(1031)2-1031×3+32-3103313+]=(1031)2-1031×3+32-1=1031(1031-3)+8⇒末两位数是08.[练习2]:1.(2006年上海市TI 杯高二年级数学竞赛试题)有一个根据某年某月某日计算“星期几”的有趣公式:d+[2.6m-0.2]+y+[4y]+ 月份 1 2 3 4 5 6 7 8 9 10 11 12[4c]-2c 除以7的余数,其中,c 表示年的前两位数字(即世纪),y 表示年的后两位数字,d 表示日,m 表示月对应的数字(见表). [x]表 示不于x 的最大整数.则2008年6月18日是星期 .2.①(2008年北京市中学生数学竞赛高一年级初试试题)以[x]表示不超过x 的最大整数,试确定[sin1]+[sin2]+[sin3]+ [sin4]+[sin5]的值.②(2011年全国高中数学联赛贵州预赛试题)设[x]表示不超过x 的最大整数,则[sin1]+[cos2]+[tan3]+[sin4]+[cos5] +[tan6]= .3.①(2005年上海市高中数学竞赛试题)设[x]表示不超过实数x 的最大整数,求集合{n|n=[20052k ],1≤k ≤2004,k ∈N}的元素个数.②(2010年全国高中数学联赛山西预赛试题)设a n =21⋅+32⋅+…+)1(+n n ,则[na n2]= . ③(2011年全国高中数学联赛福建预赛试题)对正整数n,设x n 是关于x 的方程nx 3+2x-n=0的实数根,记a n =[(n+1)x n ](n= 2,3,…)([x]表示不超过x 的最大整数).则10051(a 2+a 3+…+a 2011)= . ④(2007年全国高中数学联赛四川预赛试题)[x]表示不超过实数x 的最大整数,比如[3.14]=3,[0]=0,[-3.14]=-4.数列满足{a n }:a n =3n-2,若b n =[5na ],则b 1+b 2+…+b 2007= . 3.求和问题:[例3]:(2012年全国高中数学联赛河南预赛试题)设[x]表示不超过x 的最大整数,则[log 21]+[log 22]+[log 23]+…+ 第一讲:高斯函数 3[log 22012]= .[解析]:我们来解决一般性问题:设a ∈N +,且a ≥2,求和[log a 1]+[log a 2]+[log a 3]+…+[log a n].当a t≤k<a t+1时,[log a k]=t,t=0,1,2,…,且在区间[a t,a t+1)中的正整数有(a-1)a t个.并设a m≤n<a m+1,n=a m+b(b ∈N +),则 [log a 1]+[log a 2]+[log a 3]+…+[log a n]=(a-1)[0×a 0+1×a+2×a 2+…+(m-1)×a m-1]+mb=(a-1){[1-a a (m-1)-2)1(-a a ]a m-1+ 2)1(-a a }+mb=[a(m-1)-1-a a ]a m-1+1-a a +m(b+1) 回到本题:a=2,由210<2012<211⇒m=10,由2012-210=2012-1024=988⇒b=988⇒和为(2×9-2)29+2+10×989=18084.[练习3]:对应的m 值 11 12 1 2 3 4 5 6 7 8 9 101.①(2008年全国高中数学联赛湖北预赛试题)设[x]表示不超过x 的最大整数,则[log 21]+[log 22]+[log 23]+…+[log 2500]= .②(2010年全国高中数学联赛贵州预赛试题)设[x]表示不超过x 的最大整数,则[lg1]+[lg2]+[lg3]+…+[lg2010]= . ③(2009年北京市中学生数学竞赛高一年级初试试题)[x]表示不超过x 的最大整数,若[log 36]+[log 37]+[log 38]+…+ [log 3(n-1)]+[log 3n]=2009,试确定正整数n 的值.④(1991年第二届“希望杯”全国数学邀请赛试题){x}表示不小于实数x 的最小整数,则{log 21}+{log 22}+…+{log 21991} = .2.①(1990年第一届“希望杯”全国数学邀请赛试题)设[x]表示不超过x 的最大整数,则[1]+[2]+[3]+…+ [19901989⋅]+[-1]+[-2]+[-3]+…+[-19901989⋅]的值是 .②(2012年北京市中学生数学竞赛高中一年级初赛试题)若[x]表示不超过x 的最大整数,求满足方程[nlg2]+[nlg5]=2012的自然数n 的值.3.①(2012年全国高中数学联赛湖北预赛试题)设[x]表示不超过x 的最大整数,则∑+=+201201]222012[k k k = .②(2012年全国高中数学联赛福建预赛试题)对正整数x,记m=[2x ]+[22x ]+[32x ]+…+[k x 2],其中k 为满足2k≥x 的最小整数,符号[x]表示不超过x 的最大整数.x 与m 的差,即x-m 称为正整数x 的“亏损数”.(如x=100时,m=[2100]+[22100]+…+ [72100]=97,x-m=3,因此,数100的“亏损数”为3).则“亏损数”为9的最小正整数x 为________.4.方程问题:[例4]:(1995年全国高中数学联赛试题)用[x]表示不大于实数x 的最大整数,方程lg 2x-[lgx]-2=0的实根个数是_____.[解析]:由x ≥[x],lg 2x-[lgx]-2=0⇒lg 2x-2=[lgx]≤lgx ⇒-1≤lgx ≤2⇒[lgx]=-1,0,1,2;当[lgx]=-1时,lg 2x=1⇒lgx=-1;当[lgx]=0时,lg 2x=2⇒lgx=±2,无解;当[lgx]=1时,lg 2x=3⇒lgx=3;当[lgx]=2时,lg 2x=4⇒lgx=2⇒实根个数是3.[练习4]:1.①(2007年全国高中数学联赛湖北预赛试题)设[x]表示不大于x 的最大整数,集合A={x|x 2-2[x]=3},B={x|81<2x<8},则A ∩B= .②(2008年全国高中数学联赛江苏预赛试题)设集合A={x|x 2-[x]=2}和B={x||x|<2},其中符号[x]表示不大于x 的最大整数,则A ∩B= .③(1999年全国高中数学联赛广西预赛试题)[tanx]表示不超过tan 的最大整数,则方程[tanx]=2cos 2x 的解为 . ④(2009年上海市高中数学竞赛试题)若[a]表示不超过实数a 的最大整数,则方程[tanx]=2sin 2x 的解是 .2.①(2006年全国高中数学联赛湖南预赛试题)对于实数x,当且仅当n ≤x<n+1(n ∈N +)时,规定[x]=n.则不等式4[x]2-36[x] +45<0的解集为 .4 第一讲:高斯函数②(2009年全国高中数学联赛山东预赛试题)对任意的x ∈R,[x]表示不大于x 的最大整数,则满足[|x 2-1|]=10的x 的集合是( )(A)(-23,-11) (B)[11,23] (C)(-23,-11]∪[11,23) (D)[-23,-11)∪(11,23] ③(2009年全国高中数学联赛福建预赛试题)方程x [x]=29的实数解是 (其中[x]表示不超过x 的最大整数). 3.①(2011年全国高中数学联赛内蒙古预赛试题)方程x 2-8[x]+7=0的所有解为 .②(2007年第十八届“希望杯”全国数学邀请赛试题)若[x]表示不超过x 的最大整数,且x 2-2008[x]+2007=0,则[x]的值是 .③(1992年第三届“希望杯”全国数学邀请赛试题)[x]表示不超过实数x 的最大整数,则方程[3x-465]-2x-1=0的解是 .④(2011年全国高中数学联赛四川预赛试题)设x 为实数,定义[x]为不小于x 的最小整数,例如[π]=4,[-π]=-3,关于实数x 的方程[3x+1]=2x-21的全部实根之和等于 . 5.方程综合:[例5]:(1998年加拿大数学奥林匹克试题.2009年全国高中数学联赛安徽预赛试题)求方程[2x ]+[3x ]+[7x ]=x 的所有解([a]表示不超过实数a 的最大整数).[解析]:由方程知解x 是整数,设x=42p+q(p ∈Z,q ∈{0,1,…,41}),则(21p+[2q])+(14p+[3q ])+(6p+[7q ])=42p+q ⇒[2q ]+[3q ]+[7q]=p+q ⇒q=0,p=0,x=0;q=1,p=-1,x=-41;q=2,p=-1,x=-40;q=3,p=-1,x=-39,…,因此,方程的解集为{0, -6,-l2,-14,-18,-20,-21,-24,-26,-27,-28,-30,-32,-33,-34,-35,-36,-38,-39,-40,-41,-44,-45,-46,-47,-49,-50,- 51,-52,-53,-55,-57,-58,-59,-61,-64,-65,-67,-71,-73,-79,-85}.[练习5]:1.(2010年全国高中数学联赛福建预赛试题)将方程x 3-3[x]=4的实数解从小到大排列得x 1,x 2,…,x k ,则x 13+x 23+…+x k 3的值为 ([x]表示不超过x 的最大整数).2.①(1989年上海市高中数学竞赛试题)设[x]表示x 的整数部分,{x}=x −[x],则方程[x 3]+[x 2]+[x]={x}−1的所有实数根是 .②(1991年上海市高中数学竞赛试题)求满足[x 2−2x]=[x]2−2[x]的一切实数x.其中[x]表示不超过x 的最大整数. ③(1993年上海市高中数学竞赛试题)自然数x 使得[x]+[!x 3]+[!x 5]+[!x7]=1993.则x=_____. 3.①(2007年上海市TI 杯高二年级数学竞赛试题)求正整数n,使得[log 31]+[log 32]+[log 33]+[log 34]+…+[log 3n]=2007.其中[x]表示不超过x 的最大整数.②(2009年上海市TI 杯高二年级数学竞赛试题)对整数n>1,设x=1+21+…+n1,y=lg2+lg3+…+lgn.则满足[x]=[y]的所有整数n 构成的集合为 ([a]表示不超过实数a 的最大整数).6.方程应用:[例6]:(1989年全国高中数学联赛试题)一个正数,若其小数部分、整数部分和其自身成等比数列,则该数为__________. [解析]:设该数为x,则(x-[x])x=[x]2⇒x=251+[x](x>0);由0<x-[x]<1⇒0<215-[x]<1⇒0<[x]<251+<2⇒[x]=1 第一讲:高斯函数 5⇒x=251+. [练习6]:1.(2009年全国高中数学联赛江苏预赛试题)设a 是整数,0≤b<1.若a 2=2b(a+b),则b= . 注:本题也可以这样说:求实数x,使[x]2=2{x}x.2.①(2011年全国高中数学联赛甘肃预赛试题)设[x]表示不超过实数x 的最大整数,则在平面上,由满足[x]2+[y]2=50的点所形成的图形的面积是 .②(2011年北京市中学生数学竞赛高一年级初试试题)若[x]表示不超过x 的最大整数.求在平面直角坐标系xOy 中满足[x][y]=2011的所有点(x,y)组成的图形的面积.③(2012年全国高中数学联赛新疆预赛试题)[x]表示不超过实数x 的最大整数,则在平面直角坐标系xOy 中,满足[x][y]=2013的所有点(x,y)组成的图形面积为 .3.①(2009年全国高中数学联赛新疆预赛试题)数(3+8)2n (n ∈N +),且n ≥2009,设[x]为x 的整数部分,则[(3+8)2n]除以8的余数是( )(A)1 (B)3 (C)4 (D)7②(2009年全国高中数学联赛吉林预赛试题)(2+3)2010的小数点后一位数字是 .7.等式问题:[例7]:(1987年第19届加拿大数学奥林匹克试题)对每一个正整数n,证明:[n +1+n ]=[14+n ]=[24+n ]=[34+n ].[解析]:设正整数m 满足:m 2>4n+1;若m 为偶数,则m 2=4k>4n+1⇒k>n ⇒k ≥n+1⇒m 2≥4n+4>4n+3;若m 为奇数,则m 2=4k+1>4n+1⇒k>n ⇒k ≥n+1⇒m 2≥4n+5>4n+3;综上m 2>4n+3,即m>34+n ;特别地,取m=[14+n ]+1,满足:m 2>4n+1,则m>34+n⇒[14+n ]+1>34+n >14+n ≥[14+n ]⇒[34+n ]=[14+n ]⇒[14+n ]=[24+n ]=[34+n ];因(n +1+n )2=2n+1+2)1(+n n >2n+1+2n=4n+1⇒n +1+n >14+n ⇒[n +1+n ]≥[14+n ];且(n +1+n )2=2n+1+2)1(+n n <2n+1+2(n+1)=4n+3⇒n +1+n <34+n ⇒[n +1+n ]<[34+n ]⇒[n +1+n ]=[14+n ]=[24+n ]=[34+n ].[练习7]:1.①(1981年第44届莫斯科数学奥林匹克试题)试问:对x>1,下面的等式[][x ]=[x ]一定能成立吗?②(1948年第8届普特南数学奥林匹克试题)如果n 为一正整数,试证:[n +1+n ]=[24+n ]. 2.①(1991年第9届美国数学邀请赛试题)设r 是实数,且满足条件[r+10019]+[r+10020]+…+[r+10091]=546.求[100r]. ②(1981年第13届加拿大数学奥林匹克试题)试证方程[x]+[2x]+[4x]+[8x]+[16x]+[32x]=12354没有实数解. 3.(1989年国家理科试验班入学考试试题)通项为a n =b[c n +]+d 的数列{a n }:1,3,3,3,5,5,5,5,5,…,其中每一个正奇数m 恰好连续出现m 次.上述b 、c 、d 是侍定的整数,求b+c+d 的值.8.不等问题:[例8]:(1981年美国数学奥林匹克试题)对正整数n 和一切实数x.求证:[nx]≥1][x +2]2[x +…+nnx ][. [解析]:为方便,记a n =1][x +2]2[x +…+nnx ][.用数学归纳法证明:①当n=1时,a 1=[x],[nx]=[x]⇒原不等式成立;②假设当k<n 时,原不等式均成立,即a 1≤[x],a 2≤[2x],…,a n-1≤[(n-1)x];注意到:a k -a k-1=kkx ][⇒ka k -ka k-1=[kx]⇒na n =a 1+(2a 2-a 1) 6 第一讲:高斯函数+(3a 3-2a 2)+…+[na n -(n-1)a n-1]=a 1+(2a 2-2a 1)+(3a 3-3a 2)+…+(na n -na n-1)+(a 1+a 2+…+a n-1)=[x]+[2x]+[3x]+…+[nx]+(a 1+a 2+…+a n-1)≤n[nx]⇒a n ≤[nx].[练习8]:1.(第10届地中海地区数学奥林匹克试题)设x 为大于1的实数.证明:(][}{x x x +-}{][x x x +)+(}{][x x x +-][}{x x x +)>29.2.(2005年国家集训队训试试题)求所有正整数m 、n,使得不等式[(m+n)α]+[(m+n)β]≥[m α]+[m β]+[n(α+β)]对任意实数α、β都成立.3.(2005年国家集训队选拔考试试题)设n 是任意给定的正整数,x 是正实数.证明:∑++-=nk x kx x k x 1])1)[1(][(≤n.第一讲:高斯函数 1第一讲:高斯函数高斯函数是数论中的重要函数,从小学、初中、高中,直到大学的各级、各类数学竞赛均有涉及,是数学竞赛极独特的内容.定义:[x]表示不超过实数x 的最大整数.则y=[x]称为高斯函数,也叫取整函数.由任一实数都能写成整数部分与非负纯小数之和,即x=[x]+α(0≤α<1),这里,[x]称为x 的整数部分,而α,即x-[x]称为x 的小数部分,记{x}=x-[x].函数性质:①高斯函数y=[x]的定义域是R,值域是Z;函数y={x}的定义域是R,值域是[0,1);②函数y=[x]与y=x-[x]与y={x}的图像分别为:③函数y=[x]是一个分段表达的不减的无界函数,即当x 1≤x 2时,有[x 1]≤[x 2];y={x}是一有界、周期为1的非单调函数;等式性质:①[n+x]=n+[x],{x+n}={x},其中x ∈R,n ∈Z;②[-x]=⎩⎨⎧∉--∈-)(1][)]([Z x x Z x x ;③若n ∈N +,x ∈R,则[n nx ][]=[x],特别地,[n x ][]=[n x],[nm x][]=[mn x ](证明:由x-1<[x]≤x<[x]⇒n[x]≤nx<n([x]+1)⇒[x]≤[n nx ][]>[x]+1⇒[n nx ][]=[x])不等性质:①若x ∈R,则x-1<[x]≤x<[x]+1;②若x,y ∈R,则[x+y]≥[x]+[y],且{x}+{y}≥{x+y},一般地,若x i ∈R,则[∑=ni i x 1]≥∑=ni i x 1][,特别地,[nx]≥n[x],[b na ]≥n[b a ];③若x,y ∈R +,则[xy]≥[x][y],特别地,][][y x ≥[yx],一般地,若x i ∈R +,则[∏=ni i x 1]≥∏=ni i x 1][,特别地,[x n ]≥[x]n ,[x]≥[n x ]n;厄米特恒等式:若x ∈R,n ∈N 6,则[x]+[x+n1]+[x+n2]+…+[x+nn 1-]=[nx];证明:引入辅助函数f(x)=[nx]-([x]+[x+n 1]+[x+n 2]+…+[x+n n 1-])⇒f(x+n 1)=[nx+1]-([x+n 1]+[x+n2]+…+[x+ n n 1-]+[x+n 1+n n 1-])=[nx]+1-([x+n 1]+[x+n 2]+…+[x+n n 1-]+[x]+1)=f(x)⇒f(x)是一个以n1为周期的周期函数,而当x ∈[0,n1]时,直接计算知f(x)=0.故对任意x ∈R,厄米特等式成立. 1.函数性质:[例1]:(2010年全国高中数学联赛天津预赛试题)若关于x 的函数f(x)=|x-[x+a]|存在最大值M(a),则正实数a 的取值范是 (其中[x]表示不超过x 的最大整数).[解析]:设x+a=n+α,其中,n ∈Z,0≤α<1,则f(x)=|x-[x+a]|=|n+α-a-n|=|α-a|;①当0<a<21时,由-a ≤α-a<1-a,因|1-a|>|-a|⇒f(x)无最大值;②当a ≥21时,由-a ≤α-a<1-a,因|1-a|≤|-a|⇒f(x)有最大值.故a 的取值范是[21,+∞).[练习1]:2 第一讲:高斯函数1.(1994年全国高中数学联赛河北预赛试题)设f(x)=xa+11-21,且[m]表示不超过m 的最大整数,则[f(x)]+[f(-x)]的值域是 .解:因f(x)+f(-x)=(x a +11-21)+(x a -+11-21)=x a +11+xxa a +1-1=0⇒f(-x)=-f(x);设f(x)=k+α,其中,k ∈Z,0≤α<1,①若α=0,则f(x)=k ⇒-f(x)=-k ⇒[f(x)]=k,[f(-x)]=-k ⇒[f(x)]+[f(-x)]=0;②若α≠0,则f(x)=k+α⇒-f(x)=-k-α= -(k+1)+(1-α)⇒[f(x)]=k,[f(-x)]=-(k+1)⇒[f(x)]+[f(-x)]=-1⇒[f(x)]+[f(-x)]的值域是{-1,0}. 2.(2012年全国高中数学联赛甘肃预赛试题)设f(x)=⎩⎨⎧>-≤-)0)(1()0]([x x f x x x ,其中[x]表示不超过x 的最大整数,若f(x)=kx+k(k>0)有三个不同的实数根,则实数k 的取值范围是 . 解:令g(x)=kx+k,由图知g(2)≤1,g(3)>1⇒41<k ≤31. 3.(2008年全国高中数学联赛湖南预赛试题)某学校数学课外活动小组,在坐标纸上某沙漠设计植树方案如下:第k 棵树种植在点P k (x k ,y k )处,其中x 1=1,y 1=1,当k ≥2时,x k =x k-1+1-5[51-k ]+5[52-k ],y k =y k-1+[51-k ]-[52-k ].其中,[a]表示实数a 的整数部分,例如[206]=2,[0.6]=0.按此方案,第2008棵树种植点的坐标为 . 解:令f(k)=[51-k ]-[52-k ],则f(k+5)=[515-+k ]-[525-+k ]=[1+51-k ]-[1+52-k ]=[51-k ]-[52-k ]=f(k),故f(k)是周期为5的函数;计算可知:f(2)=0,f(3)=0,f(4)=0,f(5)=0,f(6)=1;由x k =x k-1+1-5f(k)⇒x k -x k-1=1-5f(k)⇒x 2008=x 1+(x 2- x 1)+(x 3-x 2)+…+(x 2008-x 2007)=x 1+2007-5[f(2)+f(3)+…+f(2008)]=x 1+2007-5[4001(f(2)+f(3)+…+f(6))+f(2)+f(3)]=3;同理可得y 2008=402.所以,2008棵树的种植点为(3,402).2.求值问题:[例2]:(1993年全国高中数学联赛试题)整数[310103193+]的末两位数是_______.[解析]:由[310103193+]=[3103)310(313393+-+]=[(1031)2-1031×3+32-3103313+]=(1031)2-1031×3+32-1=1031(1031-3)+8⇒末两位数是08.[练习2]:1.(2006年上海市TI 杯高二年级数学竞赛试题)有一个根据某年某月某日计算“星期几”的有趣公式:d+[2.6m-0.2]+y+ [4y ]+[4c]-2c 除以7的余数,其中,c 表示年的前两位数字(即世纪),y 表示年的后两位数字,d 表示日,m 表示月对应的数字 (见表). [x]表 示不于x 的最大整数.则2008年6月18日是星期 . 解:因c=20,y=8,d=18,m=4⇒d+[2.6m-0.2]+y+[4y ]+[4c]-2c=18+[10.2]+8+[2]+[5]-40=3≡3(mod7)⇒2008年6月18日是星期三.2.①(2008年北京市中学生数学竞赛高一年级初试试题)以[x]表示不超过x 的最大整数,试确定[sin1]+[sin2]+[sin3]+ [sin4]+[sin5]的值. 解:因为0<1<2π,2π<2、3<π,π<4<23π,23π<5、6<2π⇒sin1、sin2、sin3∈(0,1),sin4、sin5∈(-1,0)⇒[sin1]=第一讲:高斯函数 3[sin2]=[sin3]=0,[sin4]=[sin5]=-1⇒[sin1]+[sin2]+[sin3]+[sin4]+[sin5]=-2.②(2011年全国高中数学联赛贵州预赛试题)设[x]表示不超过x 的最大整数,则[sin1]+[cos2]+[tan3]+[sin4]+[cos5] +[tan6]= . 解:因为0<1<2π,2π<2<π,43π<3<π,π<4<23π,23π<5<2π,47π<6<2π⇒sin1∈(0,1),cos2∈(−1,0),tan3∈(−1, 0),sin4∈(−1,0),cos5∈(0,1),tan6∈(−1,0)⇒[sin1]+[cos 2]+[tan 3]+[sin 4]+[cos5]+[tan 6] =0+(-1)+(-1)+(-1) +0+(-1)=-4.3.①(2005年上海市高中数学竞赛试题)设[x]表示不超过实数x 的最大整数,求集合{n|n=[20052k ],1≤k ≤2004,k ∈N}的元素个数. 解:当20052k <1,即k<44时,[20052k ]=0;当1≤20052k <2,即45≤k<63时,[20052k ]=1;当2≤20052k <3,即64≤k<77时,[20052k ]=2; 当3≤20052k <4,即78≤k<89时,[20052k ]=3;当4≤20052k <5,即90≤k<100时,[20052k ]=4;当5≤20052k <6,即100≤k<109时,月份 1 2 3 4 5 6 7 8 9 10 11 12 对应的m 值111212345678910[20052k ]=5;当6≤20052k <7,即110≤k<118时,[20052k ]=6;当7≤20052k <8,即119≤k<126时,[20052k ]=7;…,集合{n|n=[20052k ], 1≤k ≤2004,k ∈N}的元素个数=1503.②(2010年全国高中数学联赛山西预赛试题)设a n =21⋅+32⋅+…+)1(+n n ,则[na n2]= . 解:由k<)1(+k k <k+21⇒2)1(+n n <a n <2)1(+n n +21n ⇒n+1<n a n 2<n+2⇒[n a n 2]=n+1. ③(2011年全国高中数学联赛福建预赛试题)对正整数n,设x n 是关于x 的方程nx 3+2x-n=0的实数根,记a n =[(n+1)x n ](n= 2,3,…)([x]表示不超过x 的最大整数).则10051(a 2+a 3+…+a 2011)= . 解:设f(x)=nx 3+2x-n,易知,当n 为正整数时,f(x)为增函数;f(1)=2>0,且当n ≥2时,f(1+n n )=n(1+n n )3+21+n n -n=3)1(+n n (- n 2+n+1)<0⇒x n ∈(1+n n ,1)⇒n<(n+1)x n <n+1⇒a n =[(n+1)x n ]=n ⇒10051(a 2+a 3+…+a 2011)=2013. ④(2007年全国高中数学联赛四川预赛试题)[x]表示不超过实数x 的最大整数,比如[3.14]=3,[0]=0,[-3.14]=-4.数列满足{a n }:a n =3n-2,若b n =[5na ],则b 1+b 2+…+b 2007= . 解:由b n =[5n a ]=[523-n ]⇒b 5k+r =[52)5(3-+r k ]=[3k+523-r ]=3k+[523-r ](r=0,1,2,3,4)⇒b 5k =3k-1,b 5k+1=b 5k+2=3k,b 5k+3=3k+1,b 5k+4=3k+2⇒b 5k-4+b 5k-3+b 5k-2+b 5k-1+b 5k =15k-10⇒b 1+b 2+…+b 2007=(b 1+b 2+…+b 5)+…+(b 401×5-4+b 401×5-3+b 401×5-2+b 401×5-1+b 401×5)+(b 401×5+1+b 401×5+2)=152)4011(401+-10×401+(3×401+3×401)=(15×201-4)401=1207411.3.求和问题:[例3]:(2012年全国高中数学联赛河南预赛试题)设[x]表示不超过x 的最大整数,则[log 21]+[log 22]+[log 23]+…+[log 22012]= .[解析]:我们来解决一般性问题:设a ∈N +,且a ≥2,求和[log a 1]+[log a 2]+[log a 3]+…+[log a n].当a t≤k<a t+1时,[log a k]=t,t=0,1,2,…,且在区间[a t,a t+1)中的正整数有(a-1)a t个.并设a m≤n<a m+1,n=a m+b(b ∈N +),则 [log a 1]+[log a 2]+[log a 3]+…+[log a n]=(a-1)[0×a 0+1×a+2×a 2+…+(m-1)×a m-1]+mb=(a-1){[1-a a (m-1)-2)1(-a a ]a m-1+ 4 第一讲:高斯函数2)1(-a a }+mb=[a(m-1)-1-a a ]a m-1+1-a a +m(b+1) 回到本题:a=2,由210<2012<211⇒m=10,由2012-210=2012-1024=988⇒b=988⇒和为(2×9-2)29+2+10×989=18084.[练习3]:1.①(2008年全国高中数学联赛湖北预赛试题)设[x]表示不超过x 的最大整数,则[log 21]+[log 22]+[log 23]+…+[log 2500]= .解:当2t ≤k<2t+1时,[log 2k]=t,t=0,1,2,…,且在区间[2t ,2t+1)中的正整数有2t 个.设f(x)=[log 2x],注意到29=512,所以, [log 21]+[log 22]+[log 23]+…+[log 2500]=∑=5001)(k k f =f(1)+∑-=1222)(k k f +∑-=12232)(k k f +∑-=12243)(k k f +∑-=12254)(k k f +∑-=12265)(k k f +∑-=12276)(k k f +∑-=12287)(k k f +∑=50028)(k k f =0+1×21+2×22+3×23+4×24+5×25+6×26+7×27+8(28-11)=3498.②(2010年全国高中数学联赛贵州预赛试题)设[x]表示不超过x 的最大整数,则[lg1]+[lg2]+[lg3]+…+[lg2010]= . 解:因为1≤k ≤9⇒[lgk]=0;10≤k ≤99⇒[lgk]=1;100≤k ≤999⇒[lgk]=2;1000≤k ≤2010⇒[lgk]=3;所以,[lg1]+ [lg2]+[lg3]+…+[lg2010]=60×1+900×2+1011×3=4923.③(2009年北京市中学生数学竞赛高一年级初试试题)[x]表示不超过x 的最大整数,若[log 36]+[log 37]+[log 38]+…+ [log 3(n-1)]+[log 3n]=2009,试确定正整数n 的值.解:由[log 36]=[log 37]=[log 38]=1⇒[log 36]+[log 37]+[log 38]=3;[log 39]=[log 310]=…=[log 326]=2⇒[log 39]+[log 310]+ …+[log 326]=36;[log 327]=[log 328]=…=[log 380]=3⇒[log 327]+[log 328]+…+[log 380]=162;[log 381]=[log 382]=…= [log 3242]=4⇒[log 381]+[log 382]+…+[log 3242]=648;3+36+162+648=849;[log 3243]=[log 3244]=…=[log 3728]=5⇒ [log 3243]+[log 3244]+…+[log 3728]=2430⇒n=474.④(1991年第二届“希望杯”全国数学邀请赛试题){x}表示不小于实数x 的最小整数,则{log 21}+{log 22}+…+{log 21991} = .解:当log 2n 为整数时,{log 2n}=[log 2n](n=20,21,…,210);当log 2n 为整数时,{log 2n}=[log 2n]+1;所以,{log 21}+{log 22}+…+{log 21991}=[log 21]+[log 22]+…+[log 21991]+1991-11;由a=2,1024=210<1991<211⇒m=10,由1991-210=967⇒b=967⇒ [log 21]+[log 22]+…+[log 21991]+1991-11=[2×9-2]29+2+10×968+1991-11=19854.2.①(1990年第一届“希望杯”全国数学邀请赛试题)设[x]表示不超过x 的最大整数,则[1]+[2]+[3]+…+ [19901989⋅]+[-1]+[-2]+[-3]+…+[-19901989⋅]的值是 .解:当k 为整数时,[k ]+[-k ]=0(k=12,22,…,19892),当k 不是整数时,设k =n+α(0<α<1),则[k ]=n,[-k ]=[-n-α]=[-(n+1)+(1-α)]=-(n+1)⇒[k ]+[-k ]=-1⇒[1]+[2]+[3]+…+[19901989⋅]+[-1]+[-2]+[-3]+…+[-19901989⋅]=-1989×1990+1989=-19892.②(2012年北京市中学生数学竞赛高中一年级初赛试题)若[x]表示不超过x 的最大整数,求满足方程[nlg2]+[nlg5]=2012的自然数n 的值.解:因为nlg2和nlg5是无理数,那么可以表示nlg2=m+a 其中m=[nlg2],a={nlg2}≠0,而nlg5=n-nlg2=n-m-a=(n-m-1)+(1- a)⇒[nlg5]=n-m-1⇒[nlg2]+[nlg5]=n-1=2012⇒n=2013.3.①(2012年全国高中数学联赛湖北预赛试题)设[x]表示不超过x 的最大整数,则∑+=+201201]222012[k k k = . 解:由1222012++k k <1⇒2012+2k <2k+1⇒2k>2012⇒k>11⇒当k>11时,[1222012++k k ]=0;当k=0时,[1222012++k k ]=1006;当k=1时,[1222012++k k]=503;当k=2时,[1222012++k k ]=250;当k=3时,[1222012++k k ]=126;当k=4时,[1222012++k k ]=63;当k=5时,[1222012++k k ]=31;当k=6时,[1222012++k k ]=16;当k=7时,[1222012++k k ]=8;当k=8时,[1222012++k k ]=4;当k=9时,[1222012++k k ]=2;当k=10、第一讲:高斯函数 511时,[1222012++k k ]=1⇒∑+=+20121]222012[k k k =1006+503+250+126+63+31+16+8+4+2+1+1=2012.②(2012年全国高中数学联赛福建预赛试题)对正整数x,记m=[2x ]+[22x ]+[32x ]+…+[k x 2],其中k 为满足2k≥x 的最小整数,符号[x]表示不超过x 的最大整数.x 与m 的差,即x-m 称为正整数x 的“亏损数”.(如x=100时,m=[2100]+[22100]+…+ [72100]=97,x-m=3,因此,数100的“亏损数”为3).则“亏损数”为9的最小正整数x 为________.解:设下x=a n ×2n+a n-1×2n-1+…+a 2×22+a 1×21+a 0×20,其中a i ∈{0,1}(i=0,1,2,…,n),则x-2[2x ]=a 0;[2x ]-2[22x]=a 1; [22x ]-2[32x ]=a 2,…,[nx 2]-2[12+n x ]=a n ⇒a 0+a 1+a 2+…+a n =(x-2[2x ])+([2x ]-2[22x ])+([22x ]-2[32x ])+…+([n x2]- 2[12+n x])=x-([2x ]+[22x ]+[32x ]+…+[12+n x ])=x-m=x 的“亏损数”⇒亏损数”为9的最小正整数x=1+2+22+…+28=511. 4.方程问题:[例4]:(1995年全国高中数学联赛试题)用[x]表示不大于实数x 的最大整数,方程lg 2x-[lgx]-2=0的实根个数是_____.[解析]:由x ≥[x],lg 2x-[lgx]-2=0⇒lg 2x-2=[lgx]≤lgx ⇒-1≤lgx ≤2⇒[lgx]=-1,0,1,2;当[lgx]=-1时,lg 2x=1⇒lgx=-1;当[lgx]=0时,lg 2x=2⇒lgx=±2,无解;当[lgx]=1时,lg 2x=3⇒lgx=3;当[lgx]=2时,lg 2x=4⇒lgx=2⇒实根个数是3.[练习4]:1.①(2007年全国高中数学联赛湖北预赛试题)设[x]表示不大于x 的最大整数,集合A={x|x 2-2[x]=3},B={x|81<2x<8},则A ∩B= .解:由81<2x <8⇒-3<x<3⇒[x]=-3,-2,-1,0,1,2;①若[x]≤-2,则x 2=2[x]+3<0,没有实数解;②若[x]=-1,则x 2=1⇒x=-1; ③若[x]=0,则x 2=3,没有符合条件的解;④若[x]=1,则x 2=5,没有符合条件的解;⑤若[x]=2,则x 2=7⇒有一个符合条件的解x=7⇒ A ∩B={-1,7}.②(2008年全国高中数学联赛江苏预赛试题)设集合A={x|x 2-[x]=2}和B={x||x|<2},其中符号[x]表示不大于x 的最大整数,则A ∩B= .解:因|x|<2⇒[x]的值可取-2,-1,0,1;当[x]=-2,则x 2=0无解;当[x]=-1,则x 2=1⇒x=-1;当[x]=0,则x 2=2无解;当[x]=1,则x 2=3⇒x=3⇒A ∩B={-1,3}.③(1999年全国高中数学联赛广西预赛试题)[tanx]表示不超过tan 的最大整数,则方程[tanx]=2cos 2x 的解为 . 解:由0≤2cos 2x ≤2⇒0≤[tanx]≤2⇒[tanx]=0,1,2;当[tanx]=0时,cosx=0,tanx 无意义;当[tanx]=1时,cosx=±22, 注意:[tanx]=1⇒x=k π+4π(k ∈Z);当[tanx]=2时,cosx=1⇒sinx=0⇒tanx=0,矛盾. ④(2009年上海市高中数学竞赛试题)若[a]表示不超过实数a 的最大整数,则方程[tanx]=2sin 2x 的解是 . 解:由0≤2sin 2x ≤2⇒0≤[tanx]≤2⇒[tanx]=0,1,2;当[tanx]=0时,sinx=0,tanx=0⇒x=k π;当[tanx]=1时,sinx=±22,注意:[tanx]=1⇒x=2k π+4π(k ∈Z);当[tanx]=2时,sinx=1⇒cosx=0⇒tanx=0无意义.2.①(2006年全国高中数学联赛湖南预赛试题)对于实数x,当且仅当n ≤x<n+1(n ∈N +)时,规定[x]=n.则不等式4[x]2-36[x] +45<0的解集为 .6 第一讲:高斯函数解:由4[x]2-36[x]+45<0⇒23<[x]<215⇒2≤[x]≤7⇒2≤x<8. ②(2009年全国高中数学联赛山东预赛试题)对任意的x ∈R,[x]表示不大于x 的最大整数,则满足[|x 2-1|]=10的x 的集合是( )(A)(-23,-11) (B)[11,23] (C)(-23,-11]∪[11,23) (D)[-23,-11)∪(11,23]解:因[|x 2-1|]=10⇔10≤|x 2-1|<11⇔-11<x 2-1≤-10,或10≤x 2-1<11⇔x ∈(-23,-11]∪[11,23),选(C).③(2009年全国高中数学联赛福建预赛试题)方程x [x]=29的实数解是 (其中[x]表示不超过x 的最大整数). 解:显然x>0;①若x ≥3,则[x]≥3⇒x [x]≥27>29;②若0<x<2,则0≤[x]<2⇒x [x]<22=4<29;③若2≤x<3,则[x]=2⇒x 2=29 ⇒x223. 3.①(2011年全国高中数学联赛内蒙古预赛试题)方程x 2-8[x]+7=0的所有解为 .解:由x ≥[x]=872+x ⇒1≤x ≤7⇒[x]=1,2,3,4,5,6,7⇒x=1,33,41,7.②(2007年第十八届“希望杯”全国数学邀请赛试题)若[x]表示不超过x 的最大整数,且x 2-2008[x]+2007=0,则[x]的值是 .解:1,2005,2006,2007.③(1992年第三届“希望杯”全国数学邀请赛试题)[x]表示不超过实数x 的最大整数,则方程[3x-465]-2x-1=0的解是 .解:设2x+1=k,则x=21-k ,3x-465=6389-k =k+6383-k ,于是原方程等价于[k+6383-k ]-k=0⇒[6383-k ]=0⇒0≤6383-k<1⇒338≤k<344⇒k=13,14⇒解是x=6,213. ④(2011年全国高中数学联赛四川预赛试题)设x 为实数,定义[x]为不小于x 的最小整数,例如[π]=4,[-π]=-3,关于实数x 的方程[3x+1]=2x-21的全部实根之和等于 . 解:设2x-21=k ∈Z,则x=412+k ,3x+1=k+1+432+k ,于是原方程等价于[432+k ]=-1,即-2<432+k ≤-1⇒-211<k ≤-27⇒k=-5,-4⇒x=-49,-47⇒所有实根之和为-4. 5.方程综合:[例5]:(1998年加拿大数学奥林匹克试题.2009年全国高中数学联赛安徽预赛试题)求方程[2x ]+[3x ]+[7x ]=x 的所有解([a]表示不超过实数a 的最大整数).[解析]:由方程知解x 是整数,设x=42p+q(p ∈Z,q ∈{0,1,…,41}),则(21p+[2q ])+(14p+[3q ])+(6p+[7q ])=42p+q ⇒[2q ]+[3q ]+[7q]=p+q ⇒q=0,p=0,x=0;q=1,p=-1,x=-41;q=2,p=-1,x=-40;q=3,p=-1,x=-39,…,因此,方程的解集为{0, -6,-l2,-14,-18,-20,-21,-24,-26,-27,-28,-30,-32,-33,-34,-35,-36,-38,-39,-40,-41,-44,-45,-46,-47,-49,-50,- 51,-52,-53,-55,-57,-58,-59,-61,-64,-65,-67,-71,-73,-79,-85}.第一讲:高斯函数 7 [练习5]:1.(2010年全国高中数学联赛福建预赛试题)将方程x 3-3[x]=4的实数解从小到大排列得x 1,x 2,…,x k ,则x 13+x 23+…+x k 3的值为 ([x]表示不超过x 的最大整数).解:由x-1<[x]≤x;①当x ≥3时,x 3-3[x]≥x 3-3x=x(x 2-3)≥3(32-3)=18;②当x ≤-3时,x 3-3[x]<x 3-3(x-1)=x(x 2-3)+3≤ -3[(-3)2-3]+3=-15;③当-3<x<3时,[x]=-3,-1,-1,0,1,2;若[x]=-3,则x 3=3[x]+4=-5,不合要求;若[x]=-2,则x 3=3[x]+4= -2⇒x=-32,合要求;若[x]=-1,则x 3=3[x]+4=-1,不合要求;若[x]=0,则x 3=3[x]+4=4,不合要求;若[x]=1,则x 3=3[x]+4= 7⇒x=37,合要求;若[x]=2,则x 3=3[x]+4=10⇒x=310,合要求⇒(-32)3+(37)3+(310)3=15.2.①(1989年上海市高中数学竞赛试题)设[x]表示x 的整数部分,{x}=x −[x],则方程[x 3]+[x 2]+[x]={x}−1的所有实数根是 .解:由[x 3]+[x 2]+[x]∈Z ⇒{x}−1∈Z ⇒{x}=0⇒x ∈Z ⇒x 3+x 2+x=-1⇒(x+1)(x 2+1)=0⇒x=-1.②(1991年上海市高中数学竞赛试题)求满足[x 2−2x]=[x]2−2[x]的一切实数x.其中[x]表示不超过x 的最大整数. 解:设[x]=n,x-[x]=α(0≤α<1),则x 2−2x=(n+α)2-2(n+α)=n 2-2n+α2+2(n-1)α,所以原方程等价于[n 2-2n+α2+2(n-1)α]=n 2-2n ⇔[α2+2(n-1)α]=0⇔0≤α2+2(n-1)α<1;当α=0时,不等式成立,此时,x=n;当α≠0时,由0≤α2+2(n-1)α<1⇔0<α<1)1(2+-n -(n-1)⇔0<x-n<1)1(2+-n -(n-1)⇔x ∈(n,1)1(2+-n +1)(n=1,2,…). ③(1993年上海市高中数学竞赛试题)自然数x 使得[x]+[!x 3]+[!x 5]+[!x7]=1993.则x=_____. 解:由[x]+[!x 3]+[!x 5]+[!x 7]=1993⇒[x]<1993⇒x<1994⇒[!x 7]=0⇒[x]+[!x 3]+[!x5]=1993⇒x>5!;设x=5!n+r(0≤r<5!=120)⇒(120n+r)+(20n+[6r ])+n=1993⇒141n+r+[6r ]=1993=14×141+19⇒n=14,r+[6r]=19⇒r=17⇒x=1697. 3.①(2007年上海市TI 杯高二年级数学竞赛试题)求正整数n,使得[log 31]+[log 32]+[log 33]+[log 34]+…+[log 3n]=2007.其中[x]表示不超过x 的最大整数.解:因为当3k≤n<3k+1时,[log 3n]=k(k=0,1,2,…),且区间[3k,3k+1)内的正整数个数=3k+1-3k=2×3k,所以,S k =[log 31]+[log 32]+ [log 33]+[log 34]+…+[log 3(3k+1-1)]=2(0×30+1×31+2×32+…+k ×3k)=(23k-43)3k +43;令(23k-43)3k+43≤2007⇒(2k- 1)3k≤2675⇒k ≤5;S 5=1391,2007-1391=6×101⇒n=36+100=829. ②(2009年上海市TI 杯高二年级数学竞赛试题)对整数n>1,设x=1+21+…+n1,y=lg2+lg3+…+lgn.则满足[x]=[y]的所有整数n 构成的集合为 ([a]表示不超过实数a 的最大整数). 解:{5,6}.6.方程应用:[例6]:(1989年全国高中数学联赛试题)一个正数,若其小数部分、整数部分和其自身成等比数列,则该数为__________. [解析]:设该数为x,则(x-[x])x=[x]2⇒x=251+[x](x>0);由0<x-[x]<1⇒0<215-[x]<1⇒0<[x]<251+<2⇒[x]=1 ⇒x=251+. [练习6]:1.(2009年全国高中数学联赛江苏预赛试题)设a 是整数,0≤b<1.若a 2=2b(a+b),则b= .解:若a 为负整数,则a 2>0,2b(a+b)<0,不可能,故a ≥0;于是a 2=2b(a +b)<2(a+1)⇒a 2-2a-2<0⇒0≤a<1+3⇒a=0,1,8 第一讲:高斯函数2;a=0时,b=0;a=1时,2b 2+2b-1=0⇒b=213-;a=2时,b 2+2b-2=0⇒b=3-1. 注:本题也可以这样说:求实数x,使[x]2=2{x}x.2.①(2011年全国高中数学联赛甘肃预赛试题)设[x]表示不超过实数x 的最大整数,则在平面上,由满足[x]2+[y]2=50的点所形成的图形的面积是 .解:由[x]2+[y]2=50⇒[x]=±1,[y]=±7;[x]=±5,[y]=±5;[x]=±7,[y]=±1.每组解有4种情况,每种情况下的面积为1⇒图形的面积是12.②(2011年北京市中学生数学竞赛高一年级初试试题)若[x]表示不超过x 的最大整数.求在平面直角坐标系xOy 中满足[x][y]=2011的所有点(x,y)组成的图形的面积.解:设[x]=a,[y]=b,即所有这样的点(x,y)组成的图形就是a ≤x<a+1,b ≤y<b+1界定的区域,它的面积为1,又2011是质数,所以满足[x][y]=2011的点(x,y)组成的图形是4个面积为1的区域,即[x]=1,[y]=2011;[x]=2011,[y]=1;[x]=−1,[y] =−2011;[x]=−2011,[y]=−1.这些图形的总面积是4.③(2012年全国高中数学联赛新疆预赛试题)[x]表示不超过实数x 的最大整数,则在平面直角坐标系xOy 中,满足[x][y]=2013的所有点(x,y)组成的图形面积为 .解:由[x][y]=2013=1×2013=3×671=11×183=33×61,共有16种情况,每种情形下的面积为1,所以,所有点(x,y)组成的图形面积为16.3.①(2009年全国高中数学联赛新疆预赛试题)数(3+8)2n (n ∈N +),且n ≥2009,设[x]为x 的整数部分,则[(3+8)2n]除以8的余数是( )(A)1 (B)3 (C)4 (D)7解:设a n =(3+8)2n +(3-8)2n =(17+122)n +(17-122)n ,则a 1=34,a 2=342-2=1154,a n+2=34a n+1-a n ⇒a 1≡2(m0d8),a 2≡2(m0d8),a 3≡34×2-2≡2(m0d8)⇒a n ≡2(m0d8);又因0<(3-8)2n <1⇒[(3+8)2n ]=a n -1⇒[(3+8)2n]≡1(m0d8).选(A).②(2009年全国高中数学联赛吉林预赛试题)(2+3)2010的小数点后一位数字是 .解:因(2+3)2010+(2-3)2010为整数,则(2+3)2010的小数部分为1-(2-3)2010,又因0<(2-3)2010<0.21005<(0.008)300,所以0.9<1-(2-3)2010<1,可知(2+3)2010的小数点后一位数字是9.7.等式问题:[例7]:(1987年第19届加拿大数学奥林匹克试题)对每一个正整数n,证明:[n +1+n ]=[14+n ]=[24+n ]=[34+n ].[解析]:设正整数m 满足:m 2>4n+1;若m 为偶数,则m 2=4k>4n+1⇒k>n ⇒k ≥n+1⇒m 2≥4n+4>4n+3;若m 为奇数,则m 2=4k+1>4n+1⇒k>n ⇒k ≥n+1⇒m 2≥4n+5>4n+3;综上m 2>4n+3,即m>34+n ;特别地,取m=[14+n ]+1,满足:m 2>4n+1,则m>34+n⇒[14+n ]+1>34+n >14+n ≥[14+n ]⇒[34+n ]=[14+n ]⇒[14+n ]=[24+n ]=[34+n ];因(n +1+n )2=2n+1+2)1(+n n >2n+1+2n=4n+1⇒n +1+n >14+n ⇒[n +1+n ]≥[14+n ];且(n +1+n )2=2n+1+2)1(+n n <2n+1+2(n+1)=4n+3⇒n +1+n <34+n ⇒[n +1+n ]<[34+n ]⇒[n +1+n ]=[14+n ]=[24+n ]=[34+n ].[练习7]:1.①(1981年第44届莫斯科数学奥林匹克试题)试问:对x>1,下面的等式[][x ]=[x ]一定能成立吗?解:设[x ]=n,由[x ]≤x <[x ]+1⇒n ≤x <n+1⇒n 2≤x <(n+1)2⇒n 2≤[x ]<(n+1)2⇒n ≤][x <n+1⇒n ≤[][x ]<n+1⇒[][x ]=n ⇒[][x ]=[x ]成立.②(1948年第8届普特南数学奥林匹克试题)如果n 为一正整数,试证:[n +1+n ]=[24+n ].第一讲:高斯函数 9解:因(n +1+n )2=2n+1+2)1(+n n <2n+1+[n+(n+1)]=4n+2⇒n +1+n <24+n ⇒[n +1+n ]≤[24+n ];若存在某个正整数n,使得[n +1+n ]≠[24+n ],则[n +1+n ]<[24+n ];设[24+n ]=k,则n +1+n <k ≤24+n⇒2n+1+2)1(+n n <k 2≤4n+2⇒2)1(+n n <k 2-(2n+1)≤2n+1⇒4n(n+1)<[k 2-(2n+1)]2≤4n(n+1)+1(因4n(n+1)与4n(n+1)+1是连续整数)⇒[k 2-(2n+1)]2=4n(n+1)+1⇒k 2=4n+2,但任意整数的平方被4除不余2,矛盾. 2.①(1991年第9届美国数学邀请赛试题)设r 是实数,且满足条件[r+10019]+[r+10020]+…+[r+10091]=546.求[100r]. 解:设[r]=n,r=n+α(0≤α<1),则[r+100i ]=[n+α+100i ]=n(当0<α+100i <1时),或n+1(当1≤α+100i<2时),设其中有 73-k 个n,k 个n+1,则(73-k)n+k(n+1)=546⇒n=7+7335k -⇒k=35,n=7⇒α+10056<1,α+10057≥1⇒10043≤α<10044⇒7+10043≤r<7+10044⇒743≤100r<744⇒[100r]=743. ②(1981年第13届加拿大数学奥林匹克试题)试证方程[x]+[2x]+[4x]+[8x]+[16x]+[32x]=12354没有实数解. 解:设f(x)=[x]+[2x]+[4x]+[8x]+[16x]+[32x],则f(x)单调不减;由f(x)≤[(1+2+4+8+16+32)x]=[63x]≤63x ⇒x ≥6312345>195;f(196)=63×196=12348⇒x<196⇒x ∈(195,196);令t=x-195,则t ∈(0,1),且f(x)=[195+t]+[2(195+t)]+ [4(195+t)]+[8(195+t)]+[16(195+t)]+[32(195+t)]=63×195+[t]+[2t]+[4t]+[8t]+[16t]+[32t]<12285+0+1+3+7+15+31 =12342⇒方程[x]+[2x]+[4x]+[8x]+[16x]+[32x]=12354没有实数解.3.(1989年国家理科试验班入学考试试题)通项为a n =b[c n +]+d 的数列{a n }:1,3,3,3,5,5,5,5,5,…,其中每一个正奇数m 恰好连续出现m 次.上述b 、c 、d 是侍定的整数,求b+c+d 的值.解:由a n+1-a n =b([c n ++1]-[c n +]),由题知,a n+1-a n =0,或2⇒b([c n ++1]-[c n +])=0,或2;由c n ++1-c n +=cn c n ++++11≤1⇒c n +<c n ++1≤c n ++1⇒[c n +]<[c n ++1]≤[c n +]+1⇒[c n ++1]-[c n +]=0,或1;显然b ≠0,当b([c n ++1]-[c n +])=2时,b=2,[c n ++1]-[c n +]=1;由a 1=2[c +1]+d=1⇒c ≥-1,d=1-2[c +1];注意到2k a =2k-1⇒2[c k +2]+d=2k-1⇒2[c k +2]+1-2[c +1]=2k-1⇒[c k +2]-[c +1]=k-1对任意的k ∈N +恒。
2010福建高考数学试卷及答案

2010福建高考数学试卷及答案【2010福建高考数学试卷及答案】第一部分选择题(共12小题,每小题5分,共60分)1. 已知函数 f (x) = x² + ax + b 是一个顶点坐标为(1, m) 且与 x 轴交于两个不等点的抛物线(3 ≤ m ≤ 4),那么 a 是____, b 是____。
【解析】函数 f (x) 是一个抛物线,顶点坐标为(1,m),说明它的对称轴 x=1,那么抛物线的方程为f(x)=(x-1)²+a+1,把点(1,m)代入方程,可以得到二元一次方程m=(1-1)²+a+1,即a=m-1。
再由于抛物线与x轴交于两个不等点,说明抛物线的表达式f(x)=x²+ax+b,在抛物线上方,即对应其自变量x的取值,函数值全部为正,即f(x)>0。
根据这一条件,可以得出b>0。
所以该题的解为:a=m-1,b>0. 【答案】a=m-1,b>0.2. 下列数列按顺序排列是________。
n₁=1,n₂=1,n₃=—5,n₄=—1,n₅=5,n₆=1,n₇=—5,n₈=________。
【解析】观察数列可以发现,n₁和n₂都是1,后面的每两项的正负号和数值相同,且前一对正负号后面都是负数和正数。
所以根据这个规律,数列继续下去应该是—5,5,—5,5,________。
所以该题的解为:5.【答案】5.3. 设 a ≠ 1,若 a² + 2a + 2 = 0, 则 a³ + 2a²+ 2a =________。
【解析】将 a³ + 2a² + 2a 写成 a(a² + 2a + 2) 的形式,可以看出括号里的内容与题干中的方程相同。
所以 a³ +2a² + 2a = a × (—2a) = (—2a²).【答案】(—2a²).4. 半径为 r 的水管里沟能流过最大的圆盘的半径是________。
全国高中数学联赛福建赛区

李毅
福州一中
陈德燕
许恭瀚
泉州五中
赵清木
三
等
奖
(67名)
三
等
奖
(67名)
陈楷民
厦门双十中学
王成焱
翁智荣
莆田一中
吴天然
彭钦一
龙岩一中
方秦金
陈雨薇
泉州五中
杨苍洲
叶智恺
福州一中
丘远青
叶韫盛
福建师大附中
连信榕
许晓毅
安溪一中
陈荣海
苏楠淇
厦门双十中学
赵祥枝
陈明豪
长乐一中
刘宇璋
黄一帆
泉州十一中
柳明全
卢皓川
福州一中
苏文新
郑文俊
福州一中
宋梅玉
傅坤隆
泉州七中
赖艳红
蔡崇泽
晋江养正中学
周彩瑛
陈炳森
漳州一中
冯真丽
丁嘉靖
泉州五中
李晖
黄垚开
永定一中
李辉
包迪
福州三中
耿熹
连庭
泉州五中
苏建民
郑思鹏
福州一中
宋梅玉
陈轶伦
厦门一中
李寅童
留永信
晋江季延中学
陈煌图
黄泽龙
厦门一中
张帆
洪世鑫
南安一中
梁淮森
江旭
厦门外国语学校
周志伟
陈晓灿
永春一中
2012年全国高中数学联赛福建赛区
获奖学生及指导教师名单
奖次
姓名
所在学校
指导教师
一
等
奖
(41名)
李君诚
龙岩一中
方秦金
陈景林
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指导教师
一
等
奖
(57名)
徐伟生
德化一中
徐建新
孙铭
厦门外国语学校
肖骁
许有疆
德化一中
陈丽真
杨震
莆田一中
肖志强
郑刘悦
福州三中
郑文祺
陈恩俊
莆田一中
肖志强
黄永招
德化一中
徐建新
许若男
厦门双十中学
张瑞炳
庄旭航
泉州五中
黄种生
杨洋
福建师大附中
林峰
何承玮
福州三中
张军
王经纬
福安一中
池水平
陈若明
厦门外国语学校
吴铭辉
林梦翔
福州一中
陈新栋
林宇哲
福州一中
龚梅勇
陈从翔
连江一中
陈志坚
王文彬
云霄立人学校
林耀东
谢钧
厦门双十中学
张瑞炳
张华林
龙岩二中
郭小峰
陈水挺
同安一中
谢继林
董张帆
福州一中
夏彦婴
曾林
仙游一中
陈凤龙
陈彦哲
厦门双十中学
黄雄
林晨超
福州一中
苏健
林煌
福州一中
危志刚
曾祥桓
平和正兴学校
叶连雄
周培聪
厦门双十中学
张瑞炳
蔡期塬
泉州五中
黄金南
庄晨帆
厦门双十中学
张瑞炳
庄佳威
厦门外国语学校
肖骁
胡致远
厦门双十中学
陈兆坚
陈荔伟
莆田二中
林伟
陈晓
莆田一中
林清利
高扬乐
平潭一中
林玉生
蒋家鑫
泉州五中
董少田
赖翔
漳州一中
林良斌
李德欣
上杭一中
林文柱
林晓明
龙岩一中
连亮曦
郑细林
莆田二中
周伟强
三
等
奖
(52名)
陈达兴
泉州五中
董少田
陈建彬
莆田一中
苏玉蓉
方子原
福州一中
陈建彬
刘英喆
厦门双十中学
黄雄
黄晨
莆田一中
肖志强
刘睿赟
武夷山一中
江丽华
阮梦瑶
龙岩一中
陈木孙
施佳宏
福州一中
李志勇
奖次
学生姓名
所在学校
指导教师
三
等
奖
(52名)
张振宇
仙游一中
林宝坚
王薇
龙海一中
洪小娇
郑辉煌
仙游一中
林宝坚
陈正玮
莆田二中
陈金亮
黄楚荧
福州一中
吴威
黄雅冠
惠安一中
陈荣桂
金光宇
厦门外国语学校
吴铭辉
林毅坤
林笃锦
胡丽婷
福州一中
吴威
张煜乾
邵武一中
高启长
林一吾
福州一中
苏健
吴姗姗
泉州五中
王辉耀
朱有基
福鼎一中
吴建文
黄哲轩
厦门双十中学
黄雄
张昕玮
厦门双十中学
张瑞炳
陈隽
永定一中
Hale Waihona Puke 包喜柯佳鑫龙海一中
洪小娇
陈星炜
长乐一中
邱宇元
许东南
安溪一中
吴志湖
韩超
厦门双十中学
张瑞炳
洪少群
晋江季延中学
林笃锦
郑启明
南安一中
廖国凤
陈冠群
莆田二中
郭铭纪
许东磊
同安一中
谢继林
张杰锋
泉州七中
陈建斌
林培辉
长乐一中
刘宇璋
巫立凡
厦门双十中学
张瑞炳
董晴谊
泉州一中
汤向明
黄怀毅
泉州五中
王辉耀
吴豪
南靖一中
李剑评
卓凌烽
福州一中
陈新栋
林俊杰
安溪一中
吴志湖
蒋奕凯
福州一中
夏彦婴
鹿鸣
厦门双十中学
张瑞炳
严堃
安溪一中
黄金南
张伟奇
长乐一中
刘宇璋
林德芳
德化一中
王琼琼
奖次
学生姓名
陈金亮
廖世昌
安溪一中
黄金南
刘必旭
福州一中
夏彦婴
奖次
学生姓名
所在学校
指导教师
二
等
奖
(45名)
张剑华
德化一中
陈修周
周晔
泉州五中
黄种生
曾嘉浩
厦门双十中学
张瑞炳
郑喆斌
莆田五中
郑毓青
傅家庆
南安一中
卓永宁
林艺彬
福州三中
林风
游志雄
仙游私立一中
李志明
黄思荣
龙海一中
叶立平
林杰
漳州一中
李两火
刘文章
泉州七中
林志敏
肖跃坚
安溪一中
苏健
林灯
福州一中
吴威
林建和
漳州一中
林良斌
施志国
福安一中
池水平
郑昕烨
福州一中
陈婷
奖次
学生姓名
所在学校
指导教师
三
等
奖
(52名)
卓武仪
南安一中
林建源
陈龙
福安一中
游明霞
黄文瀚
福州三中
杜重成
林金勇
同安一中
黄献磅
潘秋强
三明一中
李征宇
朱晓琳
泉州五中
王辉耀
黄境炀
泉州现代中学
陈永生
庄少林
晋江养正中学
许贻旺
蔡锐阳
福州一中
莆田一中
肖志强
杨磊
龙岩一中
连亮曦
陈正海
永定一中
包喜
丁晓娟
顺昌一中
何积仰
邱佳霖
同安一中
谢继林
王珍鑫
晋江养正中学
许贻旺
吴瑨
厦门一中
王淼生
吴俊杰
宁化一中
赖国强
卓亮
福州一中
刘鹏
2010年全国高中数学联赛福建赛区
获奖学生及指导教师名单
奖次
学生姓名
所在学校
指导教师
一
等
奖
(57名)
范睿托
厦门外国语学校
吴铭辉
高复铖
福州一中
危志刚
黄山筱
福州一中
危志刚
吴旋
福州一中
苏健
谢晓晖
厦门双十中学
黄雄
黄旻捷
厦门双十中学
郭俊芳
蔡宇涵
福州一中
陈德燕
邹豪风
福州一中
丘远青
肖宇光
泉州一中
汤向明
潘振忠
泉州一中
庄晓玲
奖次
学生姓名
所在学校
指导教师
一
等
奖
(57名)
蓝捷
上杭一中
林文柱
刘鸿辉
厦门双十中学
黄雄
黄国快
晋江养正中学
许贻旺
陈振雄
晋江季延中学
陈浩
王陶
厦门双十中学
张瑞炳
二
等
奖
(45名)
金迪
厦门双十中学
黄雄
吴志煌
晋江季延中学
林笃锦
张荣燊
泉州五中
黄种生
曾大通
惠安一中
陈荣桂
张志荣
平和正兴学校
叶连雄
陈少峰
晋江季延中学
陈婷
林森
福州一中
吴威
林弘杰
永春一中
李金进
林文峰
漳州一中
林良斌
田成锦
泉州七中
王雄伟
涂炼祥
龙岩一中
连亮曦
王施敏
福州一中
夏彦婴
谢崇发
龙岩一中
连亮曦
许灵达
晋江养正中学
许贻旺
颜荣圻
厦门双十中学
黄雄
黄熹之
福州一中
王欣
施嘉察
晋江养正中学
许贻旺
曾炜赫
漳州一中
张兵源
高凌斌
顺昌一中
黄敬平
林宇凯
福州一中
陈婷
张亚能
泉州七中
