基于MATLAB的渐开线花键检测项参数值的计算
渐开线花键设计计算公式

渐开线花键设计计算公式
一、基本齿形
一、尺寸计算
D F e mx=2√(0.5Db)²+(0.5DsinαD-)²-(hs/sinα) ²
三、公差和公差值
1、配合公差指齿槽宽和齿厚的公差
基本偏差对内花键的齿槽宽取基孔制H 它是作用齿槽宽的下偏差对外花键的齿厚取K=0js=(T+λ)/2 h、f、e和d它们是作用齿厚的上偏差
配合尺寸的公差
注:1、*以分度圆直径D为基础的公差,其公差单位I为:
当D≤500mm时,I=0.45 ³√D+0.001D.
当D>500mm时,I=0.004D+2.1.
**一基本齿槽宽E或基本齿厚S为基础的公差,其公差单位I为:I=0.45 ³√E+0.001E或
I=0.45 ³√S+0.001S.
式中D、E和S为mm。
2、L为分度圆周长之半,即L=πmZ/2 mm.
3、公差因素φ=m+0.0125D mm.
4、G为花键长度mm.
非配合尺寸的公差
齿向公差Fβ
内花键M值和W值计算
一、内花键量棒测量尺寸的计算公式
D’R i=D b[tanαci-tan(αci-Emax/D+invαci-inva D)]
式中:
D’R i---量棒的计算直径;
a ci---内花键与量棒接触点上的压力角,以弧度表示,αci=cos-¹。
渐开线花键计算公式及参数标注方法

渐开线花键计算公式及参数标注方法一、渐开线花键的几何参数1. 花键尺寸(Keyway Size):指的是渐开线花键的宽度,通常用顶孔(Recess)和底孔(Sockets)直径来表示。
2. 螺纹角(Helix Angle):指的是渐开线花键的螺纹线的倾斜角度。
3. 螺纹高度(Helix Height):指的是渐开线花键的螺纹线的高度,通常用顶孔和底孔之间的距离来表示。
二、渐开线花键的计算公式1.花键尺寸计算公式-花键尺寸公式由ISO2790标准规定,根据轴的直径(d)可以计算出花键尺寸。
- 花键顶孔直径(D)= 轴的直径(d)+ 0.15mm- 花键底孔直径(d1)= 轴的直径(d)+ 0.25mm2.螺纹角计算公式-螺纹角一般由图纸给出,也可以通过以下公式计算:- 螺纹角(α)= arctan(H / (π * d))其中,H为螺纹高度。
在制作渐开线花键图纸时,需要对相关参数进行标注,以便于加工和使用。
1.标注花键尺寸-在图纸上标注花键尺寸时,可以使用简化的标注方法,如在顶孔和底孔的直径符号上加上对应的数值。
2.标注螺纹角和螺纹高度-在图纸上标注螺纹角和螺纹高度时,可以使用直线段和字母表示,如在花键尺寸标注旁边加上α和H的符号,并注明对应的数值。
3.标注公差要求-在图纸上标注公差要求时,可以使用ISO系统的标准符号,如使用T字号来表示公差要求,并在标注下方注明对应的公差范围。
四、常见问题与解决方法在渐开线花键的设计和标注过程中,可能会遇到一些常见问题,下面列举几个常见问题并给出解决方法:1.如何选择合适的渐开线花键尺寸?-渐开线花键尺寸的选择需要考虑轴的直径和应力情况,一般建议按照ISO标准进行选择。
2.如何计算渐开线花键的扭矩传递能力?-渐开线花键的扭矩传递能力可以通过以下公式计算:T=(π/16)*τ*h*d,其中T为扭矩传递能力,τ为材料的抗扭转应力,h为花键的高度,d为轴的直径。
3.如何在CAD软件中绘制渐开线花键图纸?-在CAD软件中,可以使用线段和圆弧工具来绘制渐开线花键的轮廓,然后使用文字工具来标注相关参数。
基于Matlab的冷搓渐开线花键成形

南阳理工学院本科生毕业设计(论文)学院(系):机电工程系专业:机械设计制造及其自动化学生:李建峰指导教师:李超完成日期 2010 年 5 月南阳理工学院本科生毕业设计(论文)基于Matlab的冷搓渐开线花键成形工艺优化分析Process Optimization Analysis of Cold Rolling Involute Spline Forming Based on Matlab总计:毕业设计(论文)20 页表格: 2 个插图: 14 幅南阳理工学院本科毕业设计(论文)基于Matlab的冷搓渐开线花键成形工艺优化分析Process Optimization Analysis of Cold Rolling Involute Spline Forming Based on Matlab学院(系):机电工程系专业:机械设计制造及其自动化学生姓名:李建峰学号: 021408151指导教师(职称):李超(高级工程师)评阅教师:陈永辉完成日期: 2010-05-17南阳理工学院Nanyang Institute of Technology基于Matlab的冷搓渐开线花键成形工艺优化分析基于Matlab的冷搓渐开线花键成形工艺优化分析机械设计制造及其自动化专业李建峰[摘要]根据挤压成形工艺的原理,结合渐开线花键的特点,采用冷搓成形工艺进行花键成形。
借助Marc有限元软件在不同工艺参数下对成形过程进行模拟仿真,然后利用Matlab强大的计算、分析功能对所得数据进行函数拟合,获得目标函数。
最后采用遗传算法对冷搓成形的渐开线花键工艺参数进行优化分析,从而获得最优的成形工艺参数及合理的模具设计参数。
在满足花键成形精度前提下使成形力最小,达到延长模具使用寿命,提高生产效率的目的。
[关键词] 渐开线花键;冷搓;有限元;遗传算法;优化分析Process Optimization Analysis of Cold Rolling InvoluteSpline Forming Based on MatlabMechanical Design,Manufacturing and Automaction Major LI Jian-fengAbstract: According to the theory of extrusion and combining the traits of the involute spline itself, spline forming was carried out by adopting the cold roll forming technics. Under forming process was simulated by Marc software in different process parameters, objective function can be got by potential function which obtained from datas coming from the powerful calculation and analysis function on Matlab software. Finaly,process parameters of the involute spline was optimized with genetic algorithm on Matlab software and parameters of optimized forming process, reasonable die design was got. The forming force can be minimum if the process precision of spline forming was proper.Therefore the life of die was lengthened and the production efficiency was improved.Key words: Involute spline; Cold roll forming; FEM; Genetic algorithm; Optimization analyze1基于Matlab的冷搓渐开线花键成形工艺优化分析目录1绪论 (1)1.1本课题的目的和意义 (1)1.2本课题的主要研究内容 (2)1.3小结 (2)2渐开线花键冷搓成形工艺概述 (2)2.1冷搓成形工艺原理 (2)2.2冷搓成形工艺的特点 (3)2.3小结 (4)3优化设计简介 (4)3.1优化设计的发展概况 (4)3.2优化设计数学模型的分析处理 (5)3.3优化方法的选择和结果的分析 (6)3.3.1选择优化方法 (6)3.3.2分析计算结果 (6)3.4小结 (7)4渐开线花键冷搓成形过程的有限元模拟仿真分析 (7)4.1有限元分析技术应用介绍 (7)4.2冷搓渐开线花成形的模拟仿真分析 (7)4.3小结 (9)5利用Matlab对冷搓渐开线花键成形工艺优化 (9)5.1关于Matlab函数拟合 (10)5.1.1函数拟合的基本理论 (10)5.1.2冷搓渐开线花键成形函数拟合 (10)5.2Matlab的遗传算法概述 (13)5.2.1遗传算法的基本理论 (13)5.2.2遗传算法的基本内容 (14)5.2.3遗传算法的特点 (15)5.3利用Matlab遗传算法优化渐开线花键成形工艺参数 (15)5.4 小结 (17)结束语 (18)参考文献 (19)致谢 (20)2基于Matlab的冷搓渐开线花键成形工艺优化分析1 绪论1.1 本课题的目的和意义渐开线花键属于联接用关键零部件(图1-1),主要用于定心精度要求高、载荷大或经常滑动的联接,以确保联接的稳定、可靠、灵活。
渐开线花键计算说明

基于GB/T17855-1999 方法的端面花键齿承载能力计算1. 术语、代号及说明2. 计算(渐开线花键)2.1 名义切向力Ft Ft=2000 × T/D 本例:Ft=2000×T÷19.098=104.72T N2.2 单位载荷W W=Ft/z ×l ×cos αD 本例:W=104.72T/24×25×cos34 °=0.2105T N/mm 2.3 系数(1)使用系数K1(2)齿侧间隙系数K2当花键副的受力状态如图 1 所示时,渐开线花键或矩形花键的各键齿上所受的载荷大小,除取决于键齿弹性变形大小外,还取决于花键副的侧隙大小。
在压轴力的作用下,随着侧隙的变化(一半圆周间隙增大,另一半圆周间隙减小),内花键与外花键的两轴线将出现一个相对位移量e0。
其位移量e0 的大小与花键的作用侧隙(间隙)大小和制造精度高低等因素有关。
产生位移后,使载荷分布在较少的键齿上(对渐开线花键失去了自动定心的作用),因而影响花键的承载能力。
此影响用齿侧间隙系数K2 予以考虑. 通常K2 =1.1 ~3.0 。
当压轴力较小、花键副的精度较高时,可取K2=1.1 ~1.5; 当压轴力较大、花键副的精度较低时,可取K2=2.0~3.0; 当压轴力为零、只承受转矩时,K2=1.0 。
图 1 只承受压轴力F、无转矩T,内外花键的位置(3)分配系数K3 花键副的内花键和外花键的两轴线在同轴状态下,由于其齿距累积误差(分度误差)的影响,使花键副的理论侧隙(单齿侧隙)不同,各键齿所受载荷也不同。
这种影响用分配系数K3 予以考虑。
对于磨合前的花键副,当精度较高时(按GB/T 1144 标准为精密级的矩形花键或精度等级按GB/T3478.1 标准为5 级或高于5级时),K3=1.1 ~1.2; 当精度较低时(按GB/Tll44 标准为一般用的矩形花键或精度等级按GB/T3478.1 标准低于 5 级时),K3= 1.3 ~1.6 。
matlab渐开线函数

matlab渐开线函数渐开线(也称为伯努利双曲线)是一种特殊的曲线,其极坐标方程可以用来描述。
在 MATLAB 中,我们可以使用极坐标方程来绘制渐开线。
渐开线的极坐标方程通常表示为 r = a / theta,其中a 是一个常数。
在 MATLAB 中,我们可以按照以下步骤绘制渐开线函数:步骤 1,定义角度范围。
首先,我们需要定义角度的范围,通常选择一个合适的范围,比如 0 到 2pi。
步骤 2,计算极径。
根据渐开线的极坐标方程 r = a / theta,我们可以计算每个角度对应的极径值。
步骤 3,绘制曲线。
使用极坐标下的 plot 函数,将计算得到的极径和角度值转换为直角坐标系下的坐标,并绘制出渐开线的曲线。
下面是一个在 MATLAB 中绘制渐开线的示例代码: matlab.% 定义角度范围。
theta = 0:0.01:2pi;% 计算极径。
a = 1; % 常数。
r = a ./ theta;% 将极坐标转换为直角坐标。
x = r . cos(theta);y = r . sin(theta);% 绘制渐开线。
plot(x, y);title('渐开线');xlabel('x 轴');ylabel('y 轴');在这个示例中,我们定义了角度范围为 0 到 2pi,选择了常数a 为 1,并计算了极径的值。
然后将极坐标转换为直角坐标,并使用 plot 函数绘制出渐开线的曲线。
当然,你也可以根据自己的需要调整常数 a 的取值,来观察不同参数下的渐开线曲线特性。
希望这个示例能够帮助你在 MATLAB 中绘制渐开线函数。
花键测量参数计算

花键测量参数计算花键是一种常用的机械连接方式,在工程中广泛应用于轴、键和轮毂之间的连接。
花键的尺寸参数计算是设计和选择花键连接的重要步骤。
本文将详细介绍花键尺寸参数的计算方法。
花键主要由键长、键高、键宽及槽底圆角四个参数组成。
1.键长(Lk)的计算:键长是花键抵抗剪切力和扭矩的重要参数。
一般根据连接材料的性质和使用条件来确定键长。
a.当连接轴和轮毂的直径比较小时,一般取键长为连接面域内的径向长度。
b.当连接轴和轮毂的直径比较大时,一般取键长为轴的半径与轮毂的半宽之和。
c.当存在径向力的情况下,一般根据力的大小和工作条件来确定键长。
2.键高(Hk)的计算:键高是花键抵抗剪切力的主要参数。
键高需要满足一定的强度要求,一般根据连接材料的静强度来确定。
键高计算公式:Hk≥(4Ft/π*σ)^1/3其中,Ft为设计考虑的剪切力,σ为连接材料的静强度。
3.键宽(Bk)的计算:键宽是花键抗扭矩的重要参数。
键宽计算公式:Bk≥(16T/π*τ)^1/3其中,T为设计考虑的扭矩,τ为连接材料的剪切强度。
4.槽底圆角(R)的计算:槽底圆角是花键槽底部分的半径。
槽底圆角的设计主要是为了避免应力集中。
一般取槽底圆角的半径为花键宽度的1/8总结:花键的尺寸参数计算是花键连接设计的关键步骤。
根据连接轴和轮毂的直径以及受力情况来确定键长;根据连接材料的静强度来确定键高;根据设计考虑的扭矩和连接材料的剪切强度来确定键宽;槽底圆角一般取键宽度的1/8、这些参数的计算有助于确保花键连接的可靠性和稳定性。
基于Matlab的冷搓渐开线花键成形论文演示文稿

姓名:李建峰
学号:021408151 专业:机械设计制造及自动化 指导老师:王志奎
一、本课题的主要任务
1.掌握渐开线花键成形工艺及其流程; 2.掌握渐开线花键冷搓成形模具在Marc 的CAD建模和接触运动分析的技术,并分 析在不同成形工艺参数下模拟仿真成形 后的花键精度; 3.重点是利用Matlab软件,采用遗传算 法对渐开线花键成形工艺参数进行优化 分析。
6.1 遗传算法基本流程
确定优化问题的种群 生成初始种群
计算个体适应度(fitness)
是
是否满足优化问题的算法
否
选择适应度高的个体进行复制
交叉、变异
输出最优解或个体
6.2 程序及运行结果
适应度函数程序 程序运行结果数据
搜索函数程序
6.3 采用Matlab遗传算法搜索过程 曲线
6.4 优化分析的最后工艺参数
请各位老师批评与指正!
谢谢!
5.1 基于仿真的目标函数拟合
目标函数:F=(-0.1625*x1^2+11.5768*x1+0.00028571*x2^20.21743*x2+108.7428)/2
六、基于Matlab采用遗传算法 进行优化分析
遗传优化算法是基于达尔文的进化论,使用计算机技术 模拟遗传选择和适者生存的生物进化机制而发展起来的一门新 的学科,具有“生存+检测”的迭代过程的全局搜索算法。与 其它优化算法相比它具有: 1.遗传算法是对优化问题参数的编码组进行计算,而不是直接 针对参数本身。 2.遗传算法是在种群中寻优,而不是在单个个体解中开始寻优。 3.遗传算法仅根据问题本身所具有的目标函数适应度水平确定 搜索方向,而不需要其他任何先决条件或函数的导数辅助信息。 4.遗传算法中使用的选择交叉和变异这三个算子都是随机操作, 而不是确定的规则,便于搜索多峰的复杂空间。
渐开线花键计算(最全的花键计算公式)
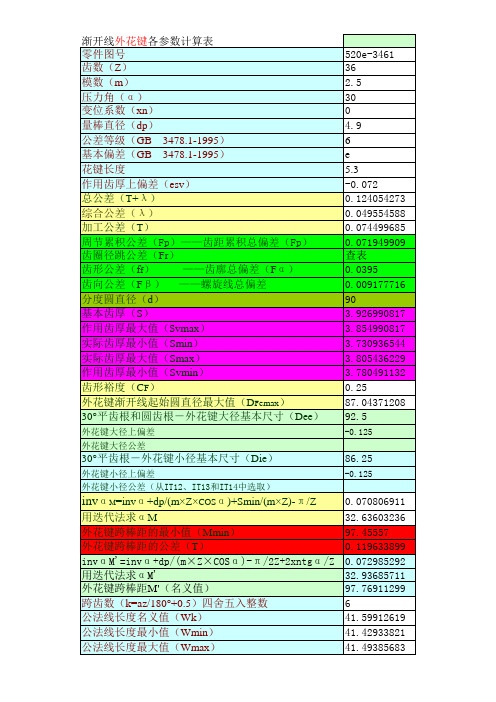
外花键大径上偏差
外花键大径公差
30°平齿根-外花键小径基本尺寸(Die)
外花键小径上偏差
外花键小径公差(从IT12、IT13和IT14中选取)
invαM=invα+dp/(m×Z×COSα)+Smin/(m×Z)-π/Z
用迭代法求αM
外花键跨棒距的最小值(Mmin) 外花键跨棒距的公差(T)
invαM'=invα+dp/(m×Z×COSα)-π/2Z+2xntgα/Z 用迭代法求αM' 外花键跨棒距M'(名义值) 跨齿数(k=az/180°+0.5)四舍五入整数 公法线长度名义值(Wk) 公法线长度最小值(Wmin)
6
h
27.5 0 0.091239434 0.036665412 0.054574022 0.051129736 查表 0.0309 0.012855055 38 2.032676542 2.032676542 1.941437108 1.99601113 1.978102521 0.1 37.65864892 39.8
公法线长度最大值(Wmax)
520e-3461 36 2.5 30 0 4.9
6 e 5.3 -0.072 0.124054273 0.049554588 0.074499685 0.071949909 查表 0.0395 0.009177716 90 3.926990817 3.854990817 3.730936544 3.805436229 3.780491132 0.25 87.04371208 92.5
-0.044
15.5745
-0.044
0.044501289
28.29702416 18.11177333 0.15482979 0.053262002 29.91557579 18.37749785 6 12.72287754 12.5932176 12.66661349
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MATLAB的渐开线花键检测项参数值的计算李平辉1,张召霞2(1.郑煤机集团,河南郑州450013;2.中科院合肥智能机械研究所,安徽合肥230027)摘要:本文针对矿山机械长壁工作面输送设备所选用的渐开线花键,给出了计算渐开线花键检测项参数值的程序流程图及Matlab程序。
经实例验证,程序计算准确快速,实用性强。
使用Matlab编程解决复杂繁琐的工程计算的方法具有推广意义。
关键词:渐开线花键;量棒直径;棒间距;跨棒距;MA TLABThe Calculation of Involute Spline Check Items Value Based on Matlab(LI Ping-hui1,ZHANG Zhao-xia2)(1.Zhengzhou Coal Mine Machinery Group Co.,Ltd,Zhengzhou 450013,China;2. Institute ofIntelligent Machines,Chinese Academy of Sciences ,Hefei 230027,China) Abstract: According to involute spline used on conveyer of longwall face, this paper gave the program flow chart and Matlab program of the calculation of involute spline check items value. The verification experiment proves that the program can achieve accurate , fast calculation, and strong practicality. Solving the complex and tedious engineering calculation by using Matlab, there is extended significance.Key words: involute spline; length bar diameter; interred spacing; distance over bar; Matlab0 引言渐开线花键联结的强度高、承载能力强,且具有精度高、齿面接触良好、能自动定心、加工方便等优点[1],现已经广泛应用在重型煤矿机械中。
矿山机械长壁工作面输送设备,通常选用30°压力角、平齿根、齿侧配合类别为H/h、公差等级为6或7级的圆柱直齿渐开线花键。
例如:刮板输送机链轮轴组中的轴、链轮等。
渐开线花键检测项参数值是检验的依据,因此在设计渐开线花键时,检测项参数值的计算尤为重要。
设计时,应在具有渐开线花键的零件图上给出检测项参数值,并列出数据表。
内花键应给出的检测项:模数m、齿数z、压力角a、公差等级和配合类别、渐开线终止圆最小直径D Fimin、作用齿槽宽最大值E vmax、实际齿槽宽最小值E min、作用齿槽宽最小值E vmin、实际齿槽宽最大值E max、齿根圆弧最小曲率半径R imin、齿距累积公差F p、齿形公差f f、齿向公差Fβ、量棒直径D Ri、棒间距M Ri;外花键应给出的检测项:模数m、齿数z、压力角a、公差等级和配合类别、渐开线起始圆最大直径D Femax、作用齿厚最大值S vmax、实际齿厚最小值S min、作用齿厚最小值S vmin、实际齿厚最大值S max、齿根圆弧最小曲率半径R emin、齿距累积公差F p、齿形公差f f、齿向公差Fβ、量棒直径D Re、跨棒距M Re。
1 检测项参数值的计算检测项包含四部分内容。
基本参数:m、z、a;花键尺寸:D Fimin、E vmax、E min、E vmin、E max、R imin(D Femax、S vmax、S min、S vmin、S max、R emin);公差等级及公差值:公差等级和配合类别、F p、f f、Fβ;量棒及M值:D Ri、M Ri(D Re、M Re)。
模数m、齿数z、花键有效长度L、压力角a、公差等级和配合类别是计算各项检测项参数值的基本参数。
花键尺寸和公差等级及公差值可参照参考文献[2]中的相关内容计算。
棒间距(跨棒距)是通过量棒间接测出的,所以量棒选择的合理与否对检测结果有着重要的影响。
量棒直径是能通过一定的计算公式求解得出的,求解出的结果称为量棒的计算直径,然后按GB 321中的R40系列选取量棒直径。
若量棒的计算直径不是R40系列数值,应选取最接近该数值较大的值[3],即向上圆整到R40系列数值。
常用刮板输送机、刮板转载机可能选用的量棒直径在10、10.6、11.2、11.8、12.5、(9) (10)(12) (13)13.2、14、15、16、17、18、19、20、21.2、22.4(均取自R40系列)之中取值。
根据量棒的计算直径按R40系列圆整出的数值通常集中在16、17、18、19、20、21.2。
但是实际生产中,检验部门往往不准备这么多种直径的量棒。
所以在计算时,量棒直径通常是自选的。
这种做法既是可取的也是经济实用的。
但是应使量棒外圆与齿廓的接触点落在分度圆及其附近的任意位置上,一般在距小径的(1/3~2/3)齿高之间为宜[4]。
1.1 内、外花键量棒直径D Ri 、D Re 的计算 1.1.1 内花键量棒直径D Ri 的确定max '[tan tan(inv inv 30)]E D D ci ci Ri b Dci ααα=--+- 式中:D'Ri ——量棒的计算直径;αci ——内花键与量棒接触点上的压力角;1cosD b ci D ciα-=D ci ——内花键与量棒接触点处直径;max min2D D ee ii D ci +=D eemax ——外花键大径最大值; D iimin ——内花键小径最小值;E max ——实际齿槽宽最大值。
内花键量棒直径D Ri 按GB 321中的R40选取量棒直径,若D'Ri 不是R40系列数值,应选取最接近D'Ri 较大的值。
1.1.2 外花键量棒直径D Re 的确定'[tan(inv min inv 30)tan ]D D ce ce Re b ZS ce Dπααα=++--- 式中:D'Re ——量棒的计算直径;αce ——外花键与量棒接触点上的压力角;1cosD b ce D ceα-=D ce ——外花键与量棒接触点处的直径;max min2D D ee ii D ce +=S min ——实际齿厚最小值。
内花键量棒直径D Re 按GB 321中的R40选取量棒直径,若D'Re 不为R40系列数值,应选取最接近D'Re 较大的值。
1.2棒间距M Ri 和跨棒距M Re 的计算 1.2.1棒间距M Ri 的计算偶数齿:max cos max min cos minD b M D Ri Rii D b M D Ri Ri i αα=-=-奇数齿:90cosmax cos max 90cos max cos minD b M D Ri RiZ i D b M D Ri RiZi αα=-=-式中:M Rimax ——内花键棒间距的最大值;M Rimin ——内花键棒间距的最小值; D Ri ——内花键量棒直径;αimax ——当E 为E max 时,内花键量棒中心圆上的压力角;αimin ——当E 为E min 时,内花键量棒中心圆上的压力角。
内花键量棒直径D Ri 已经确定,根据公式(11),分将E max 和E min 代入E ,即可求出αimax 和αimin ,进而求得棒间距M Ri 。
1inv(inv 30)D ERi i D D bα-=+- 1.2.2 跨棒距M Re 的计算偶数齿:ReRemin cos minRemax Re cos maxD b M D e D b M D e αα=+=+奇数齿:(1)(3)(2)(4)(5)(6)(7) (8)(11)(14)(15)(16)(17) 90cosReRemin cos min90cosRemax Recos maxD b M D Ze D b M D Ze αα=+=+式中:M Remin ——外花键跨棒距的最小值M Remax ——外花键跨棒距的最大值 αemin ——当S 为S min 时,外花键量棒中心圆上的压力角;αemax ——当S 为S min 时,外花键量棒中心圆上的压力角。
外花键量棒直径D Re 已确定,根据公式(16),分将S max 和S min 代入S ,即可求出αemax 和αemin ,进而求得跨棒距M Re 。
1Reinv(inv 30)D S e D D Zb πα-=++- 2 程序流程图根据计算步骤,结合程序需要,编制出程序流程图,如图1。
图1 程序流程图3 关键步骤的程序实现对于类似复杂繁琐的计算,使用高级语言编程解决是最有效的办法之一。
但是往往有些步骤在编程实现时较难处理。
在渐开线花键检测项参数值编程计算过程中,有以下几点需要注意。
3.1 计算的量棒直径按标准系列圆整以外花键量棒D Re 根据计算的量棒直径D'Re 按GB 321中R40系列圆整为例:lbbzz=[10 10.6 11.2 11.8 12.5 13.2 14... 15 16 17 18 19 20 21.2 22.4]; for i=1:15if lbbzz(1,i)<DRep continue end breakendDRe=lbbzz(1,i);lbbzz 为长壁输送设备中常用花键量棒直径(标准系列值)的矩阵,程序进入循环之后,依次检索lbbzz 矩阵中的数值,直到检索到一个大于D'Re 的数值,跳出循环,并输出该值作为外花键量棒直径。
这样才能满足“若计算的量棒直径不为R40系列数值,应选取最接近计算的量棒直径较大的值”的要求。
3.2 反求内外花键量棒中心圆上的压力角inv tan ααα=- 已知α,求解invα问题并不复杂。
但已知invα,反求α,并不容易得出结果。
如果借助编程求解,也不难实现。
类似这种问题,一般都会采用收敛算法,逐步逼近,当结果达到预定精度时,即返回当前值作为结果。
如:牛顿迭代算法。
但是Matlab 不需要这么复杂的程序,可以利用fzero 函数很方便的解决单变量函数的零点问题。
在使用fzero 时,必须为fzero 函数提供初始点或者一个初始区间。
