小学六年级数学用比例解应用题
六年级数学思维训练:比例解应用题

六年级数学思维训练:比例解应用题
一、兴趣篇
1.圆珠笔和铅笔的单价比是4:3,20支圆珠笔和21支铅笔共71.5元.圆珠笔的单价是多少?
2.一段路程分为上坡和下坡两段,这两段的长度之比是4:3.已知阿奇在上坡时每小时走3千米,下坡时每小时走4.5千米.如果阿奇走完全程用了半小时.请问:这段路程一共有多少千米?
3.有两块重量相同的铜锌合金.第一块合金中铜与锌的重量比是2:5,第二块合金中铜与锌的重量比是1:3.现在把这两块合金合铸成一块大的.求合铸所成的合金中铜与锌的重量之比.
4.甲、乙两包糖的重量比是5:3,如果从甲包取出10克放入乙包后,甲、乙两包糖的重量比变为7:5.请问:这两包糖重量的总和是多少克?
5.小明从甲地到乙地,去时每小时走5千米,回来时每小时走7千米,来回共用4小时,小明去时用了多长时间?
二、拓展篇
6.甲、乙、丙三人合买一台电视机,甲付的钱数等于乙付的钱数的2倍,也等于丙付的钱数的3倍.已知甲比丙多付了680元,请问:
(1)甲、乙、丙三人所付的钱数之比是多少?
(2)这台电视机售价多少钱?
7.两根粗细相同、材料相同的蜡烛,长度比为29:26,燃烧50分钟后,长蜡烛与短蜡烛的长度比为11:9,那么较长的那根还能燃烧多少分钟?。
六年级数学考试比例应用题练习题

六年级数学考试比例应用题练习题六年级数学毕业考试比例应用题练习题篇一(1)水果店一天运进苹果、香蕉、梨共390千克,苹果的重量是梨的1.5倍,香蕉的重量是梨的3/4,三种水果各运进多少千克?(2)一缸水,用去1/2和5桶,还剩30%,这缸水有多少桶?(3)有一快棱长20厘米的正方体木料,刨成一个底面直径的圆柱体,刨去木料的体积是多少?(4)一根钢管长10米,第一次截去它的7/10,第二次又截去余下的1/3,还剩多少米?(5)两个小组装配收音机,甲组每天装配50台,第一天完成了总任务的10%,这时乙组才开始装配,每天装配40台,完成这批任务时,甲组做了多少天?(6)修筑一条公路,完成了全长的2/3后,离中点16。
5千米,这条公路全长多少千米?(7)师徒两人合做一批零件,徒弟做了总数的2/7,比师傅少做21个,这批零件有多少个?(8)两队修一条公路,甲队每天修全长的1/5,乙队独做7.5天修好。
如果两队合修2天后,其余由乙队独修,还要几天完成?(9)仓库里有一批化肥,第一次取出总数的2/5,第二次取出总数的1/3少12袋,这时仓库里还剩24袋,两次共取出多少袋?(10)前轮在720米的距离里比后轮多转40周,如果后轮的周长是2米,求前轮的周长。
六年级数学毕业考试比例应用题练习题篇二1、为创建海华公司,张、王、李三人分别投资100万元、120万元和80万元。
在他们三人的共同努力下,到年末,公司共盈利60万元,你认为该如何合理分配这笔钱,每人分别得多少?2、甲乙两地相距360千米,一辆汽车从甲地到乙地计划7小时行完全程,汽车的速度如下表,问能否在规定的时间内行完全程?计算后简要说明3、在比例尺是的地图上,量得甲乙两地的距离为4.5厘米,如果一辆客车和货车同时从甲乙两地相对开出,经过3小时相遇。
已知客车每小时行65千米,那么这辆货车每小时行多少千米?4、在比例尺是1:3000000的地图上,量得A、B两城之间的距离是2.4厘米。
六年级数学上册按比例分配应用题

六年级数学上册按比例分配应用题1.甲、乙两人每天共做56个机器零件,甲、乙工作效率的比是3:5,问甲、乙两人每天各做多少个零件?解析:设甲每天做3x个零件,乙每天做5x个零件,则3x+5x=56,解得x=8,因此甲每天做24个零件,乙每天做40个零件。
2.石灰水是用石灰和水按1:100配成的,要配制4545千克的石灰水,需要石灰多少千克?解析:石灰和水的比是1:100,因此需要的水量是4545千克/100=45.45千克,石灰的重量也是45.45千克。
3.体育室有60根跳绳,按人数分配给甲乙两班,甲班有42人,乙班有48人,两个班各分得跳绳多少根?解析:甲班分得的跳绳数量是60×(42/90)=28根,乙班分得的跳绳数量是60×(48/90)=32根。
4.一个分数,它的分子和分母的和是80,分子和分母的比是3:7,求这个分数?解析:设分子为3x,分母为7x,则3x+7x=80,解得x=8,因此分子是24,分母是56,这个分数是24/56.5.一块长方形地,周长400米,长和宽的比是3:2,这块地的面积是多少平方米?解析:设长为3x,宽为2x,则周长为2(3x+2x)=10x,解得x=20,因此长为60米,宽为40米,面积是2400平方米。
6.甲、乙两个车间的平均人数是36人,如果两个车间人数的比是5:7,这两个车间各有多少人?解析:设甲车间的人数为5x,乙车间的人数为7x,则5x+7x=2×36,解得x=3.6,因此甲车间有18人,乙车间有25.2人,约为25人。
7.建筑工人用水泥、沙子、石子按2:3:5配制成96吨的混凝土,需要水泥、沙子、石子各多少吨?解析:设水泥、沙子、石子的比为2x:3x:5x,则2x+3x+5x=96,解得x=8,因此水泥需要16吨,沙子需要24吨,石子需要40吨。
8.一种药水是用药物和水按3:400配制成的。
1)要配制这种药水1612千克,需要药粉多少千克?2)用水60千克,需要药粉多少千克?3)用48千克药粉,可配制成多少千克的药水?解析:(1)药物和水的比是3:400,因此需要的药物重量是1612千克×(3/403)=12千克。
小学六年级简单比例运算练习题

小学六年级简单比例运算练习题一、简答题:1. 将3∶5与9∶15两个比例进行等比例的扩展。
2. 将4∶7与36∶63两个比例进行等比例的缩写。
3. 一条跑道有2000米长,如果按照比例1∶5降低长度,最后的跑道长度是多少?4. 营养饼干中蛋白质和脂肪的比例是3∶2,如果一块饼干中含有30克脂肪,那么这块饼干中蛋白质的含量是多少克?5. 一杯果汁中,橙汁和苹果汁的比例是2∶5,如果有8杯果汁,其中橙汁的杯数是多少?二、计算题:1. 小明用了50元钱买了2本书,如果每本书的价格都相同,那么一本书的价格是多少元?2. 小华用了30分钟走了7公里,如果小华以相同的速度继续行走,那么他用多少时间可以走完14公里?3. 在某学校的六年级班级中,有48个男生,比例是3∶5,那么这个班级中的女生人数是多少?4. 小明和小红一起做一个作业,小明用了1小时完成了四分之一的作业,小红用了50分钟完成了剩下的部分,请问小红用了多少时间完成了整个作业?5. 一块土地上80%是农田,剩下的部分是果园和花园,果园占土地的比例是5∶6,那么花园占土地的比例是多少?三、应用题:1. 小刚用18元钱买了2个苹果和3个梨,小华用24元钱买了4个苹果和若干个梨,请问小华买了多少个梨?2. 一栋高楼上有40层,电梯升一层需要4秒钟,小张从1楼坐电梯到了顶楼,耗时多长?3. 小明每天早上以相同的速度骑自行车上学,平均每分钟骑行3公里。
如果上学的路程是12公里,那么小明骑自行车上学需要多少时间?4. 甲、乙两个人按照比例1∶3分配了一堆零食,甲分到了12个,那么乙分到了多少个?5. 李明学习了40分钟,休息了20分钟,学习了30分钟,然后休息了10分钟。
李明一天中学习的时间和休息的时间各是多少?四、挑战题:1. 在一辆自行车上有4个轮子,如果一扇车门有5个轮子,那么需要多少扇车门才能和这辆车轮的数量比例相同?2. 一桶水中蓝色颜料和白色颜料的比例是3∶4,如果用相同的比例往桶中加入蓝色颜料和白色颜料,一共需要加多少次才可以使蓝色颜料和白色颜料达到相同的比例?3. 一块地上有80%是草地,剩下的部分是麦地和花园。
六年级数学下册解比例应用题专项练习

解比例应用题专项练习1、一幅地图,图上的4厘米,表示实际距离200千米,这幅图的比例尺是多少?2、甲、乙两地相距240千米,画在比例尺是1∶3000000的地图上,长度是多少厘米?3、在一幅地图上,用3厘米的线段表示实际距离600千米。
量得甲、乙两地的距离是4.5厘米,甲、乙两地的实际距离是多少千米?4、运来一批纸装订成练习本,每本36页,可订40本,若每本30页,可订多少本?5、在一幅比例尺是1:30000 的地图上,量得东、西两村的距离是12.3厘米,东、西两村的实际距离是多少米?6、甲地到乙地的实际距离是120千米,在一幅比例尺是1:6000000的地图上,应画多少厘米?7、一幅地图,图上的4厘米,表示实际距离200千米,这幅图的比例尺是多少?8、在一幅比例尺是1:4000 的平面图上,量得一块三角形的菜地的底是12厘米,高是8厘米,这块菜地的实际面积是多少公顷?9、一辆汽车2小时行驶130千米。
照这样的速度,从甲地到乙地共行驶5小时。
甲、乙两地相距多少千米?(用比例解)10、一辆汽车从甲地开往乙地,每小时行64千米,5小时到达。
如果要4小时到达,每小时需行驶多少千米?(用比例解)11、修一条公路,原计划每天修360米,30天可以修完。
如果要提前5天修完,每天要修多少米?(用比例解)12、修一条路,如果每天修120米,8天可以修完;如果每天修150米,可以提前几天可以修完?(用比例方法解)13、修一条公路,总长12千米,开工3天修了1.5千米。
照这样计算,修完这条路还要多少天?(用比例解答)14、修一条路,如果每天修120米,8天可以修完;如果每天多修30米,几天可以修完?(用比例方法解)15、小明买4本同样的练习本用了4.8元,138元可以买多少本这样的练习本?(用比例解答)16、工厂有一批煤,计划每天烧2.4吨,42天可以烧完。
实际每天节约12.5%,实际可以烧多少天?(比例解)17、解放军某部行军演习,4小时走了22.4千米,照这样的速度又行了6小时,一共行了多少千米?(用比例方法解)18、一对互相啮合的齿轮,主动轮有60个齿,每分转80转。
六年级数学典型比例应用题解答

六年级数学典型比例应用题解答例题、一辆汽车从甲地开往乙地,每小时行驶70千米,6小时到达,如果要4小时到达,每小时要行驶多少千米?【点拨】用比例知识解答,就要确定题中的两种量成什么比例,题中的不变量是甲乙两地的之间的路程一定,时间和速度成反比例,所以两次行驶的速度和时间的积相等,从而列出比例式进行解答【解答】设每小时要行驶X千米4x=70×6x=105【练习】1、一根圆柱,如果锯成5段,要8分钟,如果锯成10段,要多少小时?2、把一根长3米的圆柱木棒每50厘米锯成一段,共要10分钟,如果每60厘米锯成一段,共要多少分钟?例题、用边长4分米的方砖给教室铺地,要450块,如果改用边长6分米的方砖铺地,要多少块?【点拨】先弄清哪两个量成比例,成什么比例。
根据题意,房间的面积一定,则每块方砖的面积和方砖的块数成反比例。
【解答】设要X块4²×450=6²XX=200【练习】1、用同样的方砖给教室铺地,铺18平方米要用400块砖,如果铺36平方米,要多少块砖?2、同学们做广播操,每行站15人,站了12行,如果每行站18人,要站多少行?3、马东风电子车间要加工一批电子产品,计划每天加工50件,24天可以完成,实际每天比原计划多加工1/5,实际几天完成?4、一台织布机4小时织布32米,照这样计算,15小时织布多少米?5、修一条长6400米的公路,修了20天后,还剩下4800米,照这样计算,剩下的路要修多少天?1、工程队修一条水渠,原计划每天修360米,30天修完。
修10天后,每天多修40米,再修多少天就能完成任务?2、农场挖一条水渠,头5天挖了180米,照这样速度,又用了16天挖完这条水渠。
这条水渠全长多少米?3、40千克小麦能磨面粉32千克,照这样计算,7吨小麦能磨面粉多少千克?4、机床厂4天能生产小机床32台,照这样计算,要生产120台小机床需几天?5、测量小组把一米长的竹竿直立在地面上,测得它的影子长度是1.6米,同时测得电线杆的影子长度是4米,求电线杆高多少米?6、要测量一棵树的高度,量得树的影子长度是8.4米,同时用一根2米长的标杆直立在地面上,量得影子长度是1.2米,这棵树高是多少米?7、一辆汽车从甲地开往乙地,甲乙两地相距405千米,头4小时行驶了180千米,剩下的路程还要行多少小时?8、某印刷厂计划三月份印刷课本20000本,结果上旬就印刷7000本,照这样速度,三月份可以多印刷多少本?9、用5辆同样汽车运粮食一次能运22.5吨,照这样计算,要把36吨粮食一次运完,需要增加多少辆这样的汽车?10、服装厂生产制服,前3个月生产0.48万套,照这样计算,今年可以生产制服多少万套?11、农场用3辆拖拉机耕地,每天共耕225公顷,如果用5辆同样的拖拉机,每天共耕在多少公顷?12、一艘轮船,从甲地开往乙地,每小时行20千米,12小时到达,从乙地返回甲地时,每小时航行4千米,几小时可以到达?13、100千克黄豆可以榨油13千克,照这样计算,要榨豆油6.5吨,需黄豆多少吨?14、一个房间,用边长3分米的方砖铺地,需要432块,如果改用边长4分米的方砖铺地,需要多少块?17.在一幅地图上,测得甲、乙两地的图上距离是12厘米,已知甲乙两地的实际距离是480千米。
六年级数学比应用题

六年级数学比应用题一、简单的比的计算应用题(1 - 5题)1. 已知甲、乙两数的比是3:5,甲数是12,求乙数。
- 解析:- 因为甲、乙两数的比是3:5,设乙数为x,则(甲)/(乙)=(3)/(5)。
- 已知甲数是12,即(12)/(x)=(3)/(5)。
- 根据比例的性质,内项之积等于外项之积,可得3x = 12×5。
- 解得x=(12×5)/(3)=20。
2. 某班男、女生人数比是4:3,男生有24人,女生有多少人?- 解析:- 设女生有x人,因为男、女生人数比是4:3,所以(24)/(x)=(4)/(3)。
- 由比例性质可得4x = 24×3。
- 解得x=(24×3)/(4)=18人。
3. 一种药水是把药粉和水按照1:100的比配成的。
要配制这种药水4040克,需要药粉多少克?- 解析:- 药粉和水的比是1:100,那么药水就是1 + 100=101份。
- 这种药水共4040克,那么一份就是4040÷101 = 40克。
- 药粉占1份,所以需要药粉40克。
4. 学校图书馆里科技书和故事书的比是3:4,科技书有180本,故事书有多少本?- 解析:- 设故事书有x本,因为科技书和故事书的比是3:4,所以(180)/(x)=(3)/(4)。
- 根据比例性质3x=180×4。
- 解得x=(180×4)/(3)=240本。
5. 甲、乙两个数的比是5:6,它们的和是66,求甲、乙两数。
- 解析:- 甲、乙两个数的比是5:6,设甲数是5x,乙数是6x。
- 它们的和是66,则5x + 6x=66。
- 即11x = 66,解得x = 6。
- 所以甲数5x = 5×6 = 30,乙数6x=6×6 = 36。
二、比在几何中的应用题(6 - 10题)6. 一个长方形的长和宽的比是5:3,长是25厘米,宽是多少厘米?- 解析:- 设宽是x厘米,因为长和宽的比是5:3,所以(25)/(x)=(5)/(3)。
苏教版数学六年级下册专项~比例解决问题【含答案】
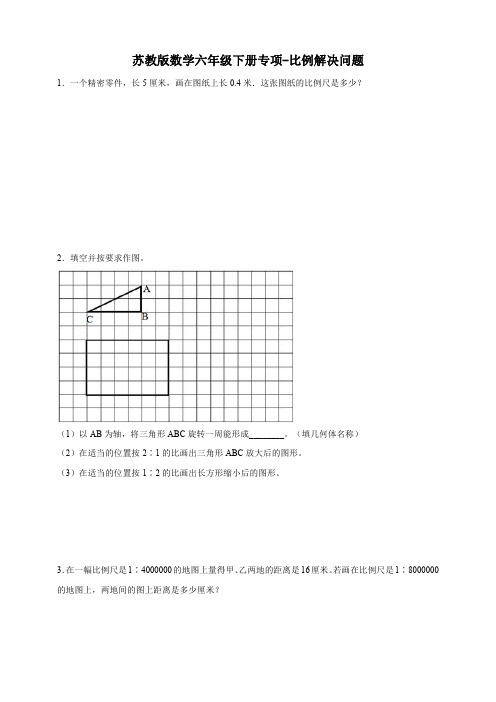
苏教版数学六年级下册专项-比例解决问题1.一个精密零件,长5厘米,画在图纸上长0.4米.这张图纸的比例尺是多少?2.填空并按要求作图。
(1)以AB为轴,将三角形ABC旋转一周能形成________。
(填几何体名称)(2)在适当的位置按2∶1的比画出三角形ABC放大后的图形。
(3)在适当的位置按1∶2的比画出长方形缩小后的图形。
3.在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。
若画在比例尺是1∶8000000的地图上,两地间的图上距离是多少厘米?4.画一画,填一填。
(1)按3∶1的比画出图形A放大后得到的图形B。
(2)按1∶2的比画出图形B缩小后得到的图形C。
我发现:放大或缩小前后的图形()变了,但()没有变,而且图形各部分长度是按一定的比变化的。
5.在一张比例尺是1∶150的建筑图纸上,量得一座大楼的长是6分米,这座大楼的实际长与宽的比是3∶1,这座大楼的实际宽是多少米?6.下图中小平行四边形按比放大后得到大平行四边形,求大平行四边形的高。
(单位:分米)12.根据图中提供的信息,完成下列问题。
(1)自来水厂要从水库取水,取水管道怎样铺最短,请在图中画出来。
(2)自来水厂到城区的送水管道经测算最短是2000米,请你测算:自来水厂到水库的取水管道最短需多少米?13.在一幅地图上,用5厘米长的线段表示实际距离100千米,这幅地图的比例尺是多少?如果甲市至乙市的铁路线路长150千米,那么这段铁路线路在这幅地图上的长度是多少厘米?14.江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。
广场绿地面积与铺装面积的比是6∶5,其中铺装面积共5000平方米,绿地面积有多少平方米?15.甲乙两城相距150千米,在一幅地图上量得甲乙两城之间的距离是5厘米,同时在这幅地图上量得乙丙两城之间的距离是8厘米。
乙丙两城之间的实际距离是多少千米?20.下图中A点是游乐场所在的位置,B点是电影院所在的位置,两地实际距离相距2千米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学六年级数学《用比例解应用题复习》教学设计
令狐采学教学目标
1.复习正反比例的意义,练习判断两种2.复习用正比例方法解答应用题。
3.复习用反比例方法解答应用题。
教学重点和难点
判断两种相关联的量成什么比例;确定解教学过程设计
(一)复习数量关系
判断两种相关联的量成不成比例,确定解1.被除数一定,除数和商。
2.一条路,已修的和未修的。
3.梯形的上、下底长度一定,梯形的面4.每块砖的面积一定,砖的块数和铺地5.挖一条水渠,参加的人数和所需要的6.从甲地到乙地所需的时间和所行走的7.单位面积一定,播种面积和总产量。
8.时间一定,速度和距离。
9.订阅《北京儿童》的份数和所需钱数(二)复习应用题
1.某工厂八月份计划造一批机床,开工第一步,先找对应关系:
第二步,判断成什么比例?(每天生产的台数请你在对应关系的旁边写上“正”字,决解设到月底可生产x台。
x=217
答:照这样速度月底可生产217台。
2.一批纸张,钉成20页一本的练习本,第一步,先找对应关系:
第二步,判断成什么比例?(纸张总页数一定请你在对应关系的旁边写上“反”字,决解钉成24页一本的练习本,可钉x本
答:如果钉成24页一本的练习本可钉500学生独立地用老师教的分析应用题的思路
(1)火车3小时行135千米,用同样的速度
(2)有一批砖,25人去搬,6小时搬完,如
(三)练习解答两步的比例应用题
1.李涛读一本书,每天读6页,30天可黑板上的对应关系变成:
解设x天读完。
答:18天可以读完。
2.在第1题的基础上,改变问题。
李涛读一本书,每天读6页,30天可以读完对应关系:
解设如果每天多读4页,x天读完。
(指导学生分析、比较。
)
以上两道题,什么发生了变化?什么没有变?练习(学生独立分析,做题。
)
1.一辆汽车从甲城开往乙城,3小时行驶
解设甲城到乙城有x千米。
3x=105×(3+1.2)
x=147
答:甲城到乙城有147km。
2.光明乡有144公顷水稻,5天收割了
解设剩下的x天可以收割完。
(再用间接设的方法做两道题。
)
1.纺织厂的织布车间过去每人看16台织
2.某机器厂原计划每天生产机器48台,
(四)总结
这节课我们主要复习了解正、反比例应用比例还是反比例,就可以正确解答了。
课堂教学设计说明
解答正、反比例应用题是有其独特的思考
第一层次,先做判断练习,判断两个相关
第二层次,进行最基本的正反比例应用题学生良好的学习习惯和学习方法。
第三层次,进行间接设的正、反比例应用
板书设计。
