「精品」高考高考数学试题分项版解析专题21几何体的表面积与体积理
空间几何体的三视图、表面积和体积 高考数学真题与解析
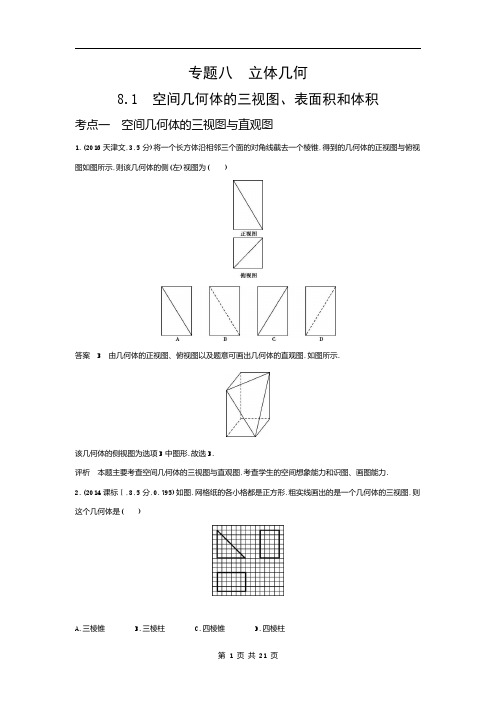
专题八立体几何8.1空间几何体的三视图、表面积和体积考点一空间几何体的三视图与直观图1.(2016天津文,3,5分)将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为()答案B由几何体的正视图、俯视图以及题意可画出几何体的直观图,如图所示.该几何体的侧视图为选项B中图形.故选B.评析本题主要考查空间几何体的三视图与直观图,考查学生的空间想象能力和识图、画图能力.2.(2014课标Ⅰ,8,5分,0.795)如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱答案B 由题中三视图可知该几何体的直观图如图所示,则这个几何体是三棱柱,故选B.3.(2014北京理,7,5分)在空间直角坐标系O-xyz 中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,2).若S 1,S 2,S 3分别是三棱锥D-ABC 在xOy,yOz,zOx 坐标平面上的正投影图形的面积,则()A.S 1=S 2=S 3B.S 2=S 1且S 2≠S 3C.S 3=S 1且S 3≠S 2D.S 3=S 2且S 3≠S 1答案D 三棱锥D-ABC 如图所示.S 1=S △ABC =12×2×2=2,S 2=12×2×2=2,S 3=12×2×2=2,∴S 2=S 3且S 1≠S 3,故选D.4.(2014课标Ⅰ理,12,5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A.62B.6C.42D.4答案B 由多面体的三视图可知该几何体的直观图为一个三棱锥,如图所示.其中面ABC⊥面BCD,△ABC 为等腰直角三角形,AB=BC=4,取BC 的中点M,连接AM,DM,则DM⊥面ABC,在等腰△BCD 中,BD=DC=25,BC=DM=4,所以在Rt△AMD 中,AD=B 2+D 2=42+22+42=6,又在Rt△ABC 中,AC=42<6,故该多面体的各条棱中,最长棱为AD,长度为6,故选B.评析本题考查空间几何体的三视图与直观图之间的互相转化,考查面面垂直性质定理的应用.同时考查考生的空间想象能力和运算求解能力.正确画出三棱锥的直观图是解决本题的关键.5.(2013课标Ⅱ,理7,文9,5分)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为()答案A设O(0,0,0),A(1,0,1),B(1,1,0),C(0,1,1),将以O、A、B、C为顶点的四面体补成一正方体后,由于OA⊥BC,所以该几何体以zOx平面为投影面的正视图为A.方法归纳由几何体直观图画三视图的要求:①注意三个视图对应的观察方向;②注意视图中虚线与实线的区别;③画出的三视图要符合“长对正,高平齐,宽相等”的基本特征.6.(2013湖南理,7,5分)已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B.2C.2-12D.2+12答案C若该正方体的放置方式如图所示,当正视的方向与正方体的任一侧面垂直时,正视图的面积最小,其值为1,当正视的方向与正方体的对角面BDD1B1或ACC1A1垂直时,正视图的面积最大,其值为2,由于正视的方向不同,因此正视图的面积S∈[1,2].故选C.评析本题考查空间几何体的三视图与直观图,考查学生空间想象能力及有关知识的应用能力,解答本题应设法求出正视图的面积的取值范围,而不应该逐项计算.7.(2011课标理,6文,8,5分)在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()答案D 由几何体的正视图和俯视图可知,该几何体应为一个半圆锥和一个有一侧面垂直于底面的三棱锥组成的组合体,故其侧视图应为D 选项.错因分析将组合体看成半圆柱和三棱锥的组合或不注意C 和D 中中线实虚的含义,易误选A 或C.评析本题主要考查空间几何体的三视图,考查学生的识图能力和空间想象能力.考点二空间几何体的表面积与体积1.(2018课标Ⅰ文,5,5分)已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A.122πB.12πC.82πD.10π答案B 本题主要考查圆柱的表面积及圆柱的轴截面.设圆柱的底面半径为r,高为h,由题意可知2r=h=22,∴圆柱的表面积S=2πr 2+2πr·h=4π+8π=12π.故选B.解题关键正确理解圆柱的轴截面及熟记圆柱的表面积公式是解决本题的关键.2.(2016课标Ⅱ文,4,5分)体积为8的正方体的顶点都在同一球面上,则该球的表面积为()A.12πB.323πC.8πD.4π答案A 设正方体的棱长为a,则a 3=8,解得a=2.设球的半径为R,则2R=3a,即R=3,所以球的表面积S=4πR 2=12π.故选A.方法点拨对于正方体与长方体,其体对角线为其外接球的直径,即外接球的半径等于体对角线的一半.3.(2016课标Ⅲ,理10,文11,5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18+365B.54+185C.90D.81答案B由三视图可知,该几何体是底面为正方形(边长为3),高为6,侧棱长为35的斜四棱柱.其表面积S=2×32+2×3×35+2×3×6=54+185.故选B.易错警示学生易因空间想象能力较差而误认为侧棱长为6,或漏算了两底面的面积而致错.4.(2015课标Ⅰ理,11,5分)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1B.2C.4D.8答案B由已知条件可知,该几何体由圆柱的一半和半球组成,其表面积为2πr2+πr2+4r2+2πr2=5πr2+4r2.由5πr2+4r2=16+20π得r=2.故选B.5.(2015北京理,5,5分)某三棱锥的三视图如图所示,则该三棱锥的表面积是()A.2+5B.4+5C.2+25D.5答案C 由三视图可得该三棱锥的直观图如图所示,其中PA=1,BC=2,取BC 的中点M,连接AM,MP,则AM=2,AM⊥BC,故AC=AB=B 2+A 2=1+4=5,由正视图和侧视图可知PA⊥平面ABC,因此可得PC=PB=B 2+A 2=1+5=6,PM=B 2+A 2=1+4=5,所以三棱锥的表面积为S △ABC +S △PAB +S △PAC +S △PBC =12×2×2+12×5×1+12×5×1+12×2×5=2+25,故选C.6.(2015陕西,理5,文5,5分)一个几何体的三视图如图所示,则该几何体的表面积为()A.3πB.4πC.2π+4D.3π+4答案D 由题中三视图知该几何体是底面半径为1,高为2的半个圆柱,故其表面积S=2×12×π×12+π×1×2+2×2=3π+4.评析本题考查三视图的概念和性质以及圆柱的表面积,考查运算及推理能力和空间想象能力.由三视图确定几何体的直观图是解题的关键.7.(2015课标Ⅱ,理9,文10,5分,0.685)已知A,B 是球O 的球面上两点,∠AOB=90°,C 为该球面上的动点.若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为()A.36πB.64πC.144πD.256π答案C ∵S △OAB 是定值,且V O-ABC =V C-OAB ,∴当OC⊥平面OAB 时,V C-OAB 最大,即V O-ABC 最大.设球O 的半径为R,则(V O-ABC )max =13×12R 2×R=16R 3=36,∴R=6,∴球O 的表面积S=4πR 2=4π×62=144π.思路分析由△OAB 的面积为定值分析出当OC⊥平面OAB 时,三棱锥O-ABC 的体积最大,从而根据已知条件列出关于R 的方程,进而求出R 值,利用球的表面积公式即可求出球O 的表面积.导师点睛点C 是动点,在三棱锥O-ABC 中,如果以面ABC 为底面,则底面面积与高都是变量,而S △OAB 为定值,因此转化成以面OAB 为底面,这样高越大,体积越大.8.(2014浙江理,3,5分)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是()A.90cm2B.129cm2C.132cm2D.138cm2答案D由三视图可知该几何体由一个直三棱柱与一个长方体组合而成(如图),其表面积为S=3×5+2×12×4×3+4×3+3×3+2×4×3+2×4×6+3×6=138(cm2).9.(2014福建文,5,5分)以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于()A.2πB.πC.2D.1答案A由题意得圆柱的底面半径r=1,母线l=1.∴圆柱的侧面积S=2πrl=2π.故选A.10.(2018浙江,3,4分)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.2B.4C.6D.8答案C本小题考查空间几何体的三视图和直观图以及几何体的体积公式.由三视图可知该几何体是直四棱柱,其中底面是直角梯形,直角梯形上,下底边的长分别为1cm,2cm,高为2 cm,直四棱柱的高为2cm.故直四棱柱的体积V=1+22×2×2=6cm3.思路分析(1)利用三视图可判断几何体是直四棱柱;(2)利用“长对正,高平齐,宽相等”的原则,可得直四棱柱的各条棱长.11.(2016山东理,5,5分)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为()A.13+23πB.13+C.13+答案C由三视图可知四棱锥为正四棱锥,底面正方形的边长为1,四棱锥的高为1,球的直径等于正四棱锥底面正方形的对角线的长,所以球的直径2R=2,即所以半球的体积为23πR3又正四棱锥的体积为13×12×1=13,所以该几何体的体积为13+故选C.易错警示不能从俯视图中正确地得到球的半径,而错误地从正视图中得到球的半径R=12.评析本题考查了空间几何体的三视图和体积公式.正确得到几何体的直观图并准确地计算是解题关键.12.(2016北京,6,5分)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.16B.13C.12D.1答案A由三视图可画出三棱锥的直观图如图所示,其底面是等腰直角三角形ACB,直角边长为1,三棱锥的高为1,故体积V=13×12×1×1×1=16.故选A.13.(2015课标Ⅰ,理6,文6,5分,0.451)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛答案B设圆锥底面的半径为R尺,由14×2πR=8得R=16π,从而米堆的体积V=14×13πR2×5=16×203π(立方尺),因此堆放的米约有16×203×1.62π≈22(斛).故选B.14.(2015课标Ⅱ,理6,文6,5分,0.426)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为()A.18B.17C.16D.15答案D如图,由已知条件可知,在正方体ABCD-A1B1C1D1中,截去三棱锥A-A1B1D1后剩余的部分即为题中三视图对应的几何体,设该正方体的棱长为a,则截去部分的体积为16a3,剩余部分的体积为a3-16a3=56a3.它们的体积之比为15.故选D.15.(2015重庆理,5,5分)某几何体的三视图如图所示,则该几何体的体积为()A.13+2πB.13π6C.7π3D.5π2答案B由三视图可知,该几何体是一个底面半径为1,高为2的圆柱和底面半径为1,高为1的半圆锥拼成的组合体.所以该几何体的体积为12×13×π×12×1+π×12×2=13π6,故选B.16.(2015浙江理,2,5分)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A.8cm3B.12cm3C.323cm3D.403cm3答案C由三视图知,该几何体是由棱长为2cm的正方体和底面边长为2cm,高为2cm的正四棱锥组合而成的几何体.所以该几何体的体积V=23+13×22×2=323cm3,故选C.17.(2015山东理,7,5分)在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为()A.2π3B.4π3C.5π3D.2π答案C如图,此几何体是底面半径为1,高为2的圆柱挖去一个底面半径为1,高为1的圆锥,故所求体积V=2π-π3=5π3.评析本题主要考查几何体的体积及空间想象能力.18.(2015湖南文,10,5分)某工件的三视图如图所示.现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为材料利用率=新工件的体积)原工件的体积A.89πB.827πC.24(2-1)3πD.8(2-1)3π答案A由三视图可知,原工件是一个底面半径为1,母线长为3的圆锥,则圆锥的高为22,新工件是该圆锥的内接正方体,如图,此截面中的矩形为正方体的对角面,设正方体的棱长为x,则22x1=22-x22,解得x=223.所以正方体的体积V1223=16227,又圆锥的体积V2=13π×12×22=223π,所以原工件材料的利用率为12=89π,故选A.19.(2014陕西理,5,5分)已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为()A.32π3B.4πC.2πD.4π3答案D 如图为正四棱柱AC 1.根据题意得AC=2,∴对角面ACC 1A 1为正方形,∴外接球直径2R=A 1C=2,∴R=1,∴V 球=4π3,故选D.20.(2014课标Ⅱ,理6,文6,5分,0.506)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.1727 B.59C.1027D.13答案C 该零件是两个圆柱体构成的组合体,其体积为π×22×4+π×32×2=34πcm 3,圆柱体毛坯的体积为π×32×6=54πcm 3,所以切削掉部分的体积为54π-34π=20πcm 3,所以切削掉部分的体积与原来毛坯体积的比值为20π54π=1027,故选C.21.(2014课标Ⅱ文,7,5分,0.495)正三棱柱ABC-A 1B 1C 1的底面边长为2,侧棱长为3,D 为BC 中点,则三棱锥A-B 1DC 1的体积为()A.3B.32C.1答案C 在正三棱柱ABC-A 1B 1C 1中,∵AD⊥BC,AD⊥BB 1,BB 1∩BC=B,∴AD⊥平面B 1DC 1,∴t1D1=13△1D1·AD=13×12×2×3×3=1,故选C.22.(2013课标Ⅰ,理8,文11,5分,0.718)某几何体的三视图如图所示,则该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π答案A由三视图可知该几何体由长方体和圆柱的一半组成.其中长方体的长、宽、高分别为4、2、2,圆柱的底面半径为2,高为4.所以该几何体的体积V=4×2×2+12π×22×4=16+8π.故选A.思路分析由三视图分析该几何体的构成,从而利用三视图中的数据计算几何体的体积.23.(2013浙江文,5,5分)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.108cm3B.100cm3C.92cm3D.84cm3答案B由三视图可知,该几何体是一个长方体截去了一个三棱锥,结合所给数据,可得其体积为6×6×3-13×12×4×4×3=100(cm3),故选B.24.(2012大纲全国,理7,文7,5分)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12D.18答案B由三视图可得,该几何体为如图所示的三棱锥S-ABC,其中底面△ABC为等腰三角形,底边AC=6,AC 边上的高为3,SB⊥底面ABC,且SB=3,所以该几何体的体积V=13×12×6×3×3=9.故选B.评析本题考查了三视图和三棱锥的体积,考查了空间想象能力.由三视图正确得到该几何体的直观图是求解的关键.25.(2011陕西文,5,5分)某几何体的三视图如图所示,则它的体积为()A.8-2π3B.8-π3C.8-2πD.2π3答案A由给出的三视图可得原几何体为正方体中挖去一圆锥,且此圆锥以正方体的上底面内切圆为底,以正方体的棱长为高.故所求几何体的体积为8-13×π×12×2=8-2π3.评析三视图是考查空间想象能力很好的一个题材,正确解答此类题目的关键是平时空间想象能力的培养,对文科学生来说,本题属中等难度题.26.(2016课标Ⅰ,6,5分)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π,则它的表面积是()A.17πB.18πC.20πD.28π答案A由三视图知该几何体为球去掉了18所剩的几何体(如图),设球的半径为R,则78×43πR3=28π3,故R=2,从而它的表面积S=78×4πR2+34×πR2=17π.故选A.27.(2016课标Ⅱ,6,5分)下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.20πB.24πC.28πD.32π答案C由三视图可得圆锥的母线长为22+(23)2=4,∴S圆锥侧=π×2×4=8π.又S圆柱侧=2π×2×4=16π,S圆柱底=4π,∴该几何体的表面积为8π+16π+4π=28π.故选C.思路分析先求圆锥的母线长,从而可求得圆锥的侧面积,再求圆柱的侧面积与底面积,最后求该几何体的表面积.28.(2017课标Ⅱ文,15,5分)长方体的长,宽,高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为.答案14π解析本题考查长方体和球的性质,考查了球的表面积公式.由题意知长方体的体对角线为球O的直径,设球O的半径为R,则(2R)2=32+22+12=14,得R2=72,所以球O的表面积为4πR2=14π.疑难突破明确长方体的体对角线为球O的直径是求解的关键.易错警示易因用错球的表面积公式而致错.29.(2013课标Ⅱ,15,5分,0.158)已知正四棱锥O-ABCD底面边长为3,则以O为球心,OA为半径的球的表面积为.答案24π解析设底面中心为E,连接OE,AE,则|AE|=12|AC|=∵体积V=13×|AB|2∴|OA|2=|AE|2+|OE|2=6.从而以OA为半径的球的表面积S=4π·|OA|2=24π.思路分析先根据已知条件直接利用锥体的体积公式求得正四棱锥O-ABCD的高,再利用勾股定理求出|OA|,最后根据球的表面积公式计算即可.30.(2013课标Ⅰ,15,5分,0.123)已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为.答案9π2解析平面α截球O所得截面为圆面,圆心为H,设球O的半径为R,则由AH∶HB=1∶2得OH=13R,由圆H的面积为π,得圆H的半径为1,+12=R2,得出R2=98,所以球O的表面积S=4πR2=4π·98=92π.31.(2013福建理,12,4分)已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是.答案12π解析由三视图知:棱长为2的正方体内接于球,故正方体的体对角线长为23,即为球的直径.所以球的表面积为232=12π.32.(2017江苏,6,5分)如图,在圆柱O 1O 2内有一个球O,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则12的值是.答案32解析本题考查空间几何体的体积.设圆柱内切球的半径为R,则由题设可得圆柱O 1O 2的底面圆的半径为R,高为2R,∴12=π2·2R 43π3=32.33.(2018天津理,11,5分)已知正方体ABCD-A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH 的体积为.答案112解析本题主要考查正方体的性质和正四棱锥的体积.由题意知四棱锥的底面EFGH 为正方形,其边长为22,即底面面积为12,由正方体的性质知,四棱锥的高为12.故四棱锥M-EFGH 的体积V=13×12×12=112.34.(2016天津理,11,5分)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m),则该四棱锥的体积为m3.答案2解析四棱锥的底面是平行四边形,由三视图可知其面积为2×1=2m2,四棱锥的高为3m,所以四棱锥的体积V=13×2×3=2m3.易错警示该题有两点容易出错:一是锥体的体积公式中的系数13易漏写;二是底面平行四边形的面积易错误地写成3×1=3m2.评析本题考查了三视图和直观图,考查了锥体的体积.35.(2016四川,13,5分)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是.答案解析由题意及正视图可知三棱锥的底面等腰三角形的底长为23,三棱锥的高为1,则三棱锥的底面积为12×22-(3)2×23=3,∴该三棱锥的体积为13×3×1=评析正确理解正视图中的数据在直观图中表示的含义很关键.36.(2014山东理,13,5分)三棱锥P-ABC中,D,E分别为PB,PC的中点,记三棱锥D-ABE的体积为V1,P-ABC的体积为V2,则12=.答案14解析如图,设S△ABD=S1,S△PAB=S2,E到平面ABD的距离为h1,C到平面PAB的距离为h2,则S 2=2S1,h2=2h1,V1=1S1h1,V2=1S2h2,∴1=1ℎ1=1.评析本题考查三棱锥的体积的求法以及等体积转化法在求空间几何体体积中的应用.本题的易错点是不能利用转化与化归思想把三棱锥的体积进行适当的转化,找不到两个三棱锥的底面积及相应高的关系,从而造成题目无法求解或求解错误.37.(2012安徽,12,5分)某几何体的三视图如图所示,则该几何体的体积等于.答案56解析由题意知,该三视图对应的几何体如图,其体积12(2+5)×4×4=56.评析本题主要考查三视图的知识,考查学生的空间想象能力.由三视图得到直观图是解题关键.38.(2011课标理,15,5分)已知矩形ABCD的顶点都在半径为4的球O的球面上,且AB=6,BC=23,则棱锥O-ABCD的体积为.答案83解析如图,连接AC,BD,交于O1,则O1为矩形ABCD所在小圆的圆心,连接OO1,则OO1⊥面ABCD,易求得O1C=23,又OC=4,∴OO1=B2-12=2,∴棱锥体积V=13×6×23×2=83.失分警示立体感不强,空间想象能力差,无法正确解出棱锥的高而得出错误结论.评析本题主要考查球中截面圆的性质及空间几何体的体积的计算,通过球这个载体考查学生的空间想象能力及推理运算能力.39.(2011课标文,16,5分)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上.若圆锥底面面积是这个球面面积的316,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为.答案13解析如图,设球的半径为R,圆锥底面半径为r,由题意得πr2=316×4πR2.=12R.体积较小的圆锥的高AO1=R-12R=12R,体积较大的圆锥的高BO1=R+12R=32R.1故这两个圆锥中,体积较小者的高与体积较大者的高的比值为13.评析本题考查球、球内接圆锥的相关问题,考查R,r的关系,由题意得到是解答本题的关键. 40.(2020课标Ⅰ文,19,12分)如图,D为圆锥的顶点,O是圆锥底面的圆心,△ABC是底面的内接正三角形,P 为DO上一点,∠APC=90°.(1)证明:平面PAB⊥平面PAC;(2)设DO=2,圆锥的侧面积为3π,求三棱锥P-ABC的体积.解析(1)由题设可知,PA=PB=PC.由于△ABC是正三角形,故可得△PAC≌△PAB,△PAC≌△PBC.又∠APC=90°,故∠APB=90°,∠BPC=90°.从而PB⊥PA,PB⊥PC,故PB⊥平面PAC,所以平面PAB⊥平面PAC.(2)设圆锥的底面半径为r,母线长为l.由题设可得rl=3,l2-r2=2.解得r=1,l=3.从而AB=3.由(1)可得PA2+PB2=AB2,故所以三棱锥P-ABC的体积为13×12×PA×PB×PC=13×12×第21页共21页。
2021-2022年高考数学专题-几何体的表面积与体积的求解

S△QAC S△PAC
S △QBC S △PBC
1 2
,由对称性得
AB
BC
AC
,又因为
QA2 AB 2
QB2 BC 2
QC 2 CA2
1, 3
S ABC 9
3
,所以 S ABC
1 2
AB2
sin 60
9
3 ,解得 AB 6, AQ 2
3,
所以 QM 3, PM 2 3, PQ 3 ,
1 3
,
S ABC
9
3 ,若要将此工艺品放入一个球形容器
(不计此球形容器的厚度)中,则该球形容器的表面积的最小值为( )
A. 42
B. 44
C. 48
D. 49
【答案】D
【分析】作 QM
AB ,连接 PM,易证 AB PM
,由 S△QAB S△PAB
1 AB QM 2 1 AB PM
1 ,得到 PM 2
3 32
3
3
2 1 x2 x2 1,解得 x 3
3 2
,所以
AD
3
,
S PAD
1 2
AD2
sin
60
33 4
,
因为 AB//CD//OM ,所以 AB 平面 APD , CD 平面 APD ,
所以
PA
AB
,
PD
CD ,
S PAB
S PCD
1 2
AB
AP
3,
因为 PB PC PA2 AB2 7 , BC 3 ,
作 PH BC 于 H ,所以 H 为 BC 的中点,所以 PH
PB2
1 2
BC
2
(完整word)高中数学立体几何表面积与体积复习.docx

空间几何体的表面积与体积考情考向分析本部分是高考考查的重点内容,主要涉及空间几何体的表面积与体积的计算.命题形式主要以填空题为主,考查空间几何体的表面积与体积的计算,涉及空间几何体的结构特征,要求考生要有较强的空间想象能力和计算能力,广泛应用转化与化归思想.1.多面体的表面积、侧面积因为多面体的各个面都是平面,所以多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=S 圆锥侧=S 圆台侧=3.柱、锥、台、球的表面积和体积名称表面积体积几何体柱体 (棱柱和圆柱 )S 表面积=S 侧+ 2S 底V=锥体 (棱锥和圆锥 )S表面积=V=台体 (棱台和圆台 )S表面积=V=球S=V=【知识拓展】1.与体积有关的几个结论(1)一个组合体的体积等于它的各部分体积的和或差.(2)底面面积及高都相等的两个同类几何体的体积相等.2.几个与球有关的切、接常用结论(1)正方体的棱长为 a,球的半径为 R,①若球为正方体的外接球,则2R= 3a;②若球为正方体的内切球,则2R= a;③若球与正方体的各棱相切,则2R= 2a.(2)若长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为 R,则 2R= a2+ b2+ c2题型一求空间几何体的表面积1.体积为 8 的正方体的顶点都在同一球面上,则该球的表面积为________.2.若三棱锥的三条侧棱两两垂直,且侧棱长都相等,其外接球的表面积是4π,则其侧棱长为________.3.各棱长均为 2 的正三棱锥的表面积是________.4.正六棱台的上、下两底面的边长分别是1cm,2cm,高是 1cm,则它的侧面积为________cm2.已知圆锥的表面积等于π2,其侧面展开图是一个半圆,则底面圆的半径为________cm.5.12 cm题型二求空间几何体的体积1.如图,在正三棱柱 ABC- A1B1C1中,已知 AB = AA1= 3,点 P 在棱 CC1上,则三棱锥 P -ABA 1的体积为 ________.2. 如图所示,已知一个多面体的平面展开图由一个边长为 1 的正方形和 4 个正三角形组成,则该多面体的体积是________.3.已知棱台的上、下底面面积分别为4,16,高为 3,则该棱台的体积为 ________.4. 已知某圆柱的侧面展开图是边长为2a, a 的矩形,求该圆柱的体积.题型三简单的等积变换1. 正三棱柱 ABC- A1B1C1的底面边长为2,侧棱长为3,D为BC的中点,则三棱锥A-B1DC 1的体积为 ________.高考汇编1.(2013 江·苏 )如图,在三棱柱 A1B1C1-ABC 中, D ,E,F 分别是 AB, AC,AA1的中点,设三棱锥 F- ADE 的体积为 V1,三棱柱 A1B1C1- ABC 的体积为 V2,则 V1∶V2= ________.2.(2014 江·苏 )设甲、乙两个圆柱的底面积分别为S,S ,体积分别为V ,V .若它们的侧面积1212相等,且S1=9,则V1的值是 ________.S4V223.(2015 江·苏 )现有橡皮泥制作的底面半径为 5,高为柱各一个.若将它们重新制作成总体积与高均保持不变,各一个,则新的底面半径为 ________.4 的圆锥和底面半径为2,高为 8 的圆但底面半径相同的新的圆锥和圆柱4.(2017.6)如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下面及母线均相切.记圆柱 O1O2的体积为 V1,球 O 的体积为 V2,则 V1的值是 ______.O2V2O.O1(第 4 题)5. (2018.10) 如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.6.(2016 江·苏 )现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥P—A1B1C1D1,下部分的形状是正四棱柱ABCD —A1B1C1D 1(如图所示 ),并要求正四棱柱的高OO1是正四棱锥的高PO1的 4 倍.(1)若 AB= 6m, PO1= 2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为 6m,则当 PO1为多少时,仓库的容积最大?解(1)V=1× 62× 2+ 62× 2× 4=312(m3) . 3(2)设 PO1= x,则 O1B1=62- x2, B1C1=2· 62- x2,∴ S A B C D=2(62-x2),1111又由题意可得下面正四棱柱的高为4x.126则仓库容积 V=3x·2(62- x2)+ 2(62- x2) ·4x=3 x(36- x2).由V′=0 得 x= 2 3或 x=- 2 3(舍去 ).由实际意义知 V 在 x= 2 3(m) 时取到最大值,故当 PO1= 2 3(m) 时,仓库容积最大.。
2021高考数学复习专题 空间几何体的表面积和体积(文 精讲)

专题8.2 空间几何体的表面积和体积【考情分析】1. 了解球、棱柱、棱锥、台的表面积和体积的计算公式. 【重点知识梳理】知识点一 圆柱、圆锥、圆台的侧面展开图及侧面积公式知识点二 柱、锥、台、球的表面积和体积【知识必备】1.设正方体的棱长为a ,则它的内切球半径r =a 2,外接球半径R =32a .2.设长方体的长、宽、高分别为a ,b ,c ,则它的外接球半径R =a 2+b 2+c 22.3.设正四面体的棱长为a ,则它的高为63a ,内切球半径r =612a ,外接球半径R =64a . 4.直棱柱的外接球半径可利用棱柱的上下底面平行,借助球的对称性,可知球心为上下底面外接圆圆心连线的中点,再根据勾股定理求球的半径.【典型题分析】高频考点一 空间几何体的的表面积【例1】(2020·新课标Ⅰ)已知A 、B 、C 为球O球面上的三个点,Ⅰ1O 为ABC 的外接圆,若Ⅰ1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A. 64πB. 48πC. 36πD. 32π【变式探究】(2020·北京卷)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).A 63+ B. 623+C. 123+D. 1223+【方法技巧】求空间几何体表面积的常见类型及思路【变式探究】(2018·全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A .122πB .12πC .82πD .10π高频考点二 空间几何体的体积的.【例2】(2020·浙江卷)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是()A. 73B.143C. 3D. 6【变式探究】【2019·北京卷】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.【变式探究】(2018·天津卷)已知正方体ABCD -A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M -EFGH 的体积为________.高频考点三 割补法求体积【例3】(2017·全国卷Ⅰ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π【方法技巧】把不规则的图形分割成规则的图形,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算其体积。
高三数学空间几何体的表面积与体积试题答案及解析

高三数学空间几何体的表面积与体积试题答案及解析1.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积是( ) A.B.16C.9D.【答案】A【解析】由已知条件可知球心在正四棱锥的高上,设球的半径为R,球心为O,正四棱锥底面中心为为E,则OE垂直棱锥底面,OE=4-R,所以(4-R)2+=R2,解得R=,所以球的表面积S=4=.【考点】正四棱锥的性质和球的表面积.2.在三棱锥中,底面为边长为的正三角形,顶点在底面上的射影为的中心,若为的中点,且直线与底面所成角的正切值为,则三棱锥外接球的表面积为__________.【答案】【解析】设M是中心,即面,∴是AE与面BCD所成角,EM是的内切圆半径r,,,在中,,∴,三棱锥外接球球心O在AM上,在中,,,即,,即,即.【考点】勾股定理、三棱锥的外接球的表面积.3.如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,,点H、G分别是线段EF、BC的中点.(1)求证:平面AHC平面;(2)(2)求此几何体的体积.【答案】(1)详见解析;(2).【解析】(1)要证面面垂直,首先证线面垂直.那么在本题中证哪条线垂直哪个面?结合条件可得,,所以面AHC,从而平面AHC平面BCE.(2)可将该几何体切割为三部分:,然后分别求出三部分的体积相加即得.(1)在菱形ABEF中,因为,所以是等边三角形,又因为H是线段EF的中点,所以因为面ABEF面ABCD,且面ABEF面ABCD=AB,所以AH面ABCD,所以在直角梯形中,AB=2AD=2CD=4,,得到,从而,所以,又AH AC=A所以面AHC,又面BCE,所以平面AHC平面BCE .6分(2)因为,所以 .12分【考点】(1)空间直线与平面的关系;(2)几何体的体积.4.一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如图所示,侧视图是一个矩形,则这个矩形的面积是()A.4B.2C.2D.【答案】B【解析】由题意可设棱柱的底面边长为a,则其体积为a2·a=2,得a=2.由俯视图易知,三棱柱的侧视图是以2为长,为宽的矩形.∴其面积为2.故选B.5.若一个正方体的表面积为S1,其外接球的表面积为S2,则=________.【答案】【解析】设正方体棱长为a,则正方体表面积为S1=6a2,其外接球半径为正方体体对角线长的,即为a,因此外接球的表面积为S2=4πr2=3πa2,则==.6.在如图所示的几何体中,四边形为正方形,四边形为等腰梯形,,,,.(1)求证:平面;(2)求四面体的体积;(3)线段上是否存在点,使平面?请证明你的结论.【答案】(1)详见解析;(2);(3)详见解析.【解析】(1)利用勾股定理得到,再结合并利用直线与平面垂直的判定定理证明平面;(2)先证明平面,从而得到为三棱锥的高,并计算的面积作为三棱锥的底面积。
高考数学专题复习:立体几何体的表面积与体积

高考数学专题复习:立体几何体的表面积与体积一、单选题1.一个圆柱的轴截面是一个面积为36的正方形,则该圆柱的体积是( ) A .54π B .36π C .16π D .8π2.在正三棱锥A BCD -中,BCD △的边长为6,侧棱长为积为( )A .754πB .75πCD 3.在菱形ABCD 中,6AB =,60A ∠=,连结BD ,沿BD 把ABD 折起,使得二面角A BD C --的大小为60,连结AC ,则四面体ABCD 的外接球的表面积为( ) A .13π B .24π C .36π D .52π 4.已知一个圆柱上,下底面的圆周都在同一个球面上,球的直径为4,圆柱底面直径为2,则圆柱的侧面积为( )A .B .C .D .5.一平面截一球得到直径为的圆面,球心到这个平面的距离为2cm ,则该球的体积为( )A .3256cm 3πB .364cm πC .364 c m 3πD .316cm 3π 6.若底面直径和高相等的圆柱的侧面积是π,则这个圆柱的体积是( ) A .π B .4π C .2π D .34π7.已知三棱锥S ABC -中,SA ⊥平面,4,60ABC SA BC BAC ==∠=︒,则三棱锥S ABC -外接球的表面积为( )A .32πB .64πC .80πD .128π8.已知一平面截一球得到直径为,则该球的体积为( )3cmA .12πB .36πC .D .108π 9.已知圆柱1OO 及其展开图如图所示,则其体积为( )A .πB .2πC .3πD .4π10.已知正四棱锥S ABCD -的底面边长为2,则该正四棱锥的体积等于( )A .43BC .D .411.已知A ,B 是球O 的球面上两点,23AOB π∠=,P 为该球面上动点,若三棱锥O PAB -体O 的表面积为( ) A .12π B .16π C .24π D .36π12.正四棱台的上、下底面边长分别是2和4,则该棱台的体积是( ) A .563 B .583 C .20 D .21二、填空题13.设体积为P ABC -外接球的球心为O ,其中O 在三棱锥P ABC -内部.若球O 的半径为R ,且球心O 到底面ABC 的距离为3R ,则球O 的半径R =__________. 14.将边长为1的正方形ABCD 沿对角线AC 折起,使ABD △为正三角形,则三棱锥A BCD -的体积为__________.15.已知正四棱台的上底边长为4,下底边长为8________. 16.如图边长为2的正方形ABCD 中,以B 为圆心的圆与AB ,BC 分别交于点E ,F ,若1tan 2CDF ∠=,则阴影部分绕直线BC 旋转一周形成的几何体的体积等于__________.三、解答题17.如图,已知圆锥的顶点为P ,O 是底面圆心,AB 是底面圆的直径,5PB =,3OB =.(1)求圆锥的表面积;(2)经过圆锥的高PO 的中点O '作平行于圆锥底面的截面,求截得的圆台的体积.18.如下图1,一个正三棱柱形容器中盛有水,底面三角形ABC 的边长为2cm ,侧棱14cm AA =,若侧面11AA B B 水平放置时(如下图2),水面恰好过AC ,BC ,11A C ,11B C 的中点.(1)求容器中水的体积;(2)当容器底面ABC 水平放置时(如图1),求容器内水面的高度.19.如果一个正四棱柱与一个圆柱的体积相等,那么我们称它们是一对“等积四棱圆柱”.将“等积四棱圆柱”的正四棱柱、圆柱的表面积与高分别记为1S 、2S 与1h 、2h .(1)若121h h ==,1=30S ,求2S 的值;(2)若12h h =,求证:12S S >.20.已知正三棱柱111ABC A B C -的底面边长为2D 为BC 的中点;(1)求该三棱柱的体积与表面积;(2)求三棱锥11D AB C -的内切球半径.21.如图,正三棱锥(底面是正三角形,侧棱长都相等)P ABC -的底面边长为2,侧棱长为3.-的表面积;(1)求正三棱锥P ABC-的体积.(2)求正三棱锥P ABC22.如图所示是在圆锥内部挖去一正四棱柱所形成的几何体,该正四棱柱上底面的四顶点在r=.圆锥侧面上,下底面落在圆锥底面内,已知圆锥侧面积为15π,底面半径为3(Ⅰ)若正四棱柱的底面边长为a(Ⅱ)求该几何体内正四棱柱侧面积的最大值.参考答案1.A【分析】设圆柱的底面半径为r ,则圆柱的高为2r ,利用圆柱的轴截面面积求出r 的值,再利用柱体体积公式可求得该圆柱的体积.【详解】设圆柱的底面半径为r ,则圆柱的高为2r ,该圆柱的轴截面面积为2436r =,解得3r =, 因此,该圆柱的体积为2223654V r r πππ=⨯=⨯⨯=.故选:A.2.B【分析】取CD 中点E ,连接BE ,在BE 上取点F ,使得23BF BE =,连接AF ,则点F 为三角形BCD的中心, 根据题意可得AF ⊥平面BCD ,求出BF =AF =半径为R ,则222)R R =+,解得R 【详解】解:取CD 中点E ,连接BE ,在BE 上取点F ,使得23BF BE =,连接AF , 则点F 为三角形BCD 的中心,根据题意可得AF ⊥平面BCD ,则该三棱锥外接球的球心O 在AF 上,BF ==,AF = 设该三棱锥外接球的半径为R ,则222)R R =+, 解得R∴该三棱锥外接球的表面积为:224475S R πππ==⨯=.故选:B .3.D【分析】取BD 的中点记为O ,分别取BCD △和ABD △的外心E 与F ,过这两点分别作平面BDC 、平面ABD 的垂线,交于点P ,则P 就是外接球的球心,先在POE △中,求解1PE =,再在PCE ,求PC 可得球半径,进而得解.【详解】如图,取BD 的中点记为O ,连接OC ,OA ,分别取BCD △和ABD △的外心E 与F ,过这两点分别作平面BDC 、平面ABD 的垂线,交于点P ,则P 就是外接球的球心,连接OP ,CP ,易知AOC ∠为二面角A BD C --的平面角为60,则AOC △是等边三角形,其边长为6=1133OE OC ==⨯在POE △中,30POE ∠=,∴tan 30=3PE OE =⋅⨯∵2=3CE OC =∴PC R ====则四面体ABCD 的外接球的表面积为2452ππ⨯=.故选:D.4.B【分析】由题意结合勾股定理可得12h = 【详解】设圆柱的高为h ,球的半径为R ,圆柱的底面半径为r ,根据题意,2,1R r ==,由勾股定理可得12h h =S 侧221rh ππ==⨯⨯=,故选:B5.A【分析】依题意求得球半径即可.【详解】依题意得球半径4R =,所以该球的体积33442564333V R πππ==⨯=(cm 3). 故选:A.6.B【分析】设出圆柱底面圆半径r 并表示出其高,借助圆柱侧面积求出r 即可作答.【详解】设圆柱底面圆半径为r ,依题意得高2h r =,于是得圆柱侧面积224S r h r πππ=⋅==,解得12r =,1h =, 所以圆柱的体积为24V Sh r h ππ==⋅=.故选:B7.A【分析】根据三棱锥中线面位置关系求解外接球的半径,进而求出外接球的表面积.【详解】 ABC 中,23,60BC BAC =∠=︒,设 ABC 的外接圆半径为r ,根据正弦定理有, 23242sin sin 60BC r r BAC ===∴=∠︒如图,1O 点为 ABC 的外心,O 三棱锥外接球的球心SA ⊥平面ABC , 1//OO SA ∴,且 OS OA =1122OO SA ∴== 1Rt AO O 中,11122,90AO r OO AO O ===∠=︒,, 22AO ∴= 即三棱锥外接球的半径为:22所以外接球的表面积为()24π·2232π=,选项A 正确,选项BCD 错误故选:A.8.B【分析】由球的截面性质求得球半径后可得体积.【详解】由题意截面圆半径为r =3R ==, 体积为334433633V R πππ==⨯=. 故选:B .9.D【分析】结合展开图求出圆柱的底面半径与高,进而结合体积公式即可求出结果.【详解】设底面半径为r ,高为h ,根据展开图得422h r ππ=⎧⎨=⎩,则41h r =⎧⎨=⎩,所以圆柱的体积为22144r h πππ=⨯⨯=,故选:D.10.A【分析】首先计算正四棱锥的高,再计算体积.【详解】如图,正四棱锥S ABCD -,SB =OB =1SO =, 则该正四棱锥的体积1422133V =⨯⨯⨯=.故选:A【分析】当点P 位于垂直于面AOB 的直径端点时,三棱锥O PAB -的体积最大,利用三棱锥O PAB -体O 的表面积. 【详解】解:如图所示,当点P 位于垂直于面AOB 的直径端点时,三棱锥O PAB -的体积最大, 设球O 的半径为R ,此时21132O PAB P AOB V V R R --==⨯=, 解得2R =,则球O 的表面积为2416R ππ=,故选:B .12.A【分析】先求出棱台的高,然后利用台体的体积公式求体积即可.【详解】由棱台的几何特征可得其高为:2h , 则其体积为:(2215624233V =⨯+⨯=. 故选:A13.3【分析】根据等边三角形的性质,结合球的几何性质、棱锥的体积公式进行求解即可.取ABC 的中心G .连接PG ,则PG ⊥平面ABC 且球心O 在PG 上.由条件知,3R OG =,连接OA ,AG ,则AG ==,设等边ABC 的边长为a ,所以等边ABC =,因此23AG ===,所以有R a 362=,于是ABC .又OP R =, 故三棱锥P ABC -的高是:1433R R R +=,所以223148)333P ABC V R R R -=⋅⋅=⋅==3R =. 故答案为:314【分析】取AC 的中点O ,连接BO ,DO ,求出底面面积以及高,然后求解体积即可.【详解】取AC 的中点O ,连接BO ,DO ,由题意,AC ⊥BO ,AC ⊥DO ,BO DO == 因为ABD △为正三角形,AB =AD =DB =1,由已知可得AO =OB =OD ,∴OBD 是直角三角形,∴DO ⊥OB ,又,OD AC AC OB O ⊥⋂=,∴OD ⊥面ABC ,∴111332A BCD D ABC ABC V V S DO --==⋅=⨯=15.112【分析】 根据已知条件,分别计算出上、下底面面积以及棱台的高,代入棱台体积公式进行计算即可得解.【详解】因为正四棱台的上底边长为4,下底边长为8所以棱台的下底面积64S =,上底面积16S '=,高3h =,所以正四棱台的体积(()11641632311233V S S h '=⋅+⋅=⋅++⋅=. 故答案为:112.16.6π【分析】阴影部分绕直线BC 旋转一周形成的几何体是一个圆柱挖掉一个半球与圆锥,分别计算其体积,然后得到答案.【详解】在Rt DCF 中12,tan 212DC CF DC CDF ==∠=⨯=, 所以211BF BC CF =-=-=,正方形ABCD 绕直线BC 旋转一周形成圆柱,圆柱的底面半径2R AB ==,高12h BC ==,其体积2211228V R h πππ==⨯⨯=; 直角CDF 绕直线BC 旋转一周形成与圆柱同底的圆锥,圆锥的底面半径2R =,高21h CF ==,其体积222211421333V R h πππ==⨯⨯=;扇形BEF 是圆的14,绕直线BC 旋转一周形成一个半球,球的半径为1r BE ==, 故其体积33314142123233V r πππ=⨯=⨯⨯=; 所以阴影部分绕直线BC 旋转一周形成的几何体是一个圆柱挖掉上述的半球与圆锥, 故其体积123428633V V V V ππππ=--=--=. 故答案为:6π.17.(1)24π;(2)21π2. 【分析】(1)由题意可知,该圆锥的底面半径3r =,母线5l =,从而可求出锥的表面积,(2)先求出大圆锥的高,从而可求出小圆锥的高,进而可得圆台的体积等于大圆锥的体积减去小圆锥的体积【详解】解:(1)由题意可知,该圆锥的底面半径3r =,母线5l =.∴该圆锥的表面积22πππ3π3524πS r rl =+=⨯+⨯⨯=.(2)在Rt POB △中,4PO ==,∵O '是PO 的中点,∴2PO '=.∴小圆锥的高2h '=,小圆锥的底面半径1322r r '==, ∴截得的圆台的体积2211321π34π2π3322V V V ⎛⎫=-=⨯⨯⨯-⨯⨯⨯= ⎪⎝⎭小台大.18.(1))3cm ;(2)3cm . 【分析】(1)在图2中,根据四棱柱的体积公式计算可得;(2)设图1中水高度为cm h ,根据水的体积相等得到方程,解得即可;【详解】解:(1)在图2中,水所占部分为四棱柱.四棱柱底面积为)222112sin 601sin 6022S cm =⨯⨯︒-⨯⨯︒=,又高为4cm所以水的体积为)34V cm ==,(2)设图1中水高度为cm h ,则212sin 602V h =⨯⨯︒⨯=3h =. 所以当容器底面ABC 水平放置时,容器内水面的高度为3cm .19.(1)18+;(2)证明见解析.【分析】设正四棱柱的底面边长为a ,圆柱的底面半径为r ,2212πa h r h =,21124S a ah =+,2222π2πS r rh =+.(1)由121h h ==,1=30S 可得答案;(2)由21h h =,得22πa r =,212124S S a ah -=+22(2π2π)r rh -+化简可得答案.【详解】设正四棱柱的底面边长为a ,圆柱的底面半径为r ,则2212πa h r h =,21124S a ah =+,2222π2πS r rh =+.(1)224130a a +⨯=,得22150a a +-=,又0a >,所以3a =,所以22π131r ⨯=⨯,得r =292π2π1πS =⨯+18=+(2)证明:21h h =,则22πa r =,212124S S a ah -=+22(2π2π)r rh -+212π4r ah =+212π2πr rh --14ah =12πrh -12π)h r =0>.得证.20.(1)1113-=ABC A B C V ,111ABC A B C S -=(2 【分析】(1)直接利用体积公式求解即可,直接求解表面积,(2)利用等体积法求法【详解】(1)111223ABC A B C V Sh -===,111222232ABC A B C S S S -=+=+=底侧(2)111111112132D AB C B AB C C ABB V V V ---===⨯= 1111113,6AB D AC D B C D AC B S S S S ====,则三棱锥11D AB C -的表面积为+设三棱锥11D AB C -的内切球半径为r ,则113r ⨯⨯=,则r =21.(1);(2【分析】(1)取BC 的中点D ,连接PD ,利用勾股定理求得PD ,可得三角形PBC 的面积,进一步可得正三棱锥P ABC -的侧面积,再求出底面积,则正三棱锥P ABC -的表面积可求; (2)连接AD ,设O 为正三角形ABC 的中心,则PO ⊥底面ABC .求解PO ,再由棱锥体积公式求解.【详解】解:(1)取BC 的中点D ,连接PD ,在Rt PBD 中,可得PD = ∴1222PBC S BC PD == 正三棱锥的三个侧面是全等的等腰三角形,∴正三棱锥P ABC -的侧面积是33PBC S =⨯=正三棱锥的底面是边长为2的正三角形,∴122sin 602ABC S =⨯⨯⨯︒=△则正三棱锥P ABC -的表面积为(2)连接AD ,设O 为正三角形ABC 的中心,则PO ⊥底面ABC .且13OD AD ==在Rt POD 中,PO ==∴正三棱锥P ABC -的体积为1133ABC S PO ⋅==.22.(Ⅰ)16123π-;(Ⅱ)【分析】 (Ⅰ)分别计算圆锥和正四棱柱的体积,再计算该几何体的体积;(Ⅱ)首先利用比例关系求得1312h +=,再利用基本不等式求得1h a 的最大值,即可得到正四棱柱侧面积的最大值【详解】解:设圆锥母线长为l ,高为h ,正四棱柱的高为1h(Ⅰ)由S rl π=圆锥侧,有315l ππ=,故5l =,由222h r l +=,故4h =, 所以圆锥体积为2211341233V r h πππ==⨯⨯=圆锥由a =2, 由图可得11h r h r -=,所以11318433r h h r --==⨯=, 故正四棱柱的体积为21816233V a h ==⨯=正四棱柱 所以该几何体的体积为16123V V π-=-圆锥正四棱柱 (Ⅱ)由图可得12r h h r =,即13243h -=,即1312h +=由13h +≥136h ==时左式等号成立,有112h a ⇒≤12h =,a =故正四棱柱侧面积14S h a =≤侧,当且仅当12h =,a =所以该几何体内正四棱柱侧面积的最大值为。
三年高考(近年-近年)高考数学试题分项版解析专题21几何体的表面积与体积理(new)

10.【2015高考新课标2,理9】已知A,B是球O的球面上两点,∠AOB=90,C为该球面上的动点,若三棱锥O—ABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π C.144π D.256π
【答案】C
【解析】如图所示,当点C位于垂直于面 的直径端点时,三棱锥 的体积最大,设球 的半径为 ,此时 ,故 ,则球 的表面积为 ,故选C.
专题21 几何体的表面积与体积
1。【2017课标3,理8】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为
A.B. C. D.
【答案】B
【解析】
【考点】圆柱的体积公式
【名师点睛】(1)求解以空间几何体的体积的关键是确定几何体的元素以及线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.
6.【 2014湖南7】一块石材表示的几何体的三视图如图2所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于()
高三数学空间几何体的表面积与体积试题

高三数学空间几何体的表面积与体积试题1.一个棱锥的三视图如图(尺寸的长度单位为m),则该棱锥的全面积是______________(单位:m2).正视图侧视图俯视图【答案】【解析】该几何体是一三棱锥,底面是底边长为2 ,高为2 的等腰三角形,有一侧面垂直于底面,底边长为2 ,高为2 的等腰三角形,另两侧面是全等等腰三角形,腰长为,底边长2 ,所以该棱锥的全面积是=。
【考点】本题主要考查三视图,几何体的面积计算。
点评:基础题,三视图是高考必考题目,因此,要明确三视图视图规则,准确地还原几何体,明确几何体的特征,以便进一步解题。
注意图中虚线,是被遮掩的棱。
2.已知正方体的外接球的体积是,则这个正方体的棱长是 ( )A.B.C.D.【答案】B【解析】由于正方体的外接球的体积是,那么根据球的表面积公式可知为,设棱长为a,则可知,故选B.【考点】正方体的外接球点评:解决的关键是理解外接球的直径就是正方体的体对角线,那么可知与棱长的关系,进而得到结论,属于基础题。
3.已知某几何体的三视图如右图所示,则该几何体的体积是()A.B.C.D.【答案】A【解析】结合已知的三视图可知,该几何体是个直三棱柱,高度为1,底面是等腰直角三角形,则可以利用三棱柱的体积,故选A.【考点】三视图,体积运算点评:根据三视图还原几何体是高考的一个热点,能通过长对正,高平齐,宽相等,来得到求解,属于基础题。
4.已知三棱锥A-BCD内接于球O,AB=AD=AC=BD=,∠BCD=60°,则球O的表面积为A.B.C.D.【答案】D【解析】因为三棱锥A-BCD内接于球O,AB=AD=AC=BD=,∠BCD=60°,球心O在高线上,连OB, OC, OD,均与OA相等。
这是一个正三棱锥,利用“小结论”,球的半径等于三棱锥高的四分之三,而底面三角形的高为,由勾股定理得,三棱锥的高h=,所以球的半径r= ,球的表面积为4π()=,故选D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题21 几何体的表面积与体积1.【2017课标3,理8】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A.B.3π4C.π2D.π4【答案】B【解析】【考点】圆柱的体积公式【名师点睛】(1)求解以空间几何体的体积的关键是确定几何体的元素以及线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.2.【2017课标II,理4】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为()A.90π B.63π C.42π D.36π【答案】B 【解析】试题分析:由题意,该几何体是一个组合体,下半部分是一个底面半径为3,高为4的圆柱,其体积213436V ππ=⨯⨯=,上半部分是一个底面半径为3,高为4的圆柱的一半,其体积()22136272V ππ=⨯⨯⨯=,该组合体的体积为:12362763V V V πππ=+=+=。
故选B 。
【考点】三视图;组合体的体积3.【2017天津,理10】已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 . 【答案】92π 【解析】设正方体边长为,则226183a a =⇒=,外接球直径为34427923,πππ3382R V R ====⨯=. 【考点】球【名师点睛】求多面体的外接球的面积和体积问题常用方法有(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心,本题就是第三种方法.4.【2016高考新课标1卷】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是() (A )17π(B )18π(C )20π(D )28π【答案】A 【解析】试题分析: 该几何体直观图如图所示:是一个球被切掉左上角的,设球的半径为R ,则37428V R 833ππ=⨯=,解得R 2=,所以它的表面积是78的球面面积和三个扇形面积之和2271=42+32=1784S πππ⨯⨯⨯⨯故选A . 考点:三视图及球的表面积与体积5.【2014高考北京理第8题】如图,正方体ABCD —A 1B 1C 1D 1的棱长为2,动点E ,F 在棱A 1B 1上,动点P ,Q 分别在棱AD ,CD 上.若EF =1,A 1E =x ,DQ =y ,DP =z (x ,y ,z 大于零),则四面体P —EFQ 的体积( )A .与x ,y ,z 都有关B .与x 有关,与y ,z 无关C .与y 有关,与x ,z 无关D .与z 有关,与x ,y 无关 【答案】D 【解析】试题分析: ∵DC ∥A 1B 1,EF =1,∴S △EFQ =12(定值).而点P 到面EFQ 的距离为P 到面A 1DCB 1的距离,为DP ·sin45°=2z .∴V 四面体P —EFQ =13×2z =13z .考点:点到面的距离;锥体的体积.6.【 2014湖南7】一块石材表示的几何体的三视图如图2所示,将该石材切削、打磨、加工成球,则能得到的最大球的半径等于() A.1 B.2 C.3 D.4【答案】B【解析】由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径,则862r r r -+-==,故选B. 【考点定位】三视图内切圆球三棱柱【名师点睛】解决有关三视图的题目,主要是根据三视图首先得到几何体的空间结构图形,然后运用有关立体几何的知识进行发现计算即可,问题在于如何正确的判定几何体的空间结构,主要是根据“长对正,高平齐,宽相等”进行判断.7.【2015高考山东,理7】在梯形ABCD 中,2ABC π∠=,//,222AD BC BC AD AB === .将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为() (A )23π(B )43π(C )53π(D )2π 【答案】C【解析】直角梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为1,母线长为2的圆柱挖去一个底面半径同样是1、高为1的圆锥后得到的组合体,所以该组合体的体积为:2215121133V V V πππ=-=⨯⨯-⨯⨯⨯=圆柱圆锥 故选C.8.【2014高考陕西版理第5题】已知底面边长为1的正四棱柱的各顶点均在同一个球面上,则该球的体积为()32.3A π.4B π.2C π4.3D π【答案】D 【解析】试题分析:根据正四棱柱的几何特征得:该球的直径为正四棱柱的体对角线,故22R ==,即得1R =,所以该球的体积224441333V R πππ===,故选D .考点:正四棱柱的几何特征;球的体积.【名师点晴】本题主要考查的是正四棱柱的几何特征;球的体积,属于容易题.解题时一定要注意正四棱柱的几何特征(实际上是一个特殊的长方体),求出球的直径,进而得到半径,然后利用球的体积公式直接运算即可9.【2014新课标,理6】如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A. 1727B. 59C. 1027D. 13【答案】C【解析】因为加工前的零件半径为3,高为6,所以体积154V π=,又因为加工后的零件,左半部为小圆柱,半径为2,高4,右半部为大圆柱,半径为3,高为2,所以体积2161834V πππ=+=,所以削掉部分的体积与原体积之比为5434105427πππ-=,故选C.10.【2015高考新课标2,理9】已知A,B 是球O 的球面上两点,∠AOB=90,C 为该球面上的动点,若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为( ) A .36π B.64π C.144π D.256π 【答案】C【解析】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时2311136326O ABC C AOB V V R R R --==⨯⨯==,故6R =,则球O 的表面积为24144S R ππ==,故选C .【考点定位】外接球表面积和椎体的体积.【名师点睛】本题以球为背景考查空间几何体的体积和表面积计算,要明确球的截面性质,正确理解四面体体积最大时的情形,属于中档题.11.【2015高考新课标1,理6】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。
问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有()(A)14斛 (B)22斛 (C)36斛 (D)66斛 【答案】B【解析】设圆锥底面半径为r ,则12384r ⨯⨯==163r =,所以米堆的体积为211163()5433⨯⨯⨯⨯=3209,故堆放的米约为3209÷1.62≈22,故选B.12.【2015高考新课标1,理11】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π,则r =()(A )1 (B )2 (C )4 (D )8 【答案】B【解析】由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r ,圆柱的高为2r ,其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π,解得r =2,故选B.13.【2016高考新课标3理数】在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是()(A )4π (B )92π(C )6π (D )323π【答案】B 【解析】试题分析:要使球的体积V 最大,必须球的半径R 最大.由题意知球的与直三棱柱的上下底面都相切时,球的半径取得最大值32,此时球的体积为334439()3322R πππ==,故选B . 考点:1、三棱柱的内切球;2、球的体积.14.【2015高考安徽,理7】一个四面体的三视图如图所示,则该四面体的表面积是()(A )1B )2(C )1+D )【答案】B【解析】由题意,该四面体的直观图如下,,ABD BCD ∆∆是等腰直角三角形,,ABC ACD ∆∆是等边三角形,则1131,60222BCD ABD ABC ACDS S S S ∆∆∆∆======,所以四面体的表面积2122BCD ABD ABC ACD S S S S S ∆∆∆∆=+++=⨯+= B.15.【2017江苏,6】如图,在圆柱12,O O 内有一个球O ,该球与圆柱的上、下面及母线均相切.记圆柱12,O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是.【答案】32【解析】设球半径为,则213223423V r r V r ππ⨯==.故答案为32. 【考点】圆柱体积【名师点睛】空间几何体体积问题的常见类型及解题策略(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解. (2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.。
