合工大Matlab上机题目3
matlab上机习题详细讲解-试题答案解析

学习指导参考P 第一次实验答案1. 设要求以0.01秒为间隔,求出y 的151个点,并求出其导数的值和曲线。
clc clearx=0:0.01:1.5;y=sqrt(3)/2*exp(-4*x).*sin(4*sqrt(3)*x+pi/3) y1=diff(y) subplot(2,1,1) plot(x,y)subplot(2,1,2) plot(x(1:150),y1)2绘制极坐标系下曲线(a,b,n 自定数据)clc clear a=10; b=pi/2; n=5;theta=0:pi/100:2*pi; rho=a*cos(b+n*theta); polar(theta,rho)3. 列出求下列空间曲面交线的程序clc clearx=[-5:0.5:5];[X,Y]=meshgrid(x); z1=X.^2-2*Y.^2;z2=X.*2-Y.*3; xlabel('x') ylabel('y') zlabel('z') surf(X,Y,z1) hold onsurf(X,Y,z2)k=find(abs(z1-z2)<0.5); x1=X(k) y1=Y(k)z3=x1.^2-2*y1.^2 hold onplot3(x1,y1,z3,'*')4、设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y 把x=0~2π间分为101点,画出以x 为横坐标,y 为纵坐标的曲线,要求有图形标注。
clc clearx=-2*pi:0.1: 2*pi;y=cos(x).*(0.5+sin(x)*3./(1+x.^2)); plot(x,y,'b*-'); title('绘图'); xlabel('x 坐标'); ylabel('y 坐标'); legend('原函数')gtext('y=cos(x)(0.5+3*sin(x)/(1+x^2))')5、求下列联立方程的解 81025695832475412743-=+-+-=-+-=++-=--+w z y x w z x w z y x w z y xclc cleara=[3,4,-7,-12;5,-7,4,2;1,0,8,-5;-6,5,-2,10]; b=[4,-3,9,-8]; c=b/a; x=c(1,1) y=c(1,2) z=c(1,3) w=c(1,4)6. 假设一曲线数据点为x = 0:2:4*pi;y = sin(x).*exp(-x/5);试将x 的间距调成 0.1,采用不同插值方法进行插值,并通过子图的形式将不同插值结果和原始数据点绘制在同一图形窗口。
matlab试题及答案

matlab试题及答案Matlab 上机考试试题考试要求:1、从10道题目中随机抽取3道独立完成,时间1小时。
(输入randperm(10),取前三个数)2、每个题目兴建一个.m的文件,命名方式ks+N.m(N为题号),然后将所选三个题目放入一个文件夹,文件名为学号+姓名。
考试完成后将文件夹通过FTP提交。
3、考试完成后要写一份报告,内容包括以下:(建一个.Doc的文档,文件名为学号+姓名)(1) 题号,题目;(2) 运行结果及其分析;(3) 图也要粘贴在文档中。
4、查阅资料写一篇2000字左右的关于matlab在电子信息中的应用的小论文或综述,也可以具体的写matlab在电子信息中某一个方面或某一个点的应用。
(打印或手写都可,打印版要交电子文档)5、所有要交的东西在1月3号之前必须交齐。
(由学习委员统一收齐交给我,电子文档也拷到学习委员处,统一拷给我)。
所交项目包括:考试报告打印版,小论文打印版(两个装订在一起,考试报告在上,小论文在下,最好做一个统一的封皮),考试报告doc文档,小论文doc文档。
Matlab 上机考试试题1.求下列联立方程的解3x+4y-7z-12w=45x-7y+4z+ 2w=-3X +8z- 5w=9-6x+5y-2z+10w=-8(1)求系数矩阵的秩; (2)求出方程组的解。
22sinx,yz,2.在[-10,10;-10,10]范围内画出函数的三维图形。
22x,y1Hs(),3.试画出系统的零极点分布图,判断系统是否稳定,同时求其单位32sss,,,221冲激响应和频率响应(幅频特性和相频特性)。
4. 将一个屏幕分4幅,选择合适的步长在右上幅与左下幅绘制出下列函数的图形。
,,cos(x),x,[,,]22(1)(曲线图);22xy(2)(曲面图)。
f(x,y),,;(-2,x,2,-4,y,4)2224,11,z5.系统传递函数为,按照以下要求求解: Hz(),,,1210.81,,zz(1)求其极零点图,判断系统的稳定性,画出系统的频谱特性;050,,n(2)当系统输入信号为:,时,画出xnnn()[5cos(0.2)2sin(0.7)],,,,, 系统的输出。
MATLAB上机模拟考试题

M A T L A B上机模拟考试题(一)(总8页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--(1)在MATLAB的命令窗口中执行_____命令,将命令窗口的显示内容清空。
()off(2)在MATLAB的命令窗口中执行_____命令,使数据输出显示为十六进制表示。
() long rat hex short e(3)下列变量名中_____是合法的。
() *y,a,1 \y,a1234 ,1 bcx ,i,j(4)已知x=0:5,则x有_____个元素。
()(5)一下运算符中哪个的优先级最高_____。
() A./ B.^ C.~=D.&(6)使用检测函数isnumeric(10)的结果是_____。
()(7)三维图形中默认视角是_____度。
() A.方位角=0 俯仰角=90B.方位角=90 俯仰角=0C.方位角= 仰俯角=30D.方位角=0 仰俯角=180(8)将符号表达式化简为因式分解因式分解因式分解因式分解形式,使用_____函数。
()(9)运行以下命令,则_____描述是正确的。
()>>syms a b cd >>A=[a b;c d] 占用的内存小于100B B.创建了5个符号变量占用的内存是a b c d的总和 D.不存在(10)已知数组a=[1 2 3;4 5 6;7 8 9],则a(:,end)是指_____元素。
(11)运行命令bitor(8,7)的结果是_____。
(12)运行以下命令:>>x=0:10; >>y1=sin(x); >>y2=5*sin(x);>>y3=[10*sin(x);20*sin(x)]; >>plot(x,y1,x,y2,x,y3) 则在一个图形窗口中,可以看到_____条曲线。
(13)符号表达式“g=sym(sin(a*z)+cos(w*v))”中的自由符号变量是_____。
MATLAB上机实验练习题及答案

MATLAB上机实验练习题及答案09级MATLAB上机实验练习题1、给出一个系数矩阵A[2 3 4;5 4 1;1 3 2],U=[1 2 3],求出线性方程组的一个精确解。
2、给出两组数据x=[0 0.3 0.8 1.1 1.6 2.3]’y=[0.82 0.72 0.63 0.60 0.55 0.50]’,我们可以简单的认为这组数据在一条衰减的指数函数曲线上,y=C1+C2e-t通过曲线拟合求出这条衰减曲线的表达式,并且在图形窗口画出这条曲线,已知的点用*表示。
3、解线性方程4、通过测量得到一组数据:5、已知一组测量值6、从某一个过程中通过测量得到:分别采用多项式和指数函数进行曲线拟合。
7、将一个窗口分成四个子窗口,分别用四种方法做出多峰函数的表面图(原始数据法,临近插值法,双线性插值法,二重三次方插值法)8、在同一窗口使用函数作图的方法绘出正弦、余弦、双曲正弦、双曲余弦。
分别使用不同的颜色,线形和标识符。
9、下面的矩阵X表示三种产品五年内的销售额,用函数pie显示每种产品在五年内的销售额占总销售额的比例,并分离第三种产品的切片。
X= 19.3 22.1 51.634.2 70.3 82.4 61.4 82.9 90.8 50.5 54.9 59.1 29.4 36.3 47.010、对应时间矢量t ,测得一组矢量y采用一个带有线性参数的指数函数进行拟合,y=a 0+a 1e -t +a 2te -t ,利用回归方法求出拟合函数,并画出拟合曲线,已知点用圆点表示。
11、请创建如图所示的结构数组(9分)12、创建如图所示的元胞数组。
(9分)13、某钢材厂从1990年到2010年的产量如下表所示,请利用三次样条插值的方法计算1999年该钢材厂的产量,并画出曲线,已知数据用‘*’表示。
要求写出达到题目要求的MATLAB 操作过程,不要求计算结果。
14、在一次化学动力学实验中,在某温度下乙醇溶液中,两种化合物反应的产物浓度与反应时间关系的原始数据如下,请对这组数据进行三次多项式拟合,并画出拟合曲线,已知数据如下。
matlab上机练习(附答案)

1.以下两种说法对吗?(1)MATLAB进行数值的表达精度与其指令窗中的数据显示精度相同。
(2)MATLAB指令窗中显示的数据有效位数不超过七位。
2.历史指令窗所记录的内容与diary指令所产生的“日志”内容有什么不同?DIARY filename causes a copy of all subsequent command window inputand most of the resulting command window output to be appended to thenamed file. If no file is specified, the file 'diary' is used.DIARY OFF suspends it.DIARY ON turns it back on.DIARY, by itself, toggles the diary state.Use the functional form of DIARY, such as DIARY('file'),when the file name is stored in a string.3.如何把用户自己的“工作目录”永久地设置在MATLAB的搜索路径上?“位于搜索路径上的目录”与“当前目录”在MATLAB中的功用相同吗?4.如何向MATLAB工作空间输入一个含有100个左右元素的一维或二维数值数组?用直接键入法?用数组编辑器?用M文件编辑器?5.运用数组算术运算符去掉下面程序里的for/end循环:x=11:15for k=1:length(x)z(k)=x(k)^2+2.3*x(k)^0.5;endx=11:15 z1=x.^2+2.3*x.^0.56.不使用数组算术运算符,重写下面的程序代码:x=[2 1 4]z=1./(1+x.^2)x=2;k=1;while i<=4,z2(k)=1/(1+i^2);i=i+1;x=x+1;end7.某公司销售电脑打印机的价格方案如下:()如果顾客只买一台打印机,则一台的基本价格为$150。
matlab上机习题详解试题答案

百度文库 - 让每个人平等地提升自我P 第一次实验答案1. 设要求以0.01秒为间隔,求出y 的151个点,并求出其导数的值和曲线。
clc clearx=0:0.01:1.5;y=sqrt(3)/2*exp(-4*x).*sin(4*sqrt(3)*x+pi/3)y1=diff(y) subplot(2,1,1) plot(x,y)subplot(2,1,2) plot(x(1:150),y1)2绘制极坐标系下曲线(a,b,n 自定数据)clc clear a=10; b=pi/2; n=5;theta=0:pi/100:2*pi; rho=a*cos(b+n*theta); polar(theta,rho)3. 列出求下列空间曲面交线的程序clc clearx=[-5:0.5:5];[X,Y]=meshgrid(x); z1=X.^2-2*Y.^2;z2=X.*2-Y.*3; xlabel('x') ylabel('y') zlabel('z') surf(X,Y,z1) hold onsurf(X,Y,z2)k=find(abs(z1-z2)<0.5); x1=X(k) y1=Y(k)z3=x1.^2-2*y1.^2 hold onplot3(x1,y1,z3,'*')4、设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y 把x=0~2π间分为101点,画出以x 为横坐标,y 为纵坐标的曲线,要求有图形标注。
clc clearx=-2*pi:0.1: 2*pi;y=cos(x).*(0.5+sin(x)*3./(1+x.^2)); plot(x,y,'b*-'); title('绘图'); xlabel('x 坐标'); ylabel('y 坐标'); legend('原函数')gtext('y=cos(x)(0.5+3*sin(x)/(1+x^2))')5、求下列联立方程的解 81025695832475412743-=+-+-=-+-=++-=--+w z y x w z x w z y x w z y xclc cleara=[3,4,-7,-12;5,-7,4,2;1,0,8,-5;-6,5,-2,10];b=[4,-3,9,-8]; c=b/a; x=c(1,1) y=c(1,2) z=c(1,3) w=c(1,4)6. 假设一曲线数据点为x = 0:2:4*pi;y = sin(x).*exp(-x/5);试将x 的间距调成 0.1,采用不同插值方法进行插值,并通过子图的形式将不同插值结果和原始数据点绘制在同一图形窗口。
MATLAB期末上机试题带答案
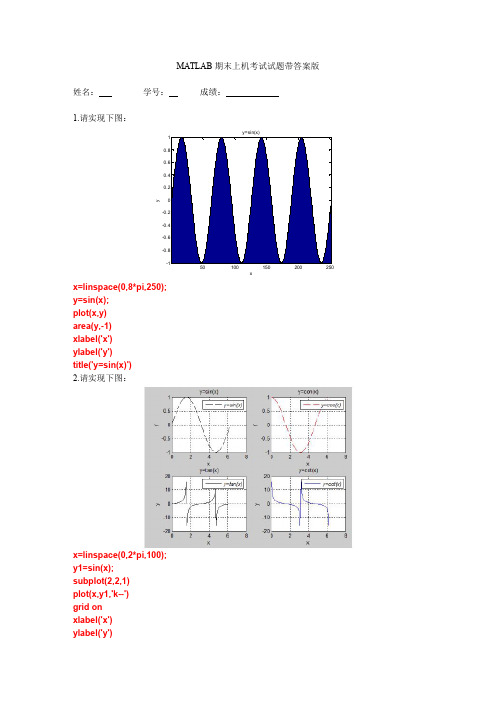
MATLAB 期末上机考试试题带答案版姓名:学号:成绩:1.请实现下图:50100150200250x y x=linspace(0,8*pi,250);y=sin(x);plot(x,y)area(y,-1)xlabel('x')ylabel('y')title('y=sin(x)')2.请实现下图:x=linspace(0,2*pi,100);y1=sin(x);subplot(2,2,1)plot(x,y1,'k--')grid onxlabel('x')ylabel('y')title('sin(x)')legend('y=sin(x)')y2=cos(x);subplot(2,2,2)plot(x,y2,'r--')grid onxlabel('x')ylabel('y')title('cos(x)')legend('y=cos(x)')y3=tan(x);subplot(2,2,3)plot(x,y3,'k-')grid onxlabel('x')ylabel('y')title('tan(x)')legend('y=tan(x)')y4=cot(x);subplot(2,2,4)plot(x,y4)grid onxlabel('x')ylabel('y')title('cot(x)')legend('y=cot(x)')3.解方程组:a=[321;1-13;24-4];b=[7;6;-2];x=a\b4.请实现下图:x y x=linspace(0,4*pi,1000);y1=sin(x);y2=sin(2*x);plot(x,y1,'--',x,y2,'b*')grid onxlabel('x');ylabel('y');title('耿蒙蒙')legend('sin(x)','sin(2*x)')5.请在x ,y 在(-2,2)内的z=xexp (-x 2-y 2)绘制网格图[x,y]=meshgrid(-2:0.1:2);z=x.*exp (-x.^2-y.^2);mesh(x,y,z)6.请实现peaks 函数:-33x Peaksy [x,y]=meshgrid(-3:1/8:3);z=peaks(x,y);mesh(x,y,z)surf(x,y,z)shading flataxis([-33-33-88])xlabel('x');ylabel('y');title('Peaks')7.请在x=[0,2],y=[-0.5*pi,7.5*pi],绘制光栅的振幅为0.4的三维正弦光栅。
Matlab上机实验题及参考解答

Matlab上机实验题及参考解答目录实验一Matlab初步实验 (2)一matlab基本功能介绍 (2)二Matlab扩展功能 (2)三练习 (2)四练习题参考解答 (3)实验二概率模型实验 (5)一复习 (5)二事件的响应 (5)三Matlab中随机数字的生成与处理 (5)四练习 (5)五练习题参考解答 (5)实验三插值与拟合 (7)实验四线性规划与非线性规划 (8)4.1 实验目的 (8)4.2 实验内容 (9)4.3 综合练习 (10)4.4 课外作业 (11)实验五数值计算 (12)5.1 实验目的 (12)5.2 实验内容 (12)4.3 综合练习 (15)4.4 课外作业 (15)实验六计算机图像处理 (16)6.1 实验目的 (16)6.2 实验内容 (16)6.3 综合练习 (17)6.4 课外作业 (19)实验七综合练习 (19)7.1 实验目的 (19)7.2 实验内容 (19)7.3 综合练习 (20)7.4 课外作业 (21)实验一 Matlab 初步实验 一 matlab 基本功能介绍1 编程环境2语法规范:for … end; if …else if …end; 3 矩阵运算 4 图形绘制二 Matlab 扩展功能1 编程练习:(1) 绘出序列kk x x r r 0(1),0.2083=+=;(2) 绘出曲线rtx t x e t 0(),0=>2 扩展功能(1) 矩阵中全部数据、部分数据的截取、更改; (2) 矩阵的初始化与赋值如:A=zeros(5,5); A(2:2:)=[1,2 3 4 5] 3 微积分基础(见实验4) 符号计算三 练习(课上编程完成下列练习,课后上机验证) 1 求和S=1+2+3+…+100; 2 求和e 1111!2!10!1...=++++3求和S 1112310!1...=++++4设A 234576138⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦, 求A 的逆、特征值和特征向量;验证Ax=λx 5 画函数图()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭6 展开 (x-1)(x-2)…(x-100)7 因式分解 x 8—y 8; 因数分解200520068 求极限312lim +∞→⎪⎭⎫⎝⎛++n n n n9 )](sin[cos 22x x y += 求dxdy10 求积分x xdx 10ln ⎰11 求积分3⎰并且画出所求的平面区域12 设x+2y=1, 2x+3y=6, y=2x 2, 画出各个方程图形,求出曲线交点.四 练习题参考解答%MatlabTrain1.m clear all % 2nd e=1; temp=1; for I=1:1:10temp=temp*I; e=e+1/temp; end e%%%%%%%%%%% clear all % 3nd S=0; temp=1;for I=1:1:100temp=temp*I; endfor J=1:1:temp S=S+1/J; end S%%%%%%%%%%%%%% clear all % 11ndx=linspace(0,4); y=1./sqrt(x.^5+1); plot(x,y) for t=1:0.1:3yt=1./sqrt(t.^5+1);hold online([t,t],[0,yt]);end%fill(t,yt,'b') %%%%%%%%%%%%% clear all% 12ndx=linspace(-2,2);y=[0.5-0.5*x; 2-2/3.*x; 2*x.^2]; plot(x,y)grid实验二概率模型实验一复习1 小结上次编程练习中存在的问题,讲述部分习题答案2 画图命令介绍:line二事件的响应(1) 获取鼠标的位置%MatlabTrain2.mclear all% 鼠标响应p=ginput(3)plot(p(:,1),p(:,2),'r*')(2) 键盘输入相应t=input('How many apples? t=');m=t+3三Matlab中随机数字的生成与处理1 随机数的生成2 产生随机数字3 产生某区间的整数4 生日模拟问题的Montecaro法设计技术、思路学生尝试编程四练习(1) 编程验证人数在不同年龄段的生日的概率计算(2) 编程实现游戏”聪明伶俐100分”(3) 编程实现两家电影院的座位数问题(4) 编程实现某图形面积的计算五练习题参考解答(1) 生日问题程序示例:%birthPro.mn=0;nStudents=30;for I=1:1000 %how many times testy=0;x=1+floor(365*rand(1,nStudents));%get nStudents random numbersfor J=1:nStudents-1for K=J+1:nStudentsif x(J)==x(K)y=1;break;endendendn=n+y;%count, n times of that there are two people's dirthday in the same dayendfreq=n/I % caculating the frequently(2) 编程实现游戏”聪明伶俐100分”参考答案%MatlabTrain2.mclear all% 鼠标响应x=floor(10*rand(1,4))t=input('填入四个数字[n1 n2 n3 n4]=');flag=0;A=0;B=0;for I=1:1:8flag=flag+1;A=0;B=0;if t==xswitch flagcase 1disp('聪明绝顶!');case 2disp('聪明!');case 3disp('有点聪明!');case 4disp('还可以!');case 5disp('聪明伶俐100分!');case 6disp('聪明伶俐90分!');case 7disp('聪明伶俐85分!');case 8disp('聪明伶俐80分!');otherwisedisp('赫赫!');endbreak;endfor J=1:1:4for K=1:1:4if x(J)==t(K) & J==KA=A+1;else if x(J)==t(K) & J~=KB=B+1;endendendends='AABB';s(1)=INT2STR(A);s(3)=INT2STR(B);disp(s);t=input('不重复填入四个数字[n1 n2 n3 n4]=');endif flag>0disp('太烂了! 正确答案是:');xend实验三插值与拟合一复习讲述聪明伶俐100分的编程中的问题二插值三拟合课堂练习2 某之股票价格from 2003 09 01 to 2004 01 02,试进行插值、拟合%TimerS.m%from 2003 09 01 to 2003 01 02clear all;dataST=[15.09 14.7514.95 14.722.88 21.8619.82 19.09];plot(dataST)四课外练习112)进行多项式拟合,求出拟合多项式,并求出多项式在t=4, 5处的值.实验四线性规划与非线性规划4.1 实验目的1 用Matlab求解线性规划2 用Matlab求解非线性规划4.2 实验内容4.2.1 线性规划求解实用格式:x=lp(c, A, b, xLB,xUB,x0,nEq)可以求解下列线性规划模型:min f=c’xs.t. Ax=<=b(其中前nEq个约束为等式约束,即等式约束的个数,其余是不等式约束<=) xLB<=x<=xUB函数中x0参数是算法迭代的初始点,任意取值例1 求解下列线性规划1)123123123123min2..360210200,1,2,3jz x x xs t x x xx x xx x xx j=--+⎧⎪++≤⎪⎪-+≤⎨⎪+-≤⎪≥=⎪⎩,2)1235635623416367min..3621060,1,,7jz x x x x xs t x x xx x xx xx x xx j=-++-⎧⎪++=⎪⎪+-=⎪⎨-+=⎪⎪++=⎪≥=⎪⎩例1求解示例c=[-2 -1 1]';%book page 72 Number 16-1A=[3 1 1;1 -1 2;1 1 -1];b=[60 10 20]';xlb=[0 0 0]';xub=[inf inf inf]';x0=[0 0 0]'; x=lp(c,A,b,xlb,xub,x0,0)% x=(15 5 0)'例2 求解示例c2=[1 -1 1 0 1 -1 0]';%book page 72 Number 16-3A2=[0 0 3 0 1 1 0;...0 1 2 -1 0 0 0;...-1 0 0 0 0 1 0;...0 0 1 0 0 1 1];b2=[6 10 0 6]';xlb2=[0 0 0 0 0 0 0]';xub2=[inf inf inf inf inf inf inf]';x02=[0 0 0 0 0 0 0]';x2=lp(c2,A2,b2,xlb2,xub2,x02,4)% unbounded4.2.2 非线性规划1)命令格式1:[X, OPTIONS]=constr(‘FUN’, X, OPTIONS,VLB,VUB)2)命令格式2:X=FMINCON(FUN,X0,A,B,Aeq,Beq)% minimizes FUN subject to the linear equalities% Aeq*X = Beq as well as A*X <= B. (Set A=[] and B=[] if no inequalities exist.)例2 求解非线性规划y x x x x s t x3211221min22 ..1=++-≤-求解示例%unconop.mfunction y=unconop(x)y=x(1).^3+2*x(1).*x(2)+2*x(2).^2;%book page 148 ex.7-1 后建立调用函数xx=fmincon('unconop',[0 0]',[-1 0],-1,[],[])%book page 148 ex.7-1 4.3 综合练习学生独立编写程序,求解一个含有2个变量的线性规划问题,要求:1)编写程序,把可行域画上阴影;2)求出最优解,在可行域上标出最优解;3)求出基本解,并在上图中表示出来;4)求出基本可行解,观察单纯形方法迭代时,顶点的变化.可行域画图与表出阴影示例:syms x y[u(1),v(1)]=solve('y=x+2','y=2*x');%求出交点坐标[u(2),v(2)]=solve('y=-x+2','y=2*x');[u(3),v(3)]=solve('y=x+2','y=-x+2');x=linspace(0,3,5); %直线作图y=[2*x;-x+2;x+2];line(x,y); gridpatch(double(u),double(v),'b'); 运行结果:4.4 课外作业1 求解线性规划131223min ..250.530,1,2,3i x x s t x x x x x i +⎧⎪+≤⎪⎨+=⎪⎪≥=⎩ (1) 求解线性规划;x *=()(2) 目标函数中c 1由1变为(-1.25)时求最优解;(3) 目标函数中c 1由1变为(-1.25),c 3由1变为2时求最优解;(4) 约束条件中53b ⎛⎫= ⎪⎝⎭变为21b -⎛⎫'= ⎪⎝⎭时,求解;(5) 约束条件中53b ⎛⎫= ⎪⎝⎭变为23b ⎛⎫'= ⎪⎝⎭时,求解[刁在筠,运筹学(第二版),高等教育出版社,2004,01 p74第20题]2 求解非线性规划y x x x x x x x 3221122233min 2223=++++ 注:无约束非线性规划问题, 命令:fminunc子函数% unconop.mfunction y=unconop(x)y=x(1).^2+2*x(1).*x(2)+2*x(2).^2+2*x(2).*x(3)+3*x(3).^2;%book page 148 ex.7-1 主函数:xx=fminunc('unconop',[0.1 0.1 1]')思考:绘出两个变量的线性规划问题的可行域、标出可行的整数解和求出可行解;演示单纯形方法的迭代过程,如j z x x s t x x x x x j 121212min 2..360200,1,2=--⎧⎪+≤⎪⎪+≤⎨⎪⎪≥=⎪⎩实验五 数值计算5.1 实验目的1 掌握代数数值计算2 掌握常微分方程数值计算5.2 实验内容5.2.1 关于多项式设多项式1110()n n n n p x a x a x a x a --=++++表示为110[,,,,]n n p a a a a -=1)求多项式的根 roots(p) %求出p(x)=0的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上机题目 三
1. 已知数组
⎪⎪⎭⎫ ⎝⎛=2312X , ⎪⎪⎭⎫ ⎝⎛=7654Y , ⎪⎪⎭⎫ ⎝⎛=257612Z , ⎪⎪⎪⎭
⎫ ⎝⎛=937654M 开展如下计算(其中有的计算会报错,要理解报错的原因是什么?):
X+Y ;X+Z ;Y+Z ;X+M ;X-Z ;Y-Z ;X-Z ;X.*Y ;X*Y ;X.*Z ;X*Z ;X.*M ;X*M ;Z*M ;X./Y ;X/Y ;X\Y ;X./Z ;X/Z ;X\Z ;X/M ;X\M ;X.^2;X^2;Z.^2;Z^2
2. 分别用矩阵求逆和矩阵除法求下列方程组的解
3. 建立一个字符串s ,其元素为:hefei anhui china ,使用class 函数察看s 的类型。
4. 将s 转化为ACSII 码,再将ACSII 码转化成字符串。
5. 取出s 的第6个元素,并察看结果。
6. 取出s 的第7个元素,并察看结果。
7. 取出s 的第10到14个元素,察看结果。
8. 在s 中查找代表省份的部分,并将其取出,赋给变量p 。
9. 在s 中查找字符i 的位置,并统计s 中有多少个字符i 。
提示:统计数组长度的函数是
“length ”
10. 将s 中的字符i ,一起替换为字符j 。
11. 将s 的第12个和13个元素替换为字符串’of ’。
12. 删除s 的第5个元素。
13. 删除s 的第7到10个元素。
14. 比较字符串’2013’与’2012’中前3个字符是否相同;比较’2013’与’2012’两个字符串整体
是否相同。
15. 创建一个一维数组,起始值为45、中止值63,步长为2,并将其直接转化为字符串。
