1999年河北省初中生毕业、升学统一考试
河北历届中考数学试卷(2000年-2011年)

2000年河北省初中升学统一考试数学试题一、填空题(本大题共10个小题;每小题2分,共20分)2.分解因式:2x3y+8x2y2+8xy3=______.3.已知:如图1,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有______对.5.已知∠A是它补角的3倍,则∠A=______.6.已知A、B两地相距s千米,甲、乙两人的速度分别是a千米/时、b千米/时,若甲从A地、乙从B地同时出发,相向而行,那么,到他们相遇时,所用的时间是______小时.7.已知:如图2,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,贝则OC的长等于______cm.8.已知:|x|=3,|y|=2,且xy<0,则x+y的值等于______.9.若关于x的一元二次方程kx2+2(k+1)x+k-1=0有两个实数根,则k的取值范围是______.10.已知:如图3,CD是⊙O的直径,AE切⊙O的于点B,DC的延长线交AB于点A,∠A=20°,则∠DBE=______.二、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的,把符合题目要求的选项前的字母填写在题后括号内)1.下列运算中正确的是[ ]A.x2²x3=x6.B.(x2)3=x5.D.3x2-2x(x+1)=-x2-2x.2.0.00813用科学记数法表示为[ ]A.8.13³10-3. B.81.3³10-4.C.8.13³10-4.D.81.3³10-3.3.已知一个多边形的外角和等于它的内角和,则这个多边形是[ ]A.三角形. B.四边形.C.五边形.D.六边形.4.已知矩形的对角线长为10cm,那么,顺次连结矩形四边中点所得的四边形周长为[ ] A.40cm.B.10cm.C.5cm.D.20cm.5.已知点M(1-a,a+2)在第二象限,则a的取值范围是[ ]A.a>-2.B.-2<a<1.C.a<-2. D.a>1.6.已知y=(a-1)x a 是反比例函数,则它的图象在[ ] A .第一、三象限. B .第二、四象限.C .第一、二象限. D .第三、四象限.7.用换元法解方程06151=+⎪⎭⎫ ⎝⎛+++x x x x 时,若设y x x =+1则原方程可化为[ ] A .y 2+6y+5=0. B .5y 2+y+6=0.C .y 2+5y+6=0. D .6y 2+5y+1=0.8.等边三角形的外接圆面积是内切圆面积的[ ] A .2倍.B .3倍.C .4倍.D .5倍.9.若等腰梯形的两条对角线互相垂直,中位线长为8cm ,则该等腰梯形的面积为[ ] A .16cm 2. B .32cm 2。
河北省历年中考理综真题及答案

2007年河北省初中毕业生升学考试一、选择题(本大题共22个小题;每小题2分,共44分。
在每小题给出的四个选项中,只有一个选项符合题意)1.下列物质的用途主要利用其化学性质的是A.金刚石制作刀具B.水作溶剂C.用16%的食盐水选种D.氧气供给呼吸2.下列做法你认为合理的是A.用甲醛溶液浸泡水产品B.用聚乙烯制作食品保鲜膜C.用添加苏丹红的饲料喂鸭子D.用水将霉变大米清洗后食用3.朝核问题引发了国际关注,核问题的关键是核能的如何利用。
已知某种核原料的原子核中含有1个质子和2个中子,那么A.该原子是一种氢原子B.该元素是金属元素C.该原子核外有3个电子D.该原子核带2个单位的正电荷4.小明从化学方程式4P+5O2===== 2P2O5中总结的信息有:①参加反应的物质是磷和氧气②反应条件是点燃③反应前后分子的总数不变④反应前后元素的种类不变。
其中正确的是A.①②③B.①②④C.①③④D.②③④5.人类的生活和生产都离不开金属。
下面对金属的利用不是..由金属活动性决定的是A.用铁回收含银废液中的银B.用锌与稀硫酸反应制取氢气C.古代金银制品能保存至今D.用铝合金制作门窗框架6.图1是a、b两种物质的溶解度曲线。
室温时,将盛有a、b饱和溶液的试管分别放入烧杯内的水中,均无晶体析出。
当向烧杯内的水中加入硝酸铵固体或浓硫酸后,图2试管内所示现象正确的是点燃图2硝酸铵浓硫酸硝酸铵a溶液浓硫酸A B CD水水水水a溶液b溶液b溶液图1温度/℃理科综合试卷第1页(共12页)理科综合试卷 第2页(共12页) 7.铁、盐酸、石灰水、硫酸铜是初中化学中常见的物质,四种物质间的反应关系如图3所示,图中两圆相交部分(A 、B 、C 、D )表示物质间反应的主要实验现象,其中描述正确的是 A .有气泡产生 B .无明显现象 C .有红色固体析出 D .有蓝色沉淀生成8.下列事实不能..用分子动理论解释的是 A .刮风时尘土飞扬 B .进入花园闻到花香C .将25m 3的石油气装入0.024m 3的钢瓶中D .50mL 酒精和50mL 水混合后的体积小于100mL 9.物质的分类方法很多,你认为下列分类合理的一组是 A .氯化钠、冰和铁都是晶体 B .橡胶、水和石墨都是绝缘体 C .空气、水银和白酒都是混合物 D .橡胶、纤维和塑料都是有机合成材料 10.下列变化中属于化学变化的是A .木炭放入冰箱除去异味B .给水通电获得氢气和氧气C .使用温度计测量温度时,液柱长度发生变化D .一束太阳光照射到三棱镜上,折射后形成一条彩色光带11.用调节好的托盘天平称量一只烧杯的质量时,当天平的右盘加上最小的砝码后,发现指针稍微向分度盘中线的左侧偏斜,为了使天平平衡,应该 A .把天平右端的平衡螺母向外旋出一些 B .把天平右端的平衡螺母向里旋进一些 C .把标尺上的游码向右移一些 D .把天平右端的底部垫高一些 12.下列做法符合科学常识的是A .电路中的保险丝熔断后,换用了更粗的保险丝B .向燃着的酒精灯中添加酒精C .用燃着的木条检验石油液化气是否泄漏D .油罐车的尾部装有一条拖在地面上的铁链 13.从图4所示实验中得出的结论不正确...的是A B CD 石灰水 稀盐酸硫酸铜 铁图3CO 2 甲 乙 丙 丁 图4O 2铁丝理科综合试卷 第3页 (共12页)A .甲实验说明流体中流速越大的位置压强越小B .乙实验说明光在同种均匀介质中沿直线传播C .丙实验说明铁丝在氧气中燃烧生成氧化铁D .丁实验说明二氧化碳不燃烧,也不支持燃烧,密度比空气大14.某同学在研究物质燃烧的条件时,做了图5所示的实验:把一条粗金属丝绕成线圈,罩在一支蜡烛的火焰上,火焰很快就熄灭了。
北京市1999年初中毕业,升学统一考试试卷

[科目] 物理[关键词] 教案/升学统一考试试卷[年级] 初三[文件] jan1.doc[标题] 北京市1999年初中毕业、升学统一考试试卷[内容]北京市1999年初中毕业、升学统一考试试卷第I卷(选择题50分)一、下列各小题均有四个选项,其中只有一个符合题意。
(共44分,每小题2分)1.在国际单位制中,力的单位是(A)千克(B)牛顿(C)焦耳(D)瓦特2.在物理实验室中,测量质量的仪器或工具是(A)量筒(B)弹簧秤(C)天平(D)气压计3.通常情况下,下列物质中属于导体的是(A)金属(B)陶瓷(C)橡胶(D)玻璃4.电能表接在家庭电路中是为了测量(A)电压(B)电流(C)电功(D)电功率5.下列简单机械中,属于省力杠杆的是(A)瓶盖起子(B)镊子(C)天平(D)定滑轮6.下列物态变化过程中,吸收热量的是(A)熔化(B)凝华(C)凝固(D)液化7.下列装置中,利用电磁感应的原理工作的是(A)发电机(B)电灯(C)电熨斗(D)电烙铁8.下列事例中,能够增大压强的是(A)在铁路的钢轨下铺设枕木(B)把书包带做得宽些(C)刀、斧、剪的刃都磨得很薄(D)在坦克的轮子上安装履带9.汽车在平直的高速公路上匀速行驶,10秒钟通过了150米的路程,汽车的速度是(A)1500米/秒(B)160米/秒(C)50米/秒(D)15米/秒10.下列物态变化过程中,属于液化现象的是(A)湿衣服变干(B)夏天的早晨,草地上出现露珠(C)冬天,水结成冰(D)放在橱里的樟脑丸越来越小11.使用幻灯机放映幻灯时,幻灯片在屏幕上所成的像是(A)倒立放大的实像(B)正立等大的实像(C)倒立缩小的实像(D)正立缩小的实像12.下列现象中,属于光的折射现象的是(A)斜插入水中的筷子,从水面上看,水下部分向上弯折了(B)从平面镜中看见自己的像(C)在太阳光照射下树木出现了影子 (D)平静的水面映出岸上的景物13.在下图所示的电路中,两个灯泡组成并联电路的是14.在右图所示的电路中,若测量通过灯泡L 1的电流,应把电流表串联接在电路中的(A)a 处 (B)b 处 (C)c 处 (D)d 处 15.阻值为10欧的两个电阻并联后,其等效电阻为(A)5欧 (B)10欧 (C)20欧 (D)40欧16.甲、乙两个物体质量相等,若它们的比热之比为2 : 1,升高的温度之比为2 : 1,则甲、乙两个物体吸收的热量之比为(A)1 : 1 (B)1 : 2 (C)1 : 4 (D)4 : 1 17.下列现象中,属于内能转化为机械能的是 (A)用打气筒打气,气筒壁发热 (B)锯木头时,锯条发热 (C)用电熨斗熨衣服(D)被加热的试管中的水蒸气膨胀做功,把管塞推出管口18.一本书放在水平桌面上,静止时,在下列各对力中属于平衡力的是 (A)书对桌面的压力和桌面对书的支持力 (B)桌子受到的重力和地面对桌子的支持力 (C)书受到的重力和书对桌面的压力 (D)书受到的重力和桌面对书的支持力19.有两个用同种材料制成的圆柱体A 和B ,A 的高度是B 的高度的3倍,将A 竖直放在水平地面上,B 竖直放在A 上,如右图(甲)所示,这时A 对地面的压强与B 之比为3 : 1,若将A 、B 倒置后仍放在水平地面上,如右图(乙)所示,则A 对B 的压强与B 对水平地面的压强之比是(A)1 : 3 (B)1 : 2 (C)4 : 1 (D)1 : 120.在右图所示的电路中,电源电压和灯泡电阻保持不变,闭合开关S ,将滑动变阻器的滑片P 向右移动,则(A)电流表示数增大,电压表示数减小 (B)电流表示数减小,电压表示数增大 (C)电流表示数增大,电压表示数增大(D)电流表示数减小,电压表示数减小 21.木块A 漂浮在容器中的水面上,它的上面放有一块石块B ,如右图所示,此时木块A 排开水的体积为V 1。
河北省历年中考理综真题及答案

理科综合试卷 第页 (共12页)12007年河北省初中毕业生升学考试一、选择题(本大题共22个小题;每小题2分,共44分。
在每小题给出的四个选项中,只有一个选项符合题意)1.下列物质的用途主要利用其化学性质的是A .金刚石制作刀具B .水作溶剂C .用16%的食盐水选种D .氧气供给呼吸2.下列做法你认为合理的是A .用甲醛溶液浸泡水产品B .用聚乙烯制作食品保鲜膜C .用添加苏丹红的饲料喂鸭子D .用水将霉变大米清洗后食用3.朝核问题引发了国际关注,核问题的关键是核能的如何利用。
已知某种核原料的原子核中含有1个质子和2个中子,那么A .该原子是一种氢原子B .该元素是金属元素C .该原子核外有3个电子D .该原子核带2个单位的正电荷4.小明从化学方程式4P+5O 2 ===== 2P 2O 5中总结的信息有:①参加反应的物质是磷和氧气 ②反应条件是点燃 ③反应前后分子的总数不变 ④反应前后元素的种类不变。
其中正确的是A .①②③B .①②④C .①③④D .②③④5.人类的生活和生产都离不开金属。
下面对金属的利用不是由金属活动性决定的是A .用铁回收含银废液中的银B .用锌与稀硫酸反应制取氢气C .古代金银制品能保存至今D .用铝合金制作门窗框架6.图1是a 、b 两种物质的溶解度曲线。
室温时,将盛有a 、b 饱和溶液的试管分别放入烧杯内的水中,均无晶体析出。
当向烧杯内的水中加入硝酸铵固体或浓硫酸后,图2试管内所示现象点燃图1温度/℃理科综合试卷 第页 (共12页)2正确的是7.铁、盐酸、石灰水、硫酸铜是初中化学中常见的物质,四种物质间的反应关系如图3所示,图中两圆相交部分(A 、B 、C 、D )表示物质间反应的主要实验现象,其中描述正确的是A .有气泡产生B .无明显现象C .有红色固体析出D .有蓝色沉淀生成8.下列事实不能用分子动理论解释的是A .刮风时尘土飞扬B .进入花园闻到花香C .将25m 3的石油气装入0.024m 3的钢瓶中D .50mL 酒精和50mL 水混合后的体积小于100mL 9.物质的分类方法很多,你认为下列分类合理的一组是A .氯化钠、冰和铁都是晶体B .橡胶、水和石墨都是绝缘体C .空气、水银和白酒都是混合物D .橡胶、纤维和塑料都是有机合成材料10.下列变化中属于化学变化的是A .木炭放入冰箱除去异味B .给水通电获得氢气和氧气C .使用温度计测量温度时,液柱长度发生变化D .一束太阳光照射到三棱镜上,折射后形成一条彩色光带 11.用调节好的托盘天平称量一只烧杯的质量时,当天平的右盘加上最小的砝码后,发现指针稍微向分度盘中线的左侧偏斜,为了使天平平衡,应该 A .把天平右端的平衡螺母向外旋出一些 B .把天平右端的平衡螺母向里旋进一些 C .把标尺上的游码向右移一些 D .把天平右端的底部垫高一些 12.下列做法符合科学常识的是A BCD 石灰水 稀盐酸硫酸铜 铁图3图2硝酸铵 浓硫酸 硝酸铵 a 溶液 浓硫酸 A B C D水水水水a 溶液b 溶液b 溶液理科综合试卷 第页 (共12页)3A .电路中的保险丝熔断后,换用了更粗的保险丝B .向燃着的酒精灯中添加酒精C .用燃着的木条检验石油液化气是否泄漏D .油罐车的尾部装有一条拖在地面上的铁链13.从图4所示实验中得出的结论不正确的是A .甲实验说明流体中流速越大的位置压强越小B .乙实验说明光在同种均匀介质中沿直线传播C .丙实验说明铁丝在氧气中燃烧生成氧化铁D .丁实验说明二氧化碳不燃烧,也不支持燃烧,密度比空气大 14.某同学在研究物质燃烧的条件时,做了图5所示的实验:把一条粗金属丝绕成线圈,罩在一支蜡烛的火焰上,火焰很快就熄灭了。
河北省2001年初中升学统一考试

河北省2001年初中升学统一考试一、填空题(本大题共10个小题,每个小题2分,共20分)1.用科学记数法表示12700的结果是____________.2.分母有理化:121-=____________.3.分解因式:2x -x y +x z -y z =____________. 4.如果∠A =35°18′,那么∠A 的余角等于____________.5.用换元法解分式方程1-x x +xx 22-+3=0时,若设y =1-x x ,则由原方程化成的关于y 的整式方程是____________.6.若三角形的三边长分别为3、4、5,则其外接圆直径的长等于____________.7.如图1,A B 是⊙O 的弦,A C 切⊙O 于点A ,且∠BAC =45°,AB =2,则⊙O 的面积为____________.(结果可保留π)图18.点A (a ,b )、B (a -1,c )均在函数y =x1的图像上,若a <0,则b ____________ c (填“>”或“<”或“=” )9.在R t △ABC 中,锐角A 的平分线与锐角B 的邻补角的平分线相交于点D ,则∠ADB =____________.10.在一次“人与自然”知识竞赛中,竞赛试题共有25道题.每道题都给出4个答案,其中只有一个答案正确.要求学生把正确答案选出来.每道题选对得4分,不选或选错倒扣2分.如果一个学生在本次竞赛中的得分不低于60分,那么,他至少选对了____________道题.二、选择题(本大题共10个小题;每个小题2分,共20分,在每个小题给出的四个选项中,只有一项是符合题目要求的,把符合题目要求的选项前的字母填写在题后的括号内)1.计算(2-1)2,结果等于( ). A . 2 B .4 C .41 D .21 12.有一边长为4的正n 边形,它的一个内角为120°则其外接圆的关径为,( ).A .34B .4C .32D .2 13.若x 1、x 2是一元二次方程3 x 2 +x -1=0的两个根,则11x +21x 的值是( ). A .-1 B .0 C .1 D .214.已知三角形三条边的长分别是2、3和a ,则a 的取值范围是( ).A .2<a <3B .0<a <5C .a >2D .1<a <515.在一元二次方程a x 2+b x +c (a ≠0)中,若a 与 c 异号,则方程( ).A .有两个不相等的实数根B .有两个相等的实数根C .没有实数根D .根的情况无法确定16.如图2,在△ABC 中,D 为AC 边上一点,∠DBC =∠A ,BC =6,A C =3,则CD 的长为( ).图2A . 1B .23C .2D .25 17.某所中学现有学生 4200人,计划一年后初中在校生增加8%,高中在校生增加11%,这样全校在校生将增加10%,这所学校现在的初中在校和高中在校生人数依次是( ).A .1400 2800B .1900 2300C . 2800 1400D .2300 190018.已知二次函数的图像经过(1 ,0 )、(2 ,0 )和(0 ,2 )三点,则该函数的解析式是( ). A .y =2x 2+x +2B .y =x 2+3x +2C .y =x 2-2x +3D .y =x 2-3x +2 19.如图3,在矩形ABCD 中,横向阴影部分是矩形,另一阴影部分是平行四边形,依照图中标注的数据,计算图中空白部分的面积,其面积是( ).图3A .bc -ab +ac +c 2B .ab -bc -ac +c 2C .a 2+ab +bc -acD .b 2-bc +a 2-ab20.已知等腰三角形三边的长为a 、b 、c ,且a =c .若关于x 的一元二次方程 ax 2-2bx +c =0的两根之差为2,则等腰三角形的一个底角是( ).A .15°B .30°C . 45°D .60°三、(本大题共2个小题,每个小题7分,共14分)21.先化简,再求值:22+-x x -22-+x x ,其中x =2. 22.已知:如图4,在正方形ABCD 中,P 是BC 上的点且BP =3PC ,Q 是CD 的中点.求证:△ADQ ∽△QCP .四、(本大题共2个小题;每个小题8分,共16分)23.如图5,⊙O 表示一个圆形工件,图中标注了有关尺寸,并且MB ︰MA =1︰4.求工件半径的长.图4 图524.某班同学参加环保知识竞赛,将学生的成绩(得分取整数)进行整理后分成五组,绘成频率分布直方图(如图6).图中从左到右各小组的小长方形的高的比是1︰3︰6︰4︰2,最右边一组的频数是6,结合直方图提供的信息,解答下列问题:图6(1)该班共有多少名同学参赛?(2)成绩落在哪组数据范围内的人数是多,是多少?(3)求成绩在60分以上(不含60分)的学生占全班参赛人数的百分率.五、(本题满分12分)25.甲乙两辆汽车在一条公路上匀速行驶.为了确定汽车的位置,我们用数轴O 表示这条公路,原点O 为零千米路标(如图7-1),并作如下约定:图7-1①速度µ>0,表示汽车向数抽正方向行驶;速度µ<0,表示汽车向数抽负方向行驶;速度µ=0,表示汽车静止.②汽车位置在数抽上的坐标S >0,表示汽车位于零千米路标的右侧;汽车位置在数抽上的坐标S <0,表示汽车位于零千米路标的左侧;汽车位置在数抽上的坐标S =0,表示汽车恰好位于零千米路标处.遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图像的形式画在了同一直角坐标繁中,如图7-2.请解答下列问题.图7-2(1)就这两个一次函数像所反映的两汽车在这条公路上行驶的状况填写如下的表格. 问项结论车别行驶方向 速度的大小(千米/小时) 出发前的位置甲车乙车 (2)甲乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,如不能相遇,请说明理由.六、(本题满分2分)26.在△ABC 中,D 为BC 边的中点,E 为AC 边上的任意一点,BE 交于AD 点O ,某学生在研究这一问题时,发现了如下的事实:(1)当AC AE =21=111+时,有AD AO =32=122+(如图8-1); (2)当AC AE =31=211+时,有AD AO =42=222+(如图8-2); (3)当AC AE =41=311+时,有AD AO =52=322+(如图8-3);图8-1 图8-2 图8-3 图8-4在图8-4中,当AC AE =n +11时,参照上述研究结论,请你猜想用n 表示ADAO 的一般结论,并给出证明(其中n 是正整数).七、(本题满分13分)27.某化工材料经销公司购进了一种化工原料共7000知克,购进价格为每千克30.物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现:单价定为70元时,日均销售60千克;单价每降低1元,日均多售出2千克.在销售过程中,每天还要支出其他费用500元(天数不足一天时,按整天计算).设销售单价为x 元,日均获利为y 元.图9 (1)求y 关于x 的二次函数关系式,并注明x 的取值范围;(2)将(1)中所求出的二次函数配方成y =a (x +a b 2)2 +ab ac 442- 的形式,写出顶点坐标;在图9所示的坐标系中画出草图;观察图像,指出单价定为多少元时日均获利最多,是多少?(3)若将这种化工原料全部售出,比较日均获利最多和销售单价最高这两种销售方式,哪一种获总利较多,多多少?八、(本题满分13分)28.如图10,在菱形ABCD 中,ABCD =10,∠BAD =60°.点M 从点A 每秒1个单位长的速度沿着AD 边向点D 移动;设点M 移动的时间为t 秒(0≤t ≤10).图10(1)点N 为BC 边上任意一点.在点M 移动过程中,线段MN 是否一定可以将菱形分割成面积相等的两部分?并说明理由;(2)点N 从点BC (与点M 出发的时刻相同)以每秒2个单位长的速度沿着BC 边向点C 移动,在什么时刻,梯形ABNM 的面积最大?并求出面积的最大值;(3)点N 从点B (与点M 出发的时刻相同)以每秒a (a ≥2)个单位长的速度沿着射线BC 方向(可以超越点C )移动,过点M 作MP ∥AB ,交BC 于点P .当△MPN ≌△ABC 时,设△MPN 与菱形ABCD 重叠部分的面积为S ,求出用t 表示S 的关系式,并求当S =0时a 的值.评析 本卷命题注重了题型的创新设计,注重了学生灵活应用勇力的考查,特别是在检测阅读理解,接受消化信息加以利用能力上下了功夫,如题10,题25,题27,其目的是传达教与学的一种新型方式-教会学生学习方法,学会如何学习是教与学的目的.压轴题是一道涉及变量、动量的几何问题,考查了“以静求动 的解题能力” 的解题能力.参考答案一、填空题(每小题2分,共20分)1.1.27×104 2.2+1 3.(x -y ) 4.54.7°(或54°42′) 5.y 2+3y +2=0 6.57.2π 8.< 9.45° 10.19二、选择题(每小题2分,共20分)题6隐含着三角形是直角三角形的条件. 题10中计分方式与平时有所不同,平时的错题得0分,而本题的错题得-2分.11.C 12. B 13.C 14.D 15.A 16.C 17.A 18.D 19.D20.B 三、(本大题共2个小题;每个小题7分,共14分) 21.解:22+-x x -22-+x x =()()()2222-+-x x x -()()()2222+-+x x x =()()()()222222-++--x x x x =()()44444222-++-+=x x x x x =482--x x . 当时x =2,原式=()42282-⨯-=42.22.证明:在正方形ABCD 中,∵Q 是CD 的中点,∴QC AD =2.∵PC BP =3,∴PC BC =4.又∵BC =2 DQ ,∴PC DQ =2.在△ADQ ∽QCP 中,QC AD =PC DQ ,∠C =∠D =90°,∴△ADQ ∽QCP .四、(本大题共2个题,每小题8分,共16分)23.解:如图,过点M 作⊙O 的直径CD ,设⊙O 的半径为xcm .∵AM ︰MB =4︰1,AB =15,∴AM =15×54=12, MB =15×51=3.由相交弦定理可知:MA ·MB =CM ·MD ,即12×3=(8+x )(8-x ),化简得:x 2=100,解得x 1=10,x 2=-10(舍去).∴工件半径的长为10cm .24.解:(1)由直方图的意义可知:小长方形高的比等于频数的比.由最右边一组的频数为6可得:各组频数依次是3,9,18,12,6.3+9+18+12+6=48,共有48个数据,即有48名学生参赛.(2)成绩落在70.5~80.5数据范围内的人数最多,人数为18.题15中△=b 2-4ac ,又因a 与c 异号,即ac <0,故△>0.题19的图形可等积变形的如下图形,这样便于计算. 题23中向两边延长OM ,分别与圆交于两点,再在应用相交弦定理,是解题的一般思路.(3)60分以上的人数是5.所占全班参赛人数的百分率为4845×100%=93.75%. 五、(本题满分12分) 25.(1)甲车:x 轴负方向(向左);40;零千米路标右侧190千米处.乙车:x 轴正方向(向右);50;零千米路标左侧80千米处.(2)甲乙两车相遇.设经过t 小时两车相遇,由⎩⎨⎧-=+-=.8050,19040s t s 得⎩⎨⎧==.70,30s t 所以经过3小时两车相遇,相遇在零千米路标右侧70千米处.六、(本题满分12分)26.解:依照题意可以猜想:当AC AE =n +11时,有AD AO =n+22成立. 证明:过点D 作DF ∥BE 交于AC 点F ,∵D 是BC 的中点,∴F 是EC 的中点. 由AC AE =n +11,可知EC AE =n 1,∴AF AE =n 2,∴AF AE =n +22,∴AD AO =AF AE =n+22. 七、(本题满分13分)27.解:(1)若销售单价为x 元,则每千克降低(70-x )元,日均多售出2(70-x )千克,日均销售量为[60+2(70-x )]千克,每千克获得为(x -30)元.依题意得:y =(x -30)[60+2(70-x )]-500=-2 x 2+260 x -6500(30≤x ≤70).(2)y =-2 (x 2-130 x )-6500=-2(x -65)+1950.顶点坐标为(65,1950).经观察可知,当单价定为65元时,日均获利最多,是1950元.(3)当日均获利最多时: 单价为65元,日均销售60+2(70-65)=70千克,那么获总利为1950×707000=195000元. 题25是代数阅读题用函数图象表示相遇问题的运动过程.解答本题要注意两点:(1)读懂背景材料,掌握其中的“约定”,特别是与常规思维不相同的“约定”,如速度小于0,S 小于0等,本题赋于了“+” “-”号新的实际意义;(2)建立准图象与实际问题的对应关系,如两直线解析式的交点表示两车相遇的位置.观察题26的图形,可看出它是相似形中一个比较常见的基本图形,过已知中L点作BE 的平行线是常见解题思路.当销售单价最高时单价为70元,日均销售60千克,将这种化工原料全部售完需607000≈117天,那么获总利为(70-30)×7000-117×500=221500元. 因为221500>19500,且221500-19500=26500元,所以,销售单价最高时获总利较多,且多获利26500元.八、(本题满分13分)28.解:(1)MN一定能在某一时刻将菱形ABCD 分割成面积相等的两部分.[方法一]对于中心对称图形,过中心的任一直线均能将图形分割成面积相等的两部分.而且菱形是中心对称图形,在点M 由A 到D 的移动过程中,一定存在一个时刻,使得线段MN 过菱形的中心.[方法二]梯形ABNM 与梯形CDMN 等高,并设高为h ,欲使面积相等,只需AM =CN . ∵AM =NC =t ,∴MD =BN =10-t .∵S梯形ABNM =2)10(t t -+·h =S 梯形CDMN ,∴存在一个时刻使将菱形分成面积相,等的两部分. (2)过B 作BE ⊥AD ,垂足为E .在Rt △ABE 中,BE 10sin60°=53,∵ AM =t ,BN =2t , ∴S 梯形ABNM =21(t +2t )×53=2315t. ∵2t ≤10,∴t ≤5时,S 梯形ABNM 最大.最大面积为2315×5=2375. (3)△ABC 是腰长为10的等腰三角形.当△MPN ≌△ABC 时,MP =10,PN =BC =10,且MP =PN ,∴BP =AM =t ,∴PC =10-t ,NC =t .过P 作PG ⊥DC ,垂足为G .在R t △PGC 中,PG =sin60°=23(10-t ).设MN 交DC 于F ,∴DC ∥MP ,且MP =PN ,∴∠NFC = NMP ∠= MNP ,∴FC =NC =t .∵重叠部分MPCF 是梯形,二次函数的应用是中考的“擦边球”,曾一度火热于各地中考试郑上,这类知识的考查有些超出初中教材范围.但题27的问题设计中先引导用配方法对二次函数变形,再利用图像观察寻找最值的方法,这实质是一种引导探索的过程,考查了学生学习能力.∴S =21(t +10)×23(10-t )=-43t 2+253. 当S =0,即-43t 2+253=0时, 解得t 1=10,t 2=-10,(舍去).∵BN =at ,BN =PN +PB =10+t ,∴at =10+t ,将t =10代入at =10+t ,解得a =2.声明:本资料由 考试吧( ) 收集整理,转载请注明出自 服务:面向较高学历人群,提供计算机类,外语类,学历类,资格类,会计类,工程类,医学类等七大类考试的全套考试信息服务及考前培训. 题28(1)要用到一个隐含的规律:“ 过中心对称图形的对称中心的任一直线均把图形分割成面积相等的两部分”.解(3)时应依据题设重新画图以利于求解.。
1999年河北省初中生毕业,升学统一考试物理试题

1999年河北省初中生毕业,升学统一考试物理试题
王久
【期刊名称】《物理教学探讨:初三年级学研期》
【年(卷),期】2000(000)002
【总页数】4页(P34-37)
【作者】王久
【作者单位】河北滦平县巴克什营镇中学
【正文语种】中文
【中图分类】G633.7
【相关文献】
1.河北省2005年初中生升学统一考试理科综合试卷物理试题分析 [J], 郭金;袁书岭
2.河北省2005年初中生升学统一考试理科综合试卷物理试题分析 [J], 郭金;袁书岭
3.从生活走向物理从物理走向社会--扬州市2005年初中毕业、升学统一考试物理试题赏析 [J], 陈国平;韩俊
4.从生活走向物理从物理走向社会——扬州市2005年初中毕业、升学统一考试物理试题赏析 [J], 陈国平;韩俊
5.河北省2005年初中生升学统一考试理科综合试卷物理试题分析 [J], 郭金; 袁书岭
因版权原因,仅展示原文概要,查看原文内容请购买。
1998年河北省中考试卷及解答
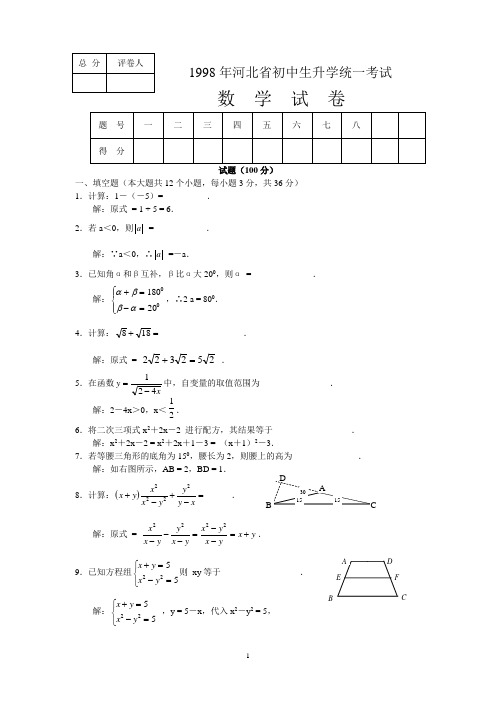
1998年河北省初中生升学统一考试数 学 试 卷试题(100分)一、填空题(本大题共12个小题,每小题3分,共36分)1.计算:1-(-5)=__________.解:原式 = 1 + 5 = 6.2.若a <0,则a =____________.解:∵a <0,∴a =-a .3.已知角α和β互补,β比α大200,则α =______________.解:αββα+=-=⎧⎨⎪⎩⎪1802000,∴2 a = 800. 4.计算:818+=___________________.解:原式 = 252322=+ .5.在函数y x =-124中,自变量的取值范围为________________. 解:2-4x >0,x <12. 6.将二次三项式x 2+2x -2 进行配方,其结果等于__________________.解:x 2+2x -2 = x 2+2x +1-3 = (x +1)2-3.7.若等腰三角形的底角为150,腰长为2,则腰上的高为_______________.解:如右图所示,AB = 2,BD = 1. 8.计算:()x y x x y y y x +-+-=2222______. 解:原式 = x x yy x y x y x yx y 2222---=--=+. 9.已知方程组x y x y +=-=⎧⎨⎩5522则 xy 等于__________________. 解:x y x y +=-=⎧⎨⎩5522 ,y = 5-x ,代入x 2-y 2 = 5,得,x = 3,y = 2,∴xy = 6.10.若等腰梯形的周长为80cm ,中位线长与腰长相等,则它的中位线长等于__________.11.已知一个扇形的半径等于一个圆的半径的2倍,且面积相等,则这个扇形的圆心角等于_____________.解:R = 2r ,ππR n r 22360= ,4n = 360,n = 900.12.在直角梯形ABCD 中,AD ∥BC ,AB ⊥AD , AB = 103,AD 、BC 的长是方程x 2-20x +75 = 0的两根,那么以D 为圆心、AD 为半径的圆与以C 为圆心、BC 为半径的圆的位置关系是_____________.解:AD 、BC 的长是方程x 2-20x +75 = 0 的两根,得,AD = 5,BC = 15,作DM ⊥BC ,则AB = DM =103,AD = BM = 5,MC = BC -MC =15-5 = 10,∴DC = 20.∴以D 为圆心、AD 为半径的圆与以C 为 圆心、BC 为半径的圆的位置关系 是外切.二、选择题(本大题共8个小题,每小题3分,在每小题给出的四个选项中,只有一项是符合题目要求的,把符合题目要求的选项前的字母填写在题后括号内)1.若 2a 与1-a 互为相反数,则a 等于 【 】 (A ) 1 (B ) -1 (C )12 (D ) 13解:依题意,得 2a = -(1-a) , a = -1,故选B .2.下列运算中,正确的是 【 】(A ) 5ab -ab = 5 (B ) x +x = x 2(C ) x 2x = 3x (D ) x 3÷x 2 = x解:显然选D .3. 分解因式 x 4 -1的结果为 【 】(A ) (x 2+1)(x 2-1) (B ) (x +1)2(x -1)2(C ) (x +1)(x -1) (x 2+1) (D )(x -1) (x +1)3解:显然选C .4.设y = x 2+x +1,则方程 x 2+x +1 = 22x x+可变形为 【 】 (A ) y 2-y -2 = 0 (B ) y 2+y +2 = 0(C ) y 2+y -2 = 0 (D ) y 2-y +2 = 0 解:依题意,得 12-=y y ,整理,得 y 2-y -2 = 0 ,故选A . 5.下列命题中,真命题为 【 】(A )对角线相等的四边形一定是矩形(B )底角相等的两个等腰三角形一定全等 DCA B M R r(C )平行四边形的一条对角线分成的两个三角形一定相似(D )有公共顶点和一条公共边的两角,若其和为1800,则这两角互为邻补角 解:选C .6.已知,如图1,∠A = 320,∠B = 450,∠C = 380,则∠DFE 等于 【 】(A ) 1200 (B ) 1150(C ) 1100 (D ) 1050 解:∠AEB =∠A + ∠C = 320 + 380 = 700, ∴∠DFE =∠AEB +∠B = 700 + 450 = 1150. 故选B . 图 17.已知,ab <0,点p (a ,b),在反比例函数y a x=的图象上,则直线y = ax + b 不经过的象限为 【 】 (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限解:∵点p (a ,b) 在反比例函数y a x=的图象上,得 b = 1, 又∵ab <0,∴a <0,∴直线y = ax + b 不经过的象限为第三象限.故选C .8.已知,如图2,在⊙O 中,直径AB ⊥CD , BE 切⊙O 于B ,且BE = BC ,CE 交AB于F ,交⊙O 于M ,连接 MO 并延长,交 ⊙O 于N .则下列结论中,正确的是 【 】(A ) CF = FM (B ) OF = FB (C ) AB 弧等于22.50(D )BC ∥MN 解:∵ 依据题目所给条件,得 ∠CBE =∠CBO +∠OBE= 450 + 900 = 1350,连接MB, ∠MBE =∠BCE =∠BEC = 22.50, 圆心角∠BOM = 450∴∠CBO = ∠BOM = 450 , ∴BC ∥MN .故选D .三、(本大题共2个小题,每小题5分,共10分)1.指出下面一组数据的中位数,并计算这组数据的方差:11 19 13 17 15解:将这组数据从小到大排列,得到11 13 15 17 19∴中位数为15 ---------------1分 x =()15191715131151=++++ --------2分 ()()()()()[]2222221519151715151513151151-+-+-+-+-=s =8 ---5分 2.已知:x y z 3460==≠,求x y z x y z +--+的值. 解:设k z y x ===643,则x = 3k ,y = 4k ,z = 6k -------------2分 ∴x y z x y z +--+ = 515643643==+--+k k k k k k k k --------------------------5分 N A D C B F O M C A B E FD四、(本大题10分) 已知,如图3,四边形ABCD 为平行四边形, 延长BA 到E ,延长DC 到F ,使BE = DF ,AF交BC 于H ,CE 交AD 于G .求证:△AGE ≌ △CHF . 证明:∵四边形ABCD 是平行四边形, ∴AB ∥CD ,AB =CD-----------------2分∵ BE = DF∴AE ∥CF , AE = CF ,四边形EAFC 是平行四边形.------------4分∴∠E =∠F , ----------------------6分 ∵AB ∥CD ,AD ∥BC ,∴∠EAG =∠D ,∠D =∠FCH------8分∴∠EAG =∠FCH ,△AGE ≌ △CHF .----------------------------10分五、列方程(或方程组)解应用题(本大题10分)从A 村到B 村的路程为12千米,甲、乙两人同时从A 村出发去B 村,1小时后,甲在乙前1千米,甲到达B 村比乙早1小时.问甲、乙两人每小时各走几千米?解:设乙每小时走x 千米,则甲每小时走(x + 1)千米.-----------------------1分 依题意得,111212=+-x x ----------------------------------5分 去分母,整理得 x 2 +x -12 = 0 -----------------------------7解这个方程,得 x 1 = 3,x 2 =-4 --------------------8分经检验, x 1 = 3,x 2 =-4 都是原方程的根,但速度不能为负数,故只取 x = 3, 此时 x + 1 = 4答:甲每小时走4千米,乙每小时走3千米.---------------------------------10分六、(本大题10分)某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料生产A 、B 两种产品,共50件,已知生产一件A 产品,需用甲种原料9千克、乙种原料3千克,可获利润700元,已知生产一件B 产品,需用甲种原料4千克、乙种原料10千克,可获利润1200元,(1)按要求安排A 、B 两种产品的生产件数,有哪几种方案?请你给设计出来.(2)设生产 A 、B 两种产品获总利润为y (元),其中一种的生产件数为x , 试写出y 与x 之间的函数关系式,并利用函数的性质说明(1)中哪种生产 方案获总利润最大?最大利润是多少?解:(1)设安排生产A 种产品x 件,则生产B 种产品(50-x )件.依题意,得 ()()⎩⎨⎧≤-+≤-+290501033605049x x x x ------------------------------------4分 解得 30≤x ≤32,∵x 为整数,∴ x 只能取30,31,32.相应的(50-x )的值为20,19,18.∴生产方案有三种: ----------------------------5分 第一种方案:生产A 种产品30件,B 种产品20件;第二种方案:生产A 种产品31件,B 种产品19件;EA B G D C F H第三种方案:生产A 种产品32件,B 种产品18件.----------------6分(2) 设安排生产A 种产品x 件,则生产B 种产品(50-x )件.依题意,得 y = 700x +1200(50-x )=-500x + 60000其中x 只能取30,31,32. -----------------------------------7分∵-500<0,∴此一次函数 y 随x 增大而减小.∴当x = 30时,y 的值最大,即按第一种生产方案安排生产,获总利润 最大.最大利润为:-500×30+60000 = 45000(元).-------10分附加题(40分)七、选择题(本大题共4个小题;每小题3分,共12分.答题要求与第二题相同)1.关于x 的方程x k k x -=-的根为 【 】(A )x = k (B )x 1 = k+1, x 2 = k -1 (C )x 1 = k, x = k+1(D )x = 2k解: 根据题意, 得⎩⎨⎧≥-≥-00x k k x 解得x = k, 故选A . 2.已知,如图4,弦AB 经过⊙O 的半径OC 的中点P ,且AP = 2,PB = 3,则⊙O 的半径等于 【 】(A )2 (B )6(C )22 (D )26解: 连接OD 交⊙O 于D, OD = R, CP = OP = 21R, ∴依据相交弦定理得: AP ·PB = CP ·PD , 即2×3 =21R ×(21R + R ) R = 22± 舍去负值, R = 22.故选C .3.已知,k >1, b = 2k, a + c = 2k 2 , ac = k 4-1,则以a 、b 、c 为边的三角形一定是 【 】(A )等边三角形 (B )等腰三角形 (C )直角三角形(D )形状无法确定 解: 依据所给条件先求出a 、b 的值, x 2 -(a + c) x + ac = 0即 x 2 -2k 2x + k 4-1 = 0解方程x 2 -2k 2x + k 4-1 = 0得 x 1 = k 2+1, x 2 = k 2-1∴a = k 2+1, c = k 2-1 (或相反)又, b = 2k,把前3式分别平方得a 2 = k 4+2k 2+1, c 2 = k 4-2k 2+1,b 2 = 4k 2发现有 c 2 + b 2 = a 2, 所以 三角形一定是直角三角形.故选C .4.已知抛物线y = x 2+2mx +m -7与x 轴的两个交点在点(1,0)两旁,则关于x 的方程14x 2+(m +1)x +m 2+5 = 0的根的情况是 (A )有两个正数根 (B )有两个负数根(C )有一个正数根和一个负数根 (D )无实数根 解: ∵抛物线与x 轴的两个交点在点(1,0)两旁, ∴a >0, 开口向上, 直线x = 1与抛物线的交点的纵坐标小于零 D CA O P B将x = 1代入y = x 2+2mx +m -7,得 1 +2m + m -7<0, m <2.方程14x 2+(m +1)x +m 2+5 = 0的判别式为 △ = (m +1)2-4×41( m 2+5) = m -2<0, ∴方程无解.故选D . 八、(本大题8分)已知,如图5,△ABC 中,∠A 的平分线AD 交BC 于D ,⊙O 过点A ,且与BC 相切于D ,与AB 、AC 分别相交于E 、F ,AD 与EF 相交于G . (1)求证:AF ·FC = GF ·DC ; (2)已知AC= 6cm ,DC = 2cm ,求FC 、GF 的长. (1)证明:连接DF ,在△AGF 和△DFC 中,∵BC 与 ⊙O 相切于D ,∴∠FAG =∠CDF∵∠FAG = ∠BAD ,又 ∠BAD =∠EFD ,∴∠CDF = ∠EFD ,EF ∥BC .∴∠AFG =∠DCF .△AGF ∽△DFC .∴FCGF DC AF =,即 AF ·FC = GF ·DC ----------------5分 (2)解:由切割线定理,得 DC 2 = AC ·FC ----------------6分∵AC = 6, DC = 2, ∴FC =()cm 32 , AF = AC -FC = ()cm 316 -----7分 由(1)知 AF ·FC = GF ·DC, ∴GF = ()cm 916 -------------8分 九、(本大题10分)已知一条抛物线经过A (0,3)、B (4,6)两点,对称轴为x =53. (1)求这条抛物线的解析式;(2)试证明这条抛物线与x 轴的两个交点中,必有一点C ,使得对于x 轴上任 意一点 D ,都有AC+BC ≤AD+BD .(1)解:设抛物线的解析式为y = ax 2+bx +c ,A 点关于35=x 的对称点为A ' 则A '(310,3) 依题意,得⎪⎪⎩⎪⎪⎨⎧==++⎪⎭⎫ ⎝⎛=++3331031064162c c b a c b a , 解得 a =89, b = 415-, c =3-------2分 ∴抛物线的解析式为y =89x 2415-x + 3 --------------------------4分 A E B D C FG O 图5(2)证明:设89x 2415-x + 3 = 0,解得 x 1 =34 , x 2 = 2. ∴抛物线与x 轴的两个交点的坐标分别是(34 ,0),(2,0)---6分 设点A 关于x 轴的对称点为E ,则E (0,3)设直线BE 的解析式为 y = mx +n ,由直线经过B ,E 两点得m =49, n =-3. ∴y = 49x -3.易知,直线与x 轴的交点坐标是(34 ,0) 设C (34 ,0),则点C 恰为抛物线与x 轴的一个交点.----------8分 在x 轴上任意取一点D ,连接AC 、AD 、BD 、ED .若点D 与点C 为同一点,则AC + BC = AD + BD ;若点D 与点C 不为同一点,在△BED 中,有BE <ED +BD .∵BE = EC + BC ,EC = AC ,ED = AD ,∴AC + BC <AD + BD .∴对于x 轴上任意一点D ,都有AC + BC <AD +-----------------10分十、(本大题10分)如图6所示,一艘轮船以20里/时的速度由西向东航行,途中接到台风警报,台风中心正以40里/时的速度由南向北移动,距台风中心2010里的圆形区域(包括边界)都属台风区.当轮船到A 处时,测得台风中心移到位于点A 正南方向B 处,且AB = 100里.(1)若这艘轮船自A 处按原速度继续航行,在途中会不会遇到台风?若会,试 求轮船最初遇到台风的时间;若不会,请说明理由;(2)现轮船自A 处立即提高船速,向位于东偏北300方向,相距60里的D 港 驶去.为使台风到来之前,到达D 港,问船速至少应提高多少(提高的 船速取整数,1336≈.)?解:(1)设途中会遇到台风, 且最初遇到台风的时间为t 小时,此时,轮船位于C 处,台风中心移到E 处,连接CE . 则有 AC = 20t, AE = AB -BE = 100-40t,EC =2010. 在△RtAEC 中, AC 2 + AE 2 = EC 2, ∴(20t)2 + (100-40t)2 =(2010)2.整理,得 t 2 -4t +3 = 0. ① ------------3分 ∵△ = (-4 )2 -4×1×3 = 4>0, ∴ 途中会遇到台风 --------------------------4分 解 ①得 t 1 = 1,t 2 = 3∴ 最初遇到台风的时间为1小时.-------------5分(2)设台风抵达D 港的时间为t 小时,此时台风中心至M 点.过D 作DF ⊥AB,垂足为F,连接DM .- ---------------------------------6分在△RtADF 中,AD = 60,∠FAD = 600,∴DF = 303,FA = 30.--------7分 又 FM = FA + AB -BM = 130-40 t, MD = 2010.∴(303)2+(130-40 t )2 = (2010)2 .整理,得 4t 2 -26t +3 9 = 0. ----------------------------8分 解得 41313,4131321+=-=t t . ∴台风抵达D 港的时间为41313-小时. -------------------------------9分 ∵轮船从A 处用41313- 小时到D 港的速度为60 41313-≈25.5. 因此,为使台风抵达D 港之前轮船到D 港,轮船至少应提速6里/时.----10分。
河北省初中生升学统一考试.doc

2005年河北省初中生升学统一考试语文试卷第一部分(1-3题,共2分)1.用诗词原句填空。
(每空1分,共2分)①几处早莺争暖树,。
(白居易《钱塘湖春行》)②,西北望,射天狼。
(苏轼《江城子•密州出猎》)2.根据要求在下列横线上写上相应的内容。
(每空1分,共4分)①《酬乐天扬州初逢席上见赠》一诗中蕴含新事物必将取代旧事物这一哲理的句子是:,。
②请你从积累的古诗中写出一个与“大海”有关的完整诗句:,。
3.根据要求完成下列两题。
(每题3分,共6分)①运用“春蚕到死丝方尽,蜡炬成灰泪始干”这一诗句,写一段完整的话,②请你根据《教学大纲》推荐的课外阅读名著,在下面横线上写出相应的内容。
读《》(名著名称),我了解到(内容):第二部分(4-25题 58分)一、阅读下面的文字,回答后面的问题。
(14分)三峡自三峡七百里中,两岸连山,略无阙处;重岩叠嶂,隐天蔽日,自非亭午夜分,不见曦月。
至于夏水襄陵,沿溯阻绝。
或王命急宣,有时朝发白帝,暮到江陵,其间千二百里,虽乘奔御风不以疾也。
春冬之时,则,。
绝巘多生怪柏,悬泉瀑布,飞漱其间。
清荣峻茂,良多趣味。
每至晴初霜旦,林寒涧肃,常有高猿长啸,属引凄异,空谷传响,哀转久绝。
故渔者歌曰:“巴东三峡巫峡长,猿鸣三声泪沾裳!”4.文章作者是北魏地理学家(人名)。
(1分)5.将文章中空缺的语句填写在下面的横线上。
(2分)答:6.解释下列句子中加着重号的词语。
(3分)①重岩叠嶂.,隐天蔽日嶂:②夏水襄陵,沿溯.阻绝溯:③虽乘奔御风不以疾.也。
疾:7.把下列的句子翻译成现代汉语。
(4分)①自非亭午夜分,不见曦月。
译文:②空谷传响,哀转久绝。
译文:8.用自己的话分别概括“三峡的山”和“夏季的水”的特点。
(4分)答:二、阅读下面的文字,回答后面的问题。
(14分)雾①雾是一种常见的天气现象。
秋冬时节,当低层大气中的水汽达到饱和状态时,低层大气中出现的水汽凝结物悬浮在空中,并使能见度的水平距离小于1 千米,气象学上把这种天气称为雾。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1999年河北省初中生毕业、升学统一考试数 学 试 题说明:本试卷共设九个大题,150分满分,答题时间为120分钟.一、 填空题本大题共10个小题,每小题3分,共30分)1.比较大小:52_____32--2.16的算术平方根是3.如图1,直线a 、b 被直线c 若∠1=1180,则∠4.不等式组⎩⎨⎧<->-2211023x x 的解集为____________5.把一个平角16等份,则每份为(用度、分、秒表示)____________. 6.函数21-=x y 的自变量x 的取值范围为_________________.7.分解因式:=--2532x x ____________________. 8.已知:如图2,在△ABC 中,∠ABC=500,∠ACB=780, 点O 为△ABC 的内心,BO 的延长线交AC 于点D ,则 ∠BDC 的度数为_________________.9.已知⊙O 1与⊙O 2的半径分别为方程01492=+-x x 的两根,若圆心距O 1O 2的长为5, 则⊙O 1与⊙O 2的位置关系为____________. 10.已知点P (1,a )在反比例函数()0≠=k xky 的图象上,其中322++=m m a (m 为实数),则这个函数的图象在第__________象限.二 、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的,把符合题目要求的选项前的字母填写在题后括号内)图 1 ABCDO图 21.如果实数a 与b 互为相反数,则a 、b 满足的关系为 【 】 A ab=1 B ab=-1 C a+b=0 D a-b=02.若正n 形的一个外角为600,则n 的值为 【 】 A 4 B 5 C 6 D 83.下列运算中,不正确的为 【 】 A ()22523x xy xy x xy -=-- B 4332842b a ab b a =⋅ C ()xy x y x x 5102532-=-⋅ D ()()993332+=+-+x x x x 4.如果a<2,那么化简()222+-a 的结果为 【 】A 4 -aB aC - aD 4 + a5.若实数m 、n 满足()02122=++-n m ,则mn 的值等于 【 】 A -1 B 1 C -2 D 26.下列各图形中,既是轴对称图形又是中心对称图形的是 【 】 A 等边三角形 B 平行四边形 C 等腰梯形 D 菱形7.已知:在△ABC 中,AB=AC ,∠BAC=1200,AD 为BC 边上的高,则下列结论中, 正确的是 【 】 A AB AD 23=B AB AD 21= C AD=BD D BD AD 22= 8.无理方程2722+=+x x x 的解为 【 】 A 4,121-==x x B x=1 C 4,121=-=x x D x=49.若菱形的周长为16,两邻角的度数之比为1∶2,则该菱形的面积为 【 】 A 34 B 38 C 310 D 31210.已知a 、b 、c 是△ABC 三条边的长,那么,方程()042=+++cx b a cx 的根的情况 【 】 A 没有实数根 B 有两个不相等的正实数根 C 有两个不相等的负实数根 D 有两个异号实数根三、(本大题共2个小题,每小题7分,共14分)1. 甲、乙两台机床同时加工直径为100毫米的零件.为了检验产品的质量,从产品中各随机抽出6件进行测量,测得的数据如下(单位:毫米)甲机床: 99 100 98 100 100 103 乙机床: 99 100 102 99 100 100(1) 分别计算上述两组数据的平均数及方差;(2) 根据(1)中计算结果,说明哪一台机床加工这种零件更符合要求.2. 已知:如图3,在△ABC 中,AD 为BC 边上的高,∠B=450,∠C=300,AD=2.求△ABC 的面积.A B CD┐ 图 3四(本大题共2个小题,每小题8分,共16分)1.先化简,再求值:1322212+++⋅⎪⎭⎫ ⎝⎛++-a a a a a a a ,其中121-=a .2.证明梯形中位线定理:已知:如图4,在梯形ABCD 中,AD ∥BC ,AM=MB ,DN=NC 求证:MN ∥BC ;()AD BC MN+=21.ADMBNC 图 4y x O 11 -1 -1图 5五、列方程(或方程组)解应用题(本大题满分10分)汛期到来之前,某施工队承担了一段300米长的河堤加固任务.加固80米后,接到防汛指挥部的指示,要求加快施工进度.为此,施工队在保证施工质量的前提下,每天多加固15米,这样一共用6天完成了任务.问接到指示后,施工队每天加固河堤多少米?六、阅读下列材料,并在横线上解答相应的问题(本大题10分)九年义务教育三年制初级中学教科书代数第三册中有以下几段文字:“对于坐标平面内任意一点M ,都有唯一的一对有序实数(x ,y )和它对应;对于任意一对有序实数(x ,y ),在坐标平面内都有唯一的一个点M 和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x 与函数y 的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.” “实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上点的坐标,一定满足这个函数的关系式.另外,已知直线上两点坐标,便可求出这条直线所对应的一次函数的解析式. 问题1:已知点A (m ,1)在直线12-=x y 上,求 m 的方法是_____________________ ____________________________________,∴m =____________________;已知点B (-2,n )在直线12-=x y 上,求 n 的方法是_____________________ ____________________________________,∴n =____________________. 问题2:已知某个一次函数的图象经过点P (3,5)和Q (-4,-9),求这个一次函数的解析式时一般先_________________________________再由已知条件可得:_______________________.解得:________________________. ∴满足已知条件的一次函数的解析式为:___________________. 这个一次函数的图象与两坐标轴的交点坐标为:_______________, 在右侧给定的平面直角坐标系中,描出这两个点,并画出这个函数的图象.像解决问题2这样,_______________________________________ _______________________________的方法,叫做待定系数法.图 6七、(本大题12分)已知:如图6,△ABC 内接于⊙O ,∠BAC 的平分线交⊙O 于点D ,交⊙O 的切线BF 于点F ,B 为切点. 求证:(1)BD 平分∠CBF ;(2)CD AF BF AB ⋅=⋅八、(本大题14分)如图7,这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图,横断面的地平线为x轴,横断面的对称轴为y轴,桥拱的DGD′部分为一段抛物线,顶点G的高度为8米,AD和A′D′是两侧高为5.5米的支柱,OA和OA′为两个方向的汽车通行区,宽都为15米,线段CD和C′D′为两段对称的上桥斜坡,其坡度为1∶4 (1)求拱桥DGD′所在抛物线的解析式及CC′的长;(2)BE和B′E′为支撑斜坡的立柱,其高都为4米,相应的AB和A′B′为两个方向的行人及非机动车通行区.试求AB和A′B′的宽;(3)按规定,汽车通过该桥下时,载货最高处和桥拱之间的距离不得小于0.4米.今有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与地面的距离均为7九、本大题满分14分如图8,正方形OABC 的顶点O 在坐标原点,且OA 边和AB 边所在直线的解析式分别为x y 43=和32534+-=x y .D 、E 分别为边OC 和AB 的中点,P 为OA 边上一动点(点P 与点O 不重合),连结DE 和CP ,其交点为Q .1. 求证:点Q 为△COP 的外心;2. 求正方形OABC 的边长;3. 当⊙Q 与AB 相切时,求点P 的坐标.4. 数学试题参考答案及平分标准说明:1.本参考答案中各题只给出了一种解法,如考生还有其它正确解法,可参照评分标准酌情给分.2.坚持每题评阅到底的原则,当考生的解答在某一步出现错误,影响了后继部分时,如果该步以后的解答未改变这一题的内容和难度,可视影响的程度决定后面部分的给分,但不得超过后继部分的一半;如果这一步后面的解答有较严重的错误,就不给分.3.解答右端所注分数,表示正确做到这一步应得的累加分数. 4.只给整数分数.一、填空题1. < ; 2. 4; 3. 620; 4. 29>x ; 5. 11015′; 6. 2>x7. ()()213-+x x ; 8. 770; 9. 内切; 10. 一、三.三、1.(1)甲x =100 乙x =100 2甲S =37 2乙S =1 ··························· 6分 (2)由(1)可知,而甲x =乙x ,2甲S >2乙S .所以乙机床加工这种零件更符合要求.········································································································································ 7分 2.解:在Rt △ADB 中,∵∠ADC=900,∠B=450,∴BD=AD=2 ···················· 2分 在Rt △ADC 中,∵∠ADC=900,∠C=300,AD=2,∴DC=ADctg300=23 ·············································································· 5分 ∴△ABC 的面积=()32232222121+=+⨯⨯=⋅BC AD ························ 7分 四、(每小题8分,共16分)解:原式 =()()()()()11222112+++⋅+-+a a a a a a a12-=a a ·························································································· 5分 当12121+=-=x 时, ·········································································· 6分原式=()()2112212112122=++=-++. - ···························································· 8分 证明:连结AN 并延长,交BC 的延长线于点E . ······················································ 1分 ∵DN=NC ,∠1=∠2,∠D=∠3, ∴△ADN ≌△ECN . ················································ 3分∴AN=EN ,AD=EC又∵AM=MB . ∴MN 是△ABE 的中位线. ∴MN ‖BC ,MN =21BE ·································· 6分∵BE =BC+EC=BC+AD ∴MN =21(BC +AD ) ··················································· 8分 五、(本大题10分)解:设施工队原计划每天加固河堤x 米,则接到指示后每天加固(x+15)米. 根据题意,得6158030080=+-+x x ······················································································ 5分 去分母,并整理.得 0200352=--x x ························································· 6分 解这个方程,得 54021-==x ,x ································································· 8分 经检验 54021-==x ,x 都是原方程的解,但52-=x 不合题意,故只取401=x . ······················································· 9分 ∴x+15=40+15=55.答:接到指示后,施工队每天加固河堤55米.10分 六、(本大题10分)问题1:将点A 的坐标(m ,1)代入y=2x-1得 1=2m-1,∴m = 1 ············· 1分 将点B 的坐标(-2,n )代入y=2x-1得 n=2 ×(-2)-1,∴n = -5 ······ 2分 问题2:设这个一次函数的解析式为y=kx+b ,························································ 3分方程组⎩⎨⎧+-=-+=b k bk 4935-------------------------4分k = 2 , b = -1 ··········································· 5分y = 2x - 1 ················································ 6分)0,21(C 、D(0, -1) ···································· 7分先设出式子中的未知系数,再根据条件求出未知 系数,从而写出这个 ································· 10分 七、(本大题12分)证明:(1)∵AD 平分∠BAC ,∴∠1=∠2. ························ 2分 ∵BF 切⊙0于点B ,∴∠3=∠1.···························· 4分又∵∠2=∠4,∴∠3=∠4,即BD 平分∠CBF.·· 6分(2)在△DBF 和△BAF 中, ∵∠3=∠1,∴∠F=∠F ,∴△DBF ∽△BAF. ············· 8分A DM BN CE1 2 3B∴AFBFAB BD =,即AB ·BF=AF ·BD. ····················· 10分 ∵∠1=∠2,∴BD=CD. ············································ 11分∴AB ·BF=AF ·BD. ······································ 12分八、(本大题14分) 解:(1)设DGD '所在的抛物线的解析式为y=ax 2+c.由题意得G(0,8),D(15,5.5). ∴⎩⎨⎧+==c a c 2255.58 解得⎪⎩⎪⎨⎧=-=8901c a∴DGD '所在的抛物线的解析式为8x 901y 2+-=. ···································· 4分 ∵41AC AD =,且AD=5.5,∴AC = 5.5 ×4 =22 (米) . ∴CC ' = 2OC =2 × (OA+AC) =2 × (15+22) =74 (米) . 答:CC '的长为74米. ················································································· 6分(2)∵41BC EB =,BE=4,∴BC=16. ··································································· 8分 ∴AB = AC - BC = 22 - 16 = 6 (米) . 答:AB 和A 'B '的宽都是6米. ································································· 10分(3)答:该大型车可以从OA (或OA ')区域安全通过. ································ 11分 在8x 901y 2+-=中,当x = 4时, 45377816901y =+⨯-=. ············································································ 13分 ∵ 04519)4.07(45377>=+-. ∴ 该大型货车可以从OA (或OA ')区域安全通过. ······························ 14分九、(本大题14分) 解:(1)∵ D 、E 分别为正方形OABC 中OC 、AB 的中点,∴DE//OA.∴ Q 也是CP 的中点.又∵ CP 是Rt △COP 的斜边,∴点Q 为△COP 的外心. ························· 3分(2)由方程组⎩⎨⎧==⎪⎩⎪⎨⎧+-==.3y ,4x .325x 34y x 43y 解得 ∴点A 的坐标为(4,3). ········································································· 5分过点A 作AF ⊥Ox 轴,垂足为点F. ∴OF = 4,AF=3.由勾股定理,得534OA 22=+=.∴正方形OABC 的边长为5. ······································································ 7分(3)如图,当△COP 的外接圆⊙Q 与AB 相切时,∵圆心Q 在直线DE 上,且DE ⊥AB , ∴E 为⊙Q 与AB 相切的切点 ···································································· 8分 又∵AE 和APO 分别是⊙Q 的切线与割线, ∴AE 2=AP ·AO.∵25AE ,5OA ==, ∴.45AP .5AP )25(2=⋅=∴当⊙Q 与AB 相切时,.415455OP =-= ·············································· 11分 作PH ⊥Ox 轴,垂足为H. ∵PH//AF ,∴.AFPHOF OH OA OP == ∴.4953415OA AF OP PH ,354415OA OF OP OH =⨯=⋅==⨯=⋅=∴点P 的坐标为).49,3(·············································································· 14分。
