基于对称方程的渐开线直齿圆锥齿轮UG参数化建模1
基于UG的齿轮参数化建模

基于UG的齿轮参数化建模齿轮是机械传动中常见的零部件,用于传递动力和转速。
在设计和制造齿轮时,参数化建模是一种有效的方法,它可以提高设计的灵活性和效率,同时可以减少错误并节省时间和成本。
在本文中,我们将介绍基于UG(Unigraphics)软件进行齿轮参数化建模的方法。
首先,我们需要打开UG软件并创建一个新的文件。
然后,在模型中选择“齿轮”功能,并设置齿轮的基本参数,如模块(modulus)、齿数、齿轮厚度、齿宽等。
这些参数将决定齿轮的几何形状和尺寸。
同时,我们还可以使用函数来定义其他参数,例如齿数、齿宽等。
通过这种方式,我们可以灵活地调整齿轮的尺寸和形状,而不需要手动修改每个参数。
另外,UG还提供了强大的几何建模工具,我们可以使用这些工具来创建齿轮的几何形状。
例如,我们可以使用“旋转”功能来绘制齿轮的基本轮廓,然后通过“变量融合”功能来添加齿形,并使用“切割”功能来创建齿形。
在建模过程中,我们还可以通过参数化建模功能来创建不同类型的齿轮,例如直齿轮、斜齿轮、螺旋齿轮等。
通过设置不同的参数,我们可以快速生成不同类型的齿轮模型,提高设计的效率和灵活性。
此外,UG还支持对齿轮模型进行分析和优化。
我们可以使用“装配分析”功能来检查齿轮的运动性能和受力情况,从而优化设计并提高其可靠性和耐用性。
总的来说,基于UG的齿轮参数化建模是一种高效、灵活和精确的设计方法。
通过这种方法,我们可以快速生成不同类型的齿轮模型,并进行准确的分析和优化,从而提高设计的效率和质量。
希望本文对您在齿轮设计中有所帮助。
基于UG的直齿圆锥齿轮的参数化、可视化设计

英文论文原文英文译文:应用图表对锥齿轮的运动学分析摘要:非定向和定向性图表技术能够应用于对锥齿轮的运动学分析中。
在这两种技术中,齿轮的运动学结构由图表方式来展现。
虽然非定向的图表的绘制相对简单,但他们只用于确定基本线路的载体节点。
另一方面,在一张定向性图表中,由于每条线代表一个对变量的诠释,所以其相对非定向性图表能传播更多信息。
本文对这两个技术进行比较,并且针对的图表技术的好处由Cincinnati Milacron T3通过对一个机制机器人的运动学分析能够充分展示定向性图表的优势。
关键词:参数化草图表达式1. 介绍近几年,应用图表技术对机器人斜面齿轮的运动学分析已逐步确立。
两种不同图表技术被应用于对机器人斜面齿轮的运动学分析中:非定向性和定向性图表技术。
非定向性图表技术是由Freudenstein率先提出的。
这一方法运用了基本电路的理念。
Freudenstein和Yang较详细地阐述了此概念,然后由Tsai开发了一个计算机算法以及机制的一个标准表示法。
这种定向线性图表技术早在六十年代就被应用于电子网络以及其他类型的物理系统中,如一维的机制转动装置。
Chou et al. 通过使用同一种方法将这些技术延伸到三维系统中。
1992年,在三维传动装置中,最重大突破是Tokad,它是多端网络刚体的一个紧凑数学模型的衍生物。
在这种衍生物中,一种所谓网络模型方法的系统方法,为三维机械系统的公式化而被开发。
Uyguroglu和Tokad 对将网络模型方法应用于空间机器人斜面齿轮的运动学和动态分析进行了详尽的阐述。
一个新的定向性图表技术被应用于斜面齿轮的相对角速度的关联中。
本文通过对非定向性图表和定向性图表技术应用于斜面齿轮的运动学分析的比较,展示出定向性图表技术优于非定向性图表技术的一面。
这一理论被Cincinnati Milacron T3通过对一个机制机器人的运动学分析充分展示。
2.机器人斜面齿轮因为机器人操纵器原理简单,而且构造简单,所以机器人操纵器通常是一个开放环路的运动学链。
基于对称方程的渐开线直齿圆柱齿轮UG参数化建模

( a hnUnv rt T i a iesy,T i nS ad n 7 0 1 hn) s i a a h n o g 2 12 ,C ia
Absr c : Thsatce h d p i td o ttes u e rc rn o l sd p rm ercm o e n t o — d rc o mai e o n ufce c tat i ril a o ne u h p rg a on q ny u e aa ti d h g me h d ie tf r t on Sm t d is f in y, h i p op sd etbih siv l e hem o h r o rn in u v y r oe sa l e n out,t t o tta se tc r es mm ercle u t n,c c ltst e dvdn n mbe fte nd t u v s tia q ai o l a uae i ig f e nu h i i ro t a hec r e eh
Ba e n S m me r c Eq a i n o v l t s p rGe r UG a a e rc M o ei g sdo y t i u t f n o u e S u a o I P r m ti d l n
Z U H ANG —T o, BI Su o AN n — Big CHu n a
过 实 例 建 模 ,证 明 了该 方 案 的 正 确 性 、 精 确 性 ,体 现 了该 方 案 理 论 严 谨 ,操 作 方 便 。
关键 词 :直齿轮 ;渐 开线 ;过 渡 曲线 ;对称 方程 ;参 数化建模
中图分类号 :T 2 H12 文献标 识码 :A d iO36 /.s . 0 — 6 32 Байду номын сангаас.1 5 o: .9 9j sn1 2 6 7 . 1 . 1 l i 0 0 0 0
直齿锥齿轮UG建模步骤小白使用

直齿锥齿轮UG建模步骤(小白使用)一、数据校核1.原图纸参数校核;校核完毕的参数保存打印,并记录原重合度值:一般在1.15~1.20间。
2.参数优化设计修改齿顶高系数保存打印,直到重合度达到满意的要求:一般达到1.25左右。
确定齿厚减薄量:根据侧隙要求来设定行齿减薄量和侧齿减薄量,确定两者的齿厚,齿厚应尽量兼顾满足图纸上的齿厚公差。
3.参数代入插件建模,将参数代入插件,注意评估变位系数是否要修改;插件自主计算时,会将行齿高变位、切变位系数加大,侧齿减薄;根据需要看是否修正。
自主建模,将参数代入.exp表达式,保存;二、锥齿自主建模1、建立如下表达式,并带入程序。
z1=18z2=12m=4.5a=22.5i=z1/z2 sigma=90B=18.73r1=m*z1/2r2=m*z2/2rb1=r1*cos(a)rb2=r2*cos(a)delta1=arctan(i)delta2=90-delta1R=r1/sin(delta1)ha1=2.673 //齿顶高hf1=5.823 //齿根高thetaa1=arctan(ha1/R)thetaf1=arctan(hf1/R)deltaha1=60.44498966 //面锥角deltahf1=49.488039 //根锥角rf1=r1-hf1*cos(delta1) //当量齿轮zv1=z1/cos(delta1)zv2=z2/cos(delta2)rv1=r1/cos(delta1)rvb1=rv1*cos(a) rva1=rv1+ha1rvf1=rv1-hf1si=8.09043-0.12-a //填入弧齿厚及减薄量及修形量yt=rvb1*cos(s)+rvb1*rad(s)*sin(s)xt=rvb1*sin(s)-rvb1*rad(s)*cos(s) 〃渐开线在 X 、Y 、Z 三个方向 的参数方程zt=02、建立草图,绘制分锥、背锥、面锥、根锥母线。
基于UG的直齿圆锥齿轮的参数化、可视化设计(1).

引言计算机的进步与制造业的发展总是相辅共荣。
越来越多的应用软件被推广与普及,如CAD/CAM、UG等一些辅助设计软件的广泛应用,就大大加快了机械零件的设计过程,缩短了产品的设计和制造周期。
UG是一个在二维和三维空间无结构网格上使用自适应多重网格方法开发的一个灵活的数值求解偏微分方程的软件工具。
其设计思想足够灵活地支持多种离散方案。
因此软件可对许多不同的用途进行再利用。
Unigraphics(简称UG)是当前世界上最先进和紧密集成、面向制造业的CAID/CAD/CAE/CAM高端软件。
它为制造行业产品开发的全过程提供解决方案,功能包括:概念设计、工程设计、性能分析和制造。
它实现了设计优化技术与基于产品和过程的知识工程的组合,显著地改进了如汽车、航天航空、机械、消费产品、医疗仪器和工具等工业的生产效率。
随着计算机性能的提高,现在在微机上就可以使用UG,这样UG的适用范围更加广阔,三维设计已经不是人们的奢侈品,会越来越多成为设计工程师的首选。
而在面对零部件批量设计的需要时,UG就不仅仅停留在制图、建模、装配、出图等基本功能的运用上。
而应实现可编辑、参数驱动等功能。
本文的设计是采用CAD数字化的思想,运用电子表格与UG的智能化接口,抽取相关零部件的参数信息,再被用来更新零部件前做手工处理。
再结合电子表格的目标搜索功能,可以对设计进行进一步的优化。
使用电子表格的前提是模型必须是参数化的,参数之间必须是相关的。
通过抽取并编辑表达式中的参数达到控制模型的目的,而其中实用的内部函数为工程计算提供了强大的引擎。
完整使用电子表格技术,则需要依赖表达式、内部函数和用户自定义函数三者的有机结合,其工作的实质就是对模型参数的驱动以更新模型。
本文以一对啮合的直齿锥齿轮在UG中的参数化、可视化设计为例。
第一章绪论1.1课题研究的目的和意义1.1.1课题研究的目的齿轮作为最重要的基础传动部件被广泛地应用于机械、冶金、石化、煤炭、水电等行业。
基于UG的渐开线直齿圆柱齿轮参数化精确造型设计

基于UG的渐开线直齿圆柱齿轮参数化精确造型设计祝林;李小明【摘要】介绍了一种利用UG的表达式和规律曲线功能建立直齿圆柱齿轮模型的方法。
该方法绘制了精确的齿廓曲线,生成的齿廓各段曲线不需任何修剪便可直接建立精确的齿轮模型。
并可通过改变模数和齿数等参数,使生成的模型自动更新,实现了建立模型的真正参数化。
%Describe expressions and laws of a UG curve method of straight tooth cylindrical gear model features.The method draws the exact tooth profile curve,tooth profile curve generating directly without any pruning can establish accurate gear models, and by changing parameters such as module and number of teeth, the generated model automatically updates, to achieve the establishment of models for real parameter.【期刊名称】《机械管理开发》【年(卷),期】2013(000)001【总页数】3页(P59-61)【关键词】直齿轮;齿廓曲线;参数化;UG【作者】祝林;李小明【作者单位】四川职业技术学院,四川遂宁 629000;四川职业技术学院,四川遂宁 629000【正文语种】中文【中图分类】TH132.4130 引言在工程机械中用作传动的渐开线直齿圆柱齿轮应用相当广泛,对直齿圆柱齿轮进行精确造型设计是工程机械进行承载分析、性能分析和动力学分析的难点。
直齿圆柱齿轮的齿廓曲线比较复杂,包括齿根圆弧、齿根过渡曲线、渐开线和齿顶圆弧。
ProE渐开线直齿轮的参数化建模教程
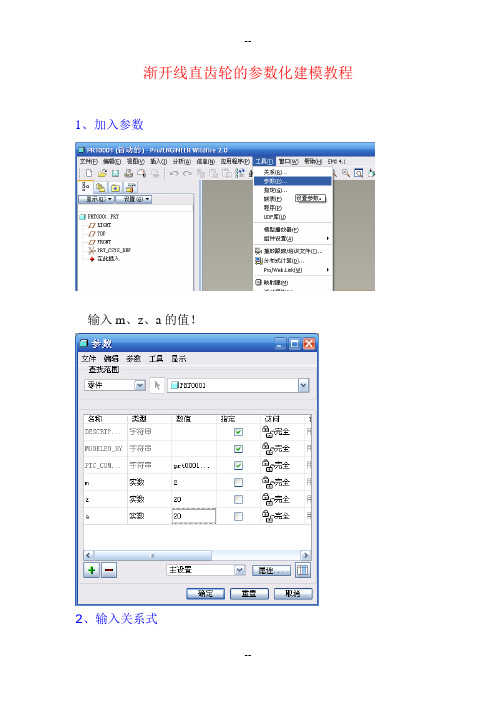
渐开线直齿轮的参数化建模教程1、加入参数输入m、z、a的值!2、输入关系式/* 参数字母含义如下:/* m-->模数/* z-->齿数/* a-->压力角/* p-->齿距/* pb-->基圆齿距/* d-->分度圆直径/* da-->齿顶圆直径/* df-->齿根圆直径/* e-->分度圆齿槽宽/*-------------------------------/*特征尺寸赋值/*-------------------------------/*定义齿轮常数(ha*&c*)/*定义齿高系数(ha*)ha=1/*定义齿顶系数(c*)c=0.25/*定义渐开线展角B=(tan(a)-(PI/180*a))/(PI/180)/*定义分度圆直径d=m*z/*定义齿顶圆直径da=(z+2*ha)*m/*定义齿根圆直径df=(z-2*(ha+c))*m/*定义基圆直径db=m*z*cos(a)/*定义齿距p=PI*m/*定义基圆齿距pb=p*cos(a)/*定义分度圆齿槽宽e=(PI*m)/2/*计算齿槽宽的夹角Angle=(e/(d/2))*(180/pi)/*定制渐开线的偏移角度d33=Angle/2/*复制的偏移角度d37=360/Z/*定义阵列的数量p43=Z-1/*定义阵列的增量d42=360/Z/*结束/*-------------------------------3、创建齿坯选取front基准面为绘图平面!将齿顶圆的直径赋予草绘尺寸,sd0=da。
如下图所示。
接受草图,返回4、创建渐开线插入基准曲线选择“从方程”,然后单击完成选取坐标系,如下:然后选择笛卡尔,如下:输入关系式:alphak=40*tThetak=(tan(alphak)-alphak*(pi/180))*(180/pi)Rk=(db/2)/cos(alphak)X=rk*cos(thetak)Y=rk*sin(thetak)Z=0/*以上由极坐标方程演变而来,Thetak为方程中展角,alphak为压力角。
基于UG二次开发的直齿、斜齿圆柱齿轮及锥齿轮的参数化建模

基于UG二次开发的直齿、斜齿圆柱齿轮及锥齿轮的参数化建模摘要在机械加工中,孔加工占机械加工的比例在30%以上,特别是在汽车与航空等行业中麻花钻的应用极为广泛。
由于长期以来,麻花钻的设计大多是靠工程师的经验来进行,在设计过程中,难免会出现重复性的工作,从而降低了设计效率。
同时通常的设计都是在二维图纸上进行设计,不能得到可视化的麻花钻三维造型,这就阻碍了麻花钻的数控刃磨加工及利用一些分析软件对麻花钻的钻削过程进行分析。
在UG中利用麻花钻参数表达式绘制麻花钻实体模型,实现麻花钻在UG的参数化设计。
从而实现产品的快速设计。
UGOpen二次开发模块是UG软件的二次开发工具集,利用该模块可对UG系统进行用户化开发,可满足用户进行各种二次开发的需求。
学习了UG二次开发的各种工具,了解了各种工具的特点和适用范围。
选择 UGOpen API编程语言,结合使用UGOpen Menu Script 和UGOpen UI Styler开发工具,实现了基于UG二次开发工具的直齿圆柱齿轮、斜齿轮、直齿锥齿轮的参数化设计。
关键词:麻花钻,二次开发,参数化,APIAbstractKey Words:parameter, gear, UGOpen, API目录第 1 章绪论 (1)1.1课题的研究背景 (1)1.2课题的研究内容和解决方法 (2)第 2 章 UG二次开发的研究 (4)2.1 UG软件概述 (4)2.1.1U G软件的功能介绍 (4)2.1.2 UG功能模块 (5)2.2 U G二次开发相关工具概述 (5)2.2.1 UGOPEN GRIP (6)2.2.2U G O P E N A P I (7)2.2.3U G O P E N M e n u S c r i p t (7)2.2.4 UGOPEN UI Styler (9)2.2.5 User Tools工具 (9)第3章二次开发方案的选择 (11)3.1列举可行的方案 (11)3.2 方案的选择 (13)3.3利用二次开发工具制作系统菜单 (14)3.3.1设置系统环境变量 (14)3.3.2制作菜单 (15)目录第4章齿轮常用的齿形曲线——渐开线 (18)4.1渐开线的形成原理 (18)4.2渐开线的数学模型 (19)4.3渐开线齿廓的绘制 (20)第 5 章直齿圆柱齿轮的参数化设计 (22)5.1 数学模型 (22)5.2 齿轮三维建模 (23)第 6章斜齿轮的参数化设计 (26)6.1 数学模型 (26)6.2 齿轮三维建模 (27)第 7 章直齿锥齿轮的参数化设计 (28)7.1 数学模型 (28)7.2 齿轮三维建模 (29)第 8 章程序设计 (30)8.1 总体方案设计 (30)8.2 对话框设计 (31)8.3 程序设计 (36)第 9 章结论 (48)致谢 (50)参考文献 (51)附录 (52)目录第1章绪论1.1课题的研究背景齿轮机构用于传递空间任意两轴之间的运动和动力,具有质量小、体积小、传动比大和效率高等优点,已广泛应用于汽车、船舶、机床、矿山冶金等领域,它几乎适用于一切功率和转速范围,是现代机械中应用最广泛的一种传动机构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2),矗>41齿,在表达式中使用方程组(1),利用规律 曲线生成齿廓曲线,注意指定cs坶参考为背锥基准 坐标系册‘面.以圆弧连接曲线端点。获得封闭的大端 齿槽截面,以锥顶点为截面线串1,以大端齿槽截面为 截面线串2,使用直纹面生成实体,与齿坯执行布尔差 运算可得锥齿轮齿槽,利用格式中特征分组把直纹与 求差添加到特征集中,以齿数=,36妒/:角度为参数。 置轴为基准轴实现圆周阵列,最终得到图5所示的参 数化的齿轮实体。
0.2
^=√髫:+,,:
(2)编辑锥齿轮计算参数 要生成渐开线,还需要由基本参数确定的计算参 数,在表达式中编辑如表2所示参数。
衰2锥齿轮计算参数 参数 分锥角/(o) 参数符号 参数计算
J茄2 ro嘲口 【),2=r0(1一sin口)一.Il棚
2
日l=(7l。,n—r0)/(rtan口) 方程坐标旋转后,由于齿根过渡曲线对称性与渐 开线对称性完全相同,建立锥齿轮齿根过渡曲线对称 方程 f蔗13=聋lcoB口2+扎sin口2 【儿3。毛sin疗2+孔c嘴口2
图I大端对称渐开线
1锥齿轮齿廓曲线
锥齿轮大端参数为标准值,因大端球面渐开线无 法展开,用近似法将大端球面齿形向背锥投影研究其 齿廓曲线,背锥展开、补全,得当量齿轮,其齿形与锥齿 轮大端的球面齿形相当,两者模数和压力角相同,当量 齿数为:;v=:/o∞d。以下均在背锥上以当量齿轮形式 研究。
图l中,渐开线l、2关于直线,,=z细7对称,
关键词锥齿轮渐开线齿根过渡曲线对称方程参数化建模
P:a删口蛐血ModeUIlg
of hIvolute Bevel
m盯ApplyiI唱UG
based蛐蛳缸证EqlI娟叽
staIt
孙岫ng Sut∞MengⅪ舯j岫
(嘶妇l UIIim蛔,%’日刀102l,CK∞)
Ab删
衄d
curve aIe
hl the
(rtall口);r为节圆半径。 如图2所示,由该方程生成的齿根过渡曲线与渐 开线并不相连,需要对方程坐标旋转来保证两曲线相 连接。
直齿圆锥齿轮大端参数为标准值,决定齿轮的几
何尺寸与形状,在表达式中设置6个基本参数,如表l 所示。
哀l锥齿轮基本参 参数 过渡曲线 图2齿根过渡曲线的生成 模数/mm 小齿轮齿数 大齿轮齿散
2直齿圆锥齿轮参数化建模
在UG中通过表达式输入锥齿轮建模所需参数, 使用草图获得齿坯,利用对称方程在背锥基准平面上 生成锥齿轮大端齿槽曲线,使用直纹面生成齿槽,圆周 阵列即可获得参数化锥齿轮。 2.1锥齿轮参数 (1)设置锥齿轮基本参数
刀具圆角半径,,o=0.3m;^。为刀具齿顶高系数,k =1.25;刀具坐标与齿轮坐标夹角臼=(km—ro)/
对称角y=一36伊/(4毛)+invⅡ,其中,invⅡ为渐 开线函数,口为大端压力角,依据关于直线对称的点坐 标计算公式建立直齿轮渐开线对称方程 f石‘2=石lI+2ta∞y(扎l一菇Iltan y)/(1+ta十y),. 【孔2=九1—2(孔I一毛ItaIl y)/(1+tan2 y) 1.3齿根过渡曲线对称方程 对于却≤41的锥齿轮在展成法加工中,基圆与齿
acc哪te】y cal砌ated.The
back咖e kI∞plalle is
FiUet
cIIIve
buih,the mled删—ace is u8ed衄a t∞l,tlle Ilsab出ty驵d
opembili哆aIe proVed.
K呵words&vel
ge缸hIvolute
帆trical
equation
第36卷第06期
文章编号:l∞4—2539(∞12106一∞47一舛
基于对称方程的渐开线直齿圆锥齿轮UG参数化建模
47
基于对称方程的渐开线直齿圆锥齿轮UG参数化建模
庄宿涛孟晓军
(泰山学院, 山东泰安27l舵1)
摘要在基于特征的渐开线直齿圆锥齿轮参数化建模中,提出了建立浙开线、齿根过渡曲线对称方
程,精确计算分界齿数与曲线起始、终止角度,构建背锥基准平面,采用直纹面为工具的解决方案,通过 实例建模,证明了该方案的实用性、可操作性。
做直线卯,约束其与以在D点重合;
③创建草图选择创建平面选项,使用成一角度平 面指令选择I平面为平面对象,OF为线性对象创建 Ⅱ平面,即为背锥基准平面。 (2)背锥基准坐标系
(3)齿廓曲线专用参数 为控制渐开线起始、终止角度及使用所提供的对 称方程创建锥齿轮大端齿槽曲线,需输入齿廓曲线专 用参数,如表3所示。
d,
n ^
【),“=儿3—2(扎3一并13tan y)/(1+tarl2 y) 该方程理论上实现了两曲线在c点相连接,但与
实际间存在微量误差,点C出现的断点可使用“桥接 曲线”保证其连续[3瑚一35。
“=d∞口/2 ^:m/石弓/2
^1-∞d(^/3)
^dm
齿宽/m 齿顶高/m
^I
k
万方数据
第36卷第06期
6
咖口。xl劬。/F
(I—I)d+b
做直线鲫,约束其与Dc在0点重合;
D点为原点创建背锥基准坐标系。 2.4锥齿轮生成
一,口/(4x
J)…
③插人基准删,以0c为*轴。以0Ⅳ为y轴,
当锥齿轮瓦≤4l齿,在表达式中使用方程组(1)、
另外还需输入齿根过渡曲线方程中的各项参数。 2.2锥齿轮齿坯 利用草图曲线功能生成等顶隙齿坯草图,由表达 式公式驱动尺寸约束。
jI
参数符号
参数初值
8 30 45 20
鲍
坐标旋转角度占2=inv%一眦taIl警,式中参数
f戈c=茗2sin疗1+y200s口l+r(p18in曰1+o∞口I)
压力角/(o) 齿顶高系数 顶隙系数 h
1.0
【,名=省2嘲曰1一,鼍sin口1+r(口1coB日1一sin臼I)
口。=arcc08(r6/rc) 其中
[1]姜海军.基于uG的直齿圆锥齿轮三维建模研究[J].煤矿机械, 加05(7):15一18. [2]王书贤,汪云,邓利军.等.基于uc的渐开线斜齿圆柱齿轮参数化 设计[J].机械传动.2011,35(5):36—38. [3]李玉龙,刘J尼.车用斜齿轮模型的uc旋转成型法研究[J].机械传 动,20略,32(”:33—35. [4】李杰,张磊,赵旗.常见齿轮过渡曲线对应齿轮弯曲应力的比较分 析[J].机械传动,20吣。32(6):101.103. [5]李玉龙,刘魁,鲍仲辅.基于渐开线齿轮展成法的参数化精确建模
机械传动
2012年
作的简单、方便。
与基准坐标系为建模保证,使用曲面特征下的直纹面
为建模工具的解决方案。通过建模实例分析,证明了 该方案的实用性、可操作性,缩短了齿轮设计周期,提 高了设计效率,在产品的系列设计、相似设计及专用 。如系统开发方面都具有较大的应用价值。
参 考 文 献
3参数化实现
以创建的两个锥齿轮模型为母体,通过改变其基 本参数即可实现参数化。 另外可以通过电子表格对基本参数编辑修改实现 参数化,选择“工具/表达式/电子表格编辑”,修改基本 参数,选择电子表格的“工具/更新公式”即可实现齿轮 模型参数变化。 当需要多个不同参数的锥齿轮时,可利用部件族 来创建。选择相同类型母体模型,选取添加到部件族电 子表格的列,输入部件编号、部件名、所需齿轮参数,选 定要创建的部件行,点击电子表格“创建部件”,即可实 现一系列直齿轮模型的创建。
顶圆压力角/(・) 根圆压力角/(o) 齿根角/(o) 根锥角/(o) 顶傩余角/(o)
^,
町 “d叶
出k d如。
a。=一(2~/也) q:一(2’・/4) 一【(k+c)m/^] ‰一‰,
①做删与^曰重合,nF与圆锥轴线重合,两者
交于O点; ②创建草图选择创建平面选项,使用点和方向平
面指令选择∞线上D点创建I平面,在该平面沿”
4结语
我们在直齿圆锥齿轮参数化建模中,分析了不同 齿数范围对建模过程的影响,建立了渐开线、齿根过渡 曲线对称方程作为建模基础,提出分界齿数为锥齿轮 不同建模形式判断,精确计算方程参变量取值控制曲 线起始、终止角度为建模手段,正确建立背锥基准平面 (上接第36页) 通过橡胶材质的驱动球与物料多点接触,有效地提高 了输送的精度。所以,本文中提出的全向滚球平台的 动态模型是正确的,平台控制算法是可行的。
L1篇篡警翟誓蝴分界齿数舢蜥
以锥齿轮建模应分两种情况:
(1)却>4l,西<由时,齿廓曲线由渐开线构成; (2)2y≤41,以>由时,齿廓曲线由渐开线与齿根
过渡曲线构成。 1.2渐开线对称方程 精确建模需要获 得锥齿轮大端齿廓曲 线。使用点关于直线 对称的坐标计算公式 实现对称渐开线的生 成,可避免使用“变换” 非参数化功能指令。
裹3齿廓曲线专用●救 参数 淅开线起始角/(。) 参数符号 参数计算
①在Ⅱ平面做OG与珊成yI=一y,约束Oc与 叫在D点重合;
②创建草图选择创建平面选项,使用点和方向平 面指令选择Oc线上D点创建Ⅲ平面。在该平面沿"
‘)4时咖却xl盯打
‘《4时伽a。xl跗y”
晰开线终止角/(a) 淅开线自变量/(a) 齿廓线对称角/(o)
p
7
万方数据
机械传动
2012年
根圆之间的齿廓曲线是齿根过渡曲线,该曲线虽不参
1.1齿廓曲线起始、终止角度 修剪渐开线会造成齿廓曲线不对称和参数丢失现 象,可通过控制方程参变量取值,精确控制齿廓渐开线 生成的起始、终止角度。 渐开线起始角度:
与齿轮啮合,但对齿轮的强度尤其是弯曲疲劳强度有
重要的影响[3]33一科4|,所以锥齿轮参数化建模必须绘 制齿根过渡曲线。 齿根过渡曲线方程[6】 f茗l=聋18irI p+yloos目+r(口sin曰+o∞口) 【儿=茗Icos口一ylsin口+r(日c08口一sill口) 式中,刀具圆角坐标
