5 改进的变步长LMS自适应滤波算法及仿真
改进的变步长LMS自适应滤波算法及其仿真

改进的变步长LMS自适应滤波算法及其仿真付瑞玲;栗红霞【期刊名称】《自动化技术与应用》【年(卷),期】2012(031)009【摘要】对变步长的(LMS)自适应算法进行了讨论,本文提出了一种新的变步长LMS自适应滤波算法,并用计算机进行了仿真,结果表明该算法在误差接近于零时步长具有缓慢的变化的特性,并且在低信噪比的环境下有更好的抗噪性能,滤波效果更好.%This paper discusses the variable step size least mean square ( LMS ) adaptive filtering algorithm. A new LMS adaptive filtering algorithm with variable step size is proposed. The simulation results show that when algorithm's error approach to zero, it has the characteristics of a slow change and better anti-noise property in low signal noise ratio environment, also the results of filtering is better.【总页数】4页(P10-13)【作者】付瑞玲;栗红霞【作者单位】黄河科技学院信息工程学院,河南郑州450000;黄河科技学院信息工程学院,河南郑州450000【正文语种】中文【中图分类】TN713【相关文献】1.改进的变步长LMS自适应滤波算法及仿真 [J], 李梅;李文杰;姚善化2.一种改进的变步长变更新速率LMS自适应滤波算法及仿真 [J], 沈大伟;贺思;李正宙;赵卫国3.一种改进的变步长LMS自适应滤波算法及其仿真 [J], 华强;夏哲雷;祝剑英4.一种新的变步长LMS自适应滤波算法仿真及性能分析 [J], 汪潮;单家方5.一种改进的变步长LMS自适应滤波算法及仿真 [J], 冯存前;张永顺因版权原因,仅展示原文概要,查看原文内容请购买。
一种改进的变步长LMS算法及其DSP实现_王俊峰

2012年第11期仪表技术与传感器InstrumentTechniqueandSensor 2012No.11基金项目:河南理工大学实验室开放基金项目(SKJA10108)收稿日期:2011-10-10收修改稿日期:2012-06-03一种改进的变步长LMS 算法及其DSP 实现王俊峰(河南理工大学计算机科学与技术学院,河南焦作454000)摘要:固定步长LMS (least mean square )算法自适应滤波器在收敛速度、时变跟踪能力与稳态误差上对步长因子的要求存在矛盾。
变步长LMS 算法的步长因子是变化的,能够有效地避免此矛盾。
在分析了2种变步长LMS 算法的基础上,提出了全新的变步长算法,并在MATLAB 环境中进行仿真,之后应用SZ -EPP5402评估板对其进行了DSP 实现。
仿真结果与DSP 实现都表明:变步长LMS 算法在一定程度上改善了收敛速度与稳态误差间矛盾,具有更快收敛速度与更小稳态误差。
关键词:最小均方误差自适应算法;变步长;数字信号处理器中图分类号:TP39文献标识码:A文章编号:1002-1841(2012)11-0128-02An Improved Variable Step LMS Algorithm and DSP RealizationWANG Jun-feng(School of Computer Science and Technology ,Henan Polytechnic University ,Jiaozuo 454000,China )Abstract :In fixed step size LMS algorithm ,there is an inconsistency between the fast algorithm convergence and the low steady state error.Variable step size LMS algorithm can resolve this problem.On the basis of analysis of two kinds of variable step size LMS algorithm ,an improved LMS adaptive algorithm was proposed.And the filter method has been tested and adopted in MAT-LAB and DSP-SZ-EPP5402.Experiments show that the realization method can effectively resolve inconsistency between the fast al-gorithm convergence and the low steady state error.Key words :LMS adaptive algorithm ;variable step size ;DSP 0引言在数字信号处理中,数字滤波技术占有极其重要的地位。
变步长LMS自适应滤波算法及其分析

过 程 中 的 不 足 , 现 了对 S S L 实 V — MS算 法 的 改 进 。理 论 分 析 和 计 算 机 仿 真 结 果 表 明 , 算 法 的 收敛 性 能 优 于 S S 本 V -
L MS算 法 另 外 , 对本 算 法 与 V - MS算 法 进 行 了 比较 , 真 结 果 表 明本 算 法 在 低 信 噪 比环 境 下 比 V - MS算 还 SI 仿 SL
l w i na i e r to e io o sg lno s a i nv r nm e t n.
p o e so t p sz d sme to d p ie se d tt , e f r h mp o e n o t e sz f r c s fse iea j t n fa a t ta y sae p ro ms t ei r v me t t h ie o u v
韩 国玺 , 春 生 , 刘 张 智
( 电子 工 程 学 院 , 肥 2 0 3 ) 合 3 0 7
摘要 : 对变步长( M ) L S 自适应滤波算法进行了讨 论 , 通过对 S m i函数修正 , i o g d 建立 了步长 因子与误差 信号之 间新
的非 线 性 函数 关 系 。新 函数 在 误 差 接 近 零 处 具 有 缓慢 变化 的特 性 , 服 了 Sg od函 数 在 自适 应稳 态 阶 段 步 长 调 整 克 im i
变步长LMS自适应滤波器算法仿真研究[1]
![变步长LMS自适应滤波器算法仿真研究[1]](https://img.taocdn.com/s3/m/1e32acf8941ea76e58fa04ce.png)
变步长LMS自适应滤波器算法仿真研究The simulation of variable step-size LMS adaptive algorithm摘要:本文分析了变步长LMS自适应滤波器算法的基本原理,并使用Matlab对其算法进行了编程设计,给出了具体的程序实现,具有比较强的借鉴作用。
关键词:自适应滤波;变步长LMS;Matlab程序设计Abstract: This paper discusses the principle of the variable step-size LMS adaptive algorithm and uses the Matlab to programme the algorithm, which can be used for reference.Key words: adaptive filtering; variable step-size LMS; Matlab1 引言滤波是当今信息处理领域的一种极其重要的技术。
滤波是从复杂的信号中提取有用的信号,同时抑制噪声和干扰信号,以便有效地利用原始信号。
滤波器实际上是一种选频系统,它对某些频率的信号予以很小的衰减,使该部分信号顺利通过;而对不需要的频率信号则予以很大的衰减,尽可能阻止这些信号通过。
总的来说,滤波器可以分为经典滤波器和现代滤波器两大类。
经典滤波器是假定输入信号x(n)中的有用成分和希望去掉的成分各占有不同的频带,即关于信号和噪声应具有一定的先验知识,这样当原始信号通过一个线性系统时无用的成分就可以滤掉。
如果有用信号和噪声的频谱相互重叠,那么通过经典滤波器就无法去除噪声或干扰。
而现代滤波器就能够解决上述问题。
现代滤波器是把信号和噪声都视为随机信号,利用它们的统计特征(如自相关函数、功率谱等)导出一套最佳的估计算法,然后用硬件或软件予以实现。
2 LMS自适应滤波器自适应滤波的研究始于20世纪50年代末,Widrow和Hoff等人最早提出了最小均方(LM S)算法。
一种改进的变步长自适应滤波器LMS算法

2004 年 8月 JOURNAL OF CIRCUITS AND SYSTEMS August , 2004 文章编号:1007-0249 (2004) 04-0115-03 一种改进的变步长自适应滤波器LMS 算法*徐凯, 纪红, 乐光新(北京邮电大学 电信工程学院,北京 100876)摘要:本文提出一种改进的LMS 算法(即MS-LMS ),并建立了步长因子µ与误差信号)(n e 之间另一种新的非线性函数关系。
该关系不仅具有原有算法在误差)(n e 接近零处缓慢变化的优点,而且低信噪比环境下比原有算法具有更好的收敛性能。
理论分析和计算机仿真结果表明,在低信噪比的环境下,改进算法的收敛速度和稳态误差的性能指标都有较大的提高,并对系统发生的突变表现出较强的鲁棒性。
关键词:自适应滤波;变步长自适应滤波算法;LMS 算法;均方误差中图分类号:TN91 文献标识码:A1 引言 自适应滤波技术在通信、自动控制领域得到广泛应用。
最常用的算法为梯度下降法,常称为最陡下降法即LMS 算法,是指Widrow 和Hoff 于1960年提出的最小均方误差算法。
由于算法采用粗糙的梯度估计得到结果,从而使算法性能欠佳,应用范围受限。
而另一方面,LMS 算法具有计算量小,易于实现等诸多特点。
尤其是这种算法是最先由统计分析法得出的一种实用算法,因此至今仍被广泛应用。
根据自适应滤波器的原理(见图1),LMS 算法迭代公式为: )()(2)()1( ),()()( ),()()(n n e n W n W n y n d n e n W n X n y T X µ+=+−==,其中,)(n X 表示n 时刻的输入信号矢量;)(n W 表示时刻n 自适应滤波器的权值;)(n d 是期望输出值,又称标准参考值;)(n e 表示时刻n 的误差;µ是控制稳定性和收敛速度的参量,称之为步长因子。
图1中的)(n v 为干扰信号。
一种改进的变步长的LMS自适应滤波算法及其仿真
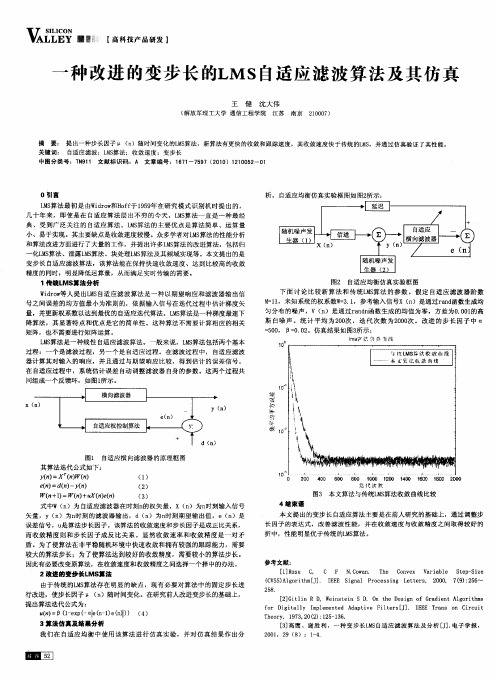
误 差信 号 ,u 是算法 步长 因子 。该 算法 的收 敛速度 和 步长 因子 是成正 比关 系 ,
本文 提 出的变 步长 自适应 算法 主 要是在 前 人研 究 的基础 上 ,通过 调整 步
长 因子 的表 达式 ,改善 滤波 性 能 ,并在 收 敛速 度 与收 敛精 度之 间 取得较 好 的
1传统 L 算法 分析 MS W do 等 人提 出LS irw M 自适应 滤 波 算法 是 一种 以期 望 响应 和滤 波 器 输 出信 号之 间误 差 的均 方值 最 小为 准则 的,依 据 输入 信 号在迭 代 过程 中估计 梯度 矢 量, 弗更新 权系 数 以达到 最优 的 自适应迭 代 算法 。L S M 算法 是一种 梯度 最速 下
逃 1 淡 数
图3 本 文算法 与传 统L S 法 收敛 曲线 比较 M算
4结束 语
式 中W ( )为 自适 应滤 波器 在 时刻n n 的权 矢量 ,X ( )为n 刻输 入信 号 n 时 矢 量 ,Y ( )为n n 时刻 的滤 波器 输 出 ,d( )为n 刻期 望 输 出值 ,e ( )是 n 时 1 1
一种新的变步长LMS自适应滤波算法及其仿真

一种新的变步长LMS自适应滤波算法及其仿真
靳翼;邵怀宗
【期刊名称】《信号处理》
【年(卷),期】2010(26)9
【摘要】传统变步长LMS算法存在收敛速度慢、易受噪声影响等缺点,为了提高算法性能,论文建立了LMS算法中步长因子μ(n)和误差信号e(n)的相关统计量之间的非线性关系,提出了一种基于改进的双曲正切函数的变步长LMS(HTLMS)算法.算法采用当前误差与上一步误差乘积的绝对值来调节步长,并引入了绝对估计误差的扰动量来更新自适应滤波器抽头向量,因而具有收敛速度快、噪声抑制能力强和稳态误差低等特点.计算机仿真结果表明,在不同信噪比条件下,与多种LMS算法相比,本文算法都具有较快的收敛速度和较好的稳态误差.
【总页数】4页(P1385-1388)
【作者】靳翼;邵怀宗
【作者单位】电子科技大学通信与信息工程学院,611731;电子科技大学通信与信息工程学院,611731
【正文语种】中文
【中图分类】TN713
【相关文献】
1.一种新的变步长LMS自适应滤波算法及其仿真 [J], 李方伟;张浩
2.一种改进的变步长变更新速率LMS自适应滤波算法及仿真 [J], 沈大伟;贺思;李
正宙;赵卫国
3.一种新的变步长LMS自适应滤波算法仿真研究 [J], 刘杰;闫清东
4.一种改进的变步长LMS自适应滤波算法及其仿真 [J], 华强;夏哲雷;祝剑英
5.一种新的变步长LMS自适应滤波算法仿真及性能分析 [J], 汪潮;单家方
因版权原因,仅展示原文概要,查看原文内容请购买。
改进的变步长LMS自适应滤波算法及其仿真

的影响可以忽略不计。当en 较小时, () () p n 也较小 , 由
于 改 进算 法 的 步 长只 与 输入 信号 有 关 , 不 受 噪声 的 而 影响 。 因此 , 有 收敛 速度 快 , 具 稳态 误 差小 的优 点 , 而 且 在 低 信 噪 比的环 境 中仍保 持 较 好 的性 能 , 具有 广 泛
的问题 , 但在 稳态性 能方 面欠佳 。在分析 了 以上 算法 的
中得到 了很 好的应用 …。然而 , 传统 的固定步长的 L MS 算法 在 收敛 速 度 、时变 系 统 的跟踪 能力 和 稳态 失调 之
间 的要 求 是存 在很 大矛 盾 的 。小 的步 长确保 稳态 时具 有 小 的失 调 , 是算 法的 收敛速 度慢 , 但 并且对 非 稳态系 统的跟 踪能力差 大的步 长 . 算法具有 更快的 收敛 速 “使
AnI rv dV r be S e — z MS Ad p ie Fl r g mp o e a i l t p Sie L a t i i a v t n e Alo i m n m ua in g rh a d Si lt t o
FU il , o - i Ru -i ng LIH ng x a
计 平均 。
+N( ) n ) n N( -1
由于 N( ) n 是零均值的噪声 , n 与 X() N() , 无关, z 并且噪声 Ⅳ ) 本身不相关, n N( 一 ) /() N( ) n 1 对 An 的
贡献 很小 , 忽略不计 , 有 可 故
本文步长在h=10 =2 0和卢=02 0 0、 0 . 5时为
《 动 技 应 02 第3卷 期 自 化 术与 用 21年 l 第9
通 信 与 信 息 处 理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0引言
由Widrow和Hoff提出的最小均方(LM S,least-mean-square)算法简单、计算量小、稳定性好,易于实现实时处理,是自适应滤波理论中应用最广泛的算法。
LM S算法的收敛速度与步长因子成反比,而稳态误差与步长因子成正比,即固定步长的LM S自适应算法在收敛速度、跟踪速度及稳态误差噪声之间的要求是相互矛盾的。
为了解决这个问题,在固定步长
LMS算法的基础上,人们发展了变步长LMS自适应滤波算法,它能够较好地解决固定步长算法的矛盾。
目前,主要的变步长算法是在迭代初始阶段误差较大时,使用较大的步长以加快收敛速度,当误差接近为零时,使用较小的步长迭代使算法的具有较小的稳态误差。
本来提出了一种新的变步长LMS算法,可以获得比较快的收敛速度,是算法的稳态误差趋于最小[1,2]。
1变步长LMS算法—SVSLMS算法分析
自适应滤波器的原理如图1所示。
图1中x(n)是时刻n时的输入信号,v(n)是噪声,d(n)是期望输出值,e(n)是误差,y(n)是滤波器的输出信号。
当输入信号x(n)发生变化时,自适应滤波器能够利用变化的误差信号e(n)来调节滤波器的参数,从而调节输出。
Sigmoid函数的变步长LM S算法:
e(n)=d(n)-X T(n)W(n)(1)μ(n)=β(1/(1+exp(-αe(n)))-0.5)(2)W(n+1)=W(n)+2μe(n)X(n)(3)式中X(n)=[x(n),x(n-1),x(n-2),…,x(n-K+1)]T,表示时刻n的输入信号矢量,由最近K个信号采样值构成。
W(n)
改进的变步长LMS自适应滤波算法及仿真
李梅,李文杰,姚善化
(安徽理工大学电气与信息工程学院,安徽淮南232001)
摘要:通过分析变步长自适应滤波算法,建立步长和误差信号之间的非线性关系,提出一种新的变步长LM S自适应滤波算法,并用计算机进行仿真,结果表明该算法在误差接近于零时步长具有缓慢变化的特性,滤波效果更好。
关键词:自适应滤波;变步长LMS算法;收敛;噪声消除
中图分类号:TM933文献标识码:A文章编号:1001-1390(2010)06-0015-03
An Improved Variable Step Size LMS Adaptive Filtering Algorithm and
Simulation
LI Mei,LI Wen-jie,YAO Shan-hua
(Institute of Electric and Information Engineering,Anhui University of Science and Technology,Huainan232001,
Anhui,China)
Abstract:This paper established the non-linear relationship between the step and the error signal based on analyzing the variable step-size adaptive filter algorithm.And a new variable step size LM S adaptive filtering algorithm has been proposed.The simulation results show that the algorithm is close to zero in the error step with the characteristics of a slow change,also the results of filtering is batter.
Key words:adaptive filtering,variable step-size LM S algorithm,convergence,noise cancellation
图1自适应滤波器原理图
Fig.1Auto-adapted filter schematic diagram
15
--
=[ω0(n ),ω1(n ),…,ωk -1(n )]T 是时刻n 自适应滤波器的权系数,K 是滤波器的阶数,控制稳定性和收敛速度的
参量(步长因子);μ是e (n )的Sigmoid 函数:
μ(n )=β(1/(1+exp (-αe (n )))-0.5)
(4)
该算法能同时获得较快的收敛速度、跟踪速度和较小的稳态误差。
但是Sigmoid 函数过于复杂,增加了计算量,而且当误差e (n )接近于0处变化时,步长μ变化很大,没有缓慢变化的特性,这是该算法的不足之处[3]。
2
新的变步长算法
图2为新的步长μ与误差e 的关系曲线。
分析步长与误差之间的关系曲线,要想提高算法的收敛速度,减少算法的稳定误差,使自适应滤波更稳定,必须在误差e (n )接近于0处变化时,步长μ缓慢变化,为了克服SVSLM S 算法在稳态阶段步长调整过程中的不足,提出了一种新的变步长LM S 算法,新算法的步长为:
μ(n )=-αexp(-e (n )2
/(2β2))+α(5)本函数与Sigmoid 函数相比,对于相同的初始误
差,当误差e (n )接近于0处变化时,即自适应稳态阶段,步长μ具有缓慢变化的特性。
当α固定,β越小,收敛速度越快。
所以,对收敛速度有高要求时,选较小的β值,
对稳态误差有高要求时,选较大的β值。
当β固定,α越小,收敛速度快[4]。
3新算法的收敛曲线
如图3所示,上面一条曲线是α=0.1,β=1.5时SVSLM S 算法的收敛曲线,下面一条曲线是α=10,β=0.3时本文新算法的收敛曲线。
通过图形可以看出新算法比SVSLMS 算法要好。
4新算法的仿真
对SVSLM S 算法以及本文算法在噪声消除中的应用进行仿真,比较两种算法下滤波器的性能。
参考输入信号x (n )是均值为0,方差为1的高斯白噪声,计算机模拟条件:(1)自适应滤波器的阶数L =2;(2)未知系
统的FIR 系数为W *=[0.8,0.5]T ,在第500个采样点时
刻未知系统发生时变,系数矢量变为W *=[0.4,0.2]T
;(3)参考输入信号x (n )是零均值,方差为1的高斯白噪
声;(4)v (n )为与x (n )不相关的高斯白噪声,其均值是零,方差为δ2
v =0.04。
仿真结果如图4~6所示,图4(a)为有用信号x (n ),图4(b)为自适应噪声消除系统的主通道中输入信号,即有
用信号与噪声的叠加d (n ),图5(a)、图5(b)分别为SVSLMS 算法下α=0.1、β=1.5(最佳值)时的自适应噪声消除系统的输出信号和收敛曲线。
图6(a)、图6(b)分别为当α=10,β=0.3时本文算法的输出信号和收敛曲线。
5
结束语
仿真结果分析:本文算法下,滤波结果与有用信
号几乎一致,去噪效果较好,很大程度的减小了稳态误差,提高了收敛精度。
图2步长与误差关系曲线
Fig.2Length of stride and the error
图3本文算法和SVSLMS 算法收敛曲线比较Fig.3Comparison of convergence curves among
SVSLMS and algorithm in this paper
(a )α固定,β变化时的曲线(b )β固定,α变化时的曲线
e (n )
u (
n )
0.10.20.3u (n )
e (n )
16--
e (n )
e (n )
e (n )
图4(a)有用信号Fig.4(b)Useful signal
图4(b)噪声和有用信号的叠加
Fig.4(b)Noise and useful signal superimposition
图5(a)输出信号Fig.5(a)Output signal
图5(b)收敛曲线Fig.5(b)Restraining curve
图6(a)输出信号图Fig.6(a)Output signal
图6(b)收敛曲线Fig.6(b)Restraining curve
参考文献
[1]沈福民.自适应信号处理[M ].西安:西安电子科技大学出版社,2001.[2]Diniz,P.S.R 著,刘郁林等译.自适应滤波算法与实现(第二版)[M ].北京:电子工业出版社,2004.
[3]覃景繁,欧阳景正.一种新的变步长自适应滤波算法[J].数据采集与处理,1997,12(3):171-194.
[4]罗小东,贾振红.一种新的变步长LM S 自适应滤波算法[J].电子学报,2006,(6).
作者简介:
李梅(1985-),女,硕士研究生,安徽理工大学控制理论与控制工程专业,现从事智能信号处理方向的研究。
Email:limei4981875@
收稿日期:2010-03-14
(田春雨编发)
17--。
