2011年高考三角函数考题特点聚焦
2011高考数学真题考点分类新编:考点14三角函数的性质(大纲版地区)

考点14三角函数的性质一、选择题1、(2011·上海高考文科·T17)若三角方程sin 0x =与sin 20x =的解集分别为,E F ,则( )(A )E F ⊄ (B )E F ⊂ (C )E F = (D )E F =∅【思路点拨】本题考查三角函数中的三角方程问题,可以先求解出各方程,然后再比较两集合的关系。
【精讲精析】对三角方程sin 0x =解得{}|()E x x k k z π==∈,对三角方程sin 20x =解得|()2k F x x k z π⎧⎫==∈⎨⎬⎩⎭,故两集合E F ⊂,故选B 2、(2011·全国高考理科·T5)设函数()cos (0)f x x ωω=>,将()y f x =的图象向右平移3π个单位长度后,所得的图象与原图象重合,则ω的最小值等于( ) (A )13(B )3 (C )6 (D )9【思路点拨】解决此题的关键是理解好三角函数周期的概念.将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,说明了3π是此函数周期的整数倍.【精讲精析】选C. 由题2()3k k Z ππω=⋅∈,解得6k ω=,令1k =,即得min 6ω=.3、(2011·全国高考文科·T7)设函数()cos (0)f x x ωω=>,将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,则ω的最小值等于( ) (A )13(B )3 (C )6 (D )9【思路点拨】解决此题的关键是理解好三角函数周期的概念.将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,说明了3π是此函数周期的整数倍.【精讲精析】选C. 由题2()3k k Z ππω=⋅∈,解得6k ω=,令1k =,即得min 6ω=.4、(2011·湖北高考理科·T3)已知函数()cos ,,f x x x x R =-∈,若()1f x ≥,则x 的取值范围为 A. |,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭ B. |22,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭C .5{|,}66x k x k k Z ππππ+≤≤+∈ D. 5{|22,}66x k x k k Z ππππ+≤≤+∈【思路点拨】先根据两角和与差的正弦公式化简()f x ,再利用单位圆或正弦曲线解不等式.【精讲精析】选B. 1()2sin(),()1,sin(),662f x x f x x ππ=+∴≥+≥即∴522,666k x k πππππ+≤-≤+即22,.3k x k k Z ππππ+≤≤+∈二、填空题5、(2011·上海高考理科·T8)函数sin cos 26y x x ππ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭的最大值为 .【思路点拨】本题考查同角三角函数的基本关系式及诱导公式,两角和与差的余弦公式,二倍角公式。
2011年高考数学重点难点讲解十五:三角函数的图象和性质(学生版)

难点15 三角函数的图象和性质三角函数的图象和性质是高考的热点,在复习时要充分运用数形结合的思想,把图象和性质结合起来.本节主要帮助考生掌握图象和性质并会灵活运用.●难点磁场(★★★★)已知α、β为锐角,且x (α+β-2π)>0,试证不等式f (x )=)sin cos ()sin cos (αββα+x x <2对一切非零实数都成立.●案例探究[例1]设z 1=m +(2-m 2)i ,z 2=cos θ+(λ+sin θ)i ,其中m ,λ,θ∈R ,已知z 1=2z 2,求λ的取值范围.命题意图:本题主要考查三角函数的性质,考查考生的综合分析问题的能力和等价转化思想的运用,属★★★★★级题目.[例2]如右图,一滑雪运动员自h =50m 高处A 点滑至O 点,由于运动员的技巧(不计阻力),在O 点保持速率v 0不为,并以倾角θ起跳,落至B 点,令OB =L ,试问,α=30°时,L 的最大值为多少?当L 取最大值时,θ为多大?命题意图:本题是一道综合性题目,主要考查考生运用数学知识来解决物理问题的能力.属★★★★★级题目.[例3]如下图,某地一天从6时到14时的温度变化曲线近似满足函数y =A sin(ωx +φ)+b .(1)求这段时间的最大温差.(2)写出这段曲线的函数解析式.命题意图:本题以应用题的形式考查备考中的热点题型,要求考生把所学的三角函数知识与实际问题结合起来分析、思考,充分体现了“以能力立意”的命题原则.属★★★★级题目.●锦囊妙计本难点所涉及的问题及解决的方法主要有:1.考查三角函数的图象和性质的基础题目,此类题目要求考生在熟练掌握三角函数图象的基础上要对三角函数的性质灵活运用.2.三角函数与其他知识相结合的综合题目,此类题目要求考生具有较强的分析能力和逻辑思维能力.在今后的命题趋势中综合性题型仍会成为热点和重点,并可以逐渐加强.3.三角函数与实际问题的综合应用.此类题目要求考生具有较强的知识迁移能力和数学建模能力,要注意数形结合思想在解题中的应用.●歼灭难点训练一、选择题1.(★★★★)函数y =-x ·cos x 的部分图象是( )2.(★★★★)函数f (x )=cos2x +sin(2π+x )是( )A.非奇非偶函数B.仅有最小值的奇函数C.仅有最大值的偶函数D.既有最大值又有最小值的偶函数 二、填空题3.(★★★★)函数f (x )=(31)|cos x |在[-π,π]上的单调减区间为_________. 4.(★★★★★)设ω>0,若函数f (x )=2sin ωx 在[-4,3ππ,]上单调递增,则ω的取值范围是_________.三、解答题5.(★★★★)设二次函数f (x )=x 2+bx +c (b ,c ∈R ),已知不论α、β为何实数恒有f (sin α)≥0和f (2+cos β)≤0.(1)求证:b +c =-1;(2)求证c ≥3;(3)若函数f (sin α)的最大值为8,求b ,c 的值.6.(★★★★★)用一块长为a ,宽为b (a >b )的矩形木板,在二面角为α的墙角处围出一个直三棱柱的谷仓,试问应怎样围才能使谷仓的容积最大?并求出谷仓容积的最大值.7.(★★★★★)有一块半径为R ,中心角为45°的扇形铁皮材料,为了获取面积最大的矩形铁皮,工人师傅常让矩形的一边在扇形的半径上,然后作其最大内接矩形,试问:工人师傅是怎样选择矩形的四点的?并求出最大面积值.8.(★★★★)设-6π≤x ≤4π,求函数y =log 2(1+sin x )+log 2(1-sin x )的最大值和最小值.9.(★★★★★)是否存在实数a ,使得函数y =sin 2x +a ·cos x +85a -23在闭区间[0,2π]上的最大值是1?若存在,求出对应的a 值;若不存在,试说明理由.。
2011年高考江西卷数学试题特点分析

2011年高考江西卷数学试题特点分析石城中学 陈 云今年是江西省使用新课标卷高考的第一年,广大教师和学生都在关心新课标下高考怎么考?高考的要求怎么样?高考的侧重点是什么?今年高考试卷非常明确地给出了回答,这份试卷告诉老师生学生,对于数学课程要求,知识点到为止,但很注重知识的横向联系与拓展,解题时一般只运用很少的知识点即可以。
新课标试题注重考查高中数学的基础知识、基本技能,基本的数学思想方法;试题依托数学知识的网络的交汇点,考查学生对高中数学基础技能和基本思想方法的掌握;试题多以能力立意,注重考查思想方法,强调知识的相互渗透,以及对学生创新意识的检验;试题对知识纵深方面的考查要求不高;对课程中新增内容和传统内容进行科学、规范的结合考查,切实体现新课程理念。
下面对今年新课标数学卷主要特点简要分析: 1.保持稳定,稍有改变试题在题型、难度、知识分布与覆盖上保持相对稳定,避免了大起大落:以文科卷为例函数与导数知识约28分,立体几何约17分,圆锥曲线约17分,三角知识约17分,数列19分,概率统计约22分,不等式、集合、向量、复数、算法及创新题各5分。
考生可能感觉题目似曾相识,与此前的模拟训练很类似,因此心情也会比较平静,能把潜力最大限度地发挥出来。
试题在题量、分值上稍有改变:选择题10小题,填空题5小题,解答题6题,共21小题,较往年减少了一个题目;减少了选择题总分值,增加了填空题分值,并在第21题增加1分;解答题对位置作了调整,理科卷立体几何作压轴题出乎意料。
2.重视基础,立足教材试题源于教材,以考查高中基础知识为主线,在基础中考查能力。
试题中较多题目相当于课本例题、练习或习题的变式题型。
如:文科卷第选择题前9个、填空题第11、12、14、15题均可在课本练习、习题及复习题中找到源型。
(文1)若()2,,x i i y i x y R -=+∈,则复数x yi +=( )A.2i -+B.2i +C.12i -D.12i +【备注】题源:选修1-2 第82页 B 组第4题;知识点:复数的四则运算及相等; (文2)若全集{1,2,3,4,5,6},{2,3},{1,4}U M N ===,则集合{5,6}等于( ) A.M N ⋃ B.M N ⋂ C.()()U U C M C N ⋃ D.()()U U C M C N ⋂ 【备注】题源:必修1 第14页 练习 第4题;知识点:集合的运算; (文3)若121()log (21)f x x =+,则()f x 的定义域为( )A.1(,0)2-B.1(,)2-+∞C.1(,0)(0,)2-⋃+∞D.1(,2)2- 【备注】题源:必修1 第96页 练习 第2题;知识点:函数定义域; (文4)曲线xy e =在点A (0,1)处的切线斜率为( )A.1B.2C.eD.1e【备注】题源:选修1-1 第62页 练习 第1题;知识点:导数的几何意义;(文5)设{n a }为等差数列,公差d = -2,n S 为其前n 项和.若1011S S =,则1a =( )A.18B.20C.22D.24【备注】题源:必修5 第39页 复习题B 组 第3题;知识点:等差数列的基本运算; (文6)观察下列各式:则234749,7343,72401===,…,则20117的末两位数字为( )A.01B.43C.07D.49【备注】题源:选修1-2 第57页 习题3-1 第1题;函数的周期性;(文8)为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:则y 对x 的线性回归方程为A.y = x-1B.y = x+1C.y = 88+12x D.y = 176 【备注】题源:必修3 第69页 复习题A 组 第6题;知识点:线性相关系数求法;(文9) 将长方体截去一个四棱锥,得到的几何体如右图所示,则该几何体的左视图为( )【备注】题源:必修2 第18页 例题6 (一样);知识点:三视图;(文11)已知两个单位向量1e ,2e 的夹角为3π,若向量1122b e e =-,21234b e e=+,则12b b ⋅=___. 【备注】题源:必修4 第94页 例题4;知识点:向量的数量积运算;(文12)若双曲线22116y x m-=的离心率e=2,则m=____.【备注】题源:选修1-1 第43页 习题2-3 B 组 ;知识点:圆锥曲线的离心率;(文14)已知角θ的顶点为坐标原点,始边为x 轴的正半轴,若()4,p y 是角θ终边上一点,且sin 5θ=-,则y=_______. 【备注】题源:必修4 第20页 习题1-4 第3题;知识点:三角函数定义;3.考查全面,强化综合今年数学试题所涉及的知识内容限定在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
2011年高考中的三角函数问题回顾

A. 4 一—
—
像与原图 合, 像重 说明要是此函 数周期的 整数倍.
由 题 意得 :
j 叫
.( k k∈z) 解 得∞: k, - i 6 , 6 则 ̄m = . O.
) .
B. 一— 5
应 选 C .
点 评 : 解 三 角 函 数 周 期 的 概 念 是 解 决 本 题 的 关键 . 然 也 理 当
帮助同学们巩固知识 , 高能力 , 提 现将 2 1 年高 考 中 的三 角 函数 01 问题 回顾 如 下 , 学 习时 参 _ . 供 考
一
移 的 区别 .
例 2 (0 1 全 国 Ⅱ文科 卷 第5 ) 函数 ) o ( > ) 2 1年 题 设 ∞o,
将y ) 图像 向 右 平 移 个 单 位 长 度 后 , 得 的 图 像 与 原 图 的 所
2 =
,
) 扩) "2 ]  ̄2- .
.
4则 ,
A 3 =
解 :1 ( )含 项 的 系 数 分 别 为 每一 项 展 开 式 中 含 项 的 系数
之和 , 3 + c: :7 . 即c十 4…+ ;c兰 0 3
( A2 2) 即 的 系 数 , r( + + 2啦+ + 弛 即A2 上 啦+ m) n( 啦) 0 =l
角 公 式 , 时 考 查 了 … 的 妙 用 , l c s snc 同 1’ 即 = o  ̄+ i2  ̄
三 、 期 问 题 周 三 角 函 数 的周 期 问题 , 般 指 的是 求 最 小 正 周 期 , 题 时 主 一 解 要 是 运 用 三 角 函 数 的有 关 公 式 ,通 过 变 形 ,最 终转 化 为 : 1 y ( )=
2011年高考数学理科试卷分类解析——三角函数
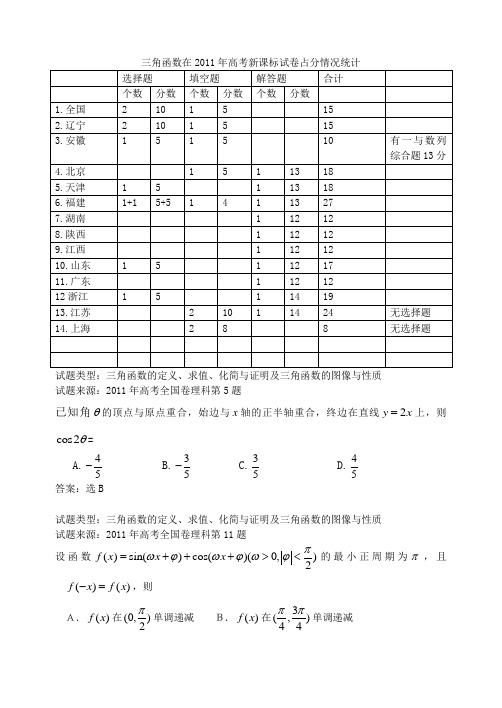
三角函数在2011年高考新课标试卷占分情况统计试题类型:三角函数的定义、求值、化简与证明及三角函数的图像与性质 试题来源:2011年高考全国卷理科第5题已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos 2θ=A.45-B.35-C.35D.45答案:选B试题类型:三角函数的定义、求值、化简与证明及三角函数的图像与性质 试题来源:2011年高考全国卷理科第11题设函数()s i n ()c o s ()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则A.()f x 在(0,)2π单调递减 B.()f x 在3(,)44ππ单调递减C.()f x 在(0,)2π单调递增 D.()f x 在3(,)44ππ单调递增答案:选A析:()sin()cos())4f x x x x πωϕωϕωϕ=+++=++.由()()f x f x -=知,()f x 为偶函数, 所以2,42k k Z ππϕπ+=+∈,又2πϕ<,则4πϕ=∴()f x x =.有余弦函数的性质(或图像)知()f x 在(0,)2π单调递减.说明:本题主要考查三角函数的恒等变形(sin cos )y a x b x x ϕ=+=+)及性质(())4f x x πϕ=++为偶函数,而()sin f x A x ω=为奇函数,所以函数要变名,令2,42k k Z ππϕπ+=+∈即可).试题类型:三角函数的定义、求值、化简与证明及三角函数的图像与性质 试题来源:2011年高考辽宁卷理科第7题 设1+=43πθsin(),则sin 2θ= A.79- B.19- C.19 D.79答案:选A试题类型:三角函数的定义、求值、化简与证明及三角函数的图像与性质试题来源:2011年高考辽宁卷理科第16题 已知函数()tan()(0,)2f x A x πωϕωϕ=+><,()y f x =的部分图像如右图,则()24f =π____________.试题类型:三角函数的定义、求值、化简与证明及三角函数的图像与性质 试题来源:2011年高考安徽卷理科第9题已知函数()sin(2)f x x ϕ=+,其中ϕ为实数,若()()6f x f π≤对x R ∈恒成立,且()()2f f ππ>,则()f x 的单调递增区间是A.,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ B.,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦C.2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ D.,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦答案:选C【解析】若()()6f x f π≤对x R ∈恒成立,则()sin()163f ππϕ=+=,所以,32k k Z ππϕπ+=+∈,,6k k Z πϕπ=+∈.由()()2f f ππ>,(k Z ∈),可知sin()sin(2)πϕπϕ+>+,即s i n 0ϕ<,所以(21),6k k Z πϕπ=++∈,代入()s i n (2f x x ϕ=+,得()sin(2)6f x x π=-+,由3222262k x k πππππ+++剟,得263k x k ππππ++剟,故选C.【命题意图】本题考查正弦函数的有界性,考查正弦函数的单调性.属中等偏难题.试题类型:三角函数的定义、求值、化简与证明及三角函数的图像与性质 试题来源:2011年高考北京卷理科第15题 已知函数()4cos sin()16f x x x π=+-。
2011年高考数学三角函数试题特点分析

r + 2 =4 v
沈新权 , : 1 等 2 1年高考数 学三 角函数试题 特点分析 0
・4 1・
题中{: , 和 21 年江西省数学高考理科 到此 法. 轨 法 、 数法 、 法等 在轨 迹 求解 中 1 01 而交 参 定义 【; 2 ; 4 +y=
A= ,T
=
中 学教 研 ( 学 ) 数
7
耵 一
詈 孑 =,
百 时取 到最 小 值 ,
题 第 1 题 ,0 1 1 2 1 年安 徽省 数学 高考 文科 试题 第 1 5
题 等.
因此 =2 又 由图像 知 当 ・
从 而
2×
例 5 若 函 数 f( )=s  ̄ (9>0) 区 间 io 0 nx 在
[詈上 调 增在 问詈詈上 调 减 0 ]单 递 ,区 [,】单 递 , ,
+ =2 竹 + k ,
则 =
(
)
得
因此
= 1 詈 2r , +
0 - ): . 7
简单 的恒 等变 换 ; 是 解 三 角 形 问题 . 题 过程 一 三 解
本题 考查 同角 三角 函数 的基 本关 系. 由
c s o2 1
_
t n a
1
+ COS
+ 了 ’ l J
,
般是 先进 行恒 等变换 , 再利 用三 角 函数 图像 和性质 解 题 . 能力 的考 查 主 要 是 演 绎 推 理 能力 、 算 能 对 计
本题 主要 考查 由 Y= s ( + ) 图 Ai 的 n
例 1 已知角 0的顶 点 为 坐 标 原 点 , 边 为 始 轴 的正 半 轴 , P( Y 是 角 0终 边 上 一 点 , 若 4, ) 且
2011年新课标高考试题分类评析——三角函数

且兼顾 了稳 中求 活 , 注重 与其 他 知 识综 合 , 现 了三 出 角与 向量 、 导数 、 列 、 数等 知识点 的综合 问题. 数 复 针 对本 章知识 特点及 考 查规 律 , 建议 同学们 在 复
习时 切实抓 好 基本 知 识 、 基本 技 能 、 本 思 想 方 法 的 基 学 习 , 足课 本 , 立 围绕考查 的上述 4个 主要 方面 , 会 体
形 结合 思想 、 归与转 化思想 等. 化
2 对 三 角 函数 图 象 与 性 质 的 考 查
■ ',
“ 衡 ’号, 代 知式 会得 一 或 平 点’ 0 入已 , 到 号 一 ( )
,
进 得 f) 或 (一 , 取 . 而 到 (一 f)一 难 舍克 O譬 o 等 以
例 3 ( 京卷 )已知 函数 - I 一4 o s ( + 北 厂z () cs i x x n
彝 芰差
终边 所通过 的平 面 I域 ( _ X 由线 性 规 划 知识 给 出) 确 来
定 , 有 新意 , 现 了在 知识 网络 交 汇 处设 计试 题 的 较 体
由正切 函数 的定 义知 , n t 一 2 又 的终 边在 第 一或 a . 第 三象 限 , 由同角关 系可求 得 CS 或 cs O 一 o 一一 5 ,
各 组 公 式 之 间 的联 系 及 推 导 过 程 . 题 过 程 需 关 注 角 解
因为 点 P 为 平 面 区 域 n 上 的一个 动点 , 以 所
图1
o 臼 . ≤ ≤
又 厂臼一 3i +CS一2i 0 D , ( √ n O ) s s( n +- 且
湖北省黄冈中学2011年高考数学题型专题冲刺精讲专题一三角函数

2011年高考题型专题冲刺精讲(数学)专题一三角函数【命题特点】纵观前五年的三角试题,我们不难发现,对三角函数的考查力度较大,题型是一大一小或两小一大,总体难度不大,解答题通常放在第一个,属容易题,要求每一位同学不失分。
主要考查三大方面;本文档由高中数学免费下载平台:数学1618(m)为您分享,更多资料尽在数学1618一.三角变换.主要考查的内容有三角函数的恒等变形(用到的公式主要有二倍角公式,辅助角公式)已知三角函数值求角(要注意已知角的范围,有的是条件直接给出,有的是三角形的内角,要留心锐角三角形的内角的限制条件).同角三角函数的基本关系式和辅助角公式等。
二.三角函数的图象与性质。
要注意图象的特征点(最高点,零点和对称中心)、特征线(对称轴)及最小正周期的求法,也要注意三角函数的最值问题,包括利用辅助公式将已知三角函数式转化为一个三角函数求最值,或转化为以某一三角函数为自变量的二次函数的最值问题。
三.解三角形问题。
正弦、余弦定理的应用。
注意面积公式的应用。
最后,要注意向量和三角函数的交汇性试题的备考,及书写格式的规范性与完整性。
同时,要控制复习的难度,重点突破以上三方面问题及理解、记忆它们涉及到的所有公式和知识点。
【试题常见设计形式】三角函数题在试卷中所处的位置基本上是第一或第二题,本章高考重点考查基础知识,仍将以容易题及中档为主,题目的难度保持稳定,估计这种情况会继续保持下去。
特点:由于三角函数中,和差化积与积化和差公式的淡出,考查主体亦发生了变化。
文科:偏重化简求值,三角函数的图象和性质。
理科:偏重三角变换,解斜三角形,与向量相结合,考查运算和图形变换也成为了一个趋势。
三角函数试题注重立足于课本,注重考查基本知识、基本公式及学生的运算能力和合理变形能力,对三角变换的要求有所降低。
三角化简、求值、恒等式证明。
图象。
最值。
解斜三角形为考查热点。
常见题型①三角函数的图象与性质;②化简和求值;③三角形中的三角函数;④最值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数, 使得这 n+ 2个数 构成递 增 的等 比数 列 . 这 t+2个数 将 l 的乘积记作 , 冉令 a lT , ≥1 = g ,n . (I) 数 列 { 的 通 项 公 式 ; 求 a} (Ⅱ) 6 设 =l a a n ta , a 求数列 { 的前 项 和 S n b} 解析 : (I) t, , t+构成 等 比数 列 , t . , 设 。t …~ 其 l£ =I
s B oA一 s B oC:2iC oB —s A oB, 有 s ( i cs 2 i cs n n s cs n i cs 即 n i A n + B)= s ( 2i B+C , n )
iC= s A, 以 n 2i 所 n
S1 M
( ! ! ± 二
但
1+t n +1 ・ a k” a f ) tn
=2 .
(
). = I
一l
( )由( )知! =2 所 以有 =2 即 c= a 又 凶为 2 1 , , 2,
Si1 ] l.. / a
所 以 S =∑ b , =∑tn +1 tn a( )・ak
= I =
GA C的周 长为 5 所 以 b= 3 ,由余弦定理得 : B , 5— a
≤ ,证E ) 一: 詈) :( ] 20 求 l 3
解 析 _ 1/ )=s cs ( )( i 。 眦 +CSS O i Xn +CSCS + OX O 1 31 "
()( ) 曰 Ⅱ由 I : 知
i
一
于 是
c(+ = s 州盯 cB手) ̄m s /A 一 3 一)
方 = c + r —2 c o B 即 ( 上 2 a cs 5—3z = ( n) +r [) 2 上 。一4上 r ×
+ =10 则 2 0,
・
.
.
三、 应用 , 考 融入 三角 形 再 现 亮点
例 5(0 年山东文 1 )在 AA C中, 21 1 7 B 内角 , c的对 曰, 边分别 为 。 6 c 已知 ,, .
r. R “ n
=
n
.
() 告的 () O =1,Ac 1求 值;2若CB △ B 的周长为5求 s ,
( ) 2 得 cs ( = , 1 +( ) 0 0 0
・ ‘
号. . B =
四 、 综 合 。 识 交 叉命 题 备 受命 题 者 的青 睐 考 知 例 7( 0 1 安 徽 文 2 )在 数 1 10之 『插 入 ,1 21 年 1 和 O H J \
.
0 <≤ j。 = : I号 c 0 詈, B
2 iC Rsn
’ . .
( t+ )- tt ) ( l )・ £ , 2 (2 … £ t 2 (
a = l T g = H +2, ≥ 1 n ,
所 以
=
=
( 由题 意 和 (I) 汁算 结 果 , 6 a ( 2)・ a Ⅱ) 中 知 =t ,+ n tt ( +3 , Y t ) n≥ 1 令 一 , 方 , 用 tn 利 a l:tn + I a ( )一 =
=
i s 2 (+ ) n A s , 詈 A = i4 n
~
=
i 。 =s(一 眦一 s 2 手) i n
7=2 ’ 竹 ) =2 … .
… . .
+ ,而 A 詈= 取,子 ,n + 詈 从 当 + 詈, 4 时2 ( 詈) = s i
最大值 2 .
例 6(0 1 2 1 年湖 南理 1 )在 AA C【 , 4, C所埘 的 7 B } 角 B, j 边分 别为 n bc 日满 足 ciA=toC ,,, . s n ( s. c
再利用 三角 函数 的性质等求解仍不会褪 色.
1
例4( 1 年四 2 1 川理1)已 0 7 知函数, ) s ( ÷1 ( = i + T n )
, ,
解析 : (I) 由正 弦 定 理 得 s Ci i s A=s A oC n n i cs . n 因 为 0<A< 所 以 s A> , 而 s C= oC I cs ≠ 订, i n 0从 i n cs . oC 义
( 卢 0 以a =,c 寻 0 < < , t l = 所 n 则 G
新课程 新学 新探究 数 学
Z) 合 选 择 项 即 可 得 答 案 应 选 C 结 二 、考 大 题 , 度 有 所 降低 难
_— l
÷, 解得 n , 以 b 2 =1所 =.
斗
考 点透 视
镯 I 一l
通过三角公式 的变形 、 转化 , 最终化 简成一角一 名形式 ,
s n / l l 斗
T : l t… .¨l t+① , t ・2 t+ c 2 T ① ×②并利用 £ f
=
・ l ・ , …f
b的 长.
=t 2 0 ( ≤i ) 得 =1 1 ≤, t+ +2 ,
) 0 。 =1
解 析 : 1 由 正 弦 定 理 得 a=2 s A, () R i b=2 s B C = n Ri , n
() 1
・
ቤተ መጻሕፍቲ ባይዱ
.
.
( )。( -O 2 cs卢- / )=cs c +s i = 4 。d 。 i s n
综t所述, i 一 o B 孚 ) 最大值为2此时『 s c ( + 的 s . 4 =
l
。 卢 d :。 。 sdi :一4 .. 2 s + ) 。 ( 一 i s ..() ..
-t
(I) 角 C的大小 ; Ⅱ) 求 ( 求 s A—cs B+ ) i n o ( 的最
斗
大值 , 并求取得最大值时角 _, 4 B的大小.
+ o( ÷ 叮 ,∈ cs 一 r R, )
( ) 厂 的最小正周期和最小值 ; 1 求_ ) (
。( )= 一 4 ( ) 知 cs卢一 2已 。( )= 4 cs卢+d
