光学工程物理光学例题详解02
光学工程物理光学例题详解02

3)光源角半径
1
b 2 f1
另一方面,由光源中心点与边
缘点发出的光在P点产生的程差之
差:
0 '
2nh(1
cos2 )
4
(板内折射角)
根据折射定律:
n' sin1 n sin2 n'1 n2
由此得:
1
1 2n'
n
h
所以光阑S的许可宽度为:
b
2
f11
W1 (1 1)W (1 0.040 )W 0.960W
W2 (1 2 )W1 (1 0.040 )W1 0.960 2W 0.922W
W3 (1 3 )W2 (1 0.067 )W2 0.933 0.922W 0.860W
那么
W4 (1 1 )4W 1 0.014W 0.960W
因此,此种情况下系统的光能损失为:
W W4 W 0.960W 1 0.960 0.04 4%
W
W
光束以很小的角度入射到一块平行平板玻璃上(如图),试
求相继从平板反射和透射的头两支光束的相对强度。设平板的
1 2
( p
s )
0.074
I1 I0
式中,I0是入射自然光强;I1是沿AB的反射光强,反射光是垂
直于图面振动的线偏振光。
对于M2,假设在绕AB轴旋转的任一位置上,入射面与图 面的夹角为 ,则沿AB的入射光可以分解为p分量和s分量, 它们之间有一定位相差,其振幅为
E p I1 sin
[解] 由题设条件知,两镜
光学工程物理光学例题详解03

mN m1 N
且有
2nd cos22N
2
mN
2
m1
N
2
整理可得
2nd(1 cos2N ) N
在一般情况下θ1N和θ2N都很小,由折射定律有n≈n0θ1N/θ2N, 而 1-cosθ2N≈θ22N/2≈(n0θ1N/n)2/2,代入上式可得
1N
1 n0
I
(
)
I0
( s in
)2
[3
2(cos2
cos5
cos7 )]
其中:
a sin
I0为宽度a的单缝衍射零级斑中心强度。 为光波波长, 为衍射角。
d
[例题] 一束s光自空气射向一透明液体界面,入射角为60°时,测得光强反射率为 14%,求此液体折射率。
n1 cos1
1 0.374 1 0.374
1.0 cos 60
1.10
再联系折射定律:
n2 sin 2 n1 sin1 1.0 sin 60 0.866
tan 2
n2 sin 2 n2 cos 2
0.866 1.10
0.787 ......... 2
6mm
即
2nh 6mm
从而
h 6 1.97mm 2n
例题 观察迈克尔逊干涉仪,看到一个由同心明、暗环所包 围的圆形中心暗斑。该干涉仪的一个臂比另一个臂长2 cm,且 λ=0.5μm。试求中心暗斑的级数,以及第6个暗环的级数。
解: 对于由虚平板产生的等倾干涉条纹, 最小值满足如
光学工程物理光学例题详解03

t( ) rect( 2 ) rect( 2 )
a
a
(2)复振幅分布为:
E~(x)
1
x2 exp[ik( f )]
E~( )eikl d
if
2f
E~(x)
1
exp[ik( f
x2 )]
E~( )eikl d
if
2f
1
exp[ik( f
m1
一个用于检验平板厚度均匀性的装置 如图所示,光阑D用于限制平板上的受光 面积,通过望远镜可以观察平板不同部位 产生的干涉条纹(平板可相对光阑平移)。 试讨论:
(1)平板从B处移到A处时,可看到有10 个暗纹从中心冒出,问A、B两处对应的平 板厚度差是多少?并决定哪端厚或薄?
(2)所用光源的光谱宽度为0.06nm,平 均波长为600nm,问能检验多厚的平板 (n=1.52)?
n
d
N
因而第N个暗环半径的表示式为 :
rN
f
tan1N
f1N
f n0
n
d
N
第一个暗环的半径为:
r1
f n0
n 0.95cm
d
(2) 为能看到干涉环,最大允许谱线宽度Δλ应满足
m1( ) (m1 1)
由此可求得最大允许的谱线宽度为
0.75 104 m
[解] (1)由所给装置知这是一等倾干涉系统,因此条纹外冒,表明厚度h
增加,故
,厚度差: hA hB
h
N
600 10 6
10 1.97 10 3 mm 1.97 m
2n
2 1.52
光学工程基础物理光学试题参考答案
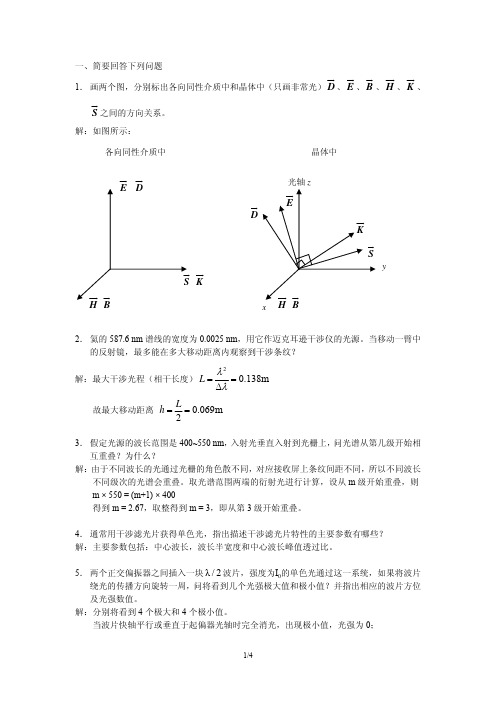
一、简要回答下列问题1. 画两个图,分别标出各向同性介质中和晶体中(只画非常光)D J J G 、E J J G 、B J G 、H JJ G 、、K J J GS J G之间的方向关系。
解:如图所示:E J J G DJ J G S J G KJ J G H JJ G BJ G 各向同性介质中DJ J G 晶体中xy光轴z2. 氦的587.6 nm 谱线的宽度为0.0025 nm ,用它作迈克耳逊干涉仪的光源。
当移动一臂中的反射镜,最多能在多大移动距离内观察到干涉条纹?解:最大干涉光程(相干长度)20.138m L λλ==Δ故最大移动距离 0.069m 2Lh ==3. 假定光源的波长范围是400~550 nm ,入射光垂直入射到光栅上,问光谱从第几级开始相互重叠?为什么?解:由于不同波长的光通过光栅的角色散不同,对应接收屏上条纹间距不同,所以不同波长不同级次的光谱会重叠。
取光谱范围两端的衍射光进行计算,设从m 级开始重叠,则 m × 550 = (m+1) × 400得到m = 2.67,取整得到m = 3,即从第3级开始重叠。
4. 通常用干涉滤光片获得单色光,指出描述干涉滤光片特性的主要参数有哪些? 解:主要参数包括:中心波长,波长半宽度和中心波长峰值透过比。
5. 两个正交偏振器之间插入一块波片,强度为I λ/20的单色光通过这一系统,如果将波片绕光的传播方向旋转一周,问将看到几个光强极大值和极小值?并指出相应的波片方位及光强数值。
解:分别将看到4个极大和4个极小值。
当波片快轴平行或垂直于起偏器光轴时完全消光,出现极小值,光强为0;当波片光轴与偏振器光轴成45度角时,光强极大,为I 0/2。
6. 正弦光栅在自身所在平面内平移或转动时,对夫琅和费衍射场或透镜后焦面上的衍射斑有什么影响?解:根据夫琅和费衍射与傅里叶变换的关系可知:正弦光栅在自身所在平面内移动时,衍射斑光强分布不变,相位分布发生一定变化; 在自身所在平面内转动时,衍射斑光强、相位分布均随之旋转。
大学物理---光学部分练习题及答案解析

PS 1 S 2r 1n 1n 2t 2r 2t 1大学物理---光学部分练习题及答案解析一、选择题1. 有一平面透射光栅,每毫米有500条刻痕,刻痕间距是刻痕宽度的两倍。
若用600nm 的平行光垂直照射该光栅,问第几级亮条纹缺级?能观察到几条亮条纹? ( C )A. 第1级,7条B. 第2级,6条C. 第3级,5条D. 第2级,3条2. 下列情形中,在计算两束反射光线的光程差时,不需要计算因半波损失而产生的额外光程的是:( D )A BCD3. 在相同的时间内,一束波长为λ的单色光在空气中和在玻璃中( C ) (A) 传播的路程相等,走过的光程相等 (B) 传播的路程相等,走过的光程不相等 (C) 传播的路程不相等,走过的光程相等 (D) 传播的路程不相等,走过的光程不相等4. 如图,S 1、S 2是两个相干光源,它们到P 点的距离分别为r 1和r 2。
路径S 1P 垂直穿过一块厚度为t 1、折射率为n 1的介质板,路径S 2P 垂直穿过厚度为t 2、折射率为n 2的另一介质板,其余部分可看作真空,这两条路径的光程差等于( B )(A) )()(111222t n r t n r +-+(B) ])1([])1([111222t n r t n r -+--+ (C) )()(111222t n r t n r ---空气油膜n=1.4 水MgF 2 n=1.38 空气玻璃 n=1.5油膜n=1.4 空气 水空气MgF 2 n=1.38玻璃 n=1.5(D) 1122t n t n -5、如图所示,平行单色光垂直照射到薄膜上,经上下两表面反射的两束光发生干涉,若薄膜的厚度为e ,并且n 1<n 2>n 3,1λ为入射光在折射率为n 1的媒质中的波长,则两束反射光在相遇点的相位差为 ( C )(A) )/(2112λπn e n (B) πλπ+)/(4121n e n (C) πλπ+)/(4112n e n(D) )/(4112λπn e n6、在真空中波长为λ的单色光,在折射率为n 的透明介质中从A 沿某路径传播到B ,若A 、B 两点相位差为3π,则此路径AB 的光程为( A )(A) 1.5 λ(B) 1.5 λ / n(C) 1.5n λ(D) 3 λ7、一束光强为I 0的自然光垂直穿过两个偏振片,且此两偏振片的透振方向成45°角,则穿过两个偏振片后的光强I 为( B )(A) 24/0I(B )4/0I(C )2/0I(D)2/20I8、波长为λ的单色光垂直入射于光栅常数为d 、缝宽为a 、总缝数为N 的光栅上。
高考物理光学知识点之几何光学分类汇编附答案解析(2)

高考物理光学知识点之几何光学分类汇编附答案解析(2)一、选择题1.如图所示,一束复色光由空气射向玻璃,发生折射而分为a 、b 两束单色光.则A .玻璃对a 、b 光的折射率满足n a >n bB .a 、b 光在玻璃中的传播速度满足v a >v bC .逐渐增大入射角,a 光将先消失D .分别通过同一双缝干涉实验装置时,相邻亮条纹间距离a 光大于b 光2.华裔科学家高锟获得2009年诺贝尔物理奖,他被誉为“光纤通讯之父”.光纤通讯中信号传播的主要载体是光导纤维,它的结构如图所示,其内芯和外套材料不同,光在内芯中传播.下列关于光导纤维的说法中正确的是A .内芯的折射率比外套的小,光传播时在内芯与外套的界面上发生全反射B .内芯的折射率比外套的大,光传播时在内芯与外套的界面上发生全反射C .波长越短的光在光纤中传播的速度越大D .频率越大的光在光纤中传播的速度越大 3.下列现象中属于光的衍射现象的是 A .光在光导纤维中传播 B .马路积水油膜上呈现彩色图样 C .雨后天空彩虹的形成 D .泊松亮斑的形成4.先后用两种不同的单色光,在相同的条件下用同双缝干涉装置做实验,在屏幕上相邻的两条亮纹间距不同,其中间距较大.....的那种单色光,比另一种单色光( ) A.在真空中的波长较短 B.在玻璃中传播的速度较大C.在玻璃中传播时,玻璃对其折射率较大D.其在空气中传播速度大5.某单色光在真空中传播速度为c ,波长为λ0,在水中的传播速度为v ,波长为λ,水对这种单色光的折射率为n ,当这束单色光从空气斜射入水中时,入射角为i ,折射角为r ,下列正确的是( ) A .v=nc,λ=n c 0B.λ0=λn,v=sinicsinrC.v=cn,λ=c vD.λ0=λ/n,v=sinrcsini6.如图所示,一细束平行光经玻璃三棱镜折射后分解为互相分离的a、b、c三束单色光。
比较a、b、c三束光,可知()A.当它们在真空中传播时,a光的速度最大B.当它们在玻璃中传播时,c光的速度最大C.若它们都从玻璃射向空气,c光发生全反射的临界角最大D.若它们都能使某种金属产生光电效应,c光照射出的光电子最大初动能最大7.如图所示,两束单色光a、b同时从空气中斜射入平行玻璃砖的上表面,进入玻璃砖中后形成复合光束c则下列说法中正确的是A.a光的能量较大B.在玻璃中a光的传播速度小于b光的传播速度C.在相同的条件下,a光更容易发生衍射D.a光从玻璃到空气的全反射临界角小于b光从玻璃到空气的全反射临界角8.甲、乙两单色光分别通过同一双缝干涉装置得到各自的干涉图样,相邻两个亮条纹的中心距离分别记为Δx1和Δx2,已知Δx1>Δx2。
高考物理光学知识点之物理光学解析含答案
D.将光源向双缝移动一小段距离
10.下列四种现象不属于光的衍射现象的是
A.太阳光照射下,架在空中的电线在地面上不会留下影子
B.不透光的圆片后面的阴影中心出现一个泊松亮斑
C.用点光源照射小圆孔,后面屏上会出现明暗相间的圆环
D.通过游标卡尺两卡脚间的狭缝观察发光的日光灯管,会看到平行的彩色条纹
A.电流i正在增大,线圈L中的磁场能也正在增大
B.电容器两极板间电压正在增大
C.电容器带电量正在减小
D.线圈中电流产生的磁场的磁感应强度正在增强
22.1966年华裔科学家高锟博士提出一个理论:直径仅几微米的玻璃纤维就可以用来做为光的波导来传输大量信息,43年后高锟因此获得2009年诺贝尔物理学奖,他被誉为“光纤通讯之父”.以下哪个实验或现象的原理和光导纤维是相同的( )
【名师点睛】人类对于光学的研究及应用非常广泛,在学习中要注意掌握不同现象在生产生活中的应用,平时要注意观察积累生活中的光现象.
5.B
解析:B
【解析】根据出现明暗条纹的条件可知,P0点到双缝的路程差为0,出现明条纹.用600nm的橙色光照射时,在光屏上的P0点和P0点上方的P1点恰好形成两列相邻的亮条纹,则 ,解得△x=λ1=600nm,则 ,可知P1点是暗条纹.故B正确,A错误.因橙光的波长大于紫光,则根据 可知,橙光的相邻亮条纹间距大于紫光的相邻亮条纹间距,若分别用上述两种光通过同一装置做单缝衍射实验,橙光的衍射现象更明显,选项CD错误;故选B.
D.宇宙飞船以接近光速的速度经过地球时,地球上的人观察到飞船上的时钟变快
19.下列说法中正确的是()
A.炽热的固体、液体和高压气体发出的光形成连续光谱
B.各种原子的明线光谱中的明线和它吸收光谱中的暗线必定一一对应
北京理工大学光学工程专业物理光学课件与习题答案

a0 a0 2
4
rect
b0
a
f , f
a0b0exp
j 0
2
sinc
a0 x
2 f
cos
a0x 2 f
0
2
sinc
b0
y f
E x,
y
a0b0
j f
exp
j
f
x2 y2 2f
0
2
sinc
a0
2
x f
cos
a0x 2 f
④ 对于夫琅和费衍射: E (P) (x, y), E (P) E (P) (x, y) (x, y) (当x y 0) E (P) E (P)(当x and (or) y 0)
或
(x, y) (x y 0)
L L (x, y)(x y 0以外的一切点)
⑤ 菲涅耳衍射:公式 E (P) E (P) E (P) 仍然成立,但
3.直边夫琅和费衍射
A step
E x, y
1
j f
exp jk
f
x2 2f
y2
f j2
x
1 2
x
f
y
f
1
L
x,
y
4
2
x
2
(当x, y 0)
x, y 当x=y=0
4.位相物体的夫琅和费衍射
A
,
rect
a0 a0 2
4
exp
j0
rect
Hole
Diffraction
pattern pattern
Square holes
Round holes
Moon coronas are due to diffraction.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.5 12
0.04
n 1 1.5 1
显然,光束从平板—空气界面反射的反射比也为0.04。设入 射光束的强度为I,则第一支反射光束的强度为
I1' I 0.04 I
第二支反射光束的强度为:
I
' 2
(1
)(1
)I
(1
)2 I
0.037 I
/
m2
)(4
107
N
s2
/
C
2
)(3 108
m
/
1
s)] 2
7.75V / m
[例题4] 一列平面光波从A点传播到B点,今在AB之间插入一 透明薄片,其厚度为 t 1mm ,折射率 n 1.5 。假定光波的波 长 0 500nm , 试计算插入透明薄片后B点位相的变化。
W4 (1 4 )W3 (1 0.067 )W3 0.933 0.860W 0.802W
因此,此种情况下系统的光能损失为:
W W4 W 0.802W 1 0.802 0.198 20%
W
W
(2)若各面的反射比均降为1%,即:
1 2 3 4 0.01
折射率为 n 1.5 。图中入射光波的S波分量Es与P波分量Ep的指
向已标出,请标出图中反射和透射光波的S波分量及P波分量的
指向。
E1p
E1s
θ1
1’
2’
n1=1.0 n2=1.50
θ2
n1=1.0
1’’
2’’
[解] 在接近正入射情况下,光束从空气—平板界面反射的 反射比为
n 12
波矢与x轴的夹角 tan1(k y ) 60
y
kx
E
k
60
x
(2)光波的振幅
A Ax2 Ay2 (2 3)2 (2)2 4(V / m)
(3)光波的频率
12 1014 6 1014 Hz
2
2
(4)光波的相速度 (5)光波的波长
V 3108 m / s
同理,计算出头两支透射光束的强度分别为:
I1'' (1 )(1 )I (1 )2 I 0.922 I
I
'' 2
(1
)(1
)I
(1
)2
2I
0.0015 I
[例题7] M1、M2是两块平行放置的玻璃片(n=1.50),背面涂 黑。一束自然光以 B 角入射到M1上的A点,反射至M2上的B 点,再出射。试确定M2以AB为轴旋转一周时,出射光强的变 化规律。
那么
W4 (1 1 )4W 1 0.014W 0.960W
因此,此种情况下系统的光能损失为:
W W4 W 0.960W 1 0.960 0.04 4%
W
W
光束以很小的角度入射到一块平行平板玻璃上(如图),试
求相继从平板反射和透射的头两支光束的相对强度。设平板的
2
( AB h c
h V
AB ) c
2 ( h h ) 2h( 1 1 )
0
0
式中 为光波在薄片内的波长。由于 0 ,所以上式又可
以写为:
n
2h (n 1) 2
0
0
式中 定义为光程差:
h(n 1)
把数值带入,计算得到:
1 1
2
1.7 12
1.7 1
0.067
4
n4 n4
1 1
2
1
1.7
1 1.7
2
1
1
1 1.7 2
1 1.7
0.067
如果入射到系统的光能为W,则相继透过各面的光能为:
[解] 由于
I
1 2
c 0 A2
所以,投射到地球表面的太阳光的电场强度为
A
(
2I
1
)2
(
2 1.33103W
1
)2
c 0
3108 m / s 8.85421012 C 2 / N m2
103V / m
[例题3]
一个功率P=100W的单色光源均匀地向空间各个方向发光。试 计算离光源10m处的光波电场强度。
E~R ( x, y) EReiC
式中,初相位C是一个常
数,可取为零。
平面波和球面波的相干叠 加
在干涉场(xOy平面)中任一点,两束光的合振幅为: E~(x, y) E~O (x, y) E~R (x, y)
考察点光强度为:
I ( x, y) E~( x, y) E~*( x, y)
EO2
ER2
2EO ER
cos k
x2 y2 2 z0
当满足: k x2 y2 2m
2z0
m=0, 1, 2, …
时,光强度为极大(亮条纹)。干涉场中亮条纹方程为
x2 y2 R2 , R 2z0m m=0, 1, 2, …
该式表明,此时干涉条纹是一组半径R与干涉级m的平
(2).该光波的振幅; (3).该光波的频率; (4).该光波的相速度; (5).该光波的波长。解 (1)由题设条件知 Nhomakorabea波数
kx 2 106
k y 2 3 106
所以
k 2 106 (1)2 ( 3)2 4 106 m1
角频率 2 106 6 108 12 1014 s1
1 2
( p
s )
0.074
I1 I0
式中,I0是入射自然光强;I1是沿AB的反射光强,反射光是垂
直于图面振动的线偏振光。
对于M2,假设在绕AB轴旋转的任一位置上,入射面与图 面的夹角为 ,则沿AB的入射光可以分解为p分量和s分量, 它们之间有一定位相差,其振幅为
E p I1 sin
[解] 光源均匀发光时,离光源10m处的光波强度为:
I P 100W 7.96 10 2W / m2
4r 2 4 (10m)2
在空气中,
V C
因此
1
00
I
1 2
c
0
A2
1 2
A2
0c
得到离光源10m处的光波电场强度为:
1
E A (2I0c) 2
[2(7.96 102W
2
500
10 3 m 10 9 m
(1.5
1)
2
10 3 rad
例题:
一光学系统由两片分离的透镜组成,两片透镜的 折射率分别为1.5和1.7,求此系统的反射光能损失。 如透镜表面镀上增透膜使表面反射率降为1%,问此系 统的光能损失又是多少?
[解] (1)系统包括4个反射面,假设光束是接近正入 射情形下通过各反射面,因而各面的反射比分别为:
Es I1 cos 由于此时的入射角也为 B ,所以:
rp 0
rs
sin(1 sin(1
2) 2)
0.3846
因此,自M2出射光的振幅为:
E
' p
0
E
' s
rs Es
(0.3846 )
I1 cos
即自M2出射光的强度为:
I2
(
E
' s
)
2
0.011I 0
[例题]
在真空中传播的一列平面电磁波,用国际单位量度时其电场可 以表示为
Ex 0
Ey 0
Ez
(102V
/
m) cos[
1014 s1( x c
t)
]
2
问该电磁波的频率、波长、振幅、周期和初位相是多少?
[解] 对照波动公式的基本形式
E Acos[2 ( x t) ]
6 10 6 m
6m
周期
T1
1
2 1014 s
0.5 1014 s 1
一、在国际标准单位制下,一单色平面光波的表示式为:
E (2 3 x0 2 y0 ) exp[ i2 10 6 (x 3y 6 108 t)]
要求:
(1).画图示意出该光波的传播方向和偏振方向(标出相 应的角度值);
cos2
结论:出射光强依M2相对于M1的方位变化,符合马吕斯 (Malus)定律。
例题8 讨论平面光波和球面光波的干涉。
解:
如图所示,有一球面光波O和一平面光波R在空间相遇,产生
干涉。
(1)在正入射时,球面光波的复振幅(近轴情形)为
E~O (x,
y)
ik
EOe
x2 y2 2 z0
平面光波的复振辐为
c
把Ez写为
Ez
(10 2V
/ m) cos[2
1014 2
s1( x c
t) ]
2
于是可见:
频率
1014 s 1 0.5 1014 Hz
2
振幅 A 102V / m
初位相 rad
2
