散列习题课
合集下载
线性代数行列式计算习题课
3 2
a bc d
a
3
b a c d
1 x2
b b
3
c a b d
1
2
a bc
d d
3 2
1
2
c c
3 2
r4 r3
a
x1
2
xn
x1 a b c d x1
n 1
a
b 2 2 x2 xn a b c d a n 1 b x 2 a
2 3 3 2
c d ( xi x j ) ni j 1c d a b a b c d
* c in *
6、 某 行 （ 列 ） 的 k倍 加 到 另 一 行 （ 列 ） 上 ， 行 列 式 值 不 变
ri k r j ( c i k c j )
第 5页
行列式按行（列）展开
行列式等于它的任一行 ( 列 ) 各元素与其对应的代数余子 式乘积之和：
D n a i1 Ai1 a i 2 Ai 2 a 1 i A1 i a 2 i A 2 i a in A in a ni Ani
5 3 1 4 3
0 4 9
20
第16页
a. 行（列）元素之和相等的行列式
1 7. D 1 1 x 1 1 1 x 1 1
b
1 x 1 1 1 1
x 1 1 1 1
bx 1
c1 c 2 c1 c 3
x x x x 1 0
1 1 x 1 1 0 x
1 x 1 1 1
x 1 1 1 1
c1 c 4
1 a b 1
c1 x
x
1 b a 1 1 x 1
离散数学-第2章 习题课
5
谓词的概念与表示
解：a) a:小张 W(x): x是工人。 W(a)
b)S(x):x是田径运动员, B(x):x是球类运动员, h:他 S(h)B(h) c) C(x):x是聪明的，B(x):x是美丽的，a:小莉 C(a) B(a) d) O(x):x是奇数。 O(m) O(2m)
28
变元的约束
例15 如果论域是集合{a,b,c}，试消去下面公式 中的量词。 a) (x) P( x) P(a) P(b) P(c) b) (x) R( x) (x) S ( x)
R(a) R(b) R(c)S (a)S (b)S (c)
c) (x)( P( x) Q( x))
(x)( I ( x) ( R( x) N ( x)))
13
命题函数与量词
例5 令P(x)，L(x)，R(x,y,z)和E(x,y)分别表示 “x是一个点”，“x是一条直线”，“z通过x和 ”和“x=y”。符号化下面得句子。 对每两个点有且仅有一条直线通过该两点。 解：
(x)(y)(( P( x) P( y ) E ( x, y)) (! z )( L( z ) R( x, y, z )))
9
命题函数与量词
e) J(x): x是教练员, L(x): x是运动员。
(x)(L(x) J(x)) f) L(x): x是运动员, S(x): x是大学生,C(x):x是国家 选手。 (x)(S(x)L(x)C(x)) g) C(x):x是国家选手,V(x)：x是健壮的。 ( x)(C(x) V(x)) h) (x)(O(x) C(x) L(x))
14
谓词公式与翻译
例6 利用谓词公式翻译下列命题 a)如果有限个数的乘积等于零，那么至少有一个因 子等于零。 b)对于每一个实数x,存在一个更大的实数y。 c)存在实数x,y和z,使得x与y之和大于x与z之积。
谓词的概念与表示
解：a) a:小张 W(x): x是工人。 W(a)
b)S(x):x是田径运动员, B(x):x是球类运动员, h:他 S(h)B(h) c) C(x):x是聪明的，B(x):x是美丽的，a:小莉 C(a) B(a) d) O(x):x是奇数。 O(m) O(2m)
28
变元的约束
例15 如果论域是集合{a,b,c}，试消去下面公式 中的量词。 a) (x) P( x) P(a) P(b) P(c) b) (x) R( x) (x) S ( x)
R(a) R(b) R(c)S (a)S (b)S (c)
c) (x)( P( x) Q( x))
(x)( I ( x) ( R( x) N ( x)))
13
命题函数与量词
例5 令P(x)，L(x)，R(x,y,z)和E(x,y)分别表示 “x是一个点”，“x是一条直线”，“z通过x和 ”和“x=y”。符号化下面得句子。 对每两个点有且仅有一条直线通过该两点。 解：
(x)(y)(( P( x) P( y ) E ( x, y)) (! z )( L( z ) R( x, y, z )))
9
命题函数与量词
e) J(x): x是教练员, L(x): x是运动员。
(x)(L(x) J(x)) f) L(x): x是运动员, S(x): x是大学生,C(x):x是国家 选手。 (x)(S(x)L(x)C(x)) g) C(x):x是国家选手,V(x)：x是健壮的。 ( x)(C(x) V(x)) h) (x)(O(x) C(x) L(x))
14
谓词公式与翻译
例6 利用谓词公式翻译下列命题 a)如果有限个数的乘积等于零，那么至少有一个因 子等于零。 b)对于每一个实数x,存在一个更大的实数y。 c)存在实数x,y和z,使得x与y之和大于x与z之积。
散列表练习(1)
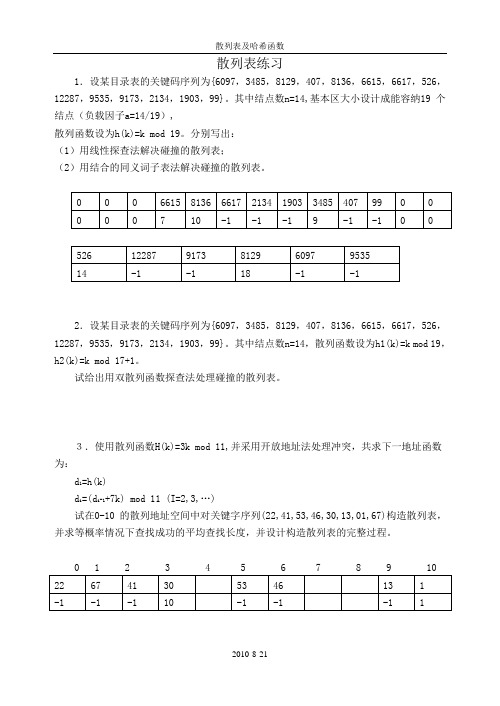
散列表练习1．设某目录表的关键码序列为{6097，3485，8129，407，8136，6615，6617，526，12287，9535，9173，2134，1903，99}。
其中结点数n=14,基本区大小设计成能容纳19 个结点（负载因子a=14/19）,散列函数设为h(k)=k mod 19。
分别写出：（1）用线性探查法解决碰撞的散列表；（2）用结合的同义词子表法解决碰撞的散列表。
2．设某目录表的关键码序列为{6097，3485，8129，407，8136，6615，6617，526，12287，9535，9173，2134，1903，99}。
其中结点数n=14，散列函数设为h1(k)=k mod 19，h2(k)=k mod 17+1。
试给出用双散列函数探查法处理碰撞的散列表。
３．使用散列函数H(k)=3k mod 11,并采用开放地址法处理冲突，共求下一地址函数为：d1=h(k)d i=(d i-1+7k) mod 11 (I=2,3,…)试在0-10 的散列地址空间中对关键字序列(22,41,53,46,30,13,01,67)构造散列表，并求等概率情况下查找成功的平均查找长度，并设计构造散列表的完整过程。
4．假设有1000 个值小于10000 的正整数，用构造散列表的方法将1000 个正整数按由小到大的次序放入表中。
负载因子a=1，试写出你的排序算法。
5．AK 的故事之英语学习篇程序名： mistake.pas输入文件名： mistake.in输出文件名： mistake.out问题描述：面对竞争日益激烈的社会，AK 深感自己的英语水平实在是太差了，他决定在英语方面下苦工。
这些日子里，AK 每天都要背大量的英语单词，阅读很多英语文章。
终于有一天，AK 很高兴的对自己说：“我的英语已经没问题了！”他决定写一篇英语文章来显示自己的水平……AK 将自己的文章交给了他的英语老师Mr. Zhu，满以为Mr. Zhu 会大加赞赏。
离散数学第2章习题课
填空设a为含命题变项pqr的重言式则公式apqr的类型为设b为含命题变项pqr的矛盾式则公式bp?qr的类型为设pq为命题变项则p?q的成真赋值为矛盾式的主析取范式为设公式a的主合取范式为m0m2m3m5则a的主析取范式为4zhejiangnormaluniversity数理信息学院浙江师范大学习题求主析取范式和合取范式1求公式pqrpqr的主析取范式2求公式pqqp的主合求公式pqq取范式3求公式pqpq?qp的主析取范式再由主析取范式求出主合取范式p的主合5zhejiangnormaluniversity数理信息学院浙江师范大学习题等值演算将公式pqr化成与之等值且仅含中联结词的公式6zhejiangnormaluniversity数理信息学院浙江师范大学习题判断公式等值用主析取范式判断p?q与pqpq是否等值7
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
数理信息学院 王艳霞
第2章 内容回顾 章
1
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
数理信息学院
内容提要
等值式和基本等值式
等值式 基本等值式 等值演算 重言式与矛盾式的判别方法
2
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
5
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
数理信息学院
习题——等值演算 等值演算 习题
将公式p 化成与之等值且仅含{┐ 将公式 →(q → r)化成与之等值且仅含 ， 化成与之等值且仅含 ∧}中联结词的公式 中联结词的公式
6
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
4
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
数理信息学院 王艳霞
第2章 内容回顾 章
1
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
数理信息学院
内容提要
等值式和基本等值式
等值式 基本等值式 等值演算 重言式与矛盾式的判别方法
2
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
5
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
数理信息学院
习题——等值演算 等值演算 习题
将公式p 化成与之等值且仅含{┐ 将公式 →(q → r)化成与之等值且仅含 ， 化成与之等值且仅含 ∧}中联结词的公式 中联结词的公式
6
浙江师范大学
ZHEJIANG NORMAL UNIVERSITY
4
排列的综合应用习题课课件-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册
索引
题型三 定序问题
例3 将A，B，C，D，E这5个字母排成一列，要求A，B，C在排列中的顺序为 “A，B，C”或“C，B，A”(可以不相邻)，则有多少种不同的排列方法？ 解 5个不同元素中部分元素A，B，C的排列顺序已定，这种问题有以下两种 常用的解法. 法一(整体法) 5 个元素无约束条件的全排列有 A55种， 由于字母A，B，C的排列顺序为“A，B，C”或“C，B，A”， 因此在上述的全排列中恰好符合“A，B，C”或“C，B，A”排列方式的排 列有AA5533×2＝40(种).
一、基础达标
1.6人站成一排，甲、乙、丙3人必须站在一起的所有排列的总数为( D )
A.A66 C.A33·A33
B.3A33 D.3！·4!
解析 甲、乙、丙三人站在一起有 A33种排法，把 3 人作为一个元素与其他 3 人 排列有 A44种排法，故共有 A33·A44，即 3！·4！种排法.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
索引
(4)如果甲、乙两人必须站两端，有多少种不同排法？ 解 甲、乙为特殊元素，先将他们排在两头位置，有 A22种，其余 6 人全排列， 有 A66种， 所以共有 A22A66＝1 440(种)不同排法.
索引
(5)如果甲不站左端，乙不站右端，有多少种不同排法？
解 法一(直接法) 甲在最右边时，其他的可全排列，有 A77种； 甲不在最右边时，可从余下 6 个位置中任选一个，有 A16种， 而乙可排在除去最右边位置后剩余的 6 个中的任意一个上，有 A16种， 其余人全排列，共有 A16A16A66＝25 920(种). 由分类加法计数原理共有 A77＋A16A16A66＝30 960(种). 法二(间接法) 8 个人全排列，共有 A88种.其中，不符合条件的有甲在最左边 时 A77种，乙在最右边时 A77种，其中都包含了甲在最左边，同时乙在最右边的 情形，共 A66种. 所以共有 A88－2A77＋A66＝30 960(种).
离散数学第七章图论习题课
利用奇数+奇数=偶数，偶数+偶数=偶数，所以， 在G中结点度数为奇数的结点，在其补图中的度 数也应为奇数，故G和其补图的奇数结点个数也 是相同的。
P286 1、在无向图G中，从结点u到结点v有一条长度为 偶数的通路，从结点u到结点v又有一条长度为奇 数的通路，则在G中必有一条长度为奇数的回路。
证明 ：
2、运用 (1) 判断有向图或无向图中通路(回路)的类型。 (2) 求短程线和距离。 (3) 判断有向图连通的类型。
三、图的矩阵表示
1、基本概念。 无向图的邻接矩阵A 根据邻接矩阵判断:各结点的度, 有向图结点 出,入度。 由Ak可以求一个结点到另一个结点长度为k 的路条数. 有向图的可达矩阵P 用P可以判定:各结点的度. 有向图的强分图。 关联矩阵M:是结点与边的关联关系矩阵. 用M判定:各结点的度
设给定图G(如由图所示)，则图G的点割集
是
．
应该填写：{f}，{c，e}。
定义 设无向图G=<V, E>为连通图，若有点集
V1V，使图G删除了V1的所有结点后，所得的子
图是不连通图，而删除了V1的任何真子集后，所
得的子图是连通图，则称V1是G的一个点割
集．若某个结点构成一个点割集，则称该结点为
割点。
a c
a c
b
d
b
d
a c
a c
b
d
b
d
推论:任何6人的人群中，或者有3人互相认识，或者有 3人彼此陌生。(当二人x,y互相认识，边(x,y)着红色， 否则着兰色。则6人认识情况对应于K6边有红K3或者 有兰K3。)
证明简单图的最大度小于结点数。
证明： 设简单图G有n个结点。对任一结点u，由于G没
P286 1、在无向图G中，从结点u到结点v有一条长度为 偶数的通路，从结点u到结点v又有一条长度为奇 数的通路，则在G中必有一条长度为奇数的回路。
证明 ：
2、运用 (1) 判断有向图或无向图中通路(回路)的类型。 (2) 求短程线和距离。 (3) 判断有向图连通的类型。
三、图的矩阵表示
1、基本概念。 无向图的邻接矩阵A 根据邻接矩阵判断:各结点的度, 有向图结点 出,入度。 由Ak可以求一个结点到另一个结点长度为k 的路条数. 有向图的可达矩阵P 用P可以判定:各结点的度. 有向图的强分图。 关联矩阵M:是结点与边的关联关系矩阵. 用M判定:各结点的度
设给定图G(如由图所示)，则图G的点割集
是
．
应该填写：{f}，{c，e}。
定义 设无向图G=<V, E>为连通图，若有点集
V1V，使图G删除了V1的所有结点后，所得的子
图是不连通图，而删除了V1的任何真子集后，所
得的子图是连通图，则称V1是G的一个点割
集．若某个结点构成一个点割集，则称该结点为
割点。
a c
a c
b
d
b
d
a c
a c
b
d
b
d
推论:任何6人的人群中，或者有3人互相认识，或者有 3人彼此陌生。(当二人x,y互相认识，边(x,y)着红色， 否则着兰色。则6人认识情况对应于K6边有红K3或者 有兰K3。)
证明简单图的最大度小于结点数。
证明： 设简单图G有n个结点。对任一结点u，由于G没
离散数学课件总复习之习题讲解
4 c8
25 c2
10 c5
11 c6
36 c7
7 3 c3 11 4 c8 17 6 c4 10 c5 7 3 c3
11
5 c1
6 c4
25 c2
11 c6
36 c7
5 c1
22 11
4 c8
25 c2
36 c7 5 c1
17
11 c6 10 c5 7 3 c3 4 c8
6 c4
25 c2
36 c7 11 5 c1 61
6 c4
11 10 c6 c5
3 c3
c7 01
4 c8
c8 1111
c5 110
c6 101
电文总码数：4×5＋ 2×25＋ 4×3＋ 4×6＋ 3×10＋ 3×11＋ 2×36＋ 4×4＝257
P295 6.9
设散列表为 HT[13] ，散列函数 H(key)=key%13 ，用闭散列法解决冲突， 对下列关键码序列12,23,45,57,20,03,78,31,15,36造表。 （1）采用线性探查法寻找下一个空位，画出相应的散列表，并计算等概率 下搜索成功的平均搜索长度和搜索不成功的平均搜索长度。 （ 2 ）采用双散列法寻找下一个空位，再散列函数 RH(key)=(7*key)%10+1 ， 寻找下一个空位的公式为 Hi＝（ Hi-1＋RH(key)）% 13，H1=H(key) 。画出 相应的散列表，并计算等概率下搜索成功的平均搜索长度。 温习：
20122012年秋季年秋季各内容重点题型讲解各内容重点题型讲解容容比比示例例题示例例题线性表线性表1515p86222p86222栈和队列栈和队列1515p133322p133322数组矩阵和串数组矩阵和串1010p185413p185413二叉树堆二叉树堆huffmanhuffman2020p248518p2485185205201010p29569p295691100p393810p393810p395824p395824搜索结构搜索结构2020p343715p343715排序排序p44092p44092p86222p86222设在一个带附加头结点的单链表中所有元素结点的数据值按递增顺序排列试编写一个函数删除表中所有大于min小于max的元素若存firstppqq温习
数据结构习题和答案
数据结构习题和答案习题课填空1、对于⼀棵⼆叉树，若⼀个结点的编号为i，则它的左孩⼦结点的编号为，双亲结点的编号为。
2、向⼀个长度为n的向量中删除第i个元素(1≤i≤n)时，需向前移动个元素。
3、在⼀棵⼆叉树中，若双分⽀结点数为5个，单分⽀结点数为6个，则叶⼦结点数为个。
4、为了实现折半查找，线性表必须采⽤⽅法存储。
顺序5、⼀种抽象数据类型包括数据对象和。
6、在以L为表头指针的带表头附加结点的单链表和循环单链表中，判断链表为空的条件分别为__________和_______。
7、数据结构被形式地定义为（D, R），其中D是的有限集合，R是D上的有限集合。
8、队列的插⼊操作在进⾏，删除操作在进⾏。
9、⼆叉搜索树的中序遍历得到的结点序列为____ ____。
10、在顺序表中插⼊或删除⼀个元素，需要平均移动元素，具体移动的元素个数与有关。
11、栈的特点是。
12、在单链表中，除了⾸元结点外，任⼀结点的存储位置由。
13、在⼀个具有n个顶点的⽆向图中，要连通所有顶点则⾄少需要条边。
14、深度为k（设根的层数为1）的完全⼆叉树⾄少有个结点，⾄多有个结点。
15、⼀棵深度为6的满⼆叉树有个分⽀结点和个叶⼦结点。
16、⼀个算法的效率可分为效率和效率。
17、队列的特点是。
18、⼀棵深度为5的满⼆叉树中的结点数为个。
19、在⼀个具有n个顶点的⽆向完全图中，包含有________条边，在⼀个具有n个顶点的有向完全图中，包含有________条边。
简答题1、已知⼀组元素为（38，26，62，94，35，50，28，55），画出按元素排列顺序输⼊⽣成的⼀棵⼆叉搜索树。
答:2、假设有⼆维数组A[0..5,0..7]，每个元素⽤相邻的6个字节存储，存储器按字节编址。
已知A的起始存储位置（基地址）为1000，计算：（1）末尾元素A57的第⼀个字节地址为；（2）若按列存储时，元素A47的第⼀个字节地址为。
(3) 数组A的体积（存储量）；(4) 若按⾏存储时，元素A14的第⼀个字节地址为。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.已知散列函数为H(K)=K mod 12,健值序 列为25，37，52，43，84，99，120， 15，26，11，70，82，采用分离链接法 处理冲突，试构造散列表，并计算查找 成功的平均查找长度。
查找成功的平均查找长度为：（4*2+8）/
12 = 4/3
5.3设有一组关键字 {29,01,13,15,56,20,87,27,69,9,10,74}，散 列函数为H(key)=key%17,采用线性探测法解决 冲突。试在0~18的散列地址空间中对该关键字 序列构造散列表，并计算成功查找的平均查找 长度。
5.4题目同上，采用平方探测法解决冲突。
5.5设有一组关键字 {92,81,58,21,57,45,161,38,117}，散列函数 为H(key)=key%13,采用双散列探测法解决第i 次冲突：H(key)=(H(key)+i* H2(key))%13,其 中， H2(key)=(key%11)+1 。试在0~12的散列 地址空间中对该关键字序列构造散列表。
③ 不同关键码值对应到相同的存储地址
④ 负载因子过大 ⑤ 数据元素过多
D： ① 线性探查法和双散列函数法
② 建溢出区法和不建溢出区法
③ 除余法和折叠法
④ 拉链法和开地址法
答案：A＝
B＝
C＝
D＝
１. ④ ① ③ ④
四、简答题
1.简述为手机号码建立一个散列表的方法。 2.简述影响产生冲突的三个因素。
五、分析题
查找长度。
（1）画表如下：
（2） 查找63,首先要与H(63)=63%16=15号单元内容比较， 即63 vs 31 ,no;
然后顺移，与46,47,32,17,63相比，一共比较了6次！ （3）查找60,首先要与H(60)=60%16=12号单元内容比较，
但因为12号单元为空（应当有空标记），所以应当只 比较这一次即可。 （4） 对于黑色数据元素，各比较1次；共6次； 对红色元素则各不相同，要统计移位的位数。“63”需要 6次，“49”需要3次，“40”需要2次，“46”需要3次， “47”需要3次， ASL=1/11（6＋2＋3×3）＝17/11≈1.55
（1）请画出所构造的散列表；（2）分别计算等 概率情况下，查找成功和查找不成功的平均查 找长度。
解：表长为10,p为7。 H（key）=（key×3）% 7 （1）
(2) 查找成功： ASL = (1+2+1+1+1+3+3) / 7 = 12 / 7 所以ASLu= （3+2+1+2+1+8+7+6+5+4）/ 10 = 39/10。
六、算法题
１.已知某哈希表的装载因子小于1，哈希函数H(key)为 关键字（标识符）的第一个字母在字母表中的序号， 处理冲突的方法为线性探测开放定址法。试编写一 个按第一个字母的顺序输出哈希表中所有关键字的 算法。
5.6已知线性表关键字集合 {21,11,13,25,48,6,39,83,30,96,108}，散列 函数为H(key)=K % 11采用分离链接法处理冲 突，试构造散列表，并计算查找成功的平均查 找长度。
5.7将关键字序列{7,8,30,11,18,9,14}散列存储 到散列表中散列表的存储空间是一个下标从0 开始的一个一维数组散列函数维：H（key）= （key×3）% p，处理冲突采用线性探测再散 列法，要求装填因子为0.7。
2. 选取散列函数H（key）=（3*key）%11，用 线性探测法处理冲突，对下列关键码序列构造 一个散列地址空间为0～10，表长为11的散列 表，{22，41，53，08，46，30，01，31，66}。
则(22*3)%11=6……0 (41*3)%11=11……2 (53*3)%11=14……5 (08*3)%11=2……2 (46*3)%11=12……6 (30*3)%11=8……2 (01*3)%11=0……3 (31*3)%11=8……5 (66*3)%11=9……0
1. 设哈希（Hash）表的地址范围为0～17，哈希函数为： H（K）＝K MOD 16。K为关键字，用线性探测法再 散列法处理冲突，输入关键字序列：
（10，24，32，17，31，30，46，47，40，63，49） 造出Hash表，试回答下列问题： 画出哈希表的示意图； 若查找关键字63，需要依次与哪些关键字进行比较？ 若查找关键字60，需要依次与哪些关键字比较？ 假定每个关键字的查找概率相等，求查找成功时的平均
3 .在开放地址散列表中，删除操作通常只能“懒惰删 除”，即需要增加一个 “删除标记(Deleted)”， 而并不是真正删除它。
4.当装填因子过大时，解决的方法是加倍扩大散列表， 这样α可以减小一半，这个过程叫做“再散列”。
5.可能将不同的关键字映射到同一个散列地址上，即 h(keyi) = h(keyj)（当keyi ≠keyj），这种现象称为 “冲突”， keyi 和keyj称为“同义词”。
二、填空
1 .常用的处理冲突的方法有两种：开放地址法和链地 址法。
2 . 发生了第 i 次冲突，试探的下一个地址将增加di， 基本公式是：hi(key) = (h(key)+di) mod TableSize ,其中di 取决于不同的解决冲突方案： 线性探测时di ＝ i 、平方探测时di ＝ ± i2 、双散 列时di ＝ i*h2(key)。
散列习题课
一、判断正误
（ ）1. p 是小于或等于 TableSize的最大素数 。 （ ）2.取11位手机号码key的后4位作为地址的 散列函数为：h(key) = atoi(key+9) 。 （ ）3.选择合适的 h(key) ，散列法的查找效率期
望是常数O(1)，它几乎与关键字的空间的大小n 无关！ （ ）4.散列方法是一个以空间换时间。 （ ）5.太小的α可能导致空间浪费，太大的α又将 付出更多的时间代价。
三、选择题
1.散列法存储的基本思想是根据 A 来决定 B ， 碰撞（冲突）指的是 C ，处理碰撞的两类主要方法 是D 。
供选择的答案
A，B： ①存储地址 ② 元素的符号 ③ 元素个数
④ 关键码值 ⑤ 非码属性 ⑥ 平均检索长度 ⑦ 负载因子 ⑧ 散列表空间
C: ①两个元素具有相同序号
② 两