异面直线及其所成角PPT课件
合集下载
高中数学异面直线所成角课件苏教版必修

异面直线所成 角为锐角或钝 角的情况需要 特别注意,因 为这两种情况 下的求解方法
不同。
在求解异面直 线所成角时, 需要注意异面 直线的方向, 因为方向不同 也会影响求解 方法的选择。
在求解异面直 线所成角时, 需要注意异面 直线是否平行, 因为平行与否 也会影响求解 方法的选择。
在求解异面直 线所成角时, 需要注意异面 直线是否垂直, 因为垂直与否 也会影响求解 方法的选择。
异面直线所成角与平行线所成 角的关系
异面直线所成角的求法
异面直线所成角的意义
异面直线所成角是描述两条异 面直线之间夹角大小的量
异面直线所成角的大小范围为 0到90度
异面直线所成角是解决异面直 线相关问题的重要工具
异面直线所成角在几何学中具 有广泛的应用价值
异面直线所成角的大小范围是(0, 90°]
异面直线所成 角的应用将进 一步拓展到其
他领域
未来将有更多 的研究和教学 成果涌现,推 动异面直线所
成角的发展
汇报人:
到 $90^{\circ}$
角的性质:异 面直线所成的 角具有唯一性
和确定性
角的计算方法: 通过平移或旋 转将异面直线 转化为相交直 线,再利用相 交直线的性质
计算角度
异面直线所成角与平面角的关系
添加标题
异面直线所成角是平面角的一 种。
添加标题
异面直线所成角的范围是[0°, 90°]。
添加标题
异面直线所成角与距离的关系: 异面直线所成角越大,距离越 小。
异面直线所成角与向量夹 角的关系
异面直线所成角在解方程 中的应用
异面直线所成角在求函数 最值中的应用
异面直线所成角在判断不 等式成立条件中的应用
异面直线所成角ppt课件

(2)求AE 和BG 所成的角是多少度?
解答:(1)∵GF∥BC ∴∠EGF(或其补角)为所
H
求.
E
o
F
R(2t)△∵EFBGF∥中,AE求得∠EGF = 45
2 2 3D
∴∠FBG(或其补角)为所求,
பைடு நூலகம்
A
23
B
Rt△BFG中,求得∠FBG
=
o
60
ppt课件
G C
10
典例展示
例2、在长方体ABCD—A1B1C1D1中,A A1= AB
平行公理 平行同一条直线的两条直线互相平行
等角定理 空间中如果两个角的两边分别对应平行,那么 这两个角相等或互补.
ppt课件
2
知识探究
异面直线所成的角
O
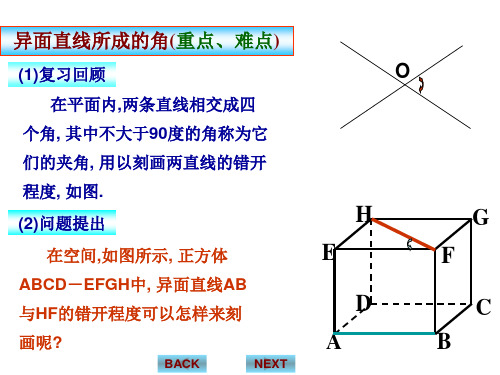
(1)旧识回顾
在平面内,两条直线相交成四个角, 其中不大于90度的角称为它们
的夹角, 如图.
(2)问题提出
在空间,如图所示, 正方体ABCD-EFGH中, 异面直线AB与HF的错开程度可以怎样来刻 画呢?
B1 A1
C1 D1
B1 A1
C1 D1
D O
A
C B
D O
A
C B
ppt课件
14
课堂小结
1、求异面直线所成的角是把空间角转化为平面角, 体现了化归的数学思想。
化归的一般步骤是: 定角
求角
定角一般方法有: (1)平移法(常用方法) (2)补形法
2、当异面直线垂直时,还可应用线面垂直的有 关知识 解决。
D1
C1
A1
B1
E
G
A
ppt课件
D F
C
B
必修2课件:异面直线所成的角
BACK NEXT
O
H E D A B F
G
C
(3)解决问题 解决问题
平移转化成相交直线所成的角,即化空间图形问题为平面图形问题 思想方法 : 平移转化成相交直线所成的角 即化空间图形问题为平面图形问题 异面直线所成角的定义: 如图,已知两条异面直线 经过空间任一点O作 异面直线所成角的定义 如图 已知两条异面直线 a , b , 经过空间任一点 作 所成的锐角(或直角 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角 或直角 叫做异面直线所成的角 ∥ ∥ 与 所成的锐角 或直角)叫做异面直线所成的角 (或夹角 或夹角). 或夹角 异面直线所成的角的范围( 0 , 90 ]
b
b′
a″ a
∠2
α
a′
O
∠1
BACK
NEXT
在求作异面直线所成的角时,O点 在求作异面直线所成的角时 点 常选在其中的一条直线上 (如线段的端点,线段的中点等) 如线段的端点 线段的中点等 如线段的端点 线段的中点
例2
如图,正方体 为侧面ADHE的中心,求 的中心, 如图,正方体ABCD-EFGH中,O为侧面 中 为侧面 的中心 (1)BE与CG所成的角? 与 所成的角? 所成的角 (2)FO与BD所成的角? 与 所成的角 所成的角?
这个角的大小与O点的位置有关吗 点位置不同时, 思考 : 这个角的大小与 点的位置有关吗 ? 即O点位置不同时 这一角的大小 点位置不同时 是否改变? 是否改变
解答: 解答: 如图
答: 这个角的大小与O点的位置无关. 点的位置无关 这个角的大小与 点的位置无关
相交所成的角为∠ 设a ′与 b ′相交所成的角为∠1, a ″与 b 所成的角为∠2 , 与 相交所成的角为 与 所成的角为∠ 公理4), ∵ a′∥a , a″ ∥a∴ a′∥ a″ (公理 ∥ ∴ ∥ 公理 同理 b′∥b″, ∴ ∠1 = ∠2 (等角定理 等角定理) ∥ 等角定理
O
H E D A B F
G
C
(3)解决问题 解决问题
平移转化成相交直线所成的角,即化空间图形问题为平面图形问题 思想方法 : 平移转化成相交直线所成的角 即化空间图形问题为平面图形问题 异面直线所成角的定义: 如图,已知两条异面直线 经过空间任一点O作 异面直线所成角的定义 如图 已知两条异面直线 a , b , 经过空间任一点 作 所成的锐角(或直角 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角 或直角 叫做异面直线所成的角 ∥ ∥ 与 所成的锐角 或直角)叫做异面直线所成的角 (或夹角 或夹角). 或夹角 异面直线所成的角的范围( 0 , 90 ]
b
b′
a″ a
∠2
α
a′
O
∠1
BACK
NEXT
在求作异面直线所成的角时,O点 在求作异面直线所成的角时 点 常选在其中的一条直线上 (如线段的端点,线段的中点等) 如线段的端点 线段的中点等 如线段的端点 线段的中点
例2
如图,正方体 为侧面ADHE的中心,求 的中心, 如图,正方体ABCD-EFGH中,O为侧面 中 为侧面 的中心 (1)BE与CG所成的角? 与 所成的角? 所成的角 (2)FO与BD所成的角? 与 所成的角 所成的角?
这个角的大小与O点的位置有关吗 点位置不同时, 思考 : 这个角的大小与 点的位置有关吗 ? 即O点位置不同时 这一角的大小 点位置不同时 是否改变? 是否改变
解答: 解答: 如图
答: 这个角的大小与O点的位置无关. 点的位置无关 这个角的大小与 点的位置无关
相交所成的角为∠ 设a ′与 b ′相交所成的角为∠1, a ″与 b 所成的角为∠2 , 与 相交所成的角为 与 所成的角为∠ 公理4), ∵ a′∥a , a″ ∥a∴ a′∥ a″ (公理 ∥ ∴ ∥ 公理 同理 b′∥b″, ∴ ∠1 = ∠2 (等角定理 等角定理) ∥ 等角定理
异面直线所成角课件

不在同一个平面上且互不相交的两条 直线。
异面直线不可能平行,也不可能相交 。
异面直线判定
两条直线若不相交,则可能为异面直 线。
异面直线所成角的定义
异面直线所成角:两条异面直 线在某个平面上投影所形成的 夹角。
异面直线所成角的取值范围: 0°到90°。
异面直线所成角的计算方法: 通过平移将两条异面直线转化 为相交直线,再计算夹角。
PART 05
异面直线所成角的扩展知 识
异面直线的其他性质
异面直线永远不会相交
由于异面直线不在同一平面内,因此它们永远不会在某一点相交 。
异面直线与平行线的关系
平行线是共面的直线,而异面直线是不同面的直线,因此平行线与 异面直线没有交点。
异面直线的方向向量
异面直线的方向向量在不同的平面上,因此它们的方向向量是垂直 的。
平面角的取值范围
锐角(0°,90°)或直角(90°)。
异面直线所成角的求法
01
02
03
定义
异面直线所成的角是指两 条异面直线在同一平面内 的射影所形成的锐角或直 角。
计算方法
通过平移将两条异面直线 变为相交直线,再通过平 面角的定义计算出所成角 的大小。
注意事项
平移过程中不能改变直线 的方向和位置,否则所求 得的角不是异面直线所成 的角。
异面直线所成角的性质
性质一
异面直线所成角是唯一 的,与平移无关。
性质二
两条异面直线所成的角 是锐角或直角,不可能
为钝角。
性质三
两条异面直线所成的角 与两条直线的夹角相等
或互补。
性质四
两条异面直线所成的角 可以通过平移、旋转和
对称等变换得到。
PART 02
高中数学人教A版必修2课件:2.1.2空间中直线与直线之间的位置关系2异面直线所成角(共20张PPT)

【例】如图,在正方体ABCD-A′B′C′D′中:
(1)哪些棱所在的直线与直线AA′垂直?
(2)哪些棱所在的直线与直线A′B垂直?
(3)直线A′B和CC′所成角是多少?
解:(1) 直线AB,BC,CD,DA, A′B′ ,B′C′,
D′
C′ C′D′, D′A′与直线AA′ 都垂直.
(2) 直线AD,BC, B′C′ ,A′D′与直线A′B
抛 砖 • 在平面内,如果两个角的两边分别对应 引 平行,那么这两个角有什么关系? 玉
抛 砖 • 在空间中,如果两个角的两边分别对应 引 平行,结论是否仍然成立呢? 玉
1、等角定理:
• 空间中如果两个角的两边分别对应平行, 那么这两个角相等或互补。
• 【定理的推论】 如果两条相交直线和另两条相交直线
• 推论2:经过_两_条_相_交直线,有且只有一个平面。 • 推论3:经过_两_条_平_行直线,有且只有一个平面。
• 公理3:如果两个不重合的平面有一个公共点,那 么它们_有_且_只_有_一_条_过_该_点_的_公_共_直_线。
• 公理4:_平_行_于_同_一_直_线_的两条直线互相平行。
• 空间中直线与直线的位置关系:
看图说话
1(1)长方体ABCD-A′B′C′D′中,有没有两条棱所
在的直线是互相垂直的异面直线?
(2)如果两条平行直线中的一条与某一条直线垂 直,那么,另一条直线是否也与这条直线垂直?
(3)垂直于同一条直线的两条直线是否平行?
C' B'
C
B
D' A'
D
A
精讲点拨
求异面直线夹角的一般步骤是: “作—证—算—答”
2、异面直线所成角:
异面直线及其夹角 PPT课件 6 人教课标版

D
C
点 C 平A面 1B A 1B .
A
B
∴直线AC与A1B为异面直线.
练习2:
已知α∩β=a,b⊂β,且b∩a=A,c⊂α,且c∥a.求证:b 和c是异面直线.
证明:证法1:如右图,因为α∩β=a,b∩a=A, 所以A∈α,又c⊂α,c∥a. 所以A∉c,在直线b上任取一点B (不同于A),则B∉α.所以b,c是异面直线.
2
AF 3 a, AP 2EC 3a.
2
P
PA中 F应用余 ,得 c弦 o sP定 A理 F2.
3
∴异面直线AF、CE所成角的余弦值是
2 3
E D
C
课堂练习1:如图,P为Δ ABC所在平面外一点,
PC⊥AB,PC=AB=2,E、F分别为PA和BC的中点。
(1)求证:EF与PC为异面直线;
不能理解为:“分别在两个平面内的两直线为异面 直线”.
演示
练习1、
1.下面两条直线是异面直线的是(C)
A.不同在一个平面内的两条直线; B.分别在某两个平面内的两条直线; C.既不平行又不相交的两条直线; D.平面内的一条直线和平面外的一条直线
2.异面直线的画法
说明: 画异面直线时 , 为了体现 它们不共面的特点。常借 助一个或两个平面来衬托.
如图:
a
b
A
a
(1)
a
b
(2)
b
(3)
BACK
NEXT
例1.如果相异点A、B和相异点C、D分别在异面直
线a,b上,那么正确的结论是( C )
A.直线AC与BD可能相交 B.直线AD和BC可能相交 C.AC与BD,AD与BC都是异面直线 D.AC与BD,AD与BC不一定都是异面直线
《异面直线及所成的角》

的中点G,连结EG, 解:连结DF,取DF的中点 ,连结 , 连结 , 的中点 CG,又E是AD的中点,故EG//AF, 的中点, , 是 的中点 , 所以∠ 所以∠GEC(或其补角)是异面直线 B (或其补角) AF、CE所成的角。 所成的角。 、 所成的角 E
G
D
F C
1 3 FG = 1 DF = 1 3 AB = 3 a. EG = AF = a. 2 2 2 4 2 4 1 7 3 CG = FG2 + FC2 = ( AB)2 + ( AB)2 = a. 4 2 4 2 在EGC中用余弦定理得cos ∠GEC = . 3 2
(2)、取值范围(00,900] )、取值范围( 取值范围 (3)、作法:平移法或补形法 )、作法: 作法 (4) 两条直线互相垂直 ①相交直线的垂直 ②异面直线的垂直
例题1 例题
设图中的正方体的棱长为a, ①图中哪些棱所在的直线与 BA1成异面直线 ②求异面直线A1B与C1C的夹 角的度数
A1
D1 B1 D A B
A
B
4、异面直线的判断
(1)、异面直线的判定定理 连结平面内一点 )、异面直线的判定定理
(2)、反证法 )、反证法
与平面外一点的直线, 与平面外一点的直线,和这个平面内不经 过此点的直线是异面直线
5、异面直线成的角
(1)、定义: 分别平行于两条异面直线 )、定义: 定义
的两条相交直线所成的锐角(或直角) 的两条相交直线所成的锐角(或直角)叫 做这两条异面直线所成的角
B1
D1 F1 C1
A1
B G C
A
思路二、 思路二、延展平面 BAA1B1,使A1E=D1A1, 则将BD1平移到AE, 则将BD 平移到AE, AE 角EAF1(或其补角 ) 即为BD 所成的角。 即为BD1与AF1所成的角。
异面直线所成角

AB AC CB
AB AC CB
2
2
2
A c B b C
AC CB 2 AC CB
2
AC CB 2 AC CB cos C
2 2
2
2
a
AC CB 2 AC CB cos( C ) AC CB 2 AC CB cos C
D1 F A1 E B1 C1
2 3
D A
5
G
3
C
2 O
1
B
2
变式1、 如图,在长方体中,AA1=AD=a, AB= 3 a,求AB1与BC1所成的角的余弦值。
B1 AD1为所求角
AD1 AB1 B1 D1 cos B1 AD1 2 AD1 AB1 D1
2 2 2
C1
B1 a
1 2 2a 2a 4
例1.正方体中,(1)哪些棱所在的直线 与直线 BA1成异面直线?(2)求直线BA1和CC1所成的 角的大小 D1
解:(1)与直线BA1成 A1 异面直线有AD、CD、 B1C1、C1D1、C1C、D1D (2)∵B1B∥C1C 易求得所成的角为 45
C1
B1
D B
C
A
∴∠A1B1B是异面直线BA1和CC1所成的角
a b
实验: 一张纸上画有 两条能相交的直线a、 b(交点在纸外). 现给你一副三角板 和量角器,限定不 许拼接纸片,不许 延长纸上的线段, 问如何能量出a、b 所成角的大小?
还等什么? 动手实验 吧。
oa o b o
o
b
o
o a
一、异面直线所成的角定义:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
如图,已知两条异面直线 a、b ,经过空间任 一点O 作直线 a´∥a,b´∥ b, 我们把a´与b´所 成的锐角(或直角)叫做异面直线a与b所成 的角(或夹角)
若两异面直线所成的角为90o,我们就说这两直线垂直。 记做a ⊥ b
b
α
a ´
.o
a
.o
b´
a ´
例2 :如图,正方形ABCD-A´B´C´D´中
空间直线2
异面直线的概念: 把不同在任何一个平面内的两条 直线叫做异面直线
问题:图中与直线AA´异面的直线有 ____________________________ 直线BC 、B´C´、DC 、D´C´ D ´ C ´
A ´
D A
B ´
C B
异面直线的判定方法:
连结平面内的一点与平面外一点的直线, 和这个 平面内不经过此点的直线 是异面直线。
A
.
.B
α
L
例1 :如图,正方形ABCD-A´B´C´D´ 中
哪些棱所在直线与直线BA´是异面直线;
解:与直线BA´是异面直线的有 直线B´C´、AD、CC´、 DD´、 D DC、D´C´。 ´
A 问题:正方体各面的对角线所 ´
C ´ B ´
在的直线中与直线 BA´是异面 直线有哪些直线?
D A B
(1)哪些棱所在直线与直线AA´垂直; (2)求直线BA´和CC´的夹角的度数; (3)求直线BA´和AD´的夹角的度数;D
´ A ´ D A B B ´ C C ´
例2 :如图,正方形ABCD-A´B´C´D´中
E、 F分别是A´B´、BB´的中点, 1 求证BE 与C´F是异面直线 2 求BE 与C´F所成角的余弦
D' A' E G
C'
B'
F
B C
D A
课堂小结: 1 异面直线定义 2异面直线所成角定义及其求法 3异面直线的判定方法:1利用定义反证法,2判定定理
