北京市2013年中考数学试题(扫描版,有答案)
2013年北京市中考数学试卷
停车位数量与日均接待游客量和单日最多接待游客量中的某个量近似成正比例
关系．根据小娜的发现，请估计，将于 2015 年举办的第十届园博会大约需要设
置的停车位数量（直接写出结果，精确到百位）．
第七届至第十届园博会游客量和停车位数量统计表：
日接待游客量 单日最多接待游 停车位数量
（万人次）
客量
（个）
（万人次）
AC，AB 的垂线，得到等边△RPQ．若 S△RPQ= ，则 AD 的长为
．
第 7页（共 51页）
五、解答题（本题共 22 分，第 23 题 7 分，第 24 题 7 分，第 25 题 8 分） 23．（7 分）（2013•北京）在平面直角坐标系 xOy 中，抛物线 y=mx2﹣2mx﹣2（m ≠0）与 y 轴交于点 A，其对称轴与 x 轴交于点 B． （1）求点 A，B 的坐标； （2）设直线 l 与直线 AB 关于该抛物线的对称轴对称，求直线 l 的解析式； （3）若该抛物线在﹣2＜x＜﹣1 这一段位于直线 l 的上方，并且在 2＜x＜3 这一 段位于直线 AB 的下方，求该抛物线的解析式．
的中点．若 AB=5，AD=12，则四边形 ABOM 的周长为
．
12．（4 分）（2013•北京）如图，在平面直角坐标系 xOy 中，已知直线 l：y=﹣x ﹣1，双曲线 y= ，在 l 上取一点 A1，过 A1 作 x 轴的垂线交双曲线于点 B1，过 B1
作 y 轴的垂线交 l 于点 A2，请继续操作并探究：过 A2 作 x 轴的垂线交双曲线于点
A．40° B．50° C．70° D．80° 5．（4 分）（2013•北京）如图，为估算某河的宽度，在河对岸选定一个目标点 A， 在近岸取点 B，C，D，使得 AB⊥BC，CD⊥BC，点 E 在 BC 上，并且点 A，E，D 在同一条直线上．若测得 BE=20m，CE=10m，CD=20m，则河的宽度 AB 等于（ ）
2013北京中考数学
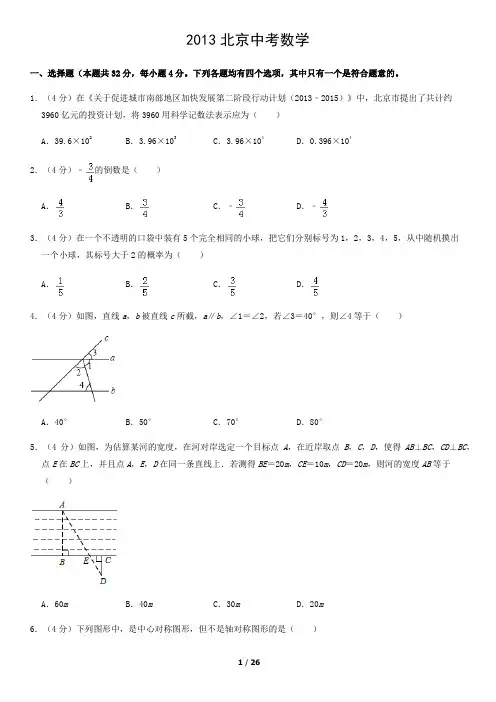
2013北京中考数学一、选择题（本题共32分，每小题4分。
下列各题均有四个选项，其中只有一个是符合题意的。
1．（4分）在《关于促进城市南部地区加快发展第二阶段行动计划（2013﹣2015）》中，北京市提出了共计约3960亿元的投资计划，将3960用科学记数法表示应为（）A．39.6×102B．3.96×103C．3.96×104D．0.396×1042．（4分）﹣的倒数是（）A．B．C．﹣D．﹣3．（4分）在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为（）A．B．C．D．4．（4分）如图，直线a，b被直线c所截，a∥b，∠1＝∠2，若∠3＝40°，则∠4等于（）A．40°B．50°C．70°D．80°5．（4分）如图，为估算某河的宽度，在河对岸选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上．若测得BE＝20m，CE＝10m，CD＝20m，则河的宽度AB等于（）A．60m B．40m C．30m D．20m6．（4分）下列图形中，是中心对称图形，但不是轴对称图形的是（）A．B．C．D．7．（4分）某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：）A．6.2小时B．6.4小时C．6.5小时D．7小时8．（4分）如图，点P是以O为圆心，AB为直径的半圆上的动点，AB＝2．设弦AP的长为x，△APO的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（）A．B．C．D．二、填空题（本题共16分，每小题4分）9．（4分）分解因式：ab2﹣4ab+4a＝．10．（4分）请写出一个开口向上，并且与y轴交于点（0，1）的抛物线的解析式，y＝．11．（4分）如图，O是矩形ABCD的对角线AC的中点，M是AD的中点．若AB＝5，AD＝12，则四边形ABOM的周长为．12．（4分）如图，在平面直角坐标系xOy中，已知直线l：y＝﹣x﹣1，双曲线y＝，在l上取一点A1，过A1作x轴的垂线交双曲线于点B1，过B1作y轴的垂线交l于点A2，请继续操作并探究：过A2作x轴的垂线交双曲线于点B2，过B2作y轴的垂线交l于点A3，…，这样依次得到l上的点A1，A2，A3，…，A n，…记点A n的横坐标为a n，若a1＝2，则a2＝，a2013＝；若要将上述操作无限次地进行下去，则a1不可能取的值是．三、解答题（本题共30分，每小题5分）13．（5分）已知：如图，D是AC上一点，AB＝DA，DE∥AB，∠B＝∠DAE．求证：BC＝AE．14．（5分）计算：（1﹣）0+|﹣|﹣2cos45°+（）﹣1．15．（5分）解不等式组：．16．（5分）已知x2﹣4x﹣1＝0，求代数式（2x﹣3）2﹣（x+y）（x﹣y）﹣y2的值．17．（5分）列方程或方程组解应用题：某园林队计划由6名工人对180平方米的区域进行绿化，由于施工时增加了2名工人，结果比计划提前3小时完成任务，若每人每小时绿化面积相同，求每人每小时的绿化面积．18．（5分）已知关于x的一元二次方程x2+2x+2k﹣4＝0有两个不相等的实数根．（1）求k的取值范围；（2）若k为正整数，且该方程的根都是整数，求k的值．四、解答题（本题共20分，每小题5分）19．（5分）如图，在▱ABCD中，F是AD的中点，延长BC到点E，使CE＝BC，连接DE，CF．（1）求证：四边形CEDF是平行四边形；（2）若AB＝4，AD＝6，∠B＝60°，求DE的长．20．（5分）如图AB是⊙O的直径，PA，PC与⊙O分别相切于点A，C，PC交AB的延长线于点D，DE⊥PO交PO的延长线于点E．（1）求证：∠EPD＝∠EDO；（2）若PC＝6，tan∠PDA＝，求OE的长．21．（5分）第九届中国国际园林博览会（园博会）已于2013年5月18日在北京开幕，以下是根据近几届园博会的相关数据绘制的统计图的一部分．（1）第九届园博会的植物花园区由五个花园组成，其中月季园面积为0.04平方千米，牡丹园面积为平方千米；（2）第九届园博会会园区陆地面积是植物花园区总面积的18倍，水面面积是第七、八界园博会的水面面积之和，请根据上述信息补全条形统计图，并标明相应数据；（3）小娜收集了几届园博会的相关信息（如下表），发现园博会园区周边设置的停车位数量与日均接待游客量和单日最多接待游客量中的某个量近似成正比例关系．根据小娜的发现，请估计，将于2015年举办的第十届园博会大约需要设置的停车位数量（直接写出结果，精确到百位）．第七届至第十届园博会游客量和停车位数量统计表：小明遇到这样一个问题：如图1，在边长为a（a＞2）的正方形ABCD各边上分别截取AE＝BF＝CG＝DH＝1，当∠AFQ＝∠BGM＝∠CHN＝∠DEP＝45°时，求正方形MNPQ的面积．小明发现，分别延长QE，MF，NG，PH交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形（如图2）请回答：（1）若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙不重叠），则这个新正方形的边长为；（2）求正方形MNPQ的面积．（3）参考小明思考问题的方法，解决问题：如图3，在等边△ABC各边上分别截取AD＝BE＝CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ．若S△RPQ＝，则AD的长为．五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．（7分）在平面直角坐标系xOy中，抛物线y＝mx2﹣2mx﹣2（m≠0）与y轴交于点A，其对称轴与x轴交于点B．（1）求点A，B的坐标；（2）设直线l与直线AB关于该抛物线的对称轴对称，求直线l的解析式；（3）若该抛物线在﹣2＜x＜﹣1这一段位于直线l的上方，并且在2＜x＜3这一段位于直线AB的下方，求该抛物线的解析式．24．（7分）在△ABC中，AB＝AC，∠BAC＝α（0°＜α＜60°），将线段BC绕点B逆时针旋转60°得到线段BD．（1）如图1，直接写出∠ABD的大小（用含α的式子表示）；（2）如图2，∠BCE＝150°，∠ABE＝60°，判断△ABE的形状并加以证明；（3）在（2）的条件下，连接DE，若∠DEC＝45°，求α的值．25．（8分）对于平面直角坐标系xOy中的点P和⊙C，给出如下的定义：若⊙C上存在两个点A、B，使得∠APB＝60°，则称P为⊙C的关联点．已知点D（，），E（0，﹣2），F（2，0）．（1）当⊙O的半径为1时，①在点D、E、F中，⊙O的关联点是．②过点F作直线l交y轴正半轴于点G，使∠GFO＝30°，若直线l上的点P（m，n）是⊙O的关联点，求m的取值范围；（2）若线段EF上的所有点都是某个圆的关联点，求这个圆的半径r的取值范围．数学试题答案一、选择题（本题共32分，每小题4分。
2013年北京市中考数学试卷-答案
（2）求出点A关于对称轴的对称点 ，然后设直线l的解析式为 ，利用待定系数法求一次函数解析式解答即可；
（3）根据二次函数的对称性判断在 这一段与在 这一段关于对称轴对称，然后判断出抛物线与直线l的交点的横坐标为 ，代入直线l求出交点坐标，然后代入抛物线求出m的值即可得到抛物线解析式．
【考点】整式的混合运算—化简求值．
17.【答案】2.5平方米
【解析】解：设每人每小时的绿化面积x平方米，由题意，得
，解得：
经检验， 是原方程的解，且符合题意．
答：每人每小时的绿化面积2.5平方米．
【提示】设每人每小时的绿化面积x平方米，根据增加2人后完成的时间比原来的时间少3小时为等量关系建立方程求出其解即可．
（2）找出k范围中的整数解确定出k的值，经检验即可得到满足题意k的值．
【考点】根的判别式，一元二次方程的解，解一元二次方程—公式法．
四、解答题
19.【答案】（1）见解析
（2）
【解析】证明：（1）在 中， ，且 ．
∵F是AD的中点，∴ ．
又∵ ，∴ ，且 ，
∴四边形CEDF是平行四边形；
（2）解：如图，过点D作 于点H．
（3）求出 ， 为等腰直角三角形，推出 ，求出 ，
得出方程 ，求出即可．
【考点】全等三角形的判定与性质，等边三角形的性质，等腰直角三角形，旋转的性质．
25.【答案】（1）①
②
（2）
【解析】解：（1）①如图1所示，过点E作 的切线设切点为R，
∵ 的半径为1，∴ ，∵ ，∴∠ ，
根据切线长定理得出 的左侧还有一个切点，使得组成的角等于 ，∴E点是 的关联点，
2013年北京市数学中考卷
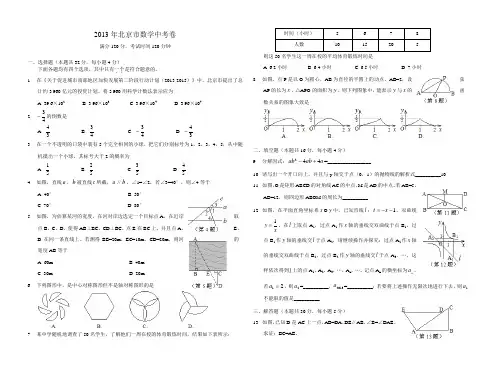
2013年北京市数学中考卷满分120分，考试时间120分钟一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的。
1. 在《关于促进城市南部地区加快发展第二阶段行动计划（2013-2015）》中，北京市提出了总计约3 960亿元的投资计划。
将3 960用科学计数法表示应为A. 39.6×102B. 3.96×103C. 3.96×104D. 3.96×104 2. 43-的倒数是 A. 34 B. 43 C. 43- D. 34-3. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为 A.51 B. 52 C. 53 D. 54 4. 如图，直线a ，b 被直线c 所截，a ∥b ，∠1=∠2，若∠3=40°，则∠4等于A. 40°B. 50°C. 70°D. 80°5. 如图，为估算某河的宽度，在河对岸边选定一个目标点A ，在近岸取点B ，C ，D ，使得AB ⊥BC ，CD ⊥BC ，点E 在BC 上，并且点A ，E ，D 在同一条直线上。
若测得BE=20m ，EC=10m ，CD=20m ，则河的宽度AB 等于A. 60mB. 40mC. 30mD. 20m 6. 下列图形中，是中心对称图形但不是轴对称图形的是7. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：则这50名学生这一周在校的平均体育锻炼时间是A. 6.2小时B. 6.4小时C. 6.5小时D. 7小时 8. 如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2，设弦函AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的数关系的图象大致是二、填空题（本题共16分，每小题4分）9. 分解因式：a ab ab 442+-=_________________10. 请写出一个开口向上，并且与y 轴交于点（0，1）的抛物线的解析式__________10 11. 如图，O 是矩形ABCD 的对角线AC 的中点，M 是AD 的中点，若AB=5，AD=12，则四边形ABOM 的周长为__________12. 如图，在平面直角坐标系x O y 中，已知直线l ：1--=x t ，双曲线xy 1=。
2013年北京市中考数学试卷
试卷第7页，总7页 2013年北京市中考数学试卷
一、选择题（本题共32分，每小题4分。
下列各题均有四个选项，其中只有一个是符合题意的。
1. 在《关于促进城市南部地区加快发展第二阶段行动计划(2013−2015)》中，北京市提出了共计约3960亿元的投资计划，将3960用科学记数法表示应为（ ）
A.39.6×102
B.3.96×103
C.3.96×104
D.0.396×104
2. −34的倒数是（ ）
A.43
B.34
C.−34
D.−43
3. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为（ ）
A.15
B.25
C.35
D.45
4. 如图，直线a ，b 被直线c 所截，a // b ，∠1=∠2，若∠3=40∘，则∠4等于( )
A.40∘
B.50∘
C.70∘
D.80∘
5. 如图，为估算某河的宽度，在河对岸选定一个目标点A ，在近岸取点B ，C ，D ，使得AB ⊥BC ，CD ⊥BC ，点E 在BC 上，并且点A ，E ，D 在同一条直线上．若测得BE ＝20m ，CE ＝10m ，CD ＝20m ，则河的宽度AB 等于（ ）
A.60m
B.40m
C.30m
D.20m
6. 下列图形中，是中心对称图形，但不是轴对称图形的是（ ）
A.
B.
C.
D.
7. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：。
年北京市中考数学试卷含答案
2013年北京市高级中等学校招生考试数学试卷满分120分，考试时间120分钟一、选择题(本题共 32分，每小题4分) 下面各题均有四个选项，其中只有一个..是符合题意的。
1.在《关于促进城市南部地区加快发展第二阶段行动计划(2013-2015 )》中，北京市提出了总计约3 960亿元的投资计划。
将 3 960用科学计数法表示应为2A. X 10B.X 103C.4X 10D.4X 102.3的倒数是4A 43 C.34 A.B.D.34433. 在-一个不透明的口袋中装有5个完全相冋的小球，把它们分别标号为1, 2, 3, 4,在 丨不透明口J 口袋中装2的概率为从中随机摸出一个小球，其标 号大于A1 f2 C.3 D.4A.B.55554. 如图，直线a ,b 被直线c 所截，a // b ，/ 仁/2, 若/ 3=40 ° , 则/ 4等于A. 40 °B. 50 OC. 70 °D. 80O5.如图，为估算某河的宽度，在河对岸边选定一个目标点 A ,在近岸取点B, C , D,使得AB 丄BC CDL BC 点E 在BC 上，并且点 A , E , D 在同一条直线上。
若测得 BE=20m EC=10mCD=20m 则河的宽度AB 等于 A. 60m B. 40m C. 30mD. 20m6. 下列图形中，是中心对称图形但不是轴对称图形的是[来源 :学科网ZXXK]7. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示:则这50名学生这一周在校的平均体育锻炼时间是A.小时B. 小时C. 小时D. 7 小时8. 如图，点P是以0为圆心，AB为直径的半圆上的动点，AB=2,设弦AP的长为x，△ APO 的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是二、填空题（本题共16分，每小题4分）_ 29. 分解因式：ab 4ab 4a= ____________________10. 请写出一个开口向上，并且与y轴交于点（0, 1）的抛物线的解析式_____________ 1011. 如图，O是矩形ABCD勺对角线AC的中点，M是AD的中点，若AB=5 AD=12,则四边形ABOM勺周长为__________12. 如图，在平面直角坐标系x O y中，已知直线：t X 1，双曲线y丄。
北京2013年中考数学真题版
2013年北京市高级中等学校招生考试数学试卷满分120分，考试时间120分钟一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的。
1. 在《关于促进城市南部地区加快发展第二阶段行动计划（2013-2015）》中，北京市提出了总计约3 960亿元的投资计划。
将3 960用科学计数法表示应为A. 39.6×102B. 3.96×103C. 3.96×104D. 3.96×104 2. 43-的倒数是 A. 34 B. 43 C. 43- D. 34-3. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为 A.51 B. 52 C. 53D. 544. 如图，直线a ，b 被直线c 所截，a ∥b ，∠1=∠2，若∠3=40°，则∠4等于A. 40°B. 50°C. 70°D. 80°5. 如图，为估算某河的宽度，在河对岸边选定一个目标点A ，在近岸取点B ，C ，D ，使得AB ⊥BC ，CD ⊥BC ，点E 在BC 上，并且点A ，E ，D 在同一条直线上。
若测得BE=20m ，EC=10m ，CD=20m ，则河的宽度AB 等于A. 60mB. 40mC. 30mD. 20m 6. 下列图形中，是中心对称图形但不是轴对称图形的是7. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：则这50名学生这一周在校的平均体育锻炼时间是A. 6.2小时B. 6.4小时C. 6.5小时D. 7小时8. 如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2，设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是二、填空题（本题共16分，每小题4分）9. 分解因式：a ab ab 442+-=_________________10. 请写出一个开口向上，并且与y 轴交于点（0，1）的抛物线的解析式__________1011. 如图，O 是矩形ABCD 的对角线AC 的中点，M 是AD 的中点，若AB=5，AD=12，则四边形ABOM 的周长为__________12. 如图，在平面直角坐标系x O y 中，已知直线：1--=x t ，双曲线xy 1=。
北京市2013年中考数学试题(解析版)
个完全相同的不透明礼盒中，准备将它们奖给小本题考核的立意相对较新，考核了学生的空间想象能力，结合图形理解两点之间距离的概念，认识两点间距离变化产生的数量关系。
采取验证法和排除法求解较为简单。
本题考点：两点间距离、线段.难度系数：0.4分解因式： ．269mn mn m ++=的代数式表示．）本题是建立在反比例函数基础上的一次函数解析式确定及与一次函数图象有关的本题考点：一次函数解析式的确定、一次函数图像与坐标轴上点的确定.据林业专家分析，树叶在光合作用后产生的分泌物能够吸附空气中的一些悬浮颗粒物，具有滞尘净化空气的作用．已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年毫克所需的银杏树叶的片数与一年滞尘毫克所需的国槐树叶的片数相同，求一片国槐树叶一年的平均滞尘量．设一片国槐树叶一年的滞尘量为毫克，则一片银杏树叶一年的滞尘量为毫克，解得检验：将带入中，不等于零，则是方程的根=CF=请根据以上信息解答下列问题：（1）补全条形统计图并在图中标明相应数据；（2）按照2011年规划方案，预计2020年北京市轨道交通运营里程将达到多少千米？（3）要按时完成截至2015年的轨道交通规划任务，从2011每年需新增运营里程多少千米？【解析】228；1000；82.75【点评】本题将北京市轨道交通发展规划与统计结合的一道考题，考查了学生对图表绘制过程的理解、阅读图表并提取有用信息的技能，借助数据处理结果做合理推测的能力。
这是北京市这几年考核统计这部分知识的常见题型本题考点：条形统计图、扇形统计图、平均数以及用样本估算总体的数学思想难度系数：0.622．操作与探究：P（1）对数轴上的点进行如下操作：先把点2，在平面直角坐标系中，对正方形及其内部的每个xOy ABCD 点进行如下操作：把每个点的横、纵坐标都乘以同一种实数到的点先向右平移个单位，再向上平移个单位（m n m 得到正方形及其内部的点，其中点的对应点分别为A B C D ''''A B ，个单位。
北京中考数学试题、答案解析版电子版本
2013北京中考数学试题、答案解析版2013年北京市高级中等学校招生考试数学试卷一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个是符合题意的。
1. 在《关于促进城市南部地区加快发展第二阶段行动计划（2013-2015）》中，北京市提出了总计约3 960亿元的投资计划。
将3 960用科学计数法表示应为 （ ）A. 39.6×102B. 3.96×103C. 3.96×104D. 3.96×104 考点：科学记数法—表示较大的数 分析:科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数． 解答：将3960用科学记数法表示为3.96×103．故选B ．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．2. 43-的倒数是 （ ）A. 34B. 43C. 43-D. 34-考点：倒数分析：据倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数 解答：D点评：本题主要考查倒数的定义，要求熟练掌握．需要注意的是： 倒数的性质：负数的倒数还是负数，正数的倒数是正数，0没有倒数． 倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数3. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为（ ） A. 51 B. 52 C. 53 D. 54 考点：概率公式分析：根据随机事件概率大小的求法，找准两点：①符合条件的情况数目，②全部情况的总数，二者的比值就是其发生的概率的大小． 解答：C点评：本题考查概率的求法与运用，一般方法：如果一个事件有n 种可能，而且这些事件的可能性相同，其中事件A 出现m 种结果，那么事件A 的概率n mA P =)(，难度适中。
北京2013年中考数学真题版
2013年北京市高级中等学校招生考试数学试卷满分120分，考试时间120分钟一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的。
1. 在《关于促进城市南部地区加快发展第二阶段行动计划（2013-2015）》中，北京市提出了总计约3 960亿元的投资计划。
将3 960用科学计数法表示应为A. 39.6×102B. 3.96×103C. 3.96×104D. 3.96×104 2. 43-的倒数是 A. 34 B. 43 C. 43- D. 34-3. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为 A.51 B. 52 C. 53D. 544. 如图，直线a ，b 被直线c 所截，a ∥b ，∠1=∠2，若∠3=40°，则∠4等于A. 40°B. 50°C. 70°D. 80°5. 如图，为估算某河的宽度，在河对岸边选定一个目标点A ，在近岸取点B ，C ，D ，使得AB ⊥BC ，CD ⊥BC ，点E 在BC 上，并且点A ，E ，D 在同一条直线上。
若测得BE=20m ，EC=10m ，CD=20m ，则河的宽度AB 等于A. 60mB. 40mC. 30mD. 20m 6. 下列图形中，是中心对称图形但不是轴对称图形的是7. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：则这50名学生这一周在校的平均体育锻炼时间是A. 6.2小时B. 6.4小时C. 6.5小时D. 7小时8. 如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2，设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是二、填空题（本题共16分，每小题4分）9. 分解因式：a ab ab 442+-=_________________10. 请写出一个开口向上，并且与y 轴交于点（0，1）的抛物线的解析式__________1011. 如图，O 是矩形ABCD 的对角线AC 的中点，M 是AD 的中点，若AB=5，AD=12，则四边形ABOM的周长为__________12. 如图，在平面直角坐标系x O y 中，已知直线：1--=x t ，双曲线xy 1=。
2013北京中考数学试题
2013年北京市高级中等学校招生考试数学试卷满分120分，考试时间120分钟一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的。
1. 在《关于促进城市南部地区加快发展第二阶段行动计划（2013-2015）》中，北京市提出了总计约3 960亿元的投资计划。
将3 960用科学计数法表示应为 A. 39.6×102B. 3.96×103C. 3.96×104D. 3.96×1042. 43-的倒数是 A. 34 B. 43 C. 43- D. 34-3. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为A.51 B. 52 C. 53 D. 54 4. 如图，直线a ，b 被直线c 所截，a ∥b ，∠1=∠2，若∠3=40°，则∠4等于A. 40°B. 50°C. 70°D. 80°5. 如图，为估算某河的宽度，在河对岸边选定一个目标点A ，在近岸取点B ，C ，D ，使得AB ⊥BC ，CD ⊥BC ，点E 在BC 上，并且点A ，E ，D 在同一条直线上。
若测得BE=20m ，EC=10m ，CD=20m ，则河的宽度AB 等于A. 60mB. 40mC. 30mD. 20m 6. 下列图形中，是中心对称图形但不是轴对称图形的是7. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：时间（小时）5 6 7 8 人数1015205则这50名学生这一周在校的平均体育锻炼时间是A. 6.2小时B. 6.4小时C. 6.5小时D. 7小时 8. 如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2，设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是二、填空题（本题共16分，每小题4分） 9. 分解因式：a ab ab 442+-=_________________10. 请写出一个开口向上，并且与y 轴交于点（0，1）的抛物线的解析式__________10 11. 如图，O 是矩形ABCD 的对角线AC 的中点，M 是AD 的中点，若AB=5，AD=12，则四边形ABOM 的周长为__________ 12. 如图，在平面直角坐标系x O y 中，已知直线l ：1--=x t ，双曲线xy 1=。
北京市2013年中考数学卷
2013年北京市高级中等学校招生考试数学试卷满分120分，考试时间120分钟一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的。
1. 在《关于促进城市南部地区加快发展第二阶段行动计划（2013-2015）》中，北京市提出了总计约3 960亿元的投资计划。
将3 960用科学计数法表示应为 A. 39.6×102 B. 3.96×103 C. 3.96×104 D. 3.96×104 2. 43-的倒数是 A. 34 B. 43 C. 43- D. 34-3. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为 A.51 B. 52 C. 53 D. 54 4. 如图，直线a ，b 被直线c 所截，a ∥b ，∠1=∠2，若∠3=40°，则∠4等于A. 40°B. 50°C. 70°D. 80°5. 如图，为估算某河的宽度，在河对岸边选定一个目标点A ，在近岸取点B ，C ，D ，使得AB ⊥BC ，CD ⊥BC ，点E 在BC 上，并且点A ，E ，D 在同一条直线上。
若测得BE=20m ，EC=10m ，CD=20m ，则河的宽度AB 等于A. 60mB. 40mC. 30mD. 20m 6. 下列图形中，是中心对称图形但不是轴对称图形的是7. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：时间（小时）5 6 7 8 人数1015205则这50名学生这一周在校的平均体育锻炼时间是A. 6.2小时B. 6.4小时C. 6.5小时D. 7小时8. 如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2，设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是二、填空题（本题共16分，每小题4分）9. 分解因式：a ab ab 442+-=_________________10. 请写出一个开口向上，并且与y 轴交于点（0，1）的抛物线的解析式__________10 11. 如图，O 是矩形ABCD 的对角线AC 的中点，M 是AD 的中点，若AB=5，AD=12，则四边形ABOM 的周长为__________ 12. 如图，在平面直角坐标系x O y 中，已知直线l ：1--=x t ，双曲线xy 1=。
2013年北京中考数学真题卷含答案解析
2013年北京市高级中等学校招生考试数学试题（含答案全解全析）(满分120分,考试时间120分钟)第Ⅰ卷(选择题,共32分)一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个．．是符合题意的.1.在《关于促进城市南部地区加快发展第二阶段行动计划(2013~2015)》中,北京市提出了总计约3960亿元的投资计划.将3960用科学记数法表示应为()A.39.6×102B.3.96×103C.3.96×104D.0.396×1042.-34的倒数是()A.43B.34C.-34D.-433.在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号大于2的概率为()A.15B.25C.35D.454.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于()A.40°B.50°C.70°D.80°5.如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC, CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于()A.60mB.40mC.30mD.20m轴对称图形的是()6.下列图形中,是中心对称图形但不是．．7.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:时间(小时)5678人数1015205则这50名学生这一周在校的平均体育锻炼时间是()A.6.2小时B.6.4小时C.6.5小时D.7小时8.如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是()第Ⅱ卷(非选择题,共88分)二、填空题(本题共16分,每小题4分)9.分解因式:ab2-4ab+4a=.10.请写出一个开口向上,并且与y轴交于点(0,1)的抛物线的解析式,y=.11.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为.12.如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=1x.在l上取一点A1,过A1作x 轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2.请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,A n,….记点A n的横坐标为a n,若a1=2,则a2=,a2013=;若要将上述操作无限次地进行下去,则a1不能取．．．的值是.三、解答题(本题共30分,每小题5分)13.已知:如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.14.计算:(1-√3)0+|-√2|-2cos45°+(14)-1.15.解不等式组:{3x>x-2, x+13>2x.16.已知x2-4x-1=0,求代数式(2x-3)2-(x+y)(x-y)-y2的值.17.列方程或方程组解应用题:某园林队计划由6名工人对180平方米的区域进行绿化,由于施工时增加了2名工人,结果比计划提前3小时完成任务.若每人每小时绿化面积相同,求每人每小时的绿化面积.18.已知关于x的一元二次方程x2+2x+2k-4=0有两个不相等的实数根.(1)求k的取值范围;(2)若k为正整数,且该方程的根都是整数,求k的值.四、解答题(本题共20分,每小题5分)19.如图,在▱ABCD中,F是AD的中点,延长BC到点E,使CE=1BC,连结DE,CF.2(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长.20.如图,AB是☉O的直径,PA,PC与☉O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.(1)求证:∠EPD=∠EDO;,求OE的长.(2)若PC=6,tan∠PDA=3421.第九届中国国际园林博览会(园博会)已于2013年5月18日在北京开幕.以下是根据近几届园博会的相关数据绘制的统计图的一部分.第六届至第九届园博会园区陆地面积和水面面积统计图第九届园博会植物花园区各花园面积分布统计图(1)第九届园博会的植物花园区由五个花园组成,其中月季园面积为0.04平方千米,牡丹园面积为平方千米;(2)第九届园博会园区陆地面积是植物花园区总面积的18倍,水面面积是第七、八两届园博会的水面面积之和,请根据上述信息补全条形统计图,并标明相应数据;(3)小娜收集了几届园博会的相关信息(如下表),发现园博会园区周边设置的停车位数量与日均接待游客量和单日最多接待游客量中的某个量近似成正比例关系.根据小娜的发现,请估计,将于2015年举办的第十届园博会大约需要设置的停车位数量(直接写出结果,精确到百位).第七届至第十届园博会游客量与停车位数量统计表日均接待游客量(万人次) 单日最多接待游客量(万人次)停车位数量(个) 第七届 0.8 6 约3 000 第八届 2.3 8.2 约4 000 第九届 8(预计) 20(预计) 约10 500 第十届 1.9(预计)7.4(预计)约22.阅读下面材料:小明遇到这样一个问题:如图1,在边长为a(a>2)的正方形ABCD 各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ 的面积.图1图2小明发现,分别延长QE,MF,NG,PH 交FA,GB,HC,ED 的延长线于点R,S,T,W,可得△RQF, △SMG,△TNH,△WPE 是四个全等的等腰直角三角形(如图2).请回答:(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙不重叠),则这个新正方形的边长为;(2)求正方形MNPQ的面积.参考小明思考问题的方法,解决问题:如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若S△RPQ=√3,则AD的长为.3图3五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.(1)求点A,B的坐标;(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;(3)若该抛物线在-2<x<-1这一段位于直线l的上方,并且在2<x<3这一段位于直线AB的下方,求该抛物线的解析式.24.在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.(1)如图1,直接写出∠ABD的大小(用含α的式子表示);(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;(3)在(2)的条件下,连结DE,若∠DEC=45°,求α的值.25.对于平面直角坐标系xOy中的点P和☉C,给出如下定义:若☉C上存在两个点A,B,使得∠APB=60°,则称P为☉C的关联点.已知点D(12,12),E(0,-2),F(2√3,0).(1)当☉O的半径为1时,①在点D,E,F中,☉O的关联点是;②过点F作直线l交y轴正半轴于点G,使∠GFO=30°,若直线l上的点P(m,n)是☉O的关联点,求m的取值范围;(2)若线段EF上的所有点都是某个圆的关联点,求这个圆的半径r的取值范围.答案全解全析：1.B 3 960=3.96×103.故选B.2.D ∵(-34)×(-43)=1,∴-34的倒数是-43.故选D.3.C 5个小球中标号大于2的有三个,故摸出标号大于2的小球的概率是35.故选C.4.C ∵∠1+∠2+∠3=180°,∠3=40°,∴∠1+∠2=140°.∵∠1=∠2,∴∠1=70°. ∵a∥b,∴∠4=∠1=70°.故选C.5.B ∵∠ABE=∠ECD=90°,∠AEB=∠DEC,∴△ABE∽△DCE,∴AB DC =BE EC,∴AB 20=2010,∴AB=40 m.故选B.6.A A 项是中心对称图形,但不是轴对称图形. B 项既是中心对称图形,又是轴对称图形. C 项不是中心对称图形,是轴对称图形.D 项既不是中心对称图形,又不是轴对称图形.故选A. 7.B x =5×10+6×15+7×20+8×550=6.4(小时).故选B.8.A 考虑三个特殊点,当AP 的长为0或2时,不构成△APO;当AP 的长为1时,△APO 为边长是1的等边三角形,其面积为√34,因为14<√34<12,所以只有选项A 符合.故选A.评析 本题考查的是函数图象的变化规律,不仅考查了定性分析,还考查了定量分析,通过构造函数处理较困难,而通过寻找特殊点较容易处理.属中档题. 9.答案 a(b-2)2解析 ab 2-4ab+4a=a(b 2-4b+4)=a(b-2)2. 10.答案 x 2+1解析 抛物线即二次函数,则函数表达式应为y=ax 2+bx+c(a≠0).∵开口向上,∴a>0.∵与y 轴交于点(0,1),∴c=1.所以满足题设条件的一个抛物线的解析式为y=x 2+1,答案不唯一.11.答案 20解析 ∵AB=5,AD=12,∴AC=13,∴BO=6.5. ∵M 、O 分别为AD 、AC 的中点, CD=5,∴MO=2.5,AM=6,∴C 四边形ABOM =AM+MO+BO+AB=6+2.5+6.5+5=20. 12.答案 -32;-13;0,-1解析 根据题意可以得到点A 1(2,-3),点B 1(2,0.5),点A 2(-1.5,0.5),点B 2(-1.5,-23),点A 3(-13,-23),点B 3(-13,-3),点A 4(2,-3),所以A 1,A 2,A 3,…,A n ,…中,三个坐标为一个循环,A 2 013是一个循环中的最后一个,故它的横坐标与A 3的横坐标相同,为-13.当A 1的横坐标为a 1时,可以分别表示出点A 1(a 1,-a 1-1),点B 1(a 1,1a 1),点A 2(-1-1a 1,1a1),点B 2(-1-1a 1,-a 1a 1+1),点A 3(-1a1+1,-a 1a 1+1),点B 3(-1a 1+1,-a 1-1).因为操作要无限次地进行下去,所以每一个点都要有意义,即分母不为0,故a 1不能取的值是-1,0.评析 读懂题目中的操作方法是解决本题的关键,属中档题. 13.证明 ∵DE ∥AB, ∴∠BAC=∠ADE.在△ABC 和△DAE 中,{∠BAC =∠ADE ,AB =DA ,∠B =∠DAE ,∴△ABC≌△DAE. ∴BC=AE.14.解析 (1-√3)0+|-√2|-2cos 45°+(14)-1=1+√2-2×√22+4 =5.15.解析 {3x >x -2, ①x+13>2x .② 解不等式①,得x>-1.解不等式②,得x<15.∴不等式组的解集为-1<x<15. 16.解析 (2x-3)2-(x+y)(x-y)-y 2=4x 2-12x+9-(x 2-y 2)-y 2=3x 2-12x+9.∵x 2-4x-1=0,∴x 2-4x=1.∴原式=3(x 2-4x)+9=12.17.解析 设每人每小时的绿化面积是x 平方米.由题意得1806x -180(6+2)x =3.解得x=2.5.经检验,x=2.5是原方程的解,且符合题意.答:每人每小时的绿化面积是2.5平方米.18.解析 (1)由题意,得Δ=4-4(2k-4)>0.∴k<52. (2)∵k 为正整数,∴k=1,2.当k=1时,方程x 2+2x-2=0的根x=-1±√3不是整数;当k=2时,方程x 2+2x=0的根x 1=-2,x 2=0都是整数.综上所述,k=2.19.解析 (1)证明:∵四边形ABCD 是平行四边形,∴AD∥BC,AD=BC.∵F是AD的中点,AD.∴FD=12BC,∴FD=CE.∵CE=12∵FD∥CE,∴四边形CEDF是平行四边形.(2)如图,过点D作DG⊥CE于点G.∵四边形ABCD是平行四边形,∴AB∥CD,CD=AB=4,BC=AD=6.∴∠1=∠B=60°.在Rt△DGC中,∠DGC=90°,∴CG=CD·cos∠1=2,DG=CD·sin∠1=2√3.BC=3,∴GE=1.∵CE=12在Rt△DGE中,∠DGE=90°,∴DE=√DG2+GE2=√13.20.解析(1)证明:∵PA、PC与☉O分别相切于点A、C, ∴PA=PC,∠APO=∠EPD.∵AB是☉O的直径,∴PA⊥AB.∵DE⊥PO,∴∠A=∠E=90°.∵∠POA=∠DOE,∴∠APO=∠EDO.∴∠EPD=∠EDO.(2)连结OC,则OC⊥PD.在Rt△PAD中,∠A=90°,PA=PC=6,tan∠PDA=34, 可得AD=8,PD=10.∴CD=4.在Rt△OCD中,∠OCD=90°,CD=4,tan∠ODC=34, 可得OC=3,OD=5.在Rt△PCO中,由勾股定理得,PO=3√5.可证得Rt△DEO∽Rt△PCO.∴OEOC =ODOP,即OE3=3√5.∴OE=√5.21.解析(1)0.03.(2)补全条形统计图如下图.第六届至第九届园博会园区陆地面积和水面面积统计图(3)3 600,3 700,3 800,3 900其中之一.评析 处理本题的关键是看清扇形图和条形图之间的关系,再按照题目要求逐一解决.属中档题.22.解析 (1)a.(2)由(1)可知,由△RQF,△SMG,△TNH,△WPE 拼成的新正方形的面积与正方形ABCD 的面积相等.∴△RAE,△SBF,△TCG,△WDH 这四个全等的等腰直角三角形的面积之和等于正方形MNPQ 的面积.∵AE=BF=CG=DH=1,∴正方形MNPQ 的面积S=4×12×1×1=2.AD 的长为23.23.解析 (1)当x=0时,y=-2.∴点A 的坐标为(0,-2).将y=mx 2-2mx-2配方,得y=m(x-1)2-m-2.∴抛物线的对称轴为直线x=1.∴点B 的坐标为(1,0).(2)由题意得点A 关于直线x=1的对称点的坐标为(2,-2).设直线l 的解析式为y=kx+b.∵点(1,0)和(2,-2)在直线l 上,∴{0=k +b ,-2=2k +b .解得{k =-2,b =2.∴直线l 的解析式为y=-2x+2.(3)由题意可知,抛物线关于直线x=1对称,直线AB 和直线l 也关于直线x=1对称. ∵抛物线在2<x<3这一段位于直线AB 的下方,∴抛物线在-1<x<0这一段位于直线l的下方.又∵抛物线在-2<x<-1这一段位于直线l的上方,∴抛物线与直线l的一个交点的横坐标为-1.∴由直线l的解析式y=-2x+2可得这个点的坐标为(-1,4).∵抛物线y=mx2-2mx-2经过点(-1,4),∴m=2.∴所求抛物线的解析式为y=2x2-4x-2.评析本题考查了一次函数、二次函数的综合运用,充分考查了二次函数图象的对称性,有一定难度.24.解析(1)∠ABD=30°-1α.2(2)△ABE为等边三角形.证明:连结AD,CD.∵∠DBC=60°,BD=BC,∴△BDC是等边三角形,∴∠BDC=60°,BD=DC.又∵AB=AC,AD=AD,∴△ABD≌△ACD,∴∠ADB=∠ADC.∴∠ADB=150°.∵∠ABE=∠DBC=60°,∴∠ABD=∠EBC.又∵BD=BC,∠ADB=∠ECB=150°,∴△ABD≌△EBC.∴AB=EB.∴△ABE是等边三角形.(3)∵△BDC是等边三角形,∴∠BCD=60°.∴∠DCE=∠BCE-∠BCD=90°.又∵∠DEC=45°,∴CE=CD=BC.∴∠EBC=15°.,∴α=30°.∵∠EBC=∠ABD=30°-α2评析本题考查了全等三角形、等边三角形、等腰三角形的相关知识,正确地构造全等三角形是解决本题的关键.属中等偏难题.25.解析(1)①D,E.②当OP=2时,过点P向☉O作两条切线PA,PB(A,B为切点),则∠APB=60°.∴点P为☉O的关联点.事实上,当0≤OP≤2时,点P是☉O的关联点;当OP>2时,点P不是☉O的关联点.∵F(2√3,0),且∠GFO=30°,∴∠OGF=60°,OF=2√3,OG=2.如图,以O为圆心,OG为半径作圆,设该圆与l的另一个交点为M.当点P在线段GM上时,OP≤2,点P是☉O的关联点;当点P在线段GM的延长线或反向延长线上时,OP>2,点P不是☉O的关联点.连结OM,可知△GOM为等边三角形.过点M作MN⊥x轴于点N,可得∠MON=30°,ON=√3.∴0≤m≤√3.(2)设该圆圆心为C.根据②可得,若点P是☉C的关联点,则0≤PC≤2r.由题意知,点E,F都是☉C的关联点,∴EC≤2r,FC≤2r.∴EC+FC≤4r.又∵EC+FC≥EF(当点C在线段EF上时,等号成立),∴4r≥EF.∵E(0,-2),F(2√3,0),∴EF=4.∴r≥1.事实上,当点C是EF的中点时,对所有r≥1的☉C,线段EF上的所有点都是☉C的关联点. 综上所述,r≥1.评析本题定义了坐标系中圆的关联点,需要对圆的相关知识熟练掌握,并通过画图观察,找到临界状态,再逐一进行验证.本题充分考查了学生的综合能力,难度较大.。
2013年北京市中考数学试卷(含答案)
2013年市高级中等学校招生考试数学试卷满分120分，考试时间120分钟一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的。
1. 在《关于促进城市南部地区加快发展第二阶段行动计划（2013-2015）》中，市提出了总计约3 960亿元的投资计划。
将3 960用科学计数法表示应为A. 39.6×102B. 3.96×103C. 3.96×104D. 3.96×1042. 43-的倒数是 A. 34 B. 43 C. 43- D. 34-3. 在一个不透明的口袋中装有5个完全相同的小球，把它们分别标号为1，2，3，4，5，从中随机摸出一个小球，其标号大于2的概率为 A.51 B. 52 C. 53 D. 54 4. 如图，直线a ，b 被直线c 所截，a ∥b ，∠1=∠2，若∠3=40°，则∠4等于A. 40°B. 50°C. 70°D. 80°5. 如图，为估算某河的宽度，在河对岸边选定一个目标点A ，在近岸取点B ，C ，D ，使得AB ⊥BC ，CD ⊥BC ，点E 在BC 上，并且点A ，E ，D 在同一条直线上。
若测得BE=20m ，EC=10m ，CD=20m ，则河的宽度AB 等于 A. 60m B. 40m C. 30m D. 20m 6. 下列图形中，是中心对称图形但不是轴对称图形的是7. 某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：时间（小时）5678人数 10 15 20 5则这50名学生这一周在校的平均体育锻炼时间是A. 6.2小时B. 6.4小时C. 6.5小时D. 7小时 8. 如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2，设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是二、填空题（本题共16分，每小题4分）9. 分解因式：a ab ab 442+-=_________________10. 请写出一个开口向上，并且与y 轴交于点（0，1）的抛物线的解析式__________10 11. 如图，O 是矩形ABCD 的对角线AC 的中点，M 是AD 的中点，若AB=5，AD=12，则四边形ABOM 的周长为__________12. 如图，在平面直角坐标系x O y 中，已知直线：1--=x t ，双曲线xy 1=。